Next Article in Journal
Cannabis Medicine 2.0: Nanotechnology-Based Delivery Systems for Synthetic and Chemically Modified Cannabinoids for Enhanced Therapeutic Performance
Previous Article in Journal
The Influence of the Type of Metal-on-Metal Hip Endoprosthesis on the Clinical, Biochemical, and Oxidative Balance Status—A Comparison of Resurfacing and Metaphyseal Implants
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Nanomaterials
Volume 15
Issue 16
10.3390/nano15161259
nanomaterials-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Research on the Poisson’s Ratio of Black Phosphorene Nanotubes Under Axial Tension

by
Xinjun Tan
1,
Touwen Fan
2,3,* and
Kaiwang Zhang
1,*
1
School of Physics and Optoelectronics, Xiangtan University, Xiangtan 411105, China
2
Research Institute of Automobile Parts Technology, Hunan Institute of Technology, Hengyang 421002, China
3
School of Science, Hunan Institute of Technology, Hengyang 421002, China
*
Authors to whom correspondence should be addressed.
Nanomaterials 2025, 15(16), 1259; https://doi.org/10.3390/nano15161259
Submission received: 23 July 2025 / Revised: 9 August 2025 / Accepted: 13 August 2025 / Published: 15 August 2025
(This article belongs to the Section Theory and Simulation of Nanostructures)
Browse Figures
Versions Notes

Abstract

In this paper, the Poisson’s ratio of black phosphorene nanotubes was examined through the molecular dynamics simulation method. Our research discovered that for the armchair black phosphorene nanotubes, the radial strain and the wall thickness strain are negatively linearly correlated with the axial strain, and both the radial Poisson’s ratio and the thickness Poisson’s ratio are positive. For the zigzag black phosphorene nanotubes, the wall thickness strain is negatively, linearly correlated with the axial strain, while the radial strain has a cubic polynomial function relationship with the axial strain. The thickness Poisson’s ratio is positive, while the radial Poisson’s ratio is a quantity related to the axial strain. As the axial strain increases, the radial Poisson’s ratio progressively diminishes from a positive value and becomes negative upon reaching a specific critical axial strain threshold. During the tensile deformation along the axial direction of the zigzag black phosphorene nanotubes, the radial strain initially decreases before subsequently increasing. Notably, the diameter of the nanotube may even surpass its initial value, demonstrating a radial expansion in response to axial tension.

Graphical Abstract

1. Introduction

Poisson’s ratio is a basic mechanical property of materials, which relates the resulting transverse strain to the applied axial strain. It refers to the negative ratio of the lateral normal strain to the longitudinal normal strain when a material is subjected to longitudinal tension or compression. According to the theory of continuum elasticity, it is feasible for a material to have a negative Poisson’s ratio (NPR). If a certain material has an NPR, it implies that when this material is under longitudinal tension, it will expand in a certain lateral direction. Nevertheless, in nature, nearly all natural materials have a positive Poisson’s ratio (PPR). Ever since the discovery of the NPR property in foam-structured materials by scholars in 1987 [1], the research on NPR materials has aroused people’s attention. NPR materials typically possess enhanced toughness and shear resistance, as well as enhanced sound absorption and vibration damping, and have been applied in fields such as medical treatment, fasteners, high-strength composite materials, sensors, biological tissue engineering, textile materials, protective engineering, etc. [2,3,4,5,6,7,8,9].
For a considerable period, materials with NPR were all artificially fabricated materials featuring hinge-like structures [5,8,10,11,12]. In 2015, Jiang [2] discovered through first-principles calculations that single-layer black phosphorene (BP) exhibits an NPR in the direction perpendicular to the BP surface when stretched along the armchair direction. This finding was experimentally verified in 2016 [13]. This was the first time that scholars discovered a natural material with a negative Poisson’s ratio, and this discovery has sparked significant interest among numerous scholars in materials with NPR. Existing research indicates that two-dimensional materials with wrinkles similar to those of black phosphene all possess the characteristic of NPR [3,4,6,9,14,15,16,17,18,19,20,21,22,23,24,25,26,27]. Additionally, some scholars contend that two-dimensional materials with honeycomb structures will all display NPR properties under appropriate strains [19]. Considering that BP exhibits a negative Poisson’s ratio in the vertical plane direction, we are curious about the result of the Poisson’s ratio in the radial direction after curling BP into black phosphorus nanotubes (BPNTs). The structural stability of BPNTs is related to their radius and environmental temperature; the larger the diameter of BPNTs, the smaller the strain energy. Theoretical research indicates that at a specific ambient temperature, when the radius of the BPNTs exceeds a certain critical value, the structural stability can be maintained [28,29,30,31,32]. Phonon spectrum calculations indicate that BPNTs exhibit stability and possess physical properties similar to that of bulk BP [29,31,33,34]. Although BPNTs have not yet been successfully prepared in the laboratory, this does not prevent scholars from exploring and researching them. Through molecular dynamics simulation and calculation methods, scholars have pointed out that phosphorene can be wound around carbon nanotubes to obtain BPNTs [35,36,37,38]. Currently, in experiments, phosphorous nanorings and nanohelices have been obtained by placing phosphorene on the surface or inside of carbon nanotubes [39,40], which is a step forward in the preparation of BPNTs. Existing theoretical research shows that BPNTs have excellent and unique physical properties and have potential application prospects in semiconductors [32,34,41,42,43,44,45], sensors [46,47,48,49], new energy [50,51,52], nanoelectromechanical device [53,54], optoelectronics [41,45,55,56], etc. Currently, research on BPNTs primarily centers on structural stability [28,30,31,54,57,58,59,60], mechanical properties [34,53,59,61,62,63], thermal properties [31,54,64,65], and electrical characteristics [34,41,42,43,44,45,56]; however, there has been no in-depth or systematic investigation into its Poisson’s ratio. The Poisson’s ratio characteristics of BPNTs and the underlying potential mechanisms still require further exploration and research by scholars. Among the existing bulk materials with negative Poisson’s ratio, the structures are basically artificially designed to have hinge-like features [1,7,66]. Almost all of the single materials with inherent negative Poisson’s ratio that have been discovered so far are 2D materials [2,13,14,15,16,17,19,20,21,22,23,24,25,27,67,68,69,70]. We are eager to know whether it is possible to obtain 1D materials with negative Poisson’s ratio by curling 2D materials with negative Poisson’s ratio to form nanotubes. If nanotubes with negative Poisson’s ratio can be obtained, the bulk materials with negative Poisson’s ratio, which are different from the structural designs of traditional negative Poisson ratio materials, can be obtained through methods such as stacking and bundling.
In this paper, we have investigated the Poisson’s ratio of BPNTs by using the molecular dynamics (MD) simulation method. The detailed calculations are elaborated in Section 2. In Section 3, the results obtained are presented. It is found that for the armchair black phosphorus nanotubes (ABPNTs), both the radial strain and the wall thickness strain are negatively linearly correlated with the axial strain. The wall thickness strain of the zigzag black phosphorene nanotubes (ZBPNTs) is negatively linearly correlated with the axial strain, while the radial strain has a cubic polynomial function relationship with the axial strain. As the axial strain increases, the radial Poisson’s ratio progressively diminishes from a positive value and becomes negative upon reaching a specific critical axial strain threshold. Finally, a brief conclusion is given in Section 4. This research contributes significantly to the application and development of black phosphorene nanotubes in the semiconductor industry.

2. Models and Methods

As shown in Figure 1, BPNTs can be rolled by BP along the vector R = ma1 + na2, where m and n are integers representing the number of lattice vectors along the a1 and a2 directions, respectively. To distinguish the phosphorous atoms of BPNTs, we label the atoms on the surface of BPNTs as P1 and the atoms inside as P2, as illustrated in Figure 1a. The chirality of BPNTs is characterized by the integer pair C (m, n). When R aligns with the x-axis (n = 0), we can obtain a zigzag phosphorene nanotube (ZBPNT), denoted as Z(m, 0); when R aligns with the y-axis (m = 0), we can obtain an armchair phosphorene nanotube (ABPNT), denoted as A(0, n). The right side of Figure 1 shows the structural diagrams of BPNTs with different chirality. Both ABPNTs and ZBPNTs possess three types of atomic bonds—Bond11 (P1 – P1), Bond22 (P2 – P2), and Bond12 (P1 – P2)—and four types of bond angles: θ111 (∠P1P1P1), θ222 (∠P2P2P2), θ221, and θ112 (∠P2P2P1 and ∠P1P1P2). We constructed models of BPNTs with varying chirality and diameters, specifically A(0, 30), A(0, 60), and A(0, 90) for ABPNTs and Z(30, 0), Z(60, 0), and Z(0, 90) for ZBPNTs. Each BPNT model contains 50 cells along the axial direction. Simulations were performed using the LAMMPS (29 August 2024) [71] open-source software package, employing the Stillinger–Weber (S-W) potential to describe the interactions between phosphorus atoms [69,72,73]. Jiang [73] used the optimized SW potential to calculate the phonon spectrum properties of BP, which are in good agreement with those obtained by ab initio calculations. Meanwhile, the two-body and three-body terms of the SW potential introduce nonlinear effects, enabling the simulation of the nonlinear properties of materials. The SW potential has also been recognized by other scholars and has achieved certain success in the research on the mechanical properties and thermodynamics of BP [69,74,75], making it a powerful tool for current molecular dynamics studies on the properties of BP.
Figure 2 shows the top views of BPNTs with different radii at the same ambient temperature. It can be seen that the larger the radius of the BPNTs, the more severe the deformation of their tube walls. We utilized the root mean square (RMS) of the atomic distances from the central axis to determine the inner and outer radii of the tube wall. Based on these measurements, we obtained the outer and inner diameter and wall thickness of the BPNTs.
Table 1 shows the inner and outer diameters and the tube wall thickness of several BPNT models with different chirality at an ambient temperature of 300 K. It can be seen from Table 1 that the value of the tube wall thickness does not increase with the increase in the radius of BPNTs. We believe that this error is caused by the deformation of the tube wall as the radius of BPNTs increases. By observing Figure 2, we find that at an ambient temperature of 300 K, as the radius of BPNTs increases, the fluctuating deformation of the tube wall becomes more obvious. In particular, ABPNTs with larger radii have wave-like undulations on their surfaces. Solving for strain can eliminate most of the errors caused by the tube wall deformation. The length strain (εl), radial strain (εd), and thickness strain (εt) of BPNTs are expressed as follows:
εl = (l − l0)/l0
εd = (d − d0)/d0
εt = (t − t0)/t0
In the above formula, l0, d0, and t0 are the length, diameter, and wall thickness of BPNTs without axial deformation, respectively, while l, d, and t correspond to the length, diameter, and wall thickness of BPNTs after axial deformation, respectively. Therefore, we believe that the deformation of the tube wall does not affect the analysis results of the functional relationship between the axial strain and the transverse strain of BPNTs.
Under the NPT ensemble, axial strain (εl) was applied to BPNTs; the εl range of BPNTs is from −0.2 to 0.4, with an interval of 0.01 between data points. The strain range where BPNTs do not undergo obvious buckling or tensile fracture is selected as the range for our data processing. We do not calculate the relevant data during the continuous change in axial strain. Instead, for each εl value, after the BPNTs reach the predetermined value of that εl and undergo sufficient relaxation at the temperature of 300 K. Subsequently, the system was further relaxed under the NVT ensemble to achieve a stable BPNTs structure, and then we calculate the corresponding inner and outer diameters as well as the tube wall thickness. Relaxation under the NVT ensemble was performed at the temperature of 300 K, with a time step of 0.2 fs and a total relaxation duration of 100 ps.
According to the definition, Poisson’s ratio ν = −ε⊥/εl, where εl denotes the longitudinal strain and ε⊥ denotes the transverse strain of the material. In continuum mechanics, two distinct conventions are commonly employed for calculating the mechanical properties of tubular structures. Under these conventions, the cross-sectional area of the tube is modeled either as a solid cylinder or as a hollow annular tube. Consequently, different methods for calculating Poisson’s ratio arise based on these two conventions [62,76].
When the nanotube is modeled as a solid cylinder, its radial Poisson’s ratio can be expressed as follows:
νd = −εd/εl
When the nanotube is modeled as a hollow tube, its thickness Poisson’s ratio can be expressed as follows:
νt = −εt/εl

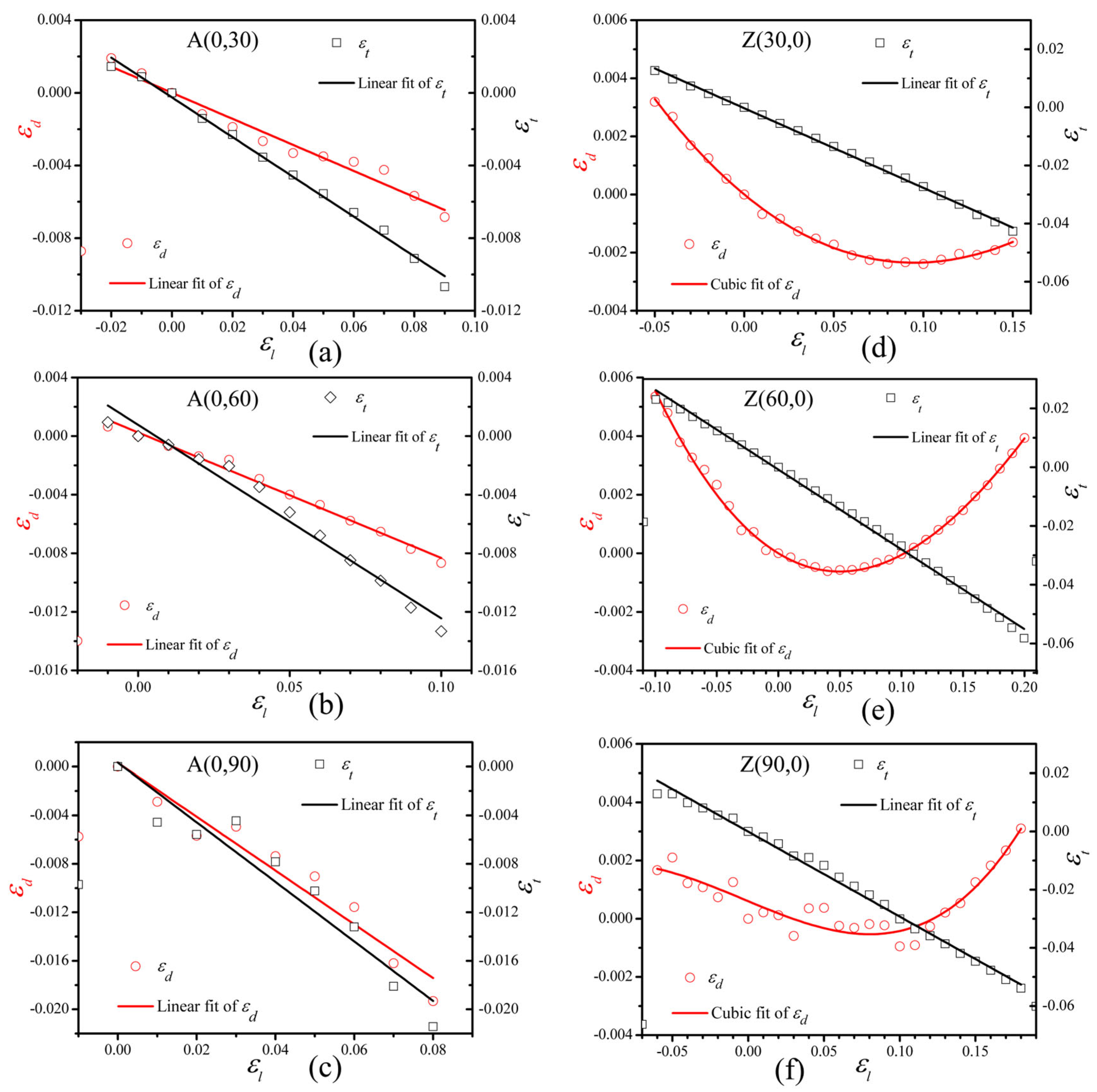
3. Results and Analysis

The ABPNT models, A(0, 30), A(0, 60), and A(0, 90), compressive buckling occurs at axial strains (εl) of −0.03, −0.02, and −0.02, respectively, while tensile fracture occurs at εl values of 0.10, 0.11, and 0.09, respectively. For the ZBPNT models, Z(30, 0), Z(60, 0), and Z(90, 0), compressive buckling or fracture is observed at εl values of −0.06, −0.11, and −0.07, respectively, and tensile fracture occurs at εl values of 0.16, 0.20, and 0.19, respectively. To ensure Poisson’s ratio calculations accurately, we selected a strain range where no significant buckling or fracture occurred in the BPNTs. After obtaining the transverse strains εd and εt under different axial strains εl, we can take εl as the x-axis and εd and εt as the y-axis to obtain the function relation graphs of εd-εl and εt-εl. Figure 3a–c shows the function relation graphs of εd-εl and εt-εl for ABPNTs, and Figure 3d–f shows the function relation graphs of εd-εl and εt-εl for ZBPNTs.
As illustrated in Figure 3a–c, the scatter plot depicts the relationship between εd-εl and εt-εl of ABPNTs. It is evident that εd and εt exhibit a predominantly linear correlation with εl. According to Formulas (3) and (4), we obtained the radial Poisson’s ratio (νd) and thickness Poisson’s ratio (νt) of A(0, 30), A(0, 60), and A(0, 90), as summarized in Table 2. Our findings indicate that both νd and νt are diameter-dependent, with an increasing trend observed as the diameter of ABPNTs increases.
Figure 3d–f illustrates the scatter plot depicting the relationships among εd, εt, and εl for ZBPNTs. It is observed that εt exhibits a predominantly linear correlation with εl, allowing for the determination of the thickness Poisson’s ratio νt through linear regression analysis. In contrast, εd does not display a linear relationship with εl. Instead, function fitting reveals that εd and εl follow a cubic polynomial relationship. This finding is consistent with the strain characteristics of the thickness observed in BP when stretched along the armchair direction [2] and parallels the strain behavior of graphene in the zigzag direction under similar conditions [14].
The results of the nonlinear fitting of εd-εl using the function y = −ν1x + ν2x2 + ν3x3 [2] are summarized in Table 3. According to the definition of νd, where νd = −∂εd/∂εl, it is derived that νd = ν1 – 2ν2εl – 3ν3εl2. νd represents the negative of the slope of the εd-εl curve. In the initial stage of tensile deformation, νd is positive, and as the tensile strain increases, νd transitions to negative values, which means that the outer diameter of the nanotube begins to expand. In Figure 3d–f, the negative Poisson’s ratio corresponds to the stage where the red solid line increases in the opposite direction after the minimum value of εd. For Z(60,0) and Z(90,0), their εd can even be positive, which means that after a process of first contracting ann then expanding, their outer diameters can exceed their initial values.
Table 4 presents a comparative analysis of the Poisson’s ratios of BPNTs obtained through various methods. The thickness Poisson’s ratios (νt) are basically close to the results of other scholars, while the radial Poisson’s ratios (νd) yield divergent results. In our view, the reason for the differences in νd observed in ZBPNTs is that some scholars, based on elastic theory, treat the deformation of BPNTs as a type of harmonic oscillator. They solve the relevant elastic coefficients and Poisson’s ratio under the presupposition of linear elastic deformation. The obtained Poisson’s ratio values either correspond to the specific εl at that time or are the expected values E(νd) within a certain deformation range. In their data processing, the corresponding functional relationship diagram between radial strain and axial strain is not provided. Therefore, in the calculation of the radial Poisson’s ratio of ZBPNTs, the nonlinear radial Poisson’s ratio fails to be presented.

4. Conclusions

In this study, molecular dynamics simulations were employed to investigate the Poisson’s ratios of armchair black phosphorene nanotubes (ABPNTs) and zigzag black phosphorene nanotubes (ZBPNTs). The results indicate that the radial Poisson’s ratio νd of ABPNTs is positively correlated with the tube diameter. Specifically, as the diameter increases, νd also increases. In our analysis, the νd values for A(0, 30), A(0, 60), and A(0, 90) were 0.072, 0.086, and 0.222, respectively. Similarly, the thickness Poisson’s ratio νt of ABPNTs exhibits a positive correlation with the diameter, with νt values of 0.110, 0.132, and 0.246 for A(0, 30), A(0, 60), and A(0, 90), respectively. Considering the influence of tube wall deformation, we estimate that in the absence of significant wall deformation, the νd value of ABPNTs is approximately 0.08, while the νt value is around 0.12.
For ZBPNTs, the thickness Poisson’s ratio νt does not exhibit a significant dependence on the diameter. In our study, the νt values for Z(30, 0), Z(60, 0), and Z(90, 0) were 0.274, 0.271, and 0.292, respectively. The relationship between the radial strain εd and axial strain εl in ZBPNTs is nonlinear and can be described by a cubic function: y = −ν1x + ν2x2 + ν3x3, where ν1, ν2, and ν3 represent the first-order, second-order, and third-order Poisson’s ratios, respectively. The radial Poisson’s ratio νd of ZBPNTs varies with axial strain εl. As ZBPNTs are stretched and εl increases, νd decreases from a positive value to a negative one, leading to an inverse expansion behavior. When εl reaches a critical value, εd may become positive, and the diameter of ZBPNTs exceeds its initial size, resulting in uniform radial expansion.
Our findings provide valuable insights into the design and application of materials with negative Poisson’s ratios. The unique tensile expansion effect observed in ZBPNTs offers potential for developing novel negative Poisson’s ratio composite materials.

Author Contributions

Conceptualization, X.T.; methodology, X.T., T.F. and K.Z.; software, K.Z.; formal analysis, T.F.; investigation, X.T. and T.F.; writing—original draft, X.T.; writing—review and editing, T.F.; visualization, X.T.; supervision, K.Z.; project administration, K.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This work is supported by the PhD innovation project of the Xiangtan University (XDCX2019B064).

Data Availability Statement

Data are contained within the article.

Acknowledgments

Thank you for the support of the Doctoral Innovation Fund of Xiangtan University (XDCX2019B064).

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Lakes, R. Foam Structures with a Negative Poisson’s Ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef]
  2. Jiang, J.-W.; Park, H.S. Negative poisson’s ratio in single-layer black phosphorus. Nat. Commun. 2014, 5, 4727. [Google Scholar] [CrossRef] [PubMed]
  3. Jiang, J.-W.; Kim, S.Y.; Park, H.S. Auxetic nanomaterials: Recent progress and future development. Appl. Phys. Rev. 2016, 3, 041101. [Google Scholar] [CrossRef]
  4. Borcea, C.S.; Ileana, S. Periodic Auxetics: Structure and Design. Q. J. Mech. Appl. Math. 2018, 71, 125–138. [Google Scholar] [CrossRef] [PubMed]
  5. Ren, X.; Das, R.; Tran, P.; Ngo, T.D.; Xie, Y.M. Auxetic metamaterials and structures: A review. Smart Mater. Struct. 2018, 27, 023001. [Google Scholar] [CrossRef]
  6. Gan, Z.; Zhuge, Y.; Thambiratnam, D.P.; Chan, T.H.; Zahra, T.; Asad, M. Recent advances in auxetics: Applications in cementitious composites. Int. J. Prot. Struct. 2022, 13, 295–316. [Google Scholar] [CrossRef]
  7. Shukla, S.; Behera, B. Auxetic fibrous structures and their composites: A review. Compos. Struct. 2022, 290, 115530. [Google Scholar] [CrossRef]
  8. Dong, S.; Hu, H. Sensors Based on Auxetic Materials and Structures: A Review. Materials 2023, 16, 3603. [Google Scholar] [CrossRef]
  9. Shukla, S.; Behera, B.K. Auxetic fibrous materials and structures in medical engineering—A review. J. Text. Inst. 2022, 114, 1078–1089. [Google Scholar] [CrossRef]
  10. Lv, Y.; Zhang, Y.; Gong, N.; Li, Z.X.; Lu, G.; Xiang, X. On the out-of-Plane Compression of a Miura-Ori Patterned Sheet. Int. J. Mech. Sci. 2019, 105022, 161–162. [Google Scholar] [CrossRef]
  11. Zhang, J.; Lu, G.; You, Z. Large deformation and energy absorption of additively manufactured auxetic materials and structures: A review. Compos. Part B Eng. 2020, 201, 108340. [Google Scholar] [CrossRef]
  12. Zhang, J.; Lu, G.; Wang, Z.; Ruan, D.; Alomarah, A.; Durandet, Y. Large deformation of an auxetic structure in tension: Experiments and finite element analysis. Compos. Struct. 2018, 184, 92–101. [Google Scholar] [CrossRef]
  13. Du, Y.; Maassen, J.; Wu, W.; Luo, Z.; Xu, X.; Ye, P.D. Auxetic Black Phosphorus: A 2D Material with Negative Poisson’s Ratio. Nano Lett. 2016, 16, 6701–6708. [Google Scholar] [CrossRef]
  14. Jiang, J.-W.; Chang, T.; Guo, X.; Park, H.S. Intrinsic Negative Poisson’s Ratio for Single-Layer Graphene. Nano Lett. 2016, 16, 5286–5290. [Google Scholar] [CrossRef]
  15. Jiang, J.-W.; Park, H.S. Negative Poisson’s Ratio in Single-Layer Graphene Ribbons. Nano Lett. 2016, 16, 2657–2662. [Google Scholar] [CrossRef]
  16. Wan, J.; Jiang, J.-W.; Park, H.S. Negative Poisson’s ratio in graphene oxide. Nanoscale 2017, 9, 4007–4012. [Google Scholar] [CrossRef] [PubMed]
  17. Yuan, K.; Li, M.-Y.; Liu, Y.-Z.; Li, R.-Z. Design and Prediction of a Novel Two-Dimensional Carbon Nanostructure with In-Plane Negative Poisson’s Ratio. J. Nanomater. 2019, 2019, 1–10. [Google Scholar] [CrossRef]
  18. Zhao, S.; Hu, H.; Kamrul, H.; Chang, Y.; Zhang, M. Development of auxetic warp knitted fabrics based on reentrant geometry. Text. Res. J. 2019, 90, 344–356. [Google Scholar] [CrossRef]
  19. Qin, G.; Qin, Z. Negative Poisson’s ratio in two-dimensional honeycomb structures. npj Comput. Mater. 2020, 6, 1–6. [Google Scholar] [CrossRef]
  20. Zhang, C.; Lu, C.; Pei, L.; Li, J.; Wang, R. Molecular Dynamics Simulation of the Negative Poisson’s Ratio in Graphene/Cu Nanolayered Composites: Implications for Scaffold Design and Telecommunication Cables. ACS Appl. Nano Mater. 2019, 3, 496–505. [Google Scholar] [CrossRef]
  21. Sun, M.; Schwingenschlögl, U. Unique Omnidirectional Negative Poisson’s Ratio in δ-Phase Carbon Monochalcogenides. J. Phys. Chem. C 2021, 125, 4133–4138. [Google Scholar] [CrossRef]
  22. Ho, V.H.; Ho, D.T.; Nguyen, C.T.; Kim, S.Y. Negative out-of-plane Poisson’s ratio of bilayer graphane. Nanotechnology 2022, 33, 255705. [Google Scholar] [CrossRef]
  23. Wang, Y.; Yu, L.; Zhang, F.; Chen, Q.; Zhan, Y.; Meng, L.; Zheng, X.; Wang, H.; Qin, Z.; Qin, G. The consistent behavior of negative Poisson’s ratio with interlayer interactions. Mater. Adv. 2022, 3, 4334–4341. [Google Scholar] [CrossRef]
  24. Yu, L.; Wang, Y.; Zheng, X.; Wang, H.; Qin, Z.; Qin, G. Emerging negative Poisson’s ratio driven by strong intralayer interaction response in rectangular transition metal chalcogenides. Appl. Surf. Sci. 2022, 610, 155478. [Google Scholar] [CrossRef]
  25. Zhu, Y.; Cao, X.; Tan, Y.; Wang, Y.; Hu, J.; Li, B.; Chen, Z. Single-Layer MoS2: A Two-Dimensional Material with Negative Poisson’s Ratio. Coatings 2023, 13, 283. [Google Scholar] [CrossRef]
  26. Ren, K.; Ma, X.; Liu, X.; Xu, Y.; Huo, W.; Li, W.; Zhang, G. Prediction of 2D IV–VI semiconductors: Auxetic materials with direct bandgap and strong optical absorption. Nanoscale 2022, 14, 8463–8473. [Google Scholar] [CrossRef] [PubMed]
  27. Wen, Y.; Gao, E.; Hu, Z.; Xu, T.; Lu, H.; Xu, Z.; Li, C. Chemically modified graphene films with tunable negative Poisson’s ratios. Nat. Commun. 2019, 10, 2446. [Google Scholar] [CrossRef]
  28. Guan, J.; Zhu, Z.; Tománek, D. High Stability of Faceted Nanotubes and Fullerenes of Multiphase Layered Phosphorus: A Computational Study. Phys. Rev. Lett. 2014, 113, 226801. [Google Scholar] [CrossRef]
  29. Guo, H.; Lu, N.; Dai, J.; Wu, X.; Zeng, X.C. Phosphorene Nanoribbons, Phosphorus Nanotubes, and Van Der Waals Multilayers. J. Phys. Chem. C 2014, 118, 14051–14059. [Google Scholar] [CrossRef]
  30. Shahnazari, A.; Ansari, R.; Rouhi, S. On the stability characteristics of zigzag phosphorene nanotubes: A finite element investigation. J. Alloy Compd. 2017, 702, 388–398. [Google Scholar] [CrossRef]
  31. Cai, K.; Wan, J.; Wei, N.; Cai, H.; Qin, Q.-H. Thermal stability of a free nanotube from single-layer black phosphorus. Nanotechnology 2016, 27, 235703. [Google Scholar] [CrossRef]
  32. Fernández-Escamilla, H.N.; Quijano-Briones, J.J.; Tlahuice-Flores, A. Chiral phosphorus nanotubes: Structure, bonding, and electronic properties. Phys. Chem. Chem. Phys. 2016, 18, 12414–12418. [Google Scholar] [CrossRef]
  33. Seifert, G.; Hernández, E. Theoretical prediction of phosphorus nanotubes. Chem. Phys. Lett. 2000, 318, 355–360. [Google Scholar] [CrossRef]
  34. Zhang, W.; Yin, J.; Zhang, P.; Ding, Y. Strain/stress engineering on the mechanical and electronic properties of phosphorene nanosheets and nanotubes. RSC Adv. 2017, 7, 51466–51474. [Google Scholar] [CrossRef]
  35. Shi, J.; Cai, K.; Liu, L.-N.; Qin, Q.-H. Self-assembly of a parallelogram black phosphorus ribbon into a nanotube. Sci. Rep. 2017, 7, 1–10. [Google Scholar] [CrossRef]
  36. Cai, K.; Liu, L.; Shi, J.; Qin, Q.H. Winding a nanotube from black phosphorus nanoribbon onto a CNT at low temperature: A molecular dynamics study. Mater. Des. 2017, 121, 406–413. [Google Scholar] [CrossRef]
  37. Cai, K.; Shi, J.; Liu, L.; Qin, Q. Fabrication of an ideal nanoring from a black phosphorus nanoribbon upon movable bundling carbon nanotubes. Nanotechnology 2017, 28, 385603. [Google Scholar] [CrossRef] [PubMed]
  38. Cai, K.; Liu, L.; Shi, J.; Qin, Q.H. Self-Assembly of a Jammed Black Phosphorus Nanoribbon on a Fixed Carbon Nanotube. J. Phys. Chem. C 2017, 121, 10174–10181. [Google Scholar] [CrossRef]
  39. Zhang, J.; Zhao, D.; Xiao, D.; Ma, C.; Du, H.; Li, X.; Zhang, L.; Huang, J.; Huang, H.; Jia, C.; et al. Assembly of Ring-Shaped Phosphorus within Carbon Nanotube Nanoreactors. Angew. Chem. Int. Ed. Engl. 2017, 56, 1850–1854. [Google Scholar] [CrossRef]
  40. Choi, Y.W.; Lee, Y.; Kim, K.; Zettl, A.; Cohen, M.L. Atomic and Electronic Structures of 1D Phosphorus Nanoring and Nanohelix. ACS Nano 2025, 19, 12155–12160. [Google Scholar] [CrossRef]
  41. Badehian, H.A.; Gharbavi, K. Effect of silicon doping on the electronic and optical properties of phosphorous nanotubes. Optik 2021, 225, 165808. [Google Scholar] [CrossRef]
  42. Fernández-Escamilla, H.N.; Guerrero-Sanchez, J.; Martínez-Guerra, E.; Takeuchi, N. Structural and Electronic Properties of Double-Walled Black Phosphorene Nanotubes: A Density Functional Theory Study. J. Phys. Chem. C 2019, 123, 7217–7224. [Google Scholar] [CrossRef]
  43. Dai, X.; Zhang, L.; Wang, Z.; Li, J.; Li, H. Effect of C and O dopant atoms on the electronic properties of black phosphorus nanotubes. Comput. Mater. Sci. 2019, 156, 292–300. [Google Scholar] [CrossRef]
  44. Li, Q.; Wang, H.; Yang, C.; Li, Q.; Rao, W. Theoretical prediction of high carrier mobility in single-walled black phosphorus nanotubes. Appl. Surf. Sci. 2018, 441, 1079–1085. [Google Scholar] [CrossRef]
  45. Li, C.; Xie, Z.; Chen, Z.; Cheng, N.; Wang, J.; Zhu, G. Tunable Bandgap and Optical Properties of Black Phosphorene Nanotubes. Materials 2018, 11, 304. [Google Scholar] [CrossRef]
  46. Ou, P.; Zhou, X.; Li, X.-Y.; Chen, Y.; Chen, C.; Meng, F.; Song, J. Single-Walled Black Phosphorus Nanotube as a NO2 Gas Sensor. Mater. Today Commun. 2022, 31, 103434. [Google Scholar] [CrossRef]
  47. Maria, J.P.; Nagarajan, V.; Chandiramouli, R. Chemosensing nature of black phosphorene nanotube towards C14H9Cl5 and C10H5Cl7 molecules – A first-principles insight. Comput. Theor. Chem. 2021, 1196, 113109. [Google Scholar] [CrossRef]
  48. Kazerooni, H.B.; Ghayour, R.; Pesaran, F. Analysis and application of zigzag phosphorene nanotube as gas nanosensor. Appl. Phys. A 2021, 127, 1–10. [Google Scholar] [CrossRef]
  49. Saravanan, S.; Nagarajan, V.; Chandiramouli, R. Adsorption insights of amine vapors on black phosphorene nanotubes—A first-principles study. Mater. Res. Express 2019, 6, 105518. [Google Scholar] [CrossRef]
  50. Cao, J.; Shi, J.; Hu, Y.; Wu, M.; Ouyang, C.; Xu, B. Lithium ion adsorption and diffusion on black phosphorene nanotube: A first-principles study. Appl. Surf. Sci. 2017, 392, 88–94. [Google Scholar] [CrossRef]
  51. Zhang, W.; Cui, Y.; Zhu, C.; Huang, B.; Yan, S.; Lou, Y.; Zhang, P. Sequential hydrogen storage in phosphorene nanotubes: A molecular dynamics study. Int. J. Hydrogen Energy 2023, 48, 23909–23916. [Google Scholar] [CrossRef]
  52. Wang, H.; Gao, Q.; Liu, C.; Cao, Y.; Liu, S.; Zhang, B.; Hu, Z.; Sun, J. Anisotropic black phosphorene nanotube anodes afford ultrafast kinetic rate or extra capacities for Li-ion batteries. Chin. Chem. Lett. 2022, 33, 3842–3848. [Google Scholar] [CrossRef]
  53. Tran, K.; Taylor, P.D.; Spencer, M.J.S. Electromechanical strain response of phosphorene nanotubes. J. Phys. Mater. 2024, 7, 035001. [Google Scholar] [CrossRef]
  54. Cuba-Supanta, G.; Fernández-Escamilla, H.N.; Guerrero-Sanchez, J.; Rojas-Tapia, J.; Takeuchi, N. Structural properties and thermal stability of multi-walled black phosphorene nanotubes and their operation as temperature driven nanorotors. Nanoscale 2020, 12, 18313–18321. [Google Scholar] [CrossRef]
  55. Guan, L.; Chen, G.; Tao, J. Prediction of the electronic structure of single-walled black phosphorus nanotubes. Phys. Chem. Chem. Phys. 2016, 18, 15177–15181. [Google Scholar] [CrossRef]
  56. Yang, J.; Xie, Y.; Wang, S.; Jiang, N.; Chen, L.; Wang, X.; Zhang, J. Manipulating the electronic, magnetic, and optical properties of single-walled armchair phosphorus nanotubes by encapsulating transition metal nanowires. Mater. Today Commun. 2022, 34, 105253. [Google Scholar] [CrossRef]
  57. Liu, P.; Pei, Q.-X.; Huang, W.; Zhang, Y.-W. Mechanical properties and fracture behaviour of defective phosphorene nanotubes under uniaxial tension. J. Phys. D Appl. Phys. 2017, 50, 485303. [Google Scholar] [CrossRef]
  58. Nguyen, V.-T. Effects of Missing Atom Defect on the Mechanical Properties of Black Phosphorene Nanotube. Int. J. Eng. Res. Appl. 2018, 8, 29–32. [Google Scholar]
  59. Sorkin, V.; Zhang, Y.-W. Effect of vacancies on the mechanical properties of phosphorene nanotubes. Nanotechnology 2018, 29, 235707. [Google Scholar] [CrossRef]
  60. Liu, P.; Pei, Q.-X.; Huang, W.; Zhang, Y.-W. Strength and buckling behavior of defective phosphorene nanotubes under axial compression. J. Mater. Sci. 2018, 53, 8355–8363. [Google Scholar] [CrossRef]
  61. Ansari, R.; Shahnazari, A.; Rouhi, S. A density-functional-theory-based finite element model to study the mechanical properties of zigzag phosphorene nanotubes. Phys. E Low-Dimens. Syst. Nanostructures 2017, 88, 272–278. [Google Scholar] [CrossRef]
  62. Chen, W.-H.; Yu, C.-F.; Chen, I.-C.; Cheng, H.-C. Mechanical property assessment of black phosphorene nanotube using molecular dynamics simulation. Comput. Mater. Sci. 2017, 133, 35–44. [Google Scholar] [CrossRef]
  63. Hao, J.; Wang, Z.; Peng, Y.; Wang, Y. Structure and elastic properties of black phosphorus nanotubes: A first-principles study. Phys. Status solidi (b) 2017, 254, 1700276. [Google Scholar] [CrossRef]
  64. Wang, L.; Wang, C. Negative/zero thermal expansion in black phosphorus nanotubes. Phys. Chem. Chem. Phys. 2018, 20, 28726–28731. [Google Scholar] [CrossRef]
  65. Hao, F.; Liao, X.; Xiao, H.; Chen, X. Thermal conductivity of armchair black phosphorus nanotubes: A molecular dynamics study. Nanotechnology 2016, 27, 155703. [Google Scholar] [CrossRef]
  66. Lakes, R.S. Negative-Poisson’s-Ratio Materials: Auxetic Solids. Annu. Rev. Mater. Res. 2017, 47, 63–81. [Google Scholar] [CrossRef]
  67. Yuan, K.; Zhao, Y.; Li, M.; Liu, Y. Predicting an ideal 2D carbon nanostructure with negative Poisson’s ratio from first principles: Implications for nanomechanical devices. Carbon Lett. 2021, 31, 1227–1235. [Google Scholar] [CrossRef]
  68. Gao, Y.; Wen, M.; Zhang, X.; Wu, F.; Xia, Q.; Wu, H.; Dong, H. Factors affecting the negative Poisson’s ratio of black phosphorus and black arsenic: Electronic effects. Phys. Chem. Chem. Phys. 2021, 23, 3441–3446. [Google Scholar] [CrossRef]
  69. Jiang, J.-W.; Rabczuk, T.; Park, H.S. A Stillinger–Weber potential for single-layered black phosphorus, and the importance of cross-pucker interactions for a negative Poisson’s ratio and edge stress-induced bending. Nanoscale 2015, 7, 6059–6068. [Google Scholar] [CrossRef] [PubMed]
  70. Ho, D.T.; Park, S.D.; Kwon, S.Y.; Park, K.; Kim, S.Y. Negative Poisson’s Ratios in Metal Nanoplates. Nat. Commun. 2014, 5, 3255. [Google Scholar] [CrossRef]
  71. Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
  72. Jiang, J.-W. An empirical description for the hinge-like mechanism in single-layer black phosphorus: The angle–angle cross interaction. Acta Mech. Solida Sin. 2017, 30, 227–233. [Google Scholar] [CrossRef]
  73. Jiang, J.-W. Parametrization of Stillinger–Weber potential based on valence force field model: Application to single-layer MoS2and black phosphorus. Nanotechnology 2015, 26, 315706. [Google Scholar] [CrossRef]
  74. Sha, Z.-D.; Pei, Q.-X.; Ding, Z.; Jiang, J.-W.; Zhang, Y.-W. Mechanical properties and fracture behavior of single-layer phosphorene at finite temperatures. J. Phys. D Appl. Phys. 2015, 48, 395303. [Google Scholar] [CrossRef]
  75. Yang, Z.; Zhao, J.; Wei, N. Temperature-dependent mechanical properties of monolayer black phosphorus by molecular dynamics simulations. Appl. Phys. Lett. 2015, 107, 023107. [Google Scholar] [CrossRef]
  76. Sorkin, V.; Zhang, Y.W. Mechanical properties of phosphorene nanotubes: A density functional tight-binding study. Nanotechnology 2016, 27, 395701. [Google Scholar] [CrossRef] [PubMed]
  77. Ansari, R.; Aghdasi, P.; Shahnazari, A. A comprehensive study of mechanical properties in armchair phosphorene nanotubes using DFT-based finite element analysis. Appl. Phys. A 2024, 130, 1–12. [Google Scholar] [CrossRef]
Nanomaterials 15 01259 g001
Figure 1. The schematic diagrams of the BPNTs. (a) The BP structure, P1 and P2 are phosphorous atoms on two different surfaces represented by brown and black, respectively. The lattice constants are a1 = 3.35 Å and a2 = 4.69 Å. (b) The perspective view of BP, the angles θ111 = θ222 = 97.31° and θ221 = θ112 = 104.91°. (c) The side view of BP, the thickness of a single layer t = 2.12 Å. (d) The curling vector R (m, n). (e,f) ABPNTs and their axial perspective views are shown. (g,h) ZBPNTs and their axial perspective views are presented. (i,j) BPNTs with chirality C (m, n) and their corresponding axial perspective views are illustrated.
Figure 1. The schematic diagrams of the BPNTs. (a) The BP structure, P1 and P2 are phosphorous atoms on two different surfaces represented by brown and black, respectively. The lattice constants are a1 = 3.35 Å and a2 = 4.69 Å. (b) The perspective view of BP, the angles θ111 = θ222 = 97.31° and θ221 = θ112 = 104.91°. (c) The side view of BP, the thickness of a single layer t = 2.12 Å. (d) The curling vector R (m, n). (e,f) ABPNTs and their axial perspective views are shown. (g,h) ZBPNTs and their axial perspective views are presented. (i,j) BPNTs with chirality C (m, n) and their corresponding axial perspective views are illustrated.
Nanomaterials 15 01259 g001
Nanomaterials 15 01259 g002
Figure 2. The thermal-induced deformation of the tube wall in BPNTs at room temperature increases with the diameter of the nanotubes.
Figure 2. The thermal-induced deformation of the tube wall in BPNTs at room temperature increases with the diameter of the nanotubes.
Nanomaterials 15 01259 g002
Nanomaterials 15 01259 g003
Figure 3. The resultant strain εd and εt vs. the applied strain εl of BPNTs. Red hollow circles represent εd vs. εl, black hollow squares denote εt vs. εl. (a–c) are the strain relationship diagrams of ABPNTs, where the black solid line and red solid line represent the linear fitting results of εt vs. εl and εd vs. εl, respectively. (d–f) are the strain relationship diagrams of ZBPNTs, where the black solid line is the linear fitting result of εt vs. εl, and the red solid line is the cubic fitting result of εd vs. εl.
Figure 3. The resultant strain εd and εt vs. the applied strain εl of BPNTs. Red hollow circles represent εd vs. εl, black hollow squares denote εt vs. εl. (a–c) are the strain relationship diagrams of ABPNTs, where the black solid line and red solid line represent the linear fitting results of εt vs. εl and εd vs. εl, respectively. (d–f) are the strain relationship diagrams of ZBPNTs, where the black solid line is the linear fitting result of εt vs. εl, and the red solid line is the cubic fitting result of εd vs. εl.
Nanomaterials 15 01259 g003
Table 1. The inner and outer diameters and wall thickness of BPNTs (Å).
Table 1. The inner and outer diameters and wall thickness of BPNTs (Å).
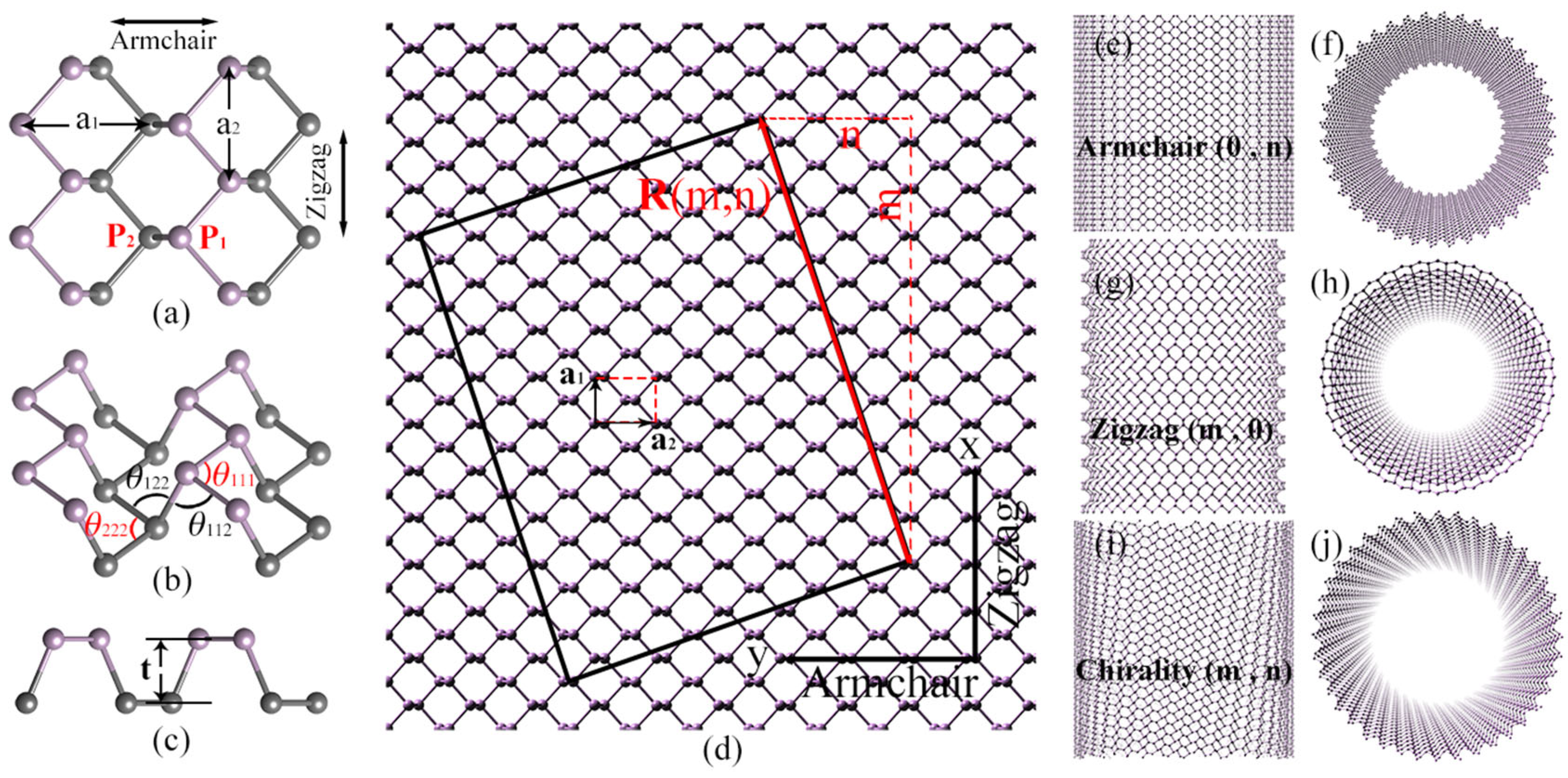
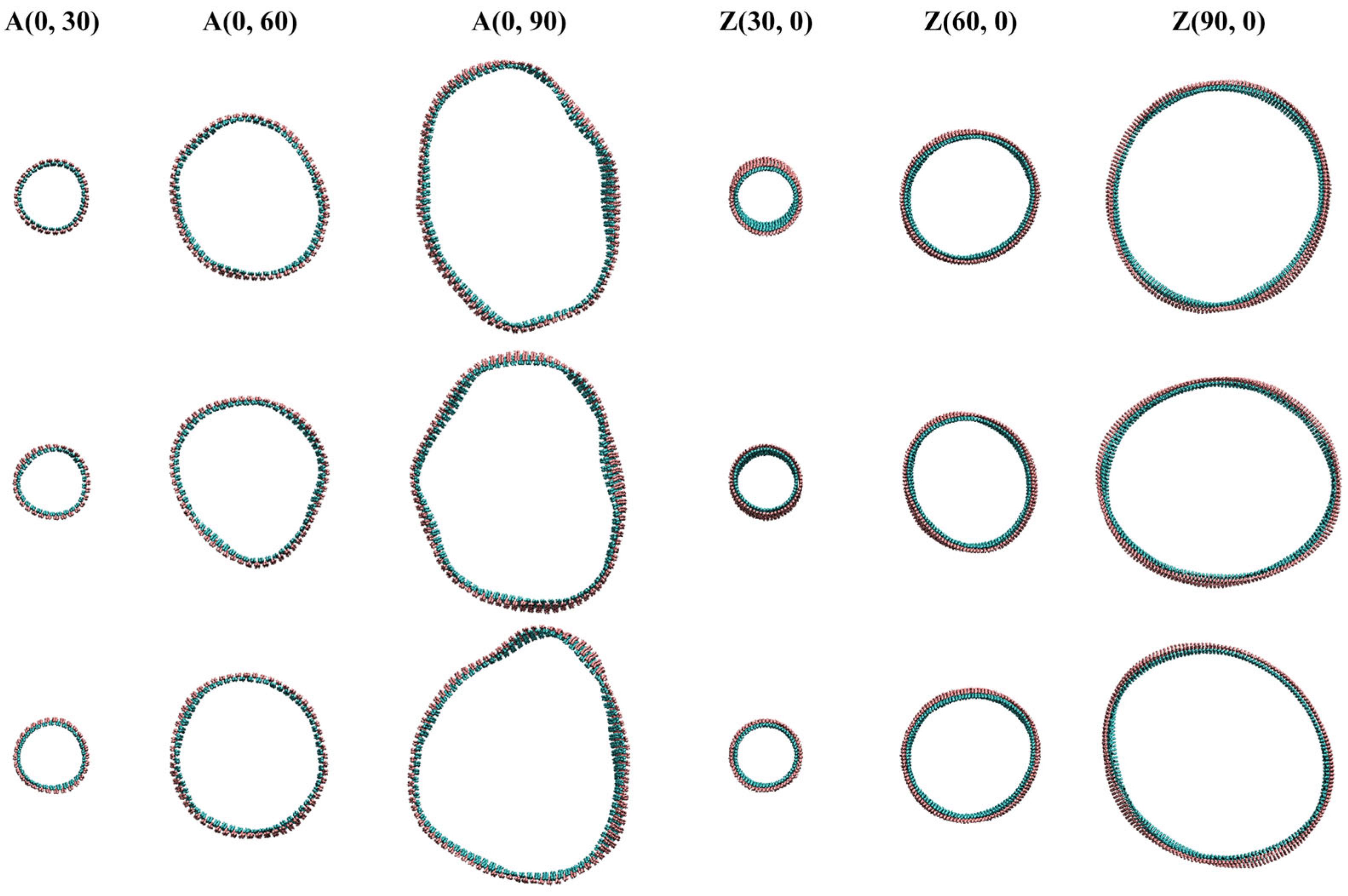
A(0, 30)A(0, 60)A(0, 90)Z(30, 0)Z(60, 0)Z(90, 0)
Dout43.9385.29124.9834.3565.6997.10
Din39.7181.11120.8830.1564.792.90
t2.112.092.052.102.112.10
Table 2. The radial Poisson’s ratio (νd) and thickness Poisson’s ratio (νt) of ABPNTs.
Table 2. The radial Poisson’s ratio (νd) and thickness Poisson’s ratio (νt) of ABPNTs.
A(0, 30)A(0, 60)A(0, 90)
νd0.0720.0860.222
νt0.1100.1320.246
Table 3. The radial Poisson’s ratio (νd) and thickness Poisson’s ratio (νt) of ZBPNTs.
Table 3. The radial Poisson’s ratio (νd) and thickness Poisson’s ratio (νt) of ZBPNTs.
Z(0, 30)Z(0, 60)Z(0, 90)
ν10.0510.0260.022
ν20.2910.2750.01
ν3−0.161−0.2441.038
νt0.2740.2710.292
Table 4. A comparative analysis of the results obtained from diverse studies.
Table 4. A comparative analysis of the results obtained from diverse studies.
ResearcherMethod and PackageABPNTs(νd)ZBPNTs
(ν1/νd)		ABPNTs(νt)ZBPNTs(νt)
This paperMD (LAMMPS)0.072–0.222−0.055~0.0880.110–0.2460.274–0.292
Chen et al. [62]Force field (COMPASS)----0.450.11
Sorkin et al. [76]Tight binding0.470.070.110.21
Ansari et al. [77]DFT-FEM----0.47--
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Tan, X.; Fan, T.; Zhang, K. Research on the Poisson’s Ratio of Black Phosphorene Nanotubes Under Axial Tension. Nanomaterials 2025, 15, 1259. https://doi.org/10.3390/nano15161259

AMA Style

Tan X, Fan T, Zhang K. Research on the Poisson’s Ratio of Black Phosphorene Nanotubes Under Axial Tension. Nanomaterials. 2025; 15(16):1259. https://doi.org/10.3390/nano15161259

Chicago/Turabian Style

Tan, Xinjun, Touwen Fan, and Kaiwang Zhang. 2025. "Research on the Poisson’s Ratio of Black Phosphorene Nanotubes Under Axial Tension" Nanomaterials 15, no. 16: 1259. https://doi.org/10.3390/nano15161259

APA Style

Tan, X., Fan, T., & Zhang, K. (2025). Research on the Poisson’s Ratio of Black Phosphorene Nanotubes Under Axial Tension. Nanomaterials, 15(16), 1259. https://doi.org/10.3390/nano15161259

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop