Mechanistic Insights into the Fracture Toughness Enhancement of Nano-TiO2 and Basalt Fiber Bar Reinforced Magnesium Phosphate Cement
Abstract
1. Introduction
2. Preparation and Experimental Test Design
2.1. Materials
2.2. Mix Proportion Design and Preparation
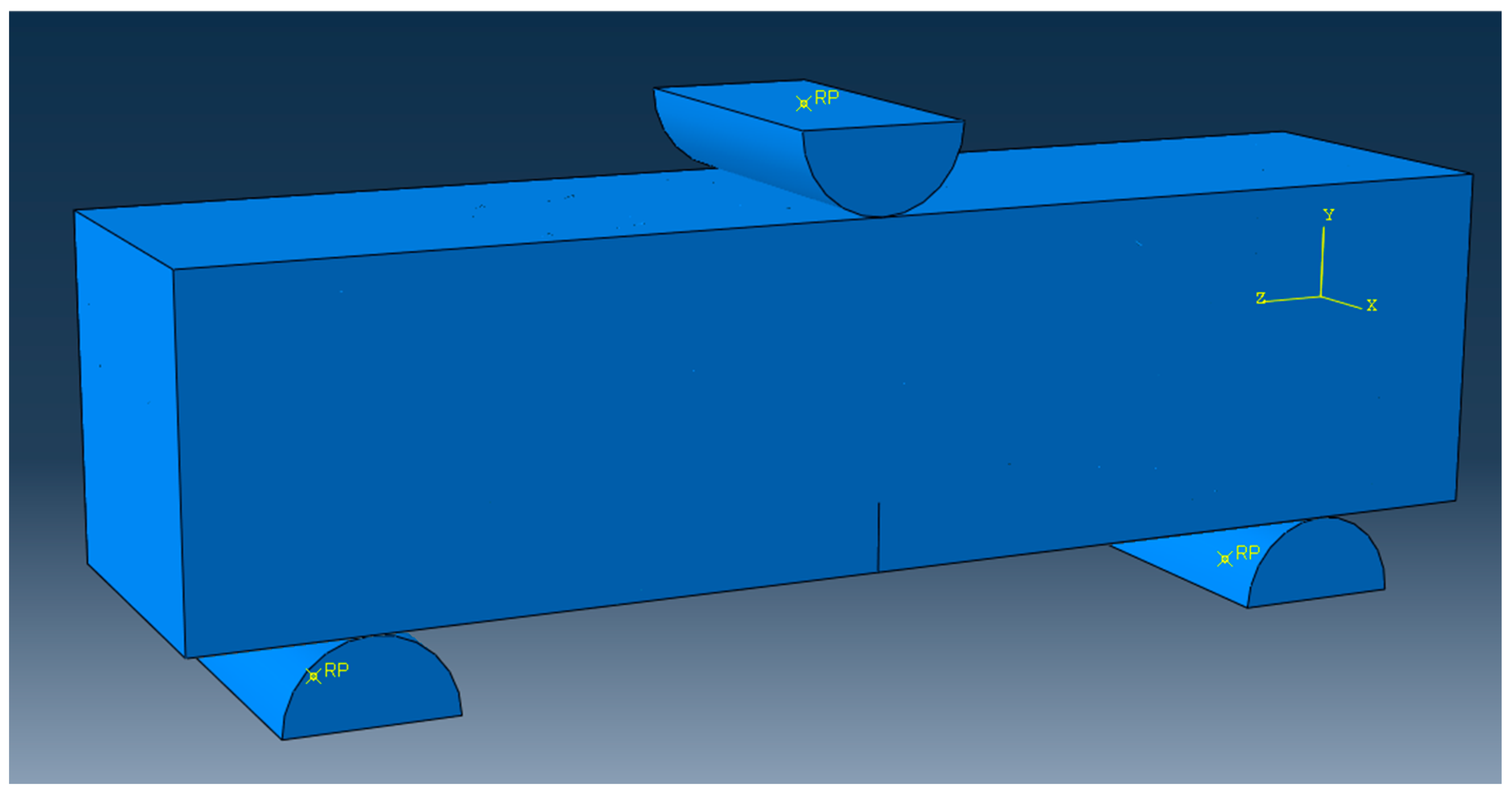
2.3. Test Methods and Data Acquisition
3. Calculation of Fracture Performance Parameters
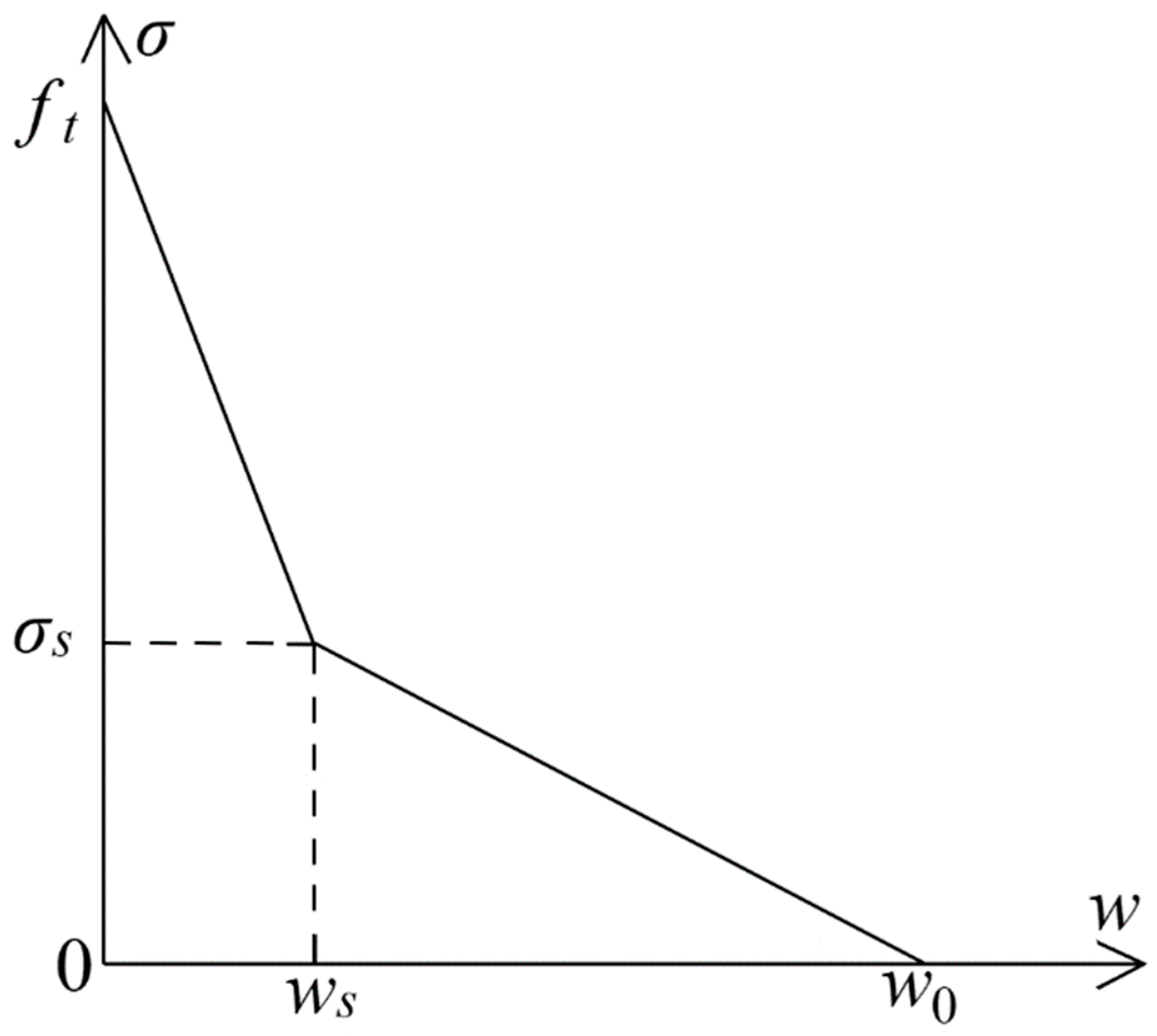
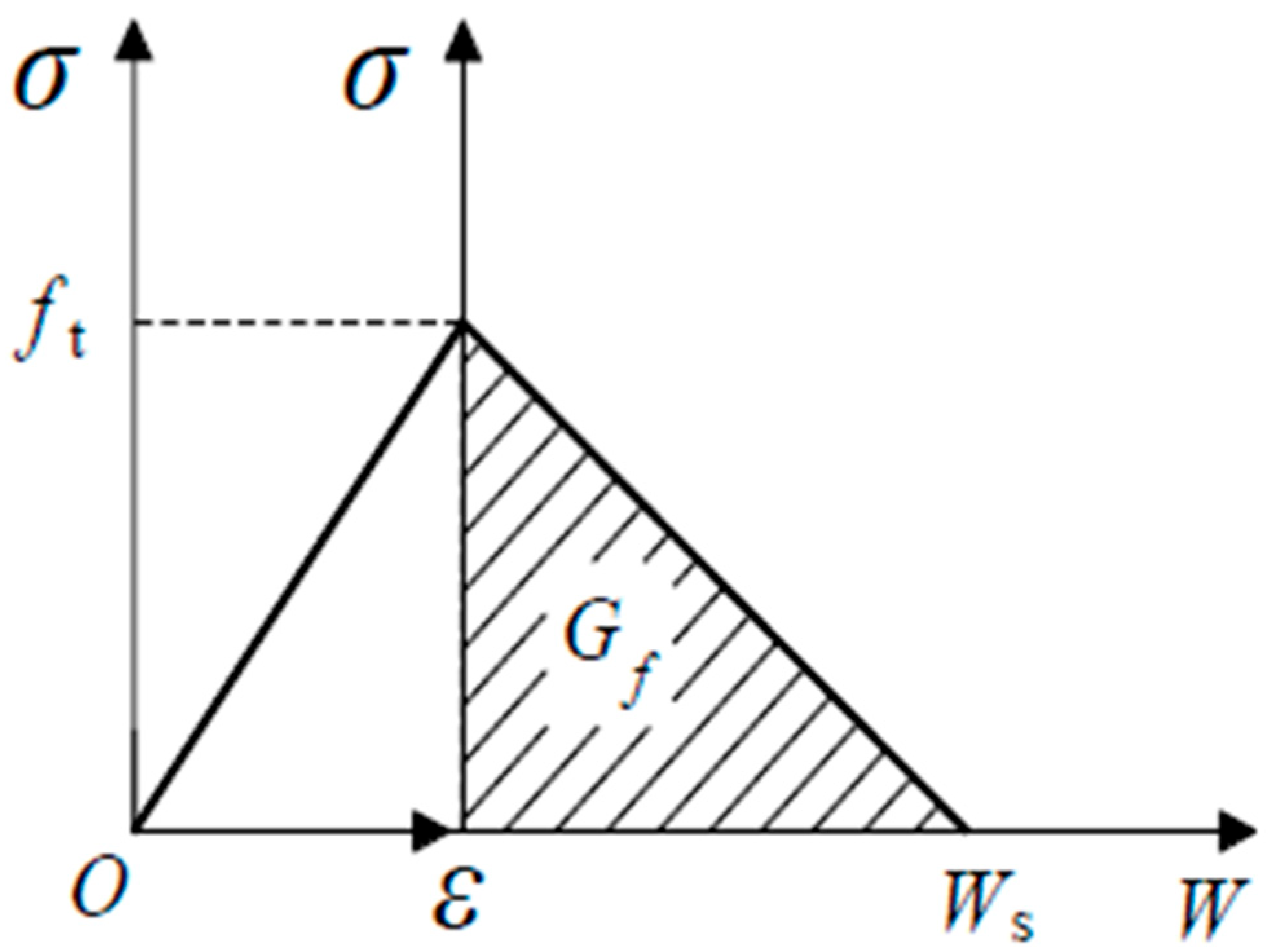
3.1. Fracture Energy
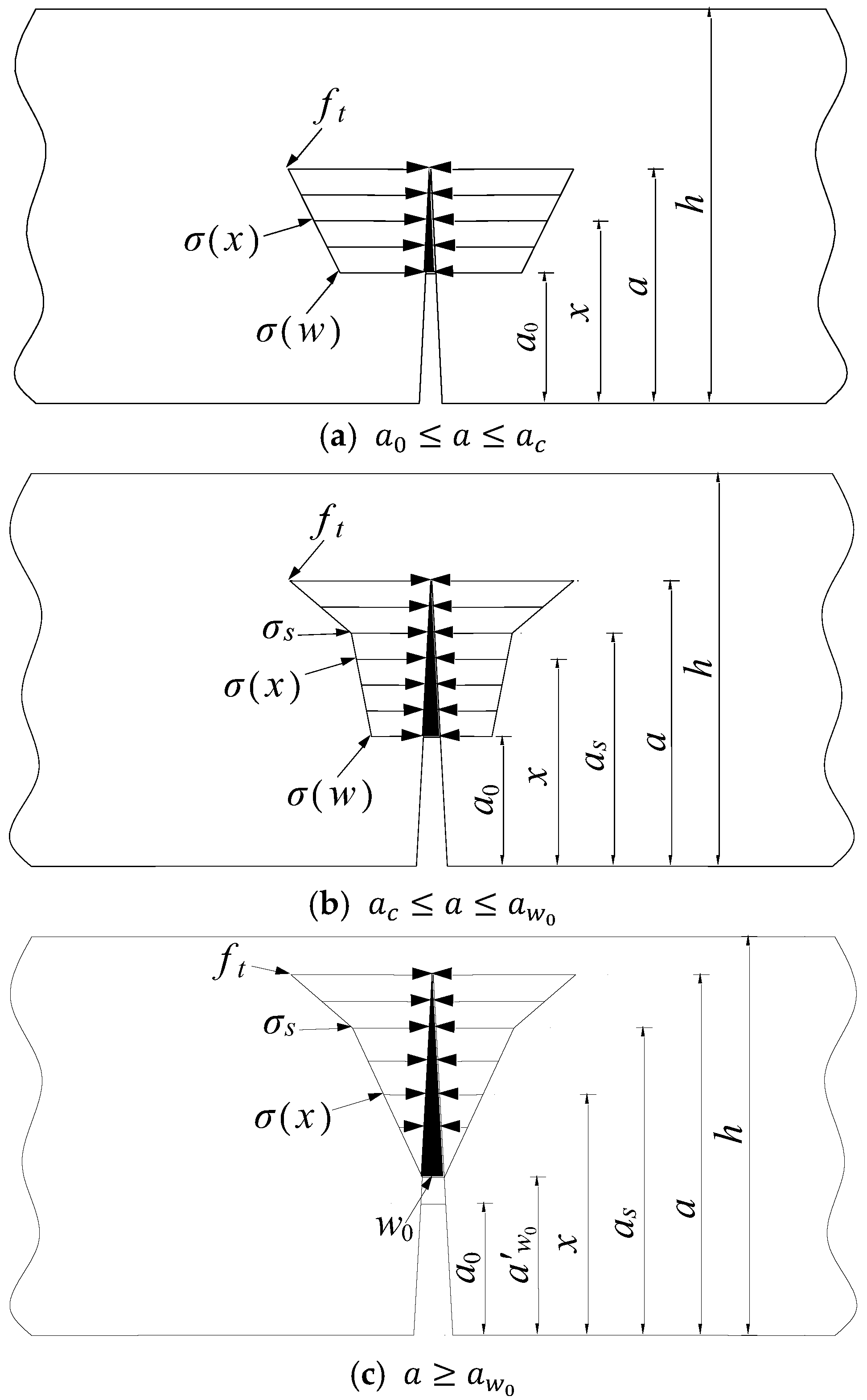
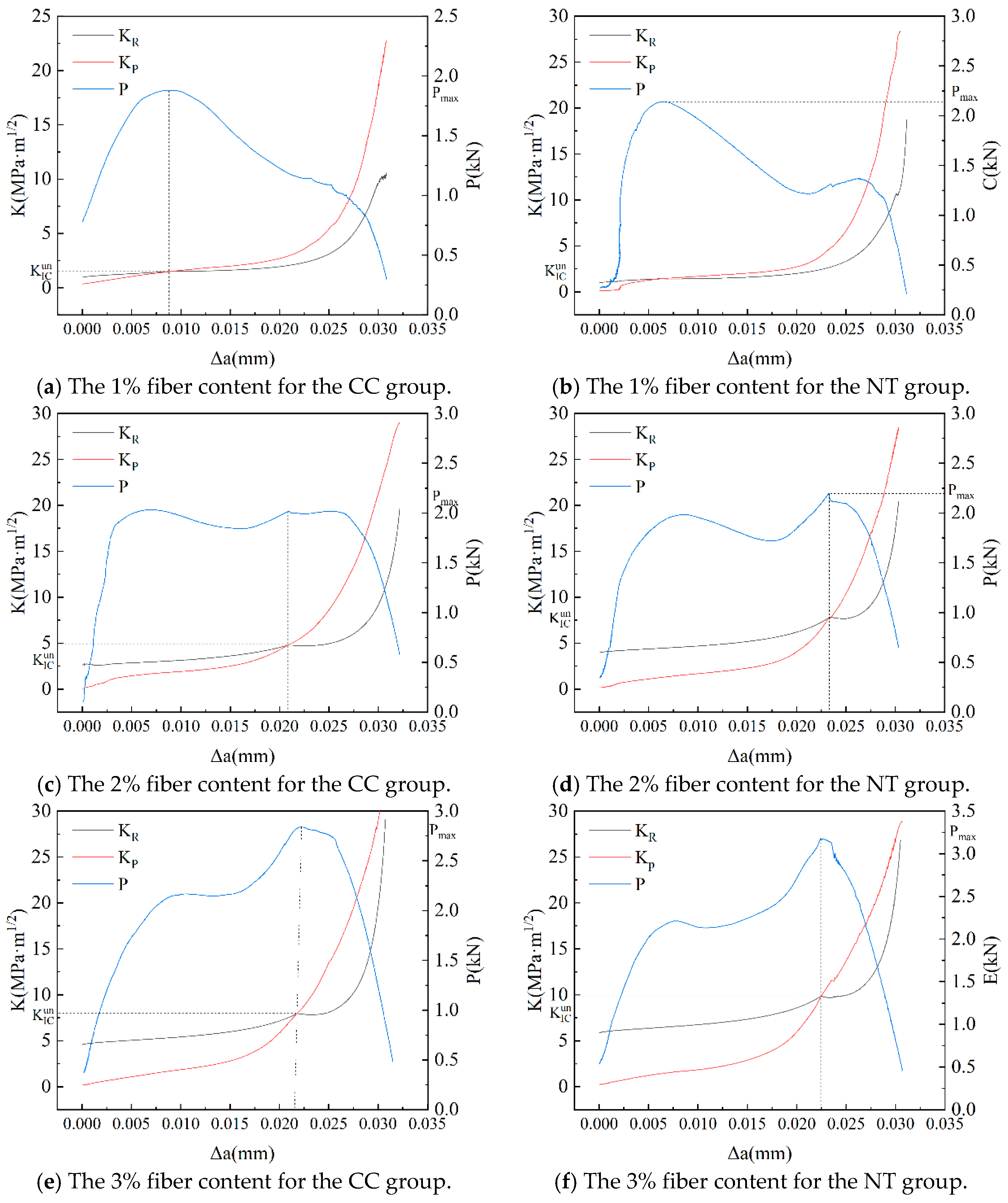
3.2. Fracture Toughness
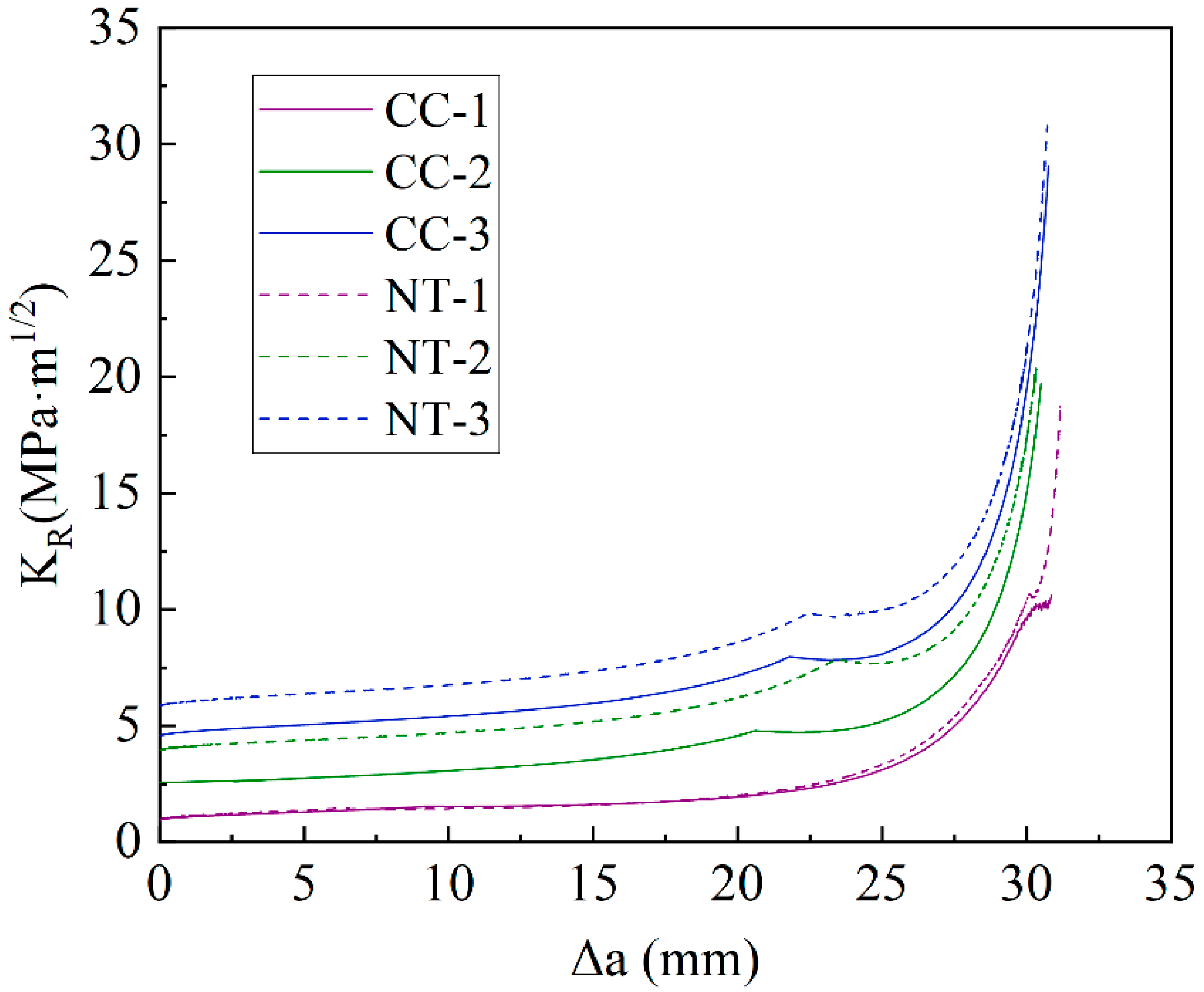
3.3. Crack Propagation Resistance
4. Numerical Simulation of MPC Fracture Testing Based on XFEM
4.1. Extended Finite Element Method
4.2. Constitutive Model Parameters Test
4.2.1. MPC Mortar
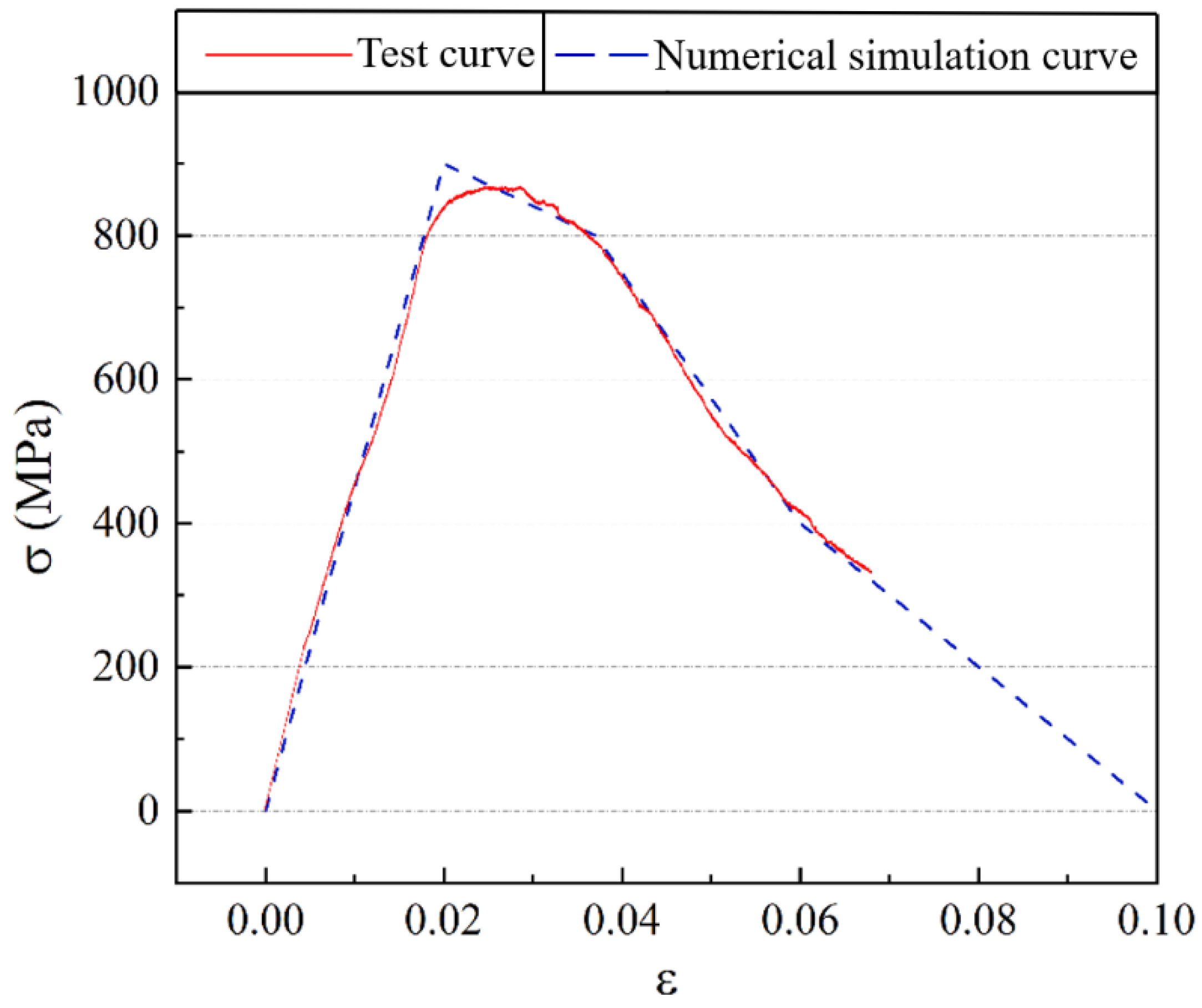
4.2.2. Basalt Fiber Bar Constitutive Relationship
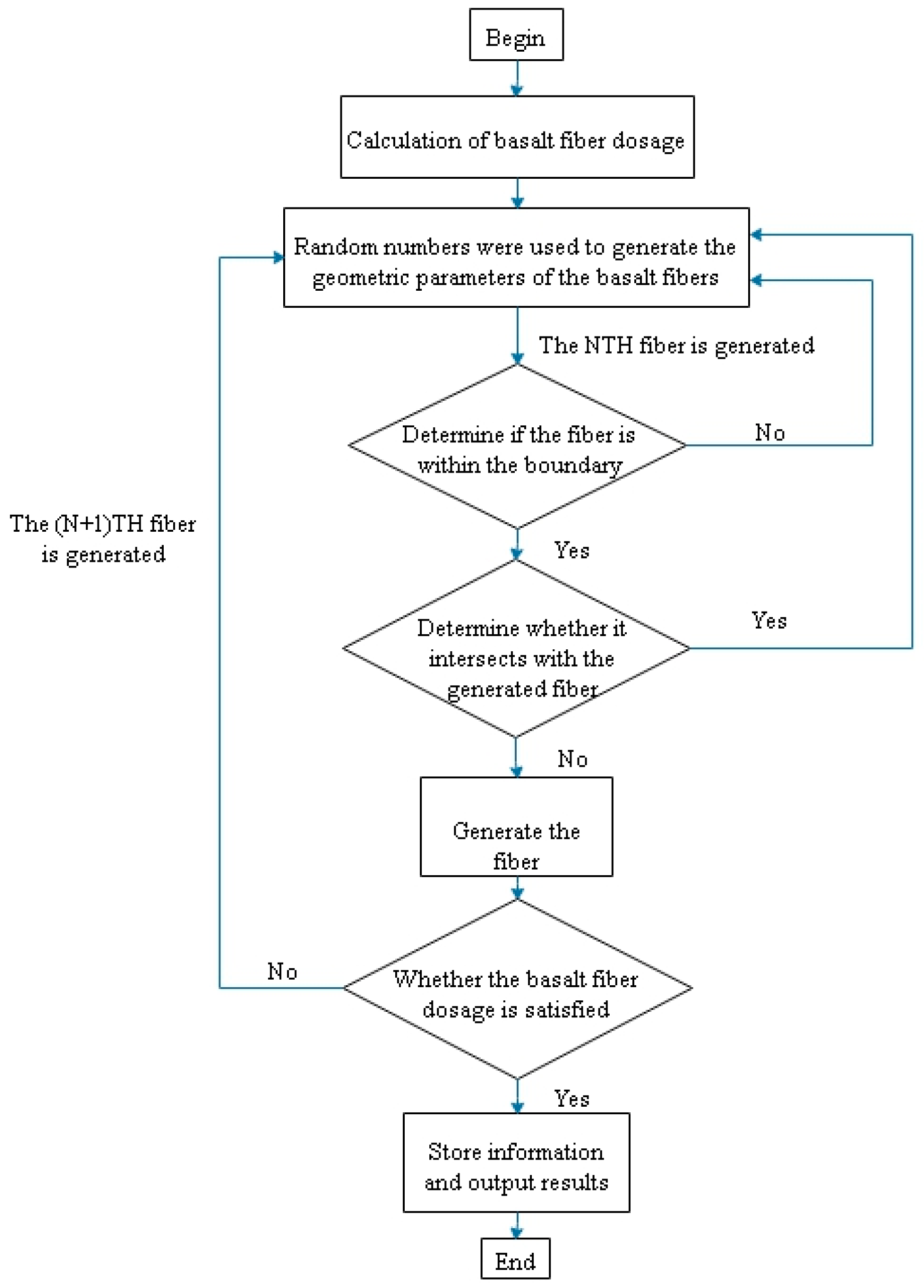
4.3. Random Fiber Generation
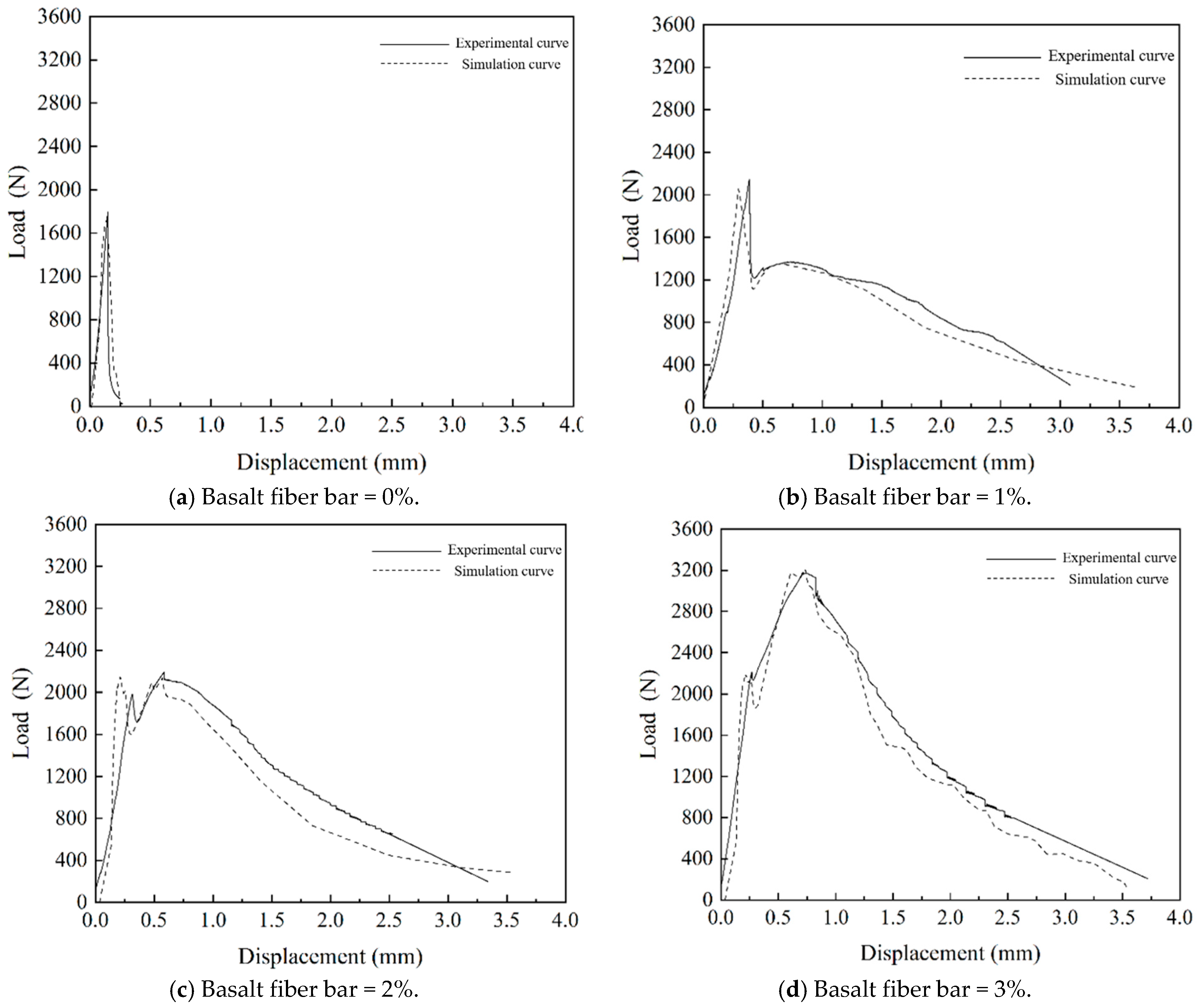
4.4. Microscale Fracture Simulation Testing and Analysis of NT and Fiber Reinforced MPC
5. Analysis of Toughening Mechanisms in NT and Basalt Fiber Bar Reinforced MPC Based on the Composite Material Theory
6. Results and Discussion
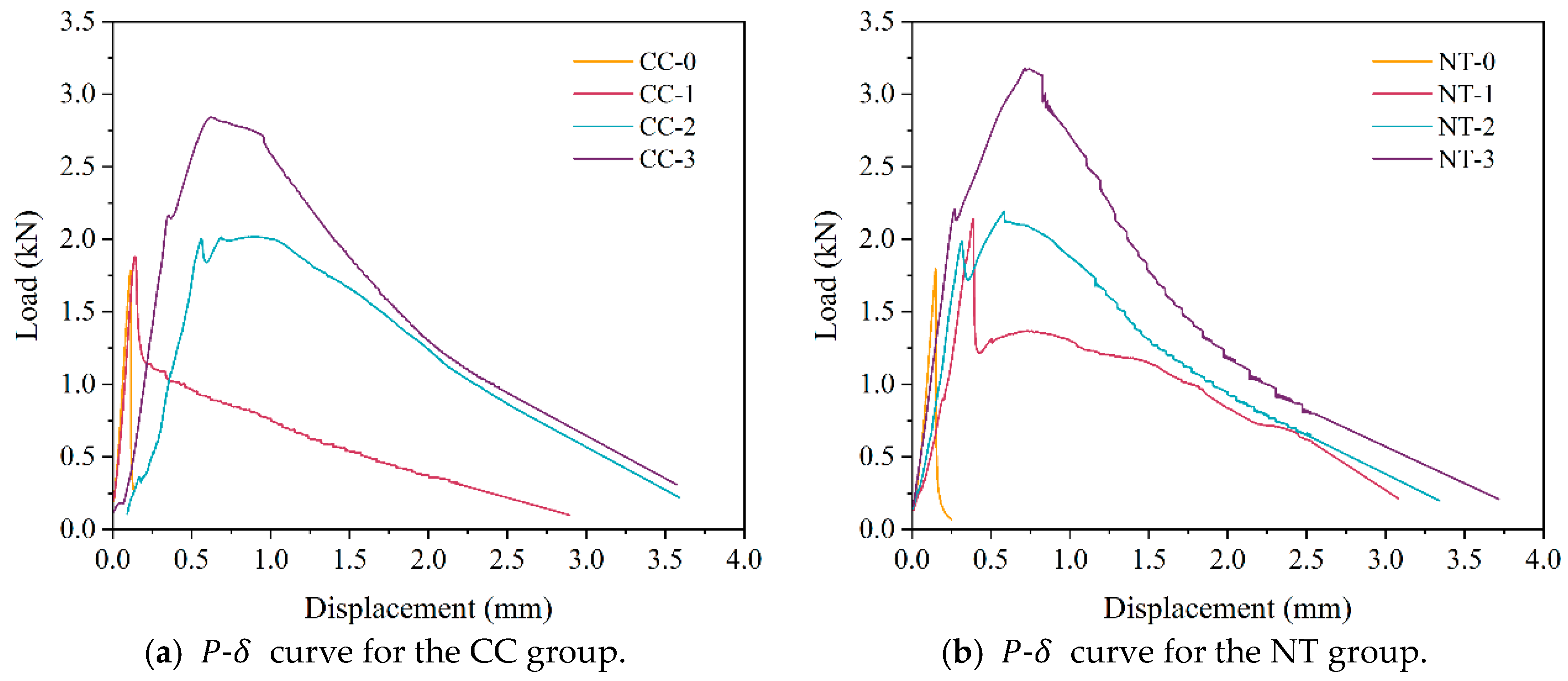
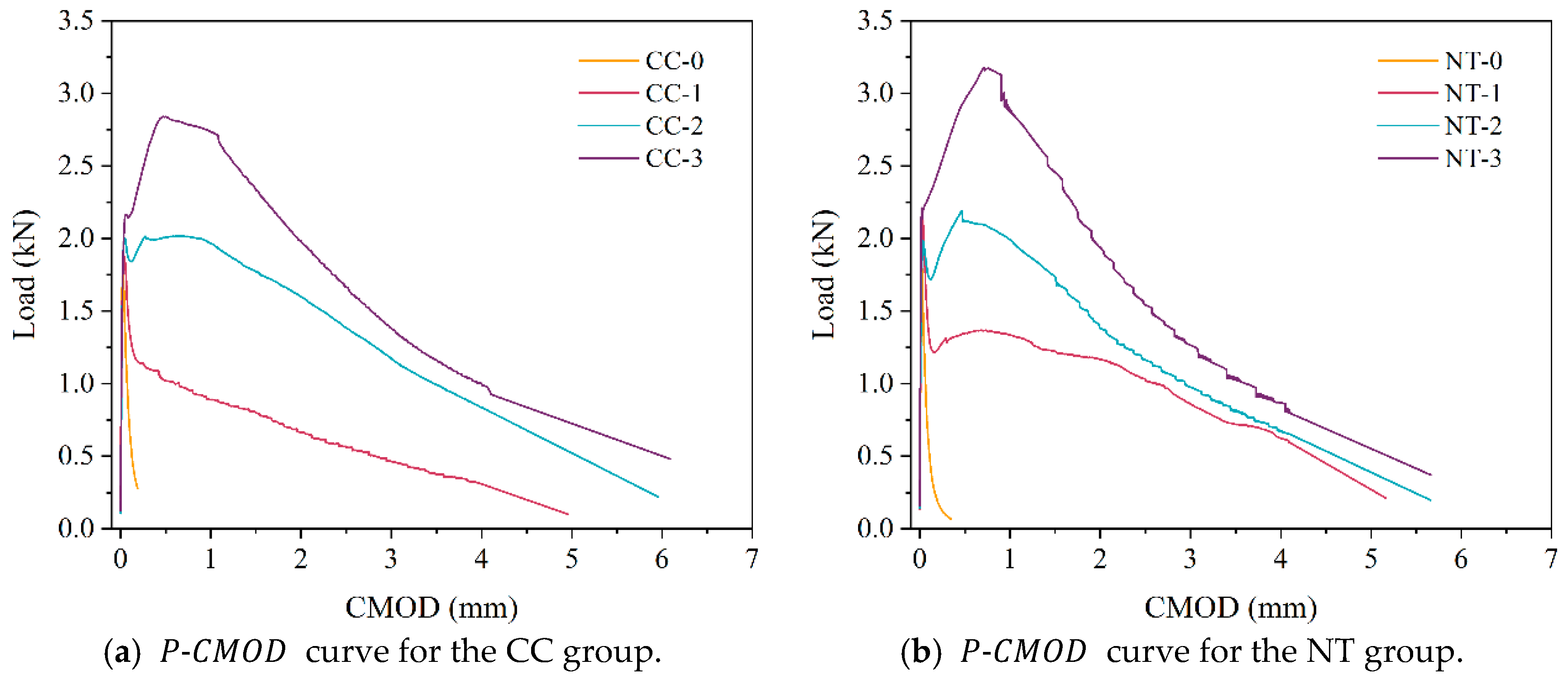
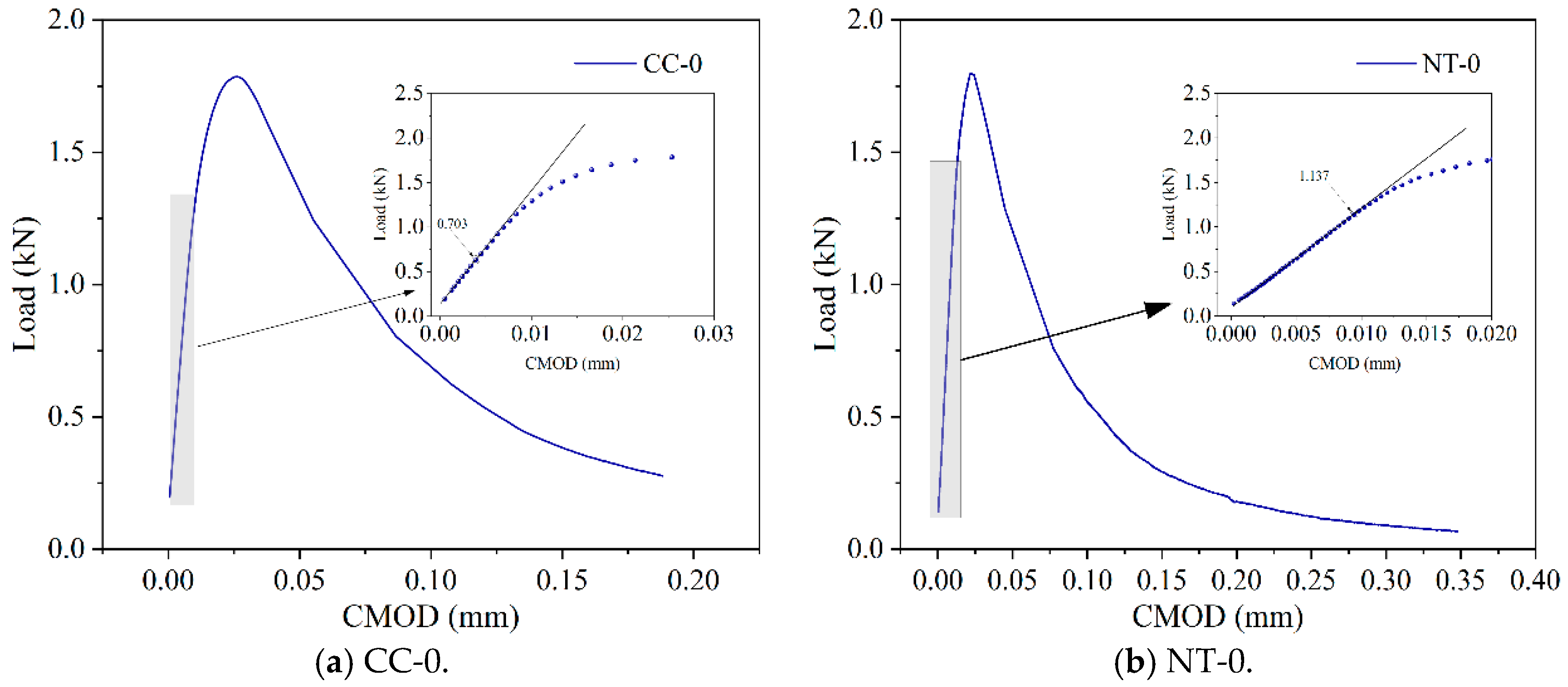
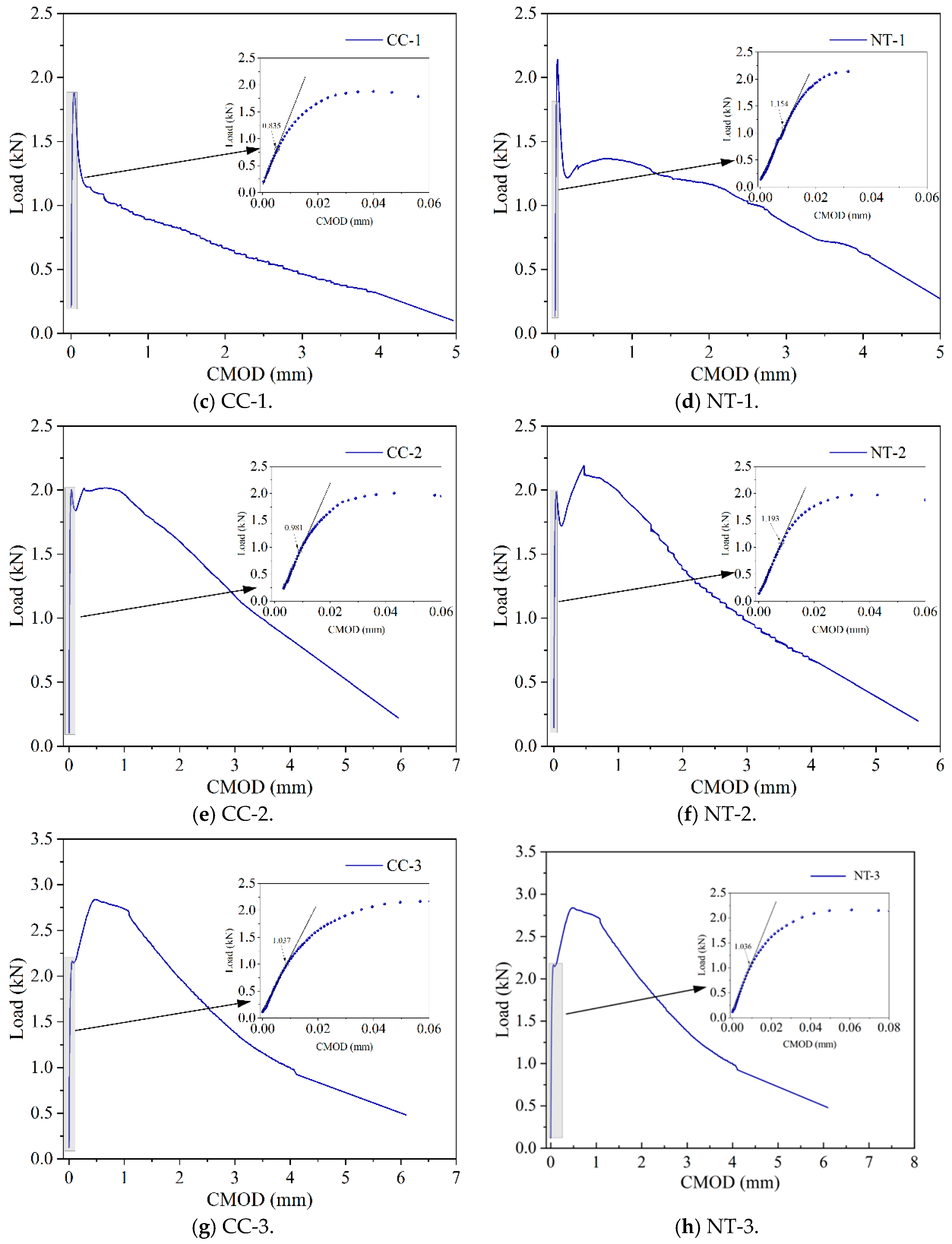
6.1. The Three-Point Bending Fracture Test
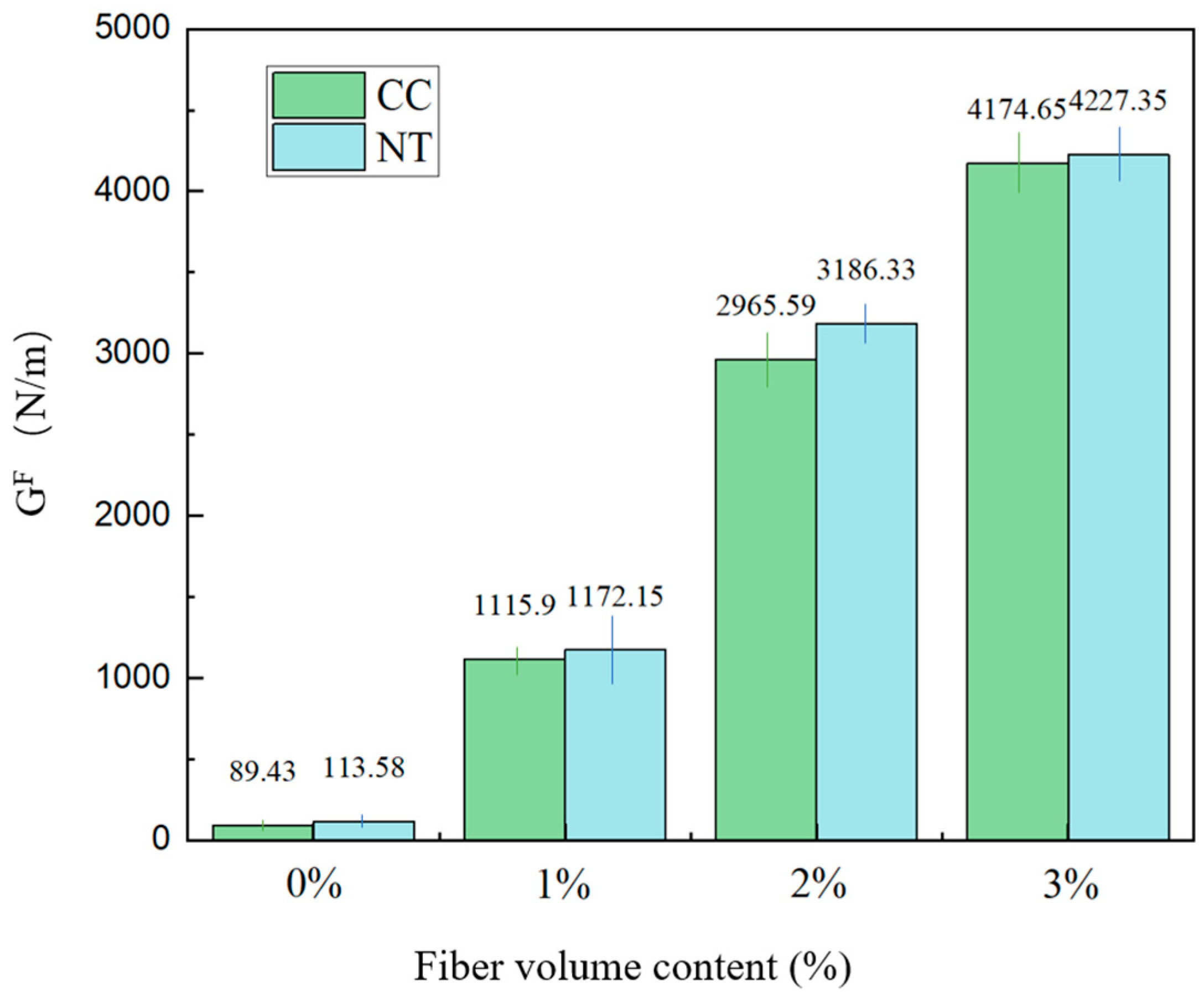
6.2. Fracture Energy
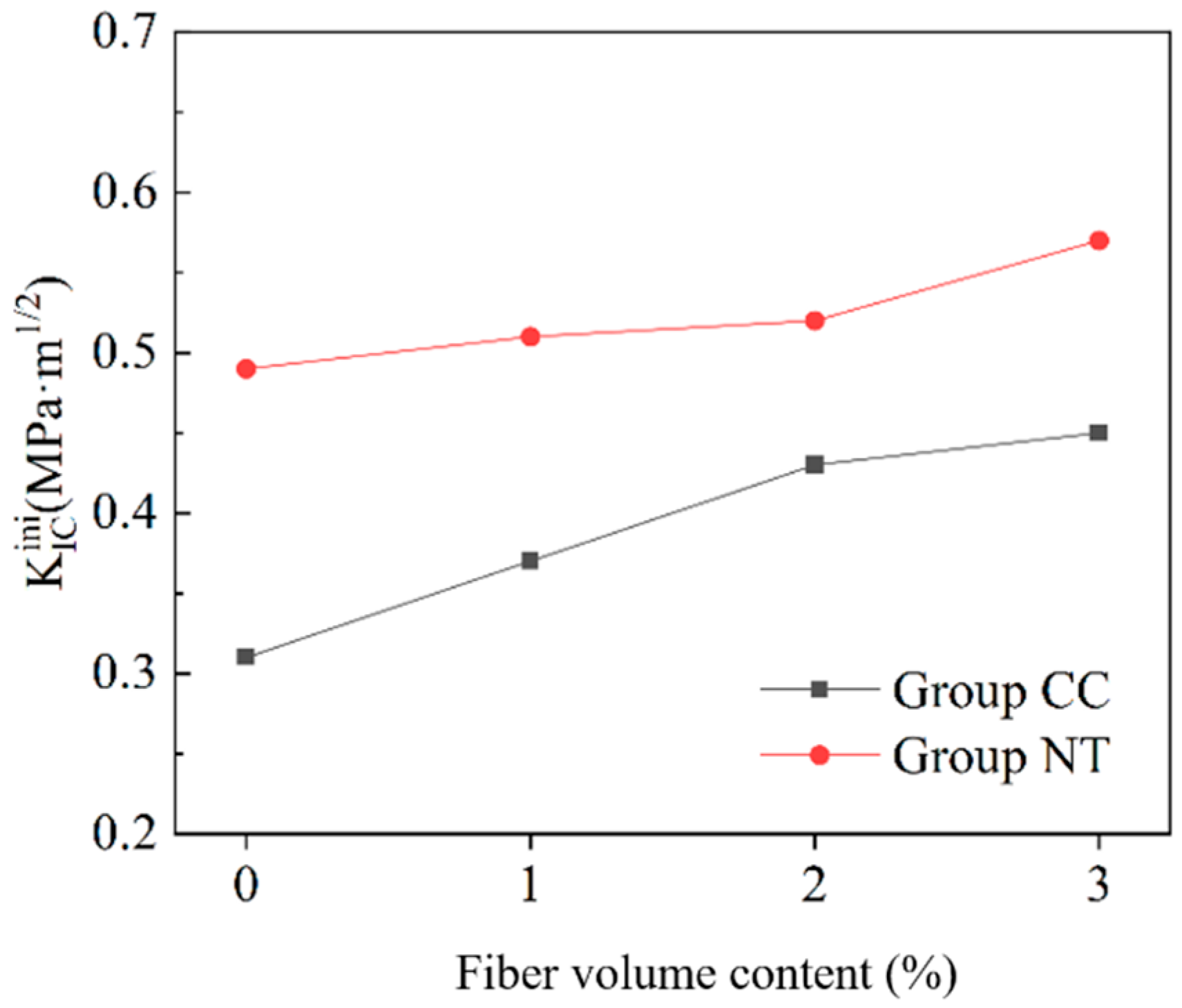
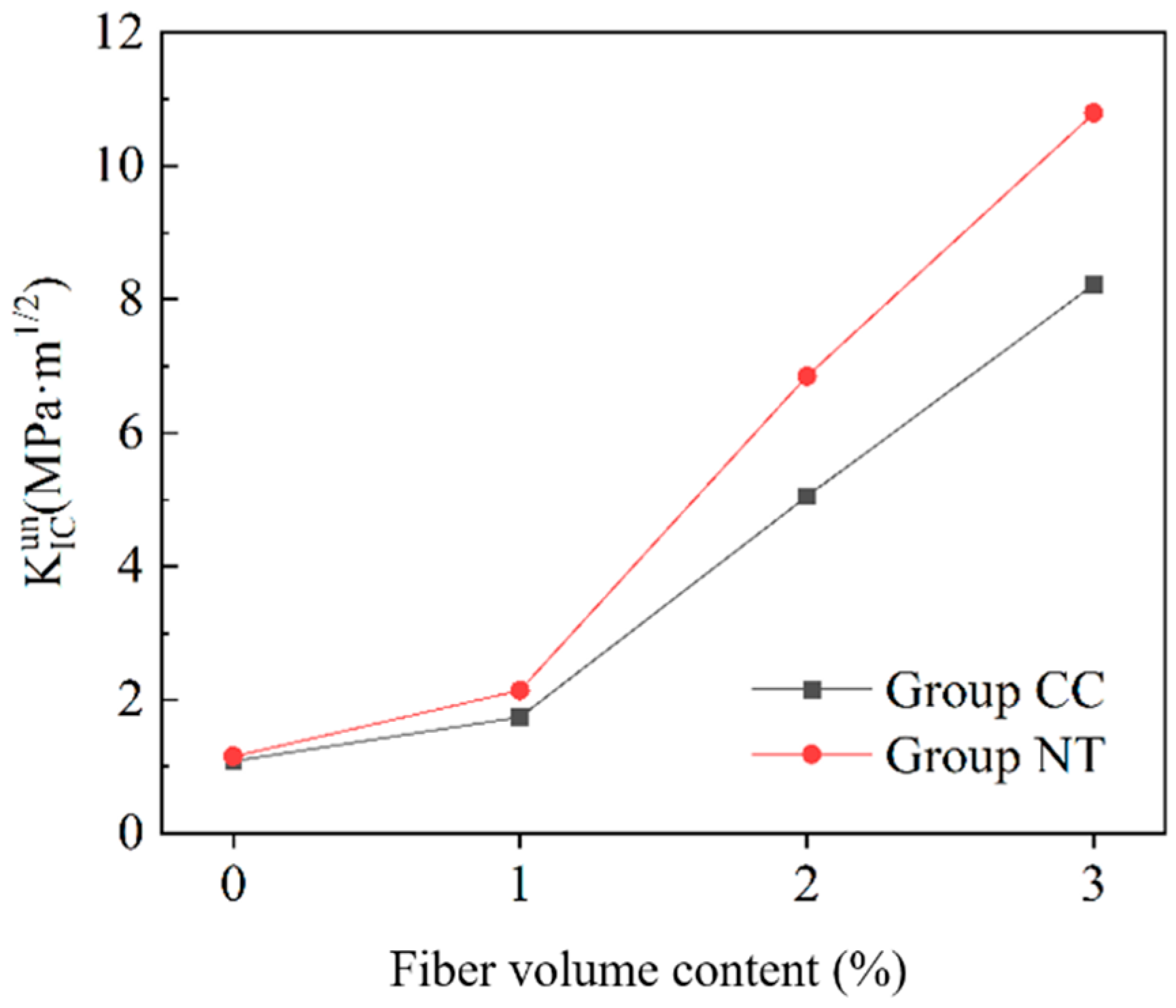
6.3. Fracture Toughness
6.4. Crack Propagation Resistance
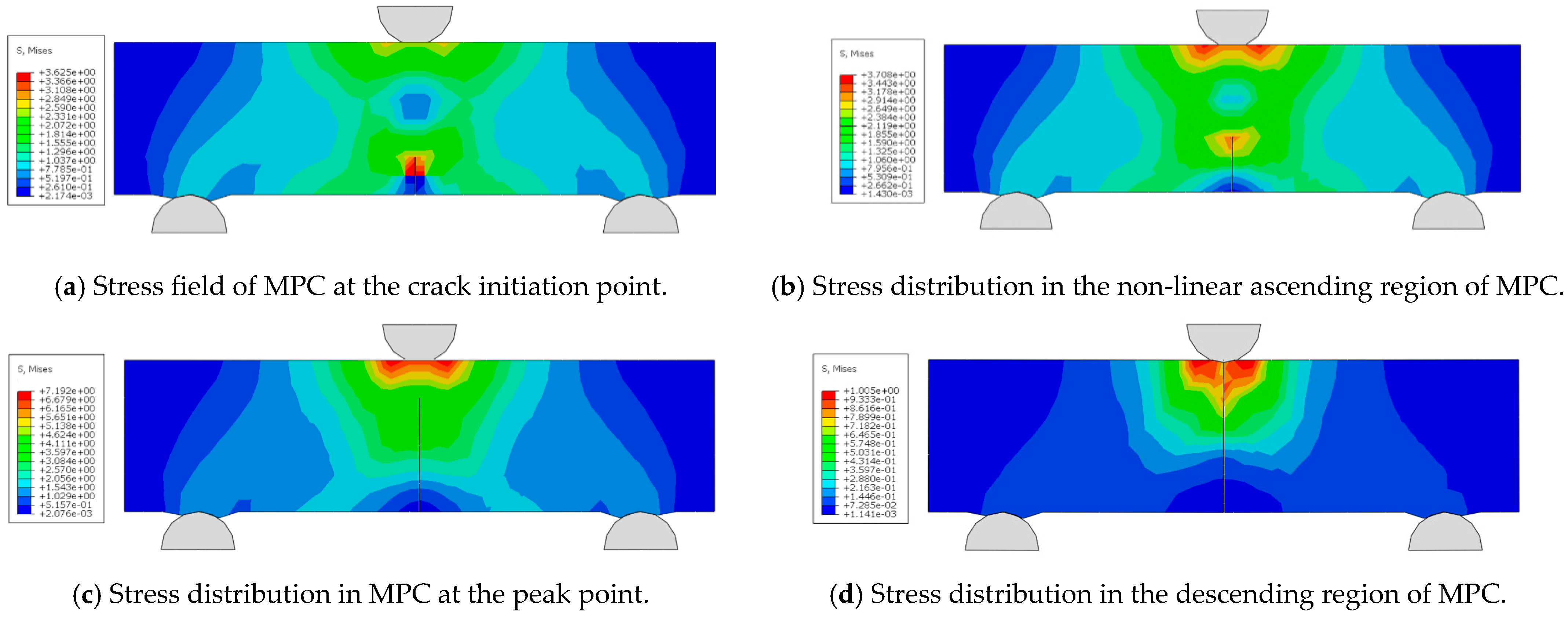
6.5. Microscale Fracture Simulation Testing and Analysis of NT and Fiber Reinforced MPC
6.6. Analysis of Toughening Mechanisms in NT and Basalt Fiber Bar Reinforced MPC Based on the Composite Material Theory
7. Conclusions, Challenges, and Future Prospects
- (1)
- Basalt fiber bars can significantly enhance the ultimate bending capacity of MPC notched beams. The improvement increases with the fiber volume fraction, and noticeable bending hardening occurs when the fiber content exceeds 2%.
- (2)
- NT also enhances the ultimate load-carrying capacity of MPC notched beams. For the same fiber volume fraction, the peak load can be increased by up to 11.7% with the addition of NT.
- (3)
- The crack propagation resistance KR of MPC shows a positive correlation with the crack propagation length and exhibits a trend of slow initial growth followed by accelerated growth. Furthermore, for the same fiber volume fraction, the NT group shows higher crack propagation resistance compared to the CC group, indicating that NT has a certain effect on improving the crack propagation resistance of MPC.
- (4)
- The formula for calculating the increment in fracture energy of MPC cementitious materials due to basalt fibers, established using composite material theory, aligns closely with experimental data, with an error within 10%.
- (5)
- The NT and basalt fiber bar reinforced MPC undergoes repeated cycles of stress concentration, cracking, and release during the fracture process until failure occurs. In contrast, this behavior is absent in the MPC without basalt fiber bars.
- (6)
- The content and diameter of basalt fiber bars are critical parameters affecting the toughness of NT and basalt fiber reinforced MPC.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Extended Finite Element Method
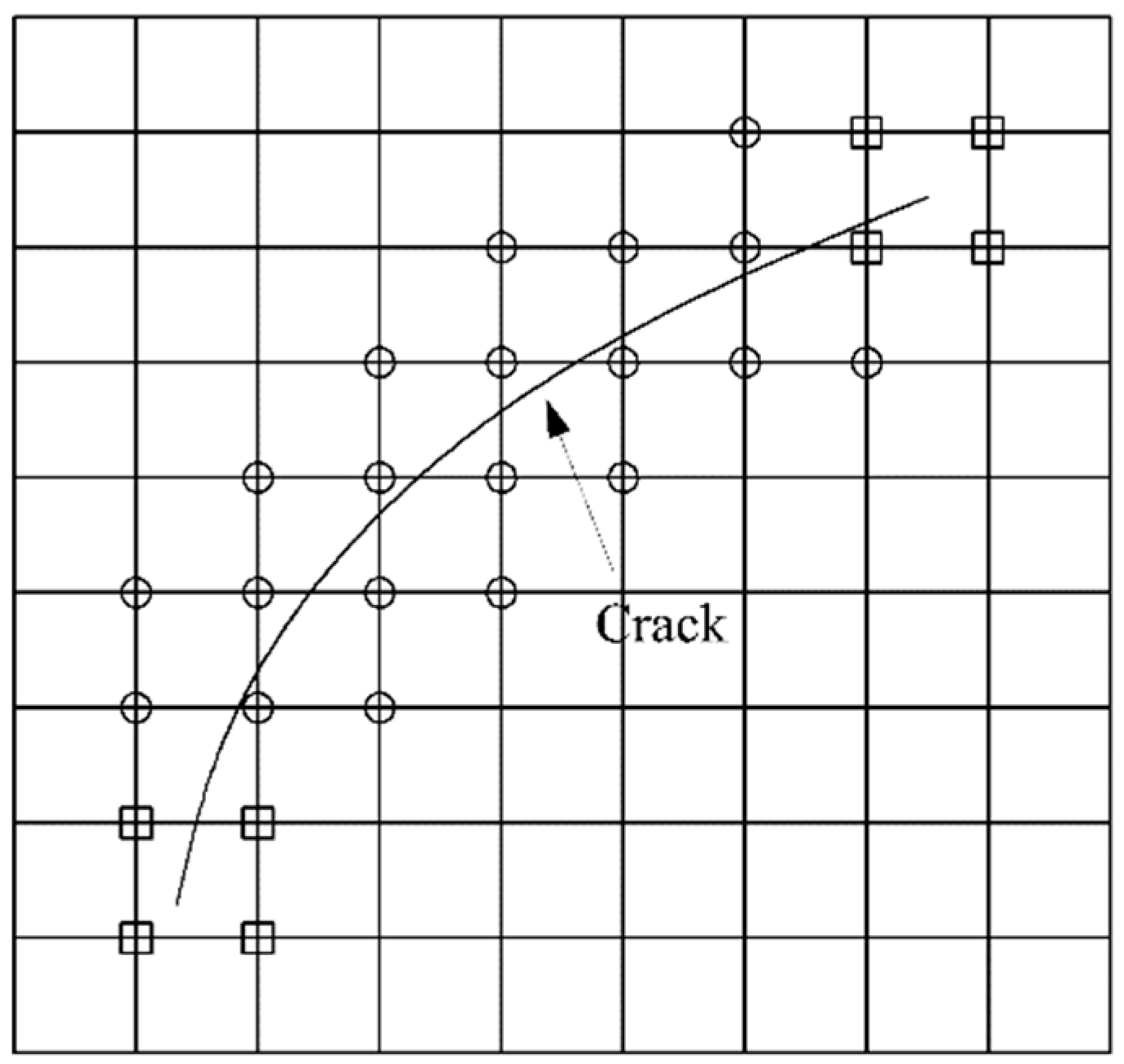
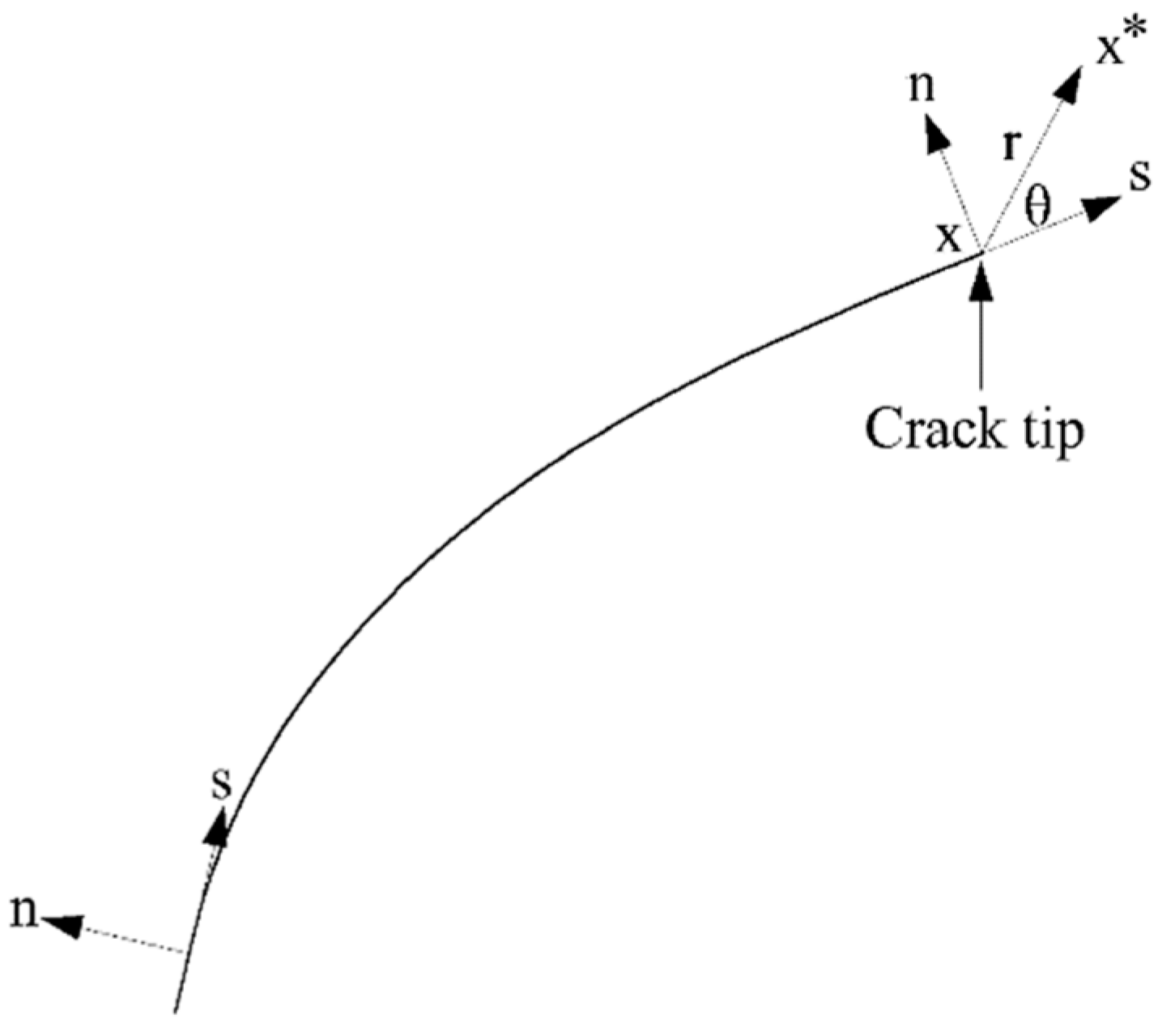
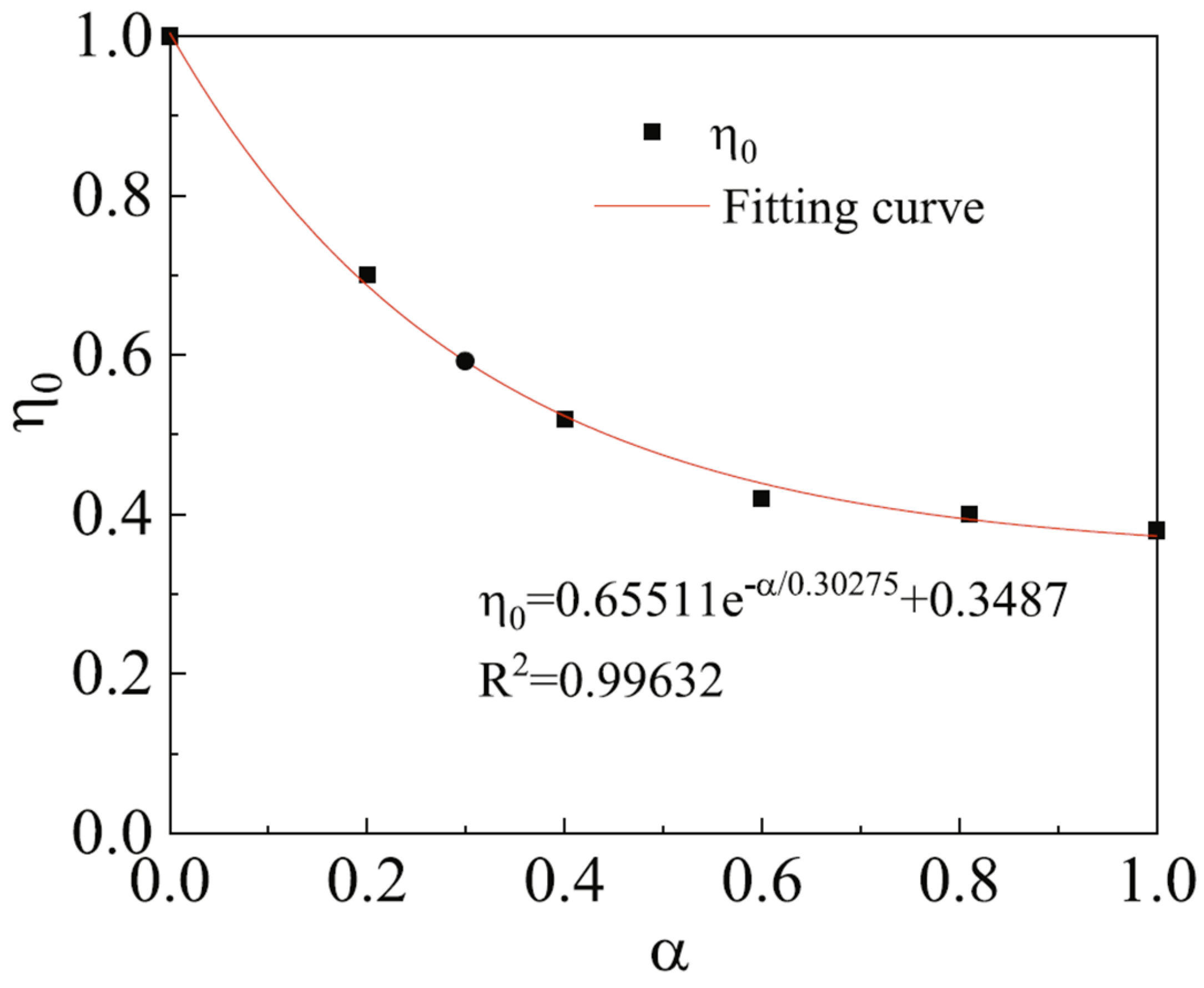
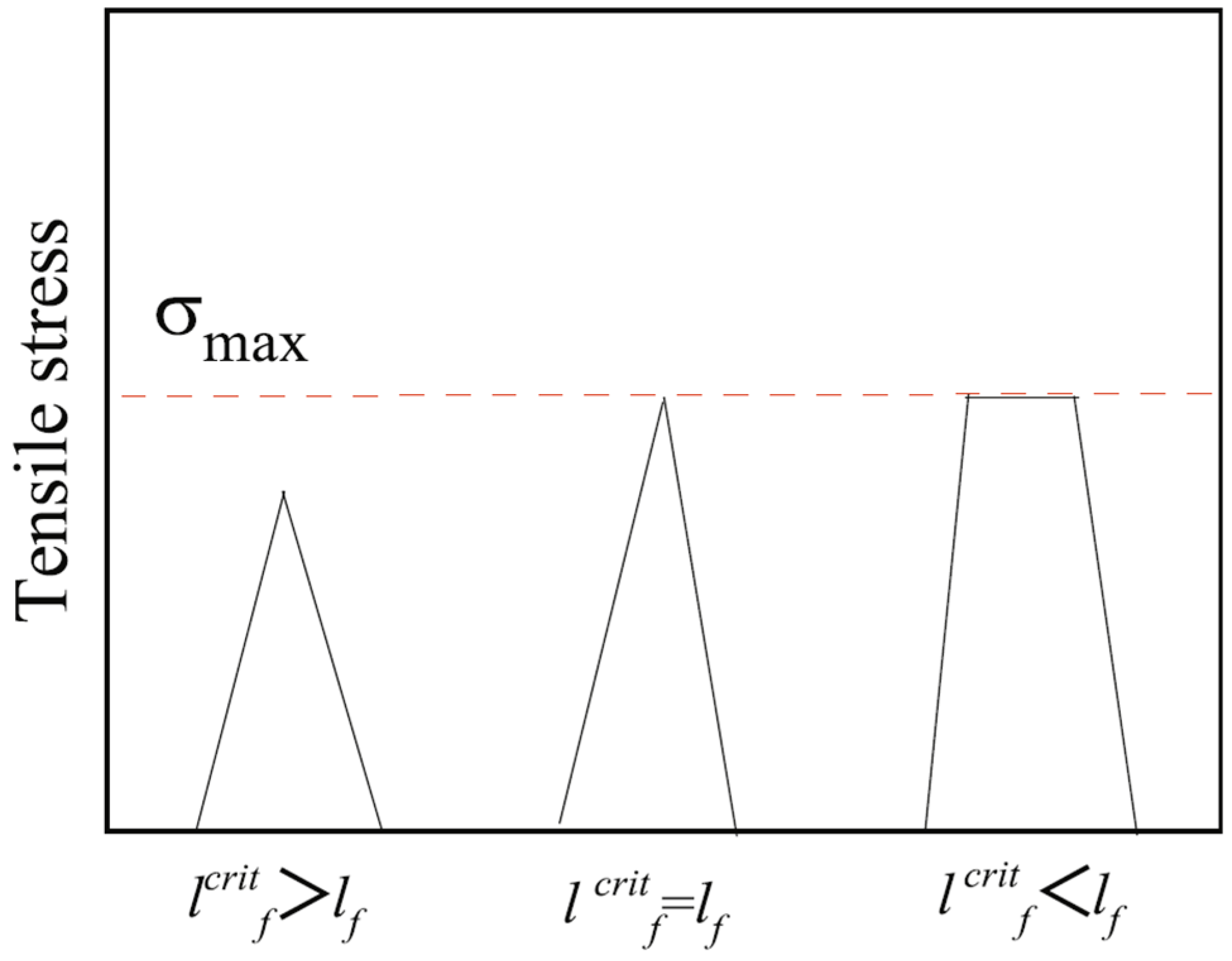
Appendix A.2. The Application of Composite Material Theory and the Establishment of Specific Parameters
References
- Hu, N.; Dai, G.-L.; Yan, B.; Liu, K. Recent development of design and construction of medium and long span high-speed railway bridges in China. Eng. Struct. 2014, 74, 233–241. [Google Scholar] [CrossRef]
- Qin, S.; Gao, Z. Developments and Prospects of Long-Span High-Speed Railway Bridge Technologies in China. Engineering 2017, 3, 787–794. [Google Scholar] [CrossRef]
- He, X.H.; Wu, T.; Zou, Y.F. Recent developments of high-speed railway bridges in China. Struct. Infrastruct. Eng. 2017, 13, 1584–1595. [Google Scholar] [CrossRef]
- Stierli, R.F.; Tarver, C.C.; Gaidis, J.M. Magnesium Phosphate Concrete Compositions. US Patent 3,960,580, 1 June 1976. [Google Scholar]
- Wang, H.J. Study on Preparation and Mechanical Behavior of Ultra-High Strength Magnesium Phosphate Cement Composites; Chongqing University: Chongqing, China, 2019. [Google Scholar] [CrossRef]
- Ezeldin, A.; Balaguru, P. Toughness Behavior of Fiber-Reinforced Rapid-Set Materials: A Preliminary Study. Cem. Concr. Aggreg. 1992, 14, 3. [Google Scholar] [CrossRef]
- Jeong, S.Y.; Wagh, A.S. Cementing The Gap Between Ceramics, Cements, And Polymers. Mater. Technol. 2003, 18, 162–168. [Google Scholar] [CrossRef]
- Qin, J.; Qian, J.; Li, Z.; You, C.; Dai, X.; Yue, Y.; Fan, Y. Mechanical properties of basalt fiber reinforced magnesium phosphate cement composites. Constr. Build. Mater. 2018, 188, 946–955. [Google Scholar] [CrossRef]
- Sim, J.; Park, C.; Moon, D.Y. Characteristics of basalt fiber as a strengthening material for concrete structures. Compos. Part B Eng. 2005, 36, 504–512. [Google Scholar] [CrossRef]
- Ma, Q.; Zhu, Y. Experimental research on the microstructure and compressive and tensile properties of nano-SiO2 concrete containing basalt fibers. Undergr. Space 2017, 2, 175–181. [Google Scholar] [CrossRef]
- Feng, H.; Shen, S.; Pang, Y.; Gao, D.; Wang, Z.; Sheikh, M.N. Mechanical properties of fiber and nano-Al2O3 reinforced magnesium phosphate cement composite. Constr. Build. Mater. 2021, 270, 121861. [Google Scholar] [CrossRef]
- Xu, X.F.; Jiang, Z.Q.; Wan, M.X.; Cui, S.A.; Liu, P.; Zeng, H.N. Experimental study on performance of reinforced concrete short columns repaired and strengthened with Basalt fiber ultra-high-performance concrete (BF-UHPC). Structures 2024, 62, 106170. [Google Scholar] [CrossRef]
- Xu, X.F.; Cui, S.A.; Xu, L.L.; Zeng, G.; Wang, X.W. Effect of different fiber sizing on basalt fiber-reinforced cement-based materials at low temperature: From macro mechanical properties to microscopic mechanism. Constr. Build. Mater. 2023, 392, 131773. [Google Scholar] [CrossRef]
- Cui, S.A.; Xu, X.F.; Yan, X.J.; Chen, Z.; Hu, C.Y.; Liu, Z.L. Experimental study on the interfacial bond between short cut basalt fiber bundles and cement matrix. Constr. Build. Mater. 2020, 256, 119353. [Google Scholar] [CrossRef]
- Cui, S.A.; Xu, X.F.; Chen, Z.; Zeng, G.; Ouyang, Q.X.; Li, G.H. Effect of different sizing agent-treated basalt fibers on bending and cracking performance of reinforced BFRC beams. Constr. Build. Mater. 2023, 365, 130037. [Google Scholar] [CrossRef]
- Liu, P.; Guo, C.; Cui, S.; Xia, W.; Wang, X.; Chen, X. Experimental study on crack propagation process of rock-concrete interface in hot-dry curing environment at different temperatures. Struct. Concr. 2023, 24, 5506–5521. [Google Scholar] [CrossRef]
- ASTM C1609/C1609M-12; Standard Test Method for Flexural Performance of Fiber-Reinforced Concrete (Using Beam With Third-Point Loading). ASTM International: West Conshohocken, PA, USA, 2019.
- Dong, S.; Zhou, D.; Ashour, A.; Han, B.; Ou, J. Flexural toughness and calculation model of super-fine stainless wire reinforced reactive powder concrete. Cem. Concr. Compos. 2019, 104, 103367. [Google Scholar] [CrossRef]
- Yin, X.; Li, Q.; Wang, Q.; Reinhardt, H.-W.; Xu, S. The double-K fracture model: A state-of-the-art review. Eng. Fract. Mech. 2023, 277, 108988. [Google Scholar] [CrossRef]
- Xu, S.; Li, Q.; Wu, Y.; Dong, L.; Lyu, Y.; Reinhardt, H.W.; Leung, C.K.Y.; Ruiz, G.; Kumar, S.; Hu, S. The theoretical basis of testing methods to determine double-K criterion for crack propagation in concrete: Technical report of the RILEM TC265-TDK. Mater. Struct. 2021, 54, 229. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, S. Correlation between tension softening relation and crack extension resistance in concrete. Front. Archit. Civ. Eng. China 2009, 3, 323–329. [Google Scholar] [CrossRef]
- Xu, S.; Guo, K.; Li, Q.; Yin, X.; Huang, B. Shear fracture performance of the interface between ultra-high toughness cementitious composites and reactive powder concrete. Compos. Struct. 2021, 275, 114403. [Google Scholar] [CrossRef]
- Xu, S.; Wang, Q.; Lyu, Y.; Li, Q.; Reinhardt, H.W. Prediction of fracture parameters of concrete using an artificial neural network approach. Eng. Fract. Mech. 2021, 258, 108090. [Google Scholar] [CrossRef]
- Xu, S.; Zhu, Y. Experimental determination of fracture parameters for crack propagation in hardening cement paste and mortar. Int. J. Fract. 2009, 157, 33–43. [Google Scholar] [CrossRef]
- Xu, S.; Gao, S. Fracture and tensile properties of polyvinyl alcohol fiber reinforced cementitious composites. J. Wuhan Univ. Technol. Mater. Sci. Ed. 2008, 23, 7–11. [Google Scholar] [CrossRef]
- Xu, S.-L.; Xu, H.-L.; Huang, B.-T.; Li, Q.-H.; Yu, K.-Q.; Yu, J.-T. Development of ultrahigh-strength ultrahigh-toughness cementitious composites (UHS-UHTCC) using polyethylene and steel fibers. Compos. Commun. 2022, 29, 100992. [Google Scholar] [CrossRef]
- Krstulović, R.; Dabić, P. A conceptual model of the cement hydration process. Cem. Concr. Res. 2000, 30, 693–698. [Google Scholar] [CrossRef]
- Bezjak, A. Nuclei growth model in kinetics analysis of cement hydration. Cem. Concr. Res. 1986, 16, 605–609. [Google Scholar] [CrossRef]
- Zhao, S.X.; Yan, H.; Wang, H.T.; Li, Y.T.; Dai, F.L. Effect of Fly Ash Content on Hydration kinetics of magnesium potassium phosphate cement. Chin. J. Mater. Res. 2017, 31, 839–846. [Google Scholar]
- Zhou, H.; Zhu, H.; Gou, H.; Yang, Z. Comparison of the Hydration Characteristics of Ultra-High-Performance and Normal Cementitious Materials. Materials 2020, 13, 2594. [Google Scholar] [CrossRef] [PubMed]
- Tan, L.X.; Luo, C.Y.; Gong, Z.C.; Huang, X.L.; Ding, Q.J. Effect of superplasticizer on early hydration property of different tricalcium silicate polymorphs. Wuhan Univer. Technol. 2012, 34, 10–16. [Google Scholar] [CrossRef]
- Xu, S.L.; Reinhardt, H.W. Crack extension resistance and fracture properties of quasi-brittle softening materials like concrete based on the complete process of fracture. Int. J. Fract. 1998, 92, 71–99. [Google Scholar] [CrossRef]
- Reinhardt, H.W.; Xu, S. Crack extension resistance based on the cohesive force in concrete. Eng. Fract. Mech. 1999, 64, 563–587. [Google Scholar] [CrossRef]
- Li, H.; Li, J.; Yuan, H. A review of the extended finite element method on macrocrack and microcrack growth simulations. Theor. Appl. Fract. Mech. 2018, 97, 236–249. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Moës, N.; Dolbow, J.; Belytschko, T. A finite element method for crack growth without remeshing. Int. J. Numer. Methods Eng. 1999, 46, 131–150. [Google Scholar] [CrossRef]
- Xu, S.L.; Reinhardt, H.W. Determination of double-K criterion for crack propagation in quasi-brittle fracture, Part II: Analytical evaluating and practical measuring methods for three-point bending notched beams. Int. J. Fract. 1999, 98, 151–177. [Google Scholar] [CrossRef]
- Huang, Z.G. Field Monitoring and Numerical Analysis on the Temperature of Long-Span Suspension Bridge; South China University of Technology: Guangzhou, China, 2016. [Google Scholar]
- Zi, G.; Belytschko, T. New crack-tip elements for XFEM and applications to cohesive cracks. Int. J. Numer. Methods Eng. 2003, 57, 2221–2240. [Google Scholar] [CrossRef]
- Yvonnet, J.; Quang, H.L.; He, Q.C. An XFEM/level set approach to modelling surface/interface effects and to computing the size-dependent effective properties of nanocomposites. Comput. Mech. 2008, 42, 119–131. [Google Scholar] [CrossRef]
- Pathak, H.; Singh, A.P.; Singh, I.V. Fatigue crack growth simulations of 3-D problems using XFEM. Int. J. Mech. Sci. 2013, 76, 112–131. [Google Scholar] [CrossRef]
- Zuk, W. Thermal and Shrinkage Stresses in Composite Beams. ACI J. Proc. 1961, 58, 327–340. [Google Scholar] [CrossRef] [PubMed]
- Kuzmanovic, V.; Savic, L.; Mladenovic, N. Computation of Thermal-Stresses and Contraction Joint Distance of RCC Dams. J. Therm. Stress. 2013, 36, 112–134. [Google Scholar] [CrossRef]
- Singh, P.R.; Rai, D.C. Effect of Piped Water Cooling on Thermal Stress in Mass Concrete at Early Ages. J. Eng. Mech. 2018, 144, 04017183. [Google Scholar] [CrossRef]


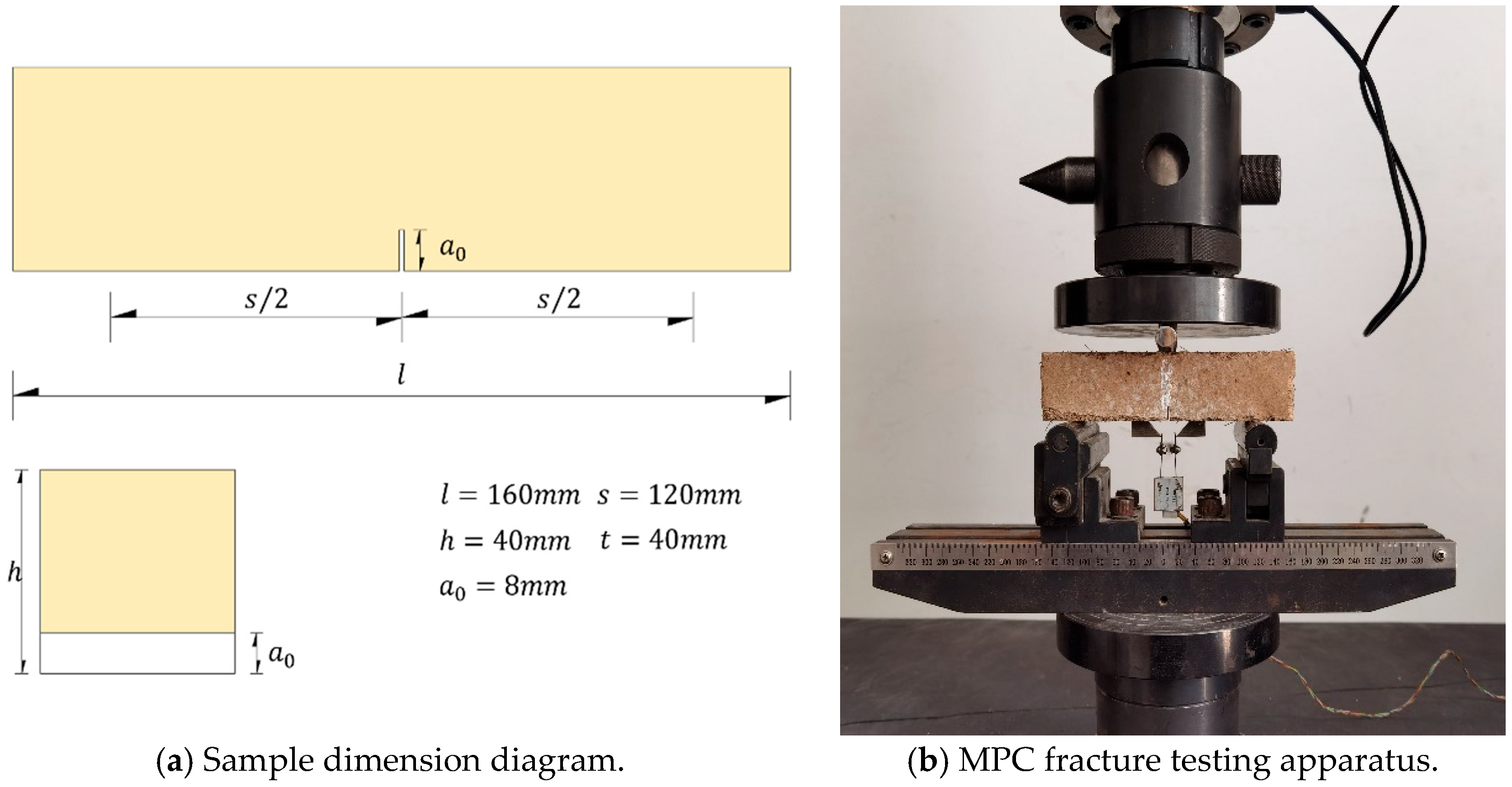

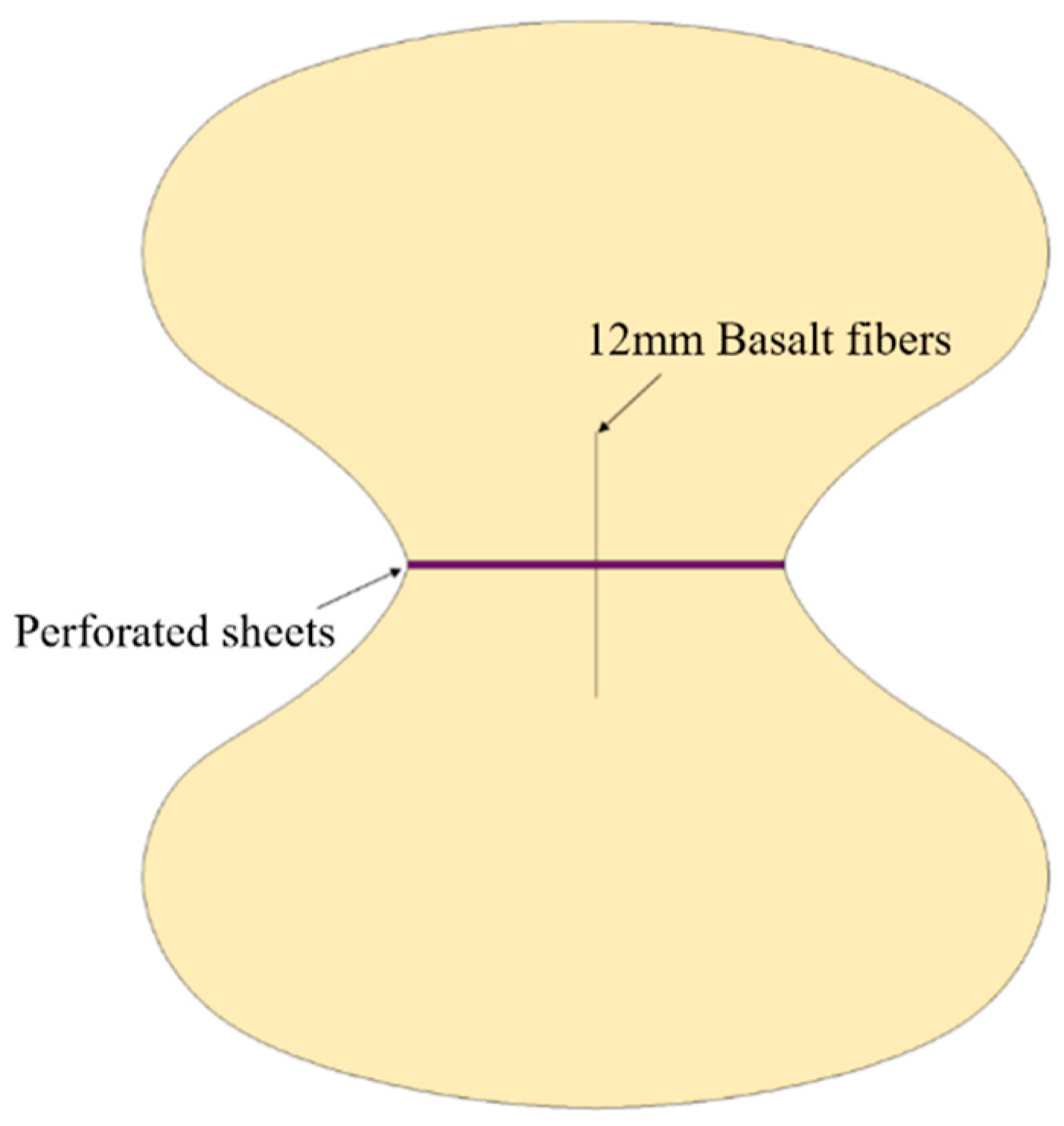

| MIX ID | Binder | Sodium Borate Decahydrate | Quartz Sand | Water | NT | Basalt Fiber Bars |
|---|---|---|---|---|---|---|
| CC-0 | 750 (MgO) + 250 (NH4H2PO4) | 52.5 | 1000 | 180 | 0 | 0 |
| CC-1 | 750 (MgO) + 250 (NH4H2PO4) | 52.5 | 1000 | 180 | 0 | 17.4 |
| CC-2 | 750 (MgO) + 250 (NH4H2PO4) | 52.5 | 1000 | 180 | 0 | 34.8 |
| CC-3 | 750 (MgO) + 250 (NH4H2PO4) | 52.5 | 1000 | 180 | 0 | 52.2 |
| NT-0 | 750 (MgO) + 250 (NH4H2PO4) | 52.5 | 1000 | 180 | 25 | 0 |
| NT-1 | 750 (MgO) + 250 (NH4H2PO4) | 52.5 | 1000 | 180 | 25 | 17.4 |
| NT-2 | 750 (MgO) + 250 (NH4H2PO4) | 52.5 | 1000 | 180 | 25 | 34.8 |
| NT-3 | 750 (MgO) + 250 (NH4H2PO4) | 52.5 | 1000 | 180 | 25 | 52.2 |
| Material | Elastic Modulus (GPa) | Poisson’s Ratio | Tensile Strength (MPa) | Fracture Toughness (N/mm) |
|---|---|---|---|---|
| Mortar | 30 | 0.2 | 3.6 | 0.114 |
| MIX ID | Primary Calculation Parameters | Error | ||||||
|---|---|---|---|---|---|---|---|---|
| NT-1 | 0.474 | 0.47 | 3.89 | 9.5 | 11.5 | 29.1 | 1081.9 | 2.0% |
| NT-2 | 0.474 | 0.39 | 4.29 | 10.46 | 15.45 | 19.41 | 3317.1 | 7.7% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.-K.; Cui, S.-A.; Li, Y.-P.; Zeng, Y.-L.; Zeng, G.; Xia, W. Mechanistic Insights into the Fracture Toughness Enhancement of Nano-TiO2 and Basalt Fiber Bar Reinforced Magnesium Phosphate Cement. Nanomaterials 2025, 15, 1183. https://doi.org/10.3390/nano15151183
Li W-K, Cui S-A, Li Y-P, Zeng Y-L, Zeng G, Xia W. Mechanistic Insights into the Fracture Toughness Enhancement of Nano-TiO2 and Basalt Fiber Bar Reinforced Magnesium Phosphate Cement. Nanomaterials. 2025; 15(15):1183. https://doi.org/10.3390/nano15151183
Chicago/Turabian StyleLi, Wei-Kang, Sheng-Ai Cui, Yu-Peng Li, Ya-Lei Zeng, Guang Zeng, and Wei Xia. 2025. "Mechanistic Insights into the Fracture Toughness Enhancement of Nano-TiO2 and Basalt Fiber Bar Reinforced Magnesium Phosphate Cement" Nanomaterials 15, no. 15: 1183. https://doi.org/10.3390/nano15151183
APA StyleLi, W.-K., Cui, S.-A., Li, Y.-P., Zeng, Y.-L., Zeng, G., & Xia, W. (2025). Mechanistic Insights into the Fracture Toughness Enhancement of Nano-TiO2 and Basalt Fiber Bar Reinforced Magnesium Phosphate Cement. Nanomaterials, 15(15), 1183. https://doi.org/10.3390/nano15151183







