Investigation of Thermoelectric Properties in Altermagnet RuO2
Abstract
1. Introduction
2. Theoretical Methods
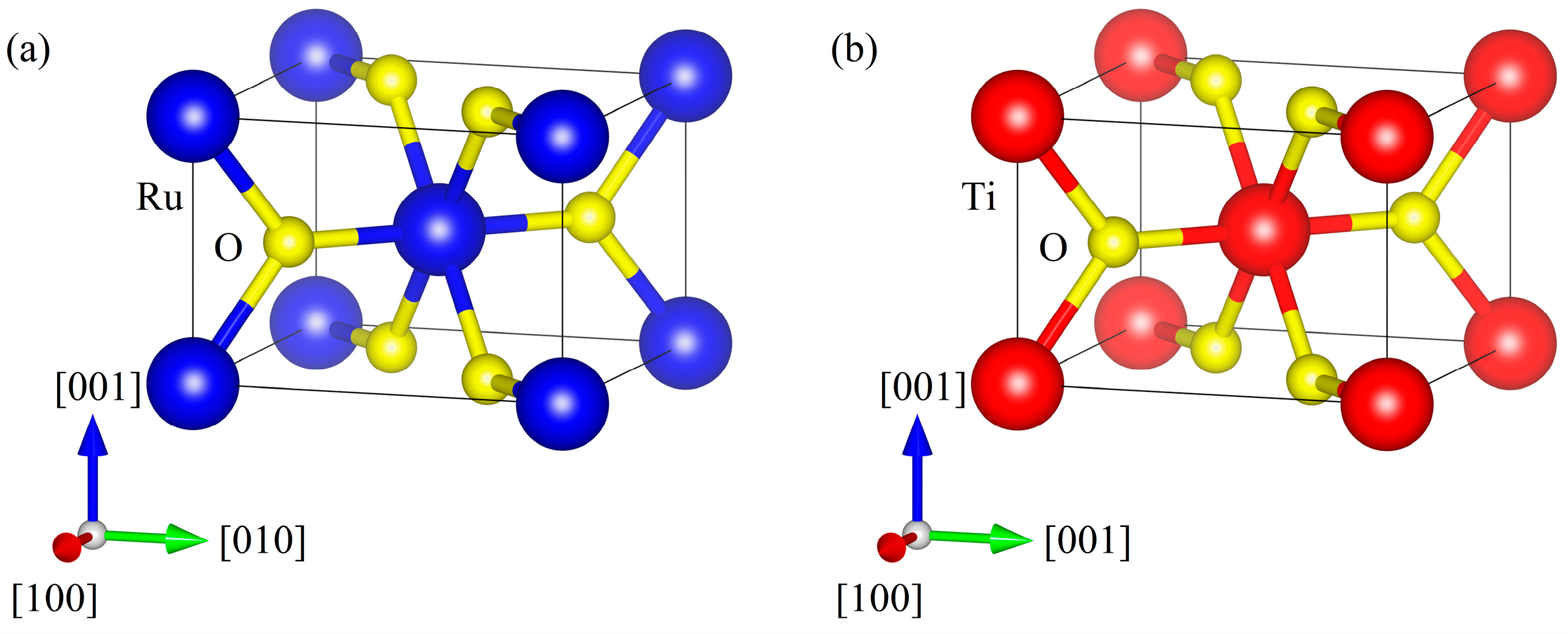
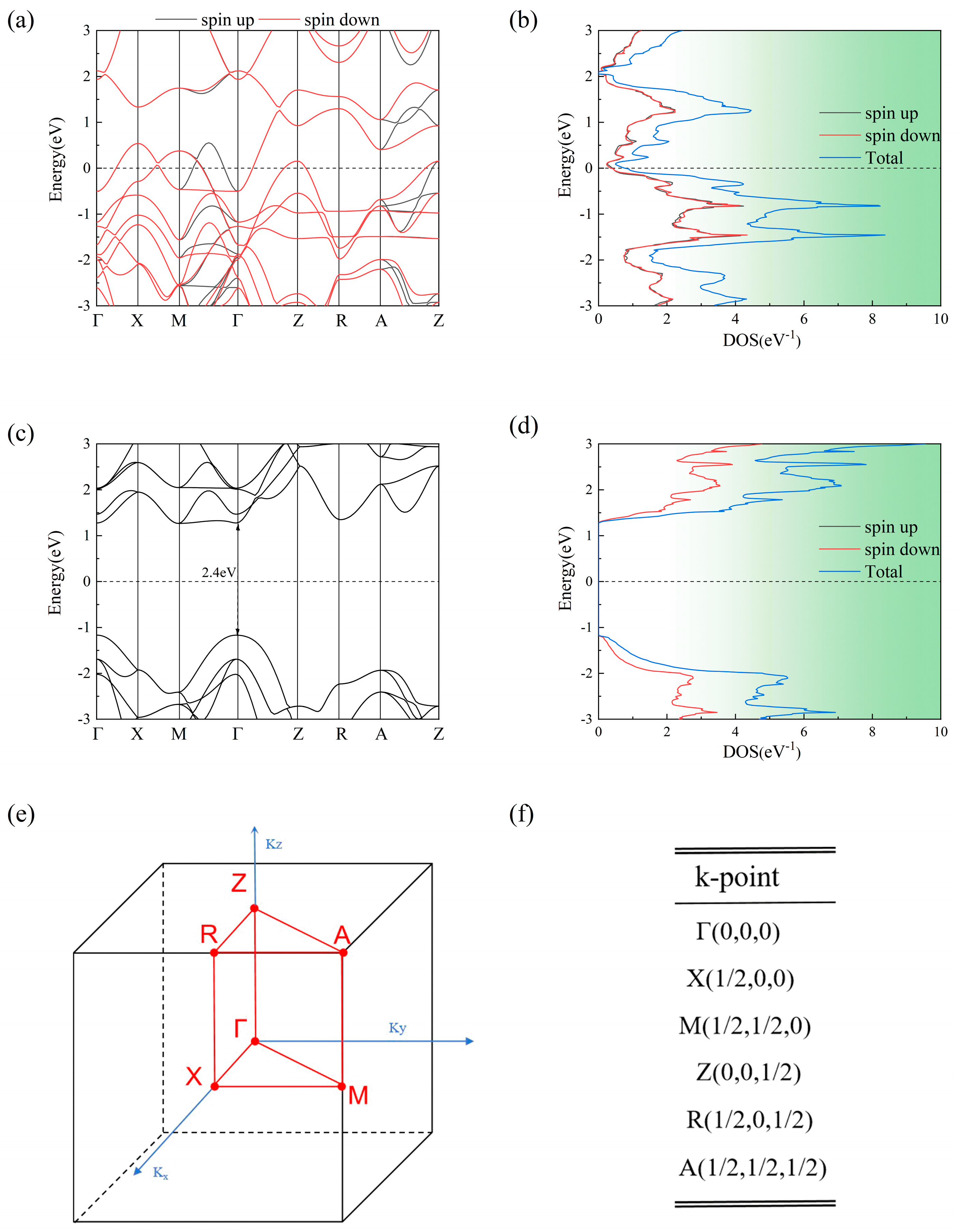
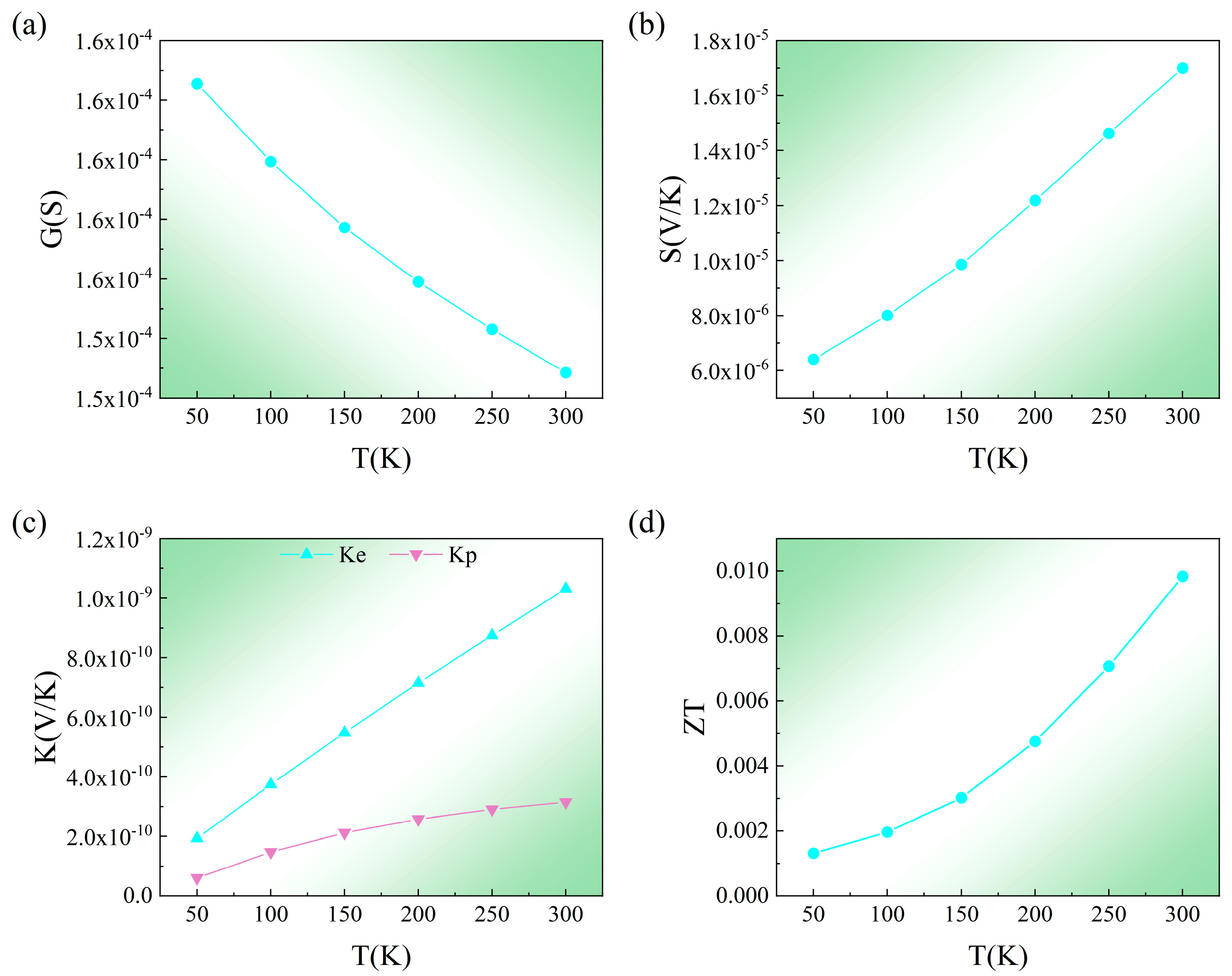
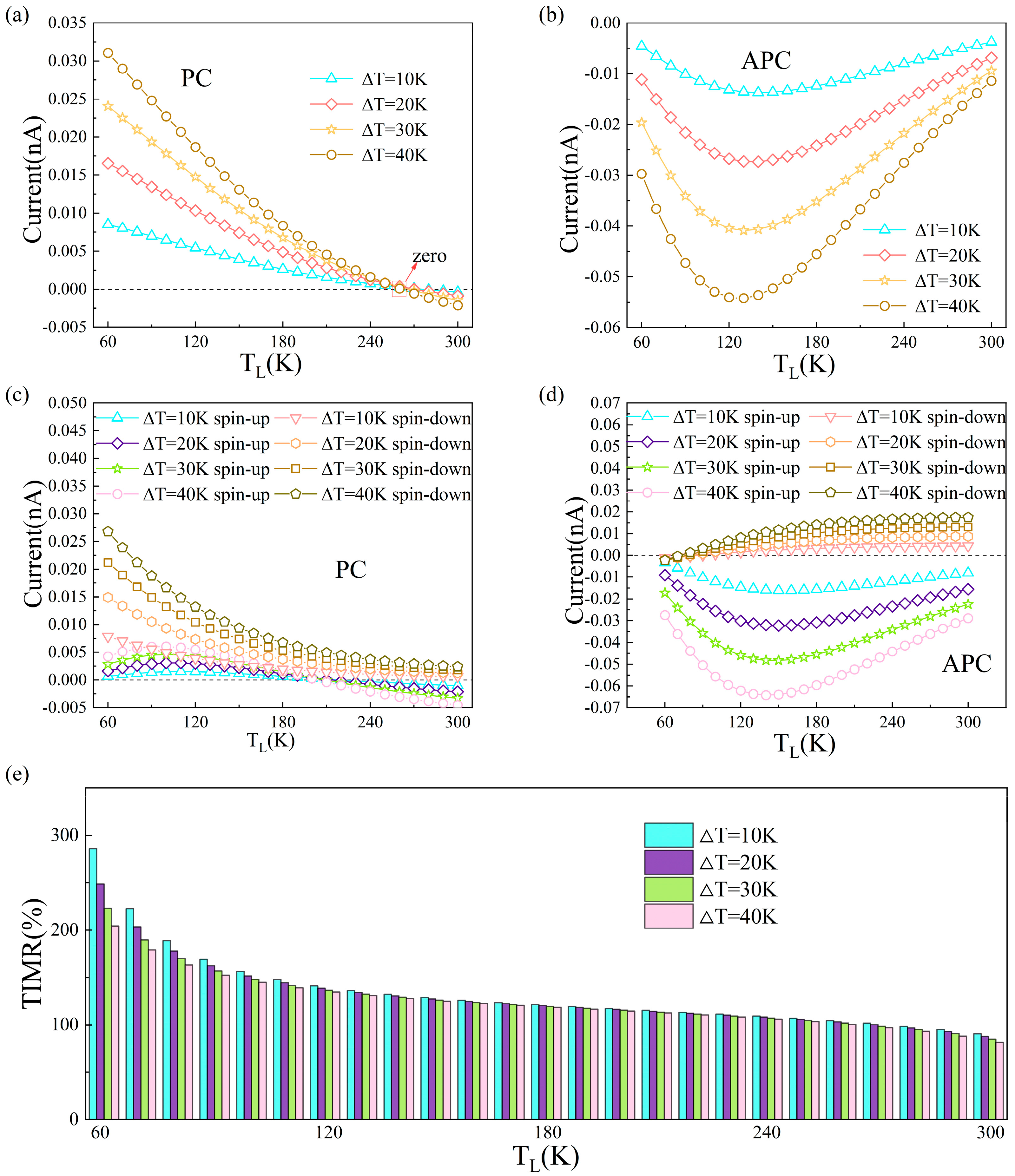
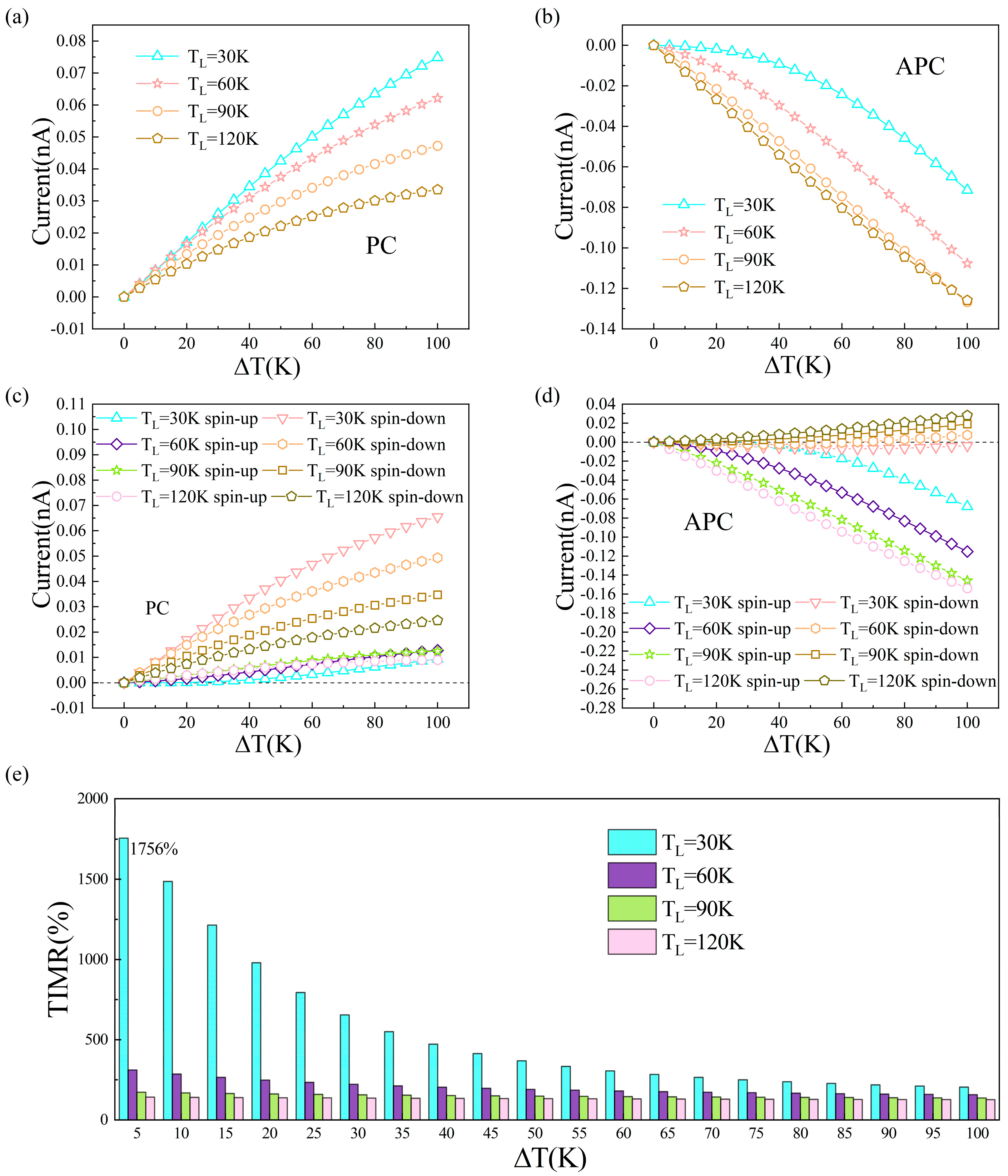
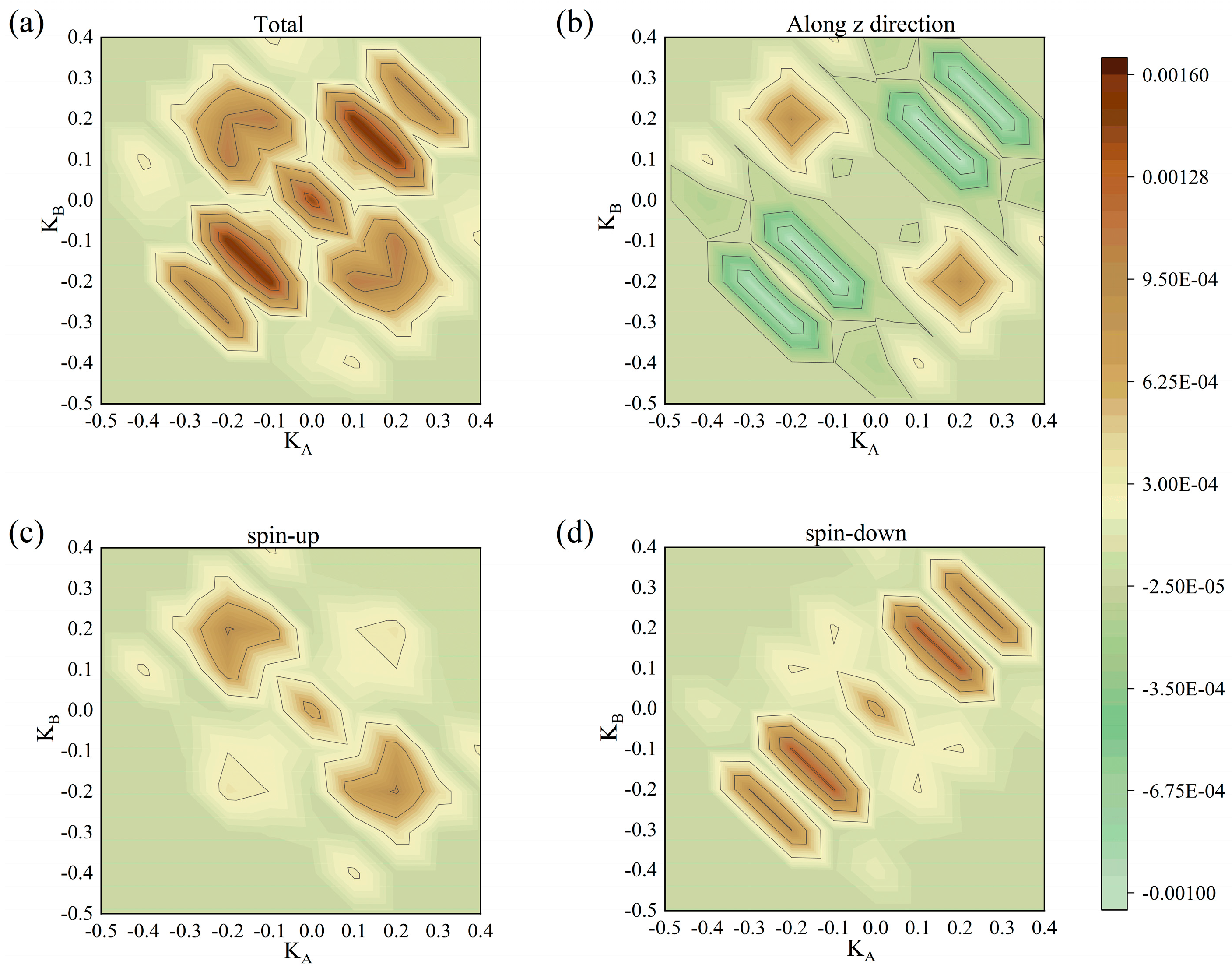
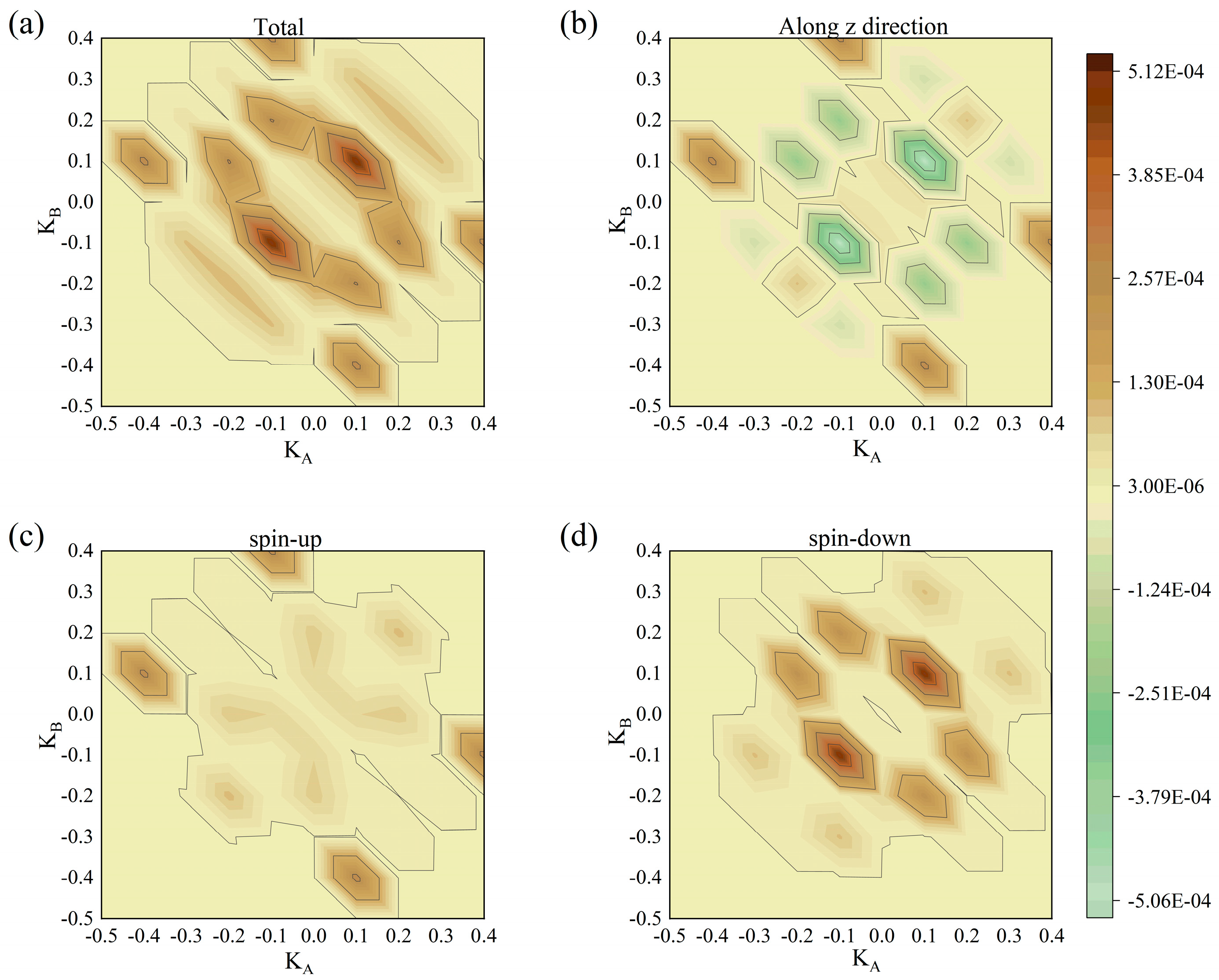
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bauer, G.E.W.; Saitoh, E.; Van Wees, B.J. Spin caloritronics. Nat. Mater. 2012, 11, 391–399. [Google Scholar] [CrossRef] [PubMed]
- Goennenwein, S.T.B.; Bauer, G.E.W. Electron spins blow hot and cold. Nat. Nanotechnol. 2012, 7, 145–147. [Google Scholar] [CrossRef] [PubMed]
- Uchida, K.; Takahashi, S.; Harii, K.; Ieda, J.; Koshibae, W.; Ando, K.; Maekawa, S.; Saitoh, E. Observation of the spin Seebeck effect. Nature 2008, 455, 778–781. [Google Scholar] [CrossRef] [PubMed]
- Jaworski, C.M.; Yang, J.; Mack, S.; Awschalom, D.D.; Heremans, J.P.; Myers, R.C. Observation of the spin-Seebeck effect in a ferromagnetic semiconductor. Nat. Mater. 2010, 9, 898–903. [Google Scholar] [CrossRef] [PubMed]
- Uchida, K.-I.; Adachi, H.; Ota, T.; Nakayama, H.; Maekawa, S.; Saitoh, E. Observation of longitudinal spin-Seebeck effect in magnetic insulators. Appl. Phys. Lett. 2010, 97, 172505. [Google Scholar] [CrossRef]
- Wu, S.M.; Pearson, J.E.; Bhattacharya, A. Paramagnetic spin Seebeck effect. Phys. Rev. Lett. 2015, 114, 186602. [Google Scholar] [CrossRef] [PubMed]
- Hirobe, D.; Sato, M.; Kawamata, T.; Shiomi, Y.; Uchida, K.-I.; Iguchi, R.; Koike, Y.; Maekawa, S.; Saitoh, E. One-dimensional spinon spin currents. Nat. Phys. 2017, 13, 30–34. [Google Scholar] [CrossRef]
- Eacret, J.S.; Gonzales, D.M.; Franks, R.G.; Burns, J.M. Immunization with merozoite surface protein 2 fused to a Plasmodium-specific carrier protein elicits strain-specific and strain-transcending, opsonizing antibody. Sci. Rep. 2019, 9, 9022. [Google Scholar] [CrossRef] [PubMed]
- Šmejkal, L.; Sinova, J.; Jungwirth, T. Beyond conventional ferromagnetism and antiferromagnetism: A phase with nonrelativistic spin and crystal rotation symmetry. Phys. Rev. X 2022, 12, 031042. [Google Scholar] [CrossRef]
- Šmejkal, L.; Sinova, J.; Jungwirth, T. Emerging research landscape of altermagnetism. Phys. Rev. X 2022, 12, 040501. [Google Scholar] [CrossRef]
- Noda, Y.; Ohno, K.; Nakamura, S. Momentum-dependent band spin splitting in semiconducting MnO2: A density functional calculation. Phys. Chem. Chem. Phys. 2016, 18, 13294–13303. [Google Scholar] [CrossRef] [PubMed]
- Hayami, S.; Yanagi, Y.; Kusunose, H. Momentum-dependent spin splitting by collinear antiferromagnetic ordering. J. Phys. Soc. Jpn. 2019, 88, 123702. [Google Scholar] [CrossRef]
- Yuan, L.D.; Wang, Z.; Luo, J.W.; Rashba, E.I.; Zunger, A. Giant momentum-dependent spin splitting in centrosymmetric low-Z antiferromagnets. Phys. Rev. B 2020, 102, 014422. [Google Scholar] [CrossRef]
- Yuan, L.D.; Wang, Z.; Luo, J.W.; Zunger, A. Prediction of low-Z collinear and noncollinear antiferromagnetic compounds having momentum-dependent spin splitting even without spin-orbit coupling. Phys. Rev. Mater. 2021, 5, 014409. [Google Scholar] [CrossRef]
- Šmejkal, L.; González-Hernández, R.; Jungwirth, T.; Sinova, J. Crystal time-reversal symmetry breaking and spontaneous Hall effect in collinear antiferromagnets. Sci. Adv. 2020, 6, eaaz8809. [Google Scholar] [CrossRef] [PubMed]
- Šmejkal, L.; Hellenes, A.B.; González-Hernández, R.; Sinova, J.; Jungwirth, T. Giant and tunneling magnetoresistance in unconventional collinear antiferromagnets with nonrelativistic spin-momentum coupling. Phys. Rev. X 2022, 12, 011028. [Google Scholar] [CrossRef]
- Wolf, S.A.; Awschalom, D.D.; Buhrman, R.A.; Daughton, J.M.; von Molnár, S.; Roukes, M.L.; Chtchelkanova, A.Y.; Treger, D.M. Spintronics: A spin-based electronics vision for the future. Science 2001, 294, 1488–1495. [Google Scholar] [CrossRef] [PubMed]
- Žutić, I.; Fabian, J.; Sarma, S.D. Spintronics: Fundamentals and applications. Rev. Mod. Phys. 2004, 76, 323. [Google Scholar] [CrossRef]
- Lenz, J.; Edelstein, S. Magnetic sensors and their applications. IEEE Sens. J. 2006, 6, 631–649. [Google Scholar] [CrossRef]
- Julliere, M. Tunneling between ferromagnetic films. Phys. Lett. A 1975, 54, 225–226. [Google Scholar] [CrossRef]
- Moodera, J.S.; Kinder, L.R.; Wong, T.M.; Meservey, R. Large magnetoresistance at room temperature in ferromagnetic thin film tunnel junctions. Phys. Rev. Lett. 1995, 74, 3273. [Google Scholar] [CrossRef] [PubMed]
- Miyazaki, T.; Tezuka, N. Giant magnetic tunneling effect in Fe/Al2O3/Fe junction. J. Magn. Magn. Mater. 1995, 139, L231–L234. [Google Scholar] [CrossRef]
- Tsymbal, E.Y.; Mryasov, O.N.; LeClair, P.R. Spin-dependent tunnelling in magnetic tunnel junctions. J. Phys. Condens. Matter 2003, 15, R109. [Google Scholar] [CrossRef]
- Zhang, X.G.; Butler, W.H. Band structure, evanescent states, and transport in spin tunnel junctions. J. Phys. Condens. Matter 2003, 15, R1603. [Google Scholar] [CrossRef]
- Chen, T.; Jiang, Y.; Keen, L. Slices of parameter space for meromorphic maps with two asymptotic values. Ergod. Theory Dyn. Syst. 2023, 43, 99–139. [Google Scholar] [CrossRef]
- Shao, D.F.; Zhang, S.H.; Li, M.; Eom, C.B.; Tsymbal, E.Y. Spin-neutral currents for spintronics. Nat. Commun. 2021, 12, 7061. [Google Scholar] [CrossRef] [PubMed]
- Dong, J.; Li, X.; Gurung, G.; Zhu, M.; Zhang, P.; Zheng, F.; Tsymbal, E.Y.; Zhang, J. Tunneling magnetoresistance in noncollinear antiferromagnetic tunnel junctions. Phys. Rev. Lett. 2022, 128, 197201. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Higo, T.; Tanaka, K.; Nomoto, T.; Tsai, H.; Idzuchi, H.; Shiga, M.; Sakamoto, S.; Ando, R.; Kosaki, H.; et al. Octupole-driven magnetoresistance in an antiferromagnetic tunnel junction. Nature 2023, 613, 490–495. [Google Scholar] [CrossRef] [PubMed]
- Qin, P.; Yan, H.; Wang, X.; Chen, H.; Meng, Z.; Dong, J.; Zhu, M.; Cai, J.; Feng, Z.; Zhou, X.; et al. Room-temperature magnetoresistance in an all-antiferromagnetic tunnel junction. Nature 2023, 613, 485–489. [Google Scholar] [CrossRef] [PubMed]
- Han, Y.; Luo, Q.; Hao, X.; Li, X.; Wang, F.; Hu, W.; Wu, K.; Lü, S.; Sadler, P.J. Reactions of an organoruthenium anticancer complex with 2-mercaptobenzanilide—A model for the active-site cysteine of protein tyrosine phosphatase 1B. Dalton Trans. 2011, 40, 11519–11529. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, K.; Pfennig, N. Fermentation of 2-methoxyethanol by Acetobacterium malicum sp. nov. and Pelobacter venetianus. Arch. Microbiol. 1988, 149, 181–187. [Google Scholar] [CrossRef]
- Shelud’kO, A.V.; Filip’eCheva, Y.A.; Telesheva, E.M.; Burov, A.M.; Evstigneeva, S.S.; Burygin, G.L.; Petrova, L.P. Characterization of carbohydrate-containing components of Azospirillum brasilense Sp245 biofilms. Microbiology 2018, 87, 610–620. [Google Scholar] [CrossRef]
- Tang, J.; Guan, D.; Xu, H.; Zhao, L.; Arshad, U.; Fang, Z.; Zhu, T.; Kim, M.; Pao, C.-W.; Hu, Z.; et al. Undoped ruthenium oxide as a stable catalyst for the acidic oxygen evolution reaction. Nat. Commun. 2025, 16, 801. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Feng, W.; Zhang, R.W.; Šmejkal, L.; Sinova, J.; Mokrousov, Y.; Yao, Y. Crystal thermal transport in altermagnetic RuO2. Phys. Rev. Lett. 2024, 132, 056701. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.Y.; Wang, Z.A.; Samanta, K.; Zhang, S.H.; Xiao, R.C.; Lu, W.J.; Sun, Y.P.; Tsymbal, E.Y.; Shao, D.F. Prediction of giant tunneling magnetoresistance in Ru O2/TiO2/RuO2 (110) antiferromagnetic tunnel junctions. Phys. Rev. B 2023, 108, 174439. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Taylor, J.; Guo, H.; Wang, J. Ab initio modeling of quantum transport properties of molecular electronic devices. Phys. Rev. B 2001, 63, 245407. [Google Scholar] [CrossRef]
- Brandbyge, M.; Mozos, J.-L.; Ordejón, P.; Taylor, J.; Stokbro, K. Density-functional method for nonequilibrium electron transport. Phys. Rev. B 2002, 65, 165401. [Google Scholar] [CrossRef]
- Hamann, D.R. Optimized norm-conserving Vanderbilt pseudopotentials. Phys. Rev. B—Condens. Matter Mater. Phys. 2013, 88, 085117. [Google Scholar] [CrossRef]
- Anisimov, V.I.; Zaanen, J.; Andersen, O.K. Band theory and Mott insulators: Hubbard U instead of Stoner, I. Phys. Rev. B 1991, 44, 943. [Google Scholar] [CrossRef] [PubMed]
- Dudarev, S.L.; Botton, G.A.; Savrasov, S.Y.; Humphreys, C.J.; Sutton, A.P. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+ U study. Phys. Rev. B 1998, 57, 1505. [Google Scholar] [CrossRef]
- Guan, D.; Xu, H.; Huang, Y.; Jing, C.; Tsujimoto, Y.; Xu, X.; Lin, Z.; Tang, J.; Wang, Z.; Sun, X.; et al. Operando studies redirect spatiotemporal restructuration of model coordinated oxides in electrochemical oxidation. Adv. Mater. 2025, 37, 2413073. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Li, W.; Wang, C.; Chen, Z.; Wu, Y.; Zhang, X.; Li, J.; Lin, S.; Chen, Y.; Pei, Y. MnTe2 as a novel promising thermoelectric material. J. Mater. 2018, 4, 215–220. [Google Scholar] [CrossRef]
- Fields, S.S.; Callahan, P.G.; Combs, N.G.; Cress, C.D.; Bennett, S.P. Orientation control and mosaicity in heteroepitaxial RuO2 thin films grown through reactive direct current sputtering. Cryst. Growth Des. 2024, 24, 4604–4612. [Google Scholar] [CrossRef]
- Katal, R.; Masudy-Panah, S.; Tanhaei, M.; Farahani, M.H.D.A.; Jiangyong, H. A review on the synthesis of the various types of anatase TiO2 facets and their applications for photocatalysis. Chem. Eng. J. 2020, 384, 123384. [Google Scholar] [CrossRef]
- Pawula, F.; Fakih, A.; Daou, R.; Hébert, S.; Mordvinova, N.; Lebedev, O.; Pelloquin, D.; Maignan, A. Multiband transport in RuO2. Phys. Rev. B 2024, 110, 064432. [Google Scholar] [CrossRef]
- Suchaneck, G. Tunnel Spin-Polarization of ferromagnetic metals and ferrimagnetic oxides and its effect on tunnel magnetoresistance. Electron. Mater. 2022, 3, 227–234. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Ning, C.; Liu, X.; Zhu, S.; Wang, S. Investigation of Thermoelectric Properties in Altermagnet RuO2. Nanomaterials 2025, 15, 1129. https://doi.org/10.3390/nano15141129
Liu J, Ning C, Liu X, Zhu S, Wang S. Investigation of Thermoelectric Properties in Altermagnet RuO2. Nanomaterials. 2025; 15(14):1129. https://doi.org/10.3390/nano15141129
Chicago/Turabian StyleLiu, Jun, Chunmin Ning, Xiao Liu, Sicong Zhu, and Shuling Wang. 2025. "Investigation of Thermoelectric Properties in Altermagnet RuO2" Nanomaterials 15, no. 14: 1129. https://doi.org/10.3390/nano15141129
APA StyleLiu, J., Ning, C., Liu, X., Zhu, S., & Wang, S. (2025). Investigation of Thermoelectric Properties in Altermagnet RuO2. Nanomaterials, 15(14), 1129. https://doi.org/10.3390/nano15141129





