Full-Space Three-Dimensional Holograms Enabled by a Reflection–Transmission Integrated Reconfigurable Metasurface
Abstract
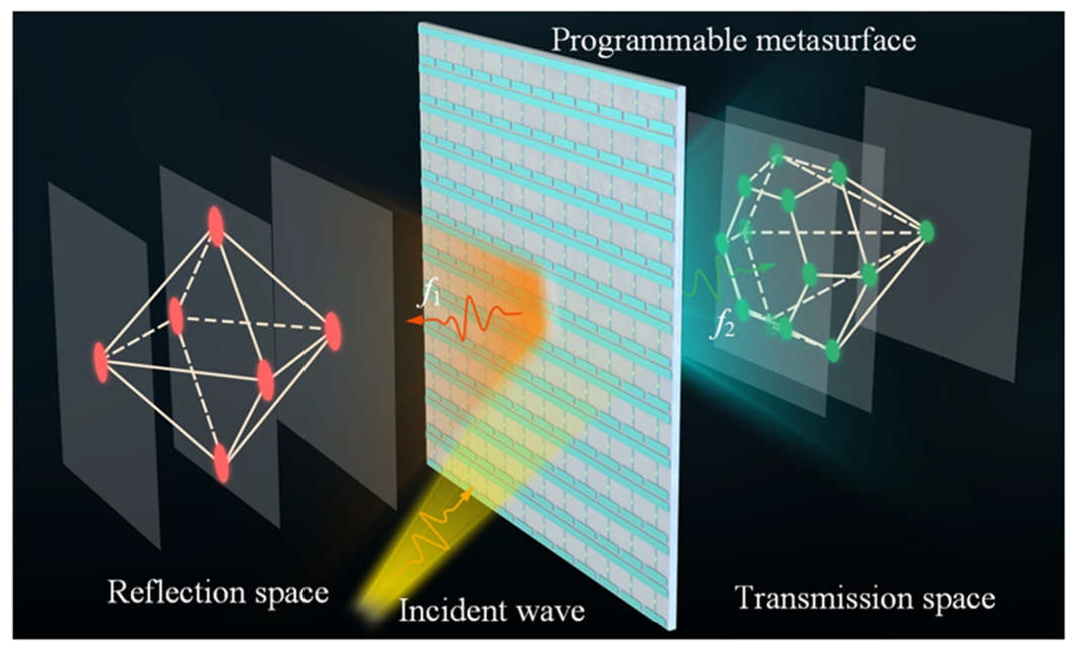
1. Introduction
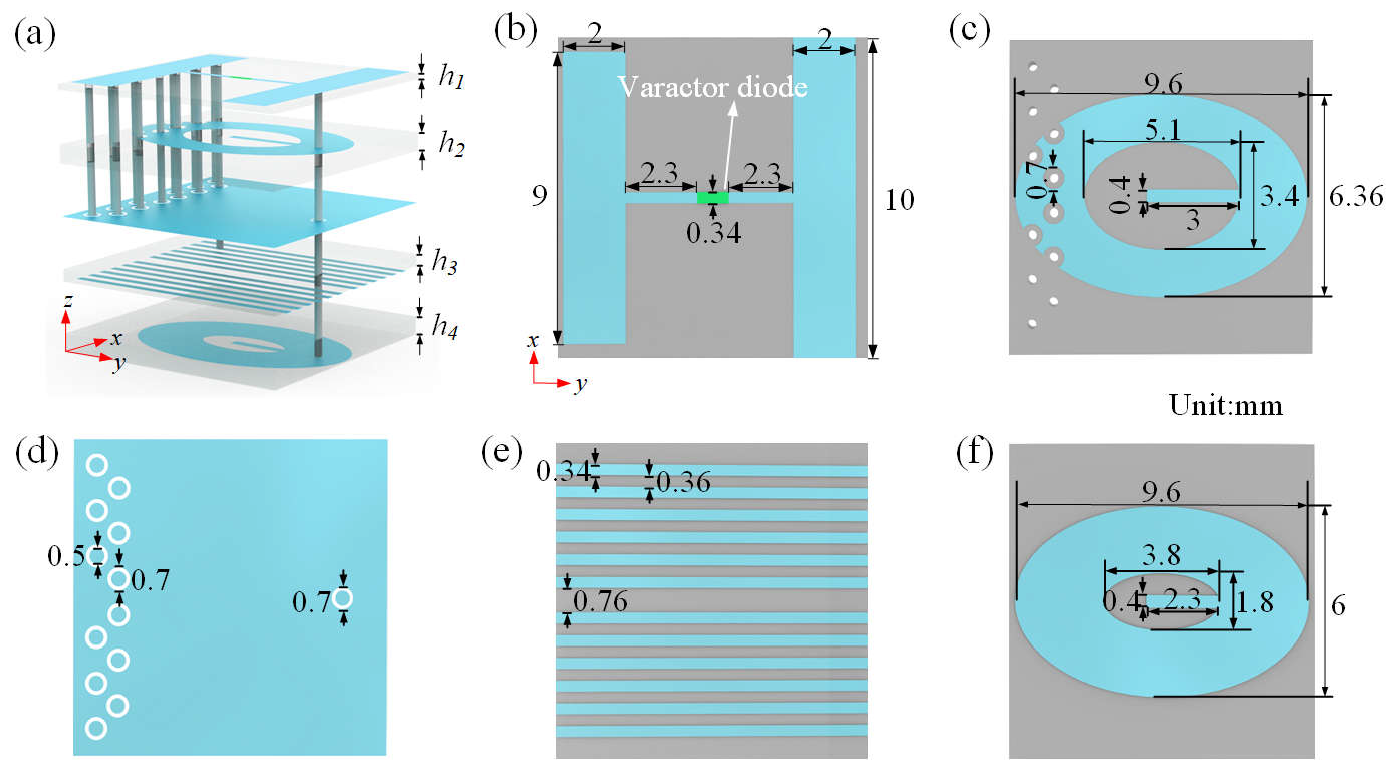
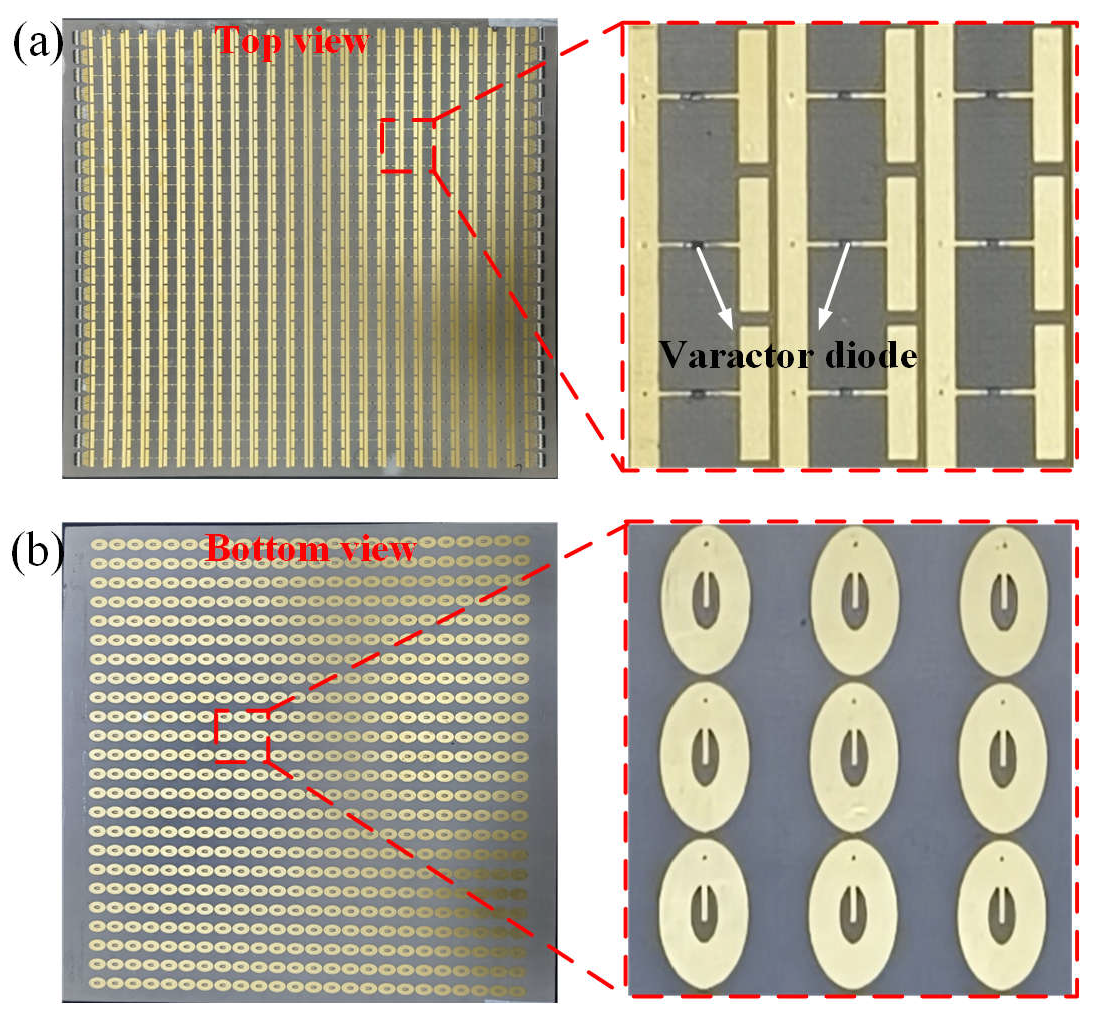
2. Metasurface Design
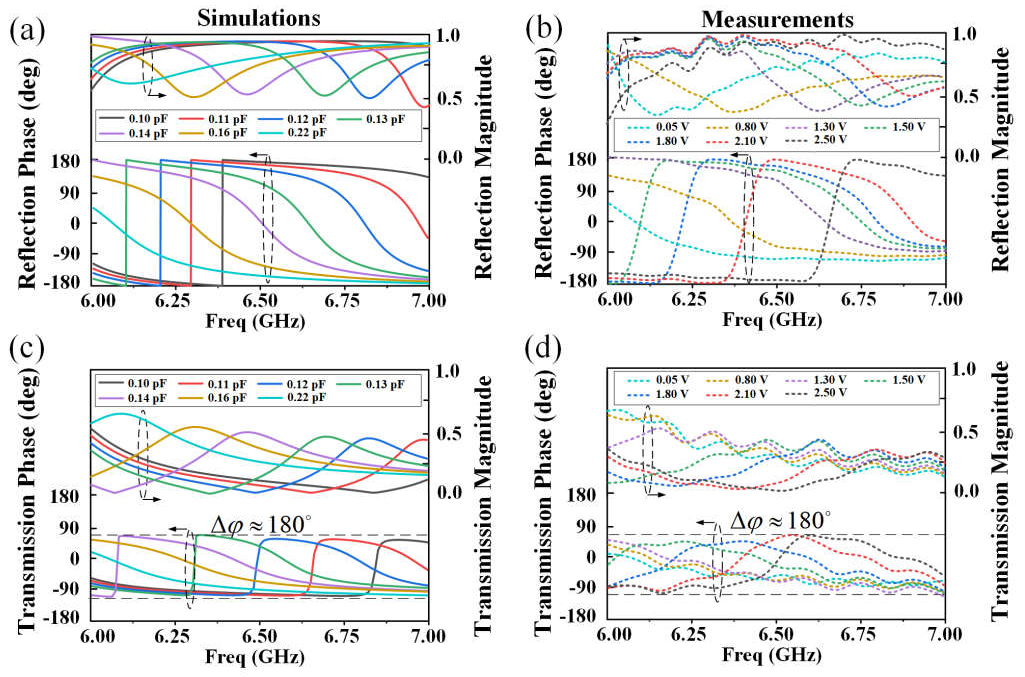
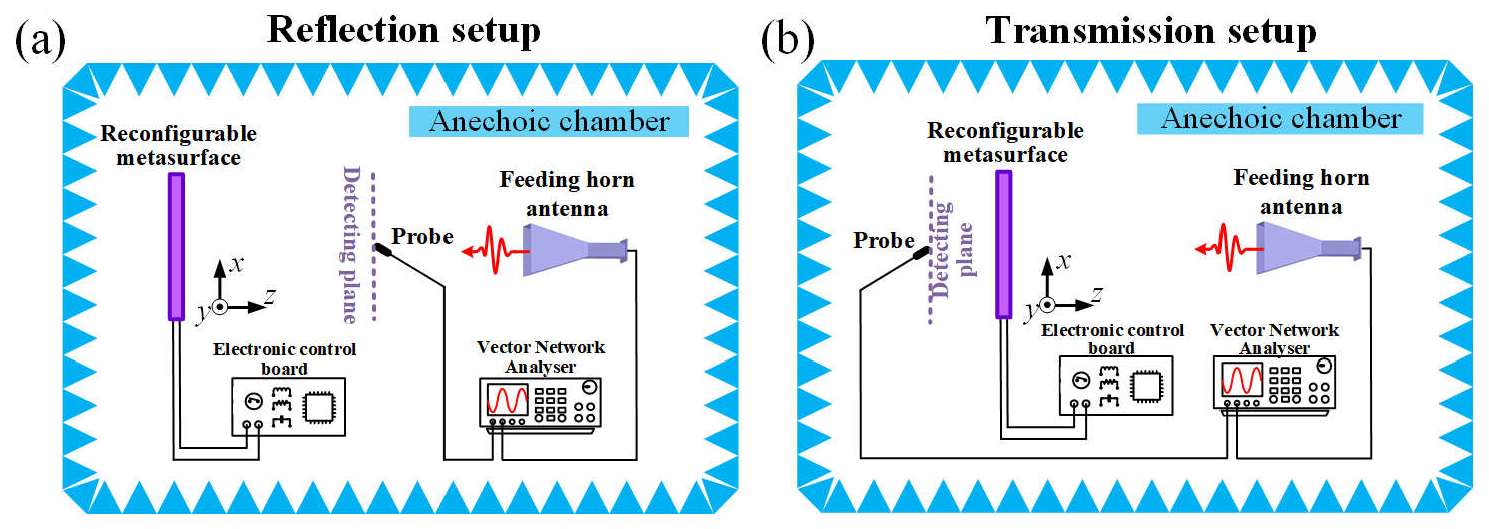
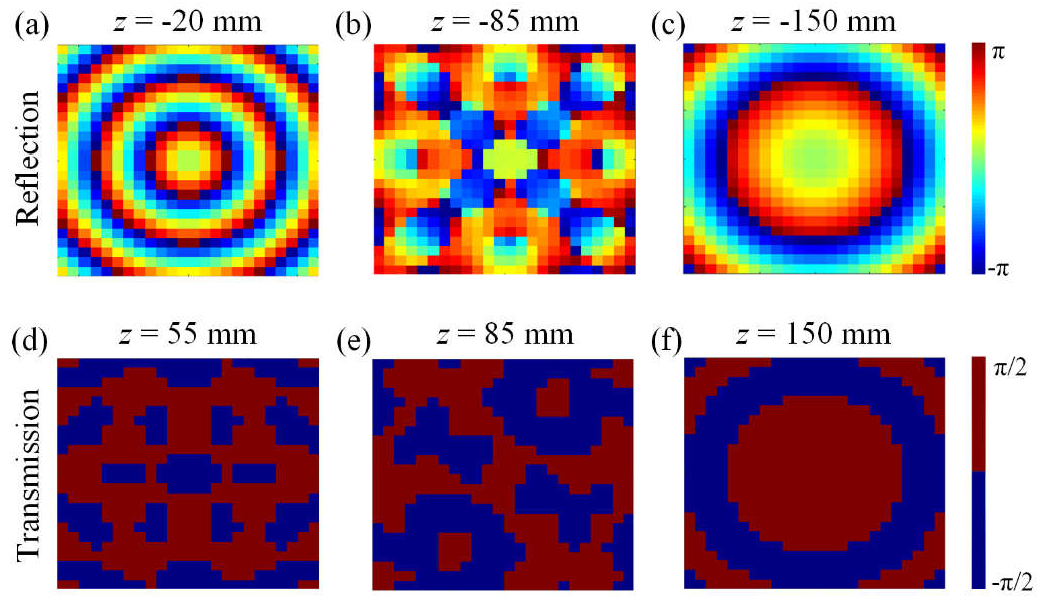
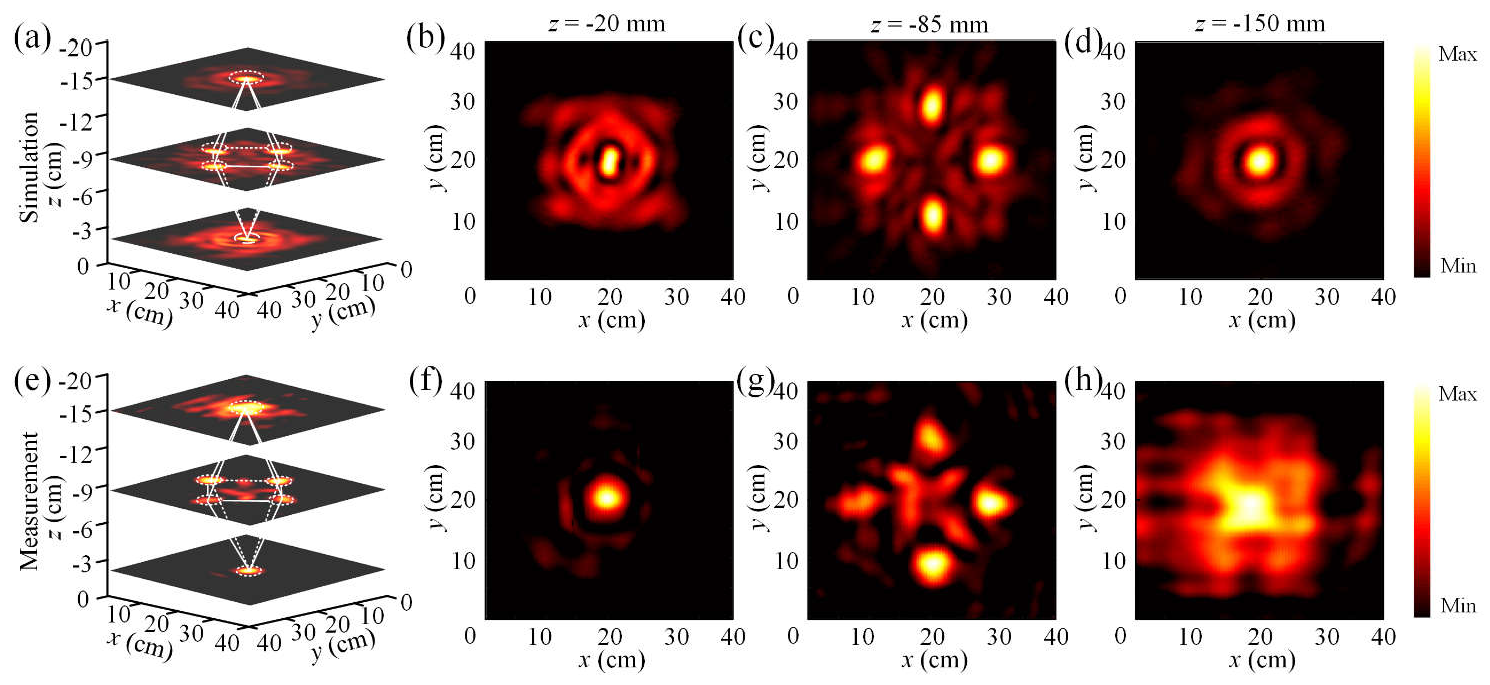
3. Principles and Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| WGS | Weighted Gerchberg–Saxton |
| FINCH | Fresnel incoherent correlation holography |
| COACH | Coded aperture correlation holography |
| CGH | Computer-generated holography |
| EM | Electromagnetic |
| OAM | Orbital angular momentum |
| 3D | Three-dimensional |
| PCB | Printed circuit board |
| SMT | Surface-mount technology |
References
- Gabor, D. A new microscope principle. Nature 1948, 161, 777. [Google Scholar] [CrossRef] [PubMed]
- Maiman, T.H. Stimulated optical radiation in ruby. Nature 1960, 187, 493–494. [Google Scholar] [CrossRef]
- Gabor, D. Microscopy by Reconstructed Wave Fronts: II. Proc. Phys. Soc. 1951, 64, 449–469. [Google Scholar] [CrossRef]
- Mertz, L.; Young, N.O. Fresnel transformations of images. Proc. Int. Conf. Opt. Instrum. Tech. 1961, 305–310. [Google Scholar]
- Rosen, J.; Brooker, G. Digital spatially incoherent Fresnel holography. Opt. Lett. 2007, 32, 912–914. [Google Scholar] [CrossRef] [PubMed]
- Vijayakumar, A.; Kashter, Y.; Kelner, R.; Rosen, J. Coded aperture correlation holography-A new type of incoherent digital holograms. Opt. Express 2016, 24, 12430–12441. [Google Scholar] [CrossRef] [PubMed]
- Lohmann, A.W.; Paris, D.P. Binary Fraunhofer Holograms, Generated by Computer. App. Opt. 1967, 6, 1739–1748. [Google Scholar] [CrossRef] [PubMed]
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.P.; Capasso, F.; Gaburro, Z. Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef] [PubMed]
- Ni, X.; Emani, N.K.; Kildishev, A.V.; Boltasseva, A.; Shalaev, V.M. Broadband light bending with plasmonic nanoantennas. Science 2012, 335, 427. [Google Scholar] [CrossRef] [PubMed]
- Yu, N.; Capasso, F. Flat optics with designer metasurfaces. Nat. Mater. 2014, 13, 139–150. [Google Scholar] [CrossRef] [PubMed]
- Sun, S.; He, Q.; Xiao, S.; Xu, Q.; Li, X.; Zhou, L. Gradient-index meta-surfaces as a bridge linking propagating waves and surface waves. Nat. Mater. 2012, 11, 426–431. [Google Scholar] [CrossRef] [PubMed]
- Hassanfiroozi, A.; Yang, Z.S.; Huang, S.H.; Cheng, W.H.; Shi, Y.; Wu, P.C. Vertically-stacked discrete plasmonic meta-gratings for broadband space-variant metasurfaces. Adv. Opt. Mater. 2023, 11, 2202717. [Google Scholar] [CrossRef]
- Díaz-Rubio, A.; Asadchy, V.S.; Elsakka, A.; Tretyakov, S.A. From the generalized reflection law to the realization of perfect anomalous reflectors. Sci. Adv. 2017, 3, e1602714. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Cui, T.J.; Zhang, L.; Xu, Q.; Wang, Q.; Wan, X.; Cheng, Q. Convolution operations on coding metasurface to reach flexible and continuous controls of terahertz beams. Adv. Sci. 2016, 3, 1600156. [Google Scholar] [CrossRef] [PubMed]
- Sun, S.; Yang, K.Y.; Wang, C.M.; Juan, T.K.; Chen, W.T.; Liao, C.Y.; Tsai, D.P. High-efficiency broadband anomalous reflection by gradient meta-surfaces. Nano Lett. 2012, 12, 6223–6229. [Google Scholar] [CrossRef] [PubMed]
- Khorasaninejad, M.; Capasso, F. Metalenses: Versatile multifunctional photonic components. Science 2017, 358, eaam8100. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Wu, P.C.; Su, V.C.; Lai, Y.C.; Chen, M.K.; Kuo, H.Y.; Tsai, D.P. A broadband achromatic metalens in the visible. Nat. Nanotechnol. 2018, 13, 227–232. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Liu, Z.; Ren, X.; Wang, S.; Su, V.C.; Chen, M.K.; Tsai, D.P. Metalens-array–based high-dimensional and multiphoton quantum source. Science 2020, 368, 1487–1490. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Hu, G.; Wang, X.; Ding, X.; Zhang, K.; Li, H.; Qiu, C.W. Single-layer spatial analog meta-processor for imaging processing. Nat. Commun. 2022, 13, 2188. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Wang, H.; Wang, J.; Liu, X.; Hao, H.; Tan, Y.S.; Ding, X. Single-shot isotropic differential interference contrast microscopy. Nat. Commun. 2023, 14, 2063. [Google Scholar] [CrossRef] [PubMed]
- Ding, X.; Wang, Z.; Hu, G.; Liu, J.; Zhang, K.; Li, H.; Qiu, C.W. Metasurface holographic image projection based on mathematical properties of Fourier transform. PhotoniX 2020, 1, 1–12. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, Y.; Guan, C.; Zhang, K.; Wu, Q.; Li, H.; Ding, X. Deep learning-enabled compact optical trigonometric operator with metasurface. PhotoniX 2022, 3, 15. [Google Scholar] [CrossRef]
- Malleboina, R.; Dash, J.C.; Sarkar, D. Design of anomalous reflectors by phase gradient unit cell-based digitally coded metasurface. IEEE Antennas Wireless Propag. Lett. 2023, 22, 2305–2309. [Google Scholar] [CrossRef]
- Wu, G.B.; Dai, J.Y.; Cheng, Q.; Cui, T.J.; Chan, C.H. Sideband-free space–time-coding metasurface antennas. Nat. Electron. 2022, 5, 808–819. [Google Scholar] [CrossRef]
- Huang, X.; Yang, H.; Zhang, D.; Luo, Y. Ultrathin dual-band metasurface polarization converter. IEEE Trans. Antennas Propag. 2019, 67, 4636–4641. [Google Scholar] [CrossRef]
- Xu, J.; Li, R.; Qin, J.; Wang, S.; Han, T. Ultra-broadband wide-angle linear polarization converter based on H-shaped metasurface. Opt. Express 2018, 26, 20913–20919. [Google Scholar] [CrossRef] [PubMed]
- Ding, F.; Deshpande, R.; Bozhevolnyi, S.I. Bifunctional gap-plasmon metasurfaces for visible light: Polarization-controlled unidirectional surface plasmon excitation and beam steering at normal incidence. Light Sci. Appl. 2018, 7, 17178. [Google Scholar] [CrossRef] [PubMed]
- Lin, Z.; Pan, X.; Yao, J.; Wu, Y.; Wang, Z.; Zhang, D.; Wang, X. Characterization of orbital angular momentum applying single-sensor compressive imaging based on a microwave spatial wave modulator. IEEE Trans. Antennas Propag. 2021, 69, 6870–6880. [Google Scholar] [CrossRef]
- Sawant, A.; Lee, I.; Choi, E. Amplitude non-uniformity of millimeter-wave vortex beams generated by transmissive structures. IEEE Trans. Antennas Propag. 2022, 70, 4623–4631. [Google Scholar] [CrossRef]
- Shi, Y.; Hu, T.T.; Meng, Z.K.; Wu, Q.W.; Cui, T.J. Demodulation method of orbital angular momentum vortex wave by few fields sampled on an extremely small partial aperture in radiation region. Appl. Phys. Rev. 2023, 10, 031418. [Google Scholar] [CrossRef]
- Meng, Z.K.; Shi, Y.; Wei, W.Y.; Zhang, Y.; Li, L. Graphene-based metamaterial transmitarray antenna design for the generation of tunable orbital angular momentum vortex electromagnetic waves. Opt. Mater. Express 2019, 9, 3709–3716. [Google Scholar] [CrossRef]
- Ma, H.F.; Cui, T.J. Three-dimensional broadband ground-plane cloak made of metamaterials. Nat. Commun. 2010, 1, 21. [Google Scholar] [CrossRef] [PubMed]
- Pendry, J.B.; Schurig, D.; Smith, D.R. Controlling electromagnetic fields. Science 2006, 312, 1780–1782. [Google Scholar] [CrossRef] [PubMed]
- Kundtz, N.; Smith, D.R. Extreme-angle broadband metamaterial lens. Nat. Mater. 2010, 9, 129–132. [Google Scholar] [CrossRef] [PubMed]
- Abdelraouf, O.A.M.; Wang, Z.; Liu, H.; Dong, Z.; Wang, Q.; Ye, M.; Wang, X.R.; Wang, Q.J.; Liu, H. Recent advances in tunable metasurfaces: Materials, design, and applications. ACS Nano 2022, 16, 13339–13369. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Cui, T.J.; Wei, J.; Liu, S.; Wan, X.; Li, Y.B.; Jiang, M.; Qiu, C.W. Electromagnetic reprogrammable coding-metasurface holograms. Nat. Commun. 2017, 8, 197. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.Y.; Huang, J.H.; Su, H.T.; Chang, S.M.; Wu, Y.C.; Huang, Y.W. Directionally asymmetric in orbital angular momentum generation using single-layer dielectric Janus metasurfaces. Adv. Opt. Mater. 2024, 12, 2401335. [Google Scholar] [CrossRef]
- Shang, G.; Hu, G.; Guan, C.; Wang, Y.; Zhang, K.; Wu, Q.; Liu, J.; Ding, X.-M.; Burokur, S.N.; Li, H.; et al. A non-interleaved bidirectional Janus metasurface with full-space scattering channels. Nanophoton. 2022, 11, 3729–3739. [Google Scholar] [CrossRef] [PubMed]
- Meftah, N.; Ratni, B.; El Korso, M.N.; Burokur, S.N. Enhanced-resolution learning-based direction of arrival estimation by programmable metasurface. Adv. Electron. Mater. 2025, 11, 2400476. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, X.; Liu, M.; Chen, J.; Du, W.; Liu, Z. Deep learning-based inverse design of multi-functional metasurface absorbers. Opt. Lett. 2024, 49, 2733–2736. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Ding, X.; Zhang, K.; Ratni, B.; Burokur, S.N.; Gu, X.; Wu, Q. Huygens metasurface holograms with the modulation of focal energy distribution. Adv. Opt. Mater. 2018, 6, 1800121. [Google Scholar] [CrossRef]
- Di, L.R.; Ianni, F.; Ruocco, G. Computer generation of optimal holograms for optical trap arrays. Opt. Express 2007, 15, 1913–1922. [Google Scholar] [CrossRef] [PubMed]
- Gerchberg, R.W.; Saxton, W.O. A practical algorithm for the determination of phase from image and diffraction plane pictures. Optik 1972, 35, 237–246. [Google Scholar]
- Kim, M.K. Digital Holographic Microscopy; Springer: Tampa, FL, USA, 2011. [Google Scholar]
- Feng, R.; Ratni, B.; Yi, J.; Zhang, H.; de Lustrac, A.; Burokur, S.N. Reprogrammable digital holograms and multibit spatial energy modulation using a reflective metasurface. ACS Appl. Electron. Mater. 2021, 3, 5272–5277. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Y.; Guo, X.; Chen, T.; Liang, H.; Hao, X.; Hou, X.; Kou, W.; Zhao, Y.; Zhou, T.; et al. A review of THz modulators with dynamic tunable metasurfaces. Nanomaterials 2019, 9, 965. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, R.; Yu, Y.; Wu, D.; Tan, Q.; Burokur, S.N. Full-Space Three-Dimensional Holograms Enabled by a Reflection–Transmission Integrated Reconfigurable Metasurface. Nanomaterials 2025, 15, 1120. https://doi.org/10.3390/nano15141120
Feng R, Yu Y, Wu D, Tan Q, Burokur SN. Full-Space Three-Dimensional Holograms Enabled by a Reflection–Transmission Integrated Reconfigurable Metasurface. Nanomaterials. 2025; 15(14):1120. https://doi.org/10.3390/nano15141120
Chicago/Turabian StyleFeng, Rui, Yaokai Yu, Dongyang Wu, Qiulin Tan, and Shah Nawaz Burokur. 2025. "Full-Space Three-Dimensional Holograms Enabled by a Reflection–Transmission Integrated Reconfigurable Metasurface" Nanomaterials 15, no. 14: 1120. https://doi.org/10.3390/nano15141120
APA StyleFeng, R., Yu, Y., Wu, D., Tan, Q., & Burokur, S. N. (2025). Full-Space Three-Dimensional Holograms Enabled by a Reflection–Transmission Integrated Reconfigurable Metasurface. Nanomaterials, 15(14), 1120. https://doi.org/10.3390/nano15141120







