High-Power-Density Miniaturized VLF Antenna with Nanocrystalline Core for Enhanced Field Strength
Abstract
1. Introduction
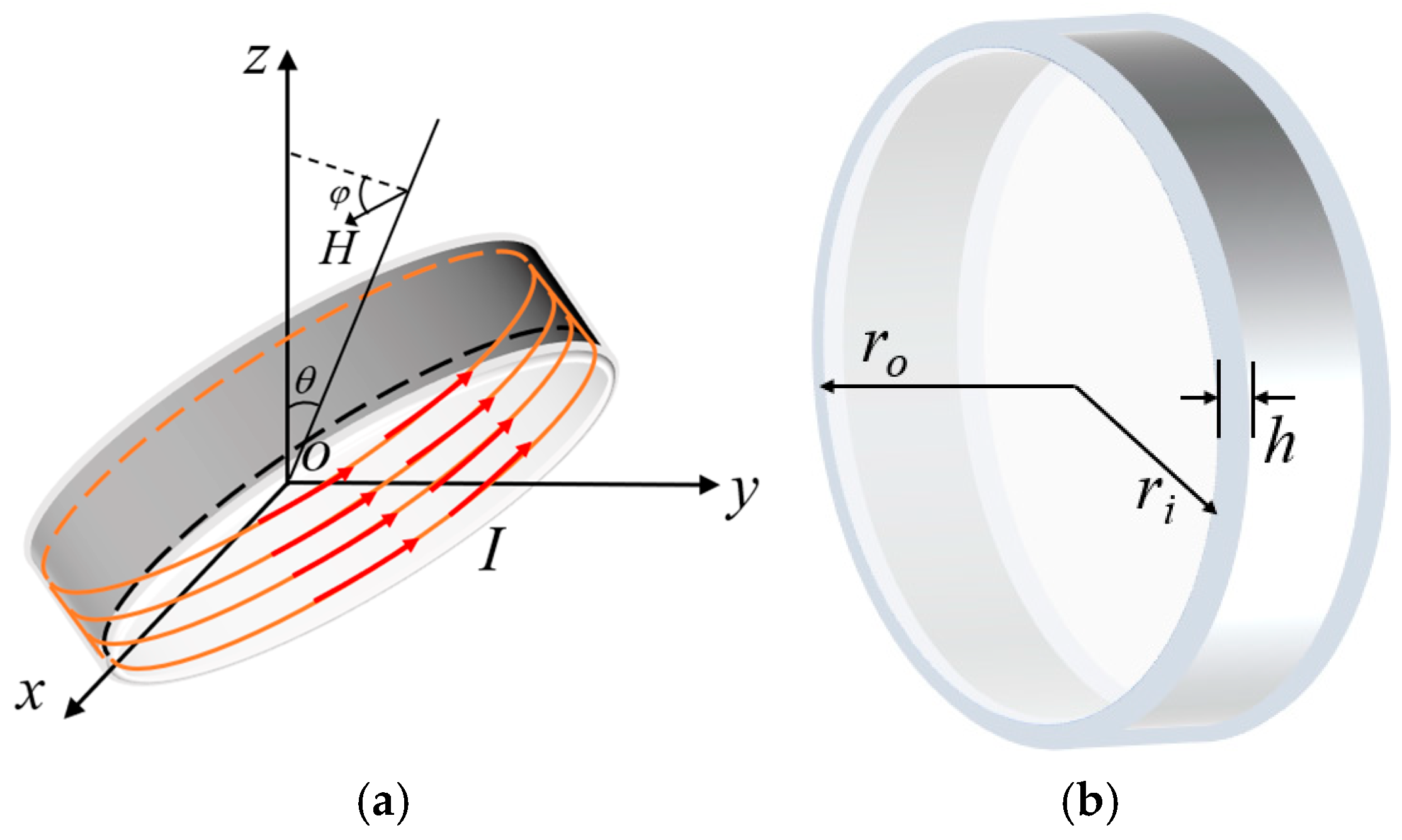
2. Basic Theory of Magnetic Loop Antenna
2.1. Radiation Performance Analysis
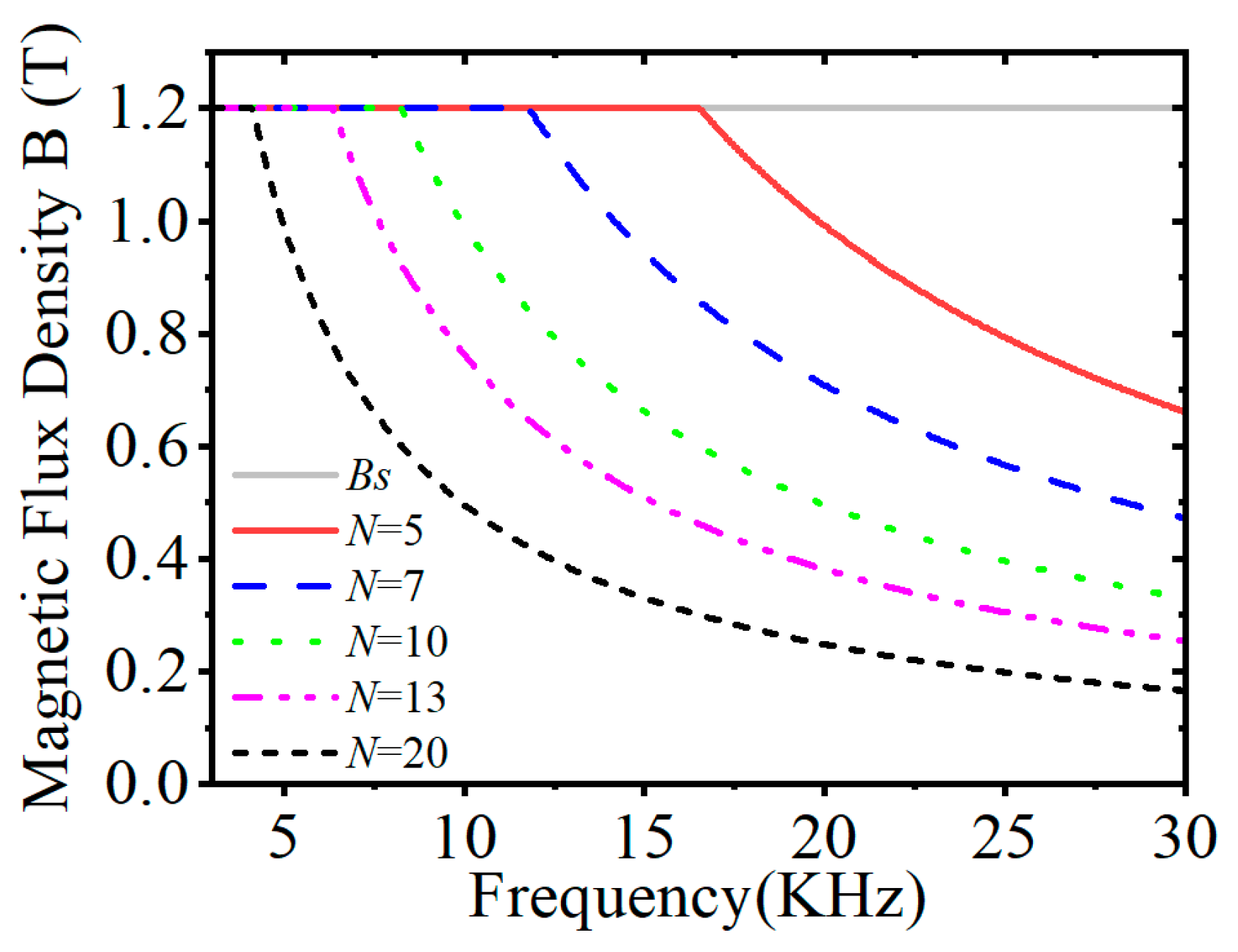
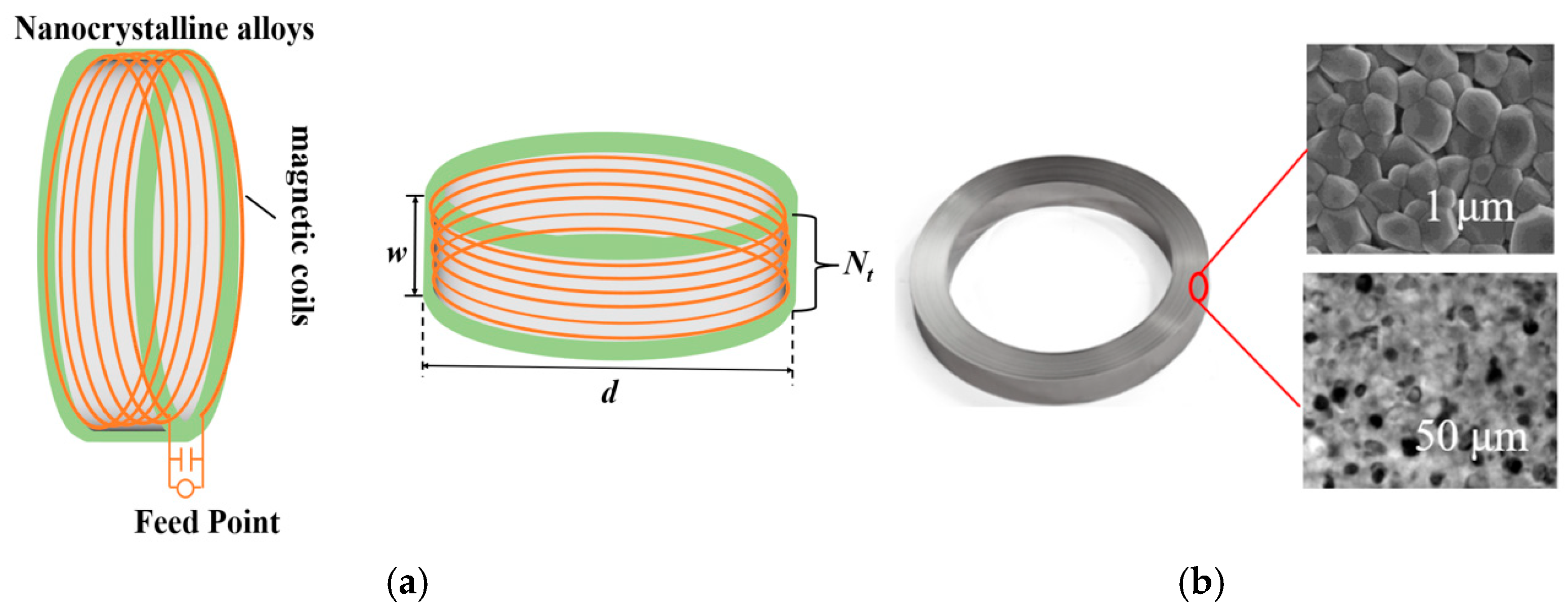
2.2. Nanocrystalline Core Ring Antenna
2.2.1. Nanocrystalline Material Properties
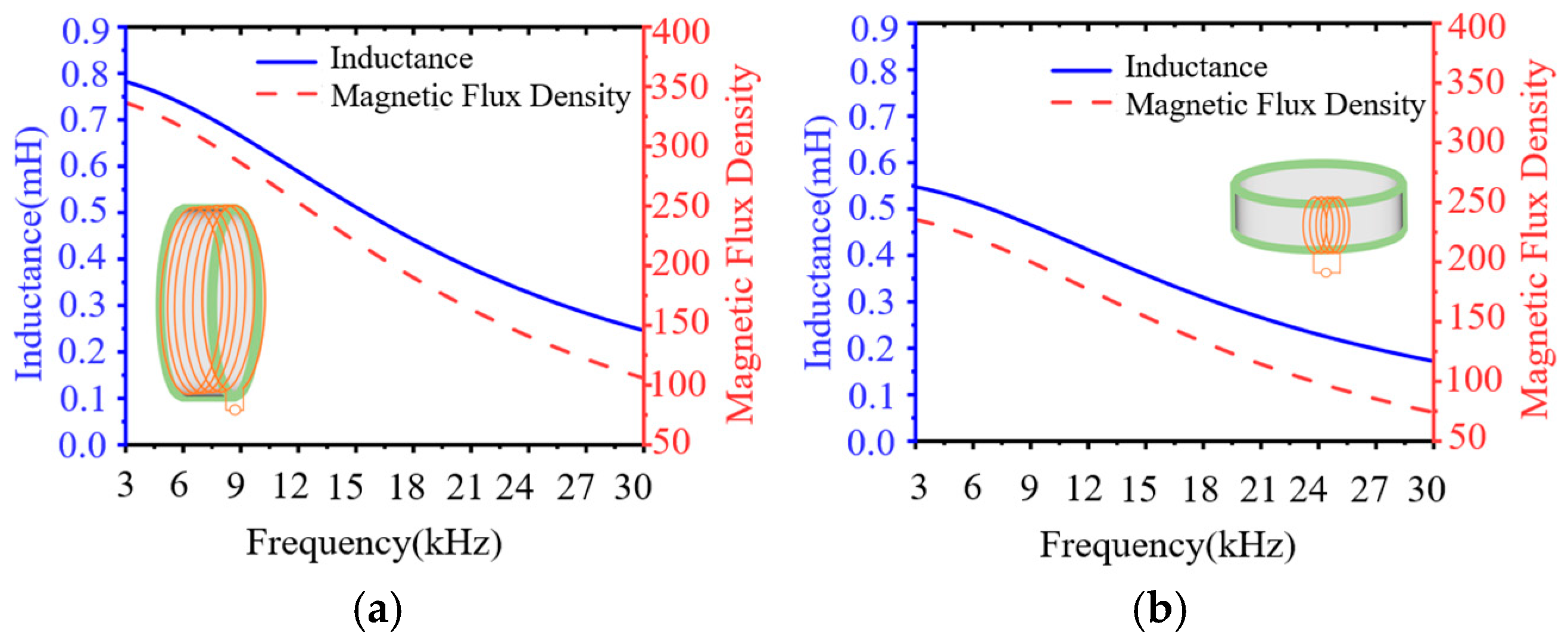
2.2.2. Ring Antenna Design Based on Nanocrystalline Materials
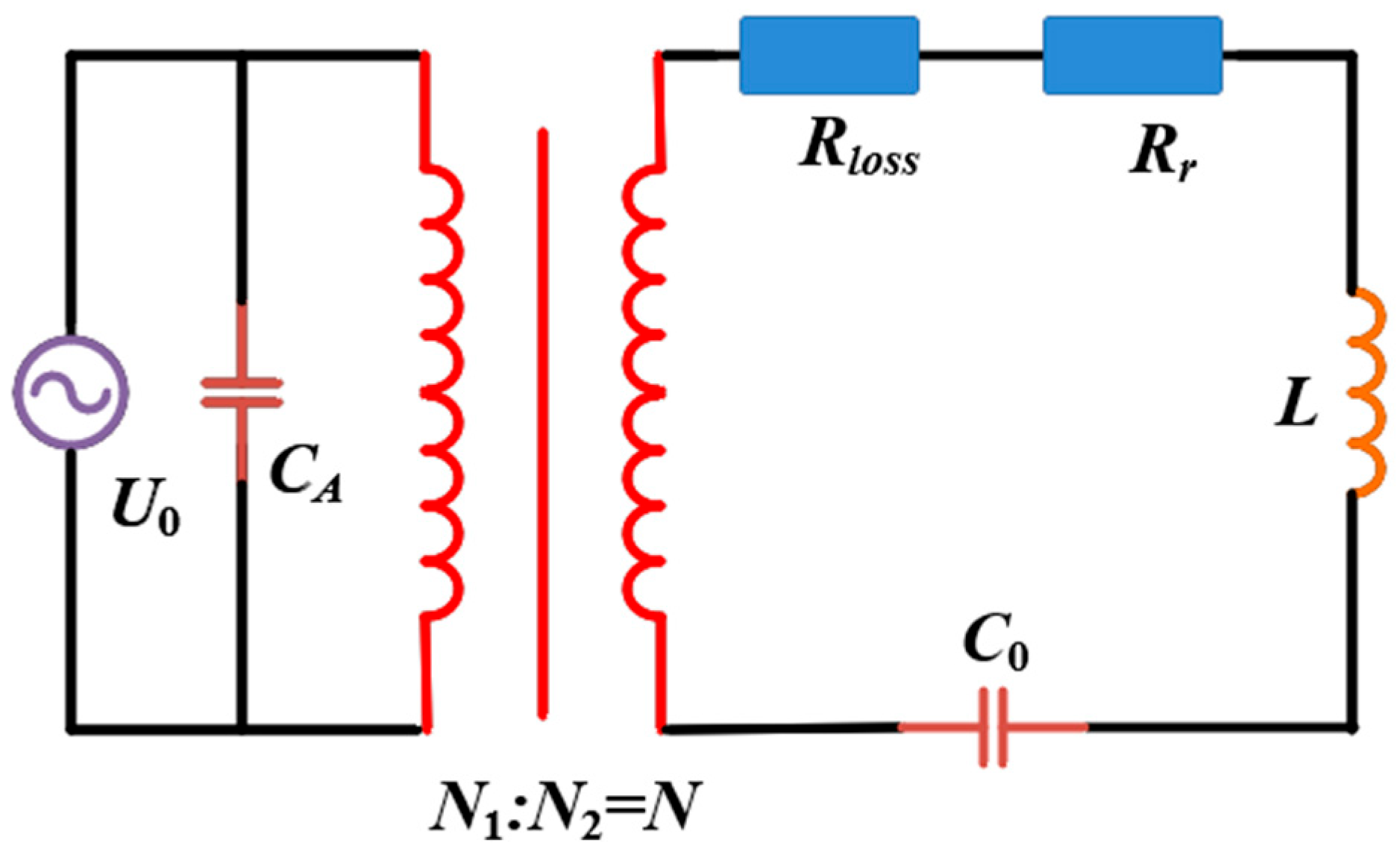
2.3. Matching Design
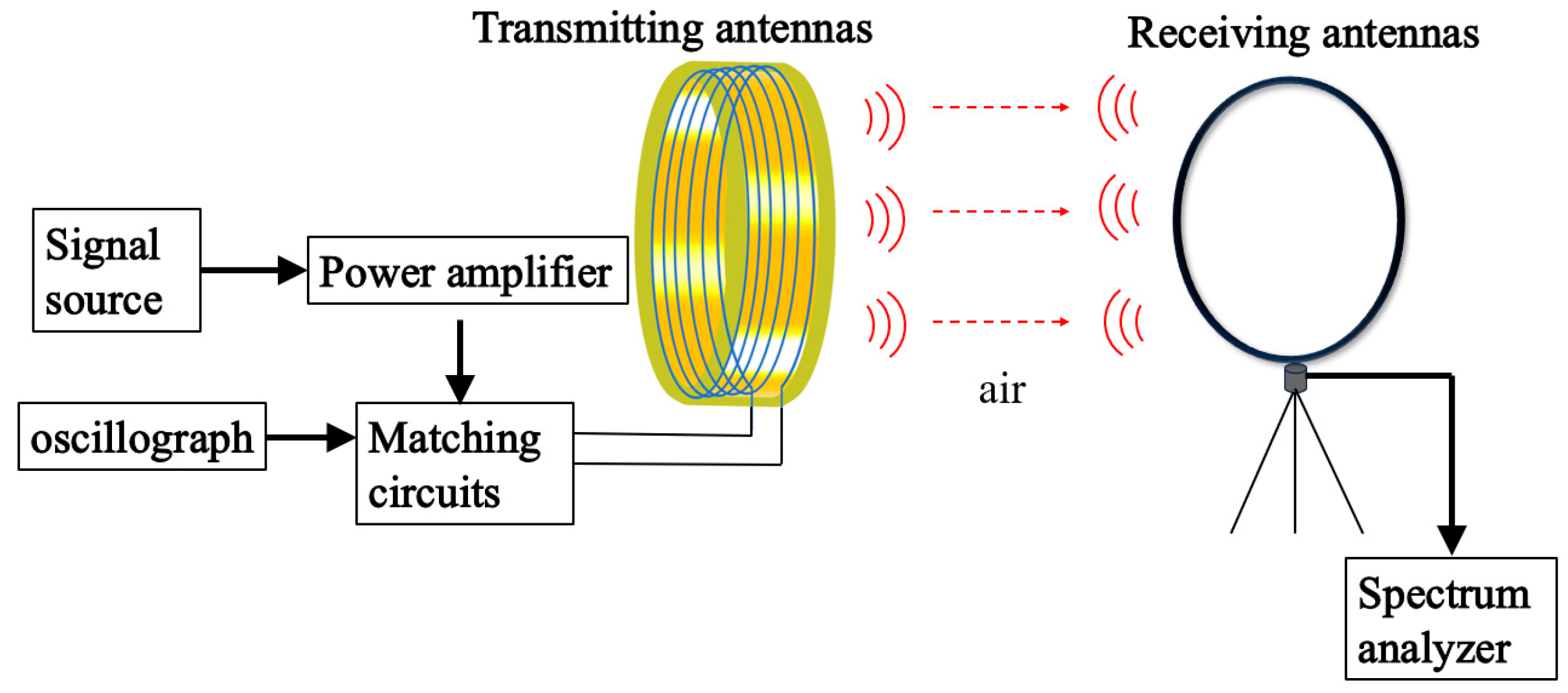
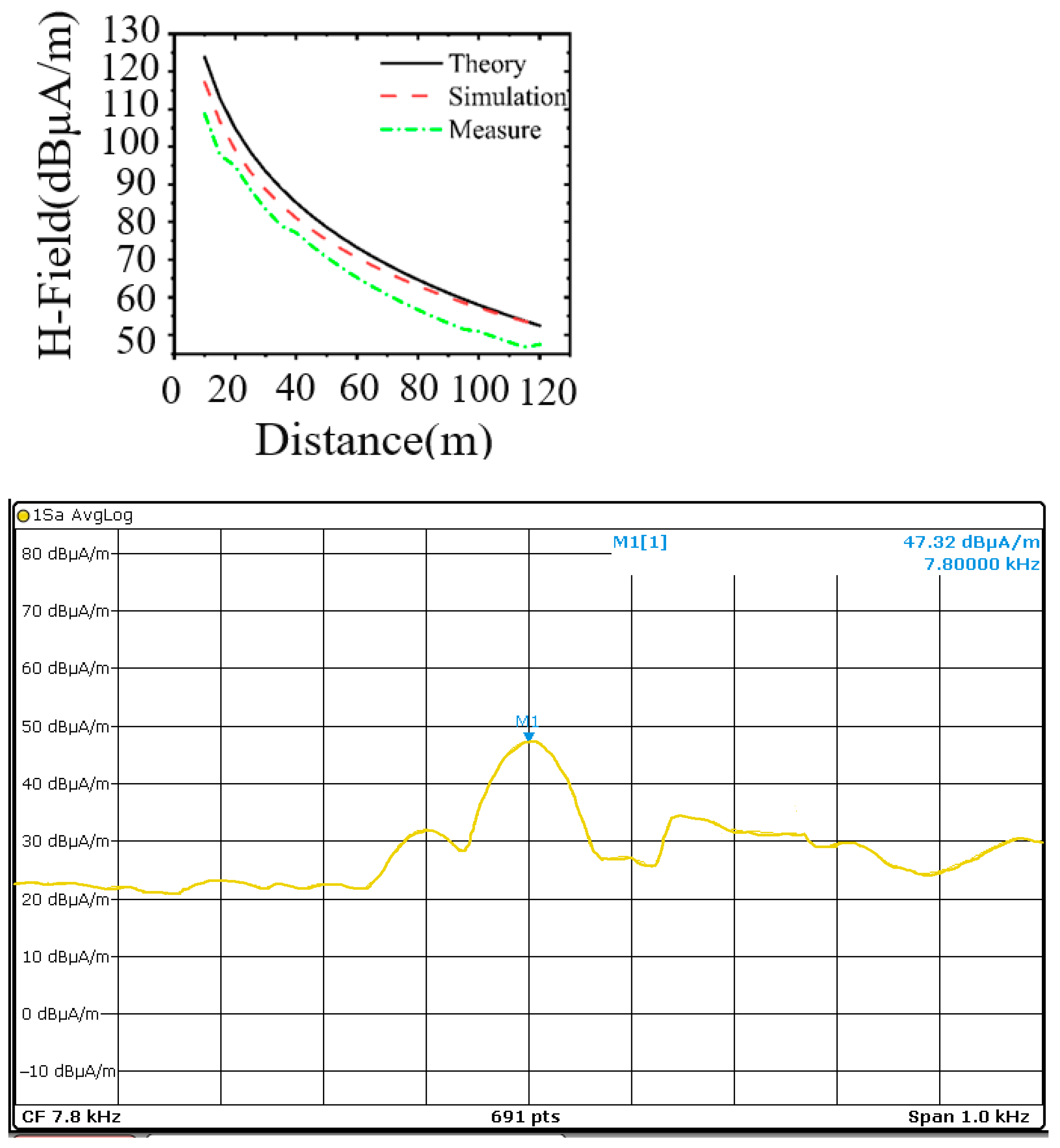
3. Experimental Verification
4. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chu, Z.; Mao, Z.; Song, K.; Jiang, S.; Min, S.; Dan, W.; Yu, C.; Wu, M.; Ren, Y.; Lu, Z.; et al. A multilayered magnetoelectric transmitter with suppressed nonlinearity for portable VLF communication. Research 2023, 6, 0208. [Google Scholar] [PubMed]
- Cui, Y.; Wang, C.; Li, L.; Li, Y.; Song, X. Single-Side Fixed Magnetoelectric Antenna Design for High-Bitrate LF Wireless Communication. IEEE Antennas Wirel. Propag. Lett. 2024, 23, 1166–1170. [Google Scholar]
- Sun, F.; Zhang, F.; Ma, X.; Ji, Y.; Fang, G. Rotating Permanent Magnet Antenna Array Based on Near-Field Polarization Modulation. IEEE Antennas Wirel. Propag. Lett. 2022, 21, 1193–1197. [Google Scholar]
- Teysseyre, P.; Briand, C.; Marshall, R.; Cohen, M. Effect of ground conductivity on VLF wave propagation. Radio Sci. 2025, 60, 1–16. [Google Scholar]
- Wang, J.; Huang, Q.; Ma, Q.; Chang, S.; He, J.; Wang, H.; Zhou, X.; Xiao, F.; Gao, C. Classification of VLF/LF lightning signals using sensors and deep learning methods. Sensors 2020, 20, 1030. [Google Scholar] [CrossRef] [PubMed]
- Xiao, N.; Wang, Y.; Chen, L.; Wang, G.; Wen, Y.; Li, P. Low-Frequency Dual-Driven Magnetoelectric Antennas With Enhanced Transmission Efficiency and Broad Bandwidth. IEEE Antennas Wirel. Propag. Lett. 2023, 22, 34–38. [Google Scholar]
- Yang, S.; Geng, J.; Zhou, H.; Wang, K.; Zhao, X.; Lu, J.; Zhao, R.; Tang, X.; Zhang, Y.; Su, D.; et al. Long-range EM communication underwater with ultracompact ELF magneto-mechanical antenna. IEEE Trans. Antennas Propag. 2022, 71, 2082–2097. [Google Scholar]
- Kurs, A.; Karalis, A.; Moffatt, R.; Joannopoulos, J.D.; Fisher, P.; Soljacic, M. Wireless power transfer via strongly coupled magnetic resonances. Science 2007, 317, 83–86. [Google Scholar] [PubMed]
- Zeng, Z.; Wu, J.; Zhang, C.; Wang, L.; Zhang, Z.; Guo, Y.; Xu, J.; Bi, K. Low-frequency metamaterial antenna based on magnetic field coupling effect. Sci. China Technol. Sci. 2025, 68, 1420204. [Google Scholar]
- Wu, J.; Zeng, Z.; Wang, L.; Xu, J.; Bi, K. Isolation transformer based very low frequency antenna with enhanced radiation characteristics. Adv. Sci. 2025, 12, 2408770. [Google Scholar]
- Valchev, V.C.; Van den Bossche, A. Inductors and Transformers for Power Electronics; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Gołkowski, M.; Park, J.; Bittle, J.; Babaiahgari, B.; Rorrer, R.A.; Celinski, Z. Novel mechanical magnetic shutter antenna for ELF/VLF radiation. In Proceedings of the 2018 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, Boston, MA, USA, 8–13 July 2018. [Google Scholar]
- Ahmed, N.; Radchenko, A.; Pommerenke, D.; Zheng, Y.R. Design and evaluation of low-cost and energy-efficient magneto-inductive sensor nodes for wireless sensor networks. IEEE Syst. J. 2018, 13, 1135–1144. [Google Scholar]
- Forget, A.; Rangraz, P.; Bousquet, J.-F. A model of the magneto-inductive link with relays to cross the air-water interface. IEEE Trans. Antennas Propag. 2024, 72, 4549–4563. [Google Scholar]






| Thickness-to-Diameter Ratio | Effective Permeability Factor m | Effective Permeability μeff |
|---|---|---|
| 0.02 | 0.1654 | 8270 |
| 0.05 | 0.16208 | 8104 |
| 0.08 | 0.22 | 11,000 |
| 0.1 | 0.2332 | 11,660 |
| 0.12 | 0.33218 | 16,609 |
| 0.15 | 0.29936 | 14,968 |
| 0.18 | 0.29856 | 14,928 |
| 0.2 | 0.20508 | 10,254 |
| 0.23 | 0.30824 | 15,412 |
| 0.25 | 0.34852 | 17,291 |
| 0.28 | 0.33508 | 16,754 |
| 0.3 | 0.37804 | 18,902 |
| Materia | Permeability | Bs | Coercion | Resistivity | Tc |
|---|---|---|---|---|---|
| silicon steel | 2000~5000 | 1.5~2.0 T | 10~50 A/m | 4 × 10−5 Ω·m | 730 °C |
| amorphous alloy | 20,000~30,000 | 1.2~1.6 T | 1~10 A/m | 1 × 10−6 Ω·m | 415 °C |
| nanocrystalline alloys | 30,000~50,000 | 1.0~1.4 T | 0.5~5 A/m | 1 × 10−7 Ω·m | 560 °C |
| ferrite | 2000~10,000 | 0.3~0.5 T | 100~500 A/m | 1 × 10−3 Ω·m | 180 °C |
| Sign | Clarification | Value |
|---|---|---|
| Ring antenna (with core) | ||
| w | Antenna width | 50 mm |
| d | Antenna ring diameter | 510 mm |
| wt | Antenna weight | 2.5 kg |
| Nt | Number of turns | 10 |
| a | Leeds wire diameter | 6 mm |
| Nanocrystalline Alloy Cores | ||
| μr | Relative permeability | 50,000 |
| ρm | density | 7.2 g/cm3 |
| cρ | Resistivity | 1.8 μΩ/m |
| Bs | Saturation magnetic field density | 1.2 T |
| tanδ | Loss angle tangent (math.) | 0.01 |
| Methodologies | Frequency | Turns | Ring Diameter | Leeds Wire Diameter | Ring Impedance | Tuning Capacitor |
|---|---|---|---|---|---|---|
| Theory | 3 kHz | 10 | 0.51 m | 6 mm | 0.16 + j16.58Ω | 3.2 μF |
| 7.8 kHz | 10 | 0.51 m | 6 mm | 0.44 + j43.12Ω | 0.47 μF | |
| 13 kHz | 10 | 0.51 m | 6 mm | 0.71 + j71.88Ω | 0.17 μF | |
| 18 kHz | 10 | 0.51 m | 6 mm | 0.99 + j99.52Ω | 0.08 μF | |
| 23 kHz | 10 | 0.51 m | 6 mm | 1.27 + j127.17Ω | 0.05 μF | |
| 28 kHz | 10 | 0.51 m | 6 mm | 1.54 + j154.81Ω | 0.04 μF | |
| Simulation | 3 kHz | 10 | 0.51 m | 6 mm | 0.16 + j3.3Ω | 16 μF |
| 7.8 kHz | 10 | 0.51 m | 6 mm | 0.48 + j8.7Ω | 2.3 μF | |
| 13 kHz | 10 | 0.51 m | 6 mm | 0.75 + j14.1Ω | 0.9 μF | |
| 18 kHz | 10 | 0.51 m | 6 mm | 1.1 + j19.5Ω | 0.45 μF | |
| 23 kHz | 10 | 0.51 m | 6 mm | 1.4 + j24.9Ω | 0.27 μF | |
| 28 kHz | 10 | 0.51 m | 6 mm | 1.7 + j30.3Ω | 0.18 μF |
| Type of Program | Sizes | Freq | Power | Magnetic Flux/ Transmission Distance | References |
|---|---|---|---|---|---|
| Magnet-based Mechanical antenna | - | 1.6 kHz | 20 W | 5 m (50 pT) | [12] |
| Loop antenna | 30 cm | 15 kHz | 200 W | 135 m | [10] |
| Relay waveguide system | 22 cm | 125 kHz | - | 40 m | [13] |
| Relay waveguide system | 12 cm | 1 kHz | 20 W | 25 m | [14] |
| Metamaterial antenna | 18 cm | 41.4 kHz | 200 W | 180 m (0.16 pT) | [9] |
| Nanomaterials antenna | 51 cm | 7.8 kHz | 1200 W | 1446 m (0.16 pT) | This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ai, W.; Wu, H.; Zhao, L.; Xie, H. High-Power-Density Miniaturized VLF Antenna with Nanocrystalline Core for Enhanced Field Strength. Nanomaterials 2025, 15, 1062. https://doi.org/10.3390/nano15141062
Ai W, Wu H, Zhao L, Xie H. High-Power-Density Miniaturized VLF Antenna with Nanocrystalline Core for Enhanced Field Strength. Nanomaterials. 2025; 15(14):1062. https://doi.org/10.3390/nano15141062
Chicago/Turabian StyleAi, Wencheng, Huaning Wu, Lin Zhao, and Hui Xie. 2025. "High-Power-Density Miniaturized VLF Antenna with Nanocrystalline Core for Enhanced Field Strength" Nanomaterials 15, no. 14: 1062. https://doi.org/10.3390/nano15141062
APA StyleAi, W., Wu, H., Zhao, L., & Xie, H. (2025). High-Power-Density Miniaturized VLF Antenna with Nanocrystalline Core for Enhanced Field Strength. Nanomaterials, 15(14), 1062. https://doi.org/10.3390/nano15141062






