First-Principles Study of Halide Modulation on Deep-Level Traps in FAPbI3
Abstract
1. Introduction
2. Calculation Methods
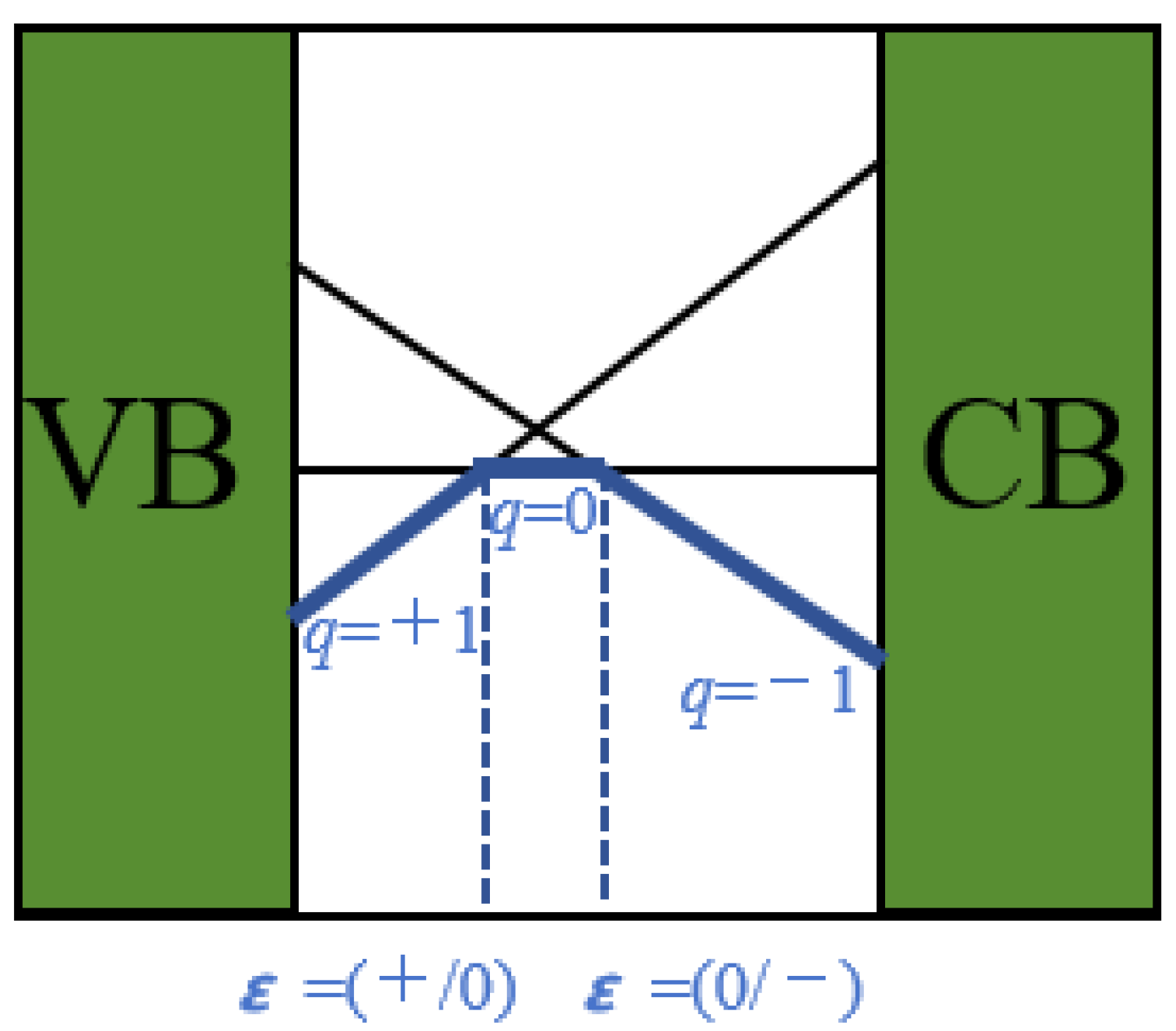
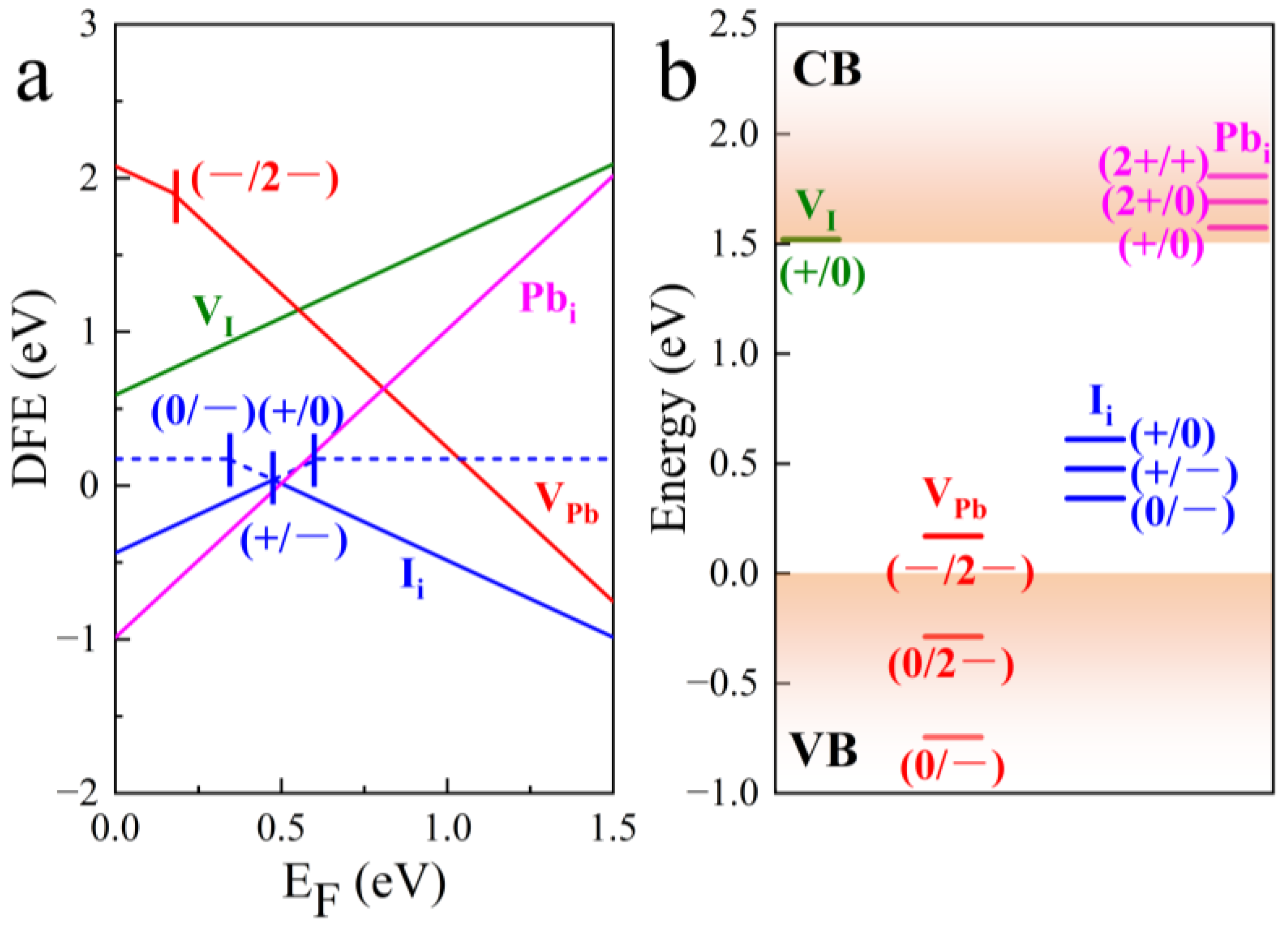
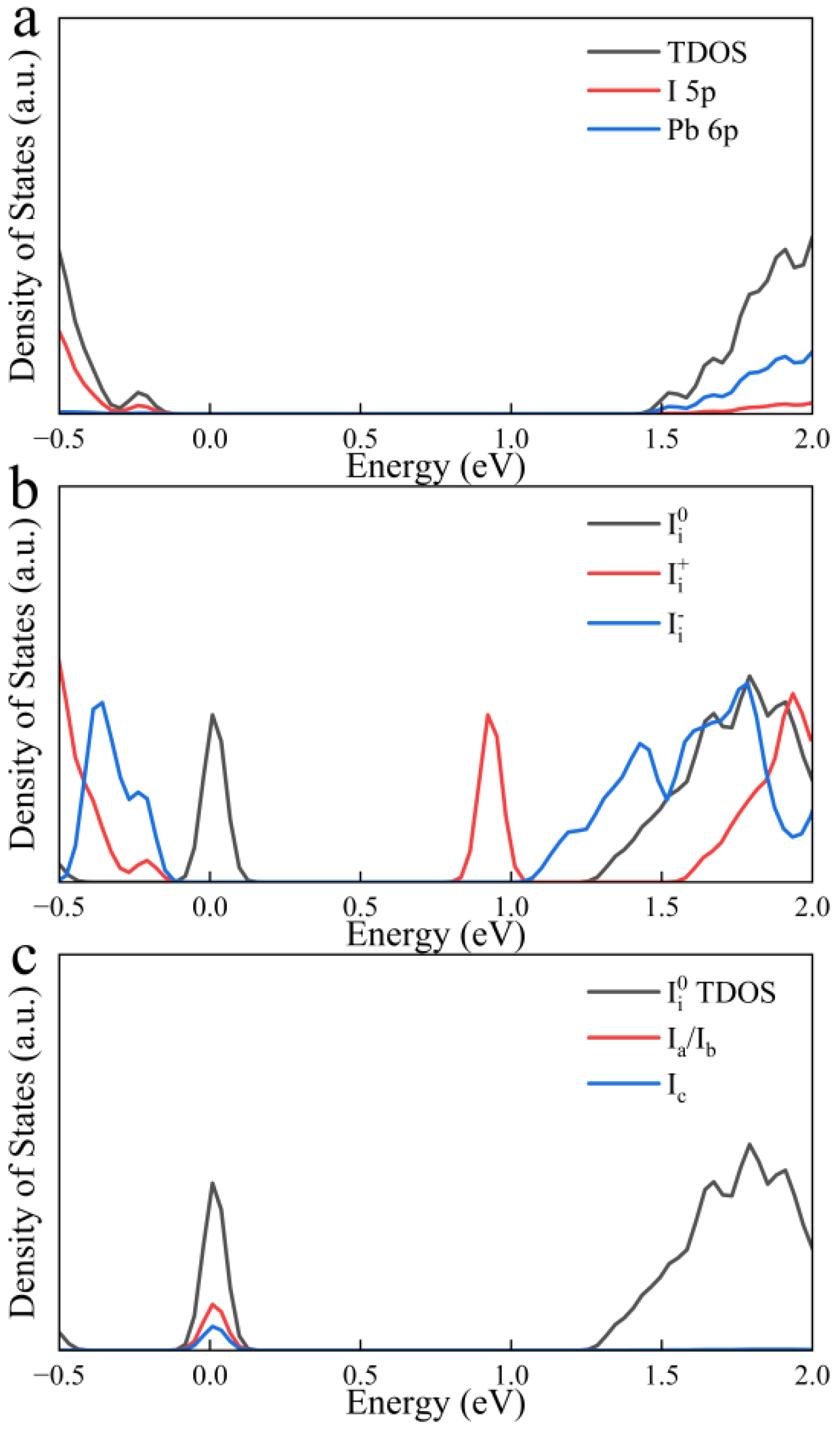
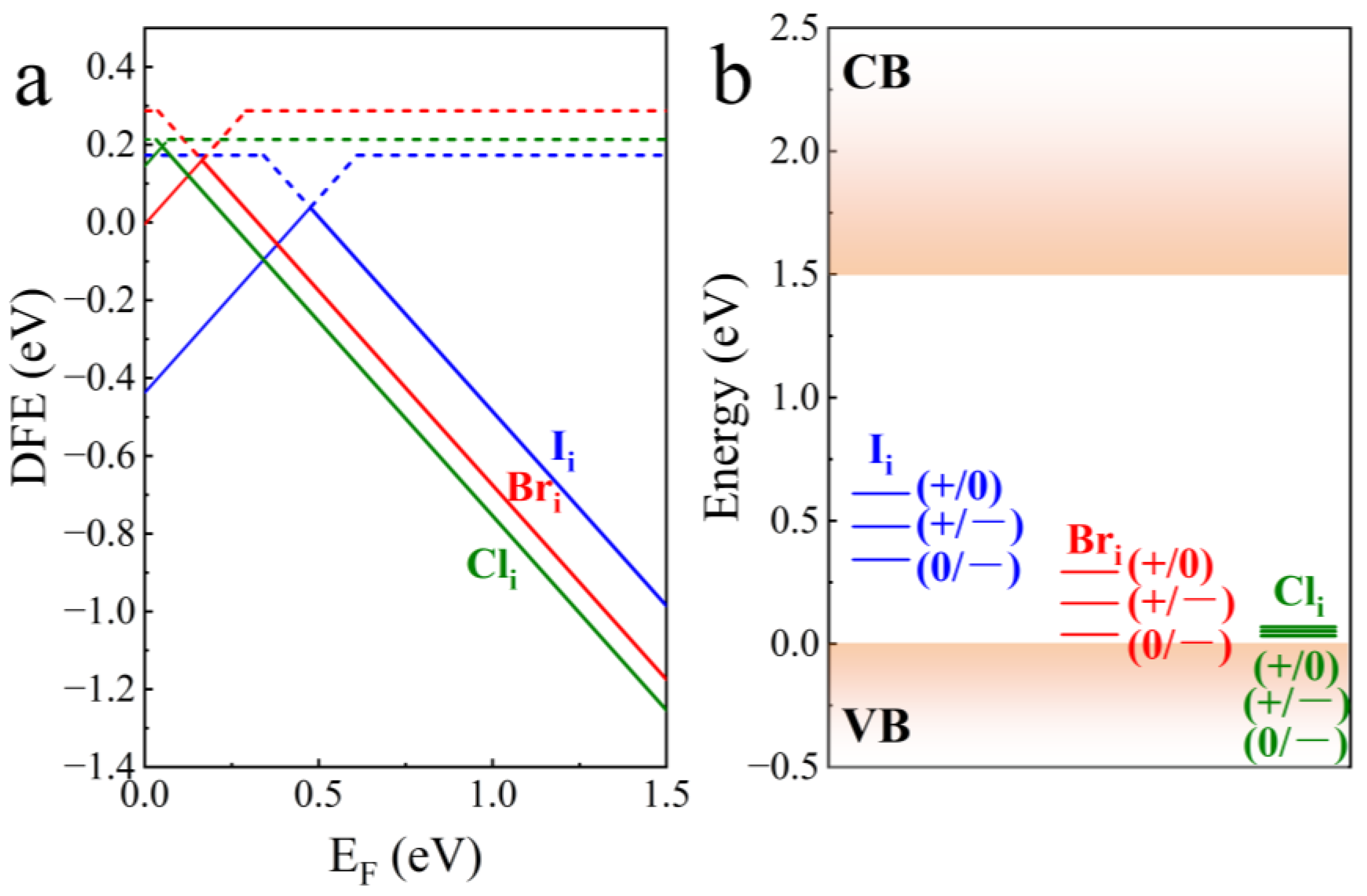
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, W.; Saliba, M.; Moore, D.T.; Pathak, S.K.; Horantner, M.T.; Stergiopoulos, T.; Stranks, S.D.; Eperon, G.E.; Alexander-Webber, J.A.; Abate, A.; et al. Ultrasmooth organic-inorganic perovskite thin-film formation and crystallization for efficient planar heterojunction solar cells. Nat. Commun. 2015, 6, 6142. [Google Scholar] [CrossRef] [PubMed]
- Lin, Q.; Armin, A.; Nagiri, R.C.R.; Burn, P.L.; Meredith, P. Electro-optics of perovskite solar cells. Nat. Photonics 2014, 9, 106–112. [Google Scholar] [CrossRef]
- Zhao, C.; Zhang, H.; Almalki, M.; Xu, J.; Krishna, A.; Eickemeyer, F.T.; Gao, J.; Wu, Y.M.; Zakeeruddin, S.M.; Chu, J.; et al. Stabilization of FAPbI(3) with Multifunctional Alkali-Functionalized Polymer. Adv. Mater. 2023, 35, e2211619. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Zhang, S.; Ji, X.; He, J.; Guo, H.; Wang, S.; Wu, W.; Zhu, W.H.; Wu, Y. Formamidinium Lead Iodide-Based Inverted Perovskite Solar Cells with Efficiency over 25% Enabled by An Amphiphilic Molecular Hole-Transporter. Angew. Chem. Int. Ed. Engl. 2024, 63, e202401260. [Google Scholar] [CrossRef]
- Kim, H.S.; Park, N.G. Soft Lattice and Phase Stability of α-FAPbI3. Adv. Energy Mater. 2024, 15, 2400089. [Google Scholar] [CrossRef]
- Kim, H.S.; Park, N.G. Future Research Directions in Perovskite Solar Cells: Exquisite Photon Management and Thermodynamic Phase Stability. Adv. Mater. 2023, 35, e2204807. [Google Scholar] [CrossRef]
- Koh, T.M.; Fu, K.; Fang, Y.; Chen, S.; Sum, T.C.; Mathews, N.; Mhaisalkar, S.G.; Boix, P.P.; Baikie, T. Formamidinium-Containing Metal-Halide: An Alternative Material for Near-IR Absorption Perovskite Solar Cells. J. Phys. Chem. C 2013, 118, 16458–16462. [Google Scholar] [CrossRef]
- Alaei, A.; Circelli, A.; Yuan, Y.; Yang, Y.; Lee, S.S. Polymorphism in metal halide perovskites. Mater. Adv. 2021, 2, 47–63. [Google Scholar] [CrossRef]
- Jacobsson, T.J.; Hultqvist, A.; García-Fernández, A.; Anand, A.; Al-Ashouri, A.; Hagfeldt, A.; Crovetto, A.; Abate, A.; Ricciardulli, A.G.; Vijayan, A.; et al. An open-access database and analysis tool for perovskite solar cells based on the FAIR data principles. Nat. Energy 2021, 7, 107–115. [Google Scholar] [CrossRef]
- Hoeksma, M.M.; Williams, R.M. Synergistic Zinc(II) and Formate Doping of Perovskites: Thermal Phase Stabilization of α-FAPbI3 and Enhanced Photoluminescence Lifetime of FA0.8MA0.2PbI3 up to 3.7 µs. Molecules 2024, 29, 516. [Google Scholar] [CrossRef]
- Ghosh, D.; Smith, A.R.; Walker, A.B.; Islam, M.S. Mixed A-Cation Perovskites for Solar Cells: Atomic-Scale Insights into Structural Distortion, Hydrogen Bonding, and Electronic Properties. Chem. Mater. 2018, 30, 5194–5204. [Google Scholar] [CrossRef]
- Liu, N.; Yam, C. First-principles study of intrinsic defects in formamidinium lead triiodide perovskite solar cell absorbers. Phys. Chem. Chem. Phys. 2018, 20, 6800–6804. [Google Scholar] [CrossRef] [PubMed]
- Ke, W.; Xiao, C.; Wang, C.; Saparov, B.; Duan, H.S.; Zhao, D.; Xiao, Z.; Schulz, P.; Harvey, S.P.; Liao, W.; et al. Employing Lead Thiocyanate Additive to Reduce the Hysteresis and Boost the Fill Factor of Planar Perovskite Solar Cells. Adv. Mater. 2016, 28, 5214–5221. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Yu, Z.; Wang, T.; Chiu, K.L.; Lin, F.; Gong, H.; Ding, L.; Cheng, Y. Full Defects Passivation Enables 21% Efficiency Perovskite Solar Cells Operating in Air. Adv. Energy Mater. 2020, 10, 2001958. [Google Scholar] [CrossRef]
- Hu, Y.; Shan, Y.; Yu, Z.; Sui, H.; Qiu, T.; Zhang, S.; Ruan, W.; Xu, Q.; Jiao, M.; Wang, D.; et al. Incorporation of γ-aminobutyric acid and cesium cations to formamidinium lead halide perovskites for highly efficient solar cells. J. Energy Chem. 2022, 64, 561–567. [Google Scholar] [CrossRef]
- Saidaminov, M.I.; Adinolfi, V.; Comin, R.; Abdelhady, A.L.; Peng, W.; Dursun, I.; Yuan, M.; Hoogland, S.; Sargent, E.H.; Bakr, O.M. Planar-integrated single-crystalline perovskite photodetectors. Nat. Commun. 2015, 6, 8724. [Google Scholar] [CrossRef]
- Kim, J.; Lee, S.H.; Lee, J.H.; Hong, K.H. The Role of Intrinsic Defects in Methylammonium Lead Iodide Perovskite. J. Phys. Chem. Lett. 2014, 5, 1312–1317. [Google Scholar] [CrossRef]
- Zhang, X.; Shen, J.X.; Turiansky, M.E.; Van de Walle, C.G. Minimizing hydrogen vacancies to enable highly efficient hybrid perovskites. Nat. Mater. 2021, 20, 971–976. [Google Scholar] [CrossRef]
- Shockley, W.; Read, W.T. Statistics of the Recombinations of Holes and Electrons. Phys. Rev. 1952, 87, 835–842. [Google Scholar] [CrossRef]
- Yang, W.; Su, R.; Luo, D.; Hu, Q.; Zhang, F.; Xu, Z.; Wang, Z.; Tang, J.; Lv, Z.; Yang, X.; et al. Surface modification induced by perovskite quantum dots for triple-cation perovskite solar cells. Nano Energy 2020, 67, 104189. [Google Scholar] [CrossRef]
- Luo, D.; Su, R.; Zhang, W.; Gong, Q.; Zhu, R. Minimizing non-radiative recombination losses in perovskite solar cells. Nat. Rev. Mater. 2019, 5, 44–60. [Google Scholar] [CrossRef]
- Zhu, X.; Wang, C.; Zhang, C.; Wang, Z.; Feng, J.; Liu, S.; Yang, D. Imidazolium-based ionic liquid for stable and highly efficient black-phase formamidinium-based perovskite solar cell. Chem. Eng. J. 2022, 434, 134759. [Google Scholar] [CrossRef]
- Ueki, T.; Itsumi, M.; Takeda, T. Octahedral void defects observed in the bulk of Czochralski silicon. Appl. Phys. Lett. 1997, 70, 1248–1250. [Google Scholar] [CrossRef]
- Ayres, J.R. Characterization of trapping states in polycrystalline-silicon thin film transistors by deep level transient spectroscopy. J. Appl. Phys. 1993, 74, 1787–1792. [Google Scholar] [CrossRef]
- Balcioglu, A.; Ahrenkiel, R.K.; Hasoon, F. Deep-level impurities in CdTe/CdS thin-film solar cells. J. Appl. Phys. 2000, 88, 7175–7178. [Google Scholar] [CrossRef]
- Kerr, L.L.; Li, S.S.; Johnston, S.W.; Anderson, T.J.; Crisalle, O.D.; Kim, W.K.; Abushama, J.; Noufi, R.N. Investigation of defect properties in Cu(In,Ga)Se2 solar cells by deep-level transient spectroscopy. Solid-State Electron. 2004, 48, 1579–1586. [Google Scholar] [CrossRef]
- Gao, Z.W.; Wang, Y.; Liu, H.; Sun, J.; Kim, J.; Li, Y.; Xu, B.; Choy, W.C.H. Tailoring the Interface in FAPbI3 Planar Perovskite Solar Cells by Imidazole-Graphene-Quantum-Dots. Adv. Funct. Mater. 2021, 31, 2101438. [Google Scholar] [CrossRef]
- Buin, A.; Comin, R.; Xu, J.; Ip, A.H.; Sargent, E.H. Halide-Dependent Electronic Structure of Organolead Perovskite Materials. Chem. Mater. 2015, 27, 4405–4412. [Google Scholar] [CrossRef]
- deQuilettes, D.W.; Laitz, M.; Brenes, R.; Dou, B.; Motes, B.T.; Stranks, S.D.; Snaith, H.J.; Bulović, V.; Ginger, D.S. Maximizing the external radiative efficiency of hybrid perovskite solar cells. Pure Appl. Chem. 2020, 92, 697–706. [Google Scholar] [CrossRef]
- Mu, C.; Pan, J.; Feng, S.; Li, Q.; Xu, D. Quantitative Doping of Chlorine in Formamidinium Lead Trihalide (FAPbI3−xClx) for Planar Heterojunction Perovskite Solar Cells. Adv. Energy Mater. 2016, 7, 1601297. [Google Scholar] [CrossRef]
- Mariotti, S.; Köhnen, E.; Scheler, F.; Sveinbjörnsson, K.; Zimmermann, L.; Piot, M.; Yang, F.; Li, B.; Warby, J.; Musiienko, A.; et al. Interface engineering for high-performance, triple-halide perovskite–silicon tandem solar cells. Science 2023, 381, 63–69. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Boyd, C.C.; Yu, Z.J.; Palmstrom, A.F.; Witter, D.J.; Larson, B.W.; France, R.M.; Werner, J.; Harvey, S.P.; Wolf, E.J.; et al. Triple-halide wide–band gap perovskites with suppressed phase segregation for efficient tandems. Science 2020, 367, 1097–1104. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Weller, M.T.; Weber, O.J.; Frost, J.M.; Walsh, A. Cubic Perovskite Structure of Black Formamidinium Lead Iodide, α-[HC(NH2)2]PbI3, at 298 K. J. Phys. Chem. Lett. 2015, 6, 3209–3212. [Google Scholar] [CrossRef]
- Chen, T.; Chen, W.-L.; Foley, B.J.; Lee, J.; Ruff, J.P.C.; Ko, J.Y.P.; Brown, C.M.; Harriger, L.W.; Zhang, D.; Park, C.; et al. Origin of long lifetime of band-edge charge carriers in organic–inorganic lead iodide perovskites. Proc. Natl. Acad. Sci. USA 2017, 114, 7519–7524. [Google Scholar] [CrossRef]
- Wu, Y.N.; Zhang, X.G.; Pantelides, S.T. Fundamental Resolution of Difficulties in the Theory of Charged Point Defects in Semiconductors. Phys. Rev. Lett. 2017, 119, 105501. [Google Scholar] [CrossRef]
- Weber, O.J.; Ghosh, D.; Gaines, S.; Henry, P.F.; Walker, A.B.; Islam, M.S.; Weller, M.T. Phase Behavior and Polymorphism of Formamidinium Lead Iodide. Chem. Mater. 2018, 30, 3768–3778. [Google Scholar] [CrossRef]
- Even, J.; Pedesseau, L.; Jancu, J.-M.; Katan, C. Importance of Spin–Orbit Coupling in Hybrid Organic/Inorganic Perovskites for Photovoltaic Applications. J. Phys. Chem. Lett. 2013, 4, 2999–3005. [Google Scholar] [CrossRef]
- Muhammad, Z.; Liu, P.; Ahmad, R.; Jalali-Asadabadi, S.; Franchini, C.; Ahmad, I. Revealing the quasiparticle electronic and excitonic nature in cubic, tetragonal, and hexagonal phases of FAPbI3. AIP Adv. 2022, 12, 025330. [Google Scholar] [CrossRef]
- Mosconi, E.; Amat, A.; Nazeeruddin, M.K.; Grätzel, M.; De Angelis, F. First-Principles Modeling of Mixed Halide Organometal Perovskites for Photovoltaic Applications. J. Phys. Chem. C 2013, 117, 13902–13913. [Google Scholar] [CrossRef]
- Pisanu, A.; Ferrara, C.; Quadrelli, P.; Guizzetti, G.; Patrini, M.; Milanese, C.; Tealdi, C.; Malavasi, L. The FA1–xMAxPbI3 System: Correlations among Stoichiometry Control, Crystal Structure, Optical Properties, and Phase Stability. J. Phys. Chem. C 2017, 121, 8746–8751. [Google Scholar] [CrossRef]
- Yin, W.-J.; Shi, T.; Yan, Y. Unusual defect physics in CH3NH3PbI3 perovskite solar cell absorber. Appl. Phys. Lett. 2014, 104, 4864778. [Google Scholar] [CrossRef]
- Freysoldt, C.; Neugebauer, J.; Van de Walle, C.G. Fully ab initio finite-size corrections for charged-defect supercell calculations. Phys. Rev. Lett. 2009, 102, 016402. [Google Scholar] [CrossRef]
- Komsa, H.P.; Pasquarello, A. Finite-size supercell correction for charged defects at surfaces and interfaces. Phys. Rev. Lett. 2013, 110, 095505. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, Y.; Kitipornchai, S.; Yang, J. Opto-electro-thermo-mechanical behaviours of perovskite plates. Int. J. Mech. Sci. 2024, 267, 109016. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, L.; Zhao, B.; Chen, H.; Liu, X.; Zhao, R.; Wang, X.; Liu, J.; Chen, Y.; Liu, M. Improving the Activity for Oxygen Evolution Reaction by Tailoring Oxygen Defects in Double Perovskite Oxides. Adv. Funct. Mater. 2019, 29, 1901783. [Google Scholar] [CrossRef]
- Freysoldt, C.; Grabowski, B.; Hickel, T.; Neugebauer, J.; Kresse, G.; Janotti, A.; Van de Walle, C.G. First-principles calculations for point defects in solids. Rev. Mod. Phys. 2014, 86, 253–305. [Google Scholar] [CrossRef]
- Meggiolaro, D.; De Angelis, F. First-Principles Modeling of Defects in Lead Halide Perovskites: Best Practices and Open Issues. ACS Energy Lett. 2018, 3, 2206–2222. [Google Scholar] [CrossRef]
- Ren, X.; Wang, J.; Lin, Y.; Wang, Y.; Xie, H.; Huang, H.; Yang, B.; Yan, Y.; Gao, Y.; He, J.; et al. Mobile iodides capture for highly photolysis- and reverse-bias-stable perovskite solar cells. Nat. Mater. 2024, 23, 810–817. [Google Scholar] [CrossRef]
- Eames, C.; Frost, J.M.; Barnes, P.R.; O’Regan, B.C.; Walsh, A.; Islam, M.S. Ionic transport in hybrid lead iodide perovskite solar cells. Nat. Commun. 2015, 6, 7497. [Google Scholar] [CrossRef]
- Azpiroz, J.M.; Mosconi, E.; Bisquert, J.; De Angelis, F. Defect migration in methylammonium lead iodide and its role in perovskite solar cell operation. Energy Environ. Sci. 2015, 8, 2118–2127. [Google Scholar] [CrossRef]
- Yang, J.-H.; Yin, W.-J.; Park, J.-S.; Wei, S.-H. Fast self-diffusion of ions in CH3NH3PbI3: The interstiticaly mechanism versus vacancy-assisted mechanism. J. Mater. Chem. A 2016, 4, 13105–13112. [Google Scholar] [CrossRef]
- Adinolfi, V.; Yuan, M.; Comin, R.; Thibau, E.S.; Shi, D.; Saidaminov, M.I.; Kanjanaboos, P.; Kopilovic, D.; Hoogland, S.; Lu, Z.H.; et al. The In-Gap Electronic State Spectrum of Methylammonium Lead Iodide Single-Crystal Perovskites. Adv. Mater. 2016, 28, 3406–3410. [Google Scholar] [CrossRef] [PubMed]
- Oner, S.M.; Sezen, E.; Yordanli, M.S.; Karakoc, E.; Deger, C.; Yavuz, I. Surface Defect Formation and Passivation in Formamidinium Lead Triiodide (FAPbI(3)) Perovskite Solar Cell Absorbers. J. Phys. Chem. Lett. 2022, 13, 324–330. [Google Scholar] [CrossRef]
- Sadoughi, G.; Starr, D.E.; Handick, E.; Stranks, S.D.; Gorgoi, M.; Wilks, R.G.; Bar, M.; Snaith, H.J. Observation and Mediation of the Presence of Metallic Lead in Organic-Inorganic Perovskite Films. ACS Appl. Mater. Interfaces 2015, 7, 13440–13444. [Google Scholar] [CrossRef]
- Mosconi, E.; Meggiolaro, D.; Snaith, H.J.; Stranks, S.D.; De Angelis, F. Light-induced annihilation of Frenkel defects in organo-lead halide perovskites. Energy Environ. Sci. 2016, 9, 3180–3187. [Google Scholar] [CrossRef]
- Wu, T.; Chen, S.; Su, Z.; Wang, Z.; Luo, P.; Zheng, Z.; Luo, J.; Ma, H.; Zhang, X.; Liang, G. Heat treatment in an oxygen-rich environment to suppress deep-level traps in Cu2ZnSnS4 solar cell with 11.51% certified efficiency. Nat. Energy 2025, 10, 630–640. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, H.; Xian, Y.; Shi, Z.; Aboa, J.N.; Fei, C.; Yang, G.; Li, N.; Selim, F.A.; Yan, Y.; et al. Enhancing charge-emitting shallow traps in metal halide perovskites by >100 times by surface strain. Joule 2025, 9, 101772. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, Z.; Cao, L.; Kou, D.; Yuan, S.; Zheng, Z.; Yang, G.; Tian, Q.; Wu, S.; Liu, S. Suppressed Interface Defects by GeSe2 Post-Deposition Treatment Enables High-Efficiency Kesterite Solar Cells. Adv. Funct. Mater. 2022, 33, 2211315. [Google Scholar] [CrossRef]
- He, J.; Fang, W.H.; Long, R. Unravelling the effects of oxidation state of interstitial iodine and oxygen passivation on charge trapping and recombination in CH(3)NH(3)PbI(3) perovskite: A time-domain ab initio study. Chem. Sci. 2019, 10, 10079–10088. [Google Scholar] [CrossRef]
- Meggiolaro, D.; Mosconi, E.; De Angelis, F. Modeling the Interaction of Molecular Iodine with MAPbI3: A Probe of Lead-Halide Perovskites Defect Chemistry. ACS Energy Lett. 2018, 3, 447–451. [Google Scholar] [CrossRef]
- Lin, C.; Zhao, Y.; Liu, Y.; Zhang, W.; Shao, C.; Yang, Z. The bandgap regulation and optical properties of alloyed Cs2NaSbX6 (X=Cl, Br, I) systems with first principle method. J. Mater. Res. Technol. 2021, 11, 1645–1653. [Google Scholar] [CrossRef]
- Noh, J.H.; Im, S.H.; Heo, J.H.; Mandal, T.N.; Seok, S.I. Chemical management for colorful, efficient, and stable inorganic-organic hybrid nanostructured solar cells. Nano Lett. 2013, 13, 1764–1769. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Zhang, X.; Wang, C.; Sun, M.; Luo, X.; Yang, Y.; Chang, S.; Zhang, D.; Duan, L. Chlorine distribution management for spectrally stable and efficient perovskite blue light-emitting diodes. Nano Energy 2021, 79, 105486. [Google Scholar] [CrossRef]
- Varnakavi, N.; Velpugonda, J.L.; Lee, N.; Nah, S.; Lin, L.Y. In Situ Synthesis of Br-Rich CsPbBr3 Nanoplatelets: Enhanced Stability and High PLQY for Wide Color Gamut Displays. Adv. Funct. Mater. 2024, 35, 2413320. [Google Scholar] [CrossRef]
- Hoover, W.G.; Ladd, A.J.C.; Moran, B. High-Strain-Rate Plastic Flow Studied via Nonequilibrium Molecular Dynamics. Phys. Rev. Lett. 1982, 48, 1818–1820. [Google Scholar] [CrossRef]
- Evans, D.J. Computer ‘‘experiment’’ for nonlinear thermodynamics of Couette flow. J. Chem. Phys. 1983, 78, 3297–3302. [Google Scholar] [CrossRef]
- Tang, W.; Fu, S.; Sun, X.; Jiao, S.; Jiang, J.; Xu, C.; Cai, H.; Wu, X.S. Structure and optical properties of Cs2TiBrxI6−x. Mater. Today Commun. 2024, 40, 109859. [Google Scholar] [CrossRef]
- Lu, H.; Liu, Y.; Ahlawat, P.; Mishra, A.; Tress, W.R.; Eickemeyer, F.T.; Yang, Y.; Fu, F.; Wang, Z.; Avalos, C.E.; et al. Vapor-assisted deposition of highly efficient, stable black-phase FAPbI 3 perovskite solar cells. Science 2020, 370, abb8985. [Google Scholar] [CrossRef]
- Osetsky, Y.; Barashev, A.V.; Béland, L.K.; Yao, Z.; Ferasat, K.; Zhang, Y. Tunable chemical complexity to control atomic diffusion in alloys. npj Comput. Mater. 2020, 6, 1–8. [Google Scholar] [CrossRef]
- Futscher, M.H.; Lee, J.M.; McGovern, L.; Muscarella, L.A.; Wang, T.; Haider, M.I.; Fakharuddin, A.; Schmidt-Mende, L.; Ehrler, B. Quantification of ion migration in CH3NH3PbI3 perovskite solar cells by transient capacitance measurements. Mater. Horiz. 2019, 6, 1497–1503. [Google Scholar] [CrossRef]
- Lyu, M.; Park, N.-G. Effect of Additives AX (A = FA, MA, Cs, Rb, NH4, X = Cl, Br, I) in FAPbI3 on Photovoltaic Parameters of Perovskite Solar Cells. Sol. RRL 2020, 4, 331. [Google Scholar] [CrossRef]
- Naik, M.H.; Jain, M. CoFFEE: Corrections For Formation Energy and Eigenvalues for charged defect simulations. Comput. Phys. Commun. 2018, 226, 114–126. [Google Scholar] [CrossRef]
- Woolard, E.W.; Einstein, A.; Furth, R.; Cowper, A.D. Investigations on the Theory of the Brownian Movement. Am. Math. Mon. 1928, 35. [Google Scholar] [CrossRef]
- Joo, S.H.; Choi, H.W. Compositional Engineering of FAPbI3 Perovskite Added MACl with MAPbBr3 or FAPbBr3. Coatings 2021, 11, 1184. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Zhang, L.; Hu, H.; Tang, Z.; Xu, B.; Park, N.G. Propylammonium Chloride Additive for Efficient and Stable FAPbI3 Perovskite Solar Cells. Adv. Energy Mater. 2021, 11, 2102538. [Google Scholar] [CrossRef]
- Ye, F.; Tian, T.; Su, J.; Jiang, R.; Li, J.; Jin, C.; Tong, J.; Bai, S.; Huang, F.; Müller-Buschbaum, P.; et al. Tailoring Low-Dimensional Perovskites Passivation for Efficient Two-Step-Processed FAPbI3 Solar Cells and Modules. Adv. Energy Mater. 2023, 14, 2302775. [Google Scholar] [CrossRef]
- Zhao, C.; Zhang, Q.; Lyu, Y.; Liu, J.; Shen, F.; Liu, H.; Kong, H.; Han, H.; Krishna, A.; Xu, J.; et al. Regulating the Crystallization of FAPbI3-Based Perovskite with a Furan Substituted Ethylammonium Additive for Achieving Highly Efficient Solar Cells. Adv. Funct. Mater. 2024, 34, 2404099. [Google Scholar] [CrossRef]
- Cao, H.; Dong, Z.; Qiu, Y.; Li, J.; Wang, Y.; Li, Z.; Yang, L.; Yin, S. Precursor Engineering of Vapor-Exchange Processes for 20%-Efficient 1 cm(2) Inverted-Structure Perovskite Solar Cells. ACS Appl. Mater. Interfaces 2020, 12, 41303–41311. [Google Scholar] [CrossRef]
- Ling, X.; Zhu, H.; Xu, W.; Liu, C.; Pan, L.; Ren, D.; Yuan, J.; Larson, B.W.; Gratzel, C.; Kirmani, A.R.; et al. Combined Precursor Engineering and Grain Anchoring Leading to MA-Free, Phase-Pure, and Stable alpha-Formamidinium Lead Iodide Perovskites for Efficient Solar Cells. Angew. Chem. Int. Ed. Engl. 2021, 60, 27299–27306. [Google Scholar] [CrossRef]
- You, S.; Xi, X.; Zhang, X.; Wang, H.; Gao, P.; Ma, X.; Bi, S.; Zhang, J.; Zhou, H.; Wei, Z. Long-term stable and highly efficient perovskite solar cells with a formamidinium chloride (FACl) additive. J. Mater. Chem. A 2020, 8, 17756–17764. [Google Scholar] [CrossRef]

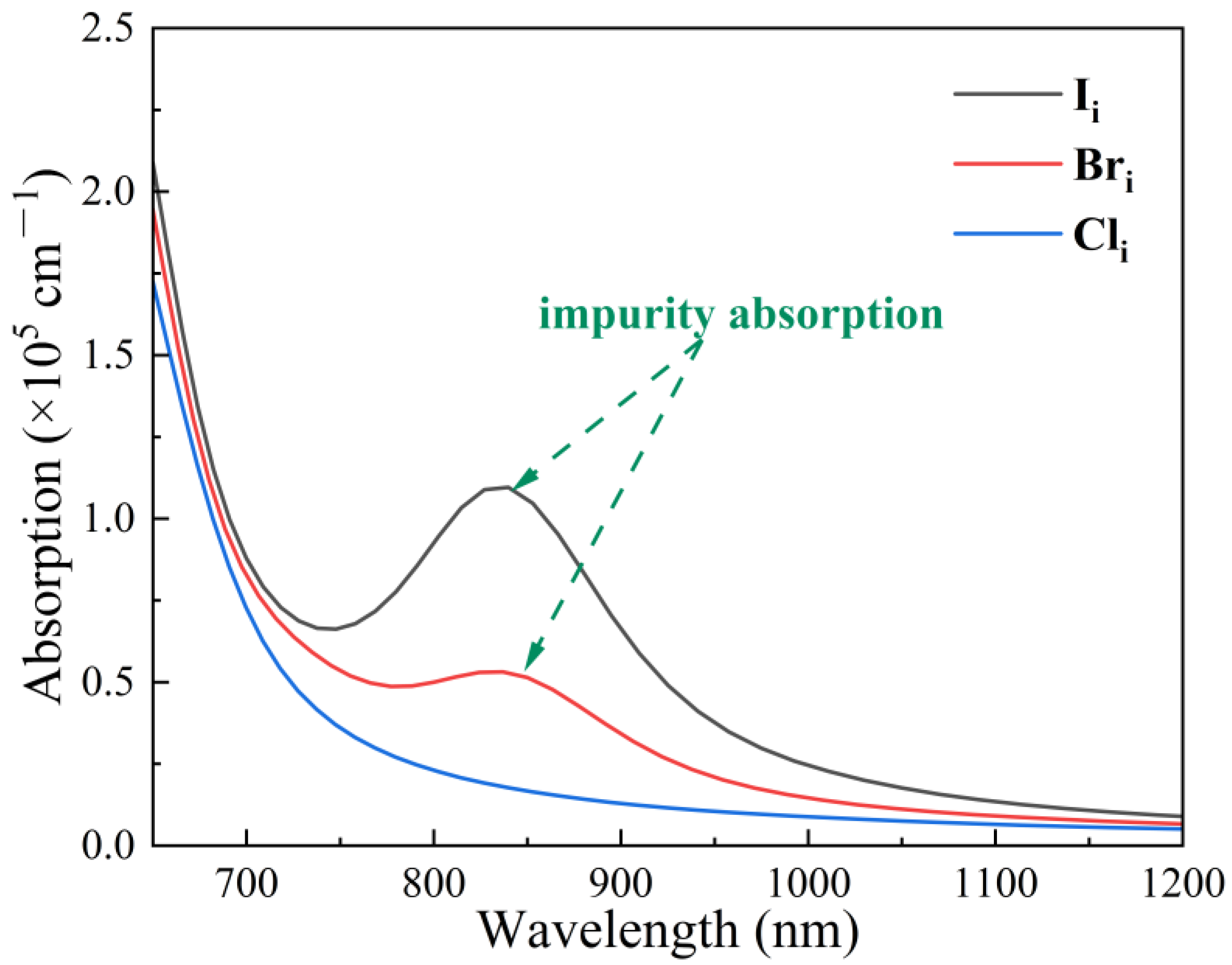
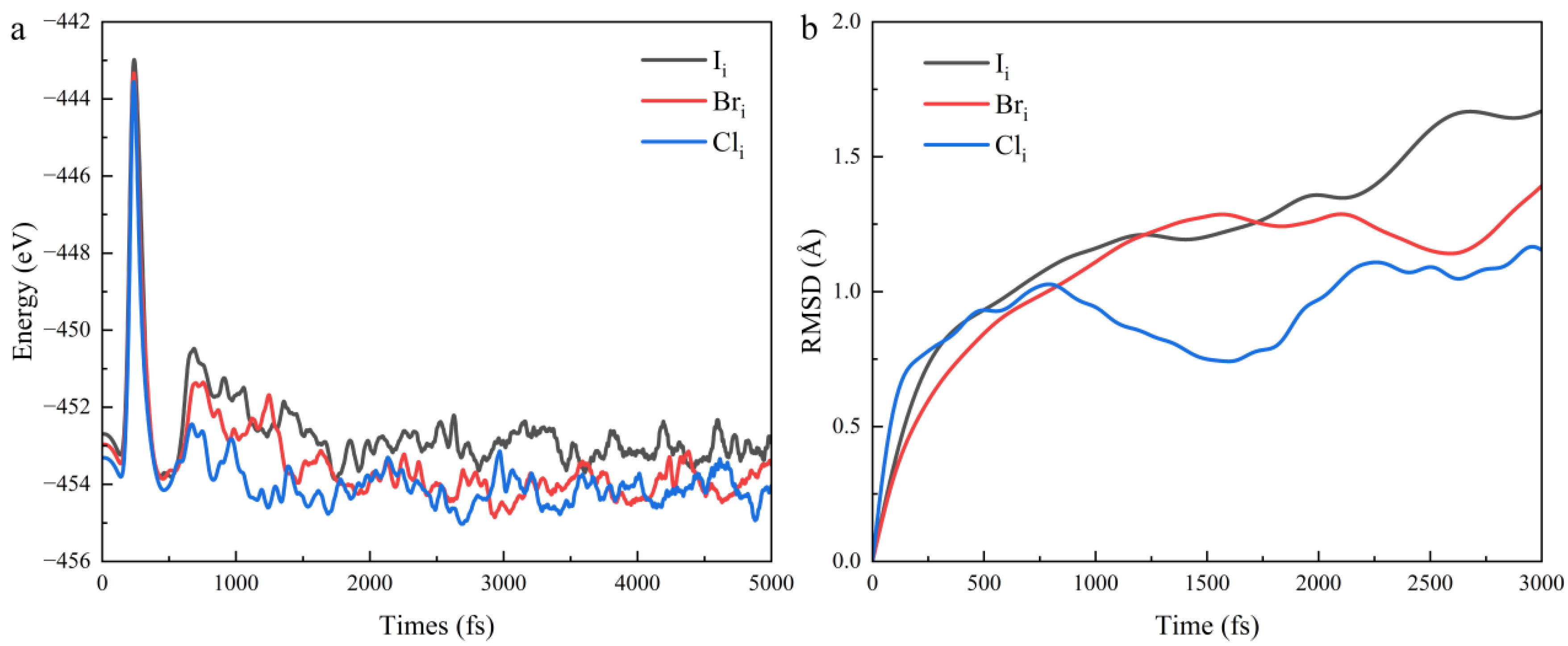
| Defect | Diffusion Coefficient cm2·s−1 |
|---|---|
| Ii | 4.53 × 10−8 |
| Bri | 3.24 × 10−8 |
| Cli | 2.67 × 10−8 |
| Device Architecture | Solution | PCE Before Solution % | PCE After Solution % | Stability Performance | Ref. |
|---|---|---|---|---|---|
| FTO/SnO2/FAPbI3/Spiro-MeOTAD/Au | FACl/FABr additive | 16.55 | 22.51/20.08 | - | [72] |
| FTO/TiO2/FAPbI2.8Cl0.2/Spiro-MeOTAD/Au | FACl dopant | 15.7 | 17.0 | - | [30] |
| FTO/TiO2/FAPbI2.9Br0.1/Spiro-MeOTAD/Au | FAPbBr3 dopant | 12.98 | 16.569 | - | [75] |
| FTO/SnO2/FAPbI3/Spiro-MeOTAD/Ag | PACl additive | 17.39 | 21.45 | 40 °C, 40%RH, AM 1.5 G, 70% PCE after 140 h. | [76] |
| FTO/SnO2/FAPbI3/Spiro-MeOTAD/Au | PFACl additive | 22.8 | 24.4 | 60 °C, 25 ± 5%RH, 85% PCE after 500 h. | [77] |
| ITO/SnO2/FAPI3/Spiro-MeOTAD/Au | FFEACl additive | 23.04 | 25.41 | 25 °C, 30%RH, AM 1.5 G, 83% PCE after 1000 h. | [78] |
| ITO/PTAA/FAPbI3/C60/BCP/Ag | FABr additive | 11.31 | 14.38 | - | [79] |
| FTO/TiO2/FAPbI3/Spiro-MeOTAD/Au | FACl + FAAC additive | 16.42 | 20.92 | 50 °C in N2, 87% PCE after 1628 h. | [80] |
| ITO/PCBM/FAMAPbI3-XBrX/P3HT/Ag | FACl additive | 18.60 | 21.02 | 25–35 °C, 10–25%, 90% PCE after 1200 h. | [81] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, J.; Tang, W.; Li, T.; Xu, C.; Zhao, M.; Ji, P.; Li, X.; Zhang, F.; Cai, H.; Wu, X. First-Principles Study of Halide Modulation on Deep-Level Traps in FAPbI3. Nanomaterials 2025, 15, 981. https://doi.org/10.3390/nano15130981
Dai J, Tang W, Li T, Xu C, Zhao M, Ji P, Li X, Zhang F, Cai H, Wu X. First-Principles Study of Halide Modulation on Deep-Level Traps in FAPbI3. Nanomaterials. 2025; 15(13):981. https://doi.org/10.3390/nano15130981
Chicago/Turabian StyleDai, Jiaqi, Wenchao Tang, Tingfeng Li, Cuiping Xu, Min Zhao, Peiqi Ji, Xiaolei Li, Fengming Zhang, Hongling Cai, and Xiaoshan Wu. 2025. "First-Principles Study of Halide Modulation on Deep-Level Traps in FAPbI3" Nanomaterials 15, no. 13: 981. https://doi.org/10.3390/nano15130981
APA StyleDai, J., Tang, W., Li, T., Xu, C., Zhao, M., Ji, P., Li, X., Zhang, F., Cai, H., & Wu, X. (2025). First-Principles Study of Halide Modulation on Deep-Level Traps in FAPbI3. Nanomaterials, 15(13), 981. https://doi.org/10.3390/nano15130981





