High-Performance and Fabrication-Tolerant 3 dB Adiabatic Coupler Based on Ultralow-Loss Silicon Waveguide by Tri-Layer Hard Mask Etching Process
Abstract
1. Introduction
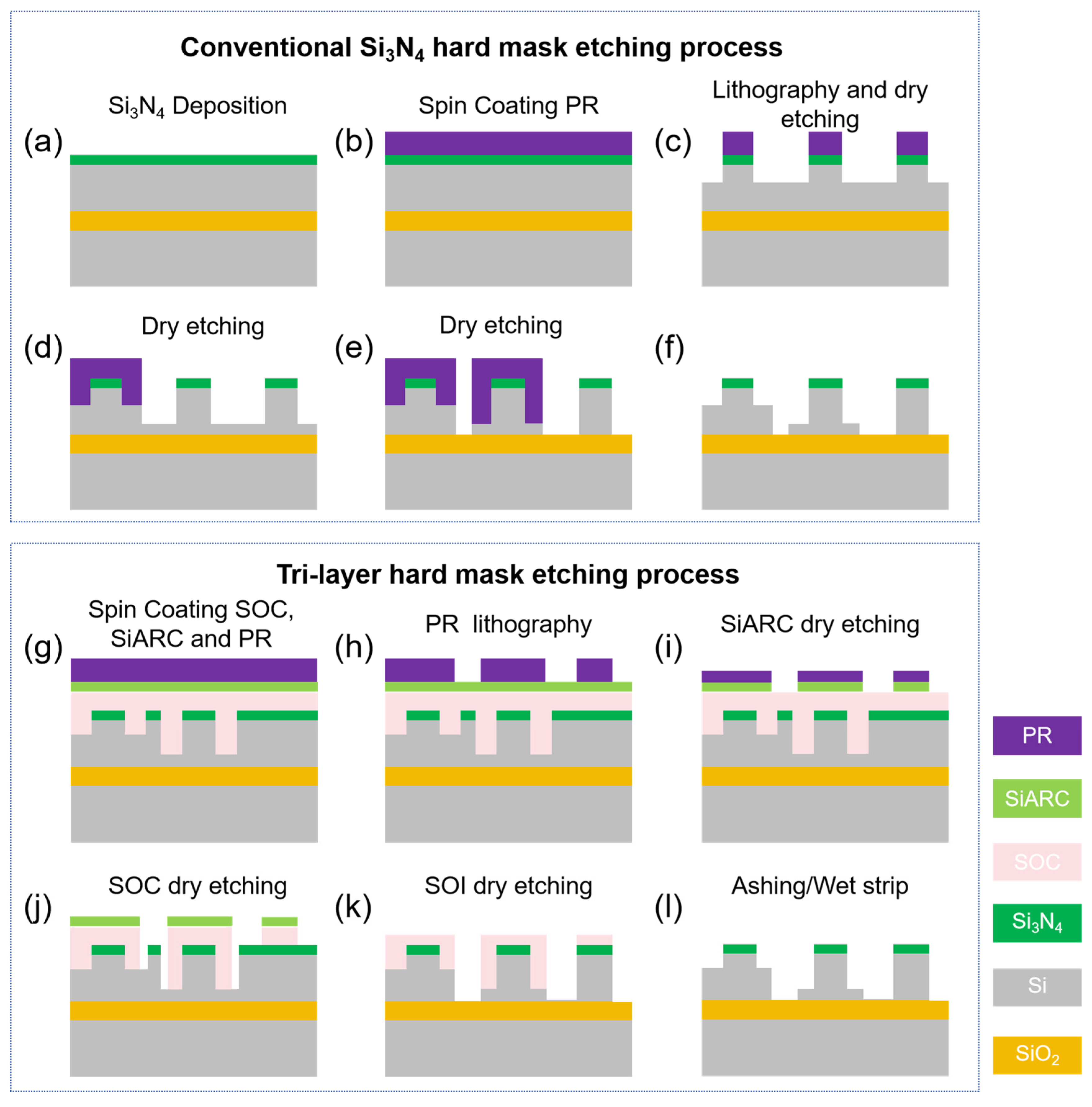
2. Tri-Layer Hard Mask Etching Process
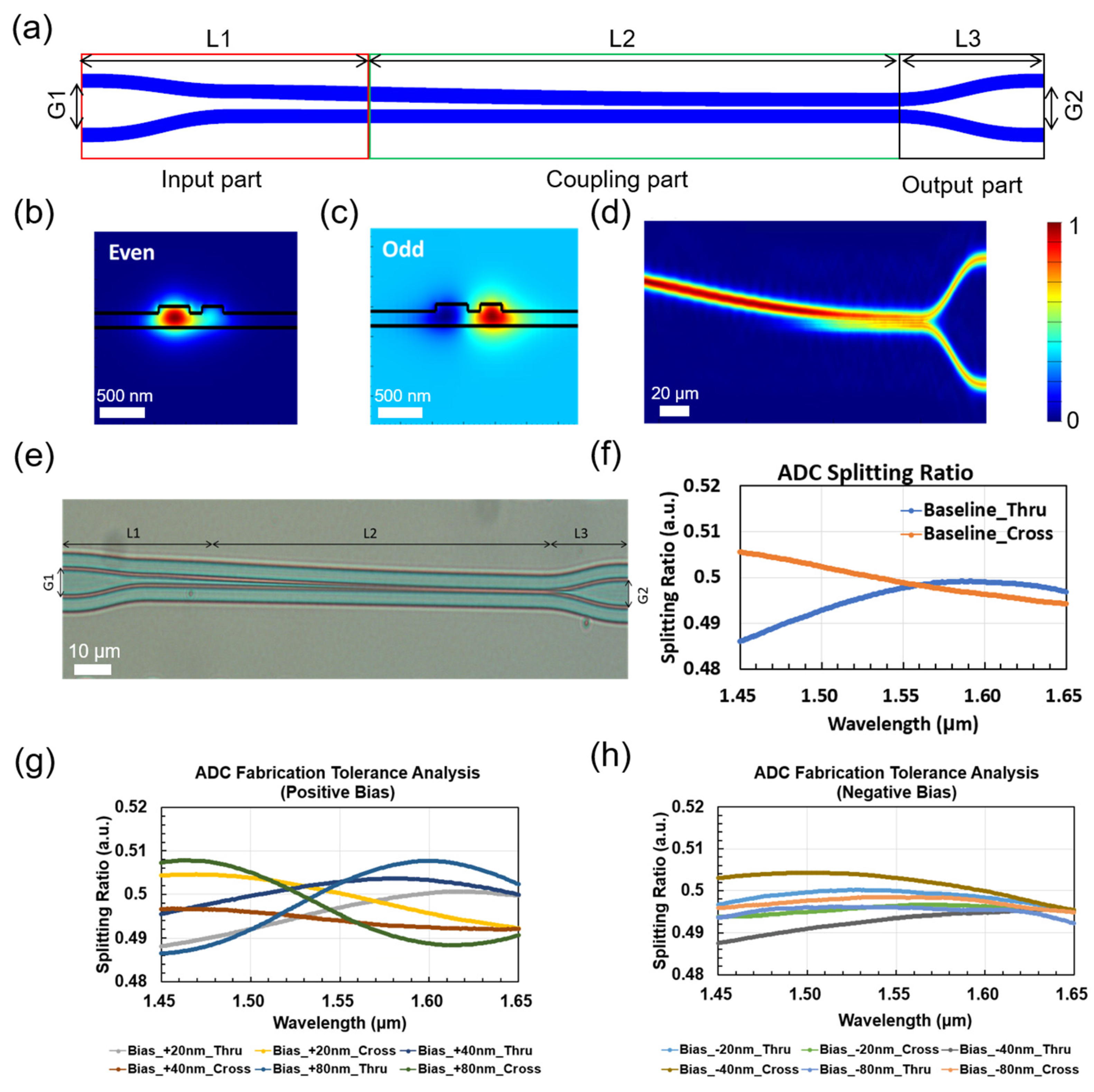
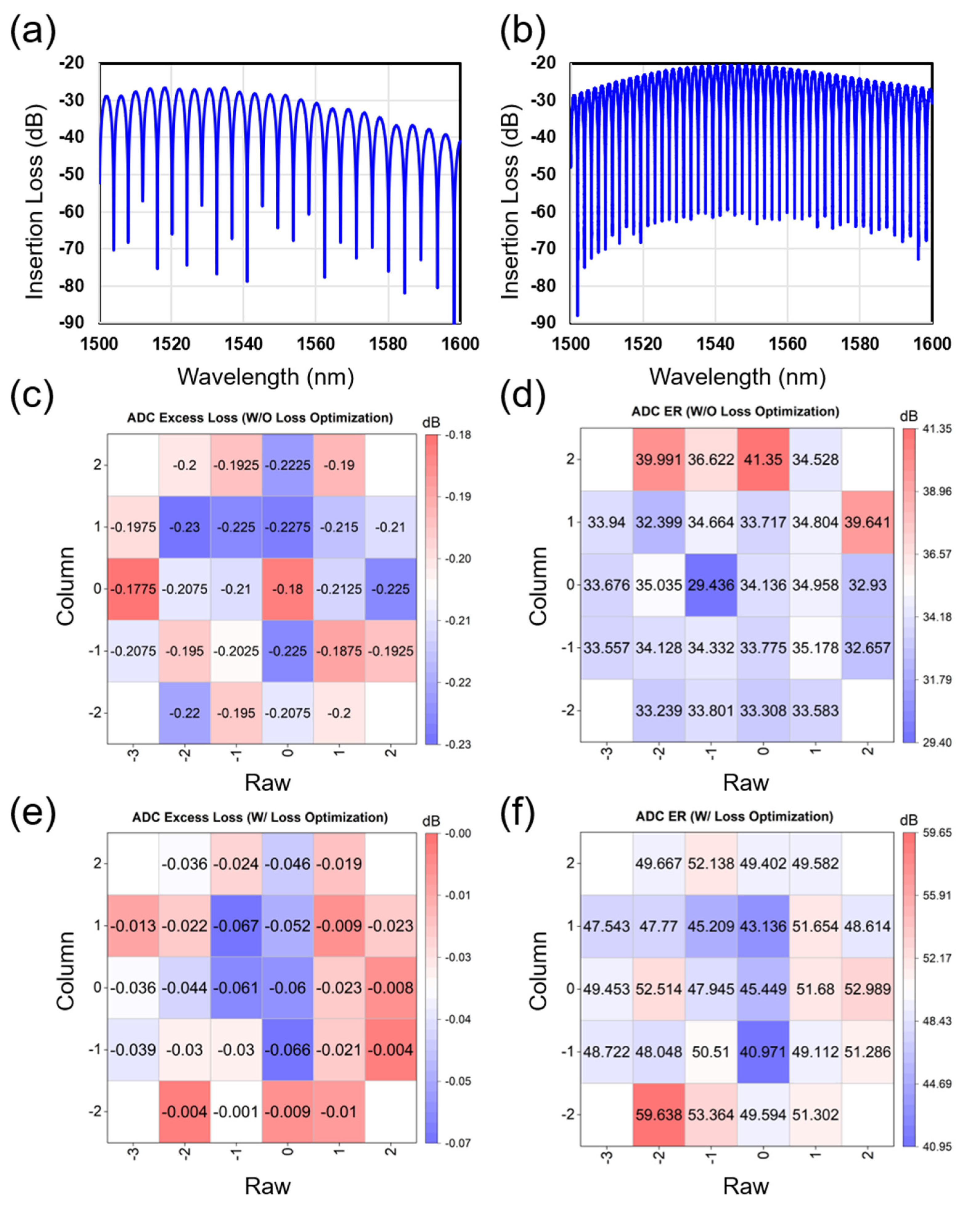
3. Adiabatic Directional Couplers
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shi, Y.C.; Zhang, Y.; Wan, Y.T.; Yu, Y.; Zhang, Y.G.; Hu, X.; Xiao, X.; Xu, H.G.; Zhang, L.; Pan, B.C. Silicon photonics for high-capacity data communications. Photonics Res. 2022, 10, A106–A134. [Google Scholar] [CrossRef]
- Pitris, S.; Moralis-Pegios, M.; Alexoudi, T.; Ban, Y.; Heyn, P.D.; Campenhout, J.V.; Lambrecht, J.; Ramon, H.; Yin, X.; Bauwelinck, J.; et al. O-band silicon photonic transmitters for datacom and computercom interconnects. J. Light. Technol. 2019, 37, 5140–5148. [Google Scholar] [CrossRef]
- Hong, S.; Zhang, L.; Wang, Y.; Zhang, M.; Xie, Y.W.; Dai, D.X. Ultralow-loss compact silicon photonic waveguide spirals and delay lines. Photonics Res. 2021, 10, 1–7. [Google Scholar] [CrossRef]
- Lu, Z.Q.; Yun, H.; Wang, Y.; Chen, Z.T.; Zhang, F.; Jaeger, N.A.F.; Chrostowski, L. Broadband silicon photonic directional coupler using asymmetric-waveguide based phase control. Opt. Express 2015, 23, 3795–3808. [Google Scholar] [CrossRef]
- Zhou, Y.; Sun, Y.H.; Wu, H.Y.; Lu, M.J.; Hu, G.H.; Yun, B.F.; Cui, Y.P. A low loss silicon waveguide bend based on width and curvature variations. Opt. Commun. 2024, 565, 130679. [Google Scholar] [CrossRef]
- Cardenas, J.; Poitras, C.B.; Robinson, J.T.; Preston, K.; Chen, L.; Lison, M. Low loss etchless silicon photonic waveguides. Opt. Express 2009, 17, 4752–4757. [Google Scholar] [CrossRef]
- Wang, X.Y.; Zhou, L.J.; Li, R.F.; Xie, J.Y.; Lu, L.J.; Wu, K.; Chen, J.P. Continuously tunable ultra-thin silicon waveguide optical delay line. Optica 2017, 4, 507–515. [Google Scholar] [CrossRef]
- Lee, K.K.; Lim, D.R.; Kimerling, L.C.; Shin, J.; Cerrina, F. Fabrication of ultralow-loss Si/SiO2 waveguides by roughness reduction. Opt. Lett. 2001, 26, 1888–1890. [Google Scholar] [CrossRef] [PubMed]
- Gao, F.; Wang, Y.; Cao, G.; Jia, X.; Zhang, F. Improvement of sidewall surface roughness in silicon-on-insulator rib waveguides. Appl. Phys. B 2005, 81, 691–694. [Google Scholar] [CrossRef]
- Bellegarde, C.; Pargon, E.; Sciancalepore, C.; Petit-Etienne, C.; Hugues, V.; Robin-Brosse, D.; Hartmann, J.M.; Lyan, P. Improvement of sidewall roughness of submicron SOI waveguides by hydrogen plasma and annealing. IEEE Photonics Technol. Lett. 2018, 30, 591–594. [Google Scholar] [CrossRef]
- Dong, P.; Qian, W.; Liao, S.; Liang, H.; Kung, C.C.; Feng, N.N.; Shafiiha, R.; Fong, J.; Feng, D.; Krishnamoorthy, A.V. Low loss shallow-ridge silicon waveguides. Opt. Express 2010, 18, 14474–14479. [Google Scholar] [CrossRef] [PubMed]
- Pafchek, R.; Tummidi, R.; Li, J.; Webster, M.; Chen, E.; Koch, T. Low-loss silicon-on-insulator shallow-ridge TE and TM waveguides formed using thermal oxidation. Appl. Opt. 2009, 48, 958–963. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Zhao, Y.; Gan, F. Ultra-broadband, Fabrication-tolerant 3-dB Power Splitter Based on Dual-layer SOI Platform. In Proceedings of the 2024 IEEE Silicon Photonics Conference (SiPhotonics), Tokyo Bay, Japan, 15–18 April 2024; pp. 1–2. [Google Scholar] [CrossRef]
- Sun, S.; He, M.; Xu, M.; Cai, X. Hybrid silicon and lithium niobate modulator. IEEE J. Sel. Top. Quantum Electron. 2020, 27, 1–12. [Google Scholar] [CrossRef]
- Chen, S.T.; Shi, Y.C.; He, S.L.; Dai, D.X. Low-loss and broadband 2 × 2 silicon thermo-optic Mach–Zehnder switch with bent directional couplers. Opt. Lett. 2016, 41, 836–839. [Google Scholar] [CrossRef]
- Deng, Q.Z.; El-Saeed, A.H.; Elshazly, A.; Lepage, G.; Marchese, C.; Kobbi, H.; Magdziak, R.; Coster, J.D.; Singh, N.; Filipcic, M.E.; et al. 32 × 100 GHz WDM filter based on ultra-compact silicon rings with a high thermal tuning efficiency of 5.85 mW/π. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 24–28 March 2024; Optica Publishing Group: Washington, DC, USA, 2024. W1A. 3. [Google Scholar]
- Qiao, L.; Tang, W.; Chu, T. 32 × 32 silicon electro-optic switch with built-in monitors and balanced-status units. Sci. Rep. 2017, 7, 42306. [Google Scholar] [CrossRef]
- Shen, Y.C.; Harris, N.C.; Skirlo, S.; Prabhu, M.; Jones, T.B.; Hochberg, M.; Sun, X.; Zhao, S.J.; Larochelle, H.; Englund, D.; et al. Deep learning with coherent nanophotonic circuits. Nat. Photonics 2017, 11, 441–446. [Google Scholar] [CrossRef]
- Hu, M.H.; Huang, J.Z.; Scarmozzino, R.; Levy, M.; Osgood-Jr, R.M. A low-loss and compact waveguide Y-branch using refractive-index tapering. IEEE Photonics Technol. Lett. 1997, 9, 203–205. [Google Scholar] [CrossRef]
- Gupta, R.K.; Chandran, S.; Das, B.K. Wavelength-independent directional couplers for integrated silicon photonics. J. Light. Technol. 2017, 35, 4916–4923. [Google Scholar] [CrossRef]
- Liu, R.F.; Lu, L.H.; Zhang, P.J.; Chang, W.J.; Liu, D.M.; Zhang, M.M. Integrated dual-mode 3-dB power splitter based on multimode interference coupler. IEEE Photonics Technol. Lett. 2020, 32, 883–886. [Google Scholar] [CrossRef]
- Chen, W.W.; Lin, J.; Li, H.X.; Wang, P.J.; Dai, S.X.; Liu, Y.X.; Yao, R.K.; Li, J.; Qiang, F.; Dai, T.G.; et al. Broadband multimode 3 dB optical power splitter using tapered couplers. Opt. Express 2022, 30, 46236–46247. [Google Scholar] [CrossRef]
- Kim, H.; Shin, H. Tailorable and broadband on-chip optical power splitter. Appl. Sci. 2019, 9, 4239. [Google Scholar] [CrossRef]
- Halir, R.; Maese-Novo, A.; Ortega-Moñux, A.; Molina-Fernández, I.; Wangüemert-Pérez, J.G.; Cheben, P.; Xu, D.X.; Schmid, J.H.; Janz, S. Colorless directional coupler with dispersion engineered sub-wavelength structure. Opt. Express 2012, 20, 13470–13477. [Google Scholar] [CrossRef] [PubMed]
- Han, L.S.; Kuo, B.P.P.; Alic, N.; Radic, S. Ultra-broadband multimode 3dB optical power splitter using an adiabatic coupler and a Y-branch. Opt. Express 2018, 26, 14800–14809. [Google Scholar] [CrossRef] [PubMed]
- Mao, D.; Wang, Y.; El-Fiky, E.; Xu, L.H.; Kumar, A.K.; Jacques, M.; Samani, A.; Carpentier, O.; Bernal, S.; Alam, M.S.; et al. Adiabatic coupler with design-intended splitting ratio. J. Light. Technol. 2019, 37, 6147–6155. [Google Scholar] [CrossRef]
- Xing, J.J.; Xiong, K.; Xu, H.; Li, Z.Y.; Xiao, X.; Yu, J.Z.; Yu, Y. Silicon-on-insulator-based adiabatic splitter with simultaneous tapering of velocity and coupling. Opt. Lett. 2013, 38, 2221–2223. [Google Scholar] [CrossRef]
- Staaks, D.; Hsu, Y.; Lee, K.Y.; Steiner, P.L.; Yu, Z.N.; Wu, J.J.; Xiao, S.G.; Yang, X.M.; Chang, T.Y. Nanoimprint lithography guiding templates for advanced magnetic media fabrication. J. Vac. Sci. Technol. B 2024, 42, 013801. [Google Scholar] [CrossRef]
- Nakajima, M.; Allen, R.D.; Somervell, M.H.; Kanno, Y.; Shibayama, W.; Takeda, S.; Kato, M.; Matsumoto, T. Development of new Si-contained hardmask for tri-layer process. In Advances in Resist Materials & Processing Technology XXVIII; International Society for Optics and Photonics: Bellingham, WA, USA, 2011; 797225. [Google Scholar]
- Shibayama, W.; Shigaki, S.; Sakamoto, R.; Onishi, R.; Bang, C.H. EUV sensitive Si containing hard mask (Si-HM) for PTD and NTD process in EUVL. In Proceedings of the Spie Advanced Lithography, San Jose, CA, USA, 24–28 February 2013. [Google Scholar]
- Liu, X.; Sheng, Z.; Zhao, Y.X.; Gan, F.W. Ultra-broadband on-chip power splitters for arbitrary ratios on silicon-on-insulator. Opt. Express 2024, 32, 2029–2038. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, Y.X.; Sheng, Z.; Gan, F.W. Compact and ultra-broadband silicon photonic adiabatic directional coupler using rib waveguides. IEEE Photonics Technol. Lett. 2024, 36, 637–640. [Google Scholar] [CrossRef]
- Guo, D.F.; Tao, C. Compact broadband silicon 3 dB coupler based on shortcuts to adiabaticity. Opt. Lett. 2018, 43, 4795–4798. [Google Scholar] [CrossRef]
- Hung, Y.J.; Li, Z.Y.; Chung, H.C.; Liang, F.C.; Jung, M.Y.; Yen, T.H.; Tseng, S.Y. Mode-evolution-based silicon-on-insulator 3 dB coupler using fast quasiadiabatic dynamics. Opt. Lett. 2019, 44, 815–818. [Google Scholar] [CrossRef]
- Tamazin, H.; El-Fiky, E.; Wang, Y.; D’Mello, Y.; Patel, D.; Kumar, A.K.; Plant, D.V. Ultra-broadband compact adiabatic coupler in silicon-on-insulator for joint operation in the C-and O-bands. In Proceedings of the CLEO: Science and Innovations, San Jose, CA, USA, 13–18 May 2018; Optica Publishing Group: Washington, DC, USA, 2018. [Google Scholar]
- Cabanillas, J.M.F.; Popović, M.A. Fast adiabatic mode evolution based on geometry-induced suppression of nearest-mode crosstalk. In Proceedings of the Conference on Lasers and Electro-Optics, San Jose, CA, USA, 13–18 May 2018; pp. 1–2. [Google Scholar]


| Type | Year | Splitting Ratio | Excess Loss (dB) | Device Length (μm) |
|---|---|---|---|---|
| ADC [31] | 2024 | 0.563:0.437 | 0.22 | 79 |
| ADC [32] | 2024 | 0.538:0.462 | 0.18 | 108 |
| ADC [26] | 2021 | 0.53:0.47 | NR | 110 |
| ADC [33] | 2018 | 0.52:0.48 | 0.3 | 70 |
| ADC [34] | 2019 | 0.56:0.44 | NR | 26.3 |
| ADC [35] | 2018 | 0.533:0.467 | NR | 100 |
| ADC [27] | 2013 | 0.51:0.49 | 0.3 | 300 |
| RAC [36] | 2018 | 0.51:0.49 | NR | NR |
| This Work | 0.516:0.484 | 0.067 | 89 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; Yu, Y.; Zhu, N.; Zhang, S.; Sun, J.; Ding, S.; Zhang, D.W. High-Performance and Fabrication-Tolerant 3 dB Adiabatic Coupler Based on Ultralow-Loss Silicon Waveguide by Tri-Layer Hard Mask Etching Process. Nanomaterials 2025, 15, 947. https://doi.org/10.3390/nano15120947
Zhang K, Yu Y, Zhu N, Zhang S, Sun J, Ding S, Zhang DW. High-Performance and Fabrication-Tolerant 3 dB Adiabatic Coupler Based on Ultralow-Loss Silicon Waveguide by Tri-Layer Hard Mask Etching Process. Nanomaterials. 2025; 15(12):947. https://doi.org/10.3390/nano15120947
Chicago/Turabian StyleZhang, Ke, Yunchu Yu, Nanfei Zhu, Senlin Zhang, Jie Sun, Shijin Ding, and David Wei Zhang. 2025. "High-Performance and Fabrication-Tolerant 3 dB Adiabatic Coupler Based on Ultralow-Loss Silicon Waveguide by Tri-Layer Hard Mask Etching Process" Nanomaterials 15, no. 12: 947. https://doi.org/10.3390/nano15120947
APA StyleZhang, K., Yu, Y., Zhu, N., Zhang, S., Sun, J., Ding, S., & Zhang, D. W. (2025). High-Performance and Fabrication-Tolerant 3 dB Adiabatic Coupler Based on Ultralow-Loss Silicon Waveguide by Tri-Layer Hard Mask Etching Process. Nanomaterials, 15(12), 947. https://doi.org/10.3390/nano15120947






