Next Article in Journal
Phase Evolution of High-Entropy Stannate Pyrochlore Oxide Synthesized via Glycine-Assisted Sol–Gel Synthesis as a Thermal Barrier Coating Material
Previous Article in Journal
Nanovesicles and Human Skin Interaction: A Comparative Ex-Vivo Study
Previous Article in Special Issue
Model and Energy Bounds for a Two-Dimensional System of Electrons Localized in Concentric Rings
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Nanomaterials
Volume 15
Issue 12
10.3390/nano15120938
nanomaterials-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Quantum Mechanics MP2 and CASSCF Study of Coordinate Quasi-Double Bonds in Cobalt(II) Complexes as Single Molecule Magnets

by
Yuemin Liu
1,2,*,
Salah S. Massoud
3,4,
Oleg N. Starovoytov
5,
Tariq Altalhi
6,
Yunxiang Gao
1 and
Boris I. Yakobson
2,6,*
1
Department of Chemistry, Prairie View A&M University, Prairie View, TX 77446, USA
2
Department of Materials Science and NanoEngineering, Rice University, Houston, TX 77005, USA
3
Department of Chemistry, University of Louisiana at Lafayette, Lafayette, LA 70504, USA
4
Department of Chemistry, Faculty of Science, Alexandria University, Moharam Bey, Alexandria 21511, Egypt
5
Center for Computation and Technology Services, Louisiana State University, Baton Rouge, LA 70803, USA
6
Chemistry Department, Taif University, Taif 21974, Saudi Arabia
*
Authors to whom correspondence should be addressed.
Nanomaterials 2025, 15(12), 938; https://doi.org/10.3390/nano15120938
Submission received: 28 April 2025 / Revised: 4 June 2025 / Accepted: 5 June 2025 / Published: 17 June 2025
(This article belongs to the Special Issue Fundamental and Applied Aspects of the Physics in Low-Dimensional Systems)
Browse Figures
Versions Notes

Abstract

:
Co(II) complexes have shown promising applications as single-molecule magnets (SMMs) in quantum computing and structural biology. Deciphering the Co(II) complexes may facilitate the development of SMM materials. Structural optimizations and calculations of chemical and magnetic properties were performed for Co(II) complexes with a tripodal tetradentate phenolate-amine ligand using MP2/aug-cc-pvdz, MP2/Def2svp, and CASSCF/Def2svp methods. The Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis unravels that Co(II) ions form unusual coordinate quasi-double bonds with ligand oxygen donor atoms, and the bond strengths range from 142.01 kcal/mol to 167.36 kcal/mol but lack further spectrometric evidence. The average 151.70 kcal/mol of the Co(II-O coordinates quasi-double bonds are formed mainly by two lone pairs of electrons from the ligand phenolate donor oxygen atoms. Dispersion forces contribute 24%, 28%, 27%, and 31% to the Co(II)-ligand interaction. Theoretical results of ZFS D, transversal ZFS E, and g-factor agree well with the experimental values. Magnetic susceptibility parameters calculated based on 5 doublet roots account for 85% of results computed 40 doublet roots are specified. These insights may aid in the rational design of SMM materials and Co(II) porphyrin fullerene conjugate for CO2 electroreduction with superior magnetic properties.

1. Introduction

Single-molecule magnets (SMMs) refer to the category of lanthanide complexes [1,2,3,4,5,6] and transition metal complexes [5,6,7,8,9,10,11] exhibiting slow magnetic relaxation and magnetic hysteresis [10,12]. With these attributes stemming from a pure molecular origin, SMMs show fundamental differences from regular bulky magnets [13]. Some transition metal ions are classified as single ion magnets (SIMs) because of magnetization resulting from 3d orbitals [14]. The SMMs have been pursued in the applications in information storage [15], quantum computing [16], spintronics [17], and structural biology [18,19,20]. Since retaining magnetization after exposure to an applied permanent magnetic field serves as the molecular basis for the applications of SMMs [21], high effective energy barriers (Ueff) for spin reversal of molecular magnetic moments are required for the paramagnetic complexes which originated from high magnetic anisotropy (D). The D tensor accounts for the axial component of the magnetic dipole–dipole interaction in Zero Field Splitting (ZFS) after degeneracy removal in the absence of a magnetic field. The SMMs with spin transitions at gigahertz (GHz) level at low magnetic fields are also called Kramer complexes. The magnetic anisotropy barrier can be defined by Ueff = |D|S2 (D refers to ZFS, and S is the total electron spin quantum numbers) for non-Kramer SMM molecules with an overall integer spin larger than ½, whereas the energy barrier can be given with Ueff = |D|(S2 − 1/4) for Kramer SMM complexes with half-integer spin [22,23]. Recently, it was found that the D indices do not have to be negative for slow magnetization relaxation in SMMs, as there are cases of SMMs with both positive and strong easy-plane anisotropy [6,24], which is true for the Co(II) complexes [25,26,27,28,29,30,31,32,33,34,35,36]. The common spin reversal demagnetization relaxation nanosecond scale of SMMs is mainly controlled by spin-lattice, magnetic dipole, and Zeeman, as well as spin–spin interaction [37]. The major spin-lattice relaxation reverses magnetization by crossing energy barriers that accompany the thermal energy exchange between the spin and lattice. If the magnetic anisotropy barrier energy Ueff is significantly larger than the thermal energy kT, then the magnetization can be maintained for a relatively long time. The spin-lattice relaxation is normally driven by three phonon-involved mechanisms, which are the Direct, Orbach, and Raman processes [37], among which the Orbach mechanism plays a predominant role in the spin-lattice relaxation [32]. The Orbach spin-lattice mechanism occurs with a relaxation rate of Ueff Arrhenius dependence [23,38]. The dynamics of the SMMs vary strongly with the temperature. The magnetic moments of SMMs usually fluctuate quickly, whereas magnetic variation is almost blocked at low temperatures. The blocking temperature refers to the temperature at which the relaxation time (τ) of the systems is 100 s for SMMs. The effective spin-reversal barrier and blocking temperature serve as two major criteria for examining the performance of SMMs [19,39].
The rational design of SMMs has been focused on enhancing the Ueff in static crystal field through polynuclear complexes, which consist of mononuclear fragments with high spin [40]. Since spin larger than 12 would not increase the magnetic anisotropy energy barrier anymore [41], the alternative strategy lies in boosting magnetic anisotropy by adjusting ligand geometry and symmetry [42]. A ligand environment can inhibit quantum tunneling of magnetization (QTM), which in turn gives rise to high magnetic degeneracy D [43,44,45,46]. The bulk groups were reported to induce spin-crossover (SCO) of Co(II) complexes by combining with environmental factors, including light, temperature, pressure, and other molecules [47]. Geometric distortions of complexes with low symmetry may cause effects on orbital degeneracy and orbital angular momentum contribution in the total magnetic moment to achieve a large magnetic anisotropy [48,49,50]. Cobalt(II) ion is capable of forming a broad variety of complexes, including 2-coordinate linear complexes [51,52], 3-coordinate trigonal planar complexes [53], 4-coordinate tetrahedral or pseudo-tetrahedral complexes [8,54,55,56,57,58], 5-coordinate distorted square pyramidal [23,59] or trigonal bipyramidal [50,60,61,62], 6-coordinate octohedral complexes [63,64,65,66,67,68,69], 7-coordinate pentagonal bipyramidal and capped trigonal prism [70,71,72], 8-coordinate square-antiprismatic [73,74,75]. Extensive efforts led to the discovery of Co(II) complexes with Ueff around 300 cm−1 [60,76], with the highest Ueff of 450 cm−1 in the absence of an applied magnetic field [51]. The pseudo-tetrahedral arrangement enables strong spin–orbit coupling between the ground and excited electronic states. Therefore, Co(II)-based SMMs with N2O2 coordination donor sets were demonstrated to show slow magnetic relaxation at zero or DC magnetic fields. The relative orientations of d-orbitals for four coordinate Co(II) complexes can vary with the distorting of coordinating arrangments [56,57,58]. Four Co(II) complexes designed are described in Figure 1, with an N2O2 coordination tripodal phenolate amine donor and distorted pseudo-tetrahedral structure, have been synthesized and revealed SMM behaviors [60,77]. A Co(II) porphyrin fullerene conjugate plays a catalytic role in the CO2 electroreduction [78,79]. Quantum mechanical (QM) simulations enable an understanding of intramolecular interactions of transitional metal complexes [9,80,81], so QM calculations will be pursued to investigate the effects of ligand molecule adjustments on magnetic properties of Co(II) complexes. Insights into Co(II) complex electronic structures specifcally coordinate bond enable the further development of SMMs materials and Co(II) porphyrin fullerene hybrid systems for CO2 electroreduction.

2. Materials and Methods

Structural models of four cobalt complexes were built based on the crystallographic structure [77], which are depicted in Figure 1. Computational simulations of the four compounds were performed using Gaussian-16 [82] and the ORCA software package (version 5.01) [83]. Structural optimizations of the four complexes were carried out using Becke–Perdew (BP86) functional [84,85,86] and Karlsruhe basis sets of the valence double-ζ basis set with polarization functions (def2SVP) on main-group and transition-metal elements [87]. The resolution of identity and chain of the sphere (RIJCOSX) approximations [88] were employed in conjunction with a variety of auxiliary basis sets to fit Coulomb’s potential [89]. An auxiliary basis set -/JK type was applied for structural optimization.
After structural optimization, the unrestricted open-shell MP2/Def2SVP calculations were conducted for the computations of intramolecular interaction and natural bond analysis of the complexes, followed by evaluations of the spin contaminations using the Gaussian-16 program.
The optimized geometries were also used for multiconfigurational (CASSCF) calculations of the Spin–Hamiltonian (SH) parameters and the magnetic properties of the complexes [90]. The minimal activity was applied for seven electrons 3d7 of Co(II) ion. The roots of states stemming from the quartet and doublet multiplicities were considered for the 3d7 configuration. There were 10 quartet roots for 4F and 4P and 40 doublet roots, which are 2G, 2P, 2H, 2D, 2D, and 2F. These roots were taken into consideration with the same weights, and then the CASSCF computation was implemented as state-averaged CASSCF. The dynamic correlation effect was considered using the highly contracted N-electrons valence perturbation theory to second order (NEVPT-SC) [91]. The DKH formalism was applied to account for the scalar relativistic effect in the structural optimization and calculations of magnetic properties. The mean-field approximation was made to take spin–orbit coupling into account.
The spin Hamiltonian (SH) parameters were extracted for 1–4, fitting both the χMT vs. T and M(H) data using PHI software version 3 [92]. To prevent any overparameterization, only an isotropic g factor and spin Hamiltonian are considered in the fittings, with some corrections for the intermolecular interactions at low temperatures for the complexes.

3. Results and Discussions

3.1. Structural Parameter and Molecular Geometry

The spin operator values in the single point MP2/Def2SVP calculations of the four complexes are included in Table 1. The cobalt-metal-ions-to-ligand (M-L) donor bond lengths, cobalt-ions-to-ligand (L-M-L) donor bond angles, geometric indices τ of the four complexes, natural bond orbital (NBO) charges for ligand donor atoms and cobalt(II) ions are listed in Table 2, Table 3, Table 4 and Table 5, respectively. The optimized geometry for complex 1 is depicted with the hydrogen atoms hidden for clarity in Figure 2a, and the two extremes for the 4-coordinate pseudo-tetrahedral chromophore and the 5-coordinate distorted trigonal bipyramidal structures are illustrated in Figure 2b and Figure 2c, respectively. The structural effect of the bridge length (CH2)2 and (CH2)3 between two nitrogen donors on the 5-coordinate complex 3 and 4-coordinate complex 4 is shown in Figure 3. Unrestricted open shell MP2 calculations allow α spin and opposite β spin electrons to have two sets of orbitals, respectively. Spin contamination occurs due to the fact that the wavefunction calculated from the unrestricted procedure may deviate from the eigenfunction of the overall spin operator <S2>. Spin-contaminated wavefunction can cause errors in energies, geometries, and population analyses [93]. The Gaussian-16 contains an annihilation process to lower the spin contamination. Our calculations produce a spin operator S2 value of 3.7575 before annihilation and 3.75 after annihilation, which are very close to the actual 3.75 manually calculated by the equation S2 = s(s + 1) = 3/2(3/2 + 1) = 3.75 where s represent the spin of system. Therefore, the simulation results of our work demonstrate low spin contaminations and high accuracies. Table 2 indicates that the N1-Co(II) bond lengths range from 2.06 Å to 2.20 Å, and the O-Co(II) bond length ranges can be largely categorized as those with tripodal phenolate amine (1.90 Å to 1.97 Å) and those with small molecule methanol or water (2.11 Å to 2.13 Å). While complexes 1 to 3 show relatively close N1-Co(II) bond parameters of 2.19, 2.17, and 2.16 Å, respectively, complex 4 has the shortest N1-Co(II) bond length of 2.06 Å. The N2-Co(II) bond length parameters share a similar range from 2.06 Å to 2.20 Å to that for N1-Co(II) of the complex series with an exception for the two slightly short 2.12 Å and 2.11 Å for ligand 1 and ligand 3, respectively. The Co(II)-N bond lengths of the four complexes fall in the ranges of other experimental results [94]. The bond lengths of O-Co(II) (1.90 Å to 1.97 Å) involved with the ligand are shorter than both N-Co(II) and O-Co(II) with small molecules of methanol or water. These values are also shorter than the Co(II)-O coordinate bonds of 1.952 to 2.239 Å were reported by Kim et al. [95]. The Co(III)-O bond length of 1.90 Å was observed in the pressure-response study [96]. Therefore, the Co(II) ion probably forms relatively stronger with ligands than with methanol, and complex 4 has the most compact structure for its four shortest without a fifth coordination bond with methanol in the four complexes. Table 3 shows that there are six coordination bond angles for 4-coordinate complex 4, and ten coordinate bond angles exist for 5-coordinate complexes 1 to 3. The most obvious difference lies in the bond angle N1-Co(II)-N2 for the four complexes. For the first 1–3 complexes, the short linker -(CH2)2- between the two ligand donor nitrogen atoms leads to the bond angle values of N1-Co(II)-N2 of 82°, 83°, and 84° for complexes 1−3, respectively. On the other hand, complex 4 shows an N1-Co(II)-N2 angle of 101° due to a long bridge -(CH2)3- between the two donor nitrogen atoms, as indicated in Figure 1. The bond angles are usually expressed in geometric parameters or indices, which are more informative [97,98,99]. Just like the three octahedral distortion parameters for describing the twisted octahedral geometry [97,100,101,102] caused by the Jahn–Teller electron–photon coupling for reducing symmetry [103], the two largest coordination bond angles can be used to derive geometric index τ values for evaluating the structural deviation from tetrahedral and trigonal bipyramidal for complexes 1 to 4. The τ4 values of 4-coordinate complexes range from 0 for square planar geometry to 1 for tetrahedral structure (τ4 = −0.00709α − 0.00709β + 2.55, α and β represent the two largest angles out of six bond angles) [99,104]. The τ5 values range from 0 for the square pyramidal structure to trigonal bipyramidal geometry (τ5 = −0.01667α + 0.01667β, α and β are the two largest angles out of ten bond angles) [98]. These parameters include τ4 of 4-coordinate for Co(II) 1 to 4 while the small ligands methanol or water are ignored in complexes 1 to 3 and τ5 for 5-coordinate values for complexes 1 to 3. Table 4 shows that τ4 increases from 0.75623, 0.76332, 0.79877, and 0.82004 for complexes 1 to 4, respectively. Complexes 1–3 have distorted tetrahedral structures when coordinating bonds with methanol or water are neglected, and complex 4 exhibits the closest geometries to a tetrahedron. Considering the Co(II)-O with methanol or water renders the distorted trigonal bipyramidal structures with the geometric factors τ5 of 0.75015, 0.76682, and 0.73348 for compound 1 to 3, respectively. It is known that the complexes with coordination 4 can adopt geometries from square planar to tetrahedral geometries, which are illustrated in Figure 2b, and 5-coordination complexes may have geometries from square pyramidal to trigonal bipyramidal geometries, which are illustrated in Figure 2c. The d-orbital energy splitting of tetrahedral complexes is relatively small even if the coordinated ligand molecules exhibit strong crystal field because of lower coordination number. The d-orbital splitting constant usually does not exceed spin pairing energy, so electrons occupy the high energy d-orbitals instead of pairing up in the low energy d-orbitals. As a redult, tetrahedral complexes exhibit high spin configurations. With a same coordination number of 4, the sqaure planar strcutures have significantly lower energies of dxz, dyz, and dz2 due to the lack of electron repulsion along z-axis. In the square plane configuration, the dx2-y2 has the highest energy and the dxy orbital shows a slightly lower level. The square planar complexes always have large crystal field splitting for low spin configuration because of equatorial coordination bond. The deviation from tetrhedral to square planar geometry most likely leads to a relatively stronger crystal field splitting. According to hole (empty orbital) formalism, the tetrahedral goemetry with dn electrons shares a same symmetry with a oectahedral configuration of n holes (empty orbitals) for the splitting of the d-orbitals for tetrhedral complexs occurs oppositely to that for the octahedral geometry [105]. The NBO charges are assigned based on a localized representation of electron density, which enables a more accurate description of atomic partial charges [106,107]. Table 5 exhibits a largely normal pattern of NBO partial charges of N1, N2, O1, and O2 for the four Co(II) complexes, with a little exception that −0.40 a.u. of O1 and −0.41 O2 for complex 1 are 0.08 a.u. and 0.07 a.u. lower than 0.48 a.u. for all other coordinating oxygen atoms. The NBO partial charges for coordinating nitrogen range from 0.32 a.u. to 0.35 a.u., consistently lower than those for oxygen atoms. Overall, Co(II)-O (ligand) bond lengths are relatively shorter than the corresponding Co(II)-N bond distances. Co(II)-O (MeOH) in complexes 1–3 and Co(II)-O and Co(II)-N bonds in complex 4 represent the shortest likely most stable, respectively, among the four complexes. The results of distortion indices indicate that complexes 1–3 adopt Trigonal Bipyramid rather than Square Pyramid. If the coordinate bonds by small methanol or water are ignored, all the complexes belong to pseudo-tetrahedron (See Figure 2). The NBO partial charges of coordinate bond atoms seem insensitive to the impacts from different functional groups such tert-butyl, methyl, and chlorine.

3.2. Intramolecular Correlation Energy of Complexes and NBO-Based Perturbation Theory Energy Analysis

The major intramolecular interactions are evaluated using truncated fragments with basis set superposition correction (BSSE), solvation correction, and NBO-based perturbation theory energy analysis. The intramolecular π–π interaction energies between the dipodal phenolates are summarized for the most compact complex 4 of complexes in Table 6. The interacting pairs for dipodal branches of complex 4 are illustrated in Figure 4a,b. The two-way delocalization interactions include interactions from ligand donor atoms to central Co(II) and those from central Co(II) to ligand donor atoms to central Co(II) in the NBO-based perturbation theory energy analysis. The detailed Co(II)-O2 and Co(II)-N1 delocalization components from ligand donor atoms to central Co(II) ion in complex 1 are shown in Table 7. The representative delocalization interactions from ligand donor atoms O2, N1, and O3 to Co(II) are depicted in Figure 5, Figure 6, and Figure 7 for Co(II)-O2, Co(II)-N1, and Co(II)-O3, respectively. The delocalization components Co(II)-O2 and Co(II)-N1 from Co(II) to ligand donor atoms in complex 1 are depicted in Table 8. The two types of intramolecular interaction forces between ligand molecules and cobalt(II) ions are summarized for all four complexes in Table 9. The percentages of the dispersion force between ligand and central ions are depicted in Figure 8a. The delocalization interactions between methanol molecules or water and cobalt ions for the first three complexes are summarized in Table 10. Energetic contributions by functional groups methyl, tert-butyl, chlorine, ethyl, and isopropyl are summarized based on the Fock Matrix in NBO Basis (see Table 11 and Figure 8b).
The intramolecular π–π interaction was able to influence physical properties such as molecular fluorescence and magnetic properties [80,108,109,110]. The tripodal phenolate amines have two phenyl rings, and intramolecular π–π interaction is characterized in complex 4 with the most compact geometry based on the short bond length in Table 1. The inclusion of correlation plays a critical part in the evaluation of π–π interaction [111,112]. The correlation energy usually refers to the difference between true total energy and the Hartree–Fock limit. There are two major static and dynamic components in correlation energy. HF treats the many-body wavefunction as a single Slater determinant, while the calculation of the real total energy requires a combination of many Slater determinants. The approximation accounts for the lack of nondynamic correlation energy. The dynamical correlation refers to the lowering of real instantaneous coulomb repulsion by the assumption of all other electrons as an average distribution charge. HF already contains the static exchange-correlation between parallel spin electrons based on the anti-symmetry principle. Our results in Table 6 suggest that there is neither attraction nor repulsion associated with the moiety pair if the two CH2 directly bonded to the N1 atom are not included, which is described in Figure 4a. On the other hand, the inclusion of CH2 in the phenolate interaction yields a repulsive force of 20.97 kcal/mol. This implies that a certain extent of spatial tension happens between the two CH2 on the N1 atom even if the C-N1-C is 110°, which is shown in Figure 4b. It is worthwhile pointing out that the 110° C-N1-C angle is slightly larger than the 107° H-N-H in ammonia, and the smaller angle but larger size of CH2 than the H atom can rationalize the repulsive force in complex 4.
The Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis can provide insights into the intramolecular delocalization interactions within complex molecules. The metal ion coordination chemistry serves as a Lewis acid or electrophile, whereas ligand is treated as a Lewis base or nucleophile. The delocalization interactions due to the charge transfer from the ligand to the central cobalt ion usually involve bonding type orbitals of ligand and antibonding orbitals of central Co(II) ion. Weak opposite delocalization interaction also occurs because of the other way charge transfers from central cobalt ion to ligands and resultant delocalizations. Our NBO-based analyses show that the ligand provides donor oxygen atom lone pair bonding type orbitals (LP), oxygen core bonding type orbitals (CR), and O-C bonding orbital in the O-related delocalization, and the cobalt(II) ion offers lone pair antibonding orbitals (LP*) and Rydberg antibonding orbitals (RY*) accordingly. A coordinate bond is defined as a two-center covalent bond in which two electrons derive from the same nonmetal donor atom [113]. The coordinate bond in this work is described as delocalizations from LP orbitals of ligand donor oxygen or nitrogen atoms to the LP* orbitals of Co(II), and the rest of the types of delocalizations between the same ligand donor atoms and acceptor Co(II) are treated as the components of dispersion force. The dispersion force includes delocalization between LP orbitals and RY* orbitals, delocalization between O-C bonding orbitals and LP* orbitals, delocalization between core bonding orbitals (CR) and LP* orbitals, and delocalizations between O-C bonding orbitals and RY* orbitals. Unrestricted open shell calculations manage α spin orbitals and β spin orbitals separately for cobalt(II) ion, and each type of above delocalizations is also classified in terms of α and β spin orbitals accordingly. Table 7 shows that the coordinate bond has 10 delocalization interactions between O2 (for all labels of atoms, see Figure 2a) α spin lone pair bonding orbitals and Co(II) α spin lone pair antibonding orbitals, contributing 75.09 kcal/mol to the O2-Co(II) interaction in complex 1. Other 13 delocalization interactions that are responsible for 9.12 kcal/mol are considered the dispersion force from oxygen atom O2 to cobalt ion α spin orbitals. Similarly, 92.27 kcal/mol of coordinate bond force results from the 19 delocalization interactions between O2 β spin lone pair bonding orbitals of LP 117β, LP 118β and LP 119β and Co(II) β spin lone pair antibonding orbitals. The remaining 13 delocalization interactions contribute 9.10 kcal/mol, accounting for the dispersion force between O2 β spin bonding orbitals and Co(II) β spin antibonding orbitals. Figure 5 shows four major delocalization interactions between Co(II) and ligand donor oxygen atom O2. Figure 5b indicates 25 kcal/mol contributed by the delocalization from ligand O2 lone pair bonding orbital 118α to Co(II) lone pair antibonding orbital 113α, and Figure 5c exhibits 40 kcal/mol yielded by the delocalization from ligand oxygen atom O2 lone pair bonding orbital 118β to Co(II) lone pair antibonding orbital 110β. Additionally, Figure 5d exhibits 17 kcal/mol introduced by the delocalization from ligand O2 lone pair bonding orbital 118α to Co(II) lone pair antibonding orbital 114α of Co(II). Figure 5e shows 19 kcal/mol contributed by the delocalization from ligand O2 lone pair bonding orbital 119α to Co(II) lone pair antibonding orbital 113α, and Figure 5c exhibits 28 kcal/mol introduced by the delocalization from ligand O2 lone pair bonding orbital 119β to Co(II) lone pair antibonding orbital 110β. Interestingly, 29 delocalization interactions, which account for 167.36 kcal/mol of the O2-Co(II) coordinate bond, come from three lone pair bonding orbitals 117(117α + 117β), 118(118α + 118β), and 119(119α + 119β). The 11 delocalization interactions out of the 29 ones, which involve lone pair orbital 117, lead to 16.61 kcal/mol, implying it unlikely makes a significant part of the coordinate bond. The eight delocalization interactions resulting from lone pair orbital 118 provide 88.91 kcal/mol, whereas ten delocalization interactions enabled by lone pair orbital 119 give rise to 61.84 kcal/mol. Therefore, the lone pair orbital 118 and 119 probably form two separate coordinate bonds between donor O2 and Co(II). Furthermore, the O2 lone pair bonding orbitals exhibit quasi-σ bond features with hybridizations sp2.06 and sp2.78 for 118α and 118β, respectively, and the O2 lone pair bonding orbitals display a quasi-π bond character with essentially pure p-type hybridizations sp15.47 and sp13.68 for 119α and 119β, respectively. The slightly longer Co(II)-O coordinate bonds of 1.952 to 2.239 Å were studied [95], but bond types were not further characterized experimentally. Since we have no additional experimental evidence, the delocalization interactions of 167.36 kcal/mol between O2 LP orbitals to Co(II) LP* orbitals can be tentatively termed as an unusual coordinate quasi-double bond, which is illustrated in Figure 5a. The ratio of β spin coordinate bond over α spin coordinate bond is 1.2 for O2-Co(II), implying the unpaired electrons occupying the β spin bonding orbitals. The results collected in Table 7 and Figure 5a show that 26 non-coordinate bond delocalization interactions account for a dispersion force of 18.22 kcal/mol between O2 lone pair bonding orbitals and Co(II) lone pair antibonding orbitals. Similarly, Table 7 and Figure 6 display that 10 delocalization interactions originating from lone pair orbital 125 (125α + 125β) produce 49.10 kcal/mol for the coordinate bond force of N1-Co(II), and the rest of the 39 delocalization interactions provide 49.10 kcal/mol for dispersion force of N1-Co(II). The ratio of β spin coordinate bond over α spin coordinate bond is 1.5 for N1-Co(II), suggesting the unpaired electrons occurring in the β spin antibonding orbitals. It is worthwhile to notice that coordinate bond strength Co(II)-O2 is triple that of Co(II)-N1. Table 8 presents the opposite delocalization interactions due to charge transfer from Co(II) ion to ligand O2 and N1, all of which are considered dispersion forces between Co(II) ion and ligand donor atoms. There are 23 delocalization interactions between Co(II) ion α spin orbitals and O2 antibonding orbitals for 5.49 kcal/mol and 3.22 kcal/mol result from 17 delocalization interactions between Co(II) ion β spin orbitals and O2 antibonding orbitals. There are 26 delocalization interactions between Co(II) ion α spin orbitals and N1 antibonding orbitals for 1.97 kcal/mol and 1.51 kcal/mol result from 22 delocalization interactions between Co(II) ion β spin orbitals and N1 antibonding orbitals. Table 9 shows a summary of the coordinate bonds and dispersion forces between ligand and Co(II) ion for the four complexes. While averaged coordinate bond energies are 51.60 kcal/mol and 55.34 kcal/mol for Co(II)-N1 and Co(II)-N2, respectively, the Co(II)-O1 and Co(II)-O2 contribute averaged coordinate bond strengths of 149.24 kcal/mol and 154.56 kcal/mol, respectively. This consistently suggests the occurrences of uncommon coordinate double bonds in the four complexes. These findings are supported by the relatively short Co(II)-O bond length of (1.89–1.97 Å) in the four complexes illustrated in the previous section. The short coordinate bonds give rise to stronger ligand fields, which in turn enable larger splitting of the d-orbitals for higher energy but lower intensity of the d-d transition bands following Laporte election rules [114]. The UV-visible bands 485, 495, 553, and 541 nm with low absorptivity are consistent with the strong Co(II)-O coordinate bonds for the four complexes [77]. The charge transfer (CT) bands occur at 368–373 nm in cobalt (II) complexes [115]. The shoulder band wavelength (λmax) 380 nm for complexes 2 and 4 probably indicates the CT resulting from the oxygen LP to Co(II) LP* delocalization for Co(II)-O with a bond length of 1.89–1.95 Å in our previous UV/Vis spectral work [77]. The coordinate bond energies of Co(II) ion β spin orbitals are 1.2–1.6-fold of those from Co(II) ion α spin orbitals. The ligand-to-metal ion charge transfer is 11–12-fold of those from central ions to ligands, proposing the four complexes belong to ligand-to-metal charge transfer compounds [116]. The coordinate bonds constitute 76%, 72%, 73%, and 69% for complexes 1 to 4, respectively, and percentages of dispersion forces are 24%, 28%, 27%, and 31% in Figure 8a. Table 10 and Figure 7 show a summary of the coordinate bonds and dispersion forces between MeOH and Co(II) ion for the first three complexes. The Co(II)-O coordinate bonds provide binding energies of 67.88 kcal/mol, 63.89 kcal/mol, and 68.85 kcal/mol for complexes 1–3, respectively, and these bonds with small ligand molecules belong to regular coordinate bonds. The 10 delocalizations interactions stemmed from lone pair orbital 124 (124α + 124β) of donor O3 offer an interaction energy of 63.10 kcal/mol, meanwhile other 10 delocalization interactions led by lone pair orbital 123 (123α + 123β) of ligand donor atom O3 give rise to 4.78 kcal/mol. The coordinate bond strengths between MeOH and Co(II) ions are constitute 68%, 66%, and 69% of overall interaction between for complexes 1–3 respectively.
The Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis is also performed for functional groups methyl, tert-butyl, chlorine, ethyl, and isopropyl (see Table 11 and Figure 8b). While R1 methyl contributes 90 kcal/mol, the R1 tert-butyl provides 205 kcal/mol, which is almost double that of methyl. The R2 chlorine and methyl interact with the rest part of the molecule slightly differently and offer delocalization energy of 70 and 86 kcal/mol, respectively. The R3 groups isopropyl, ethyl, and methyl gave rise to 137 kcal/mol, 94 kcal/mol, and 55 kcal/mol, respectively, to the complexes through the N2 atom. Interestingly, the aromatic methyl group contributes 35 kcal/mol more than the amine methylation. Therefore, selections of proper functional groups at appropriate positions on tripodal tetradentate phenolate amines permit fine-tuning of the chemical and magnetic properties of SMM candidates.

3.3. Effect of Correlation Dispersion Force and Magnetic Axial and Transverse ZFS

Magnetic susceptibility parameters are simulated using the CASSCF method. The direct current (DC) induced equilibrium magnetic behaviors are focused in this work, and the alternating current (AC) involved dynamic magnetizations, which had been the topic in previous efforts [77]. There are 10 quartet roots and 40 doublet roots specified in the CASSCF simulations of the complexes. Contributions to ZFS D from 10 quartet roots and 40 doublet roots in the CASSCF calculation are listed in Table 12. The single point energies from Gaussian-16 calculations are compared with the lowest energy of the quartet roots from the CASSCF simulation in Table 13. The calculation results of axial D, transverse ZFS E, isotropic g factors, and the experimental spin Hamiltonian (SH) magnetic susceptibility ZFS D indices and g factors, which are extracted by fitting both the magnetic susceptibility χMT vs. temperature T and magnetization [92], are shown in Table 14. Comparisons of the theoretical magnetic susceptibility parameters and experimental values are represented in Figure 9. The first- and second order perturbation to the effective Hamiltonian is reported to be significant for excitation from the ground configuration and lower excitation levels [117]. Comparisons are made between the results of calculations using 40 doublet roots and those using 5 doublets for axial zero-field splitting (ZFS) D and transverse ZFS E from the second order perturbation and effective Hamiltonian calculation of spin–orbit coupling (SOC) in Table 15. Comparisons between theoretical magnetic susceptibility parameters and experimental values are described in Figure 10. Results in Table 12 indicate that the 40 doublet roots contribute 24%, 23%, 23%, and 23% to the ZFS D tensor for four complexes respectively. The doublet and quartet spin states both occur in the complexes, and the contributions to the overall electronic and magnetic properties depend on variety of factors such as, ligand field strength and spin–orbit coupling [118]. The effects of the above factors will be further investigated using the ab initio ligand field theory (AILFT) in future work [119]. Table 13 shows that the lowest energies of quartet roots from CASSCF calculations—100.38 kcal/mol, 100.54 kcal/mol, 105.48 kcal/mol, and 99.96 kcal/mol—are lower than those of HF energies for the complexes. Furthermore the missing correlation energies of −2632.19 kcal/mol (−10.40 kcal/mol per electron), −3008.97 kcal/mol (−10.56 kcal/mol per electron), −3129.20 kcal/mol (−11.30 kcal/mol per electron), and −3273.84 kcal/mol (−11.25 kcal/mol per electron) for the four complexes respectively may prevent accurate CASSCF evaluations of energy levels of 40 doublet roots and 10 quartet roots as well as the magnetic susceptibility parameters. Table 14 demonstrates the spin–orbit coupling dominates in axial D tensor with 32.118 cm−1, 34.468 cm−1, 35.724 cm−1, and 31.106 cm−1 for complexes 1 to 4, respectively, whereas the corresponding spin–spin contribution of −0.028 cm−1, 0.031 cm−1, −0.031 cm−1, and 0.024 cm−1, which are almost negligible to the second order perturbation D tensor. Similar trends about spin–spin coupling occur to the second order perturbation calculations of the transverse E tensor and the effective Hamiltonian simulation of both axial D tensor and transverse E tensor. The axial D tensors are 5-, 5-, 6-, and 4-fold, respectively, for complexes 1–4 of transverse E tensors in both the second order perturbation and effective Hamiltonian calculations. The experimental values for axial D tensors and g factors are listed for the complexes in Table 14. The experimental D tensor values are 29.060 cm−1, 22.680 cm−1, 28.790 cm−1, and 30.860 cm−1 for complexes 1 to 4, respectively, and the second order perturbation calculations provide D tensor values which are 110.4%, 151.8%, 124.0%, and 100.7% of the experimental counterparts, respectively. Table 14 indicates that the average of the theoretical second order perturbation D tensors is 121.8% of the experimental results, and the effective Hamiltonian computation presents an average 110.5% of the experimental value which is also described in Figure 9a. While Figure 9b presents a perfect correlation with R2 of 0.9988 between the theoretical Effective Hamiltonian and the second order perturbation ZFS D tensors, a poor inverse correlation of R2 0.2648 occurs between theoretical Effective Hamiltonian and experimental ZFS D tensors (Figure 9c). The low correlation may be attributed to a lack of major correlation energy in the CASSCF calculations. It is known that combination of strong correlations and spin–orbit coupling can lead to highly anisotropic exchange interactions [9,60,120,121]. The lack of capturing the dynamic correlation energy leads to less accurate energy calculations due to failure to account for the instantaneous interaction among electrons [122]. Figure 9d shows that the axial tensor D exhibits an inverse correlation with respect to the transverse E tensor with an R2 value of 0.8409. Our computations yield ZFS D parameters 28–31 cm−1, which are close to 35–42 cm−1 by Mitsuhashi et al. [64]. The Lande or Gyromagnetic ratio (g-factor) is defined as the ratio of a molecule’s magnetic moment to its angular moment [123], and its magnitude reflects how strongly the spin and orbital of a molecule are modulated by an applied magnetic field. The electronic structure of the phenolate donor in Co(II) complexes was shown to exert strong effects on the g-factors of the compounds [124]. The theoretical and experimental values of g-factors are listed for the complexes in Table 14, and the comparisons suggest that theoretical g factors agree well with experimental results, with an average percent of 98.10% of theoretical values over experimental results. The simulation results of g-factors (gx = 2.028 to 2.052, gy = 2.221 to 2.251, and gz = 2.372 to 2.387) agree well with those (gx = 2.11 to 2.15, gy = 2.11 to 2.15, and gz = 2.48 to 2.56) of previous works [64]. Specifying 5 doublet roots rather than 40 doublet roots could allow quick evaluations of large number of complex candidates. The result in Table 15 suggests the simulation including 5 doublet roots instead of 40 doublet roots can cover 87.88% of axial D tensor values calculated using second order perturbation, and 87.98% in the effective Hamiltonian calculation. Similarly, the second order perturbation method calculation with 5 doublet roots specified gives 90.00% transverse E tensor obtained the second order perturbation method where 40 doublet roots are considered (Seen in Figure 10a), and the percentage turns to 90.88% in the effective Hamiltonian computation which is exemplified in Figure 10b. The Co(II) complex with high anisotropy of magnetic sustability D of −140 ± 30 cm–1 was reported [125]. In the future, we hope to establish an accurate structural model for Co(II) complexes, which will help the development of Co(II)-tripodal phenolate amines or other ligands of high magnetic sustainability.

4. Discussion

Crystal packing in a crystal lattice can significantly impact the magnetic properties of Co(II) complexes. Density functional theory (DFT) based molecular dynamics will be performed to investigate the effect of crystal packing on forces, stresses, and other properties of the SMMs. The inconsistencies between theoretical and experimental axial ZFS D for the complexes probably result from an inappropriate treatment of correlation energy in the CASSCF calculation.

5. Conclusions

The four Co(II) complexes were characterized using MP2 and CASSCF methods. The short Co(II)-O (ligand) coordinate bonds with lengths of 1.89 Å to 1.97 Å are identified as unusual coordinate quasi-double bonds in the optimized geometries. The strengths of Co(II)-O coordination bonds range from 142.01 kcal/mol to 167.36 kcal/mol, whereas Co(II)-N bond energies only have 48.93 kcal/mol to 60.11 kcal/mol. The delocalization energies of Co(II)-O coordination bonds of ligand are two-fold of those for Co(II)-O coordinate bonds of methanol, which are 67.88 kcal/mol, 63.89 kcal/mol, and 68.85 kcal/mol for complex 1 to 3 separately. The lone pair orbital 118 and 119 of ligand donor O2 probably form two separate coordinate bonds between donor O2 and Co(II). The O2 lone pair bonding orbitals show quasi-σ bond feature with hybridizations sp2.06 and sp2.78 for 118α and 118β, respectively, and the O2 lone pair bonding orbitals demonstrate a quasi-π bond character with essentially pure p-type hybridizations sp15.47 and sp13.68 for 119α and 119β, respectively. The delocalization interactions of 167.36 kcal/mol between O2 lone pair bonding orbitals to Co(II) lone pair antibonding orbitals can be tentatively termed as an unusual coordinate quasi-double bond due to the absence of direct supporting experimental results. The dispersion forces constitute 24%, 28%, 27%, and 31% of the ligand–central ion interaction. The MP2 calculation indicated the π–π interaction does not occur between the two phenolate moieties, but a repulsive force of 20.97 kcal/mol exists between two CH2 groups bonded to N1 atoms. The delocalization energy for the ligand to the central metal ion is 11-fold that of the opposite central Co(II) to ligands, suggesting that the complexes are dominated by the ligand-to-metal charge transfer (LMCT). The tert-butyl group on the phenyl ring provides the highest 204.74 kcal/mol to intramolecular interaction energy among methyl, ethyl, chloro, and tert-butyl groups. This work shows that spin–orbit coupling constitutes the major component of both axial and transverse ZFS. The axial ZFS D has three-fold of the transverse ZFS E, and the axial ZFS D is inversely correlated with the transverse ZFS values in the complexes. Our results propose that computations specifying 5 doublet roots can cover 85% of D and E numerical values from the calculations, including 40 doublet roots. The Effect Hamiltonian method generates more accurate D and E numerical values than those from the second order perturbation approach. This work suggests that the bulky tert-butyl and the longer spacer [CH2]2 can tune dispersion forces in the Co(II) complexes to boost large magnetic susceptibility. Our results imply the need to employ an MP2 type of complete active space strategy for the simulation of SMM materials. Our calculations suggest that the combination of bulky electron donating groups and the linker [CH2]2 can be utilized to pursue Co(II) compounds of promising magnetic properties and Co(II) porphyrin fullerene conjugate systems for CO2 electroreduction.

Author Contributions

Conceptualization, Y.L., S.S.M.; methodology, Y.L.; software, Y.L., S.S.M., and O.N.S.; validation, Y.L.; formal analysis, Y.L.; investigation, Y.L., S.S.M., B.I.Y., and Y.G.; resources, Y.L.; data curation, Y.L.; writing—original draft preparation, Y.L., B.I.Y., S.M.; writing—review and editing, Y.L.; visualization, Y.L.; supervision, Y.L.; project administration, Y.L.; funding acquisition, Y.G., Y.L., B.I.Y., T.A. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Department of Energy (grant FOA Number 0002931). T.A. and B.I.Y. acknowledge the Taif University Research Support Project TURSPHC2025/1, Saudi Arabia.

Data Availability Statement

Data are contained within the article.

Acknowledgments

The authors thank the Department of Chemistry, Prairie View A&M University, for their support. T.A. and B.I.Y. acknowledge the Taif University Research Support Project TURSPHC2025/1, Saudi Arabia. We would like to thank Orion Ciftja for his continues support to the project on quantum mechanical simulations of nanoparticle-Co(II) complexe conjugate for the reduction reaction of CO2 and other applications. We acknowledge the computational time funding (1000000 SU) from the Louisiana Optical Network Initiative, Allocation ID 2736. This support is vital, as it enables us to compare experimental results with theoretical calculations and make progress in studying Single-Molecule Magnets (SMMs).  We also acknowledge the support from the HPC LSU System and User Support teams.We acknowledge the computational time funding (1000000 SU) from the Louisiana Optical Network Initiative, Allocation ID 2736. This support is vital, as it enables us to compare experimental results with theoretical calculations and make progress in studying Single-Molecule Magnets (SMMs).  We also acknowledge the support from the HPC LSU System and User Support teams.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Coronado, E. Molecular magnetism: From chemical design to spin control in molecules, materials and devices. Nat. Rev. Mater. 2020, 5, 87–104. [Google Scholar] [CrossRef]
  2. Zhu, Z.; Tang, J. Lanthanide single-molecule magnets with high anisotropy barrier: Where to from here? Natl. Sci. Rev. 2022, 9, nwac194. [Google Scholar] [CrossRef] [PubMed]
  3. Zhu, Z.; Guo, M.; Li, X.-L.; Tang, J. Molecular magnetism of lanthanide: Advances and perspectives. Coord. Chem. Rev. 2019, 378, 350–364. [Google Scholar] [CrossRef]
  4. Mautner, F.A.; Bierbaumer, F.; Fischer, R.C.; Tubau, À.; Speed, S.; Ruiz, E.; Massoud, S.S.; Vicente, R.; Gómez-Coca, S. Insights into the Spin Dynamics of Mononuclear Cerium(III) Single-Molecule Magnets. Inorg. Chem. 2022, 61, 11124–11136. [Google Scholar] [CrossRef]
  5. Shao, D.; Wang, X.-Y. Development of Single-Molecule Magnets†. Chin. J. Chem. 2020, 38, 1005–1018. [Google Scholar] [CrossRef]
  6. Feng, M.; Tong, M.-L. Single Ion Magnets from 3d to 5f: Developments and Strategies. Chem. A Eur. J. 2018, 24, 7574–7594. [Google Scholar] [CrossRef]
  7. Craig, G.A.; Murrie, M. 3d single-ion magnets. Chem. Soc. Rev. 2015, 44, 2135–2147. [Google Scholar] [CrossRef]
  8. Zadrozny, J.M.; Xiao, D.J.; Atanasov, M.; Long, G.J.; Grandjean, F.; Neese, F.; Long, J.R. Magnetic blocking in a linear iron(I) complex. Nat. Chem. 2013, 5, 577–581. [Google Scholar] [CrossRef]
  9. Kumar Sahu, P.; Kharel, R.; Shome, S.; Goswami, S.; Konar, S. Understanding the unceasing evolution of Co(II) based single-ion magnets. Coord. Chem. Rev. 2023, 475, 214871. [Google Scholar] [CrossRef]
  10. Guo, F.S.; Day, B.M.; Chen, Y.C.; Tong, M.L.; Mansikkamäki, A.; Layfield, R.A. A Dysprosium Metallocene Single-Molecule Magnet Functioning at the Axial Limit. Angew. Chem. Int. Ed. Engl. 2017, 56, 11445–11449. [Google Scholar] [CrossRef]
  11. Yin, X.; Deng, L.; Ruan, L.; Wu, Y.; Luo, F.; Qin, G.; Han, X.; Zhang, X. Recent Progress for Single-Molecule Magnets Based on Rare Earth Elements. Materials 2023, 16, 3568. [Google Scholar] [CrossRef] [PubMed]
  12. Sessoli, R.; Gatteschi, D.; Caneschi, A.; Novak, M.A. Magnetic bistability in a metal-ion cluster. Nature 1993, 365, 141–143. [Google Scholar] [CrossRef]
  13. Wernsdorfer, W. Molecular Nanomagnets. In Advanced Magnetic Nanostructures; Sellmyer, D., Skomski, R., Eds.; Springer: Boston, MA, USA, 2006; pp. 147–181. [Google Scholar]
  14. Freedman, D.E.; Harman, W.H.; Harris, T.D.; Long, G.J.; Chang, C.J.; Long, J.R. Slow Magnetic Relaxation in a High-Spin Iron(II) Complex. J. Am. Chem. Soc. 2010, 132, 1224–1225. [Google Scholar] [CrossRef]
  15. Mannini, M.; Pineider, F.; Sainctavit, P.; Danieli, C.; Otero, E.; Sciancalepore, C.; Talarico, A.M.; Arrio, M.A.; Cornia, A.; Gatteschi, D.; et al. Magnetic memory of a single-molecule quantum magnet wired to a gold surface. Nat. Mater. 2009, 8, 194–197. [Google Scholar] [CrossRef]
  16. Moreno-Pineda, E.; Wernsdorfer, W. Measuring molecular magnets for quantum technologies. Nat. Rev. Phys. 2021, 3, 645–659. [Google Scholar] [CrossRef]
  17. Greenspon, A.S.; Marceaux, B.L.; Hu, E.L. Robust lanthanide emitters in polyelectrolyte thin films for photonic applications. Nanotechnology 2018, 29, 075302. [Google Scholar] [CrossRef]
  18. Boulon, M.-E.; Cucinotta, G.; Luzon, J.; Degl’Innocenti, C.; Perfetti, M.; Bernot, K.; Calvez, G.; Caneschi, A.; Sessoli, R. Magnetic Anisotropy and Spin-Parity Effect Along the Series of Lanthanide Complexes with DOTA. Angew. Chem. Int. Ed. 2013, 52, 350–354. [Google Scholar] [CrossRef] [PubMed]
  19. Woodruff, D.N.; Winpenny, R.E.P.; Layfield, R.A. Lanthanide Single-Molecule Magnets. Chem. Rev. 2013, 113, 5110–5148. [Google Scholar] [CrossRef]
  20. Yatoo, M.; Habib, F.; Ahmad, Z.; Ahmad, S.; Husain, A. A Concise Review of Single-Molecule Magnets, Carbon Nanotubes and Hybrids Between Them. Preprints 2023. [Google Scholar] [CrossRef]
  21. Duan, Y.; Rosaleny, L.E.; Coutinho, J.T.; Giménez-Santamarina, S.; Scheie, A.; Baldoví, J.J.; Cardona-Serra, S.; Gaita-Ariño, A. Data-driven design of molecular nanomagnets. Nat. Commun. 2022, 13, 7626. [Google Scholar] [CrossRef]
  22. Etesse, J.; Holzäpfel, A.; Ortu, A.; Afzelius, M. Optical and spin manipulation of non-Kramers rare-earth ions in a weak magnetic field for quantum memory applications. Phys. Rev. A 2021, 103, 022618. [Google Scholar] [CrossRef]
  23. Mondal, S.; Lunghi, A. Unraveling the Contributions to Spin-Lattice Relaxation in Kramers Single-Molecule Magnets. J. Am. Chem. Soc. 2022, 144, 22965–22975. [Google Scholar] [CrossRef] [PubMed]
  24. Pedersen, K.S.; Sigrist, M.; Sørensen, M.A.; Barra, A.-L.; Weyhermüller, T.; Piligkos, S.; Thuesen, C.A.; Vinum, M.G.; Mutka, H.; Weihe, H.; et al. [ReF6]2−: A Robust Module for the Design of Molecule-Based Magnetic Materials. Angew. Chem. Int. Ed. 2014, 53, 1351–1354. [Google Scholar] [CrossRef]
  25. Sato, R.; Suzuki, K.; Minato, T.; Shinoe, M.; Yamaguchi, K.; Mizuno, N. Field-induced slow magnetic relaxation of octahedrally coordinated mononuclear Fe(iii)-, Co(ii)-, and Mn(iii)-containing polyoxometalates. Chem. Commun. 2015, 51, 4081–4084. [Google Scholar] [CrossRef] [PubMed]
  26. Vallejo, J.; Castro, I.; Ruiz-García, R.; Cano, J.; Julve, M.; Lloret, F.; De Munno, G.; Wernsdorfer, W.; Pardo, E. Field-Induced Slow Magnetic Relaxation in a Six-Coordinate Mononuclear Cobalt(II) Complex with a Positive Anisotropy. J. Am. Chem. Soc. 2012, 134, 15704–15707. [Google Scholar] [CrossRef]
  27. Palii, A.V.; Korchagin, D.V.; Yureva, E.A.; Akimov, A.V.; Misochko, E.Y.; Shilov, G.V.; Talantsev, A.D.; Morgunov, R.B.; Aldoshin, S.M.; Tsukerblat, B.S. Single-Ion Magnet Et4N[CoII(hfac)3] with Nonuniaxial Anisotropy: Synthesis, Experimental Characterization, and Theoretical Modeling. Inorg. Chem. 2016, 55, 9696–9706. [Google Scholar] [CrossRef]
  28. Wang, Y.-L.; Chen, L.; Liu, C.-M.; Zhang, Y.-Q.; Yin, S.-G.; Liu, Q.-Y. Field-Induced Slow Magnetic Relaxation and Gas Adsorption Properties of a Bifunctional Cobalt(II) Compound. Inorg. Chem. 2015, 54, 11362–11368. [Google Scholar] [CrossRef]
  29. Meng, Y.-S.; Mo, Z.; Wang, B.-W.; Zhang, Y.-Q.; Deng, L.; Gao, S. Observation of the single-ion magnet behavior of d8 ions on two-coordinate Co(i)–NHC complexes. Chem. Sci. 2015, 6, 7156–7162. [Google Scholar] [CrossRef]
  30. Liu, X.; Sun, L.; Zhou, H.; Cen, P.; Jin, X.; Xie, G.; Chen, S.; Hu, Q. Single-Ion-Magnet Behavior in a Two-Dimensional Coordination Polymer Constructed from CoII Nodes and a Pyridylhydrazone Derivative. Inorg. Chem. 2015, 54, 8884–8886. [Google Scholar] [CrossRef]
  31. Mondal, A.K.; Jover, J.; Ruiz, E.; Konar, S. Investigation of easy-plane magnetic anisotropy in P-ligand square-pyramidal CoII single ion magnets. Chem. Commun. 2017, 53, 5338–5341. [Google Scholar] [CrossRef]
  32. Mondal, A.K.; Goswami, T.; Misra, A.; Konar, S. Probing the Effects of Ligand Field and Coordination Geometry on Magnetic Anisotropy of Pentacoordinate Cobalt(II) Single-Ion Magnets. Inorg. Chem. 2017, 56, 6870–6878. [Google Scholar] [CrossRef]
  33. Cahier, B.; Perfetti, M.; Zakhia, G.; Naoufal, D.; El-Khatib, F.; Guillot, R.; Rivière, E.; Sessoli, R.; Barra, A.-L.; Guihéry, N.; et al. Magnetic Anisotropy in Pentacoordinate NiII and CoII Complexes: Unraveling Electronic and Geometrical Contributions. Chem. A Eur. J. 2017, 23, 3648–3657. [Google Scholar] [CrossRef] [PubMed]
  34. El-Khatib, F.; Cahier, B.; Shao, F.; López-Jordà, M.; Guillot, R.; Rivière, E.; Hafez, H.; Saad, Z.; Girerd, J.-J.; Guihéry, N.; et al. Design and Magnetic Properties of a Mononuclear Co(II) Single Molecule Magnet and Its Antiferromagnetically Coupled Binuclear Derivative. Inorg. Chem. 2017, 56, 4601–4608. [Google Scholar] [CrossRef] [PubMed]
  35. Shao, D.; Shi, L.; Zhang, S.-L.; Zhao, X.-H.; Wu, D.-Q.; Wei, X.-Q.; Wang, X.-Y. Syntheses, structures, and magnetic properties of three new chain compounds based on a pentagonal bipyramidal Co(ii) building block. CrystEngComm 2016, 18, 4150–4157. [Google Scholar] [CrossRef]
  36. Świtlicka-Olszewska, A.; Palion-Gazda, J.; Klemens, T.; Machura, B.; Vallejo, J.; Cano, J.; Lloret, F.; Julve, M. Single-ion magnet behaviour in mononuclear and two-dimensional dicyanamide-containing cobalt(ii) complexes. Dalton Trans. 2016, 45, 10181–10193. [Google Scholar] [CrossRef]
  37. Briganti, M.; Santanni, F.; Tesi, L.; Totti, F.; Sessoli, R.; Lunghi, A. A Complete Ab Initio View of Orbach and Raman Spin–Lattice Relaxation in a Dysprosium Coordination Compound. J. Am. Chem. Soc. 2021, 143, 13633–13645. [Google Scholar] [CrossRef]
  38. Accorsi, S.; Barra, A.-L.; Caneschi, A.; Chastanet, G.; Cornia, A.; Fabretti, A.C.; Gatteschi, D.; Mortalò, C.; Olivieri, E.; Parenti, F.; et al. Tuning Anisotropy Barriers in a Family of Tetrairon(III) Single-Molecule Magnets with an S = 5 Ground State. J. Am. Chem. Soc. 2006, 128, 4742–4755. [Google Scholar] [CrossRef]
  39. Lu, F.; Guo, W.-X.; Zhang, Y.-Q. Largely Enhancing the Blocking Energy Barrier and Temperature of a Linear Cobalt(II) Complex through the Structural Distortion: A Theoretical Exploration. Inorg. Chem. 2022, 61, 295–301. [Google Scholar] [CrossRef] [PubMed]
  40. Murrie, M. Cobalt(ii) single-molecule magnets. Chem. Soc. Rev. 2010, 39, 1986–1995. [Google Scholar] [CrossRef]
  41. Oshio, H.; Nakano, M. High-spin molecules with magnetic anisotropy toward single-molecule magnets. Chemistry 2005, 11, 5178–5185. [Google Scholar] [CrossRef]
  42. Fukui, K.; Ohya-Nishiguchi, H.; Hirota, N. The relation between zero-field splittings and distortions along the normal coordinates in transition metal complexes. Mol. Phys. 1990, 71, 1269–1283. [Google Scholar] [CrossRef]
  43. Murugesan, S.; Stöger, B.; Carvalho, M.D.; Ferreira, L.P.; Pittenauer, E.; Allmaier, G.; Veiros, L.F.; Kirchner, K. Synthesis and Reactivity of Four- and Five-Coordinate Low-Spin Cobalt(II) PCP Pincer Complexes and Some Nickel(II) Analogues. Organometallics 2014, 33, 6132–6140. [Google Scholar] [CrossRef] [PubMed]
  44. Krzystek, J.; Zvyagin, S.A.; Ozarowski, A.; Fiedler, A.T.; Brunold, T.C.; Telser, J. Definitive Spectroscopic Determination of Zero-Field Splitting in High-Spin Cobalt(II). J. Am. Chem. Soc. 2004, 126, 2148–2155. [Google Scholar] [CrossRef] [PubMed]
  45. Devkota, L.; SantaLucia, D.J.; Wheaton, A.M.; Pienkos, A.J.; Lindeman, S.V.; Krzystek, J.; Ozerov, M.; Berry, J.F.; Telser, J.; Fiedler, A.T. Spectroscopic and Magnetic Studies of Co(II) Scorpionate Complexes: Is There a Halide Effect on Magnetic Anisotropy? Inorg. Chem. 2023, 62, 5984–6002. [Google Scholar] [CrossRef]
  46. Kremer, S.; Henke, W.; Reinen, D. High-spin-low-spin equilibriums of cobalt(2+) in the terpyridine complexes Co(terpy)2X2.nH2O. Inorg. Chem. 1982, 21, 3013–3022. [Google Scholar] [CrossRef]
  47. Izumiyama, N.; Fujii, S.; Kato, K.; Tokunaga, R.; Hayami, S.; Nakaya, M. Spin-crossover cobalt(ii) complexes exhibiting temperature- and concentration-dependent optical changes in solution. Dalton Trans. 2024, 53, 9547–9553. [Google Scholar] [CrossRef]
  48. Craven, M.; Nygaard, M.H.; Zadrozny, J.M.; Long, J.R.; Overgaard, J. Determination of d-Orbital Populations in a Cobalt(II) Single-Molecule Magnet Using Single-Crystal X-ray Diffraction. Inorg. Chem. 2018, 57, 6913–6920. [Google Scholar] [CrossRef]
  49. Palii, A.V.; Clemente-Juan, J.M.; Coronado, E.; Klokishner, S.I.; Ostrovsky, S.M.; Reu, O.S. Role of Orbital Degeneracy in the Single Molecule Magnet Behavior of a Mononuclear High-Spin Fe(II) Complex. Inorg. Chem. 2010, 49, 8073–8077. [Google Scholar] [CrossRef]
  50. Gomez-Coca, S.; Cremades, E.; Aliaga-Alcalde, N.; Ruiz, E. Mononuclear single-molecule magnets: Tailoring the magnetic anisotropy of first-row transition-metal complexes. J. Am. Chem. Soc. 2013, 135, 7010–7018. [Google Scholar] [CrossRef]
  51. Bunting, P.C.; Atanasov, M.; Damgaard-Møller, E.; Perfetti, M.; Crassee, I.; Orlita, M.; Overgaard, J.; van Slageren, J.; Neese, F.; Long, J.R. A linear cobalt(II) complex with maximal orbital angular momentum from a non-Aufbau ground state. Science 2018, 362, eaat7319. [Google Scholar] [CrossRef]
  52. Yao, X.N.; Du, J.Z.; Zhang, Y.Q.; Leng, X.B.; Yang, M.W.; Jiang, S.D.; Wang, Z.X.; Ouyang, Z.W.; Deng, L.; Wang, B.W.; et al. Two-Coordinate Co(II) Imido Complexes as Outstanding Single-Molecule Magnets. J. Am. Chem. Soc. 2017, 139, 373–380. [Google Scholar] [CrossRef] [PubMed]
  53. Eichhöfer, A.; Lan, Y.; Mereacre, V.; Bodenstein, T.; Weigend, F. Slow magnetic relaxation in trigonal-planar mononuclear Fe(II) and Co(II) bis(trimethylsilyl)amido complexes--a comparative study. Inorg. Chem. 2014, 53, 1962–1974. [Google Scholar] [CrossRef]
  54. Rechkemmer, Y.; Breitgoff, F.D.; van der Meer, M.; Atanasov, M.; Hakl, M.; Orlita, M.; Neugebauer, P.; Neese, F.; Sarkar, B.; van Slageren, J. A four-coordinate cobalt(II) single-ion magnet with coercivity and a very high energy barrier. Nat. Commun. 2016, 7, 10467. [Google Scholar] [CrossRef] [PubMed]
  55. Fataftah, M.S.; Zadrozny, J.M.; Rogers, D.M.; Freedman, D.E. A Mononuclear Transition Metal Single-Molecule Magnet in a Nuclear Spin-Free Ligand Environment. Inorg. Chem. 2014, 53, 10716–10721. [Google Scholar] [CrossRef]
  56. Wu, C.-M.; Tsai, J.-E.; Lee, G.-H.; Yang, E.-C. Slow magnetization relaxation in a tetrahedrally coordinated mononuclear Co(ii) complex exclusively ligated with phenanthroline ligands. Dalton Trans. 2020, 49, 16813–16820. [Google Scholar] [CrossRef]
  57. Cui, H.H.; Lu, F.; Chen, X.T.; Zhang, Y.Q.; Tong, W.; Xue, Z.L. Zero-Field Slow Magnetic Relaxation and Hysteresis Loop in Four-Coordinate Co(II) Single-Ion Magnets with Strong Easy-Axis Anisotropy. Inorg. Chem. 2019, 58, 12555–12564. [Google Scholar] [CrossRef] [PubMed]
  58. Ziegenbalg, S.; Hornig, D.; Görls, H.; Plass, W. Cobalt(II)-Based Single-Ion Magnets with Distorted Pseudotetrahedral [N2O2] Coordination: Experimental and Theoretical Investigations. Inorg. Chem. 2016, 55, 4047–4058. [Google Scholar] [CrossRef]
  59. Ferentinos, E.; Tzeli, D.; Sottini, S.; Groenen, E.; Ozerov, M.; Poneti, G.; Kaniewska-Laskowska, K.; Krzystek, J.; Kyritsis, P. Magnetic anisotropy and structural flexibility in the field-induced single ion magnets [Co{(OPPh 2 )(EPPh 2 )N} 2 ], E = S, Se, explored by experimental and computational methods. Dalton Trans. 2023, 52, 2036–2050. [Google Scholar] [CrossRef]
  60. Massoud, S.S.; Perez, Z.E.; Courson, J.R.; Fischer, R.C.; Mautner, F.A.; Vančo, J.; Čajan, M.; Trávníček, Z. Slow magnetic relaxation in penta-coordinate cobalt(ii) field-induced single-ion magnets (SIMs) with easy-axis magnetic anisotropy. Dalton Trans. 2020, 49, 11715–11726. [Google Scholar] [CrossRef]
  61. Mora-Fonz, M.J.; Catlow, C.R.; Lewis, D.W. Oligomerization and cyclization processes in the nucleation of microporous silicas. Angew. Chem. Int. Ed. Engl. 2005, 44, 3082–3086. [Google Scholar] [CrossRef]
  62. Jurca, T.; Farghal, A.; Lin, P.H.; Korobkov, I.; Murugesu, M.; Richeson, D.S. Single-molecule magnet behavior with a single metal center enhanced through peripheral ligand modifications. J. Am. Chem. Soc. 2011, 133, 15814–15817. [Google Scholar] [CrossRef]
  63. Bamberger, H.; Albold, U.; Dubnická Midlíková, J.; Su, C.-Y.; Deibel, N.; Hunger, D.; Hallmen, P.P.; Neugebauer, P.; Beerhues, J.; Demeshko, S.; et al. Iron(II), Cobalt(II), and Nickel(II) Complexes of Bis(sulfonamido)benzenes: Redox Properties, Large Zero-Field Splittings, and Single-Ion Magnets. Inorg. Chem. 2021, 60, 2953–2963. [Google Scholar] [CrossRef]
  64. Mitsuhashi, R.; Hosoya, S.; Suzuki, T.; Sunatsuki, Y.; Sakiyama, H.; Mikuriya, M. Hydrogen-bonding interactions and magnetic relaxation dynamics in tetracoordinated cobalt(ii) single-ion magnets. Dalton Trans. 2019, 48, 395–399. [Google Scholar] [CrossRef] [PubMed]
  65. Böhme, M.; Ziegenbalg, S.; Aliabadi, A.; Schnegg, A.; Görls, H.; Plass, W. Magnetic relaxation in cobalt(ii)-based single-ion magnets influenced by distortion of the pseudotetrahedral [N2O2] coordination environment. Dalton Trans. 2018, 47, 10861–10873. [Google Scholar] [CrossRef] [PubMed]
  66. Plyuta, N.; Petrusenko, S.; Kokozay, V.N.; Cauchy, T.; Lloret, F.; Julve, M.; Cano, J.; Avarvari, N. Field-induced mononuclear cobalt(II) single-molecule magnet (SMM) based on a benzothiadiazole-ortho-vanillin ligand †. Dalton Trans. 2022, 51, 4760–4771. [Google Scholar] [CrossRef]
  67. Landart-Gereka, A.; Quesada-Moreno, M.M.; Díaz-Ortega, I.F.; Nojiri, H.; Ozerov, M.; Krzystek, J.; Palacios, M.A.; Colacio, E. Large easy-axis magnetic anisotropy in a series of trigonal prismatic mononuclear cobalt(ii) complexes with zero-field hidden single-molecule magnet behaviour: The important role of the distortion of the coordination sphere and intermolecular interactions in the slow relaxation. Inorg. Chem. Front. 2022, 9, 2810–2831. [Google Scholar] [CrossRef]
  68. Tupolova, Y.P.; Shcherbakov, I.N.; Korchagin, D.V.; Tkachev, V.V.; Lebedev, V.E.; Popov, L.D.; Zakharov, K.V.; Vasiliev, A.N.; Palii, A.V.; Aldoshin, S.M. Fine-Tuning of Uniaxial Anisotropy and Slow Relaxation of Magnetization in the Hexacoordinate Co(II) Complexes with Acidoligands. J. Phys. Chem. C 2020, 124, 25957–25966. [Google Scholar] [CrossRef]
  69. Mičová, R.; Rajnák, C.; Titiš, J.; Bieńko, A.; Moncoľ, J.; Samoľová, E.; Boča, R. Easy-axis magnetic anisotropy in tetragonally elongated cobalt(ii) complexes beyond the spin-Hamiltonian formalism. Dalton Trans. 2023, 52, 7885–7892. [Google Scholar] [CrossRef]
  70. Pilichos, E.; Font-Bardia, M.; Cano, J.; Escuer, A.; Mayans, J. Slow magnetic relaxation for cobalt(ii) complexes in axial bipyramidal environment: An S = 1/2 spin case. Dalton Trans. 2022, 51, 8986–8993. [Google Scholar] [CrossRef]
  71. Mondal, A.K.; Mondal, A.; Konar, S. Slow Magnetic Relaxation in a One-Dimensional Coordination Polymer Constructed from Hepta-Coordinate Cobalt(II) Nodes. Magnetochemistry 2020, 6, 45. [Google Scholar] [CrossRef]
  72. Shao, D.; Zhang, S.-L.; Shi, L.; Zhang, Y.-Q.; Wang, X.-Y. Probing the Effect of Axial Ligands on Easy-Plane Anisotropy of Pentagonal-Bipyramidal Cobalt(II) Single-Ion Magnets. Inorg. Chem. 2016, 55, 10859–10869. [Google Scholar] [CrossRef]
  73. Chen, L.; Wang, J.; Wei, J.-M.; Wernsdorfer, W.; Chen, X.-T.; Zhang, Y.-Q.; Song, Y.; Xue, Z.-L. Slow magnetic relaxation in a mononuclear eight-coordinate cobalt(II) complex. J. Am. Chem. Soc. 2014, 136, 12213–12216. [Google Scholar] [CrossRef] [PubMed]
  74. Ruamps, R.; Batchelor, L.J.; Maurice, R.; Gogoi, N.; Jiménez-Lozano, P.; Guihéry, N.; de Graaf, C.; Barra, A.-L.; Sutter, J.-P.; Mallah, T. Origin of the Magnetic Anisotropy in Heptacoordinate NiII and CoII Complexes. Chem. A Eur. J. 2013, 19, 950–956. [Google Scholar] [CrossRef]
  75. Kopotkov, V.A.; Korchagin, D.V.; Sasnovskaya, V.D.; Gilmutdinov, I.F.; Yagubskii, E.B. A Series of Field-Induced Single-Ion Magnets Based on the Seven-Coordinate Co(II) Complexes with the Pentadentate (N3O2) H2dapsc Ligand. Magnetochemistry 2019, 5, 58. [Google Scholar] [CrossRef]
  76. Habib, F.; Luca, O.R.; Vieru, V.; Shiddiq, M.; Korobkov, I.; Gorelsky, S.I.; Takase, M.K.; Chibotaru, L.F.; Hill, S.; Crabtree, R.H.; et al. Influence of the Ligand Field on Slow Magnetization Relaxation versus Spin Crossover in Mononuclear Cobalt Complexes. Angew. Chem. Int. Ed. 2013, 52, 11290–11293. [Google Scholar] [CrossRef]
  77. Massoud, S.S.; Mautner, F.A.; Sakiyama, H.; Louka, F.R.; Salem, N.H.M.; Fischer, R.C.; Torvisco, A.; Guizouarn, T.; Velmurugan, G.; Comba, P.; et al. SMM Behavior in Distorted Trigonal Bipyramidal and Tetrahedral Cobalt(II) Complexes Based on Tripodal Tetradentate Phenolic Amines. Eur. J. Inorg. Chem. 2025, 28, e202400777. [Google Scholar] [CrossRef]
  78. Dong, X.; Xin, Z.; He, D.; Zhang, J.-L.; Lan, Y.-Q.; Zhang, Q.-F.; Chen, Y. Boosting CO2 electroreduction performance over fullerene-modified MOF-545-Co promoted by π–π interaction. Chin. Chem. Lett. 2023, 34, 107459. [Google Scholar] [CrossRef]
  79. Subedi, D.; Jang, Y.; Ganesan, A.; Schoellhorn, S.; Reid, R.; Verbeck, G.; D’Souza, F. Donor-acceptor conjugates derived from cobalt porphyrin and fullerene via metal-ligand axial coordination: Formation and excited state charge separation. J. Porphyr. Phthalocyanines 2021, 25, 533–546. [Google Scholar] [CrossRef]
  80. Liu, Y.; Gallo, A.A.; Liu, Y.; Hall, M.B.; Johnson, B.R. QM evaluation of the intramolecular aromatic π-π interactions of Ir(I) complex transition states. J. Mol. Struct. 2023, 1291, 135907. [Google Scholar] [CrossRef]
  81. Lunghi, A.; Sanvito, S. Computational design of magnetic molecules and their environment using quantum chemistry, machine learning and multiscale simulations. Nat. Rev. Chem. 2022, 6, 761–781. [Google Scholar] [CrossRef]
  82. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Rev. C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
  83. Neese, F. The ORCA program system. WIREs Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
  84. Perdew, J.P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B 1986, 33, 8822–8824. [Google Scholar] [CrossRef]
  85. Becke, A.D. Density functional calculations of molecular bond energies. J. Chem. Phys. 1986, 84, 4524–4529. [Google Scholar] [CrossRef]
  86. Becke, A.D.; Johnson, E.R. A density-functional model of the dispersion interaction. J. Chem. Phys. 2005, 123, 154101. [Google Scholar] [CrossRef]
  87. Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
  88. Neese, F.; Wennmohs, F.; Hansen, A.; Becker, U. Efficient, approximate and parallel Hartree–Fock and hybrid DFT calculations. A ‘chain-of-spheres’ algorithm for the Hartree–Fock exchange. Chem. Phys. 2009, 356, 98–109. [Google Scholar] [CrossRef]
  89. Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef]
  90. Jung, J.; Atanasov, M.; Neese, F. Ab Initio Ligand-Field Theory Analysis and Covalency Trends in Actinide and Lanthanide Free Ions and Octahedral Complexes. Inorg. Chem. 2017, 56, 8802–8816. [Google Scholar] [CrossRef] [PubMed]
  91. Angeli, C.; Cimiraglia, R.; Evangelisti, S.; Leininger, T.; Malrieu, J.P. Introduction of n-electron valence states for multireference perturbation theory. J. Chem. Phys. 2001, 114, 10252–10264. [Google Scholar] [CrossRef]
  92. Chilton, N.F.; Anderson, R.P.; Turner, L.D.; Soncini, A.; Murray, K.S. PHI: A powerful new program for the analysis of anisotropic monomeric and exchange-coupled polynuclear d- and f-block complexes. J. Comput. Chem. 2013, 34, 1164–1175. [Google Scholar] [CrossRef]
  93. Glaesemann, K.R.; Schmidt, M.W. On the Ordering of Orbital Energies in High-Spin ROHF. J. Phys. Chem. A 2010, 114, 8772–8777. [Google Scholar] [CrossRef] [PubMed]
  94. Zanders, D.; Boysen, N.; Land, M.A.; Obenlüneschloß, J.; Masuda, J.D.; Mallick, B.; Barry, S.T.; Devi, A. Co(II) Amide, Pyrrolate, and Aminopyridinate Complexes: Assessment of their Manifold Structural Chemistry and Thermal Properties. Eur. J. Inorg. Chem. 2021, 2021, 5119–5136. [Google Scholar] [CrossRef]
  95. Kim, H.-C.; Mitra, S.; Veerana, M.; Lim, J.-S.; Jeong, H.-R.; Park, G.; Huh, S.; Kim, S.-J.; Kim, Y. Cobalt(II)-coordination polymers containing glutarates and bipyridyl ligands and their antifungal potential. Sci. Rep. 2019, 9, 14983. [Google Scholar] [CrossRef] [PubMed]
  96. Chin, Y.-Y.; Lin, H.-J.; Hu, Z.; Kuo, C.-Y.; Mikhailova, D.; Lee, J.-M.; Haw, S.-C.; Chen, S.-A.; Schnelle, W.; Ishii, H.; et al. Relation between the Co-O bond lengths and the spin state of Co in layered Cobaltates: A high-pressure study. Sci. Rep. 2017, 7, 3656. [Google Scholar] [CrossRef]
  97. Buron-Le Cointe, M.; Hébert, J.; Baldé, C.; Moisan, N.; Toupet, L.; Guionneau, P.; Létard, J.F.; Freysz, E.; Cailleau, H.; Collet, E. Intermolecular control of thermoswitching and photoswitching phenomena in two spin-crossover polymorphs. Phys. Rev. B 2012, 85, 064114. [Google Scholar] [CrossRef]
  98. Addison, A.W.; Rao, T.N.; Reedijk, J.; van Rijn, J.; Verschoor, G.C. Synthesis, structure, and spectroscopic properties of copper(II) compounds containing nitrogen–sulphur donor ligands; the crystal and molecular structure of aqua[1,7-bis(N-methylbenzimidazol-2′-yl)-2,6-dithiaheptane]copper(II) perchlorate. J. Chem. Soc. Dalton Trans. 1984, 1349–1356. [Google Scholar] [CrossRef]
  99. Yang, L.; Powell, D.R.; Houser, R.P. Structural variation in copper(i) complexes with pyridylmethylamide ligands: Structural analysis with a new four-coordinate geometry index, τ4. Dalton Trans. 2007, 955–964. [Google Scholar] [CrossRef]
  100. Alonso, J.A.; Martínez-Lope, M.J.; Casais, M.T.; Fernández-Díaz, M.T. Evolution of the Jahn−Teller Distortion of MnO6 Octahedra in RMnO3 Perovskites (R = Pr, Nd, Dy, Tb, Ho, Er, Y): A Neutron Diffraction Study. Inorg. Chem. 2000, 39, 917–923. [Google Scholar] [CrossRef]
  101. Marchivie, M.; Guionneau, P.; Letard, J.-F.; Chasseau, D. Photo-induced spin-transition: The role of the iron(II) environment distortion. Acta Crystallogr. Sect. B 2005, 61, 25–28. [Google Scholar] [CrossRef]
  102. McCusker, J.K.; Rheingold, A.L.; Hendrickson, D.N. Variable-Temperature Studies of Laser-Initiated 5T2 → 1A1 Intersystem Crossing in Spin-Crossover Complexes:  Empirical Correlations between Activation Parameters and Ligand Structure in a Series of Polypyridyl Ferrous Complexes. Inorg. Chem. 1996, 35, 2100–2112. [Google Scholar] [CrossRef]
  103. Köppel, H.; Barentzen, H. The Jahn-Teller Effect: Fundamentals and Implications for Physics and Chemistry; Springer: Berlin/Heidelberg, Germany, 2009; Volume 97. [Google Scholar]
  104. Okuniewski, A.; Rosiak, D.; Chojnacki, J.; Becker, B. Coordination polymers and molecular structures among complexes of mercury(II) halides with selected 1-benzoylthioureas. Polyhedron 2015, 90, 47–57. [Google Scholar] [CrossRef]
  105. Šebová, M.; Boca, R.; Dlhan, L.; Nemec, I.; Papankova, B.; Pavlik, J.; Fuess, H. Direct determination of zero-field splitting in Co(II) complexes by FAR infrared spectroscopy. Inorganica Chim. Acta 2012, 383, 143–151. [Google Scholar] [CrossRef]
  106. Weinhold, F.; Landis, C.R.; Glendening, E.D. What is NBO analysis and how is it useful? Int. Rev. Phys. Chem. 2016, 35, 399–440. [Google Scholar] [CrossRef]
  107. Weinhold, F. Natural bond orbital analysis: A critical overview of relationships to alternative bonding perspectives. J. Comput. Chem. 2012, 33, 2363–2379. [Google Scholar] [CrossRef]
  108. Mizukami, S.; Houjou, H.; Sugaya, K.; Koyama, E.; Tokuhisa, H.; Sasaki, T.; Kanesato, M. Fluorescence Color Modulation by Intramolecular and Intermolecular π−π Interactions in a Helical Zinc(II) Complex. Chem. Mater. 2005, 17, 50–56. [Google Scholar] [CrossRef]
  109. Liu, Y.; Liu, Y.; Murru, S.; Tzeng, N.; Srivastava, R.S. Quantum mechanics study of repulsive π–π interaction and flexibility of phenyl moiety in the iron azodioxide complex. J. Mol. Struct. 2015, 1097, 226–230. [Google Scholar] [CrossRef]
  110. Ciliberto, E.; Doris, K.A.; Pietro, W.J.; Reisner, G.M.; Ellis, D.E.; Fragala, I.; Herbstein, F.H.; Ratner, M.A.; Marks, T.J. The.pi.-.pi. interactions and bandwidths in molecular metals. A chemical, structural, photoelectron spectroscopic, and Hartree-Fock-Slater study of monomeric and cofacially joined dimeric silicon phthalocyanines. J. Am. Chem. Soc. 1984, 106, 7748–7761. [Google Scholar] [CrossRef]
  111. Carter-Fenk, K.; Liu, M.; Pujal, L.; Loipersberger, M.; Tsanai, M.; Vernon, R.M.; Forman-Kay, J.D.; Head-Gordon, M.; Heidar-Zadeh, F.; Head-Gordon, T. The Energetic Origins of Pi-Pi Contacts in Proteins. J. Am. Chem. Soc. 2023, 145, 24836–24851. [Google Scholar] [CrossRef]
  112. Kowalski, P.H.; Krzemińska, A.; Pernal, K.; Pastorczak, E. Dispersion Interactions between Molecules in and out of Equilibrium Geometry: Visualization and Analysis. J. Phys. Chem. A 2022, 126, 1312–1319. [Google Scholar] [CrossRef]
  113. Khare, E.; Holten-Andersen, N.; Buehler, M.J. Transition-metal coordinate bonds for bioinspired macromolecules with tunable mechanical properties. Nat. Rev. Mater. 2021, 6, 421–436. [Google Scholar] [CrossRef]
  114. Laporte, O.; Meggers, W.F. Some Rules of Spectral Structure*. J. Opt. Soc. Am. 1925, 11, 459–463. [Google Scholar] [CrossRef]
  115. Schnaubelt, L.; Petzold, H.; Speck, J.M.; Rüffer, T.; Hörner, G.; Lang, H. Spin Transition and Charge Transfer in Co2+/Co3+ Complexes of Meridional Ligands Holding Nearby Redox-active Triarylamine. Z. Anorg. Allg. Chem. 2018, 644, 1257–1267. [Google Scholar] [CrossRef]
  116. May, A.M.; Dempsey, J.L. A new era of LMCT: Leveraging ligand-to-metal charge transfer excited states for photochemical reactions. Chem. Sci. 2024, 15, 6661–6678. [Google Scholar] [CrossRef] [PubMed]
  117. Tuszyński, J.A. First- and second-order contributions to the effective Hamiltonian parameters for Gd3+(8S) and Mn2+(6S). J. Magn. Magn. Mater. 1986, 54–57, 1481–1482. [Google Scholar] [CrossRef]
  118. Kumar, S.; Arumugam, S.; Schwarz, B.; Ehrenberg, H.; Mondal, K. Static and Dynamic Magnetic Properties of a Co(II)-Complex with N2O2 Donor Set—A Theoretical and Experimental Study. Eur. J. Inorg. Chem. 2023, 26, e202200774. [Google Scholar] [CrossRef]
  119. Rao, S.V.; Maganas, D.; Sivalingam, K.; Atanasov, M.; Neese, F. Extended Active Space Ab Initio Ligand Field Theory: Applications to Transition-Metal Ions. Inorg. Chem. 2024, 63, 24672–24684. [Google Scholar] [CrossRef]
  120. Lloret, F.; Julve, M.; Cano, J.; Ruiz-García, R.; Pardo, E. Magnetic properties of six-coordinated high-spin cobalt(II) complexes: Theoretical background and its application. Inorganica Chim. Acta 2008, 361, 3432–3445. [Google Scholar] [CrossRef]
  121. Khosla, A.L.; Jacko, A.C.; Merino, J.; Powell, B.J. Spin-orbit coupling and strong electronic correlations in cyclic molecules. Phys. Rev. B 2017, 95, 115109. [Google Scholar] [CrossRef]
  122. Šulka, M.; Šulková, K.; Dubecký, M. Unveiling hidden dynamic correlations in CASSCF correlation energies by Hartree–Fock nodes. J. Chem. Phys. 2024, 161, 114112. [Google Scholar] [CrossRef]
  123. Landé, A. Über den anomalen Zeemaneffekt (Teil I). Z. Phys. 1921, 5, 231–241. [Google Scholar] [CrossRef]
  124. Sakiyama, H.; Kimura, R.; Oomiya, H.; Mitsuhashi, R.; Fujii, S.; Kanaizuka, K.; Muddassir, M.; Tamaki, Y.; Asato, E.; Handa, M. Relationship between Structure and Zero-Field Splitting of Octahedral Nickel(II) Complexes with a Low-Symmetric Tetradentate Ligand. Magnetochemistry 2024, 10, 32. [Google Scholar] [CrossRef]
  125. Pankratova, Y.A.; Nelyubina, Y.V.; Novikov, V.V.; Pavlov, A.A. High-Spin Cobalt(II) Complex with Record-Breaking Anisotropy of the Magnetic Susceptibility According to Paramagnetic NMR Spectroscopy Data. Russ. J. Coord. Chem. 2021, 47, 10–16. [Google Scholar] [CrossRef]
Nanomaterials 15 00938 g001
Figure 1. Structures of four Co(II) complexes based on the ligand tripodal tetradentate phenolate amine ligands.
Figure 1. Structures of four Co(II) complexes based on the ligand tripodal tetradentate phenolate amine ligands.
Nanomaterials 15 00938 g001
Nanomaterials 15 00938 g002
Figure 2. Structure of complex 1 with hydrogen atoms omitted for clarity and d orbital diagrams of the geometries for 4-coordinate and 5-coordinate complexes. (a) Structure of complex 1 with hydrogen atoms omitted for clarity. (b) The geometries for 4-coordinate complexes. (c) The geometries for 5-coordinate complexes.
Figure 2. Structure of complex 1 with hydrogen atoms omitted for clarity and d orbital diagrams of the geometries for 4-coordinate and 5-coordinate complexes. (a) Structure of complex 1 with hydrogen atoms omitted for clarity. (b) The geometries for 4-coordinate complexes. (c) The geometries for 5-coordinate complexes.
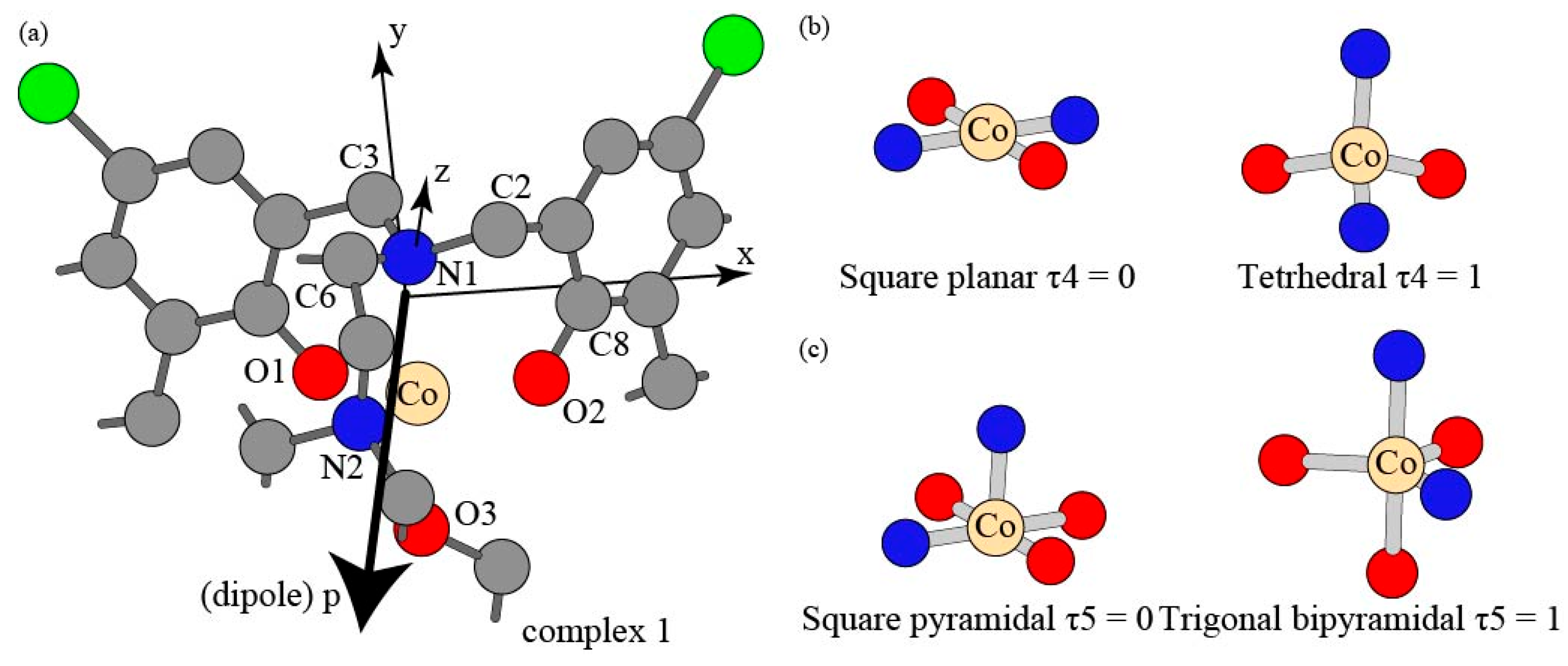
Nanomaterials 15 00938 g002
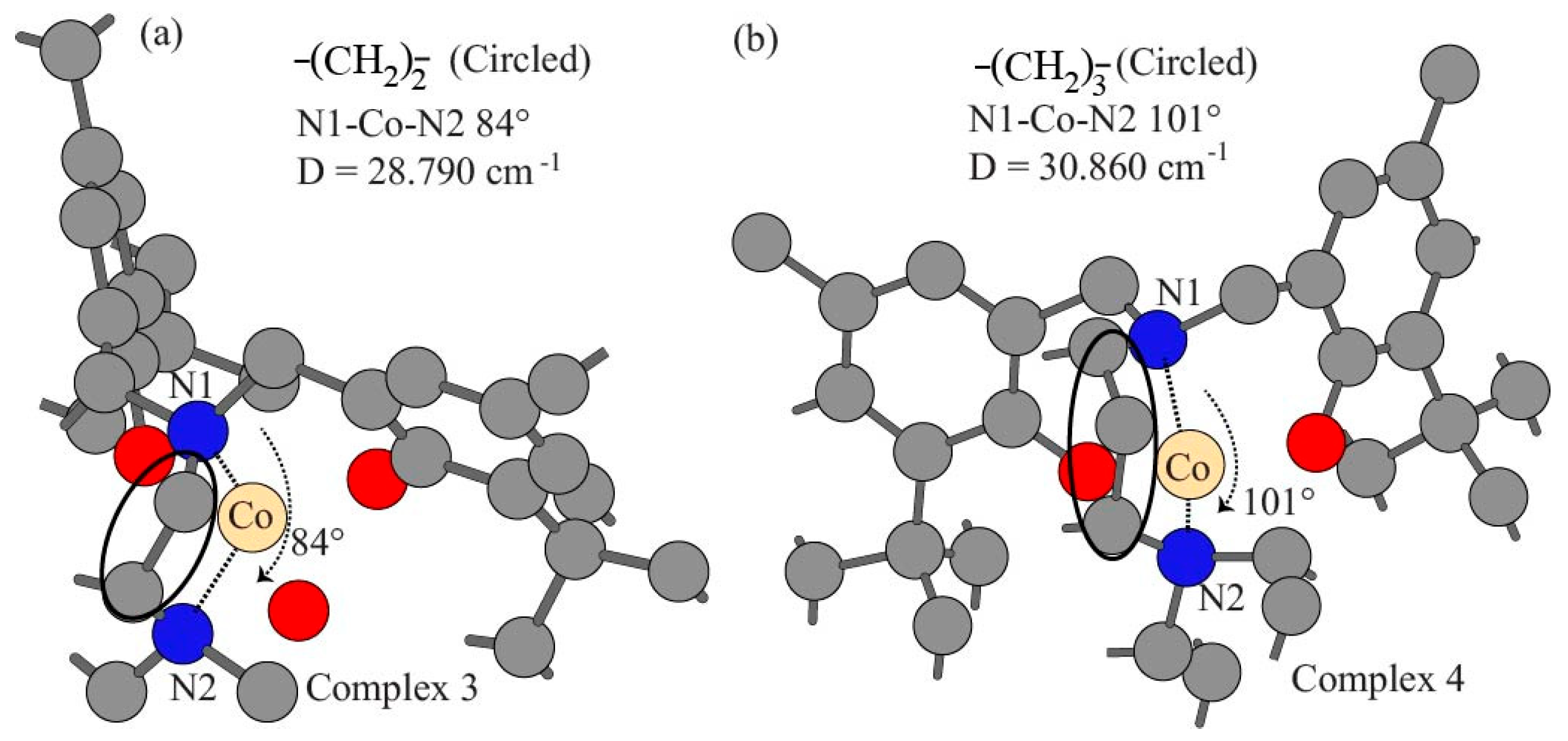
Nanomaterials 15 00938 g003
Figure 3. Comparison of the N-Co(II)-N angles between complexes 3 and 4. (a) The N-Co(II)-N angles in complex 3. (b) The N-Co(II)-N angles in complex 4.
Figure 3. Comparison of the N-Co(II)-N angles between complexes 3 and 4. (a) The N-Co(II)-N angles in complex 3. (b) The N-Co(II)-N angles in complex 4.
Nanomaterials 15 00938 g003
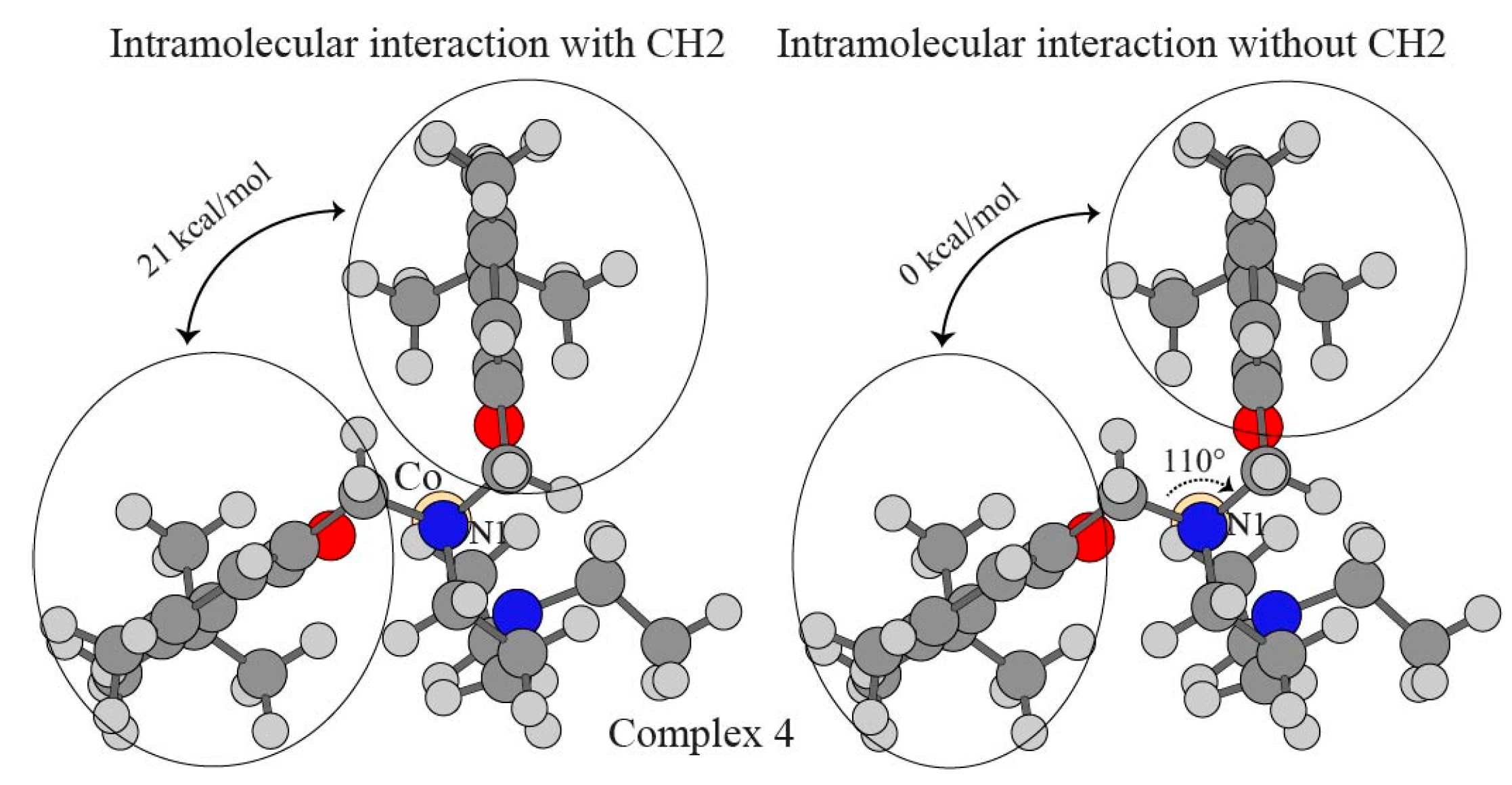
Nanomaterials 15 00938 g004
Figure 4. Intramolecular π–π within the complexes.
Figure 4. Intramolecular π–π within the complexes.
Nanomaterials 15 00938 g004
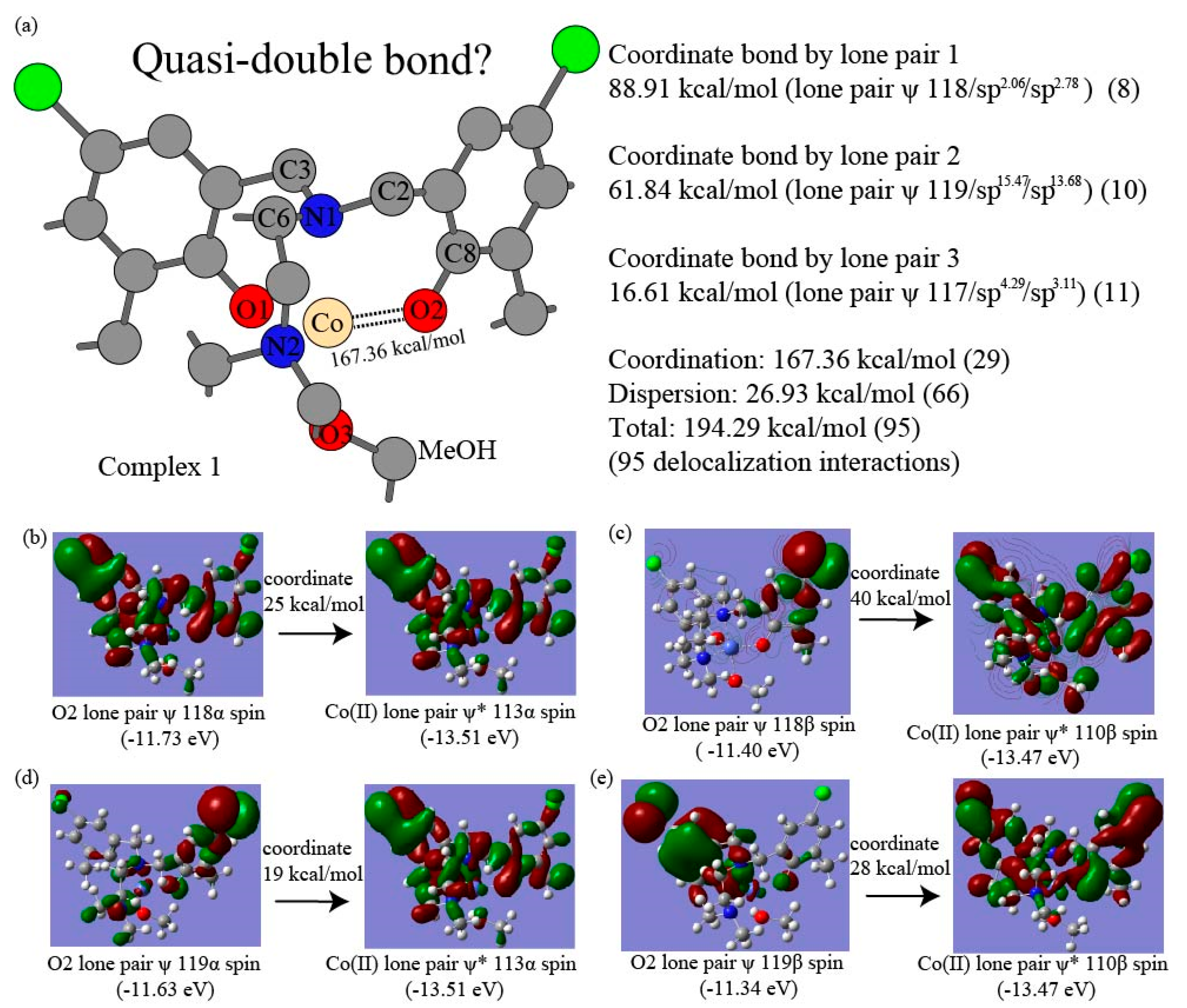
Nanomaterials 15 00938 g005
Figure 5. The delocalization interactions between donor atom O2 of ligand and central Co(II) ion in complex 1. (a) The Co(II)-O2 coordinate bond energies in complex 1; (b) The delocalization from O2 ψ lone pair 118α spin orbital to Co(II) ψ* lone pair 113α spin orbital; (c) The delocalization from O2 ψ lone pair 118β spin orbital to Co(II) ψ* lone pair 110β spin orbital; (d) The delocalization from O2 ψ lone pair 119α spin orbital to Co(II) ψ* lone pair 113α spin orbital; (e) The delocalization from O2 ψ lone pair 119β spin orbital to Co(II) ψ* lone pair 110β spin orbital (The ψ represents bonding orbitals and ψ* indicates antibonding orbitals).
Figure 5. The delocalization interactions between donor atom O2 of ligand and central Co(II) ion in complex 1. (a) The Co(II)-O2 coordinate bond energies in complex 1; (b) The delocalization from O2 ψ lone pair 118α spin orbital to Co(II) ψ* lone pair 113α spin orbital; (c) The delocalization from O2 ψ lone pair 118β spin orbital to Co(II) ψ* lone pair 110β spin orbital; (d) The delocalization from O2 ψ lone pair 119α spin orbital to Co(II) ψ* lone pair 113α spin orbital; (e) The delocalization from O2 ψ lone pair 119β spin orbital to Co(II) ψ* lone pair 110β spin orbital (The ψ represents bonding orbitals and ψ* indicates antibonding orbitals).
Nanomaterials 15 00938 g005
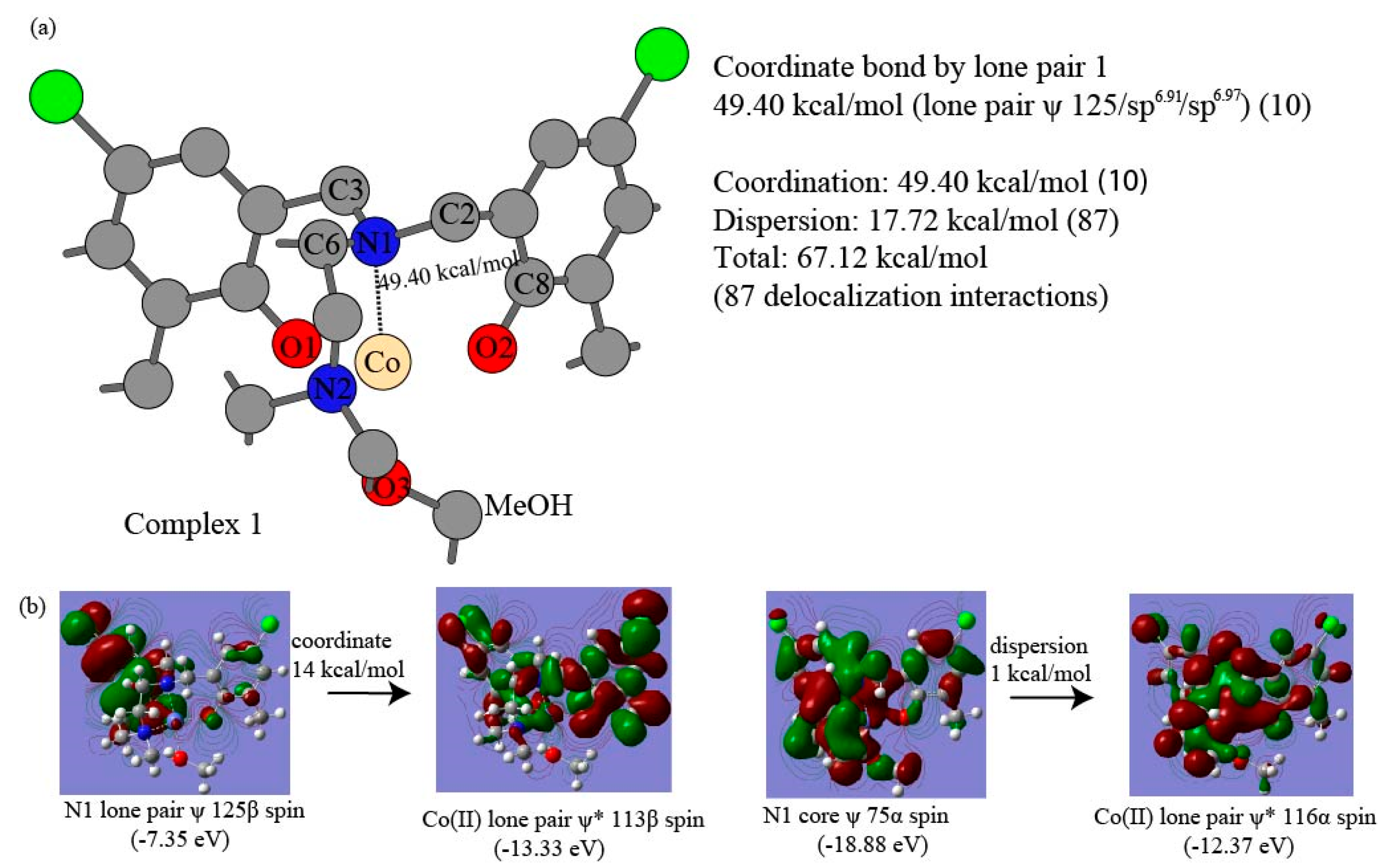
Nanomaterials 15 00938 g006
Figure 6. The delocalization interactions between donor atom N1 of ligand and central Co(II) ion in complex 1. (a) The Co(II)-N1 coordinate bond energies in complex 1. (b) The two out of 49 delocalization interactions between donor N1 and Co(II) ion (The ψ represents bonding orbitals and ψ* indicates antibonding orbitals).
Figure 6. The delocalization interactions between donor atom N1 of ligand and central Co(II) ion in complex 1. (a) The Co(II)-N1 coordinate bond energies in complex 1. (b) The two out of 49 delocalization interactions between donor N1 and Co(II) ion (The ψ represents bonding orbitals and ψ* indicates antibonding orbitals).
Nanomaterials 15 00938 g006
Nanomaterials 15 00938 g007
Figure 7. The delocalization interactions between donor atom O3 of methanol and central Co(II) ion in complex 1: (a) The Co(II)-O3 coordinate bond energies, (b) The two out of 52 delocalization interactions between donor O3 and Co(II) ion (The ψ represents bonding orbitals and ψ* indicates antibonding orbitals).
Figure 7. The delocalization interactions between donor atom O3 of methanol and central Co(II) ion in complex 1: (a) The Co(II)-O3 coordinate bond energies, (b) The two out of 52 delocalization interactions between donor O3 and Co(II) ion (The ψ represents bonding orbitals and ψ* indicates antibonding orbitals).
Nanomaterials 15 00938 g007
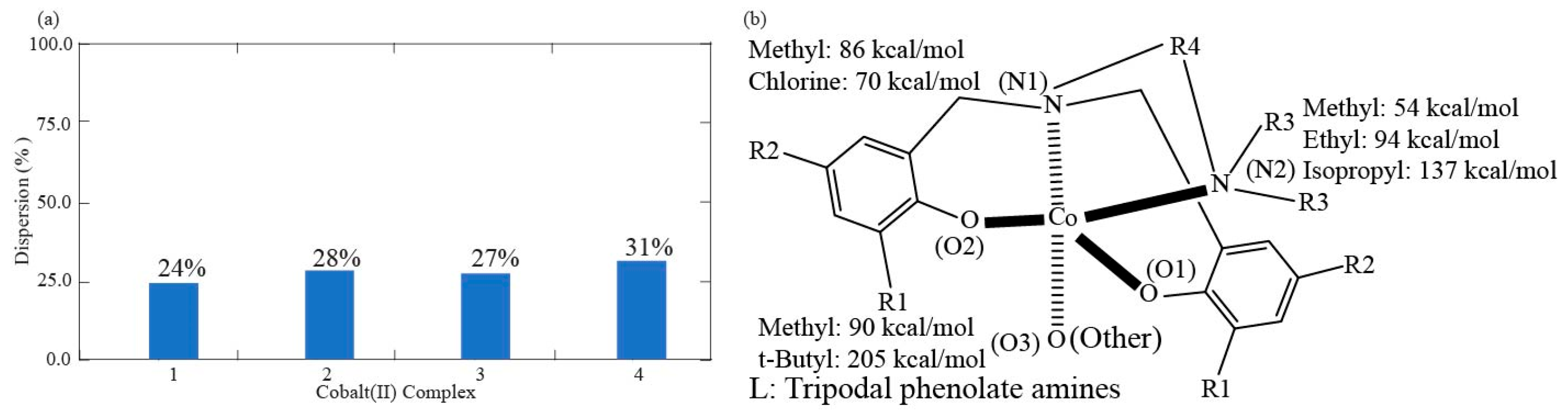
Nanomaterials 15 00938 g008
Figure 8. Percentages of dispersion between ligands and Co(II) and interaction contribution of different groups in the ligand. (a) Percentages of dispersion forces between ligand and Co(II) of four complexes; (b) The delocalization interactions contributed by groups in the rational design of ligands.
Figure 8. Percentages of dispersion between ligands and Co(II) and interaction contribution of different groups in the ligand. (a) Percentages of dispersion forces between ligand and Co(II) of four complexes; (b) The delocalization interactions contributed by groups in the rational design of ligands.
Nanomaterials 15 00938 g008
Nanomaterials 15 00938 g009
Figure 9. Comparisons of theoretical magnetic susceptibility parameters with experimental values. (a) Comparison between the second perturbation axial ZFS D and experimental counterpart. (b) Correlation between the effective Hamiltonian axial ZFS D and second perturbation counterpart. (c) Correlation between the effective Hamiltonian axial ZFS D tensor and the experimental axial ZFS D index. (d) Correlation between the effective Hamiltonian axial ZFS D results and the effective Hamiltonian transverse ZFS E values.
Figure 9. Comparisons of theoretical magnetic susceptibility parameters with experimental values. (a) Comparison between the second perturbation axial ZFS D and experimental counterpart. (b) Correlation between the effective Hamiltonian axial ZFS D and second perturbation counterpart. (c) Correlation between the effective Hamiltonian axial ZFS D tensor and the experimental axial ZFS D index. (d) Correlation between the effective Hamiltonian axial ZFS D results and the effective Hamiltonian transverse ZFS E values.
Nanomaterials 15 00938 g009
Nanomaterials 15 00938 g010
Figure 10. Comparison between theoretical magnetic susceptibility. (a) Comparison of the axial ZFS D values between the calculations of 40 doublet roots and those of 5 doublet roots. (b) Comparison of the transverse ZFS E values between the calculations, including 40 doublet roots and those specifying 5 doublet roots.
Figure 10. Comparison between theoretical magnetic susceptibility. (a) Comparison of the axial ZFS D values between the calculations of 40 doublet roots and those of 5 doublet roots. (b) Comparison of the transverse ZFS E values between the calculations, including 40 doublet roots and those specifying 5 doublet roots.
Nanomaterials 15 00938 g010
Table 1. Comparison of calculated and actual values of the spin operator of four Co(II) complexes.
Table 1. Comparison of calculated and actual values of the spin operator of four Co(II) complexes.
Complex1234
Overall atoms57697884
Total Mass486.30542.41515.60539.67
Before annihilation3.75753.75753.75753.7575
After annihilation 3.753.753.753.75
Theoretical value3.753.753.753.75
Table 2. Coordination bond lengths for the optimized structures of four Co(II) complexes (Å).
Table 2. Coordination bond lengths for the optimized structures of four Co(II) complexes (Å).
ComplexMean1234
Co(II)-N12.152.192.172.162.06
Co(II)-N22.152.122.202.112.06
Co(II)-O11.941.951.951.971.89
Co(II)-O21.931.941.941.931.90
Co(II)-O32.12 *2.112.132.13 
* The averages are calculated for the three available values.
Table 3. The LG-M-LG bond angles of four Co(II) complexes (degree°).
Table 3. The LG-M-LG bond angles of four Co(II) complexes (degree°).
ComplexMean1234
N1-Co(II)-O29192919191
N1-Co(II)-O19491929399
N1-Co(II)-N288828384101
N2-Co(II)-O1112107108113118
N2-Co(II)-O2123130133120107
O1-Co(II)-O2124123119127126
N1-Co(II)-O3175175179171 
N2-Co(II)-O394 *939693 
O1-Co(II)-O391 *908896 
O2-Co(II)-O388 *918983 
* The averages are calculated for the three available values.
Table 4. Geometric index based on L-M-L bond angles for four Co(II) complexes.
Table 4. Geometric index based on L-M-L bond angles for four Co(II) complexes.
Complex1234
τ40.756230.763320.798770.82004
τ50.750150.766820.73348 
Table 5. The Natural Bond Orbital (NBO) partial charge for the donor atoms with MP2/DeF2SVP using Gaussian 16 Revision B.01.
Table 5. The Natural Bond Orbital (NBO) partial charge for the donor atoms with MP2/DeF2SVP using Gaussian 16 Revision B.01.
AtomMean1234
Co(II)2.182.172.182.172.19
N1−0.34−0.35−0.33−0.34−0.35
N2−0.34−0.32−0.35−0.33−0.34
O1−0.46−0.40−0.48−0.48−0.48
O2−0.46−0.41−0.48−0.48−0.48
O3−0.43 *−0.42−0.41−0.47 
* The averages are calculated for the three available values.
Table 6. Intramolecular π–π force between the dipodal phenolates (restricted open shell MP2).
Table 6. Intramolecular π–π force between the dipodal phenolates (restricted open shell MP2).
pi–pi (no CH2) aΔEgas bΔΔEgasBSSE cΔΔEsolv dΔE
pi–pi (with CH2)70.335.16−54.5220.97
pi–pi (no CH2)−4.233.350.980.10
a All methods used the aug-cc-pVDZ basis set. b ΔEgas = Edimer(gas) − Emonomer,a(gas) − Emonomer,b(gas). c ΔΔEgasBSSE denotes the counterpoise correction for the basis set superposition error. d ΔΔEsolv = (ΔE dimer(solv) − ΔE monomer,a(solv) − ΔE monomer,b(solv)) − ΔEgas, where ΔEsolv denotes solvation free energy.
Table 7. Delocalization energy from ligands to Co(II) ion in the Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis for O2-Co(II) and N1-Co(II) of complex 1 (The relevant atoms are labeled in Figure 2. Unit: kcal/mol), LP represents lone pair bonding orbitals, LP* indicates lone pair antibonding orbitals, RY denotes the Rydberg orbital, RY* stands for antibonding Rydberg orbitals, CR is the abbreviation of inner core Co(II) orbitals, and BD represents bonding orbitals.
Table 7. Delocalization energy from ligands to Co(II) ion in the Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis for O2-Co(II) and N1-Co(II) of complex 1 (The relevant atoms are labeled in Figure 2. Unit: kcal/mol), LP represents lone pair bonding orbitals, LP* indicates lone pair antibonding orbitals, RY denotes the Rydberg orbital, RY* stands for antibonding Rydberg orbitals, CR is the abbreviation of inner core Co(II) orbitals, and BD represents bonding orbitals.
O2-Co(II)N1-Co(II)
DonorOrbitalAcceptorOrbitalEnergyDonorOrbitalAcceptorOrbitalEnergy
O2LP 117αCo(II)LP* 113α3.70N1LP 125αCo(II)LP* 113α3.42
O2LP 117αCo(II)LP* 114α0.78N1LP 125αCo(II)LP* 114α0.15
O2LP 117αCo(II)LP* 115α0.84N1LP 125αCo(II)LP* 115α3.82
O2LP 117αCo(II)LP* 116α1.13N1LP 125αCo(II)LP* 116α12.55
O2LP 118αCo(II)LP* 113α25.26     
O2LP 118αCo(II)LP* 114α16.95     
O2LP 119αCo(II)LP* 113α18.59     
O2LP 119αCo(II)LP* 114α4.29     
O2LP 119αCo(II)LP* 115α3.40     
O2LP 119αCo(II)LP* 116α0.15     
Coordinate 1075.09   419.94
O2LP 117αCo(II)RY* 133α0.03N1LP 125αCo(II)RY* 134α0.06
O2LP 117αCo(II)RY* 137α0.05N1-C2BD 5αCo(II)LP* 113α0.07
O2LP 118αCo(II)RY* 133α0.05N1-C2BD 5αCo(II)LP* 114α0.38
O2LP 118αCo(II)RY* 134α0.07N1-C2BD 5αCo(II)LP* 115α0.61
O2LP 119αCo(II)RY* 133α0.20N1-C2BD 5αCo(II)LP* 116α0.79
O2LP 119αCo(II)RY* 135α0.05N1-C3BD 6αCo(II)LP* 113α0.04
O2-C8BD 1αCo(II)LP* 113α2.97N1-C3BD 6αCo(II)LP* 114α0.37
O2-C8BD 1αCo(II)LP* 114α1.76N1-C3BD 6αCo(II)LP* 115α0.53
O2-C8BD 1αCo(II)LP* 115α0.12N1-C3BD 6αCo(II)LP* 116α0.71
O2CR 72αCo(II)LP* 113α2.34N1-C6BD 7αCo(II)LP* 113α0.03
O2CR 72αCo(II)LP* 114α1.35N1-C6BD 7αCo(II)LP* 114α0.34
O2CR 72αCo(II)LP* 115α0.09N1-C6BD 7αCo(II)LP* 115α0.59
O2-C8BD 1αCo(II)RY* 133α0.04N1-C6BD 7αCo(II)LP* 116α0.77
     N1CR 75αCo(II)LP* 113α0.41
     N1CR 75αCo(II)LP* 114α0.03
     N1CR 75αCo(II)LP* 115α0.34
     N1CR 75αCo(II)LP* 116α0.98
     N1-C3BD 6αCo(II)RY* 133α0.04
     N1-C6BD 7αCo(II)RY* 133α0.03
Dispersion 139.12   197.12
O2LP 117βCo(II)LP* 110β5.87N1LP 125βCo(II)LP* 110β1.44
O2LP 117βCo(II)LP* 111β0.39N1LP 125βCo(II)LP* 111β0.26
O2LP 117βCo(II)LP* 112β0.28N1LP 125βCo(II)LP* 112β4.82
O2LP 117βCo(II)LP* 113β1.53N1LP 125βCo(II)LP* 113β13.76
O2LP 117βCo(II)LP* 114β0.29N1LP 125βCo(II)LP* 114β9.05
O2LP 117βCo(II)LP* 115β0.72N1LP 125βCo(II)LP* 116β0.13
O2LP 117βCo(II)LP* 116β1.08     
O2LP 118βCo(II)LP* 110β35.90     
O2LP 118βCo(II)LP* 111β7.60     
O2LP 118βCo(II)LP* 112β0.11     
O2LP 118βCo(II)LP* 114β0.50     
O2LP 118βCo(II)LP* 115β1.88     
O2LP 118βCo(II)LP* 116β0.71     
O2LP 119βCo(II)LP* 110β28.07     
O2LP 119βCo(II)LP* 111β2.27     
O2LP 119βCo(II)LP* 112β2.13     
O2LP 119βCo(II)LP* 114β0.59     
O2LP 119βCo(II)LP* 115β1.71     
O2LP 119βCo(II)LP* 116β0.64     
Coordinate 1992.27   629.46
O2LP 117βCo(II)RY* 137β0.04N1-C3BD 6βCo(II)LP* 133β0.03
O2LP 119βCo(II)RY* 133β0.20N1-C6BD 5βCo(II)LP* 110β0.41
O2-C8BD 1βCo(II)LP* 110β3.91N1-C6BD 5βCo(II)LP* 111β0.12
O2-C8BD 1βCo(II)LP* 111β0.69N1-C6BD 5βCo(II)LP* 112β0.48
O2-C8BD 1βCo(II)LP* 112β0.11N1-C6BD 5βCo(II)LP* 113β0.77
O2-C8BD 1βCo(II)LP* 114β0.06N1-C6BD 5βCo(II)LP* 114β0.09
O2-C8BD 1βCo(II)LP* 116β0.28N1-C3BD 6βCo(II)LP* 110β0.34
O2CR 72βCo(II)LP* 110β2.94N1-C3BD 6βCo(II)LP* 111β0.10
O2CR 72βCo(II)LP* 111β0.42N1-C3BD 6βCo(II)LP* 112β0.45
O2CR 72βCo(II)LP* 112β0.07N1-C3BD 6βCo(II)LP* 113β0.72
O2CR 72βCo(II)LP* 114β0.06N1-C3BD 6βCo(II)LP* 114β0.10
O2CR 72βCo(II)LP* 115β0.03N1-C2BD 7βCo(II)LP* 110β0.40
O2CR 72βCo(II)LP* 116β0.29N1-C2BD 7βCo(II)LP* 111β0.07
     N1-C2BD 7βCo(II)LP* 112β0.46
     N1-C2BD 7βCo(II)LP* 113β0.75
     N1-C2BD 7βCo(II)LP* 114β0.08
     N1CR 75βCo(II)LP* 110β0.32
     N1CR 75βCo(II)LP* 111β0.08
     N1CR 75βCo(II)LP* 112β0.39
     N1CR 75βCo(II)LP* 113β0.96
Dispersion139.10   207.12
O2 LP 117-Co(II)1116.61N1 LP 125-Co(II)1049.40
O2 LP 118-Co(II)888.91     
O2 LP 119-Co(II)1061.84     
Co(II) β/α)) 1.2    1.5
Coordinate Tot29167.36   1049.40
Dispersion Tot2618.22   3914.24
Table 8. Delocalization energy from Co(II) ion to ligands in the Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis for O2-Co(II) and N1-Co(II) of complex 1 (Unit: kcal/mol). LP represents lone pair bonding orbitals, LP* indicates lone pair antibonding orbitals, RY denotes the bonding Rydberg orbital, RY* stands for antibonding Rydberg orbitals, CR is the abbreviation of inner Co(II) orbitals, BD represents bonding orbitals, and BD* inciates antibonding orbitals.
Table 8. Delocalization energy from Co(II) ion to ligands in the Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis for O2-Co(II) and N1-Co(II) of complex 1 (Unit: kcal/mol). LP represents lone pair bonding orbitals, LP* indicates lone pair antibonding orbitals, RY denotes the bonding Rydberg orbital, RY* stands for antibonding Rydberg orbitals, CR is the abbreviation of inner Co(II) orbitals, BD represents bonding orbitals, and BD* inciates antibonding orbitals.
Co(II)-O2Co(II)-N1
DonorOrbitalAcceptorOrbitalEnergyDonorOrbitalAcceptorOrbitalEnergy
Co(II)CR/LP/LP*O2BD*/RY*Co(II)CR/LP/LP*N1BD*/RY*
 α 235.49   261.97
 β 173.22   221.51
Dispersion Tot408.71   483.48
Table 9. Summary of the delocalization energy of Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis for the four complexes (Unit: kcal/mol).
Table 9. Summary of the delocalization energy of Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis for the four complexes (Unit: kcal/mol).
Complex
Number of Atoms		1234
57697884
DonorAcceptor
N1 LPCo(II) α spin LP*19.9420.3919.9922.37
N2 LPCo(II) α spin LP*23.3719.7821.6824.61
O1 LPCo(II) α spin LP*75.0963.8467.3368.20
O2 LPCo(II) α spin LP*66.1062.4966.6569.21
LigandCo(II) α other45.2153.9051.9269.60
N1 LPCo(II) β spin LP*29.4628.5429.7335.99
N2 LPCo(II) β spin LP*32.3430.0034.0835.50
O1 LPCo(II) β spin LP*92.2780.3683.6687.47
O2 LPCo(II) β spin LP*82.7479.5282.5987.66
LigandCo(II) β other44.7654.2252.2871.38
Co(II) α spin otherN1 other1.971.982.372.82
Co(II) α spin otherN2 other2.952.173.163.27
Co(II) α spin otherO1 other5.495.085.526.12
Co(II) α spin otherO2 other5.305.615.205.75
Co(II) α spin otherother atoms7.4710.4110.879.43
Co(II) β spin otherN1 other1.511.131.581.95
Co(II) β spin otherN2 other1.991.931.91.95
Co(II) β spin otherO1 other3.223.042.923.19
Co(II) β spin otherO2 other3.353.352.633.13
Co(II) β spin otherOther atoms8.0110.5410.5112.61
N1-Co(II) β/α1.51.51.41.51.6
N2-Co(II) β/α1.51.41.51.61.4
O1-Co(II) β/α1.31.21.31.21.3
O2-Co(II) β/α1.31.31.31.21.3
LP1 N1-Co(II)(Mean) 51.6049.4048.9349.7258.36
LP1 O2-Co(II)(Mean) 14.5516.6115.3813.1313.08
LP2 O2-Co(II)(Mean) 80.7388.9185.4364.8783.71
LP3 O2-Co(II)(Mean) 59.2861.8443.3972.9958.88
N1-Co(II)(Mean) 51.6049.4048.9349.7258.36
N2-Co(II)(Mean) 55.3455.7149.7855.7660.11
O1-Co(II)(Mean) 154.56167.36144.20150.99155.67
O2-Co(II)(Mean) 149.24148.84142.01149.24156.87
L-M coordination410.74421.31384.92405.71431.01
L-M dispersion110.8289.97108.12104.2140.98
L-M interaction521.56511.28493.04509.91571.99
M-L dispersion45.8541.2645.2446.6650.22
L-M/M-L ratio11.2512111111
Dispersion156.66131.23153.36150.86191.20
Total interaction567.40552.54538.28556.57622.21
coordination %72.576%72%73%69%
Dispersion %27.524%28%27%31%
Table 10. Summary of the delocalization energy of Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis for methanol-involved coordinations in three complexes (Unit: kcal/mol).
Table 10. Summary of the delocalization energy of Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis for methanol-involved coordinations in three complexes (Unit: kcal/mol).
Complex
Number of Atoms		1234
57697884
DonorAcceptor
O3 LPCo(II) α spin LP*30.1828.5230.76 
MeOHCo(II) α other10.9112.0413.27 
O3 LPCo(II) β spin LP*37.7035.3738.09 
MeOHCo(II) β other11.1112.2213.26 
Co(II) α spin otherMeOH4.874.572.59 
Co(II) β spin otherMeOH4.754.342.40 
L-M O3-Co(II) β/α(Mean) 1.21.21.21.2 
LP(ψ 124)-M O3-Co(II)62.1763.1059.1864.24 
LP(ψ 123)-M O3-Co(II)4.704.784.714.61 
L-M O3-Co(II)66.8767.8863.8968.85 
L-M dispersion24.2722.0224.2626.53 
L-M interaction91.1489.9088.1595.38 
M-L dispersion7.849.628.914.99 
L-M/M-L ratio12.6791019 
Dispersion32.4531.7934.1731.40 
Total interaction98.9899.5297.06100.37 
coordination %67.768%66%69% 
Dispersion %32.332%34%31% 
Table 11. Summary of the delocalization energy of Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis for functional-groups-involved interactions in three complexes (Unit: kcal/mol).
Table 11. Summary of the delocalization energy of Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis for functional-groups-involved interactions in three complexes (Unit: kcal/mol).
Complex1234
R1 89.9389.89205.43204.50
R270.17 70.1586.1685.13
R355.39 136.9454.3394.47
Ligand 2956.99 3056.882238.293857.57
Table 12. The contributions of ZFS D from 40 doublet roots and 10 quartet roots in the second perturbation computation.
Table 12. The contributions of ZFS D from 40 doublet roots and 10 quartet roots in the second perturbation computation.
SpinRootComplex 1Complex 2Complex 3Complex 4
3/200.0000.0000.0000.000
3/217.5397.3726.27514.511
3/220.5042.1850.6901.884
3/236.5916.8699.2262.736
3/249.5059.92310.8784.597
3/250.0910.0740.0580.071
3/260.0460.0340.0260.007
3/270.0900.0630.1030.005
3/280.0010.0380.0000.008
3/290.0750.0210.0890.001
3/2Tot24.44226.57927.34523.82
1/20−0.226−0.1910.6812.610
1/210.4640.334−0.0440.166
1/223.4123.5002.4100.216
1/23−0.0110.0020.0110.381
1/24−0.2480.013−0.828−0.008
1/25−0.096−0.055−0.128−0.031
1/26−0.732−0.671−0.034−1.331
1/270.0970.2868.5387.684
1/286.2375.737−1.118−1.038
1/29−0.025−0.026−0.003−0.231
1/2100.0000.012−0.003−0.266
1/211−0.009−0.008−0.0470.029
1/212−0.086−0.139−0.0550.028
1/213−0.149−0.111−0.010−0.210
1/214−0.142−0.075−0.167−0.071
1/215−0.168−0.166−0.165−0.017
1/2160.005−0.036−0.018−0.555
1/217−0.105−0.198−0.112−0.180
1/218−0.156−0.095−0.1780.097
1/219−0.000−0.1410.115−0.035
1/2200.1160.2580.0780.068
1/2210.0260.0020.0010.161
1/2220.7480.9070.7760.634
1/223−0.432−0.259−0.107−0.343
1/224−0.026−0.189−0.258−0.200
1/225−0.165−0.169−0.111−0.076
1/226−0.214−0.197−0.311−0.082
1/227−0.266−0.283−0.340−0.096
1/228−0.066−0.047−0.107−0.010
1/229−0.125−0.059−0.1050.045
1/230−0.050−0.072−0.035−0.044
1/231−0.051−0.058−0.054−0.044
1/2320.006−0.033−0.070−0.054
1/233−0.038−0.0390.005−0.020
1/234−0.000−0.0010.007−0.020
1/2350.0450.0430.0660.014
1/2360.0200.0040.001−0.000
1/237−0.004−0.003−0.001−0.001
1/238−0.003−0.004−0.003−0.004
1/2390.0930.1190.1000.124
1/2Tot7.6767.8928.3777.290
Tot 32.11834.47135.72231.11
3/2 76%77%77%77%
1/2 24%23%23%23%
Table 13. Calculated MP2, HF energies, and major correlation energies with MP2/Def2SVP method using Gaussian 16 Revision B.01.
Table 13. Calculated MP2, HF energies, and major correlation energies with MP2/Def2SVP method using Gaussian 16 Revision B.01.
Complex1234
Lowest CASSCF−3444.3676637−3600.3760521−2799.8676682−2840.8954558
HF(Hartree)−3444.2077057−3600.2158344−2799.6995722−2840.7361725
MP2(Hartree)−3448.4023597−3605.0109351−2804.6862648−2845.9533635
CASSCF-HF (kcal/mol)−100.38−100.54−105.48−99.96
MP2-HF (kcal/mol)−2632.19−3008.97−3129.20−3273.84
Number of electrons253285277291
 MP2-HF (kcal/mol)/e−10.40−10.56−11.30−11.25
CASSCF-HF (kcal/mol)−100.38−100.54−105.48−99.96
Table 14. The axial zero-field splitting (ZFS)(D) and transverse ZFS(E) from spin–spin coupling (SSC), second order spin–orbit coupling (SOC), and effective Hamiltonian with CASSCF/Def2SVP method using ORCA package (version 5.01). D-tensor spin–orbit coupling is calculated using Pederson–Khanna (PK) algorithm (Unit: cm −1).
Table 14. The axial zero-field splitting (ZFS)(D) and transverse ZFS(E) from spin–spin coupling (SSC), second order spin–orbit coupling (SOC), and effective Hamiltonian with CASSCF/Def2SVP method using ORCA package (version 5.01). D-tensor spin–orbit coupling is calculated using Pederson–Khanna (PK) algorithm (Unit: cm −1).
Complex1234
Number of atoms57697884
2nd order SOC D32.11834.46835.72431.106
SSC D−0.0280.031−0.0310.024
2nd order D32.09034.43735.69331.082
2nd order SOC E6.8376.6875.9808.125
SSC E−0.0070.009−0.0080.004
2nd order E6.8306.6965.9728.121
2nd order D/E5564
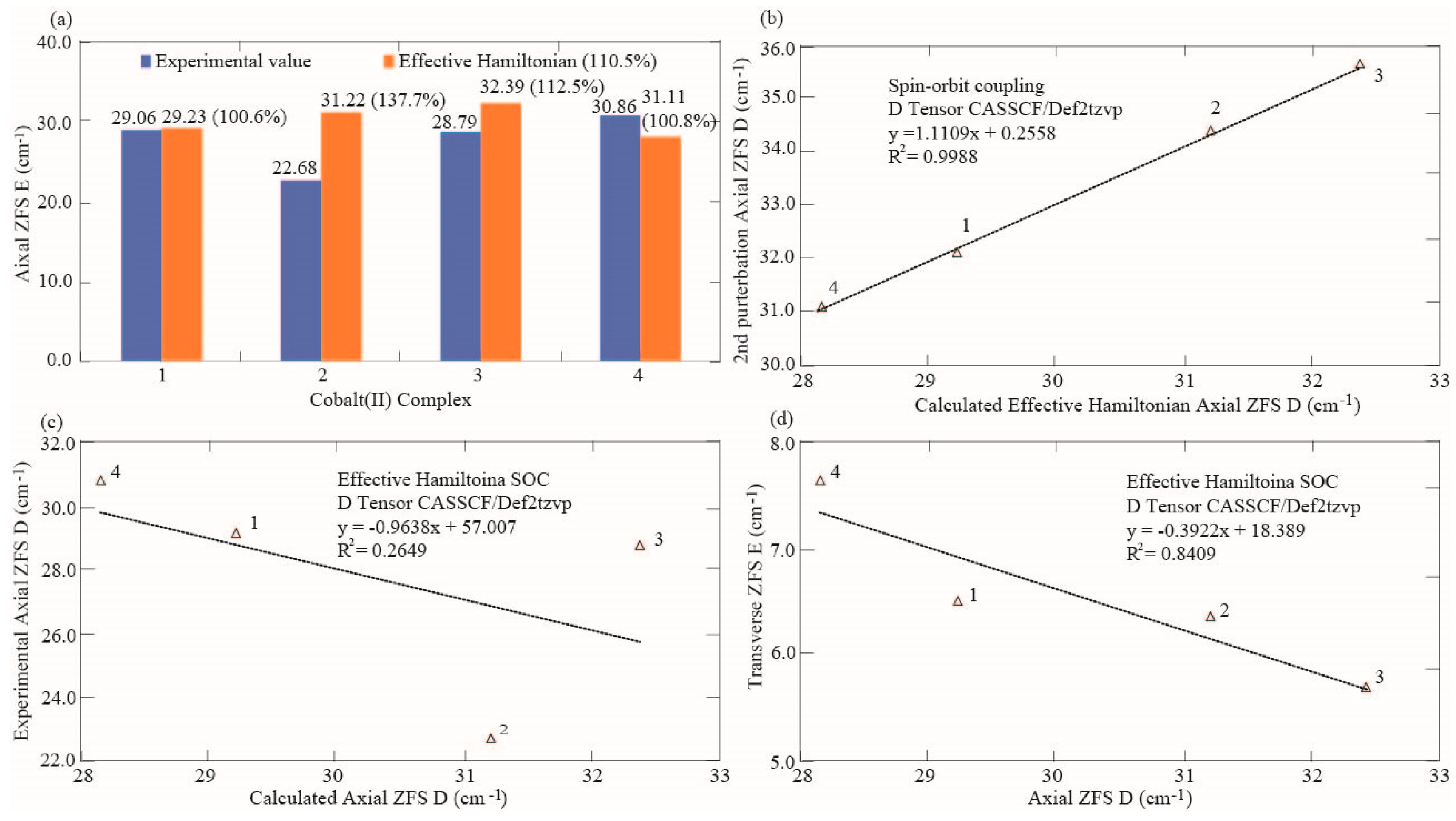
Effective Hamiltonian D29.23331.22032.39228.173
Effective Hamiltonian E6.4726.3005.6897.637
Effective Hamiltonian D/E5564
Experimental D based on (χM)29.06022.68028.79030.860
2nd order perturbation D (%)110.4151.8124.0100.7
Effective Hamiltonian D (%)100.6137.7112.591.3
Theoretical iso g factor2.2162.2252.2192.220
Theoretical gx factor2.0462.0402.0282.052
Theoretical gy factor2.2292.2482.2512.221
Theoretical gz factor2.3722.3872.3762.386
Experimental g factor2.2752.2492.3042.262
Theoretical g factor (%)97.498.996.398.1
Table 15. Comparison between the results of calculations using 40 doublet roots and those using 5 doublets for axial zero-field splitting (ZFS) D and transverse ZFS E from the second order perturbation calculation of spin–orbit coupling (SOC) and Effective Hamiltonian with CASSCF/Def2SVP method using ORCA package (version 5.01). D-tensor spin–orbit coupling is calculated using Pederson–Khanna (PK) algorithm (Unit: cm−1).
Table 15. Comparison between the results of calculations using 40 doublet roots and those using 5 doublets for axial zero-field splitting (ZFS) D and transverse ZFS E from the second order perturbation calculation of spin–orbit coupling (SOC) and Effective Hamiltonian with CASSCF/Def2SVP method using ORCA package (version 5.01). D-tensor spin–orbit coupling is calculated using Pederson–Khanna (PK) algorithm (Unit: cm−1).
Complex1234Mean
Number of Atoms57697884 
2nd Order Perturbation D 40 Roots32.11834.46835.72431.106 
2nd Order Perturbation D 5 Roots28.42430.99530.17527.561 
2nd Order Perturbation D 5 Roots %88.5%89.9%84.5%88.6%87.88%
Effective Hamiltonian D 40 Roots29.23331.22032.39228.173 
Effective Hamiltonian D 5 Roots25.89628.19627.24925.040 
Effective Hamiltonian D 5 Roots %88.6%90.3%84.1%88.9%87.89%
2nd Order Perturbation E 40 Roots 6.8376.6875.9808.125 
2nd Order Perturbation E 5 Roots6.5086.6894.8538.092 
2nd Order Perturbation E 5 Roots %95.2%100%81.2%99.6%94.00%
Effective Hamiltonian E 40 Roots6.4726.3005.6897.637 
Effective Hamiltonian E 5 Roots5.9896.2034.2127.524 
Effective Hamiltonian E 5 Roots %92.5%98.5%74.0%98.5%97.88%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Liu, Y.; Massoud, S.S.; Starovoytov, O.N.; Altalhi, T.; Gao, Y.; Yakobson, B.I. Quantum Mechanics MP2 and CASSCF Study of Coordinate Quasi-Double Bonds in Cobalt(II) Complexes as Single Molecule Magnets. Nanomaterials 2025, 15, 938. https://doi.org/10.3390/nano15120938

AMA Style

Liu Y, Massoud SS, Starovoytov ON, Altalhi T, Gao Y, Yakobson BI. Quantum Mechanics MP2 and CASSCF Study of Coordinate Quasi-Double Bonds in Cobalt(II) Complexes as Single Molecule Magnets. Nanomaterials. 2025; 15(12):938. https://doi.org/10.3390/nano15120938

Chicago/Turabian Style

Liu, Yuemin, Salah S. Massoud, Oleg N. Starovoytov, Tariq Altalhi, Yunxiang Gao, and Boris I. Yakobson. 2025. "Quantum Mechanics MP2 and CASSCF Study of Coordinate Quasi-Double Bonds in Cobalt(II) Complexes as Single Molecule Magnets" Nanomaterials 15, no. 12: 938. https://doi.org/10.3390/nano15120938

APA Style

Liu, Y., Massoud, S. S., Starovoytov, O. N., Altalhi, T., Gao, Y., & Yakobson, B. I. (2025). Quantum Mechanics MP2 and CASSCF Study of Coordinate Quasi-Double Bonds in Cobalt(II) Complexes as Single Molecule Magnets. Nanomaterials, 15(12), 938. https://doi.org/10.3390/nano15120938

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop