Anomalous Nonlinear Optical Effects by Intensity-Dependent Phase-Variation Compensation in Photonic Crystals Containing Hyperbolic Metamaterials
Abstract
1. Introduction
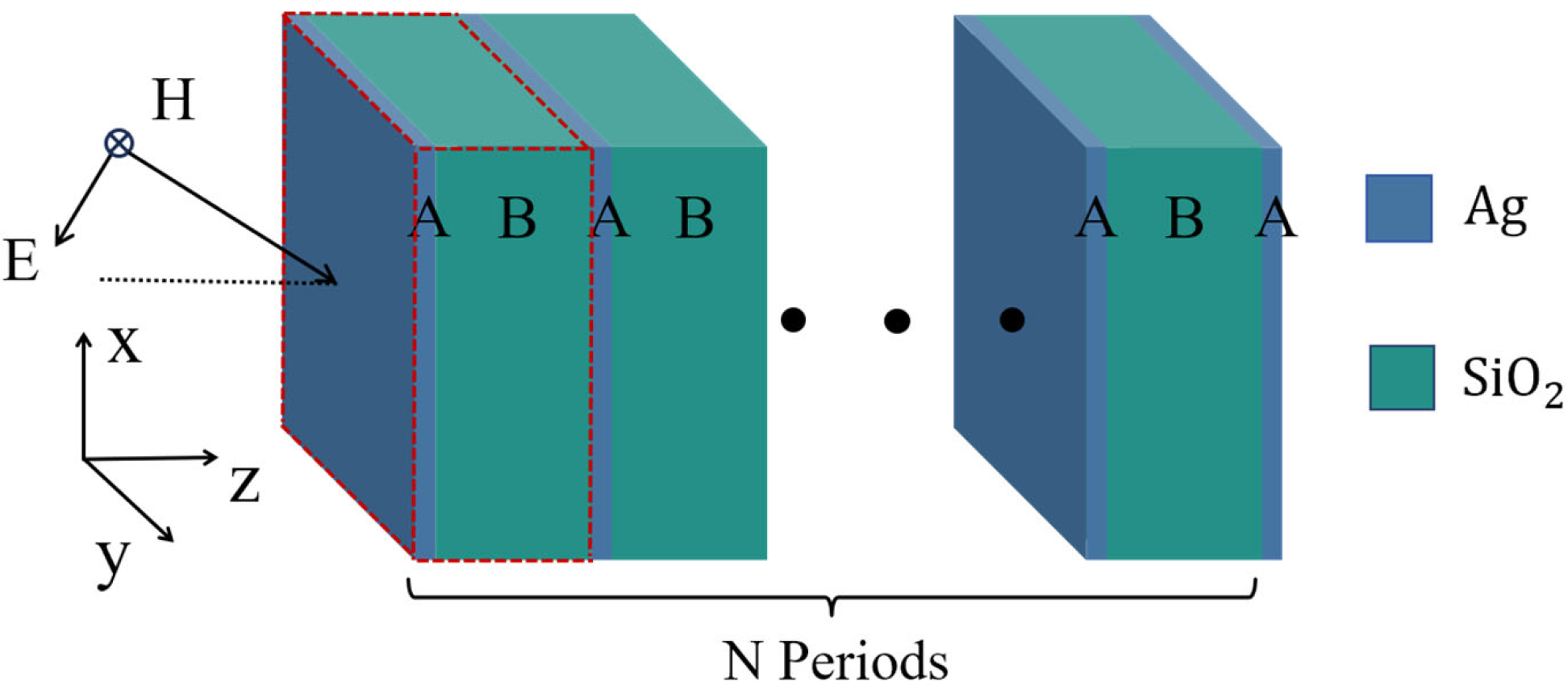
2. Theoretical Model
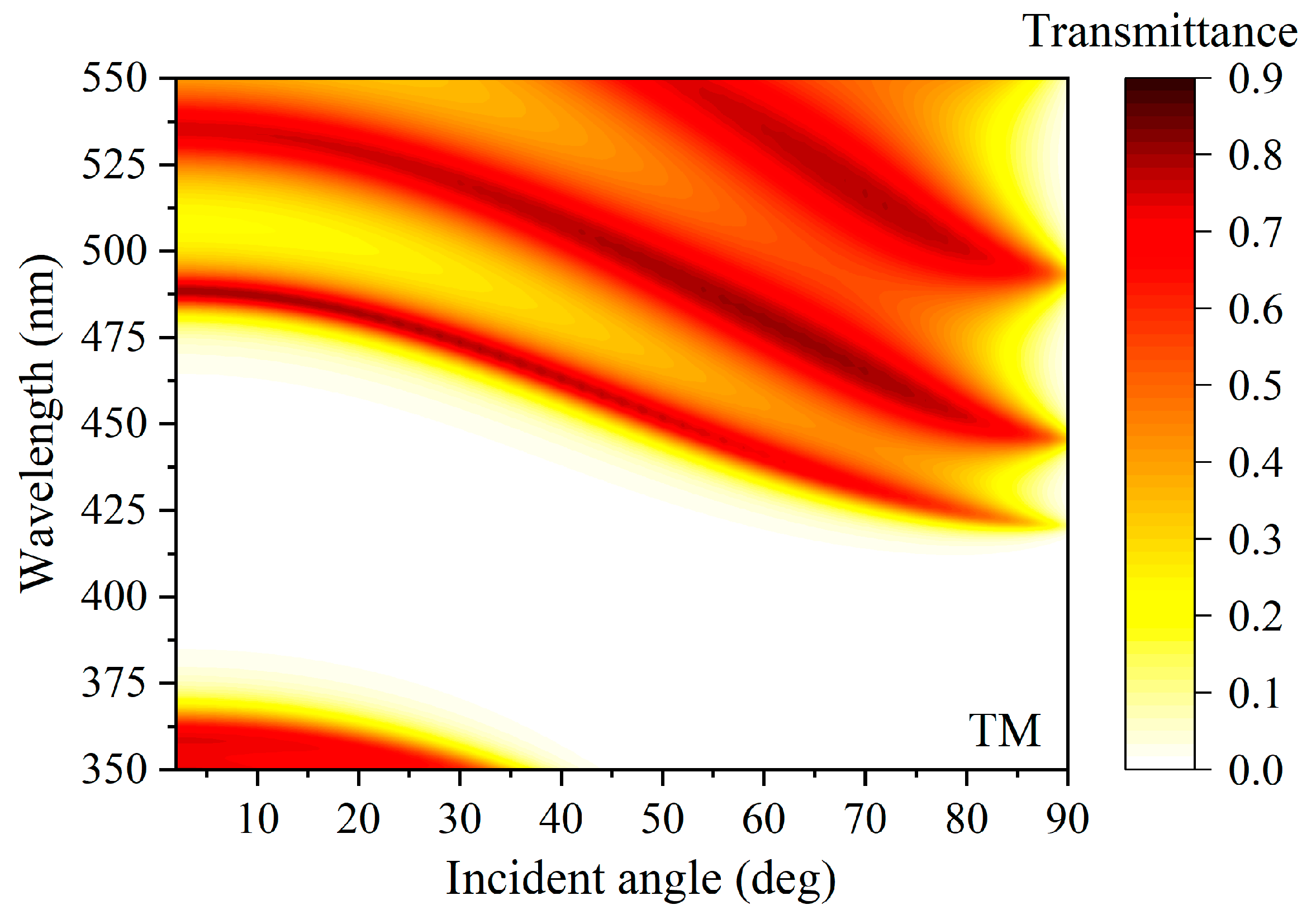
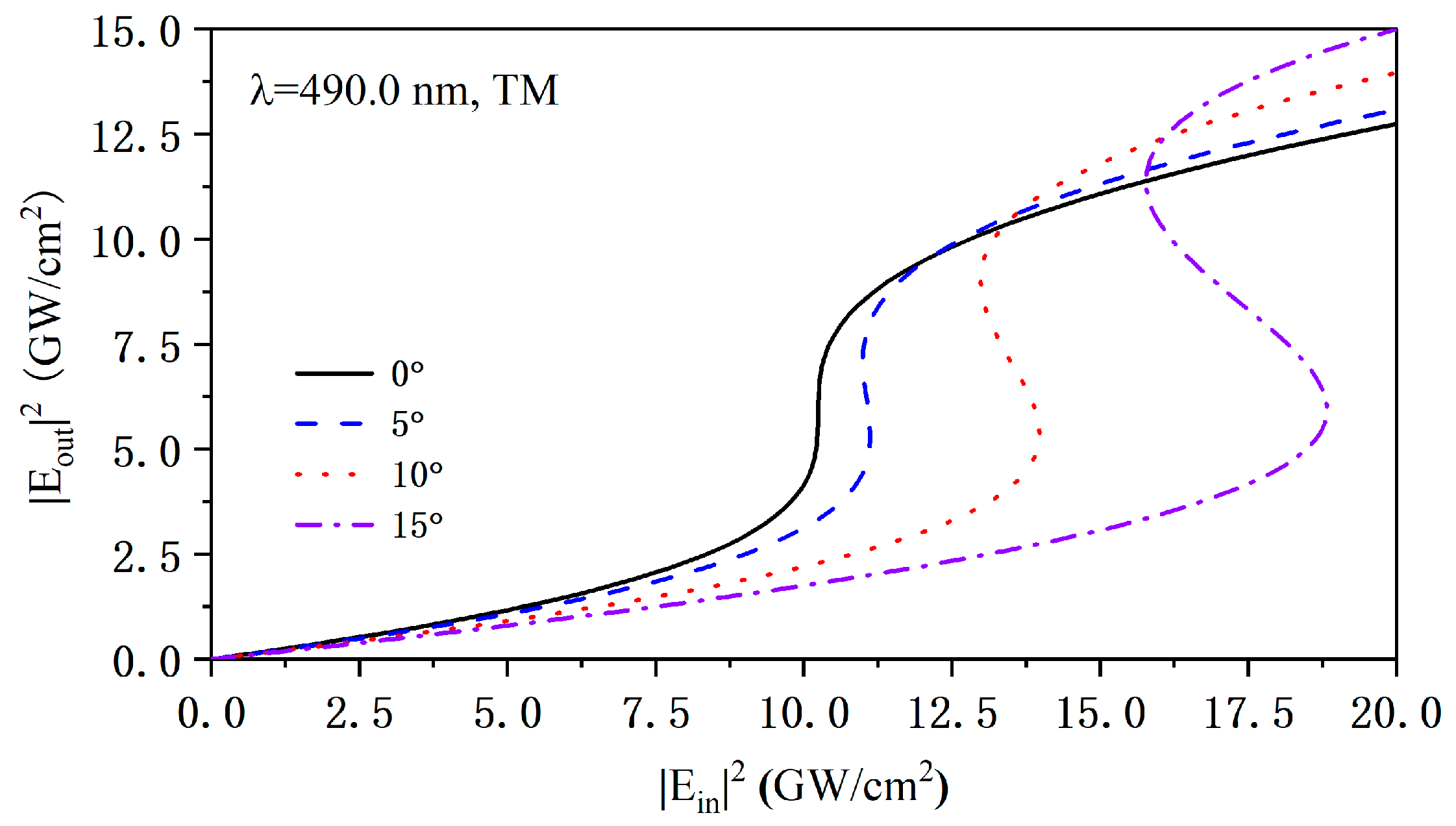
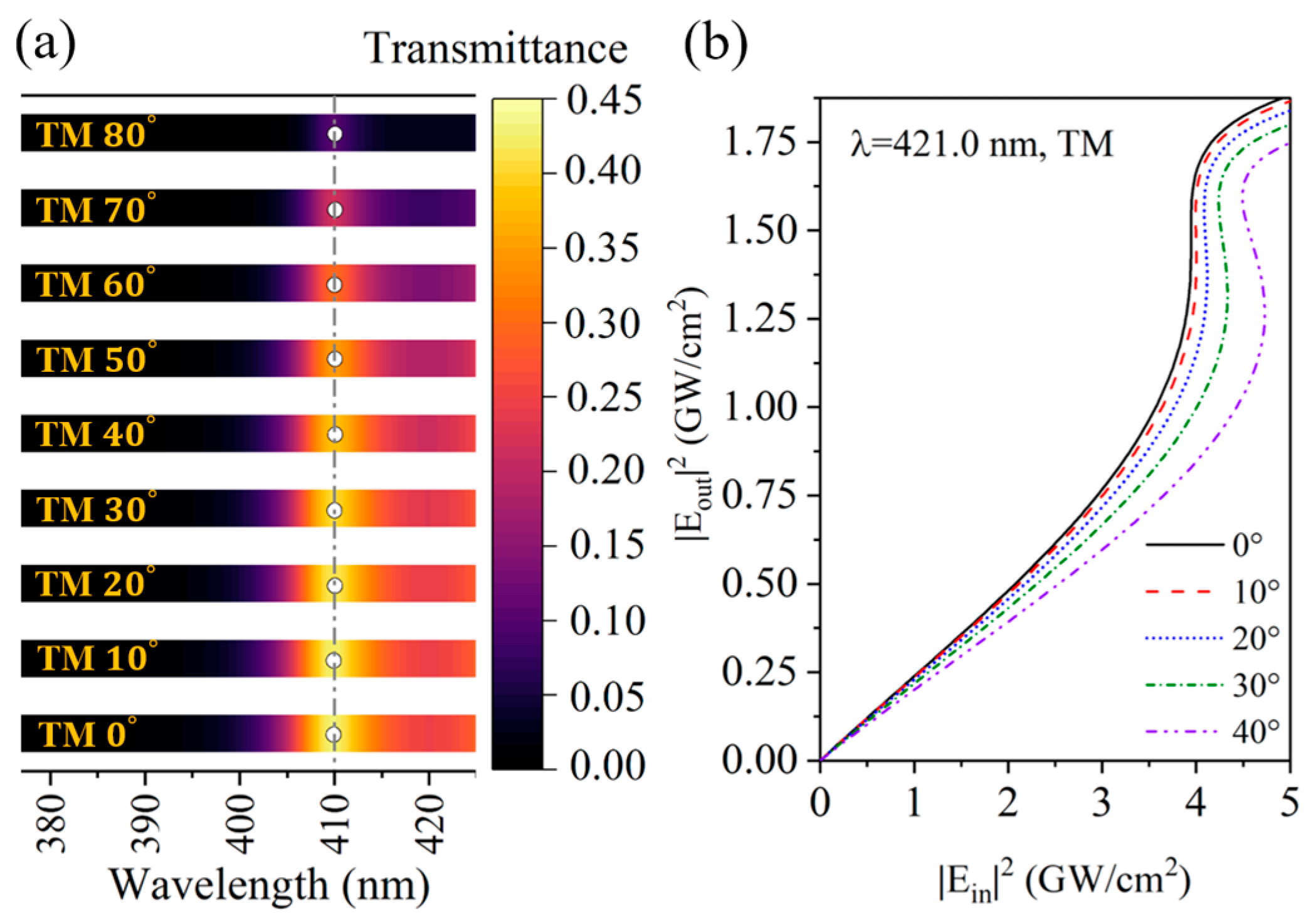
3. Nonlinear Optical Effects in Metal–Dielectric Photonic Crystals
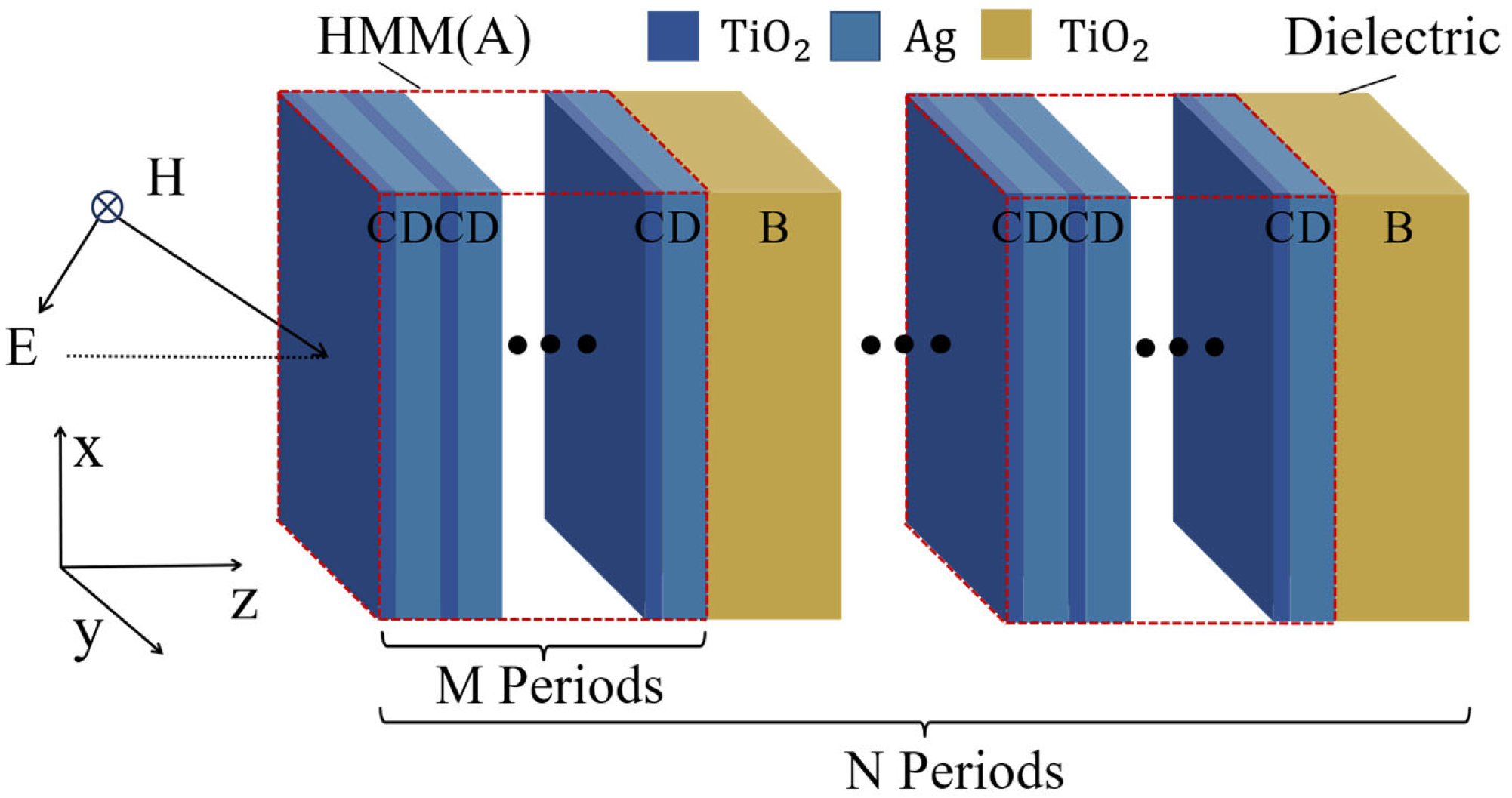
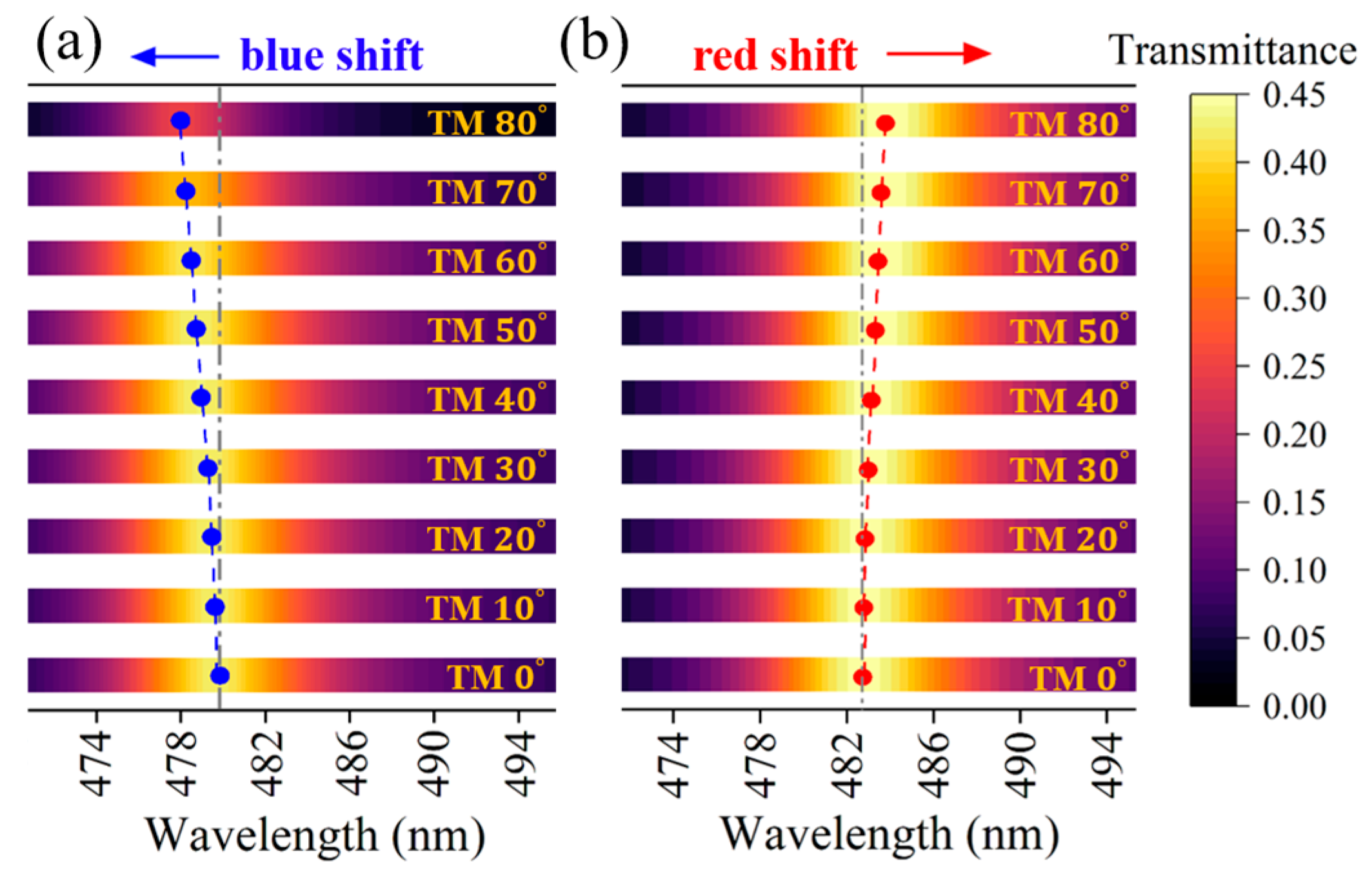
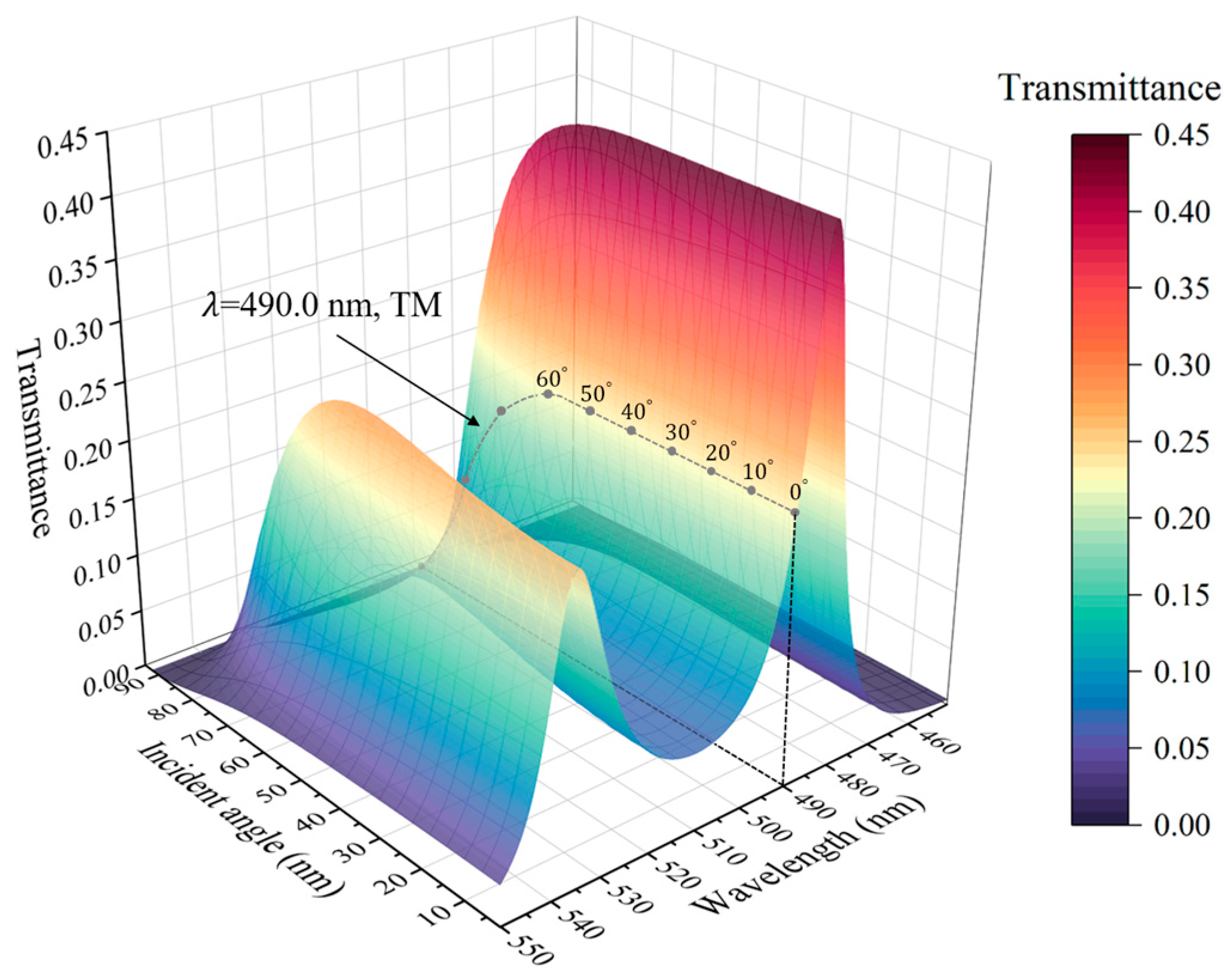
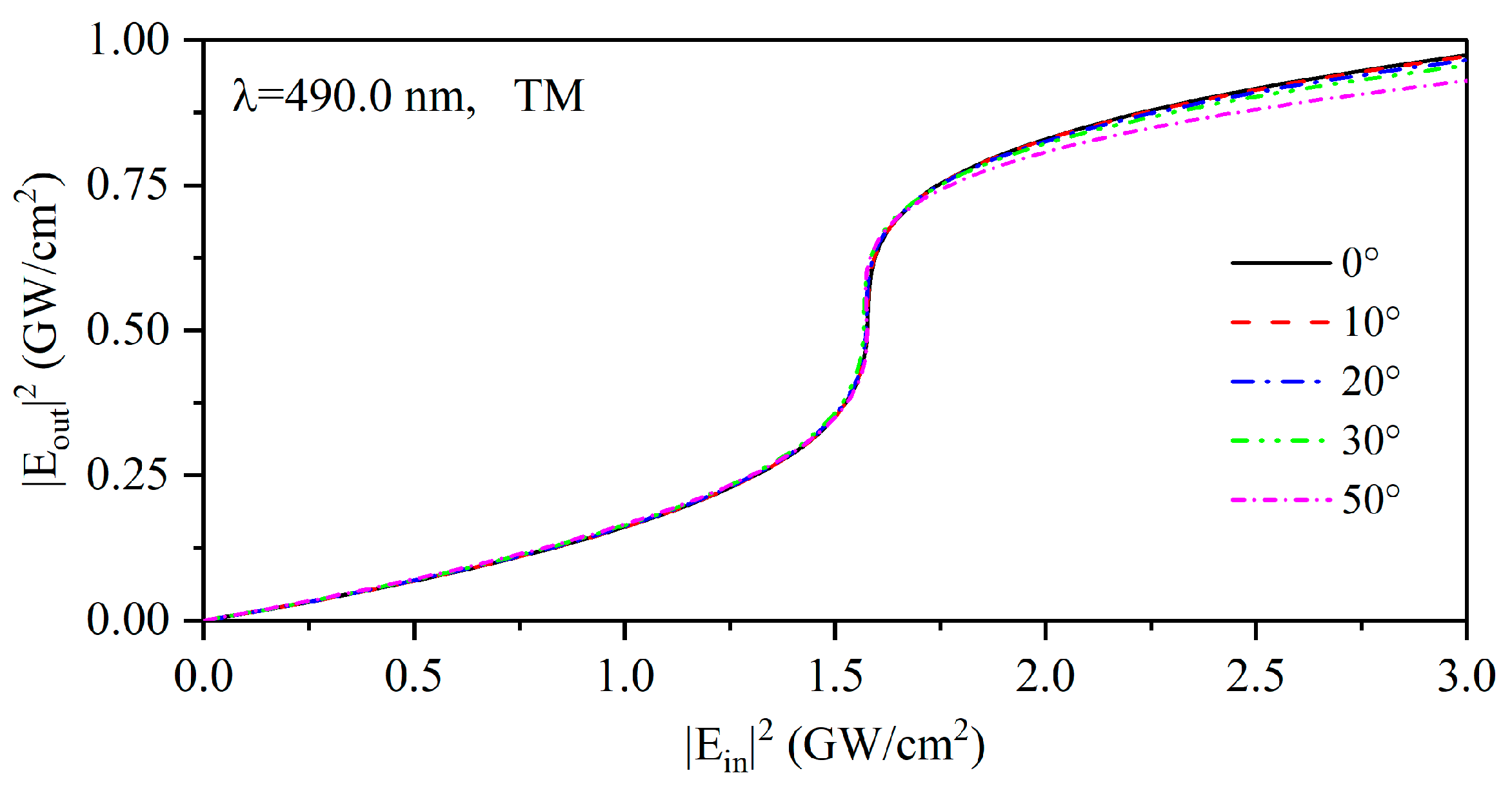
4. Anomalous Nonlinear Optical Effects in Photonic Crystals Containing Hyperbolic Metamaterials
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Maker, P.D.; Terhune, R.W.; Nisenoff, M.; Savage, C.M. Effects of Dispersion and Focusing on the Production of Optical Harmonics. Phys. Rev. Lett. 1962, 8, 21–22. [Google Scholar] [CrossRef]
- Ricard, D.; Roussignol, P.; Flytzanis, C. Surface-mediated enhancement of optical phase conjugation in metal colloids. Opt. Lett. 1985, 10, 511–513. [Google Scholar] [CrossRef] [PubMed]
- You, J.W.; Bongu, S.R.; Bao, Q.; Panoiu, N.C. Nonlinear optical properties and applications of 2D materials: Theoretical and experimental aspects. Nanophotonics 2018, 8, 63–97. [Google Scholar] [CrossRef]
- Reshef, O.; De Leon, I.; Alam, M.Z.; Boyd, R.W. Nonlinear optical effects in epsilon-near-zero media. Nat. Rev. Mater. 2019, 4, 535–551. [Google Scholar] [CrossRef]
- Xu, J.; Peng, Y.; Jiang, J.; Qian, S.; Jiang, L. Nonlinear optical bistability based on epsilon-near-zero mode in near-infrared band. Opt. Lett. 2023, 48, 3235–3238. [Google Scholar] [CrossRef]
- Bennink, R.S.; Yoon, Y.-K.; Boyd, R.W.; Sipe, J.E. Accessing the optical nonlinearity of metals with metal–dielectric photonic bandgap structures. Opt. Lett. 1999, 24, 1416–1418. [Google Scholar] [CrossRef]
- Lepeshkin, N.N.; Schweinsberg, A.; Piredda, G.; Bennink, R.S.; Boyd, R.W. Enhanced Nonlinear Optical Response of One-Dimensional Metal-Dielectric Photonic Crystals. Phys. Rev. Lett. 2004, 93, 123902. [Google Scholar] [CrossRef]
- Scalora, M.; Mattiucci, N.; D’Aguanno, G.; Larciprete, M.; Bloemer, M.J. Nonlinear pulse propagation in one-dimensional metal-dielectric multilayer stacks: Ultrawide bandwidth optical limiting. Phys. Rev. E 2006, 73, 016603. [Google Scholar] [CrossRef]
- Yablonovitch, E. Inhibited Spontaneous Emission in Solid-State Physics and Electronics. Phys. Rev. Lett. 1987, 58, 2059–2062. [Google Scholar] [CrossRef]
- Maes, B.; Bienstman, P.; Baets, R. Switching in coupled nonlinear photonic-crystal resonators. J. Opt. Soc. Am. B 2005, 22, 1778–1784. [Google Scholar] [CrossRef]
- Razskazovskaya, O.; Luu, T.T.; Trubetskov, M.; Goulielmakis, E.; Pervak, V. Nonlinear absorbance in dielectric multilayers. Optica 2015, 2, 803–811. [Google Scholar] [CrossRef]
- Du, G.-q.; Jiang, H.-t.; Wang, Z.-s.; Chen, H. Optical nonlinearity enhancement in heterostructures with thick metallic film and truncated photonic crystals. Opt. Lett. 2009, 34, 578–580. [Google Scholar] [CrossRef] [PubMed]
- Husakou, A.; Herrmann, J. Steplike Transmission of Light through a Metal-Dielectric Multilayer Structure due to an Intensity-Dependent Sign of the Effective Dielectric Constant. Phys. Rev. Lett. 2007, 99, 127402. [Google Scholar] [CrossRef] [PubMed]
- Larciprete, M.C.; Belardini, A.; Cappeddu, M.G.; de Ceglia, D.; Centini, M.; Fazio, E.; Sibilia, C.; Bloemer, M.J.; Scalora, M. Second-harmonic generation from metallodielectric multilayer photonic-band-gap structures. Phys. Rev. A 2008, 77, 013809. [Google Scholar] [CrossRef]
- Iliew, R.; Etrich, C.; Lederer, F.; Staliunas, K. Nonlinear all-photonic-crystal Fabry–Perot resonator with angle-independent bistability. Opt. Lett. 2010, 35, 3907–3909. [Google Scholar] [CrossRef]
- Lu, H.; Li, W.; Xue, C.-H.; Jiang, H.-t.; Jiang, X.; Chen, H. High-efficiency nonlinear platform with usage of metallic nonlinear susceptibility. Opt. Lett. 2013, 38, 1283–1285. [Google Scholar] [CrossRef]
- Lu, H.; Xue, C.-h.; Jiang, H.-t.; Chen, H. Optical phase conjugation enhancement in one-dimensional nonlinear photonic crystals containing single-negative materials. J. Opt. Soc. Am. B 2011, 28, 856–860. [Google Scholar] [CrossRef]
- Owens, D.T.; Fuentes-Hernandez, C.; Hales, J.M.; Perry, J.W.; Kippelen, B. Nonlinear optical properties of induced transmission filters. Opt. Express 2010, 18, 19101–19113. [Google Scholar] [CrossRef]
- Acharyya, J.N.; Rao, D.N.; Adnan, M.; Raghavendar, C.; Gangineni, R.B.; Prakash, G.V. Giant Optical Nonlinearities of Photonic Minibands in Metal–Dielectric Multilayers. Adv. Mater. Interfaces 2020, 7, 2000035. [Google Scholar] [CrossRef]
- Xue, C.; Jiang, H.; Chen, H. Highly efficient all-optical diode action based on light-tunneling heterostructures. Opt. Express 2010, 18, 7479–7487. [Google Scholar] [CrossRef]
- Fink, Y.; Winn, J.N.; Fan, S.; Chen, C.; Michel, J.; Joannopoulos, J.D.; Thomas, E.L. A Dielectric Omnidirectional Reflector. Science 1998, 282, 1679–1682. [Google Scholar] [CrossRef] [PubMed]
- Choi, Y.-K.; Ha, Y.-K.; Kim, J.-E.; Park, H.Y.; Kim, K. Antireflection film in one-dimensional metallo-dielectric photonic crystals. Opt. Commun. 2004, 230, 239–243. [Google Scholar] [CrossRef]
- Smith, D.R.; Pendry, J.B.; Wiltshire, M.C.K. Metamaterials and Negative Refractive Index. Science 2004, 305, 788–792. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Zhou, L.; Chan, C.T.; Sheng, P. Photonic Band Gap from a Stack of Positive and Negative Index Materials. Phys. Rev. Lett. 2003, 90, 083901. [Google Scholar] [CrossRef]
- Kaipurath, R.M.; Pietrzyk, M.; Caspani, L.; Roger, T.; Clerici, M.; Rizza, C.; Ciattoni, A.; Di Falco, A.; Faccio, D. Optically induced metal-to-dielectric transition in Epsilon-Near-Zero metamaterials. Sci. Rep. 2016, 6, 27700. [Google Scholar] [CrossRef]
- Marinica, D.C.; Kazansky, A.K.; Borisov, A.G. Electrical control of the light absorption in quantum-well functionalized junctions between thin metallic films. Phys. Rev. B 2017, 96, 245407. [Google Scholar] [CrossRef]
- Poddubny, A.; Iorsh, I.; Belov, P.; Kivshar, Y. Hyperbolic metamaterials. Nat. Photonics 2013, 7, 948–957. [Google Scholar] [CrossRef]
- Drachev, V.P.; Podolskiy, V.A.; Kildishev, A.V. Hyperbolic metamaterials: New physics behind a classical problem. Opt. Express 2013, 21, 15048–15064. [Google Scholar] [CrossRef]
- Ferrari, L.; Wu, C.; Lepage, D.; Zhang, X.; Liu, Z. Hyperbolic metamaterials and their applications. Prog. Quantum Electron. 2015, 40, 1–40. [Google Scholar] [CrossRef]
- Xue, C.-h.; Ding, Y.; Jiang, H.-t.; Li, Y.; Wang, Z.-s.; Zhang, Y.-w.; Chen, H. Dispersionless gaps and cavity modes in photonic crystals containing hyperbolic metamaterials. Phys. Rev. B 2016, 93, 125310. [Google Scholar] [CrossRef]
- Krishna, K.H.; Sreekanth, K.V.; Strangi, G. Dye-embedded and nanopatterned hyperbolic metamaterials for spontaneous emission rate enhancement. J. Opt. Soc. Am. B 2016, 33, 1038–1043. [Google Scholar] [CrossRef]
- Kim, M.; Kim, S.; Kim, S. Optical bistability based on hyperbolic metamaterials. Opt. Express 2018, 26, 11620–11632. [Google Scholar] [CrossRef] [PubMed]
- Wu, F.; Lu, G.; Xue, C.; Jiang, H.; Guo, Z.; Zheng, M.; Chen, C.; Du, G.; Chen, H. Experimental demonstration of angle-independent gaps in one-dimensional photonic crystals containing layered hyperbolic metamaterials and dielectrics at visible wavelengths. Appl. Phys. Lett. 2018, 112, 041902. [Google Scholar] [CrossRef]
- Shen, K.-S.; Li, X.-K.; Zheng, Y.; Liu, H.-C.; Dong, S.-Q.; Zhang, J.; Xia, S.-Q.; Dong, C.; Sun, X.-L.; Zhang, X.-Z. Near-infrared ITO-based photonic hypercrystals with large angle-insensitive bandgaps. Opt. Lett. 2022, 47, 917–920. [Google Scholar] [CrossRef]
- Wu, F.; Lu, G.; Guo, Z.; Jiang, H.; Xue, C.; Zheng, M.; Chen, C.; Du, G.; Chen, H. Redshift gaps in one-dimensional photonic crystals containing hyperbolic metamaterials. Phys. Rev. Appl. 2018, 10, 064022. [Google Scholar] [CrossRef]
- Lu, G.; Zhou, X.; Zhao, Y.; Zhang, K.; Zhou, H.; Li, J.; Diao, C.; Liu, F.; Wu, A.; Du, G. Omnidirectional photonic bandgap in one-dimensional photonic crystals containing hyperbolic metamaterials. Opt. Express 2021, 29, 31915–31923. [Google Scholar] [CrossRef]
- He, J.; Cada, M. Combined distributed feedback and Fabry–Perot structures with a phase-matching layer for optical bistable devices. Appl. Phys. Lett. 1992, 61, 2150–2152. [Google Scholar] [CrossRef]
- Bloemer, M.J.; Scalora, M. Transmissive properties of Ag/MgF2 photonic band gaps. Appl. Phys. Lett. 1998, 72, 1676–1678. [Google Scholar] [CrossRef]
- Jamshidi-Ghaleh, K.; Safari, Z.; Moslemi, F. Angular and polarization dependence of all optical diode in one-dimensional photonic crystal. Eur. Phys. J. D 2015, 69, 1–5. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, X.; Qin, H.; Li, J.; Chen, H.; Li, X.; Liu, F.; Wang, T.; Lu, G.; Du, G. Anomalous Nonlinear Optical Effects by Intensity-Dependent Phase-Variation Compensation in Photonic Crystals Containing Hyperbolic Metamaterials. Nanomaterials 2025, 15, 903. https://doi.org/10.3390/nano15120903
Yu X, Qin H, Li J, Chen H, Li X, Liu F, Wang T, Lu G, Du G. Anomalous Nonlinear Optical Effects by Intensity-Dependent Phase-Variation Compensation in Photonic Crystals Containing Hyperbolic Metamaterials. Nanomaterials. 2025; 15(12):903. https://doi.org/10.3390/nano15120903
Chicago/Turabian StyleYu, Xiangting, Haoyuan Qin, Junyang Li, Hong Chen, Xudong Li, Fen Liu, Tongbiao Wang, Guang Lu, and Guiqiang Du. 2025. "Anomalous Nonlinear Optical Effects by Intensity-Dependent Phase-Variation Compensation in Photonic Crystals Containing Hyperbolic Metamaterials" Nanomaterials 15, no. 12: 903. https://doi.org/10.3390/nano15120903
APA StyleYu, X., Qin, H., Li, J., Chen, H., Li, X., Liu, F., Wang, T., Lu, G., & Du, G. (2025). Anomalous Nonlinear Optical Effects by Intensity-Dependent Phase-Variation Compensation in Photonic Crystals Containing Hyperbolic Metamaterials. Nanomaterials, 15(12), 903. https://doi.org/10.3390/nano15120903






