The Elevated-Temperature Nano-Mechanical Properties of a PDMS–Silica-Based Superhydrophobic Nanocomposite Coating
Abstract
1. Introduction
2. Materials and Methods
3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Luo, Q.; Peng, J.; Chen, X.; Zhang, H.; Deng, X.; Jin, S.; Zhu, H. Recent Advances in Multifunctional Mechanical–Chemical Superhydrophobic Materials. Front. Bioeng. Biotechnol. 2022, 10, 947327. [Google Scholar] [CrossRef] [PubMed]
- Roshan, S.; Sarabi, A.A.; Jafari, R.; Momen, G. One-step fabrication of superhydrophobic nanocomposite with superior anticorrosion performance. Prog. Org. Coat. 2022, 169, 106918. [Google Scholar] [CrossRef]
- Pirich, R.; Weir, J.; Leyble, D.; Chu, S. In modeling & simulation of nanostructures for superhydrophobic coatings. In Proceedings of the 2012 IEEE Long Island Systems, Applications and Technology Conference (LISAT), Farmingdale, NY, USA, 4 May 2012; pp. 1–4. [Google Scholar]
- Wang, Y.; Li, M.; Lv, T.; Wang, Q.; Chen, Q.; Ding, J. Influence of different chemical modifications on the icephobic properties of superhydrophobic surfaces in a condensate environment. J. Mater. Chem. A 2015, 3, 4967–4975. [Google Scholar] [CrossRef]
- Khan, M.Z.; Militky, J.; Petru, M.; Tomková, B.; Ali, A.; Tören, E.; Perveen, S. Recent advances in superhydrophobic surfaces for practical applications: A review. Eur. Polym. J. 2022, 178, 111481. [Google Scholar] [CrossRef]
- Schaeffer, D.A.; Polizos, G.; Smith, D.B.; Lee, D.F.; Hunter, S.R.; Datskos, P.G. Optically transparent and environmentally durable superhydrophobic coating based on functionalized SiO2 nanoparticles. Nanotechnology 2015, 26, 055602. [Google Scholar] [CrossRef]
- Zhang, Z.; Ge, B.; Men, X.; Li, Y. Mechanically durable, superhydrophobic coatings prepared by dual-layer method for anti-corrosion and self-cleaning. Colloids Surf. A Physicochem. Eng. Asp. 2016, 490, 182–188. [Google Scholar] [CrossRef]
- Qing, Y.; Yang, C.; Hu, C.; Zheng, Y.; Liu, C. A facile method to prepare superhydrophobic fluorinated polysiloxane/ZnO nanocomposite coatings with corrosion resistance. Appl. Surf. Sci. 2015, 326, 48–54. [Google Scholar] [CrossRef]
- Yu, J.; Qin, L.; Hao, Y.; Kuang, S.; Bai, X.; Chong, Y.-M.; Zhang, W.; Wang, E. Vertically Aligned Boron Nitride Nanosheets: Chemical Vapor Synthesis, Ultraviolet Light Emission, and Superhydrophobicity. ACS Nano 2010, 4, 414–422. [Google Scholar] [CrossRef]
- Boinovich, L.B.; Emelyanenko, A.M. The behaviour of fluoro- and hydrocarbon surfactants used for fabrication of superhydrophobic coatings at solid/water interface. Colloids Surf. A Physicochem. Eng. Asp. 2015, 481, 167–175. [Google Scholar] [CrossRef]
- Tao, C.; Yan, H.; Yuan, X.; Yao, C.; Yin, Q.; Zhu, J.; Ni, W.; Yan, L.; Zhang, L. Synthesis of shape-controlled hollow silica nanostructures with a simple soft-templating method and their application as superhydrophobic antireflective coatings with ultralow refractive indices. Colloids Surf. A Physicochem. Eng. Asp. 2016, 501, 17–23. [Google Scholar] [CrossRef]
- Buehler, M.J.; Misra, A. Mechanical behavior of nanocomposites. MRS Bull. 2019, 44, 19–24. [Google Scholar] [CrossRef]
- Sebastian, D.; Yao, C.-W. Effect of poly(dimethylsiloxane) binder in a silica-based superhydrophobic coating on mechanical properties, surface roughness, and wettability. Mrs. Commun. 2020, 10, 512–518. [Google Scholar] [CrossRef]
- Arora, G.; Pathak, H. Nanoindentation characterization of polymer nanocomposites for elastic and viscoelastic properties: Experimental and mathematical approach. Compos. Part C Open Access 2021, 4, 100103. [Google Scholar] [CrossRef]
- Liang, X. Visualization of Nanomechanical Properties of Polymer Composites Using Atomic Force Microscopy. Polym. J. 2023, 55, 913–920. [Google Scholar] [CrossRef]
- Bor, B.; Giuntini, D.; Domènech, B.; Swain, M.V.; Schneider, G.A. Nanoindentation-based study of the mechanical behavior of bulk supercrystalline ceramic-organic nanocomposites. J. Eur. Ceram. Soc. 2019, 39, 3247–3256. [Google Scholar] [CrossRef]
- Ornaghi, H.L.; Lazzari, L.K.; Kerche, E.F.; Neves, R.M. Dynamic Mechanical Behavior of Polymer Nanocomposites. In Mechanics of Nanomaterials and Polymer Nanocomposites; Abdellaoui, H.M.R.S., Siengchin, S., Eds.; Springer Nature: Singapore, 2023; pp. 147–161. [Google Scholar]
- Shan, L.; Tan, C.Y.; Shen, X.; Ramesh, S.; Zarei, M.S.; Kolahchi, R.; Hajmohammad, M.H. The effects of nano-additives on the mechanical, impact, vibration, and buckling/post-buckling properties of composites: A review. J. Mater. Res. Technol. 2023, 24, 7570–7598. [Google Scholar] [CrossRef]
- Mahmoud, Z.H.; Al-Salman, H.N.K.; Kianfar, E. Nanoindentation: Introduction and applications of a non-destructive analysis. Nano TransMed 2024, 3, 100057. [Google Scholar] [CrossRef]
- Wang, J.; Yang, C.; Liu, Y.; Li, Y.; Xiong, Y. Using Nanoindentation to Characterize the Mechanical and Creep Properties of Shale: Load and Loading Strain Rate Effects. ACS Omega 2022, 7, 14317–14331. [Google Scholar] [CrossRef]
- Yang, C.; Liu, Y.; Wang, J.; Wu, D.; Liu, L.; Su, Z.; Xiong, Y. Application of nanoindentation technique in mechanical characterization of organic matter in shale: Attentive issues, test protocol, and technological prospect. Gas Sci. Eng. 2023, 113, 204966. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, D.; Zhao, J. Control of fracture toughness of kerogen on artificially-matured shale samples: An energy-based nanoindentation analysis. Gas Sci. Eng. 2024, 124, 205266. [Google Scholar] [CrossRef]
- Huang, H.; Zhang, W.; Shi, H.; Ni, J.; Ding, L.; Yang, B.; Zheng, Y.; Li, X. Experimental investigation of microscale mechanical alterations in shale induced by fracturing fluid contact. Gas Sci. Eng. 2024, 124, 205264. [Google Scholar] [CrossRef]
- Wang, J.; Dziadkowiec, J.; Liu, Y.; Jiang, W.; Zheng, Y.; Xiong, Y.; Peng, P.A.; Renard, F. Combining atomic force microscopy and nanoindentation helps characterizing in-situ mechanical properties of organic matter in shale. Int. J. Coal Geol. 2024, 281, 104406. [Google Scholar] [CrossRef]
- Karimzadeh, A.; Koloor, S.S.R.; Ayatollahi, M.R.; Bushroa, A.R.; Yahya, M.Y. Assessment of Nano-Indentation Method in Mechanical Characterization of Heterogeneous Nanocomposite Materials Using Experimental and Computational Approaches. Sci. Rep. 2019, 9, 15763. [Google Scholar] [CrossRef] [PubMed]
- Ryou, H.; Romberg, E.; Pashley, D.H.; Tay, F.R.; Arola, D. Nanoscopic dynamic mechanical properties of intertubular and peritubular dentin. J. Mech. Behav. Biomed. Mater. 2012, 7, 3–16. [Google Scholar] [CrossRef]
- Yan, C.; Bor, B.; Plunkett, A.; Domènech, B.; Maier-Kiener, V.; Giuntini, D. Nanoindentation creep of supercrystalline nanocomposites. Mater. Des. 2023, 231, 112000. [Google Scholar] [CrossRef]
- Holz, H.; Merle, B. Novel nanoindentation strain rate sweep method for continuously investigating the strain rate sensitivity of materials at the nanoscale. Mater. Des. 2023, 236, 112471. [Google Scholar] [CrossRef]
- Vandamme, M.; Ulm, F.-J. Nanogranular origin of concrete creep. Proc. Natl. Acad. Sci. USA 2009, 106, 10552–10557. [Google Scholar] [CrossRef]
- Liu, K.; Jin, Z.; Zeng, L.; Ostadhassan, M.; Xu, X. Understanding the creep behavior of shale via nano-DMA method. Energy Rep. 2021, 7, 7478–7487. [Google Scholar] [CrossRef]
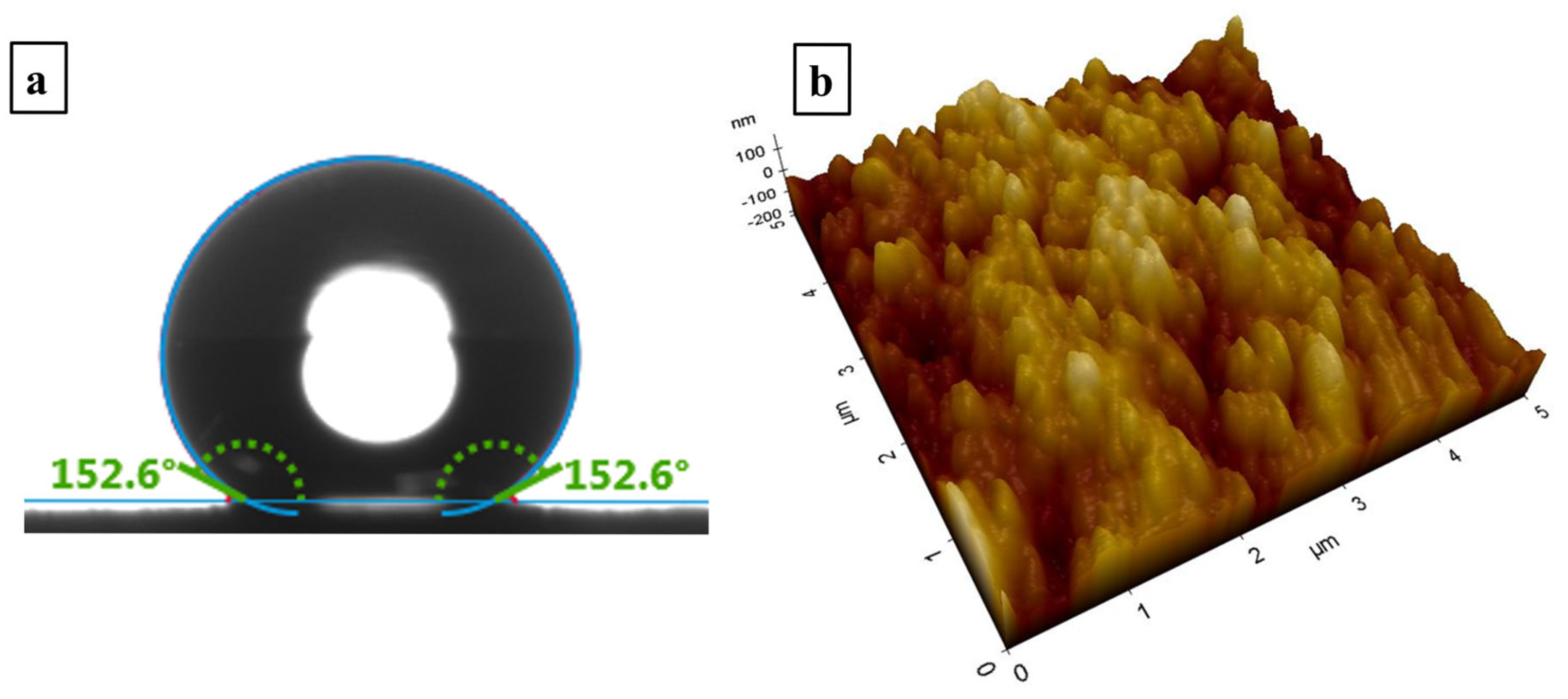

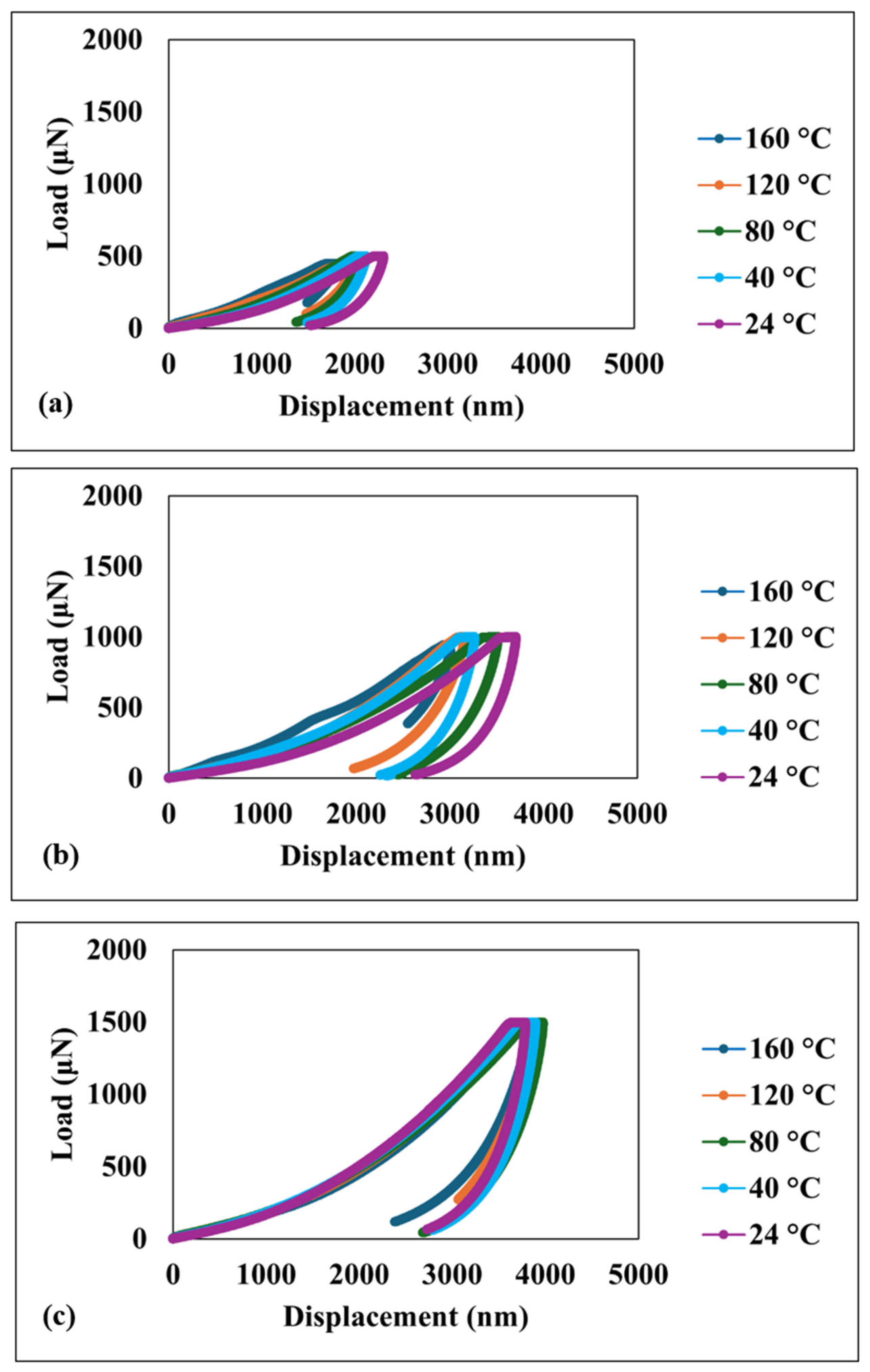

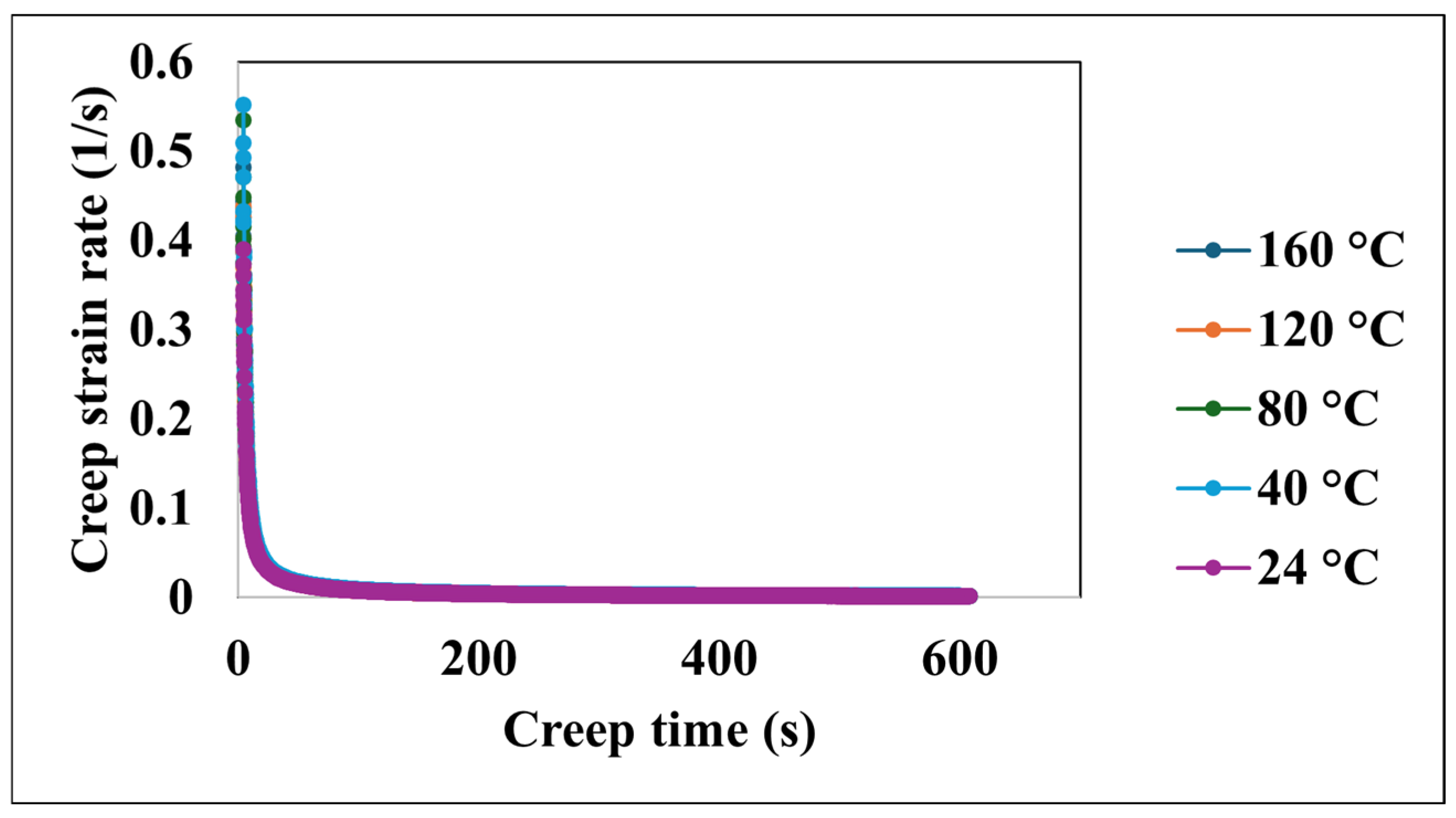
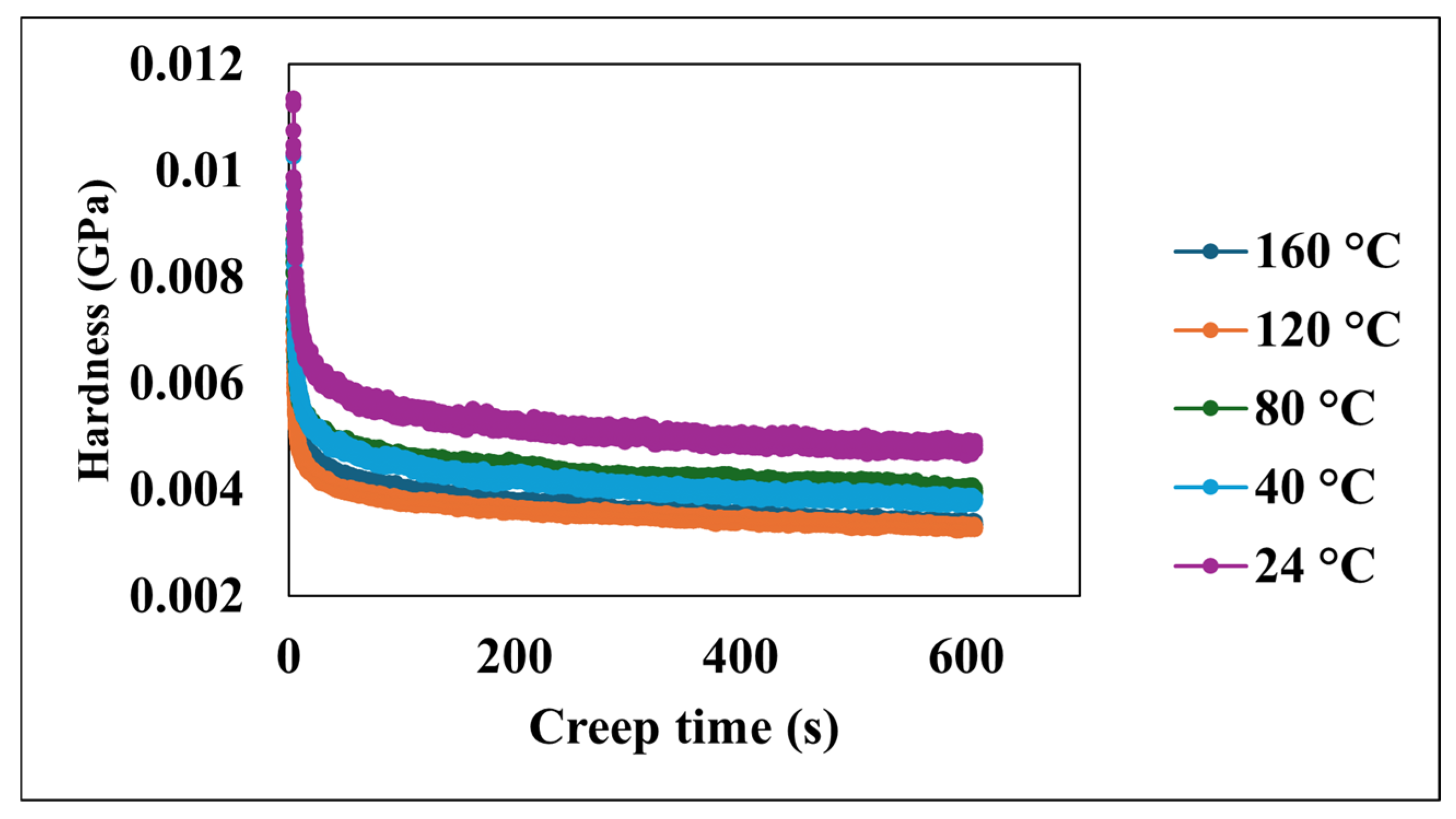
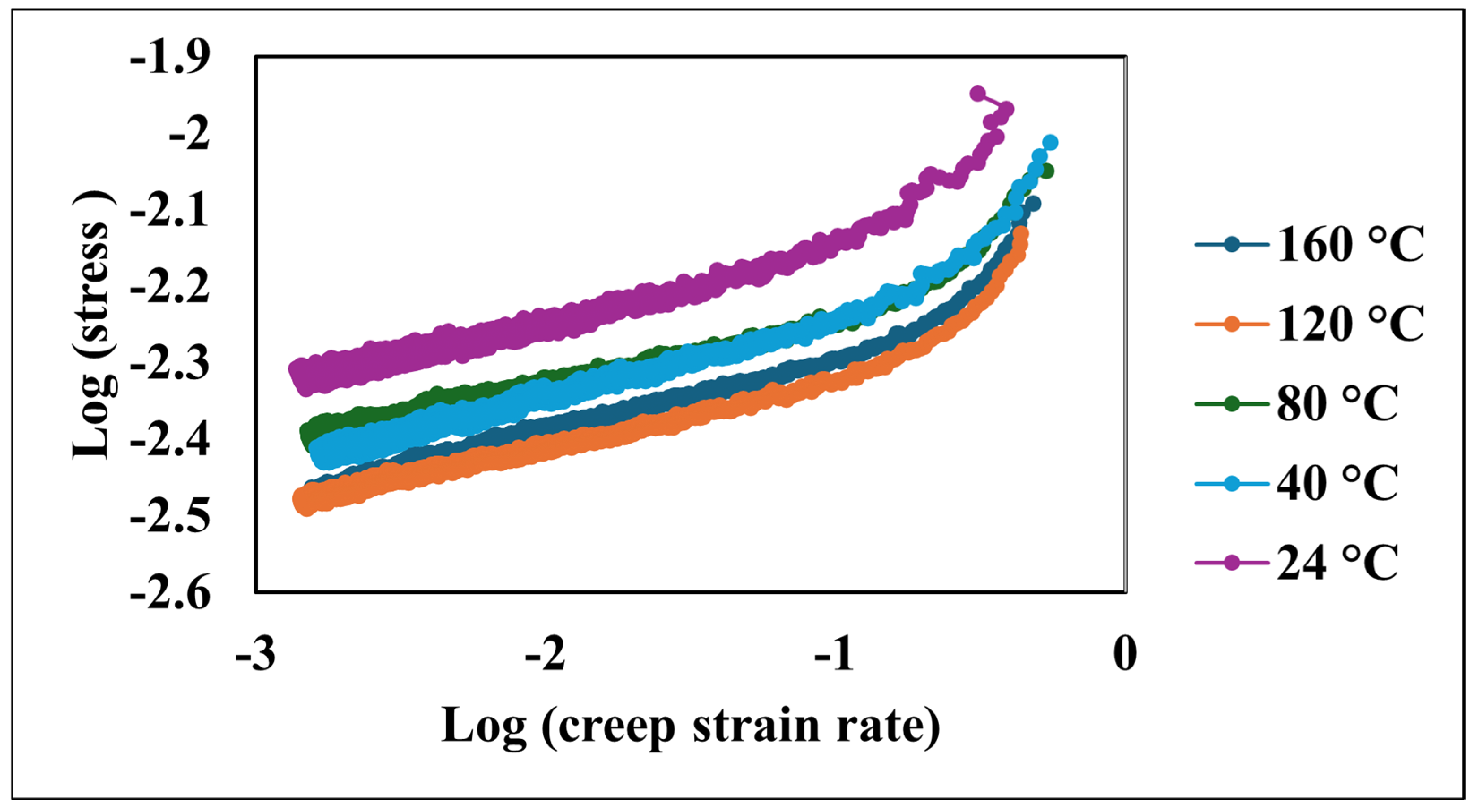
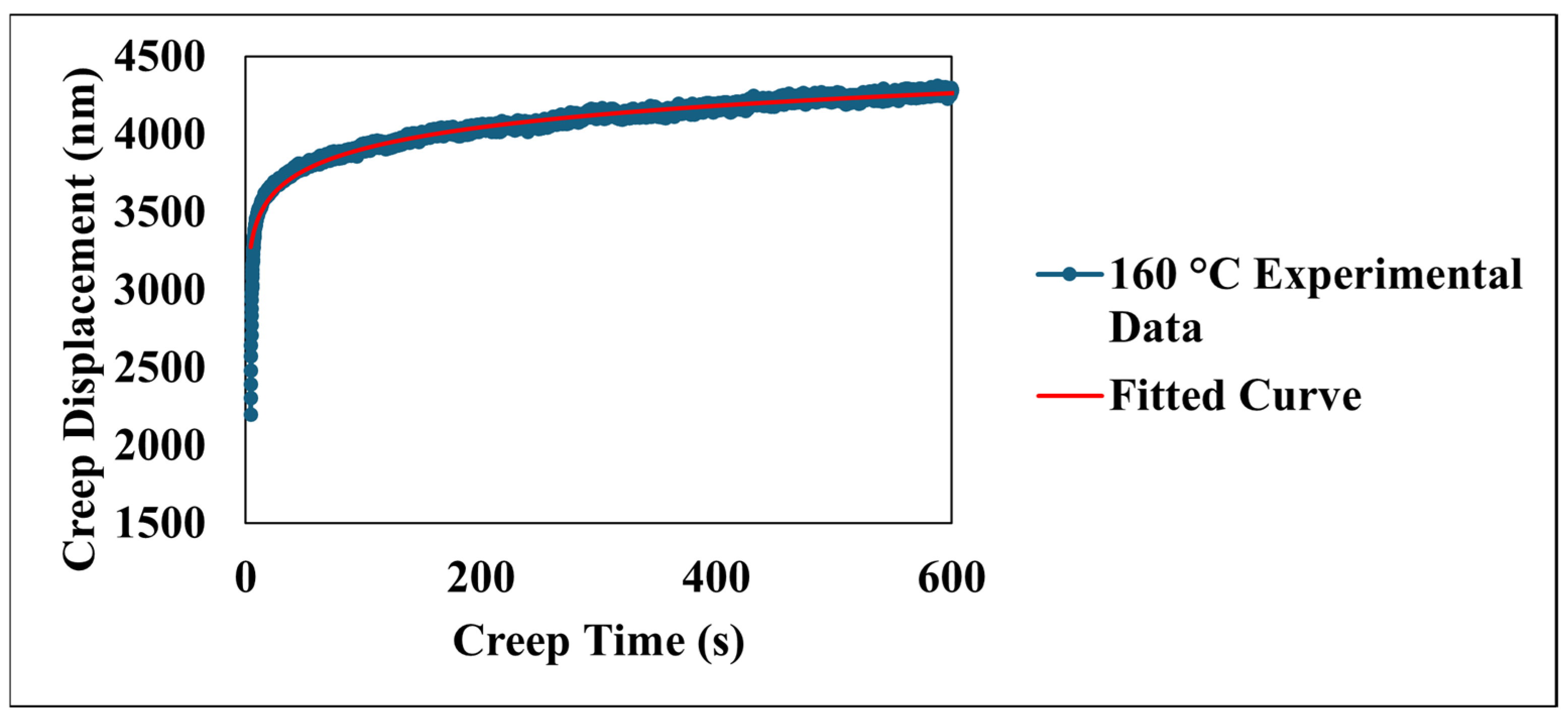
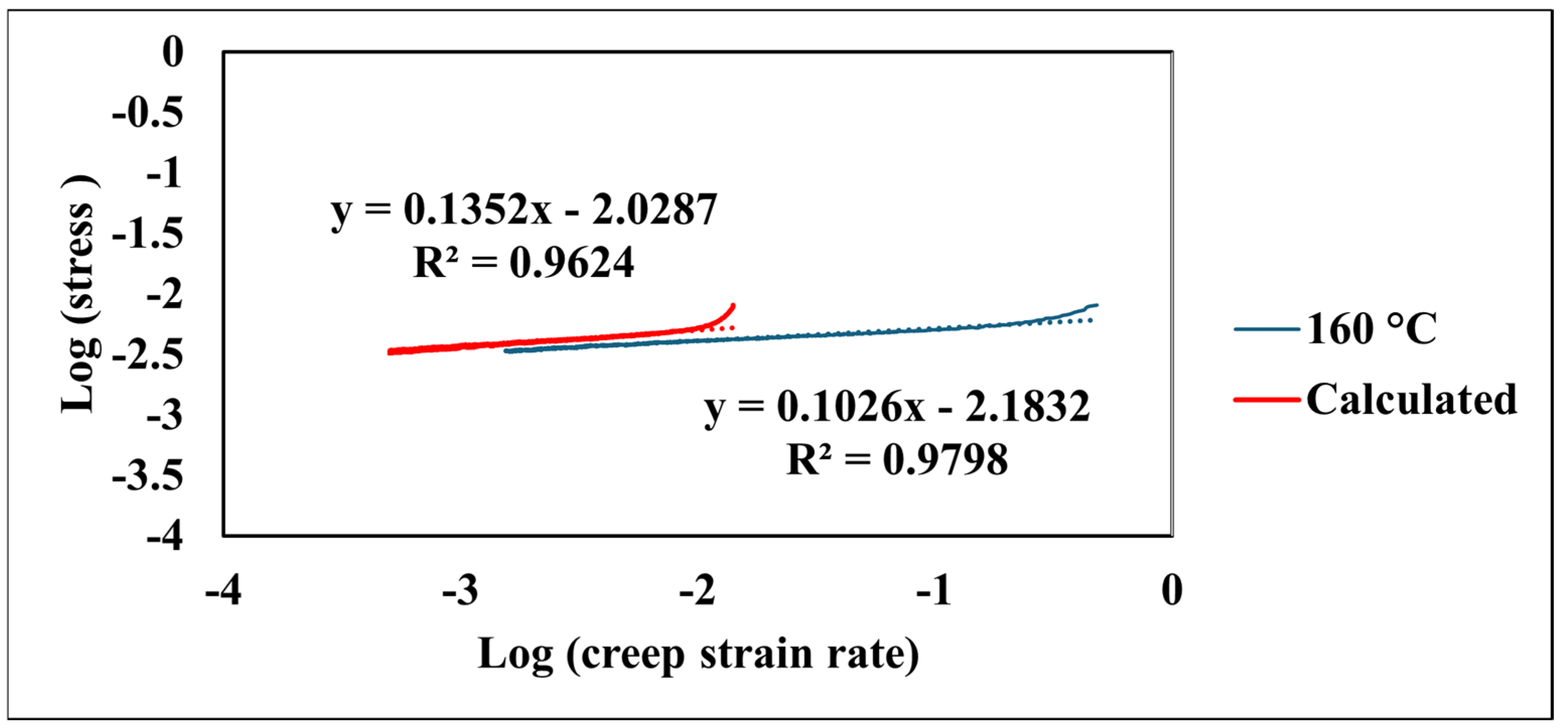
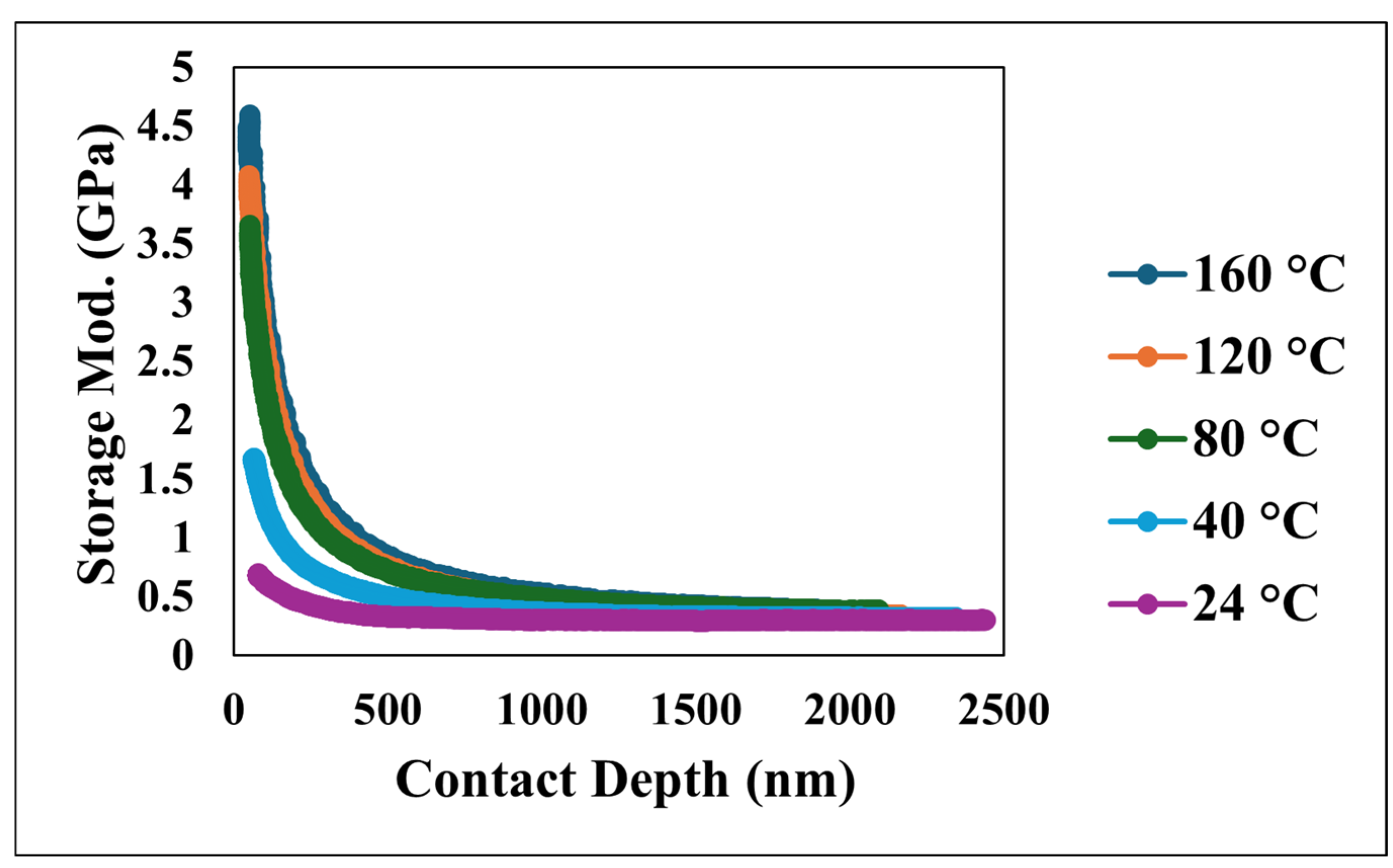
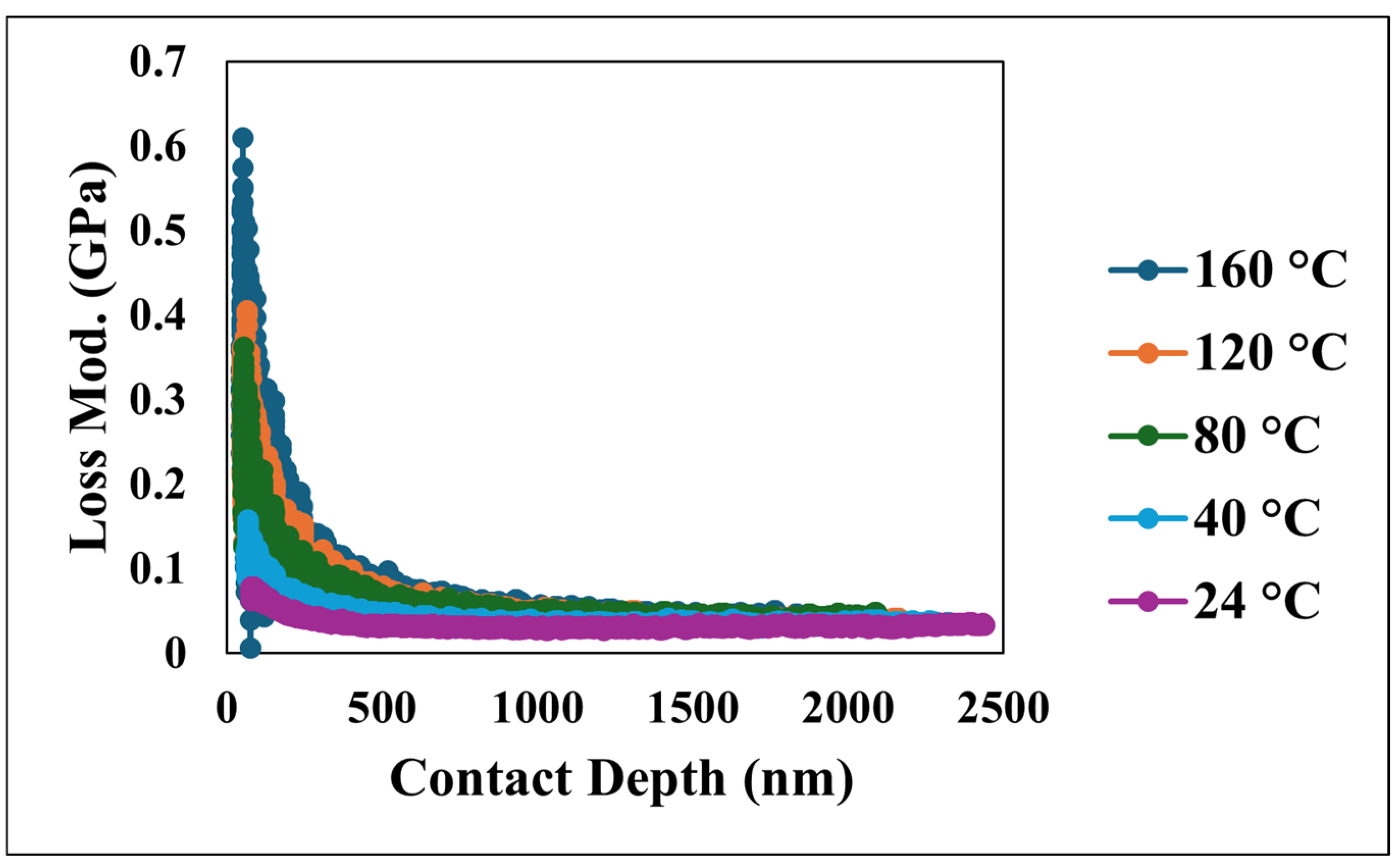
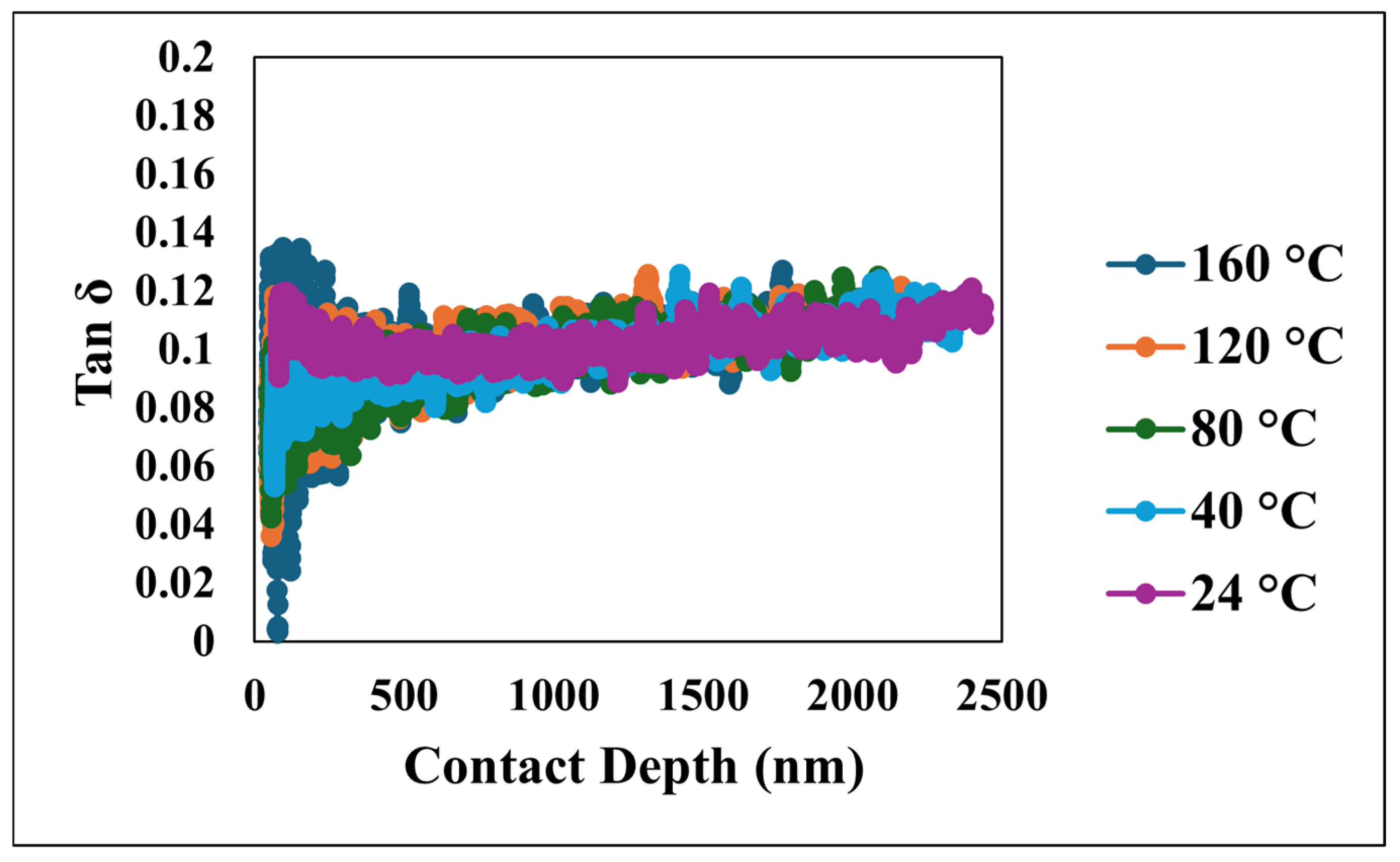
| Coefficient | 1/m | a1 | R2 |
|---|---|---|---|
| 24 °C case | 0.09 | −2.06 | 0.95 |
| 40 °C case | 0.10 | −2.14 | 0.97 |
| 80 °C case | 0.08 | −2.16 | 0.96 |
| 120 °C case | 0.09 | −2.24 | 0.97 |
| 160 °C case | 0.10 | −2.18 | 0.98 |
| Coefficient | a | b | c | d | R2 |
|---|---|---|---|---|---|
| 24 °C case | 1044 | −0.2016 | 187.1 | 2699 | 0.94 |
| 40 °C case | 1078 | −0.1581 | 215 | 2479 | 0.95 |
| 80 °C case | 1257 | −0.1641 | 201.1 | 3038 | 0.95 |
| 120 °C case | 1618 | −0.1051 | 190.6 | 3013 | 0.94 |
| 160 °C case | 1359 | −0.0008 | 199.6 | 3517 | 0.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, C.-W.; Lian, I.; Zhou, J.; Bernazzani, P.; Jao, M. The Elevated-Temperature Nano-Mechanical Properties of a PDMS–Silica-Based Superhydrophobic Nanocomposite Coating. Nanomaterials 2025, 15, 898. https://doi.org/10.3390/nano15120898
Yao C-W, Lian I, Zhou J, Bernazzani P, Jao M. The Elevated-Temperature Nano-Mechanical Properties of a PDMS–Silica-Based Superhydrophobic Nanocomposite Coating. Nanomaterials. 2025; 15(12):898. https://doi.org/10.3390/nano15120898
Chicago/Turabian StyleYao, Chun-Wei, Ian Lian, Jiang Zhou, Paul Bernazzani, and Mien Jao. 2025. "The Elevated-Temperature Nano-Mechanical Properties of a PDMS–Silica-Based Superhydrophobic Nanocomposite Coating" Nanomaterials 15, no. 12: 898. https://doi.org/10.3390/nano15120898
APA StyleYao, C.-W., Lian, I., Zhou, J., Bernazzani, P., & Jao, M. (2025). The Elevated-Temperature Nano-Mechanical Properties of a PDMS–Silica-Based Superhydrophobic Nanocomposite Coating. Nanomaterials, 15(12), 898. https://doi.org/10.3390/nano15120898






