Improvement in Heat Transfer in Hydrocarbon and Geothermal Energy Coproduction Systems Using Carbon Quantum Dots: An Experimental and Modeling Approach
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Synthesis of Carbon Quantum Dots
2.3. Characterization of Carbon Quantum Dots
2.3.1. Density
2.3.2. The Specific Heat Capacity (Cp)
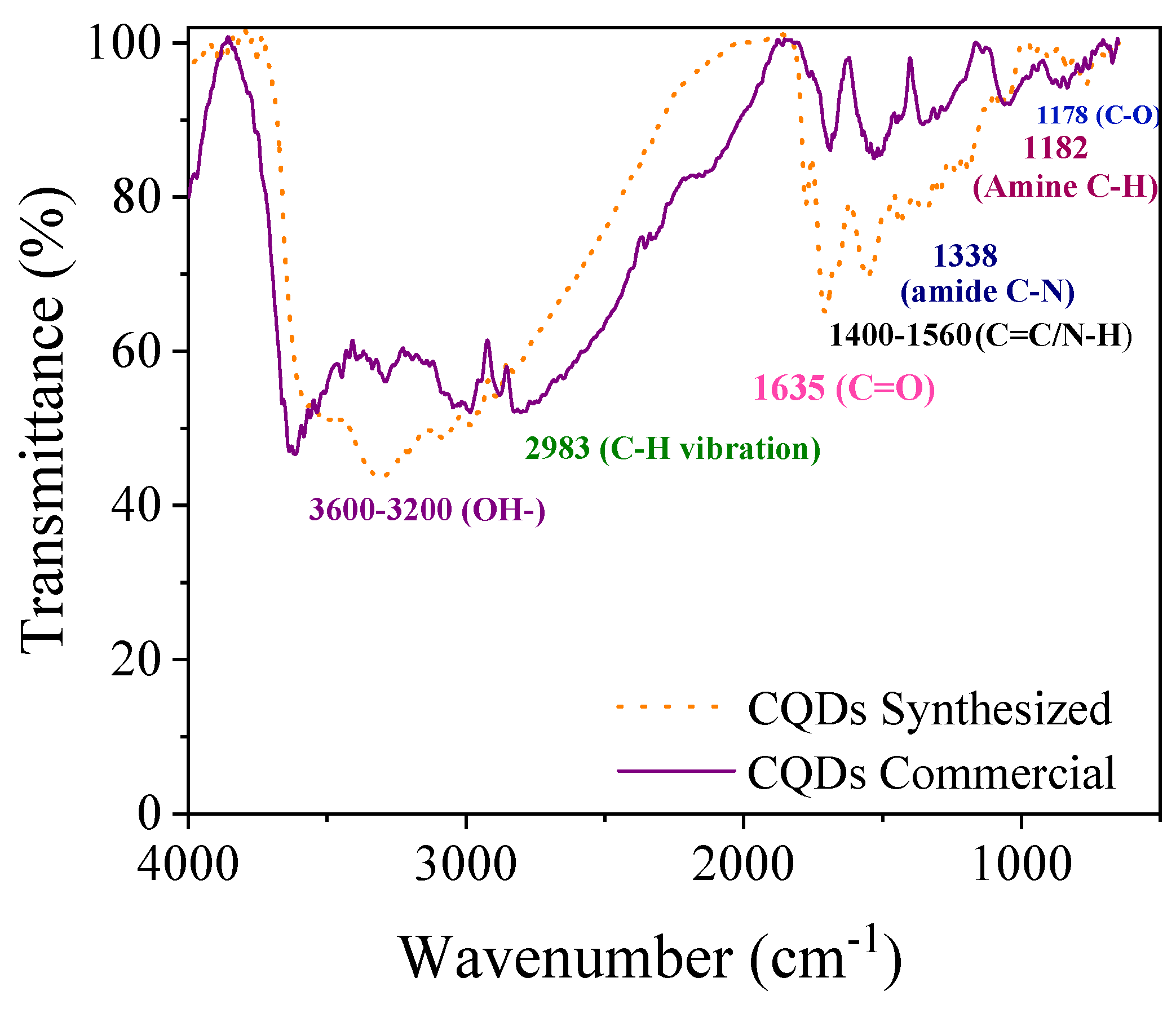
2.3.3. Fourier Transform Infrared Spectroscopy (FTIR) Analysis
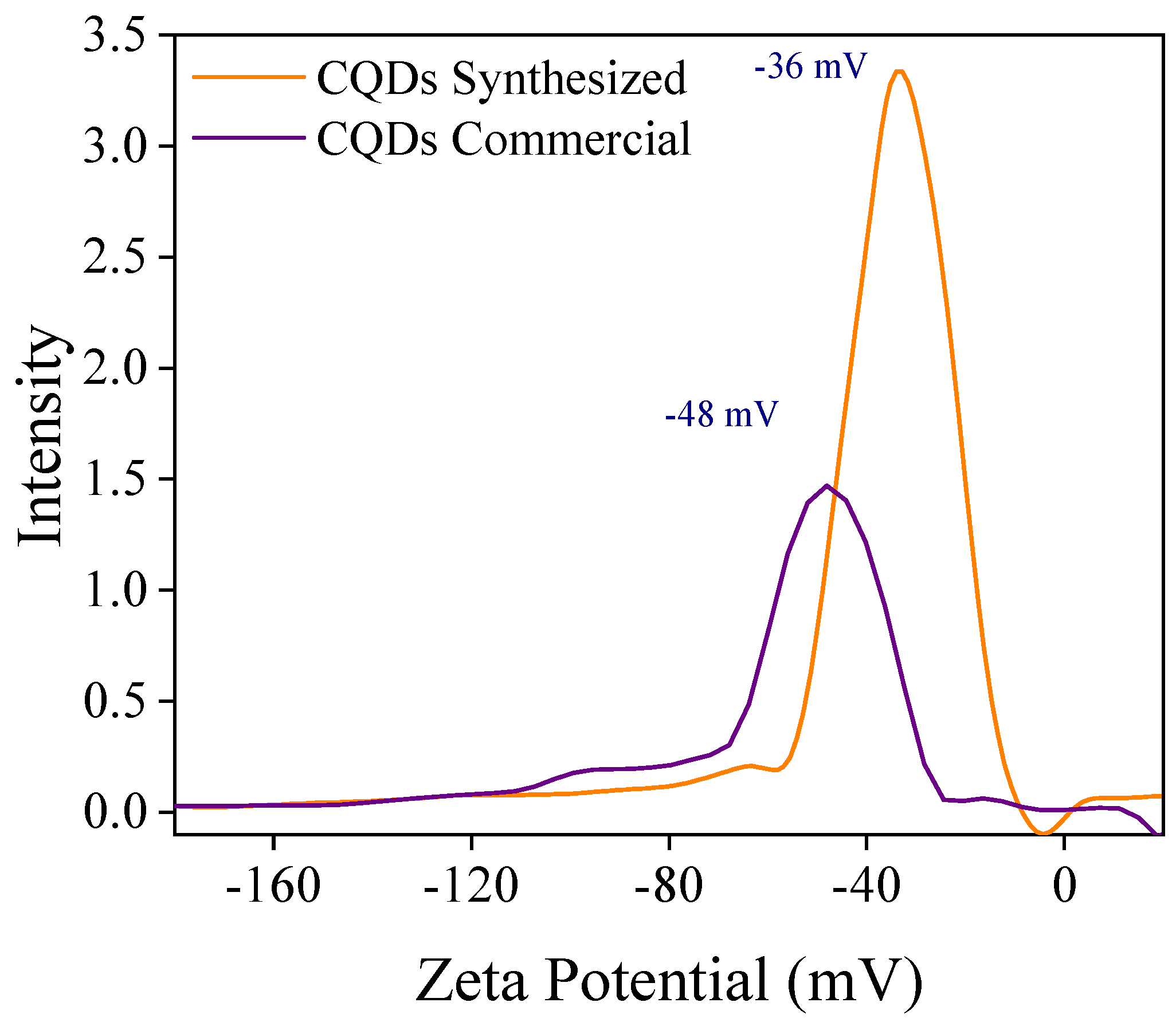
2.3.4. Particle Size and Surface Charge
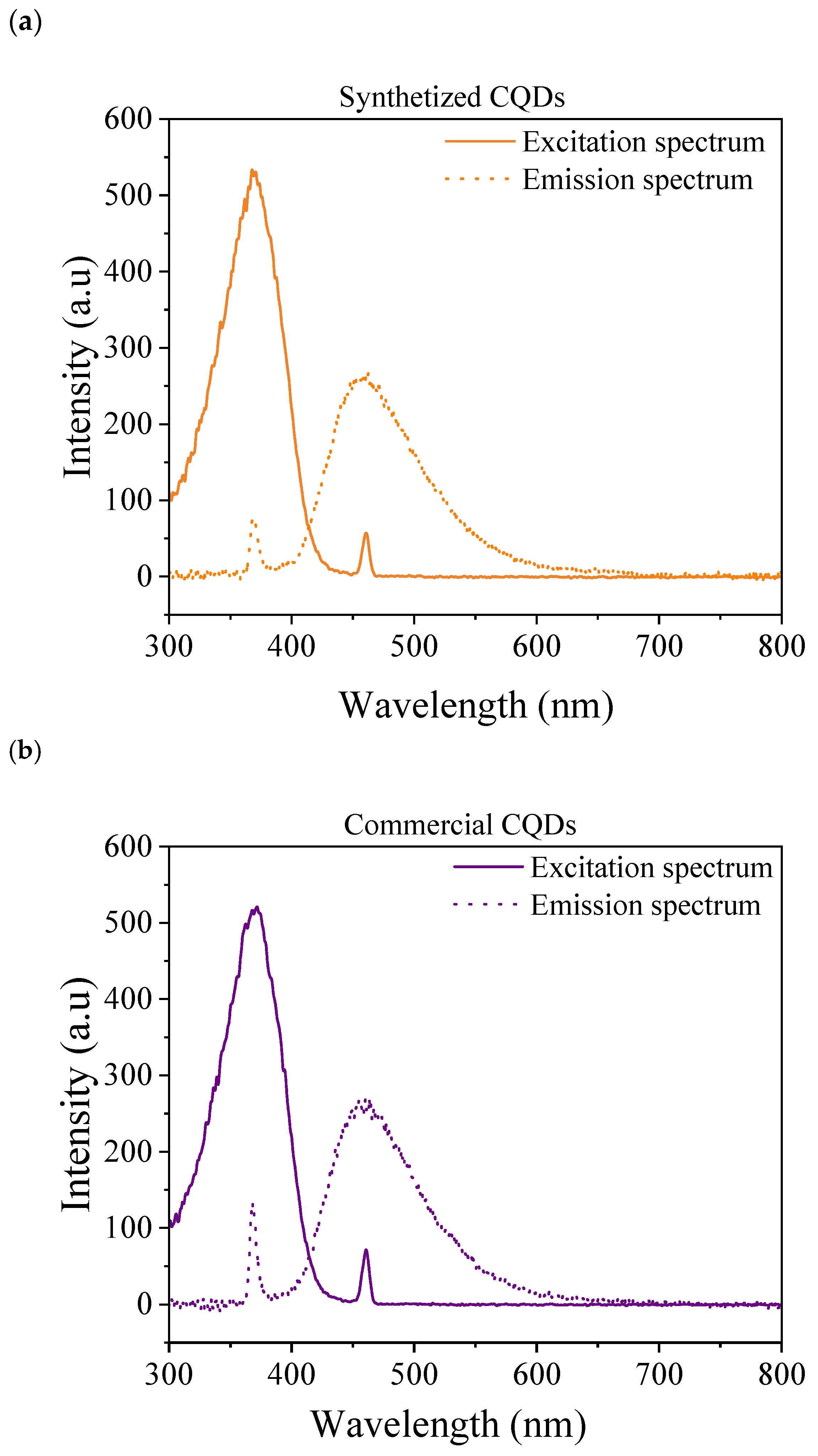
2.3.5. Fluorescence Measurements
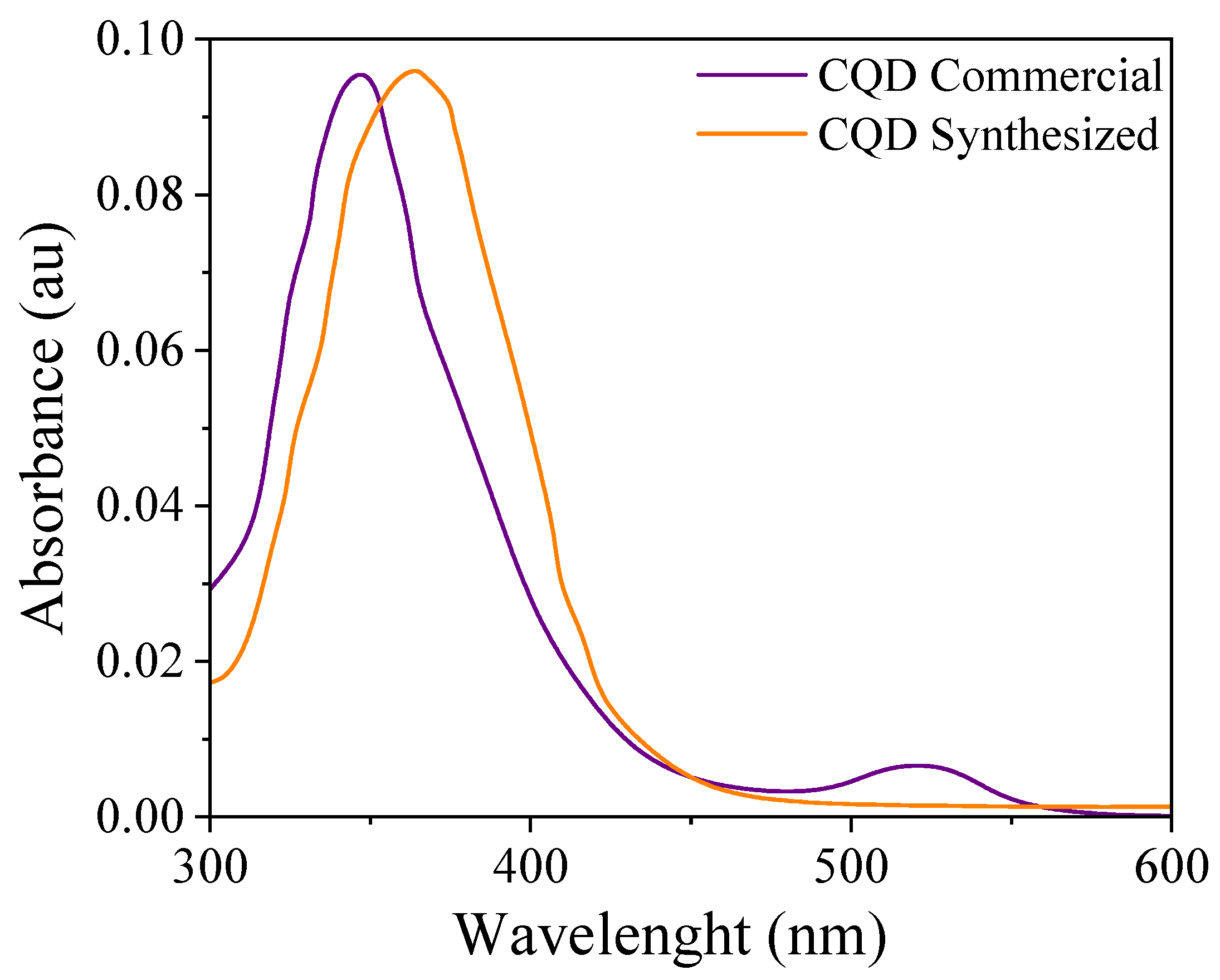
2.3.6. UV–VIS Absorption
2.4. Nanofluid Formulations
2.5. Thermal Conductivity
3. Simulation of the Use of CQDs in Brine as Heating Fluid for ORC Cycles
4. Results and Discussion
4.1. Characterization of CQDs
4.2. Thermal Conductivity
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
List of Symbols
| Cycle efficiency. | |
| Heat transferred to the evaporator | |
| Power consumed by the pumping system of the evaporator circuit on the hot-fluid side. | |
| Pumping power consumed to move the working fluid within the power cycle. | |
| Surface area of the evaporator | |
| Logarithmic mean temperature difference. | |
| Overall heat-transfer coefficient | |
| Resistance in the evaporator | |
| i-th thermal resistance | |
| Convection heat transfer coefficient of the hot fluid side | |
| Nusselt number | |
| Reynolds number | |
| Prandtl number | |
| Thermal conductivity of nanofluid | |
| (m) | Inner diameter of the pipe that comprises the evaporator |
| Friction factor in the evaporator | |
| Rugosity | |
| Thermal conductivity of the nanoparticles, | |
| Thermal conductivity of the base fluid | |
| Volumetric fraction of nanoparticles in the nanofluid. | |
| Sphericity | |
| Sphericity parameter | |
| The particle size | |
| Density of nanoparticles | |
| Heat capacity of nanofluid | |
| Boltzmann constant | |
| Viscosity of the nanofluid. |
References
- Chappidi, S.; Kumar, A.; Singh, J. Geothermal Energy Extraction from Abandoned Oil and Gas Wells Using Mono and Hybrid Nanofluids. Geothermics 2023, 114, 102794. [Google Scholar] [CrossRef]
- Lund, J.W.; Toth, A.N. Direct Utilization of Geothermal Energy 2020 Worldwide Review. Geothermics 2021, 90, 101915. [Google Scholar] [CrossRef]
- Ang, T.Z.; Salem, M.; Kamarol, M.; Das, H.S.; Nazari, M.A.; Prabaharan, N. A Comprehensive Study of Renewable Energy Sources: Classifications, Challenges and Suggestions. Energy Strategy Rev. 2022, 43, 100939. [Google Scholar] [CrossRef]
- Wang, K.; Yuan, B.; Ji, G.; Wu, X. A Comprehensive Review of Geothermal Energy Extraction and Utilization in Oilfields. J. Pet. Sci. Eng. 2018, 168, 465–477. [Google Scholar] [CrossRef]
- Afifa; Arshad, K.; Hussain, N.; Ashraf, M.H.; Saleem, M.Z. Air Pollution and Climate Change as Grand Challenges to Sustainability. Sci. Total Environ. 2024, 928, 172370. [Google Scholar] [CrossRef]
- Soltani, M.; Moradi Kashkooli, F.; Alian Fini, M.; Gharapetian, D.; Nathwani, J.; Dusseault, M.B. A Review of Nanotechnology Fluid Applications in Geothermal Energy Systems. Renew. Sustain. Energy Rev. 2022, 167, 112729. [Google Scholar] [CrossRef]
- Jello, J.; Baser, T. Utilization of Existing Hydrocarbon Wells for Geothermal System Development: A Review. Appl. Energy 2023, 348, 121456. [Google Scholar] [CrossRef]
- Cano, N.A.; Céspedes, S.; Redondo, J.; Foo, G.; Jaramillo, D.; Martinez, D.; Gutiérrez, M.; Pataquiba, J.; Rojas, J.; Cortés, F.B.; et al. Power from Geothermal Resources as a Co-Product of the Oil and Gas Industry: A Review. ACS Omega 2022, 7, 40603–40624. [Google Scholar] [CrossRef] [PubMed]
- Céspedes, S.; Cano, N.A.; Foo, G.; Jaramillo, D.; Martinez, D.; Gutiérrez, M.; Pataquiba, J.; Rojas, J.; Cortés, F.B.; Franco, C.A. Technical and Environmental Feasibility Study of the Co-Production of Crude Oil and Electrical Energy from Geothermal Resources: First Field Trial in Colombia. Processes 2022, 10, 568. [Google Scholar] [CrossRef]
- Bohórquez-Araque, A.; Garavito-Reyes, H. Feasibility Analysis of the Implementation of Geothermal Energy in Waters Associated for the Production of Hydrocarbons. Rev. Fuentes El Reventón Energético 2020, 19, 33–43. [Google Scholar]
- Santos, L.; Dahi Taleghani, A.; Elsworth, D. Repurposing Abandoned Wells for Geothermal Energy: Current Status and Future Prospects. Renew Energy 2022, 194, 1288–1302. [Google Scholar] [CrossRef]
- Liu, X.; Falcone, G.; Alimonti, C. A Systematic Study of Harnessing Low-Temperature Geothermal Energy from Oil and Gas Reservoirs. Energy 2018, 142, 346–355. [Google Scholar] [CrossRef]
- Mukherjee, S.; Wciślik, S.; Chandra Mishra, P.; Chaudhuri, P. Nanofluids: Critical Issues, Economics and Sustainability Perspectives. Particuology 2024, 87, 147–172. [Google Scholar] [CrossRef]
- Diglio, G.; Roselli, C.; Sasso, M.; Jawali Channabasappa, U. Borehole Heat Exchanger with Nanofluids as Heat Carrier. Geothermics 2018, 72, 112–123. [Google Scholar] [CrossRef]
- Ahmed, M.A.; Shuaib, N.H.; Yusoff, M.Z.; Al-Falahi, A.H. Numerical Investigations of Flow and Heat Transfer Enhancement in a Corrugated Channel Using Nanofluid. Int. Commun. Heat Mass Transf. 2011, 38, 1368–1375. [Google Scholar] [CrossRef]
- Jin, X.; Wang, R.; Huang, L.; Shao, C. Effect of Interfacial Layer around Core-Shell Nanoparticles on Thermal Conductivity of Nanofluids. Powder Technol. 2023, 429, 118945. [Google Scholar] [CrossRef]
- Wole-Osho, I.; Okonkwo, E.C.; Adun, H.; Kavaz, D.; Abbasoglu, S. An Intelligent Approach to Predicting the Effect of Nanoparticle Mixture Ratio, Concentration and Temperature on Thermal Conductivity of Hybrid Nanofluids. J. Therm. Anal. Calorim. 2021, 144, 671–688. [Google Scholar] [CrossRef]
- Du, R.; Jiang, D.D.; Wang, Y.; Wei Shah, K. An Experimental Investigation of CuO/Water Nanofluid Heat Transfer in Geothermal Heat Exchanger. Energy Build 2020, 227, 110402. [Google Scholar] [CrossRef]
- Duangthongsuk, W.; Wongwises, S. Heat Transfer Enhancement and Pressure Drop Characteristics of TiO2-Water Nanofluid in a Double-Tube Counter Flow Heat Exchanger. Int. J. Heat Mass Transf. 2009, 52, 2059–2067. [Google Scholar] [CrossRef]
- Javadi, H.; Urchueguia, J.F.; Ajarostaghi, S.S.M.; Badenes, B. Impact of Employing Hybrid Nanofluids as Heat Carrier Fluid on the Thermal Performance of a Borehole Heat Exchanger. Energies 2021, 14, 2892. [Google Scholar] [CrossRef]
- Jahanbin, A.; Semprini, G.; Pulvirenti, B. Nanofluid Suspensions as Heat Carrier Fluids in Single U-Tube Borehole Heat Exchangers. In Proceedings of the Journal of Physics: Conference Series, Online, 20–22 September 2021; IOP Publishing Ltd.: Bristol, UK, 2021; Volume 2116. [Google Scholar]
- Das, R.; Bandyopadhyay, R.; Pramanik, P. Carbon Quantum Dots from Natural Resource: A Review. Mater. Today. Chem. 2018, 8, 96–109. [Google Scholar] [CrossRef]
- Pourmadadi, M.; Rahmani, E.; Rajabzadeh-Khosroshahi, M.; Samadi, A.; Behzadmehr, R.; Rahdar, A.; Ferreira, L.F.R. Properties and Application of Carbon Quantum Dots (CQDs) in Biosensors for Disease Detection: A Comprehensive Review. J. Drug Deliv. Sci. Technol. 2023, 80, 104156. [Google Scholar] [CrossRef]
- Zhao, D.L.; Chung, T.S. Applications of Carbon Quantum Dots (CQDs) in Membrane Technologies: A Review. Water Res. 2018, 147, 43–49. [Google Scholar] [CrossRef] [PubMed]
- Quaid, T.; Ghalandari, V.; Reza, T. Effect of Synthesis Process, Synthesis Temperature, and Reaction Time on Chemical, Morphological, and Quantum Properties of Carbon Dots Derived from Loblolly Pine. Biomass 2022, 2, 250–263. [Google Scholar] [CrossRef]
- Pirsaheb, M.; Asadi, A.; Sillanpää, M.; Farhadian, N. Application of Carbon Quantum Dots to Increase the Activity of Conventional Photocatalysts: A Systematic Review. J. Mol. Liq. 2018, 271, 857–871. [Google Scholar] [CrossRef]
- Rani, U.A.; Ng, L.Y.; Ng, C.Y.; Mahmoudi, E. A Review of Carbon Quantum Dots and Their Applications in Wastewater Treatment. Adv. Colloid. Interface Sci. 2020, 278, 102124. [Google Scholar] [CrossRef]
- Medina, O.E.; Rosales, S.; Garzón, N.; López, D.; Taborda, E.A.; Ordóñez, J.C.; Fernández, S.A.; Cortés, F.B.; Franco, C.A. Advances in Quantum Dot Applications for the Oil and Gas Industry: Current Trends and Future Directions. Energy Fuels 2024, 38, 21793–21831. [Google Scholar] [CrossRef]
- Rosales, S.; Zapata, K.; Cortes, F.B.; Rojano, B.; Diaz, C.; Cortes, C.; Jaramillo, D.; Vasquez, A.; Ramirez, D.; Franco, C.A. Simultaneous Detection of Carbon Quantum Dots as Tracers for Interwell Connectivity Evaluation in a Pattern with Two Injection Wells. Nanomaterials 2024, 14, 789. [Google Scholar] [CrossRef]
- Franco, C.A.; Candela, C.H.; Gallego, J.; Marin, J.; Patiño, L.E.; Ospina, N.; Patiño, E.; Molano, M.; Villamil, F.; Bernal, K.M.; et al. Easy and Rapid Synthesis of Carbon Quantum Dots from Mortiño (Vaccinium Meridionale Swartz) Extract for Use as Green Tracers in the Oil and Gas Industry: Lab-to-Field Trial Development in Colombia. Ind. Eng. Chem. Res. 2020, 59, 11359–11369. [Google Scholar] [CrossRef]
- Pham, X.H.; Park, S.M.; Ham, K.M.; Kyeong, S.; Son, B.S.; Kim, J.; Hahm, E.; Kim, Y.H.; Bock, S.; Kim, W.; et al. Synthesis and Application of Silica-Coated Quantum Dots in Biomedicine. Int. J. Mol. Sci. 2021, 22, 10116. [Google Scholar] [CrossRef]
- Giraldo, L.J.; Galeano-Caro, D.; Franco, C.A.; Archila, J.; Villamil, F.; Cortés, F.B.; Franco, C.A. Development of a Novel Green Bio-Nanofluid from Sapindus Saponaria for Enhanced Oil Recovery Processes. Processes 2022, 10, 1057. [Google Scholar] [CrossRef]
- Soltan, Y.I.; Nasser, M.S.; Almomani, F.; Mahmoud, K.A.; Onaizi, S.A. Thermal Conductivity of Different Materials Nanofluids Nanofluids of MXenes, Metal Organic Frameworks, and Other Nanostructured Materials in Heat Transfer Applications: Review. J. Mater. Res. Technol. 2024, 31, 2723–2761. [Google Scholar] [CrossRef]
- Razzaq, I.; Xinhua, W.; Rasool, G.; Sun, T.; Shflot, A.S.; Malik, M.Y.; Abbas, K.; Ali, S.; Ali, A. Nanofluids for Advanced Applications: A Comprehensive Review on Preparation Methods, Properties, and Environmental Impact. ACS Omega 2025, 10, 5251–5282. [Google Scholar] [CrossRef] [PubMed]
- Dickes, R.; Ziviani, D.; van den Broek, M.; de Paepe, M.; Quoilin, S.; Lemort, V. ORCmKit: An Open-Source Library for Organic Rankine Cycle Modelling and Analysis. In Proceedings of the ECOS 2016-29th International Conference on Efficiency, Cost, Optimisation, Simulation and Environmental Impact of Energy Systems, Portorož, Slovenia, 19–23 June 2016. [Google Scholar]
- Bell, I.H.; Wronski, J.; Quoilin, S.; Lemort, V. Pure and Pseudo-Pure Fluid Thermophysical Property Evaluation and the Open-Source Thermophysical Property Library CoolProp. Ind. Eng. Chem. Res. 2014, 53, 2498–2508. [Google Scholar] [CrossRef]
- Apmann, K.; Fulmer, R.; Soto, A.; Vafaei, S. Thermal Conductivity and Viscosity: Review and Optimization of Effects of Nanoparticles. Materials 2021, 14, 1–75. [Google Scholar] [CrossRef]
- Hamilton, R.L. Thermal Conductivity of Heterogeneous Two-Component Systems. Ind. Eng. Chem. Fundam. 1962, 1, 187–191. [Google Scholar] [CrossRef]
- Iqbal, M.; Kouloulias, K.; Sergis, A.; Hardalupas, Y. Critical Analysis of Thermal Conductivity Enhancement of Alumina–Water Nanofluids. J. Therm. Anal. Calorim. 2023, 148, 9361–9389. [Google Scholar] [CrossRef]
- Xuan, Y.; Li, Q.; Hu, W. Aggregation Structure and Thermal Conductivity of Nanofluids. AIChE J. 2003, 49, 1038–1043. [Google Scholar] [CrossRef]
- Muzychka, Y.S.; Yovanovich, M.M. Convective Heat Transfer. In Handbook of Fluid Dynamics, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2016; pp. 14.1–14.58. ISBN 9781439849576. [Google Scholar]
- Jang, S.P.; Choi, S.U.S. Effects of Various Parameters on Nanofluid Thermal Conductivity. J. Heat Transf. 2007, 129, 617–623. [Google Scholar] [CrossRef]
- Jung, J.Y.; Yoo, J.Y. Thermal Conductivity Enhancement of Nanofluids in Conjunction with Electrical Double Layer (EDL). Int. J. Heat Mass Transf. 2009, 52, 525–528. [Google Scholar] [CrossRef]
- Kumar, D.H.; Patel, H.E.; Kumar, V.R.R.; Sundararajan, T.; Pradeep, T.; Das, S.K. Model for Heat Conduction in Nanofluids. Phys. Rev. Lett. 2004, 93, 144301. [Google Scholar] [CrossRef]
- Zhou, X.F.; Gao, L. Thermal Conductivity of Nanofluids: Effects of Graded Nanolayers and Mutual Interaction. J. Appl. Phys. 2008, 103, 083503. [Google Scholar] [CrossRef]
- Ríos, E.H.; Guzmán, J.D.; Ribadeneira, R.; Bailón-García, E.; Acevedo, E.R.; Vélez, F.; Franco, C.A.; Riazi, M.; Cortes, F.B. Effect of the Oil Content on Green Hydrogen Production from Produced Water Using Carbon Quantum Dots as a Disruptive Nanolectrolyte. Int. J. Hydrogen Energy 2024, 76, 353–362. [Google Scholar] [CrossRef]
- Mandal, T.; Mishra, S.R.; Singh, K.; Agarwalla, H.; Masto, R.E.; Kumar, M.; Singh, V. Fluorescent Carbon Nanomaterials from Coal and Its Derivatives: Structure, Properties, and Applications. J. Nanopart. Res. 2023, 25, 125. [Google Scholar] [CrossRef]
- Karelovic, A.; Galdames, G.; Medina, J.C.; Yévenes, C.; Barra, Y.; Jiménez, R. Mechanism and Structure Sensitivity of Methanol Synthesis from CO2 over SiO2-Supported Cu Nanoparticles. J. Catal. 2019, 369, 415–426. [Google Scholar] [CrossRef]
- Rahman, M.A.; Hasnain, S.M.M.; Pandey, S.; Tapalova, A.; Akylbekov, N.; Zairov, R. Review on Nanofluids: Preparation, Properties, Stability, and Thermal Performance Augmentation in Heat Transfer Applications. ACS Omega 2024, 9, 32328–32349. [Google Scholar] [CrossRef]
- FIde, K.; Tsuji, T.; Suzuki, T.; Setoura, K. Brownian Dynamics Simulation of Microscale Thermophoresis in Liquid. ACS Omega 2025, 10, 4526–4533. [Google Scholar] [CrossRef]
- Pisarevsky, M.I.; Struchalin, P.G.; Balakin, B.V.; Kutsenko, K.V.; Maslov, Y.A. Experimental Study of Nanofluid Heat Transfer for Geothermal Applications. Renew Energy 2024, 221, 119631. [Google Scholar] [CrossRef]
- Hu, X.; Yin, D.; Chen, X.; Xiang, G. Experimental Investigation and Mechanism Analysis: Effect of Nanoparticle Size on Viscosity of Nanofluids. J. Mol. Liq. 2020, 314, 113604. [Google Scholar] [CrossRef]
- Hashimoto, S.; Yano, K.; Hirota, Y.; Uchiyama, H.; Tsutsui, S. Analysis of Enhancement Mechanism for Thermal Conductivity of Nanofluids by Inelastic X-Ray Scattering. Int. J. Heat Mass Transf. 2021, 173, 121245. [Google Scholar] [CrossRef]
- Chen, M.; Zou, C.; Tang, W.; Huang, Y.; Sun, H. Experimental and Modeling Studies of N-Doped Carbon Quantum Dot Nanofluids for Heat Transfer Systems. Diam. Relat. Mater. 2022, 129, 109394. [Google Scholar] [CrossRef]
- Mousavi, H.; Ghomshe, S.M.T.; Rashidi, A.; Mirzaei, M. Hybrids Carbon Quantum Dots as New Nanofluids for Heat Transfer Enhancement in Wet Cooling Towers. Heat Mass Transf. 2022, 58, 309–320. [Google Scholar] [CrossRef]
- Zou, L.; Yang, X.; Tan, J.; Sun, Y. S-N Curve Modeling Method of Aluminum Alloy Welded Joints Based on the Fatigue Characteristics Domain. Fract. Struct. Integr. 2017, 11, 137–148. [Google Scholar] [CrossRef]
- Li, T.; Li, S.; Zhao, J.; Lu, P.; Meng, L. Sphericities of Non-Spherical Objects. Particuology 2012, 10, 97–104. [Google Scholar] [CrossRef]
- Seibert, J.R.; Keleş, Ö.; Wang, J.; Erogbogbo, F. Infusion of Graphene Quantum Dots to Modulate Thermal Conductivity and Dynamic Mechanical Properties of Polymers. Polymer 2019, 185, 121988. [Google Scholar] [CrossRef]
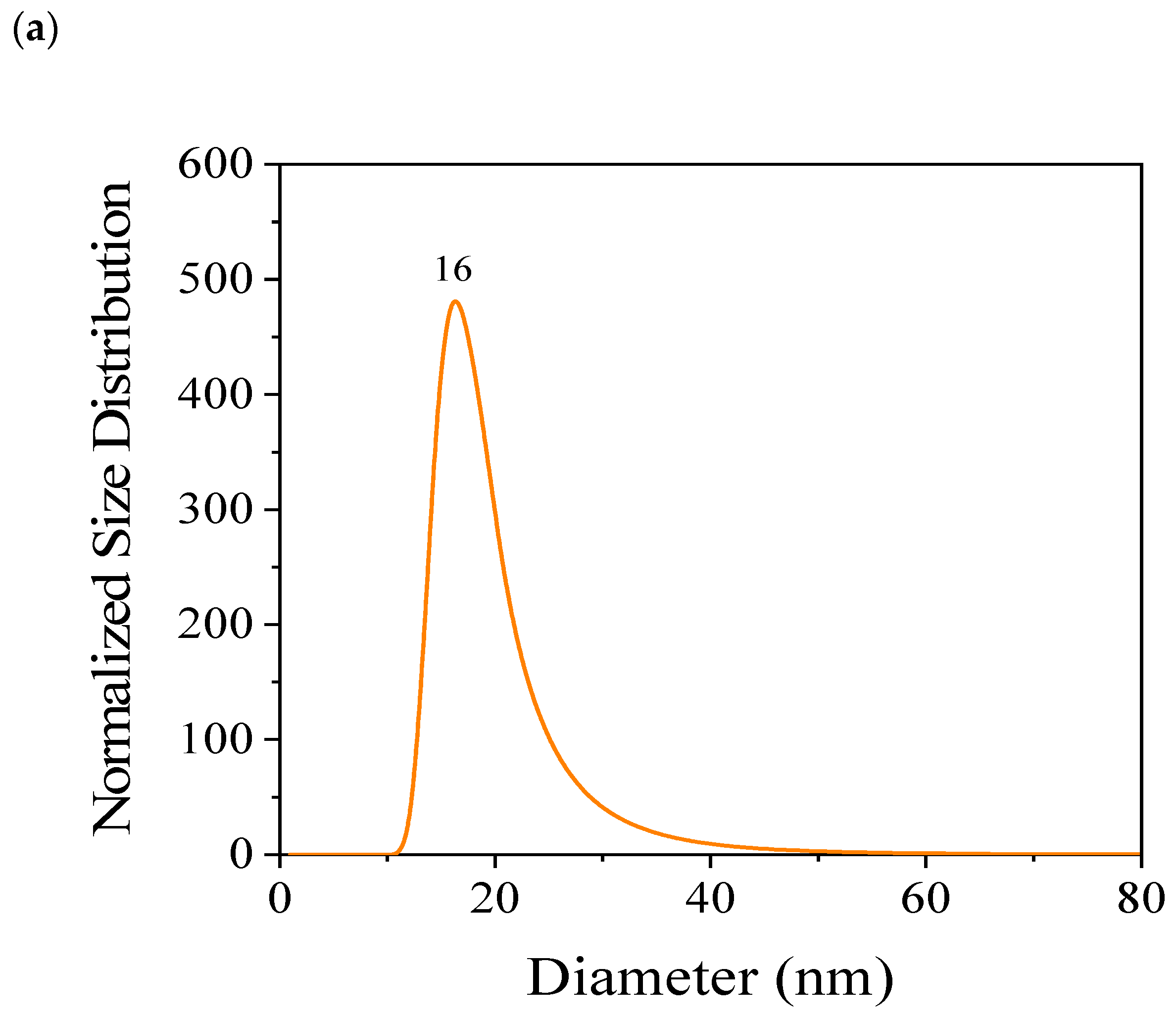
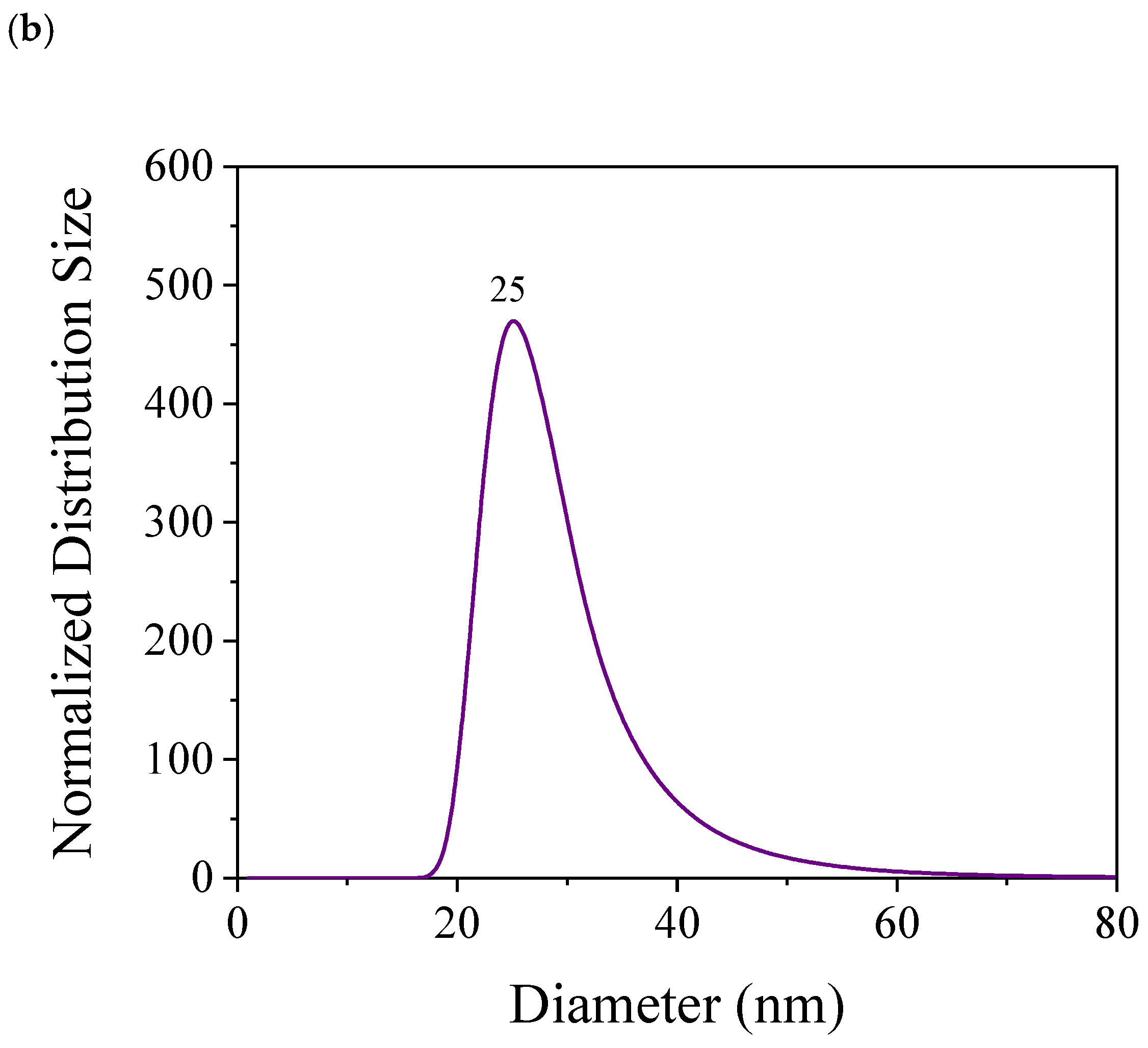
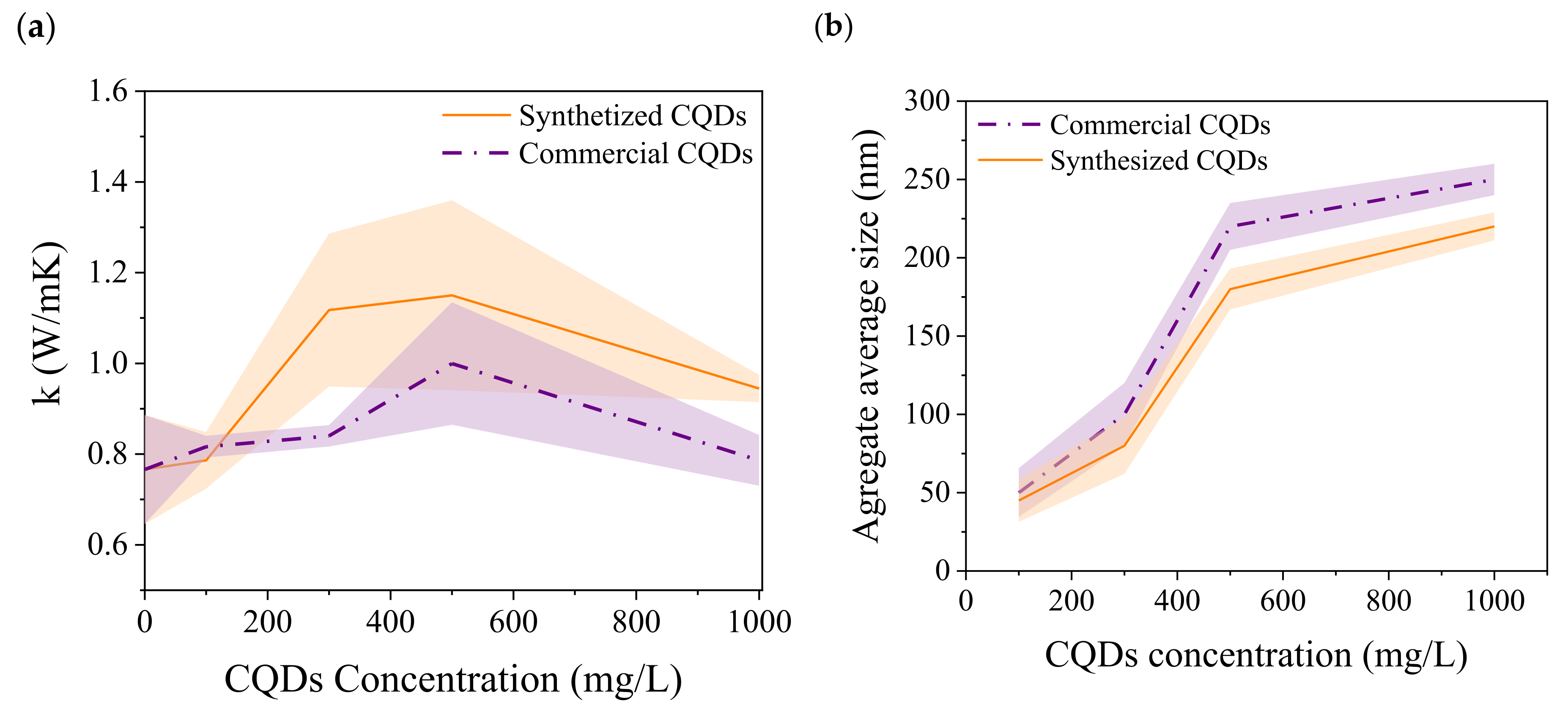
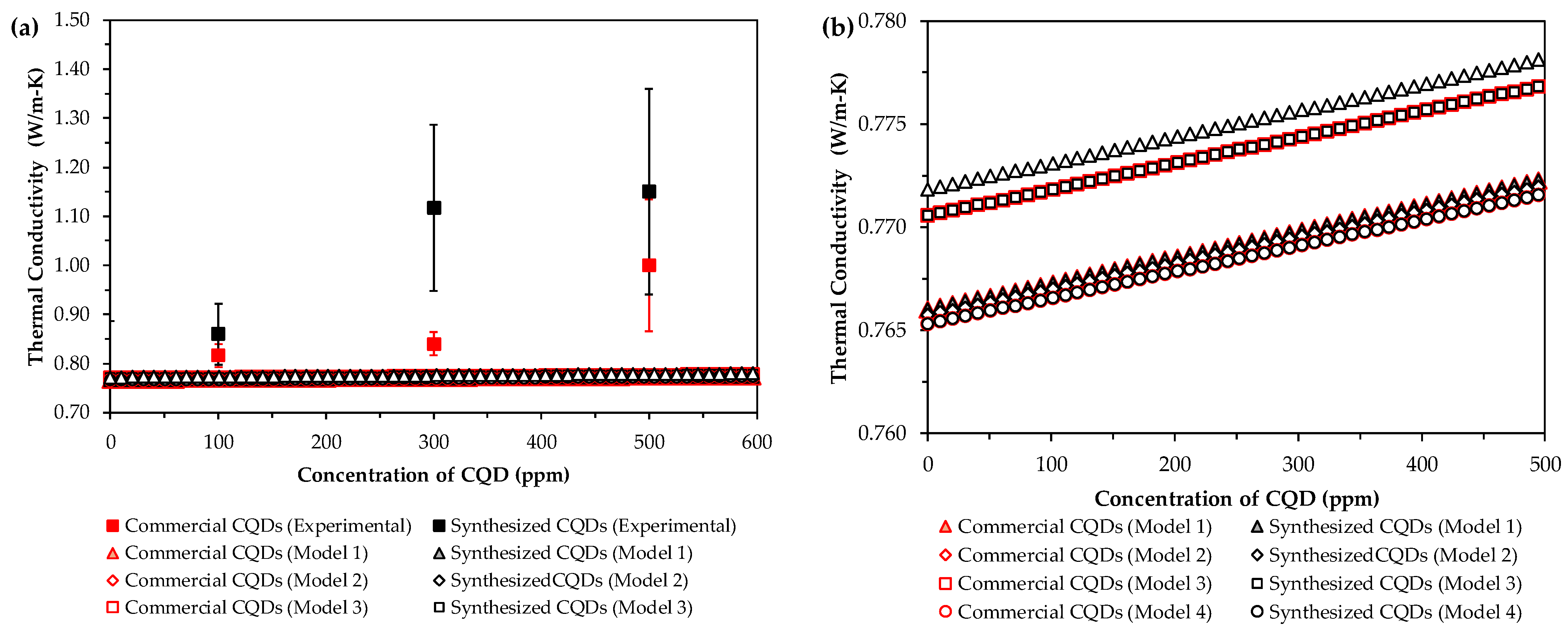
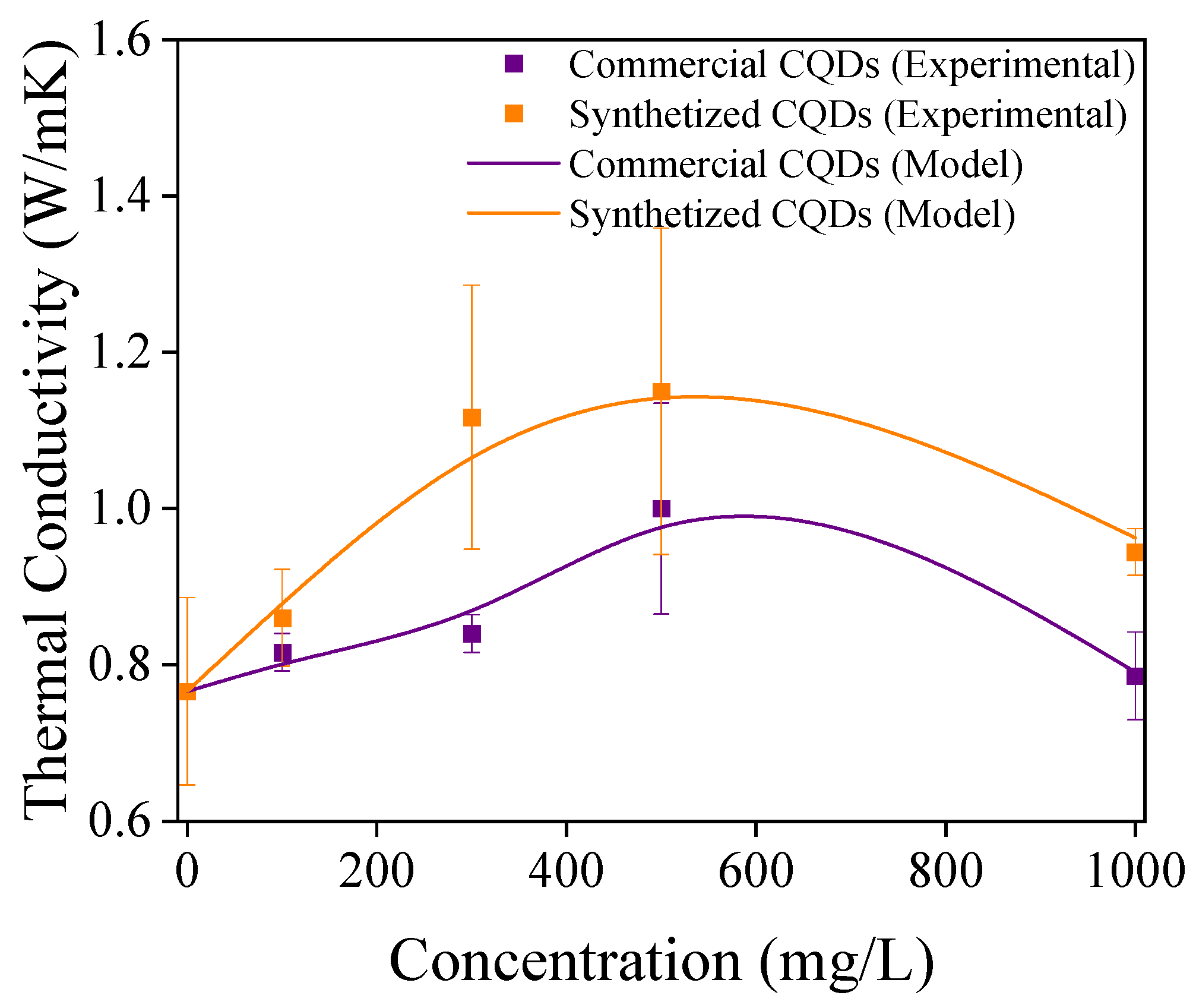
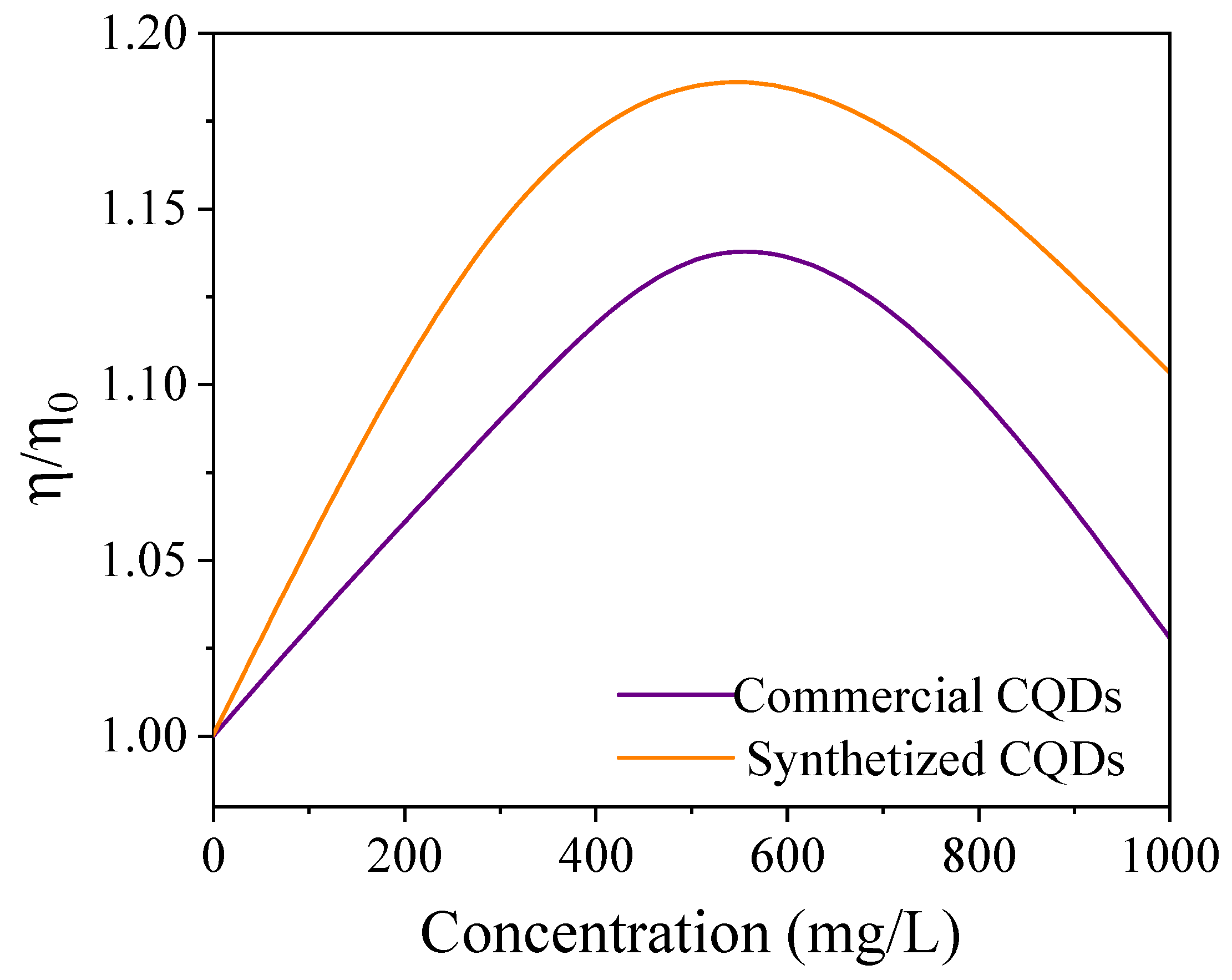
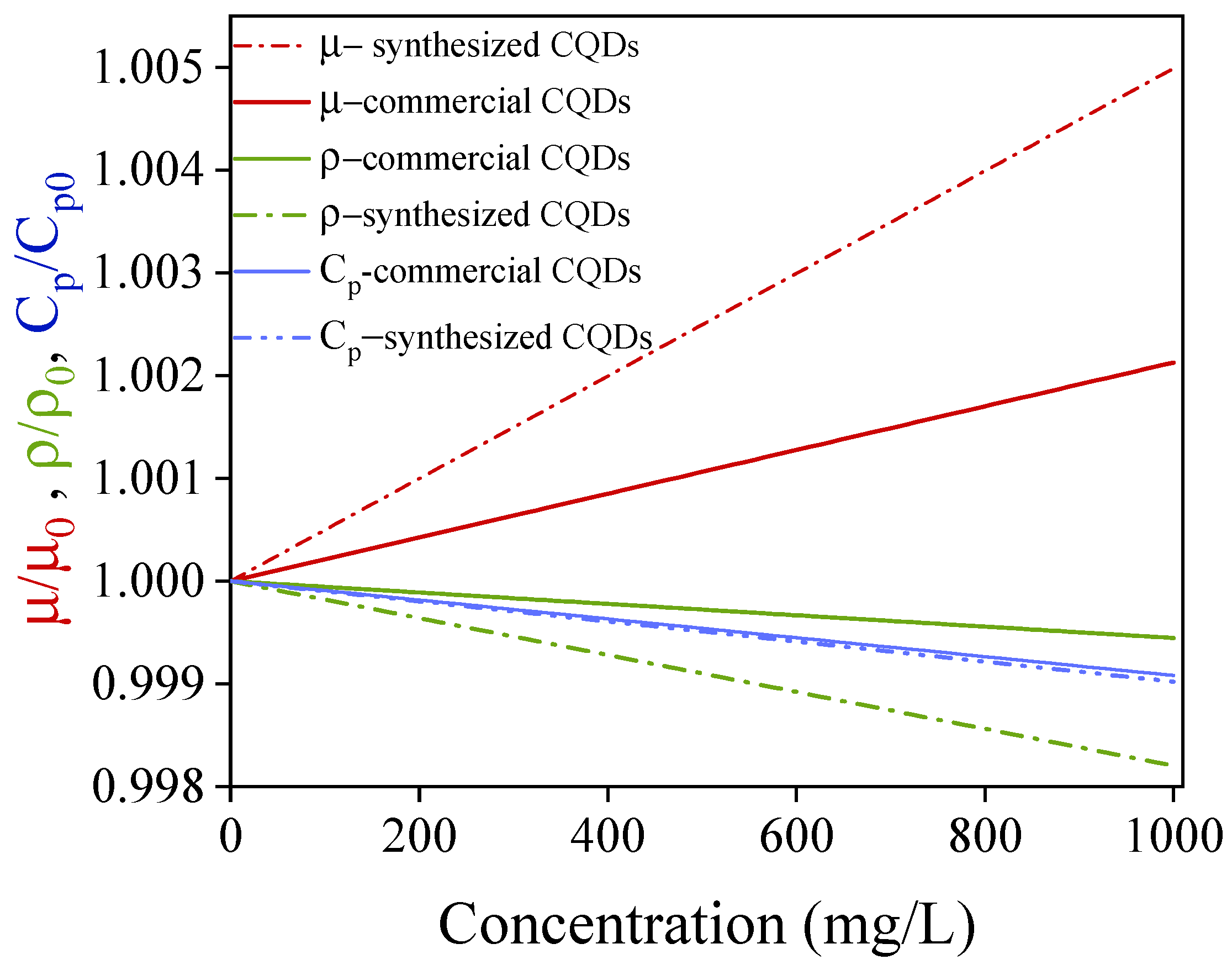
| Component | Concentration (g/L) |
|---|---|
| Sodium Chloride (NaCl) | 6.82 |
| Potassium chloride (KCl) | 0.093 |
| Hexahydrate magnesium chloride (MgCl26H2O) | 0.634 |
| Calcium chloride dehydrated (CaCl22H2O) | 0.543 |
| Number | Model | Reference |
|---|---|---|
| 1 | [41] | |
| 2 | [42] | |
| 3 | [43] | |
| 4 | where | [44] |
| 5 | [45] |
| CQDs | Density ± 0.012 (g/cm3) | Heat Capacity ± 0.017 (J/g·°C) |
|---|---|---|
| Commercial | 1.175 | 0.350 |
| Synthesized | 0.501 | 0.100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Villada, Y.; Giraldo, L.J.; Estenoz, D.; Riazi, M.; Ordoñez, J.; Taborda, E.A.; Bastidas, M.; Franco, C.A.; Cortés, F.B. Improvement in Heat Transfer in Hydrocarbon and Geothermal Energy Coproduction Systems Using Carbon Quantum Dots: An Experimental and Modeling Approach. Nanomaterials 2025, 15, 879. https://doi.org/10.3390/nano15120879
Villada Y, Giraldo LJ, Estenoz D, Riazi M, Ordoñez J, Taborda EA, Bastidas M, Franco CA, Cortés FB. Improvement in Heat Transfer in Hydrocarbon and Geothermal Energy Coproduction Systems Using Carbon Quantum Dots: An Experimental and Modeling Approach. Nanomaterials. 2025; 15(12):879. https://doi.org/10.3390/nano15120879
Chicago/Turabian StyleVillada, Yurany, Lady J. Giraldo, Diana Estenoz, Masoud Riazi, Juan Ordoñez, Esteban A. Taborda, Marlon Bastidas, Camilo A. Franco, and Farid B. Cortés. 2025. "Improvement in Heat Transfer in Hydrocarbon and Geothermal Energy Coproduction Systems Using Carbon Quantum Dots: An Experimental and Modeling Approach" Nanomaterials 15, no. 12: 879. https://doi.org/10.3390/nano15120879
APA StyleVillada, Y., Giraldo, L. J., Estenoz, D., Riazi, M., Ordoñez, J., Taborda, E. A., Bastidas, M., Franco, C. A., & Cortés, F. B. (2025). Improvement in Heat Transfer in Hydrocarbon and Geothermal Energy Coproduction Systems Using Carbon Quantum Dots: An Experimental and Modeling Approach. Nanomaterials, 15(12), 879. https://doi.org/10.3390/nano15120879










