Non-Bosonic Damping of Spin Waves in van der Waals Ferromagnetic Monolayers
Abstract
1. Introduction
2. Materials and Methods
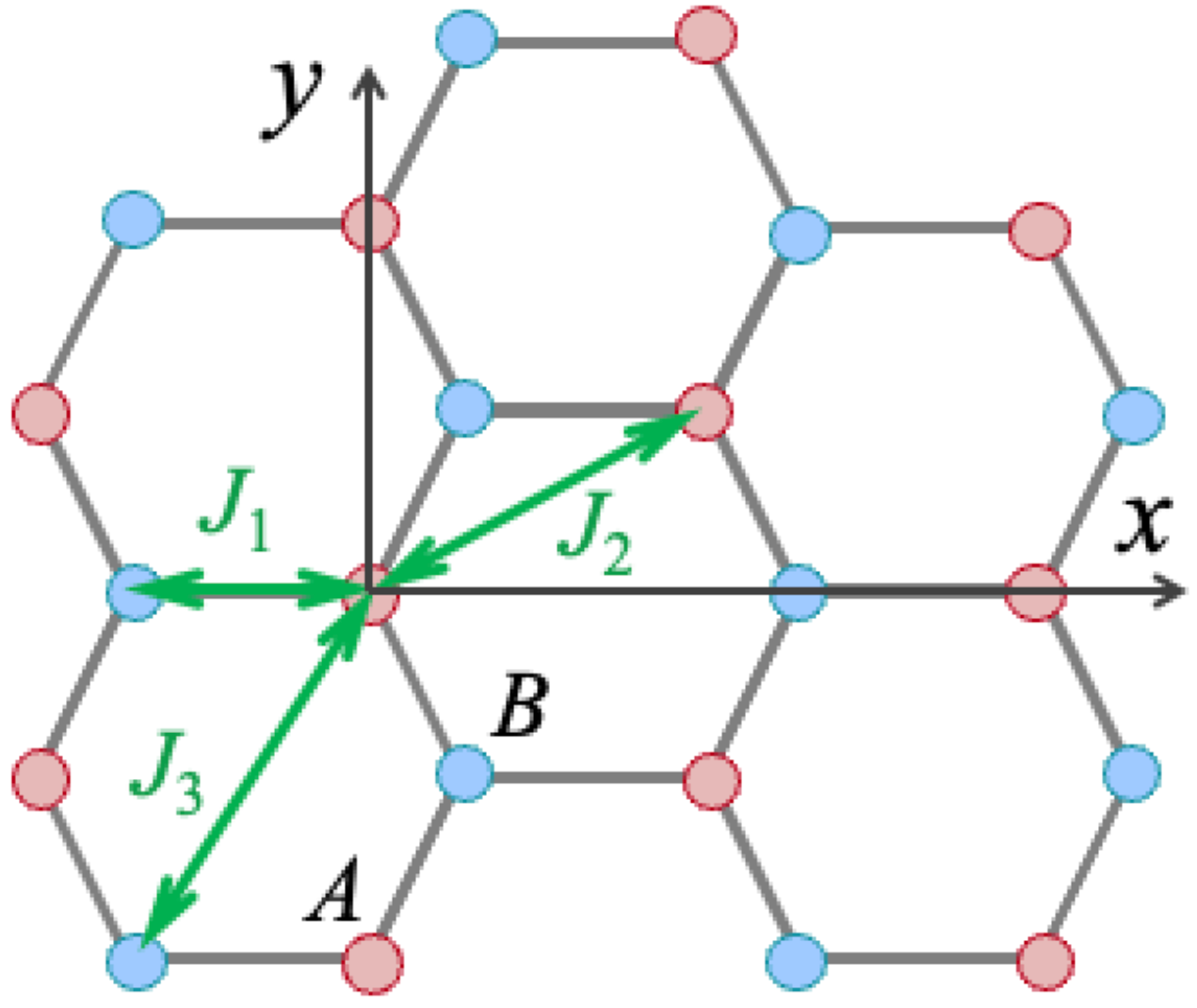
2.1. Background Theory
2.2. Spin Waves in Lowest Order
3. Results
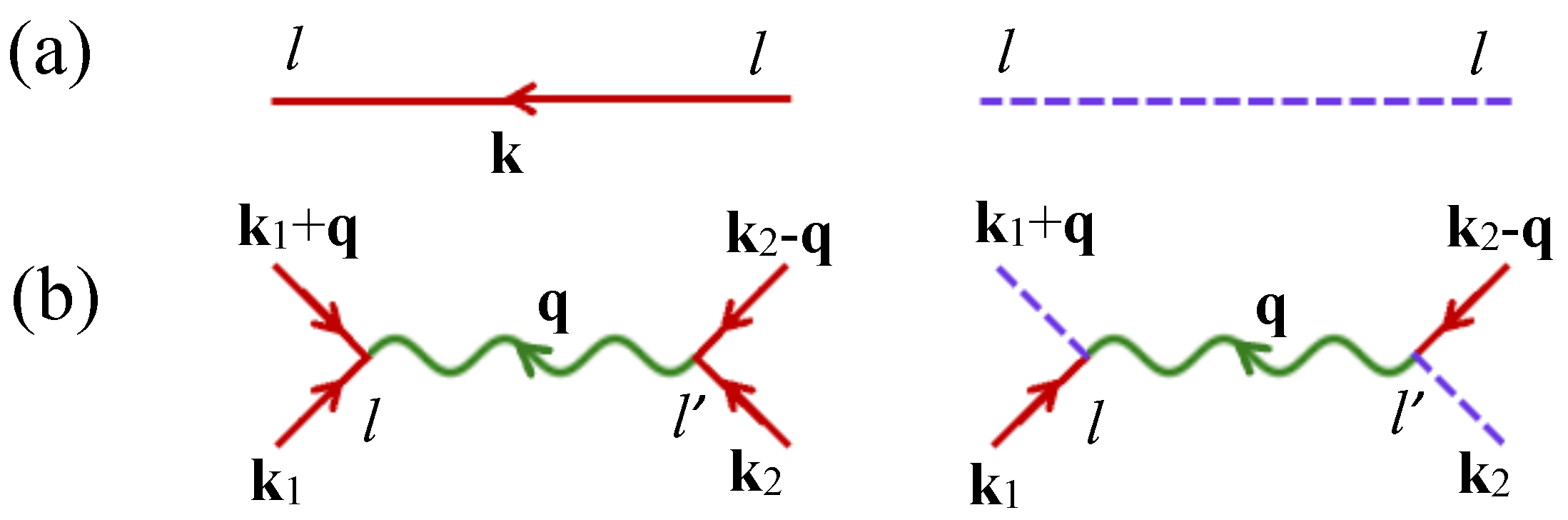
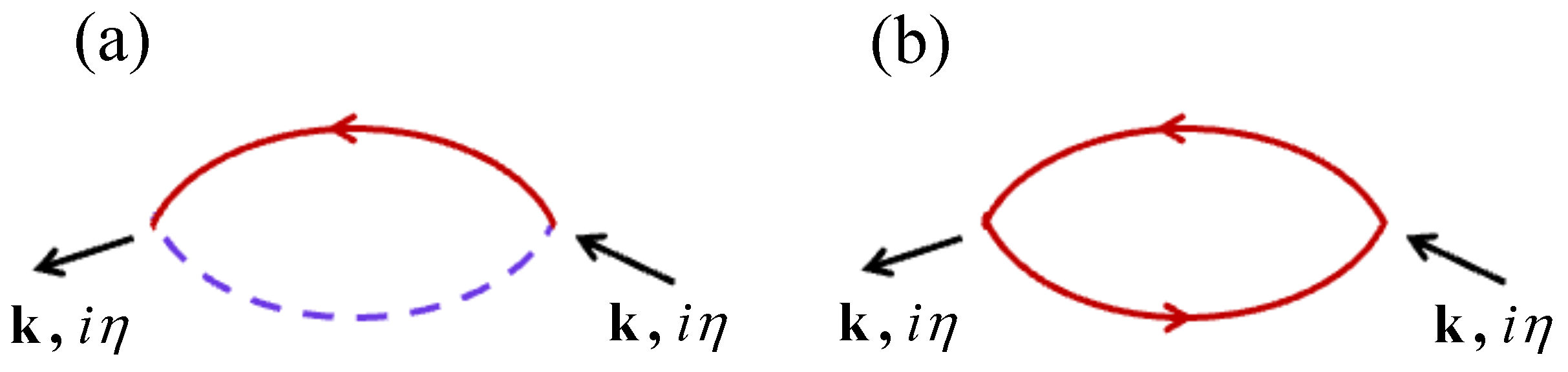
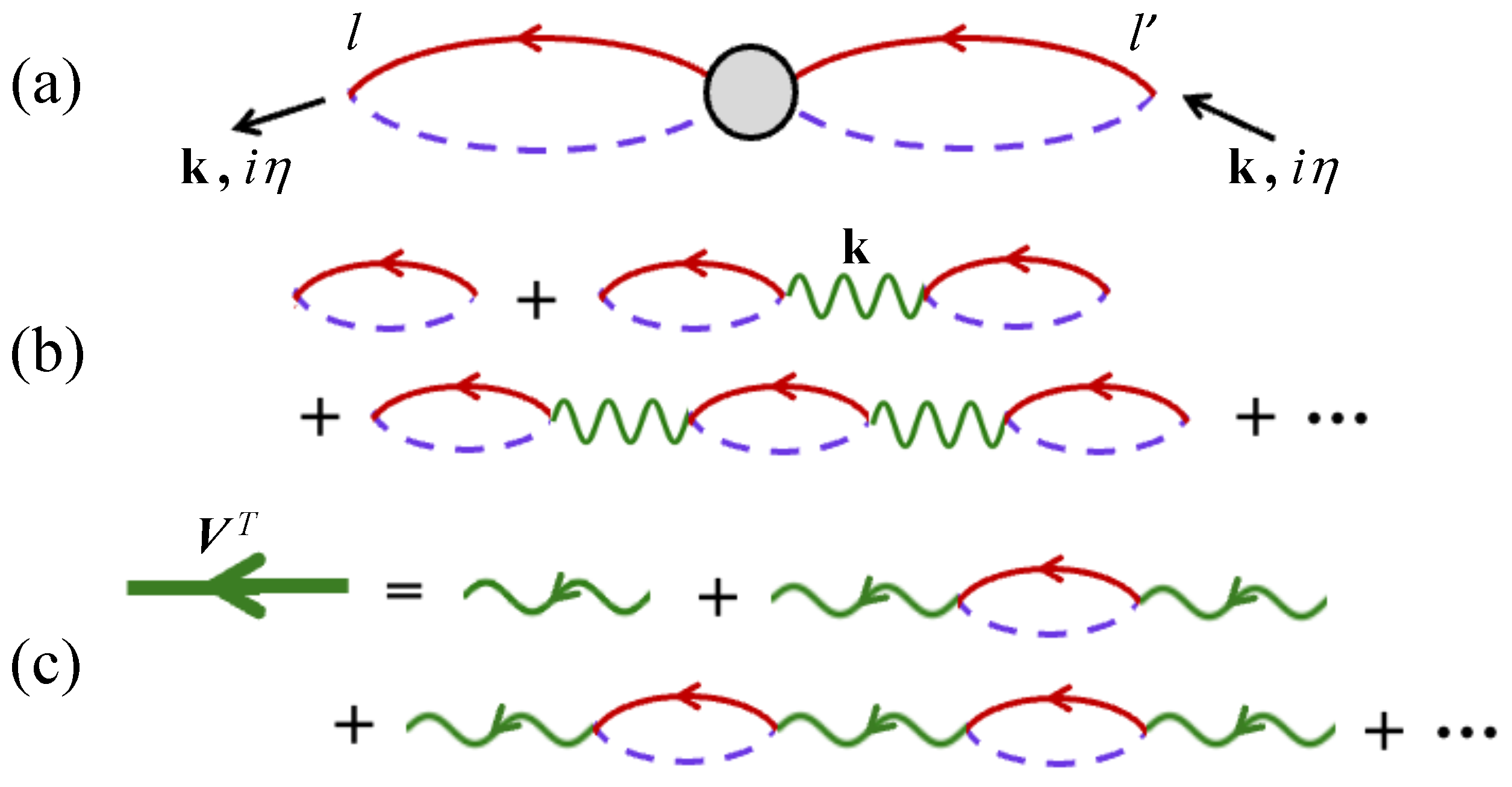
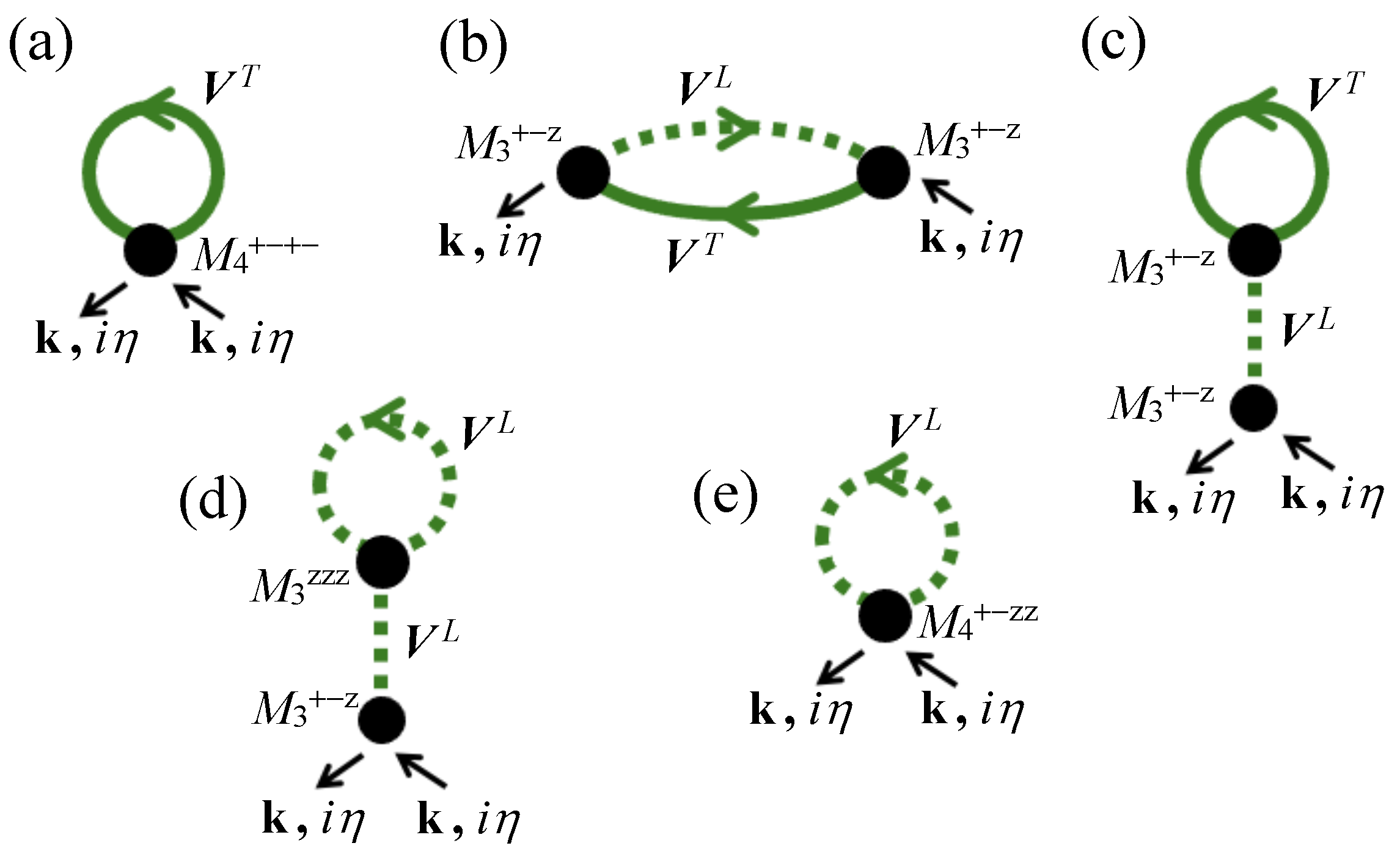
3.1. Inclusion of Spin Wave Interactions
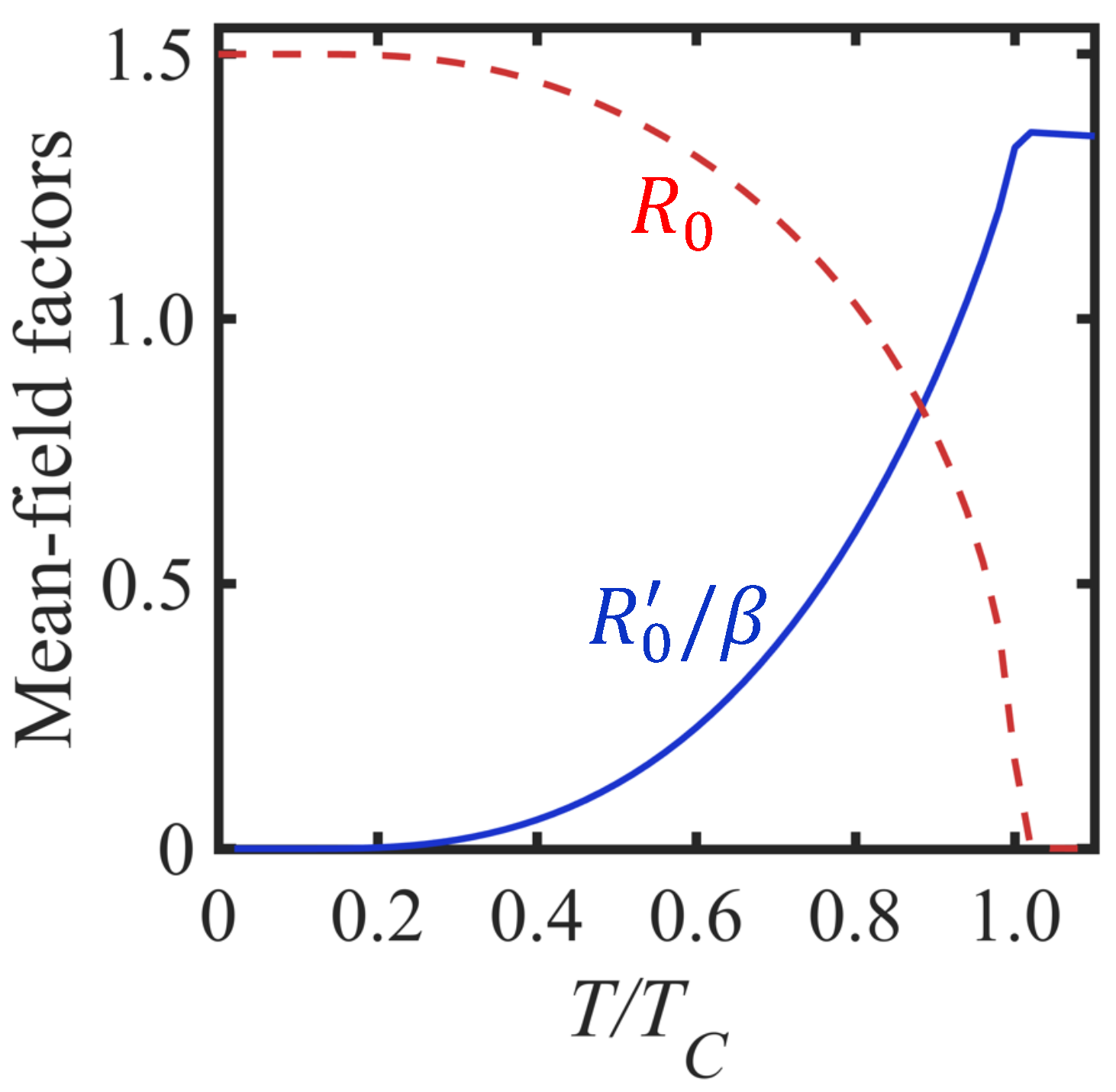
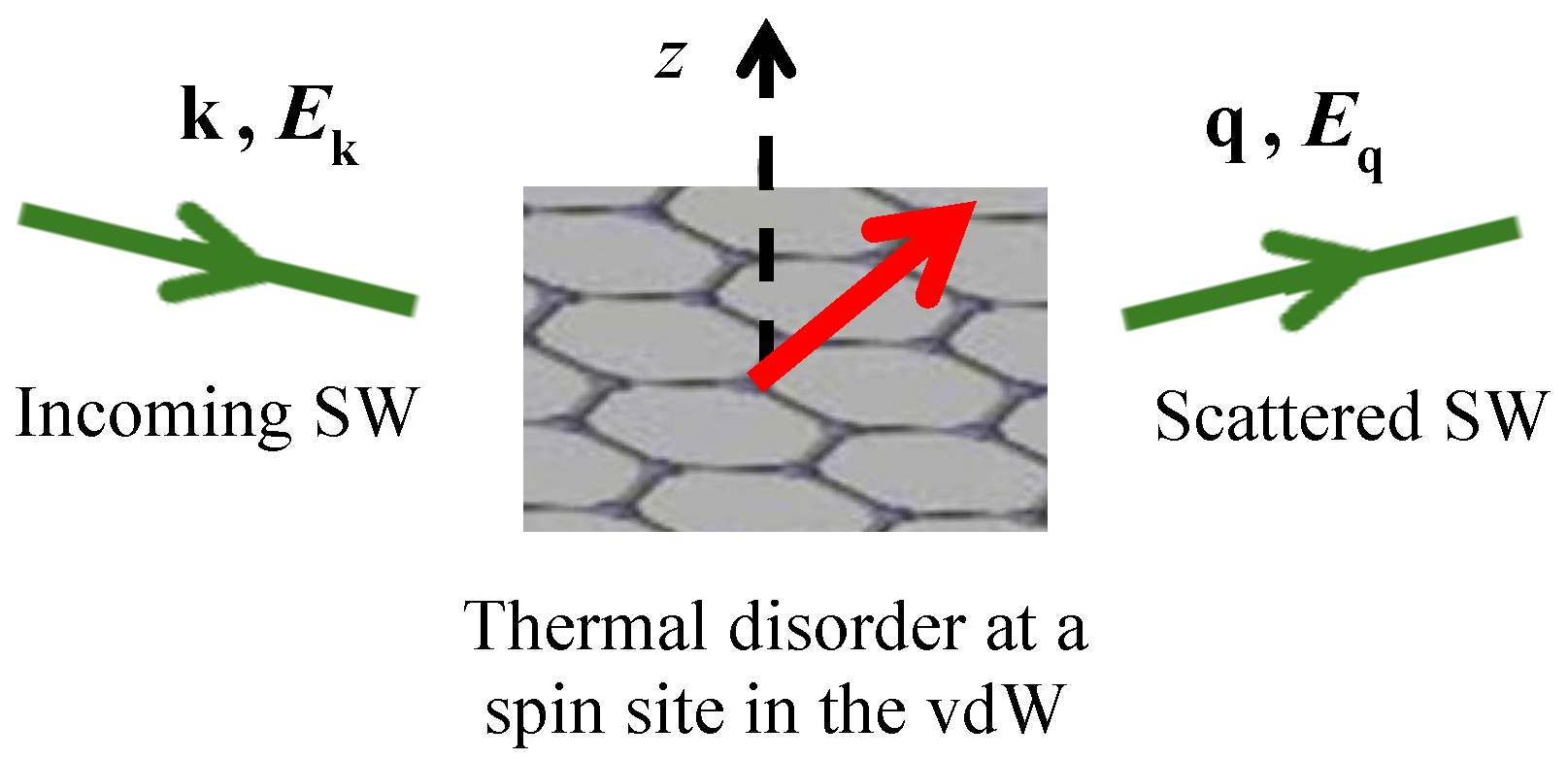
3.2. Spin Disorder Damping Results
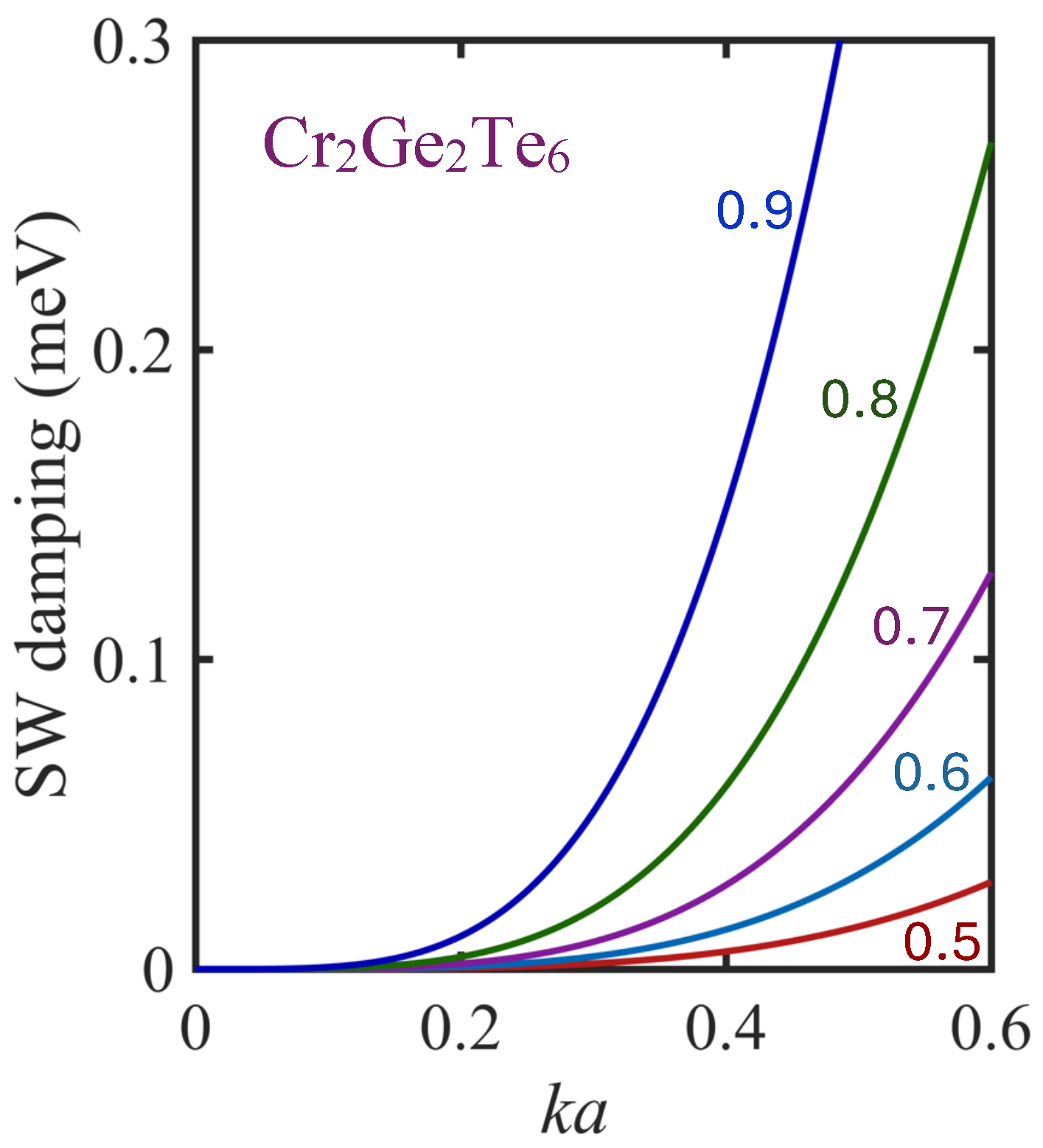
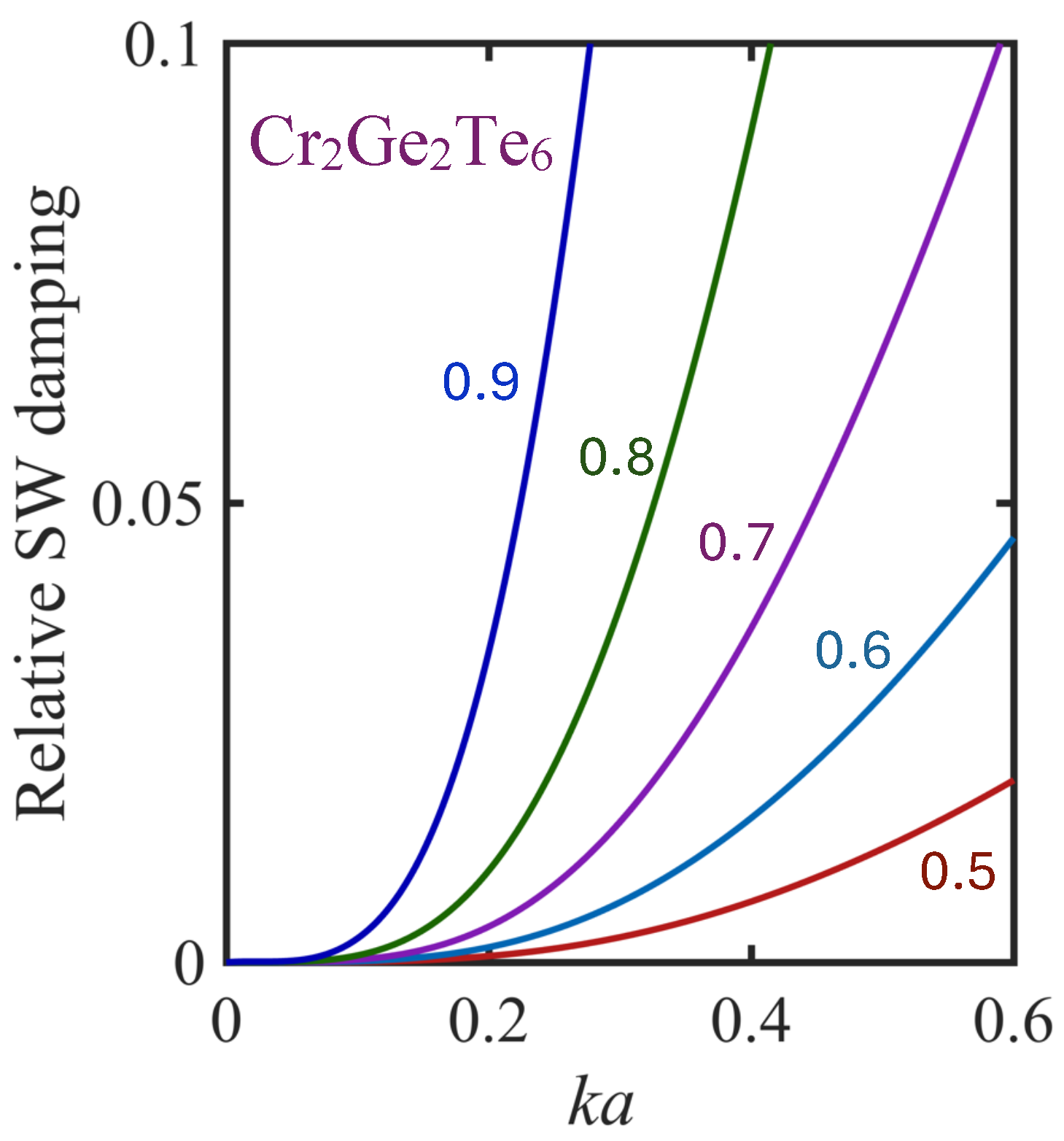
3.3. Results for Cr2Ge2Te6
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Keffer, F. Spin waves. Encycl. Phys. 1966, 18, 1. [Google Scholar]
- Akhiezer, A.I.; Bar’yakhtar, V.G.; Peletminskii, S.V. Spin Waves; North-Holland: Amsterdam, The Netherlands, 1968. [Google Scholar]
- Gurevich, A.G.; Melkov, G.A. Magnetization Oscillations and Waves; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Stancil, D.D.; Prabhakar, A. Spin Waves: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- White, R.M. Quantum Theory of Magnetism: Magnetic Properties of Materials, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Arias, R.; Mills, D.L. Extrinsic contributions to the ferromagnetic resonance response of ultrathin films. Phys. Rev. B 1999, 60, 7395. [Google Scholar] [CrossRef]
- Hou, H.Y.; Yang, M.; Qiu, J.; Yang, I.S.; Chen, X.B. Anomalous behaviors of spin waves studied by inelastic light scattering. Crystals 2019, 9, 357. [Google Scholar] [CrossRef]
- Azevedo, A.; Oliveira, A.B.; de Aguiar, F.M.; Rezende, S.M. Extrinsic contributions to spin-wave damping and renormalization in thin Ni50Fe50 films. Phys. Rev. B 2000, 62, 5331. [Google Scholar] [CrossRef]
- Boone, C.T.; Katine, J.A.; Childress, J.R.; Tiberkevich, V.; Slavin, A.; Zhu, J.; Cheng, X.; Krivorotov, I.N. Resonant nonlinear damping of quantized spin waves in ferromagnetic nanowires: A spin torque ferromagnetic resonance study. Phys. Rev. Lett. 2009, 103, 167601. [Google Scholar] [CrossRef] [PubMed]
- Lenk, B.; Ulrichs, H.; Garbs, F.; Munzerberg, M. The building blocks of magnonics. Phys. Rep. 2011, 507, 107. [Google Scholar] [CrossRef]
- Barman, A.; Sinha, J. Spin Dynamics and Damping in Ferromagnetic Thin Films and Nanostructures; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Gubbiotti, G. (Ed.) Three-Dimensional Magnonics; Jenny Stanford Publishing: Singapore, 2019. [Google Scholar]
- Tang, C.; Alahmed, L.; Mahdi, M.; Xiong, Y.; Inman, J.; McLaughlin, N.J.; Zollitsch, C.; Kim, T.H.; Du, C.R.; Kurebayashi, H.; et al. Spin dynamics in van der Waals magnetic systems. Phys. Rep. 2023, 1032, 1–36. [Google Scholar] [CrossRef]
- Holstein, T.; Primakoff, H. Field dependence of the intrinsic domain magnetization of a ferromagnet. Phys. Rev. 1940, 58, 1098. [Google Scholar] [CrossRef]
- Dyson, F.J. Thermodynamic behavior of an ideal ferromagnet. Phys. Rev. 1956, 102, 1230. [Google Scholar] [CrossRef]
- Maleev, S.V. Scattering of slow neutrons in ferromagnets. Sov. Phys. JETP 1958, 64, 654. [Google Scholar]
- Kittel, C. Quantum Theory of Solids; Wiley: Hoboken, NJ, USA, 1987. [Google Scholar]
- Rezende, S.M. Fundamentals of Magnonics; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Mattis, D.C. The Theory of Magnetism; Harper and Row: New York, NY, USA, 1965. [Google Scholar]
- Psaltakis, G.C.; Cottam, M.G. The generalised drone-fermion method and the semi-invariant approach for spin systems. J. Phys. A: Math. Gen. 1981, 14, 2149. [Google Scholar] [CrossRef]
- Spencer, H.J. Quantum-field-theory approach to the Heisenberg ferromagnet. Phys. Rev. 1968, 167, 434. [Google Scholar] [CrossRef]
- Reinecke, T.L.; Stinchcombe, R.B. The anisotropic Heisenberg ferromagnet with arbitrary field direction. I. Thermodynamics. J. Phys. C Solid State Phys. 1974, 7, 527. [Google Scholar] [CrossRef]
- Reinecke, T.L.; Stinchcombe, R.B. The anisotropic Heisenberg ferromagnet with arbitrary field direction. II. Correlation functions. J. Phys. C Solid State Phys. 1974, 7, 548. [Google Scholar] [CrossRef]
- Psaltakis, G.C.; Cottam, M.G. Theory of spin-wave interactions in S = 1 two-sublattice uniaxial magnets. J. Phys. C Solid State Phys. 1982, 15, 4847. [Google Scholar] [CrossRef]
- Cottam, M.G.; Stinchcombe, R.B. Thermodynamic properties of a Heisenberg antiferromagnet. J. Phys. C Solid State Phys. 1970, 3, 2283. [Google Scholar] [CrossRef]
- Stinchcombe, R.B. Thermal and magnetic properties of the transverse Ising model. J. Phys. C Solid State Phys. 1973, 6, 2459. [Google Scholar] [CrossRef]
- Cottam, M.G. Theory of dipole-dipole interactions in ferromagnets. I. The thermodynamic properties. J. Phys. C Solid State Phys. 1971, 4, 2658. [Google Scholar] [CrossRef]
- Vaks, V.G.; Larkin, A.I.; Pikin, S.A. Thermodynamics of an ideal ferromagnetic substance. Sov. Phys.-JETP 1968, 26, 188. [Google Scholar]
- Vaks, V.G.; Larkin, A.I.; Pikin, S.A. Spin waves and correlation functions in a ferromagnetic. Sov. Phys.-JETP 1968, 26, 647. [Google Scholar]
- Pikalev, E.M.; Savchenko, M.A.; Solyom, J. Thermodynamics and Correlation Functions of a Heisenberg Antiferromagnet. Sov. Phys.-JETP 1969, 28, 734. [Google Scholar]
- Solyom, J. Spin waves and thermodynamic properties of unaxial antiferromagnets. Sov. Phys.-JETP 1969, 28, 1251. [Google Scholar]
- Izyumov, Y.A.; Kassan-Ogly, F.A. A diagram technique for spin operators Heisenberg Hamiltonian. Phys. Met. Metallogr. 1970, 30, 1. [Google Scholar]
- Kashchenko, M.P.; Balakhonov, N.F.; Kurbatov, L.V. Spin waves in an Heisenberg ferromagnetic substance with single-ion anisotropy. Sov. Phys.-JETP 1973, 37, 201. [Google Scholar]
- Tarasenko, V.V.; Kharitonov, R.E. Spin-spin relaxation of surface waves in a Heisenberg ferromagnet. Sov. Phys.-Solid State 1974, 16, 1031. [Google Scholar]
- Burch, K.S.; Mandrus, D.; Park, J.G. Magnetism in two-dimensional van der Waals materials. Nature 2018, 563, 47. [Google Scholar] [CrossRef]
- Gibertini, M.; Koperski, M.; Morpurgo, A.F.; Novoselov, K.S. Magnetic 2D materials and heterostructures. Nat. Nanotech. 2019, 14, 408. [Google Scholar] [CrossRef]
- Gong, C.; Zhang, X. Two-dimensional magnetic crystals and emergent heterostructure devices. Science 2019, 363, 706. [Google Scholar] [CrossRef]
- Wang, M.C.; Huang, C.C.; Cheung, C.H.; Chen, C.Y.; Tan, S.G.; Huang, T.W.; Zhao, Y.; Wu, G.; Feng, Y.P.; Wu, H.C.; et al. Prospects and opportunities of 2D van der Waals magnetic systems. Ann. Phys. 2020, 532, 1900452. [Google Scholar] [CrossRef]
- Kim, K.; Lee, J.U.; Cheong, H. Raman spectroscopy of two-dimensional magnetic van der Waals materials. Nanotechnology 2019, 30, 452001. [Google Scholar] [CrossRef]
- Khan, Y.; Obaidulla, S.M.; Habib, M.R.; Gayen, A.; Liang, T.; Wang, X.; Xu, M. Recent breakthroughs in two-dimensional van der Waals magnetic materials and emerging applications. Nano Today 2020, 34, 100902. [Google Scholar] [CrossRef]
- Zhang, X.X.; Li, L.; Weber, D.; Goldberger, J.; Mak, K.F.; Shan, J. Gate-tunable spin waves in antiferromagnetic atomic bilayers. Nat. Mater. 2020, 19, 838. [Google Scholar] [CrossRef]
- Blei, M.; Lado, J.L.; Song, Q.; Dey, D.; Erten, O.; Pardo, V.; Comin, R.; Tongay, S.; Botana, A.S. Synthesis, engineering, and theory of 2D van der Waals magnets. Appl. Phys. Revs. 2021, 8, 021301. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197. [Google Scholar] [CrossRef]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109. [Google Scholar] [CrossRef]
- Mermin, N.D.; Wagner, H. Absence of ferromagnetism or antiferromagnetism in one- or two-dimensional Isotropic Heisenberg models. Phys. Rev. Lett. 1966, 17, 1133. [Google Scholar] [CrossRef]
- Jin, W.; Kim, H.H.; Ye, Z.; Li, S.; Rezaie, P.; Diaz, F.; Siddiq, S.; Wauer, E.; Yang, B.; Li, C.; et al. Raman fingerprint of two terahertz spin wave branches in a two-dimensional honeycomb Ising ferromagnet. Nat. Commun. 2018, 9, 5122. [Google Scholar] [CrossRef] [PubMed]
- Kapoor, L.N.; Mandal, S.; Adak, P.C.; Patankar, M.; Manni, S.; Thamizhavel, A.; Deshmukh, M.M. Observation of standing spin waves in a van der Waals magnetic material. Adv. Mater. 2021, 33, 2005105. [Google Scholar] [CrossRef]
- Sun, Y.; Xiao, R.C.; Lin, G.T.; Zhang, R.R.; Ling, L.S.; Ma, Z.W.; Luo, X.; Lu, W.J.; Sun, Y.P.; Sheng, Z.G. Effects of hydrostatic pressure on spin-lattice coupling in two-dimensional ferromagnetic Cr2Ge2Te6. Appl. Phys. Lett. 2018, 112, 072409. [Google Scholar] [CrossRef]
- Ge, W.; Xu, K.; Xia, W.; Yu, Z.; Wang, H.; Liu, X.; Zhao, J.; Wange, X.; Yu, N.; Zoue, Z.; et al. Raman spectroscopy and lattice dynamical stability study of 2D ferromagnetic semiconductor Cr2Ge2Te6 under high pressure. J. Alloy. Compd. 2020, 819, 153368. [Google Scholar] [CrossRef]
- O’Neill, A.; Rahman, S.; Zhang, Z.; Schoenherr, P.; Yildirim, T.; Gu, B.; Su, G.; Lu, Y.; Seidel, J. Enhanced room temperature ferromagnetism in highly strained 2D semiconductor Cr2Ge2Te6. ACS Nano 2022, 17, 735. [Google Scholar] [CrossRef] [PubMed]
- Mkhitaryan, V.V.; Ke, L. Self-consistently renormalized spin-wave theory of layered ferromagnets on the honeycomb lattice. Phys. Rev. B 2021, 104, 064435. [Google Scholar] [CrossRef]
- Costa Filho, R.N.; Cottam, M.G.; Farias, G.A. Microscopic theory of dipole-exchange spin waves in ferromagnetic films: Linear and nonlinear processes. Phys. Rev. B 2000, 62, 6545. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Akbari-Sharbaf, A.; Cottam, M.G. Spin-wave damping in ferromagnetic stripes with inhomogeneous magnetization. Phys. Rev. B 2011, 83, 214423. [Google Scholar] [CrossRef]
- Demokritov, S.O.; Slavin, A.N. Magnonics: From Fundamentals to Applications; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- McMichael, R.D.; Stiles, M.D.; Chen, P.J.; Egelhoff, W.F.J. Ferromagnetic resonance linewidth in thin films coupled to NiO. J. Appl. Phys. 1998, 83, 7037. [Google Scholar] [CrossRef]
- McMichael, R.D.; Twisselmann, D.J.; Kunz, A. Localized ferromagnetic resonance in inhomogeneous thin films. Phys. Rev. Lett. 2003, 90, 227601. [Google Scholar] [CrossRef]
- Reinecke, T.L.; Stinchcombe, R.B. Spin-wave damping in ferromagnets in the ordered regime. Phys. Rev. B 1978, 17, 1297. [Google Scholar] [CrossRef]
- Lockwood, D.J.; Cottam, M.G.; So, V.C.Y.; Katiyar, R.S. Raman scattering from one-magnon excitations in FeF2. J. Phys. C Solid State Phys. 1984, 17, 6009. [Google Scholar] [CrossRef]
- Abrikosov, A.A.; Gor’kov, L.P.; Dzyaloshinskii, I.Y. Quantum Field Theoretical Methods in Statistical Physics, 2nd ed.; Pergamon: Oxford, UK, 1965. [Google Scholar]
- Mahan, G.D. Many-Particle Physics; Kluwer Academic: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Economou, E.N. Green’s Functions in Quantum Physics, 3rd ed.; Springer: Berlin/Springer, Germany, 2006. [Google Scholar]
- Nolting, W. Fundamentals of Many-Body Physics: Principles and Methods; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Coleman, P. Introduction to Many-Body Physics; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Cottam, M.G.; Haghshenasfard, Z. Many-Body Theory of Condensed Matter Systems: An Introductory Course; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Coey, J.M.D. Magnetism and Magnetic Materials; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics; Saunders College: Philadelphia, PA, USA, 1976. [Google Scholar]
- Hussain, B.; Cottam, M.G. Dipole-exchange spin waves in two-dimensional van der Waals ferromagnetic films and stripes. J. Phys. C Condens. Matter 2022, 34, 445801. [Google Scholar] [CrossRef]
- Moriya, T. Theory of light scattering by magnetic crystals. J. Phys. Soc. Jpn. 1967, 23, 490. [Google Scholar] [CrossRef]
- Loudon, R. Theory of the temperature dependence of first-order light scattering by ordered spin systems. J. Phys. C Solid State Phys. 1970, 3, 872. [Google Scholar] [CrossRef]
- de Jongh, L.J.; Miedema, A.R. Experiments on Simple Magnetic Model Systems; Taylor and Francis: London, UK, 1974. [Google Scholar]
- Cottam, M.G.; Haghshenasfard, Z. Damping of dipole-exchange spin waves in ferromagnetic thin films at elevated temperatures. J. Phys. Condens. Matter 2021, 33, 235802. [Google Scholar] [CrossRef]
- Stinchcombe, R.B.; Horwitz, G.; Englert, F.; Brout, R. Thermodynamic behavior of the Heisenberg ferromagnet. Phys. Rev. 1963, 130, 155. [Google Scholar] [CrossRef]
- Power, S.R.; Ferreira, M.S. Indirect exchange and Ruderman-Kittel-Kasuya-Yosida (RKKY) interactions in magnetically-doped graphene. Crystals 2013, 3, 49. [Google Scholar] [CrossRef]
- MATLAB, version: 9.13.0 (R2022b); The MathWorks Inc.: Natick, MA, USA, 2022.
- Yang, S.; Chen, Y.; Jiang, C. Strain engineering of two-dimensional materials: Methods, properties, and applications. Info. Mat. 2021, 3, 397. [Google Scholar] [CrossRef]
- Wang, N.; Tang, H.; Shi, M.; Zhang, H.; Zhuo, W.; Liu, D.; Meng, F.; Ma, L.; Ying, J.; Zou, L.; et al. Transition from ferromagnetic semiconductor to ferromagnetic metal with enhanced Curie temperature in Cr2Ge2Te6 via organic ion intercalation. J. Am. Chem. Soc. 2019, 141, 17166. [Google Scholar] [CrossRef]
- Harris, A.B.; Kumar, D.; Halperin, B.I.; Hohenberg, P.C. Dynamics of an antiferromagnet at low temperatures: Spin-wave damping and hydrodynamics. Phys. Rev. B 1971, 3, 961. [Google Scholar] [CrossRef]
- Schultheiss, H.; Vogt, K.; Hillebrands, B. Direct observation of nonlinear four-magnon scattering in spin-wave microconduits. Phys. Rev. B 2012, 86, 054414. [Google Scholar] [CrossRef]
- Li, Y.H.; Cheng, R. Moiré magnons in twisted bilayer magnets with collinear order. Phys. Rev. B 2020, 094404, 102. [Google Scholar] [CrossRef]
- Olsen, T. Magnetic anisotropy and exchange interactions of two-dimensional FePS3, NiPS3 and MnPS3 from first principles calculations. J. Phys. D: Appl. Phys. 2021, 54, 314001. [Google Scholar] [CrossRef]
- Liang, Y.; Yun, G.; Yang, H.; Bai, N.; Cao, Y. Dirac points and flat bands in two-dimensional magnonic crystals with honeycomb–kagome structure. AIP Adv. 2024, 14, 035242. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cottam, M.G.; Hussain, B. Non-Bosonic Damping of Spin Waves in van der Waals Ferromagnetic Monolayers. Nanomaterials 2025, 15, 768. https://doi.org/10.3390/nano15100768
Cottam MG, Hussain B. Non-Bosonic Damping of Spin Waves in van der Waals Ferromagnetic Monolayers. Nanomaterials. 2025; 15(10):768. https://doi.org/10.3390/nano15100768
Chicago/Turabian StyleCottam, Michael G., and Bushra Hussain. 2025. "Non-Bosonic Damping of Spin Waves in van der Waals Ferromagnetic Monolayers" Nanomaterials 15, no. 10: 768. https://doi.org/10.3390/nano15100768
APA StyleCottam, M. G., & Hussain, B. (2025). Non-Bosonic Damping of Spin Waves in van der Waals Ferromagnetic Monolayers. Nanomaterials, 15(10), 768. https://doi.org/10.3390/nano15100768







