Accurate Deep Potential Model of Temperature-Dependent Elastic Constants for Phosphorus-Doped Silicon
Abstract
1. Introduction
2. Materials and Methods
2.1. Generation of DP Model
2.2. DFT and MD Simulation Settings
2.3. Elastic Constants Calculation
3. Results and Discussion
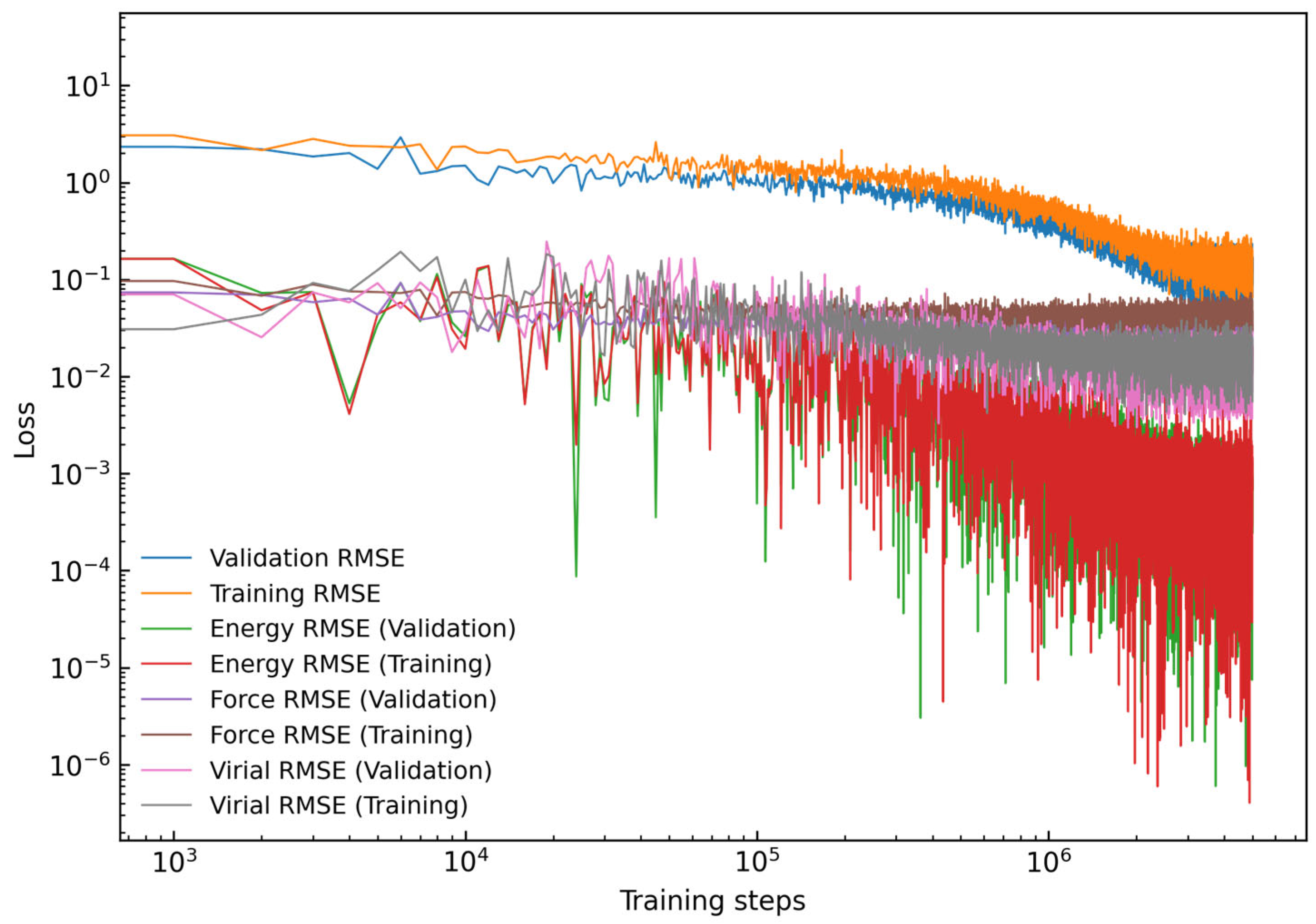
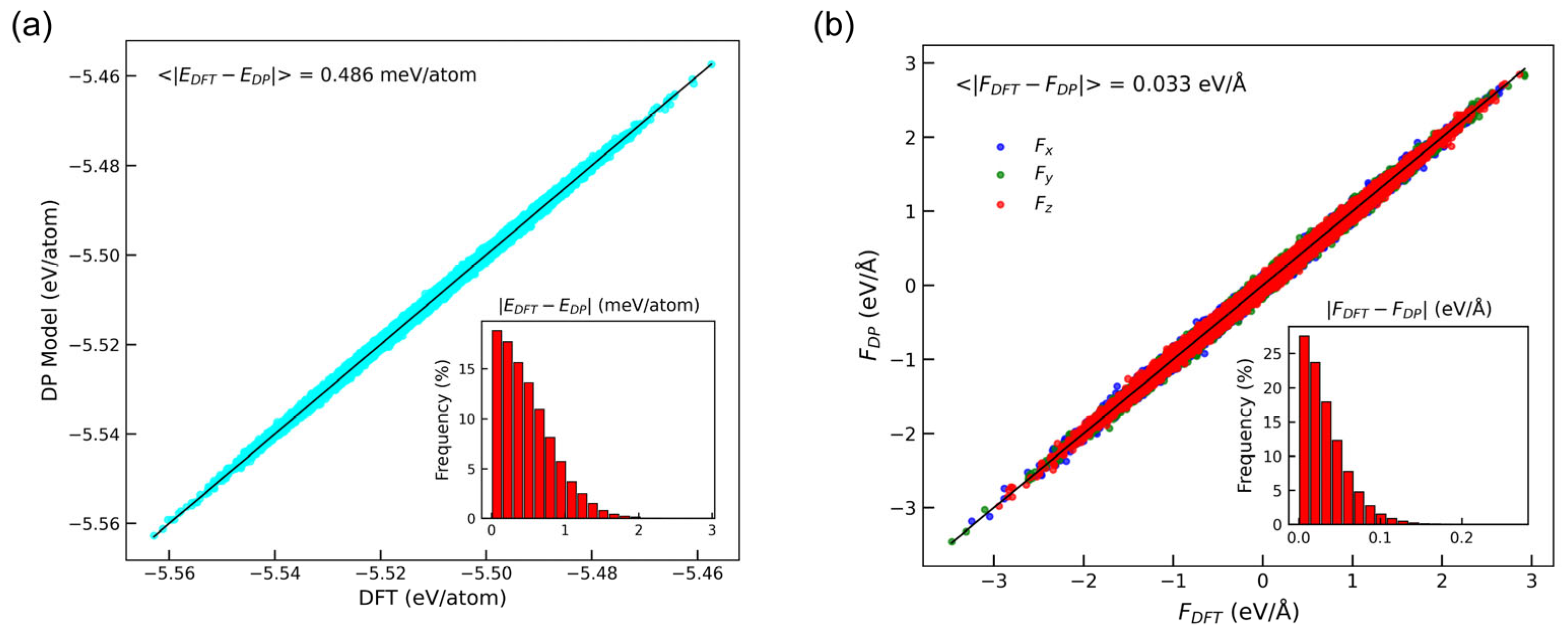
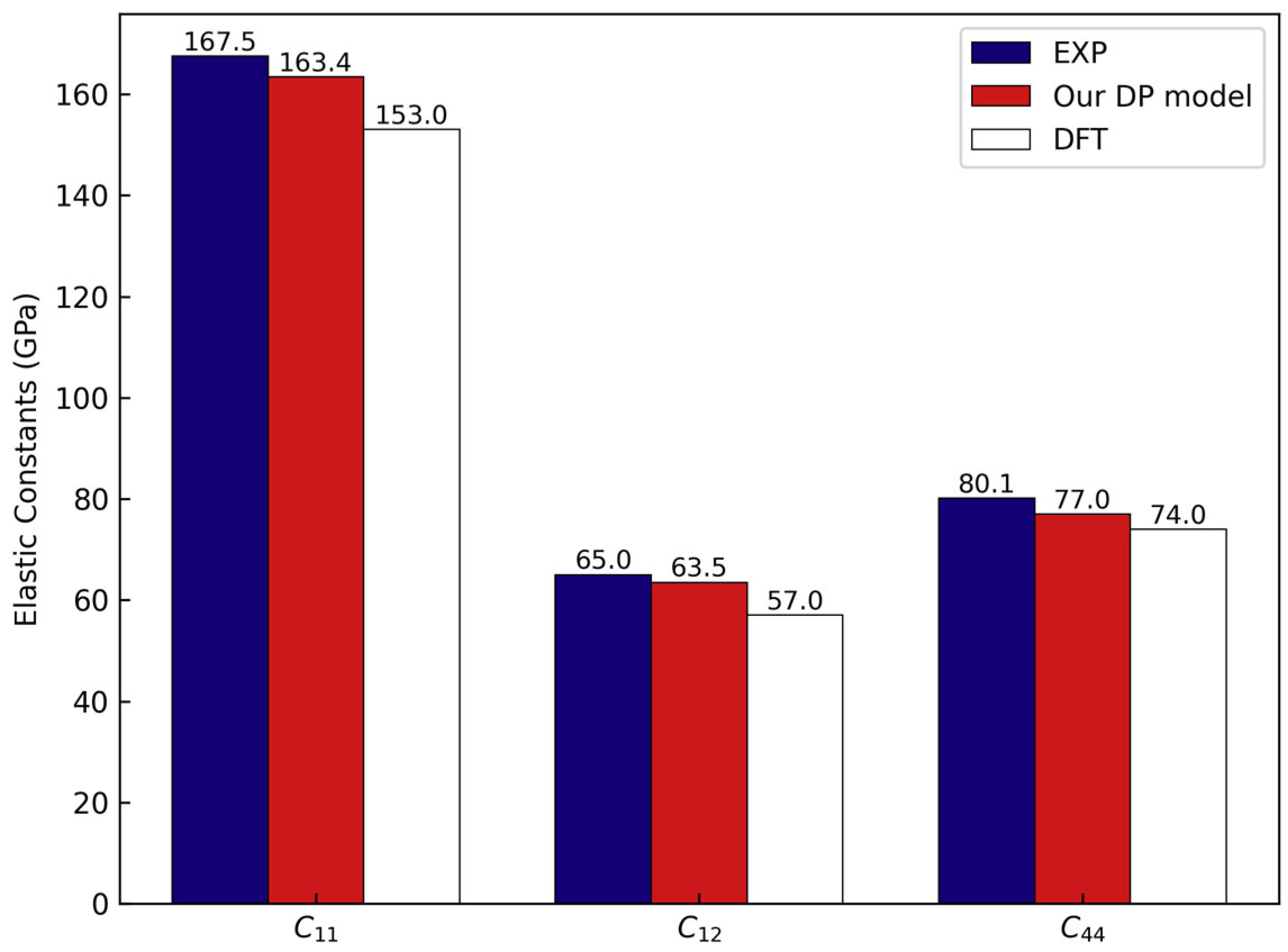
3.1. Accuracy of DP Model
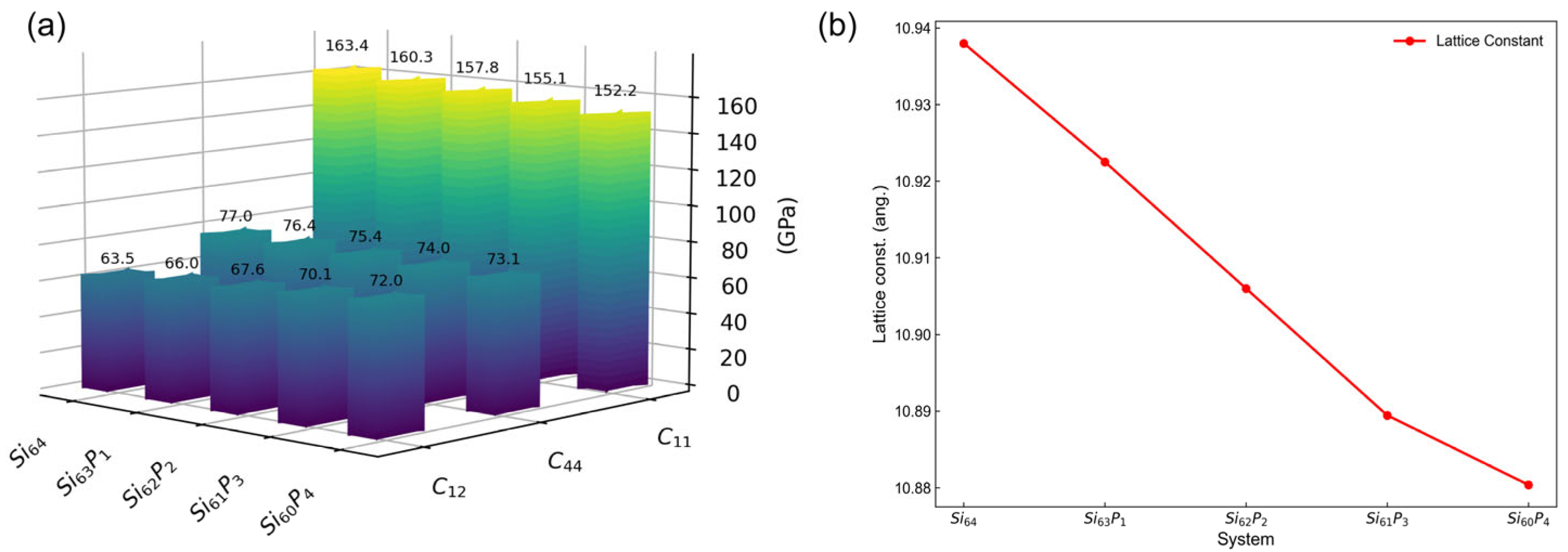
3.2. Dopant Concentration Dependence of Elastic Constants
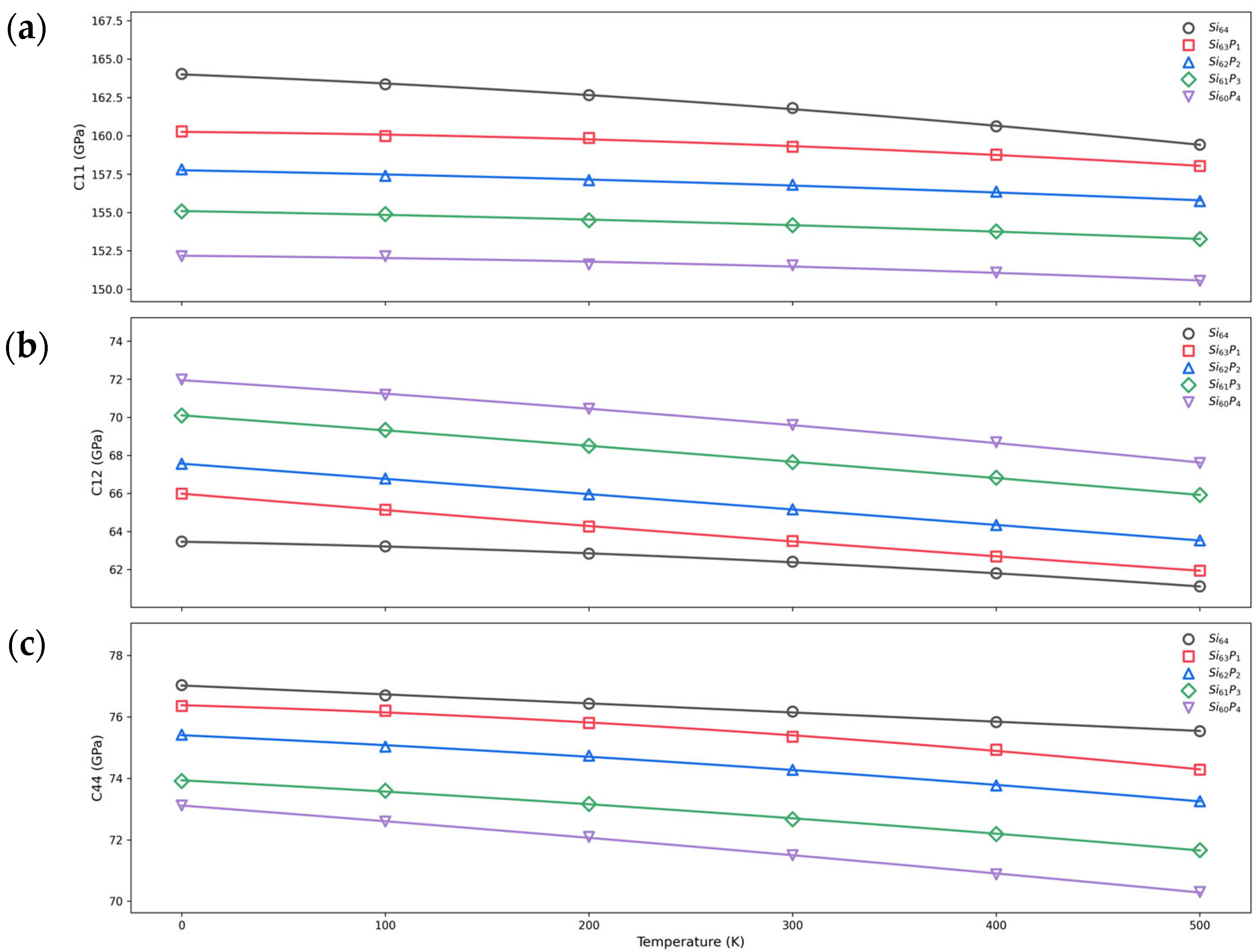
3.3. Temperature Dependence of Elastic Constants
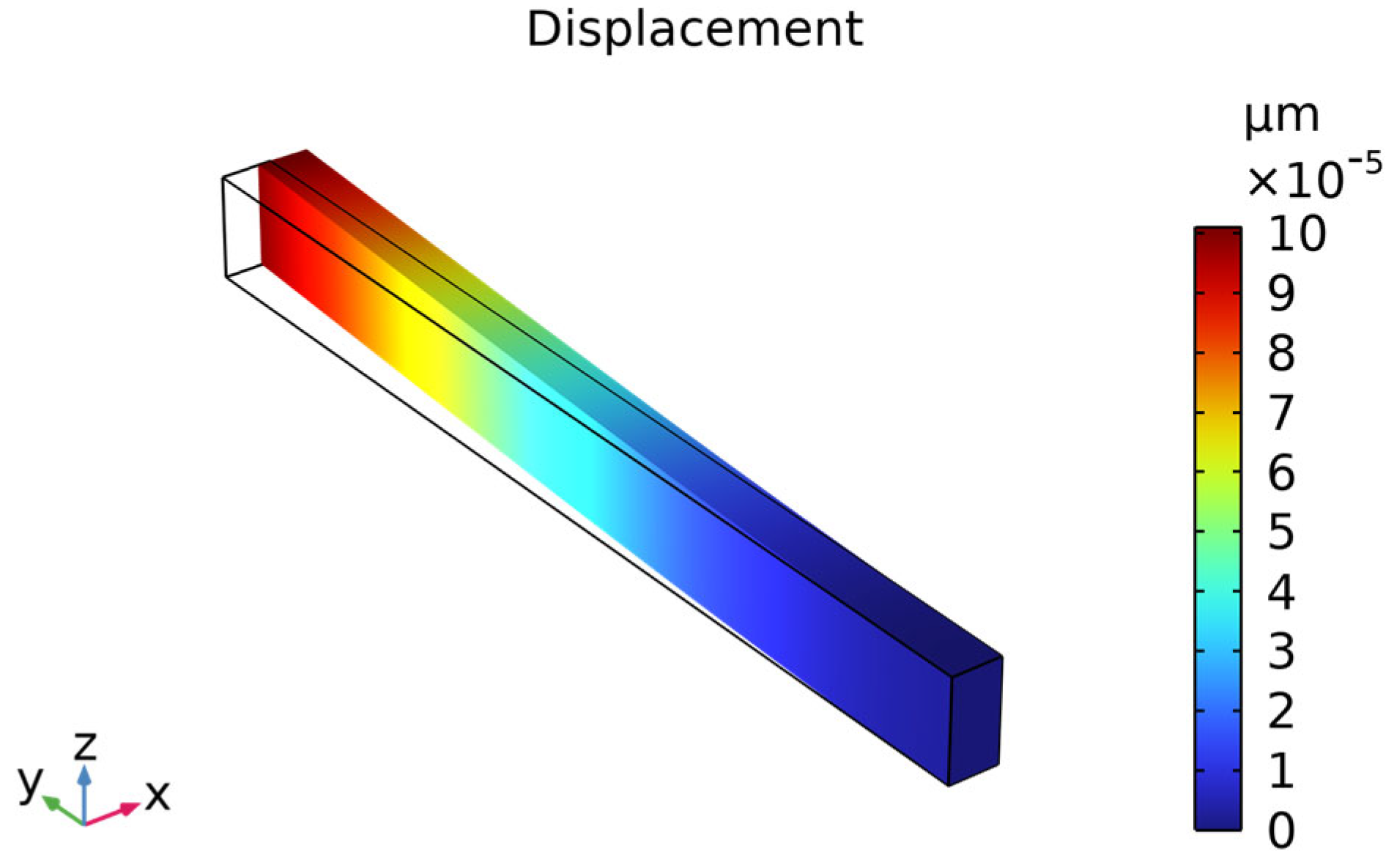
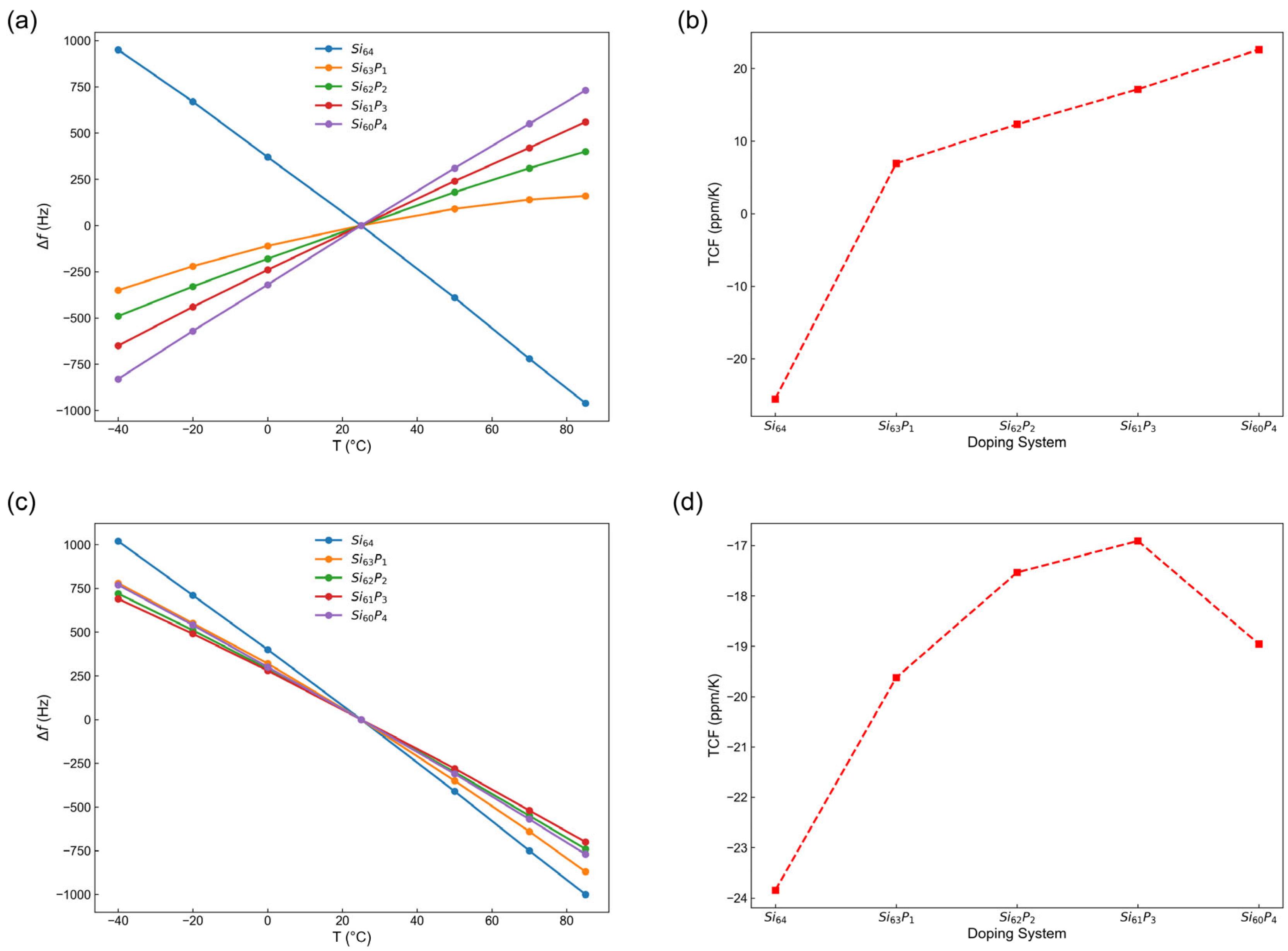
3.4. Temperature Stability of MEMS Resonators
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rajai, P.; Ahmed, H.; Straeten, M.; Xereas, G.; Ahamed, M.J. Analytical modeling of n-type doped silicon elastic constants and frequency-compensation of Lamé mode microresonators. Sens. Actuators A Phys. 2019, 297, 111508. [Google Scholar] [CrossRef]
- Jaakkola, A.; Prunnila, M.; Pensala, T.; Dekker, J.; Pekko, P. Determination of doping and temperature-dependent elastic constants of degenerately doped silicon from MEMS resonators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2014, 61, 1063–1074. [Google Scholar] [CrossRef]
- Wu, G.; Xu, J.; Ng, E.J.; Chen, W. MEMS Resonators for Frequency Reference and Timing Applications. J. Microelectromechanical Syst. 2020, 29, 1137–1166. [Google Scholar] [CrossRef]
- Ng, E.J.; Hong, V.A.; Yang, Y.; Ahn, C.H.; Everhart, C.L.M.; Kenny, T.W. Temperature Dependence of the Elastic Constants of Doped Silicon. J. Microelectromechanical Syst. 2014, 24, 730–741. [Google Scholar] [CrossRef]
- Ono, N.; Kitamura, K.; Nakajima, K.; Shimanuki, Y. Measurement of Young′s Modulus of Silicon Single Crystal at High Temperature and Its Dependency on Boron Concentration Using the Flexural Vibration Method. Jpn. J. Appl. Phys. 2000, 39, 368. [Google Scholar] [CrossRef]
- Jaakkola, A.; Prunnila, M.; Pensala, T. Temperature compensated resonance modes of degenerately n-doped silicon MEMS resonators. In Proceedings of the 2012 IEEE International Frequency Control Symposium (FCS), Baltimore, MA, USA, 20–24 May 2012; pp. 1–5. [Google Scholar]
- Hajjam, A.; Rahafrooz, A.; Pourkamali, S. Sub-100 ppb/°C temperature stability in thermally actuated high frequency silicon resonators via degenerate phosphorous doping and bias current optimization. In Proceedings of the 2010 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 6–8 December 2010; pp. 7.5.1–7.5.4. [Google Scholar]
- Csavinszky, P.; Einspruch, N.G. Effect of Doping on the Elastic Constants of Silicon. Phys. Rev. B 1963, 132, 2434–2440. [Google Scholar] [CrossRef]
- Hall, J.J. Electronic effects in the elastic constants of n-type silicon. Phys. Rev. B 1967, 161, 756. [Google Scholar] [CrossRef]
- Samarao, A.K.; Ayazi, F. Temperature compensation of silicon resonators via degenerate doping. IEEE Trans. Electron Devices 2011, 59, 87–93. [Google Scholar] [CrossRef]
- Keyes, R.W. Electronic effects in the elastic properties of semiconductors. In Solid State Physics; Elsevier: Amsterdam, The Netherlands, 1968; Volume 20, pp. 37–90. [Google Scholar]
- Khan, F.S.; Allen, P.B. Temperature Dependence of the Elastic Constants of p+ Silicon. Phys. Status Solidi (B) 1985, 128, 31–38. [Google Scholar] [CrossRef]
- Wang, F.; Wu, H.-H.; Dong, L.; Pan, G.; Zhou, X.; Wang, S.; Guo, R.; Wu, G.; Gao, J.; Dai, F.-Z.; et al. Atomic-scale simulations in multi-component alloys and compounds: A review on advances in interatomic potential. J. Mater. Sci. Technol. 2023, 165, 49–65. [Google Scholar] [CrossRef]
- Li, R.; Lee, E.; Luo, T. A unified deep neural network potential capable of predicting thermal conductivity of silicon in different phases. Mater. Today Phys. 2020, 12, 100181. [Google Scholar] [CrossRef]
- Morawietz, T.; Artrith, N. Machine learning-accelerated quantum mechanics-based atomistic simulations for industrial applications. J. Comput. Aided Mol. Des. 2021, 35, 557–586. [Google Scholar] [CrossRef] [PubMed]
- Mortazavi, B.; Zhuang, X.; Rabczuk, T.; Shapeev, A.V. Atomistic modeling of the mechanical properties: The rise of machine learning interatomic potentials. Mater. Horiz. 2023, 10, 1956–1968. [Google Scholar] [CrossRef]
- Deringer, V.L.; Caro, M.A.; Csányi, G. Machine Learning Interatomic Potentials as Emerging Tools for Materials Science. Adv. Mater. 2019, 31, e1902765. [Google Scholar] [CrossRef]
- Wu, S.; Yang, X.; Zhao, X.; Li, Z.; Lu, M.; Xie, X.; Yan, J. Applications and Advances in Machine Learning Force Fields. J. Chem. Inf. Model. 2023, 63, 6972–6985. [Google Scholar] [CrossRef]
- Tersoff, J. New empirical approach for the structure and energy of covalent systems. Phys. Rev. B 1988, 37, 6991–7000. [Google Scholar] [CrossRef] [PubMed]
- Tersoff, J. Empirical interatomic potential for silicon with improved elastic properties. Phys. Rev. B 1988, 38, 9902–9905. [Google Scholar] [CrossRef]
- Tersoff, J. Modeling solid-state chemistry: Interatomic potentials for multicomponent systems. Phys. Rev. B 1989, 39, 5566–5568. [Google Scholar] [CrossRef]
- Stillinger, F.H.; Weber, T.A. Computer simulation of local order in condensed phases of silicon. Phys. Rev. B 1985, 31, 5262. [Google Scholar] [CrossRef]
- Mishin, Y. Machine-learning interatomic potentials for materials science. Acta Mater. 2021, 214, 116980. [Google Scholar] [CrossRef]
- Mo, P.; Li, C.; Zhao, D.; Zhang, Y.; Shi, M.; Li, J.; Liu, J. Accurate and efficient molecular dynamics based on machine learning and non von Neumann architecture. npj Comput. Mater. 2022, 8, 107. [Google Scholar] [CrossRef]
- Mortazavi, B. Recent Advances in Machine Learning-Assisted Multiscale Design of Energy Materials. Adv. Energy Mater. 2024, 15, 2403876. [Google Scholar] [CrossRef]
- Marx, D.; Hutter, J. Ab Initio Molecular Dynamics: Basic Theory and Advanced Methods; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Yu, H.; Giantomassi, M.; Materzanini, G.; Wang, J.; Rignanese, G. Systematic assessment of various universal machine-learning interatomic potentials. Mater. Genome Eng. Adv. 2024, 2, e58. [Google Scholar] [CrossRef]
- He, X.; Liu, J.; Yang, C.; Jiang, G. Predicting thermodynamic stability of magnesium alloys in machine learning. Comput. Mater. Sci. 2023, 223, 112111. [Google Scholar] [CrossRef]
- Zuo, Y.; Chen, C.; Li, X.-G.; Deng, Z.; Chen, Y.; Behler, J.; Csányi, G.; Shapeev, A.V.; Thompson, A.P.; Wood, M.A.; et al. Performance and Cost Assessment of Machine Learning Interatomic Potentials. J. Phys. Chem. A 2020, 124, 731–745. [Google Scholar] [CrossRef]
- Ko, T.W.; Ong, S.P. Recent advances and outstanding challenges for machine learning interatomic potentials. Nat. Comput. Sci. 2023, 3, 998–1000. [Google Scholar] [CrossRef]
- Behler, J.; Parrinello, M. Generalized neural-network representation of high-dimensional potential-energy surfaces. Phys. Rev. Lett. 2007, 98, 146401. [Google Scholar] [CrossRef] [PubMed]
- Takamoto, S.; Okanohara, D.; Li, Q.-J.; Li, J. Towards universal neural network interatomic potential. J. Mater. 2023, 9, 447–454. [Google Scholar] [CrossRef]
- Bartók, A.P.; Payne, M.C.; Kondor, R.; Csányi, G. Gaussian Approximation Potentials: The Accuracy of Quantum Mechanics, without the Electrons. Phys. Rev. Lett. 2010, 104, 136403. [Google Scholar] [CrossRef]
- Thompson, A.; Swiler, L.; Trott, C.; Foiles, S.; Tucker, G. Spectral neighbor analysis method for automated generation of quantum-accurate interatomic potentials. J. Comput. Phys. 2015, 285, 316–330. [Google Scholar] [CrossRef]
- Drautz, R. Atomic cluster expansion for accurate and transferable interatomic potentials. Phys. Rev. B 2019, 99, 014104. [Google Scholar] [CrossRef]
- Shapeev, A.V. Moment Tensor Potentials: A Class of Systematically Improvable Interatomic Potentials. Multiscale Model. Simul. 2016, 14, 1153–1173. [Google Scholar] [CrossRef]
- Jacobs, R.; Morgan, D.; Attarian, S.; Meng, J.; Shen, C.; Wu, Z.; Xie, C.Y.; Yang, J.H.; Artrith, N.; Blaiszik, B.; et al. A practical guide to machine learning interatomic potentials—Status and future. Curr. Opin. Solid State Mater. Sci. 2025, 35, 101214. [Google Scholar] [CrossRef]
- Zhao, Y.; Fan, J.; Su, L.; Song, T.; Wang, S.; Qiao, C. SNAP: A communication efficient distributed machine learning framework for edge computing. In Proceedings of the 2020 IEEE 40th International Conference on Distributed Computing Systems (ICDCS), Singapore, 29 November–1 December 2020; pp. 584–594. [Google Scholar]
- Bochkarev, A.; Lysogorskiy, Y.; Drautz, R. Graph Atomic Cluster Expansion for Semilocal Interactions beyond Equivariant Message Passing. Phys. Rev. X 2024, 14, 021036. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, L.; Han, J.; E, W. DeePMD-kit: A deep learning package for many-body potential energy representation and molecular dynamics. Comput. Phys. Commun. 2018, 228, 178–184. [Google Scholar] [CrossRef]
- Çanlı, M.; Ilhan, E.; Arıkan, N. First-principles calculations to investigate the structural, electronic, elastic, vibrational and thermodynamic properties of the full-Heusler alloys X2ScGa (X = Ir and Rh). Mater. Today Commun. 2021, 26, 101855. [Google Scholar] [CrossRef]
- Zhang, L.; Han, J.; Wang, H.; Car, R.; E, W. Deep Potential Molecular Dynamics: A Scalable Model with the Accuracy of Quantum Mechanics. Phys. Rev. Lett. 2018, 120, 143001. [Google Scholar] [CrossRef]
- Zhao, J.; Feng, T.; Lu, G.; Yu, J. Insights into the local structure evolution and thermophysical properties of NaCl–KCl–MgCl2–LaCl3 melt driven by machine learning. J. Mater. Chem. A 2023, 11, 23999–24012. [Google Scholar] [CrossRef]
- Zhang, W.; Zhou, L.; Yang, B.; Yan, T. Molecular dynamics simulations of LiCl ion pairs in high temperature aqueous solutions by deep learning potential. J. Mol. Liq. 2022, 367, 120500. [Google Scholar] [CrossRef]
- An, Y.; Hu, T.; Pang, Q.; Xu, S. Observing Li Nucleation at the Li Metal–Solid Electrolyte Interface in All-Solid-State Batteries. ACS Nano 2025, 19, 14262–14271. [Google Scholar] [CrossRef]
- Wen, T.; Zhang, L.; Wang, H.; E, W.; Srolovitz, D.J. Deep potentials for materials science. Mater. Futures 2022, 1, 022601. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, H.; Chen, W.; Zeng, J.; Zhang, L.; Wang, H.; E, W. DP-GEN: A concurrent learning platform for the generation of reliable deep learning based potential energy models. Comput. Phys. Commun. 2020, 253, 107206. [Google Scholar] [CrossRef]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; In′t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS-a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Zeng, J.; Zhang, D.; Lu, D.; Mo, P.; Li, Z.; Chen, Y.; Rynik, M.; Huang, L.; Li, Z.; Shi, S.; et al. DeePMD-kit v2: A software package for deep potential models. J. Chem. Phys. 2023, 159, 054801. [Google Scholar] [CrossRef]
- He, R.; Wu, H.; Zhang, L.; Wang, X.; Fu, F.; Liu, S.; Zhong, Z. Structural phase transitions in SrTi O3 from deep potential molecular dynamics. Phys. Rev. B 2022, 105, 064104. [Google Scholar] [CrossRef]
- Shi, Y.; He, R.; Zhang, B.; Zhong, Z. Revisiting the phase diagram and piezoelectricity of lead zirconate titanate from first principles. Phys. Rev. B 2024, 109, 174104. [Google Scholar] [CrossRef]
- Pang, Y.; Lian, X. Transfer Learning in Interatomic Potential: A Deep Potential Generator (DP-GEN) Framework; Brown University: Providence, RI, USA, 2024. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Togo, A. First-principles phonon calculations with phonopy and phono3py. J. Phys. Soc. Jpn. 2023, 92, 012001. [Google Scholar] [CrossRef]
- Squire, D.; Holt, A.; Hoover, W. Isothermal elastic constants for argon. theory and Monte Carlo calculations. Physica 1969, 42, 388–397. [Google Scholar] [CrossRef]
- Lutsko, J.F. Generalized expressions for the calculation of elastic constants by computer simulation. J. Appl. Phys. 1989, 65, 2991–2997. [Google Scholar] [CrossRef]
- Van Workum, K.; Yoshimoto, K.; de Pablo, J.J.; Douglas, J.F. Isothermal stress and elasticity tensors for ions and point dipoles using Ewald summations. Phys. Rev. E 2005, 71, 061102. [Google Scholar] [CrossRef]
- Van Workum, K.; Gao, G.; Schall, J.D.; Harrison, J.A. Expressions for the stress and elasticity tensors for angle-dependent potentials. J. Chem. Phys. 2006, 125, 144506. [Google Scholar] [CrossRef] [PubMed]
- Krief, M.; Ashkenazy, Y. Calculation of elastic constants of embedded-atom-model potentials in the NVT ensemble. Phys. Rev. E 2021, 103, 063307. [Google Scholar] [CrossRef]
- Clavier, G.; Desbiens, N.; Bourasseau, E.; Lachet, V.; Brusselle-Dupend, N.; Rousseau, B. Computation of elastic constants of solids using molecular simulation: Comparison of constant volume and constant pressure ensemble methods. Mol. Simul. 2017, 43, 1413–1422. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, H.; Guo, L.; Yan, Z.; Zheng, J.; Zhou, W.; Xue, J. Deep learning inter-atomic potential for irradiation damage in 3C-SiC. Comput. Mater. Sci. 2023, 233, 112693. [Google Scholar] [CrossRef]
- Liu, Y.; He, X.; Mo, Y. Discrepancies and error evaluation metrics for machine learning interatomic potentials. npj Comput. Mater. 2023, 9, 174. [Google Scholar] [CrossRef]
- McSkimin, H.J. Measurement of elastic constants at low temperatures by means of ultrasonic waves-data for silicon and germanium single crystals, and for fused silica. J. Appl. Phys. 1953, 24, 988–997. [Google Scholar] [CrossRef]
- Råsander, M.; Moram, M.A. On the accuracy of commonly used density functional approximations in determining the elastic constants of insulators and semiconductors. J. Chem. Phys. 2015, 143, 144104. [Google Scholar] [CrossRef] [PubMed]
- Kamiyama, E.; Sueoka, K. Method for estimating elastic modulus of doped semiconductors by using ab initio calculations—Doping effect on Young’s modulus of silicon crystal. AIP Adv. 2023, 13, 085224. [Google Scholar] [CrossRef]
- Khanolkar, A.; Wang, Y.; Dennett, C.A.; Hua, Z.; Mann, J.M.; Khafizov, M.; Hurley, D.H. Temperature-dependent elastic constants of thorium dioxide probed using time-domain Brillouin scattering. J. Appl. Phys. 2023, 133, 195101. [Google Scholar] [CrossRef]
- Yokoyama, T.; Chaveanghong, S. Anharmonicity in elastic constants and extended x-ray-absorption fine structure cumulants. Phys. Rev. Mater. 2019, 3, 033607. [Google Scholar] [CrossRef]
- Al-Nuaimi, N.A.M.; Thränhardt, A.; Gemming, S. Impact of B and P Doping on the Elastic Properties of Si Nanowires. Nanomaterials 2025, 15, 191. [Google Scholar] [CrossRef]



| Iter. | Length (ps) | T (K) | Ensemble |
|---|---|---|---|
| 0 | 1 | 0, 100, 200, 300, 400, 500 | NPT |
| 1 | 1 | 0, 100, 200, 300, 400, 500 | NPT |
| 2 | 3 | 0, 100, 200, 300, 400, 500 | NPT |
| 3 | 3 | 0, 100, 200, 300, 400, 500 | NPT |
| 4 | 5 | 0, 100, 200, 300, 400, 500 | NPT |
| 5 | 10 | 0, 100, 200, 300, 400, 500 | NPT |
| 6 | 10 | 0, 100, 200, 300, 400, 500 | NPT |
| 7 | 20 | 0, 100, 200, 300, 400, 500 | NPT |
| 8 | 20 | 0, 100, 200, 300, 400, 500 | NPT |
| 9 | 30 | 0, 100, 200, 300, 400, 500 | NPT |
| 10 | 30 | 0, 100, 200, 300, 400, 500 | NPT |
| 11 | 50 | 0, 100, 200, 300, 400, 500 | NPT |
| System | (GPa) | (ppm/K) | (ppb/K2) | (GPa) | (ppm/K) | (ppb/K2) | (GPa) | (ppm/K) | (ppb/K2) |
|---|---|---|---|---|---|---|---|---|---|
| Si64 | 161.8 | −61.5 | −50.1 | 62.4 | −83.8 | −88.2 | 76.2 | −39.1 | −2.1 |
| Si63P1 | 159.3 | −31.8 | −41.6 | 63.5 | −125.5 | 21.5 | 75.4 | −61.2 | −60.2 |
| Si62P2 | 156.8 | −26.8 | −18.7 | 65.2 | −124.2 | −3.8 | 74.3 | −61.4 | −35.6 |
| Si61P3 | 154.2 | −25.4 | −18.6 | 67.7 | −125.2 | −17.6 | 72.7 | −65.8 | −30.8 |
| Si60P4 | 151.5 | −24.0 | −28.5 | 69.6 | −129.5 | −54.8 | 71.5 | −81.0 | −19.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, M.; Bie, X.; Wang, Y.; Li, Y.; Zhai, Z.; Lyu, H.; Zou, X. Accurate Deep Potential Model of Temperature-Dependent Elastic Constants for Phosphorus-Doped Silicon. Nanomaterials 2025, 15, 769. https://doi.org/10.3390/nano15100769
Gao M, Bie X, Wang Y, Li Y, Zhai Z, Lyu H, Zou X. Accurate Deep Potential Model of Temperature-Dependent Elastic Constants for Phosphorus-Doped Silicon. Nanomaterials. 2025; 15(10):769. https://doi.org/10.3390/nano15100769
Chicago/Turabian StyleGao, Miao, Xiaorui Bie, Yi Wang, Yuhang Li, Zhaoyang Zhai, Haoqi Lyu, and Xudong Zou. 2025. "Accurate Deep Potential Model of Temperature-Dependent Elastic Constants for Phosphorus-Doped Silicon" Nanomaterials 15, no. 10: 769. https://doi.org/10.3390/nano15100769
APA StyleGao, M., Bie, X., Wang, Y., Li, Y., Zhai, Z., Lyu, H., & Zou, X. (2025). Accurate Deep Potential Model of Temperature-Dependent Elastic Constants for Phosphorus-Doped Silicon. Nanomaterials, 15(10), 769. https://doi.org/10.3390/nano15100769







