Dynamical Characteristics of Isolated Donors, Acceptors, and Complex Defect Centers in Novel ZnO
Abstract
1. Introduction
2. Theoretical Background
2.1. Crystal Structure
Intrinsic Defects in ZnO
2.2. The Rigid-Ion Model
2.3. Green’s Function Approach
2.3.1. The Perfect Lattice Green’s Functions
2.3.2. The Imperfect Lattice Green’s Functions
2.3.3. Perturbation Matrices
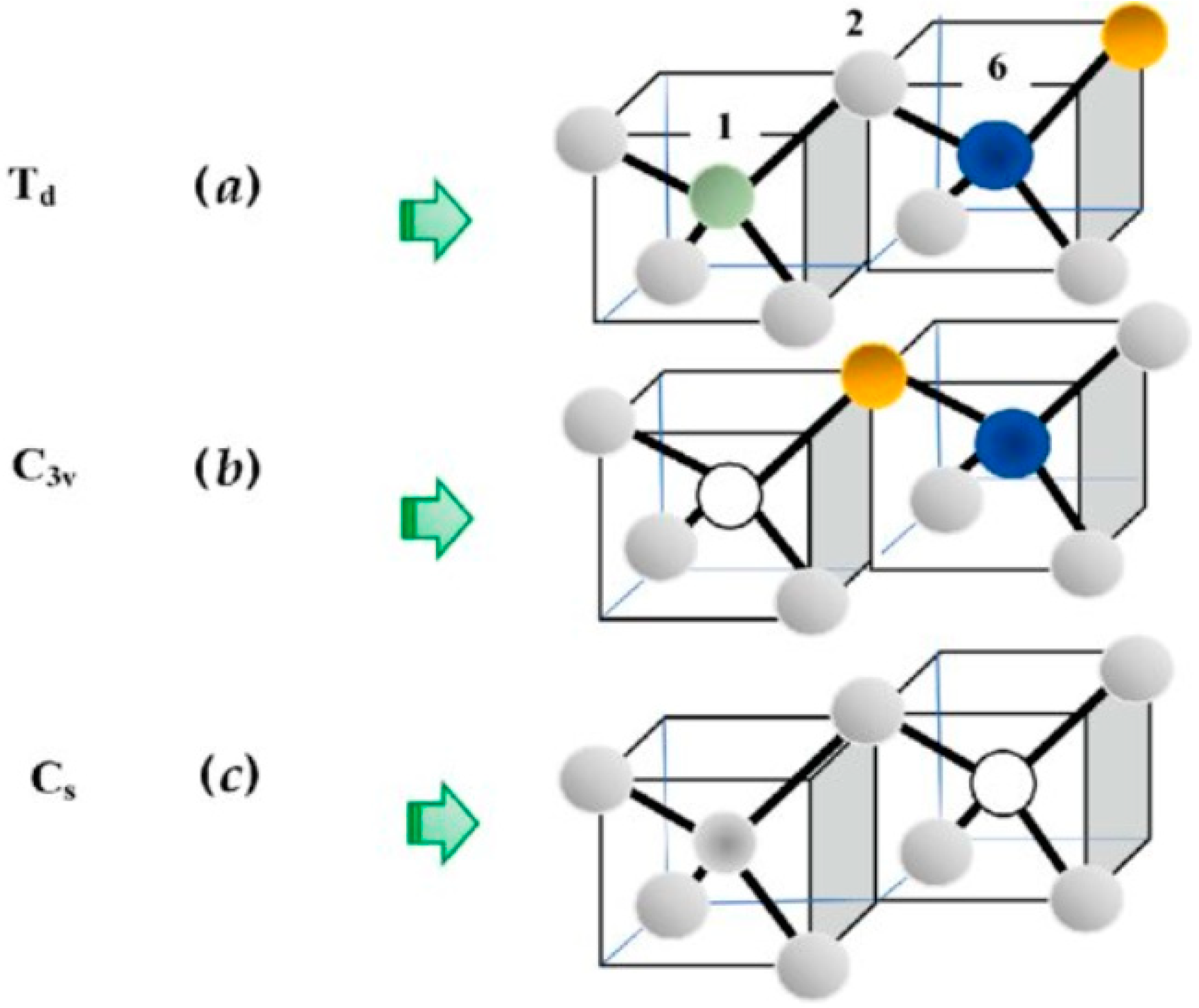
- (a)
- Isolated Defects: Symmetry
- (b)
- NN Pair Defects: Symmetry
- (c)
- Complex Defects: or Symmetry
3. Numerical Computation Results and Discussion
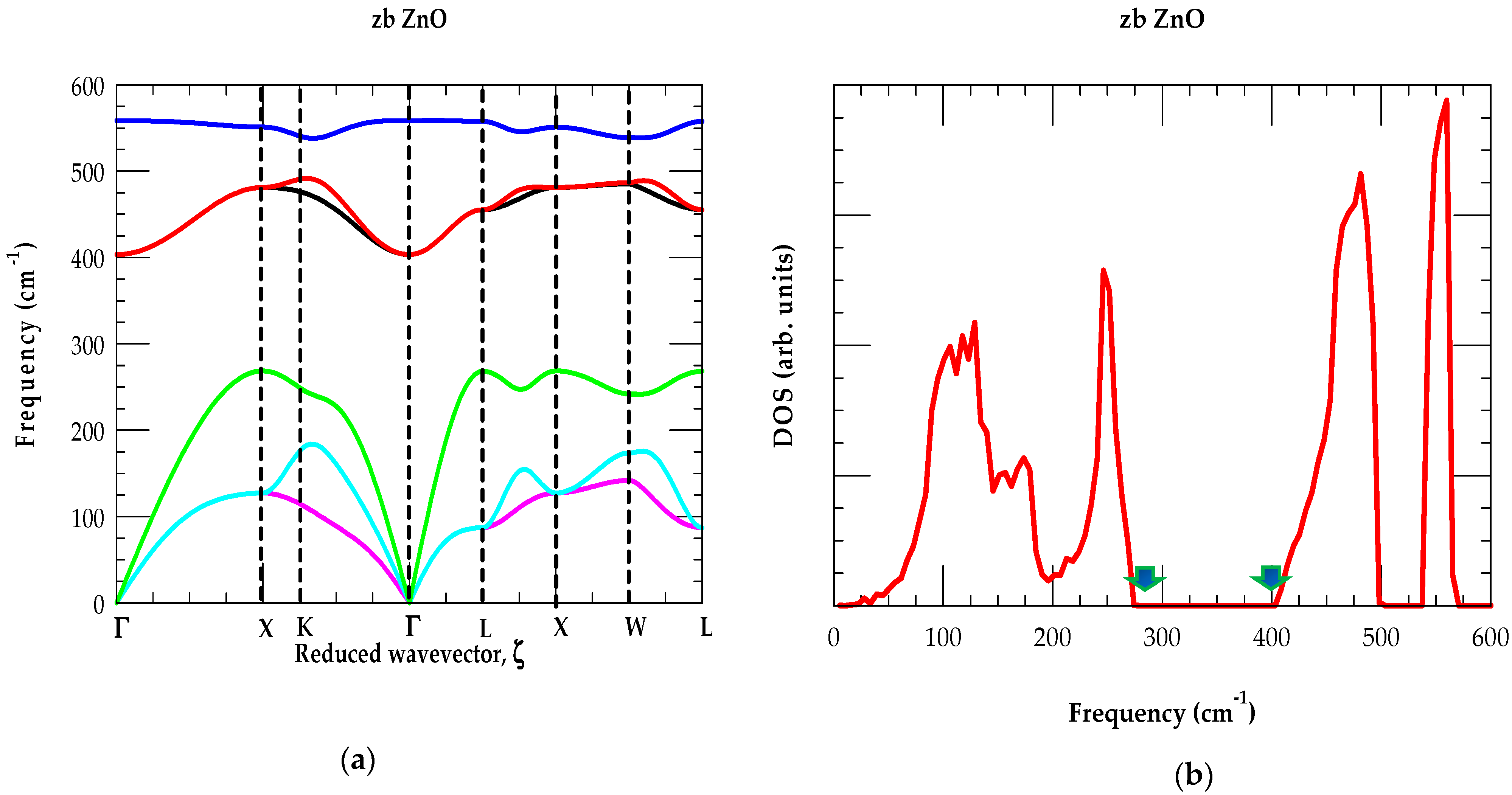
3.1. Theoretical Framework of Phonons
Lattice Dynamics of ZnO
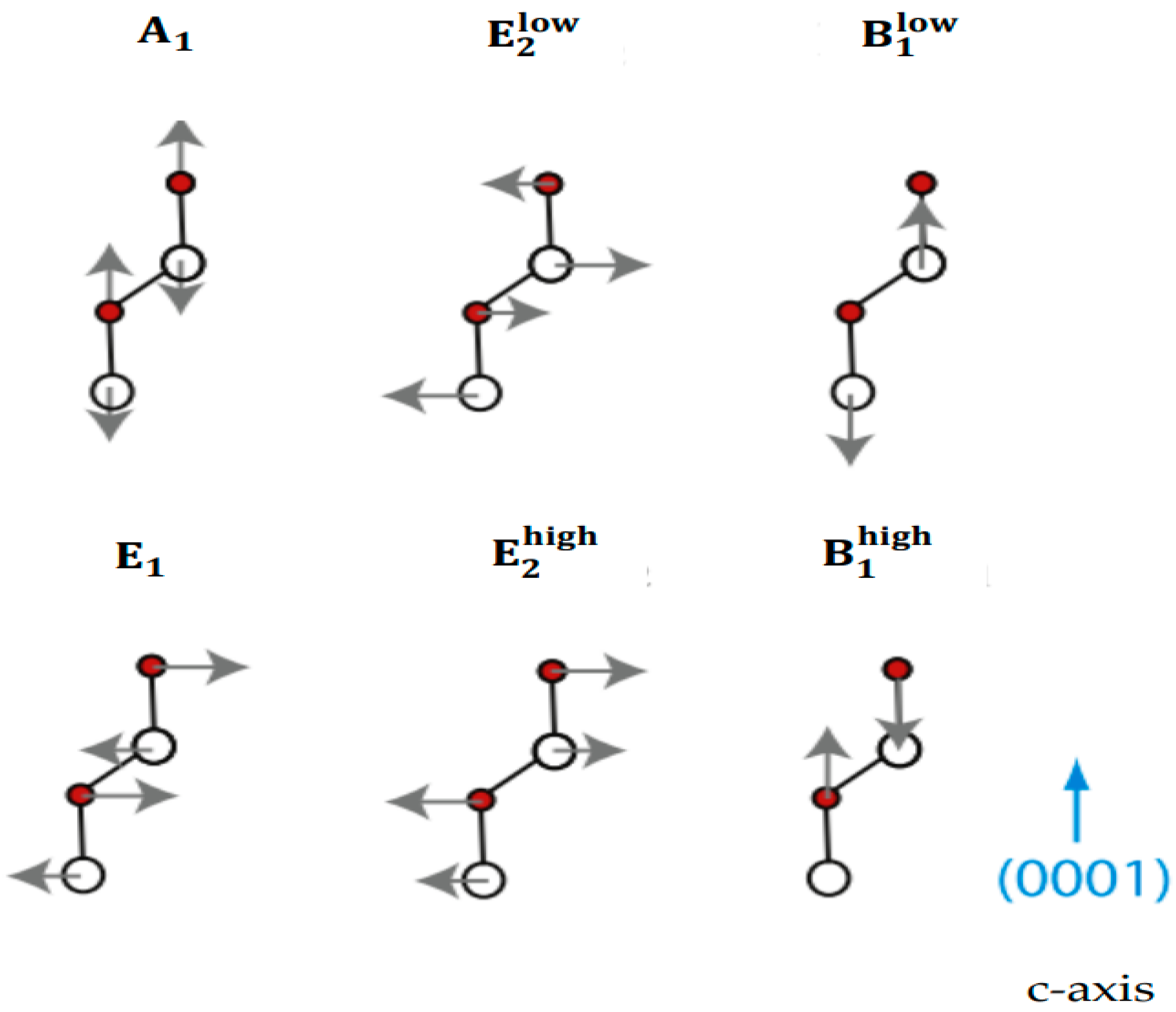
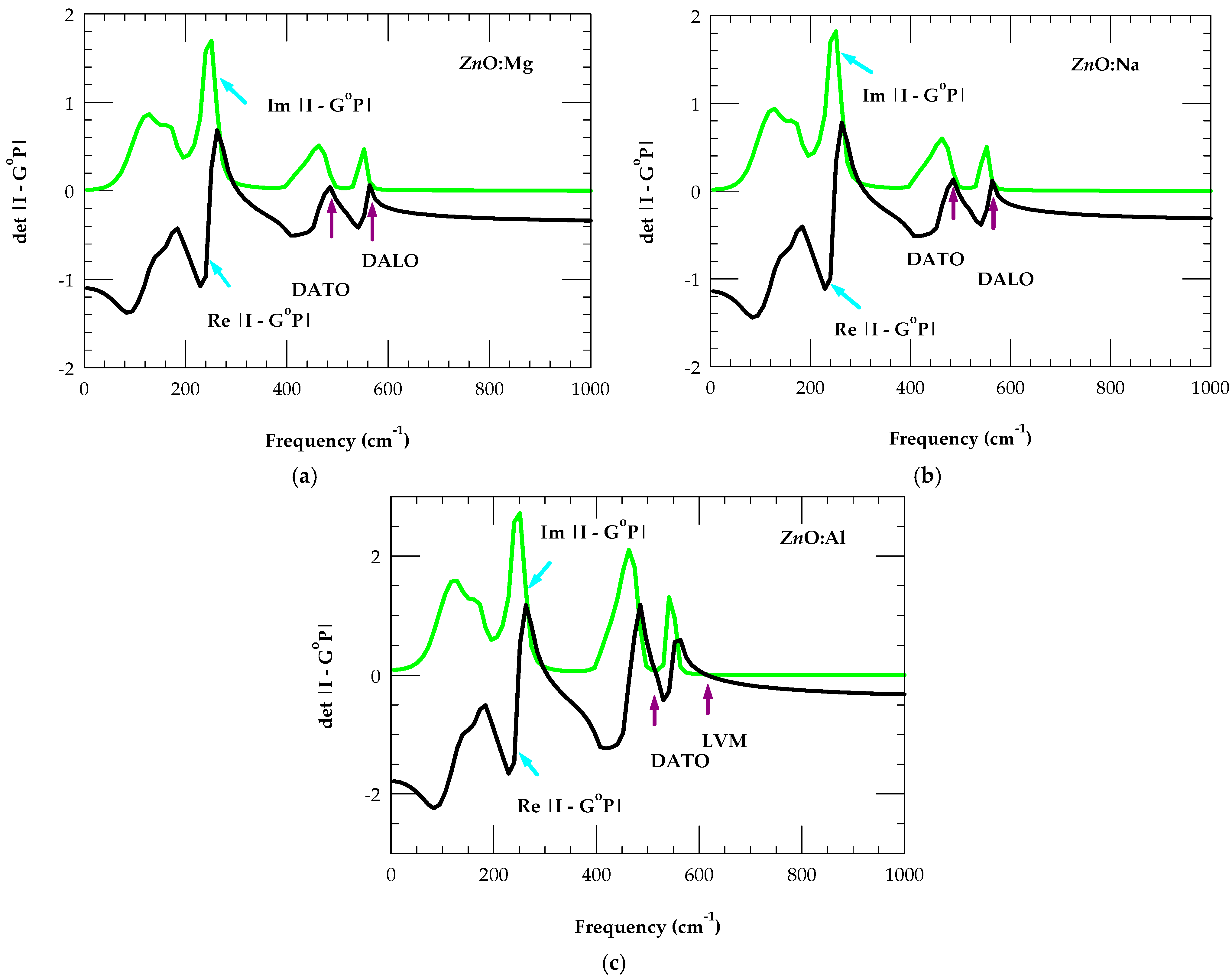
3.2. Chemical Trends of Impurity–Host Interactions
Long-Wavelength Optical Phonons in Alloys
3.3. Vibrational Modes of Isolated Defects in zb ZnO
Impurity Modes of Closest Mass Isoelectronic Donor and Acceptor on the Zn (O) Sites in ZnO
3.4. Impurity Vibrational Modes of in ZnO
4. Concluding Remarks
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Udayagiri, H.; Sana, S.S.; Dogiparthi, L.K.; Vadde, R.; Varma, R.S.; Koduru, J.R.; Ghodake, G.S.; Somala, A.R.; Boya, V.K.N.; Kim, S.-C.; et al. Phytochemical fabrication of ZnO nanoparticles and their antibacterial and anti-bioflm activity. Sci. Rep. 2024, 14, 19714. [Google Scholar] [CrossRef] [PubMed]
- Mutukwa, D.; Taziwa, R.T.; Khotseng, L. A Review of Plant-Mediated ZnO Nanoparticles for Photodegradation and Antibacterial Applications. Nanomaterials 2024, 14, 1182. [Google Scholar] [CrossRef] [PubMed]
- Jha, S.; Rani, R.; Singh, S. Biogenic Zinc Oxide Nanoparticles and Their Biomedical Applications: A Review. J. Inorg. Organomet. Polym. Mater. 2023, 33, 1437–1452. [Google Scholar] [CrossRef]
- Natu, K.; Laad, M.; Ghule, B.; Shalu, A. Transparent and flexible zinc oxide-based thin-film diodes and thin-film transistors: A review. J. Appl. Phys. 2023, 134, 190701. [Google Scholar] [CrossRef]
- Hazarika, R.; Kalita, B. Site selective behavior of B, C and N doping in MgO monolayers towards spintronic and optoelectronic applications. Mater. Sci. Semicond. Process. 2023, 162, 1075. [Google Scholar] [CrossRef]
- Balu, K.; Kaliyamoorthy, S.; Mani, D.; Aguiar, A.; Sobral, M.C.M.; Muthuvel, I.; Kumaravel, S.; Avula, B.; Sobral, A.J.F.N.; Ahn, Y.-H. Porphyrins and ZnO hybrid semiconductor materials: A review. Inorg. Chem. Commun. 2023, 154, 110973. [Google Scholar] [CrossRef]
- Tian, W.; Lu, H.; Li, L. Nanoscale Ultraviolet Photodetectors Based on One-Dimensional Metal Oxide Nanostructures. Nano Res. 2015, 8, 382–405. [Google Scholar] [CrossRef]
- Willander, M.; Nur, O.; Zhao, Q.X.; Yang, L.L.; Lorenz, M.; Cao, B.Q.; Zuniga-Perez, J.; Czekalla, C.; Zimmermann, G.; Grundmann, M.; et al. Zinc Oxide Nanorod Based Photonic Devices: Recent Progress in Growth, Light Emitting Diodes and Lasers. Nanotechnology 2009, 20, 332001. [Google Scholar] [CrossRef]
- Consonni, V.; Briscoe, J.; Karber, E.; Li, X.; Cossuet, T. ZnO Nanowires for Solar Cells: A Comprehensive Review. Nanotechnology 2019, 30, 362001. [Google Scholar] [CrossRef]
- Zhu, L.; Zeng, W. Room-Temperature Gas Sensing of ZnO Based Gas Sensor: A Review. Sens. Actuators A 2017, 267, 242–261. [Google Scholar] [CrossRef]
- Abdullahi, Y.Z.; Ersan, F. Stability and electronic properties of XO (X = Be, Mg, Zn, Cd) biphenylene and graphenylene networks: A first-principles study. Appl. Phys. Lett. 2023, 123, 252104. [Google Scholar] [CrossRef]
- Pushpalatha, C.; Suresh, J.; Gayathri, V.S.; Sowmya, S.V.; Augustine, D.; Alamoudi, A.; Zidane, B.; Albar, N.H.M.; Patil, S. Zinc Oxide Nanoparticles: A Review on Its Applications in Dentistry, Nanoparticles. Front. Bioeng. Biotechnol. 2022, 10, 917990. [Google Scholar] [CrossRef] [PubMed]
- Sharma, D.K.; Shukla, S.; Sharma, K.K.; Kumar, V. A review on ZnO: Fundamental properties and applications. Mater. Today Proc. 2022, 49, 3028–3035. [Google Scholar] [CrossRef]
- Zahoor, R.; Abdul, J.; Ilyas, S.Z.; Ahmed, S.; Hassan, A. Optoelectronic and solar cell applications of ZnO nanostructures. Results Surf. Interfaces 2021, 2, 100003. [Google Scholar] [CrossRef]
- Singh, J.P.; Singh, V.; Sharma, A.; Pandey, G.; Chae, K.H.; Lee, S. Approaches to synthesize MgO nanostructures for diverse applications. Heliyon 2020, 6, e04882. [Google Scholar] [CrossRef]
- Özgür, Ü.; Alivov, Y.I.; Liu, C.; Teke, A.; Reshchikov, M.A.; Doğan, S.; Avrutin, V.; Cho, S.-J.; Morkoç, H. A comprehensive review of ZnO materials and devices. J. Appl. Phys. 2005, 98, 041301. [Google Scholar] [CrossRef]
- Dincer, I. Renewable energy and sustainable development: A crucial review. Renew. Sust. Energ. Rev. 2000, 4, 157–175. [Google Scholar] [CrossRef]
- Talwar, D.N.; Becla, P. Microhardness, Young’s and Shear Modulus in Tetrahedrally Bonded Novel II-Oxides and III-Nitrides. Materials 2025, 18, 494. [Google Scholar] [CrossRef]
- Winer, I.; Shter, G.E.; Mann-Lahav, M.; Grader, G.S. Effect of solvents and stabilizers on sol–gel deposition of Ga-doped zinc oxide TCO films. J. Mater. Res. 2011, 26, 1309–1315. [Google Scholar] [CrossRef]
- Minami, T. Present status of transparent conducting oxide thin-film development for Indium-Tin-Oxide (ITO) substitutes. Thin Solid Film. 2008, 516, 5822–5828. [Google Scholar] [CrossRef]
- Sohn, S.; Han, Y.S. Transparent conductive oxide (TCO) films for organic light emissive devices (OLEDs). In Organic Light Emitting Diode—Material, Process and Devices; InTechOpen: London, UK, 2011; pp. 233–274. [Google Scholar]
- Qiu, T.; Akinoglu, E.M.; Luo, B.; Konarova, M.; Yun, J.; Gentle, I.R. Nanosphere lithography: A versatile approach to develop transparent conductive films for optoelectronic applications. Adv. Mater. 2022, 34, 2103842. [Google Scholar] [CrossRef] [PubMed]
- Song, D.; Widenborg, P.; Chin, W.; Aberle, A.G. Investigation of lateral parameter variations of Al-doped zinc oxide films prepared on glass substrates by rf magnetron sputtering. Sol. Energy Mater. Sol. Cells 2002, 73, 1–20. [Google Scholar] [CrossRef]
- Jang, M.S.; Ryu, M.K.; Yoon, M.H.; Lee, S.H.; Kim, H.K.; Onodera, A.; Kojima, S. A study on the Raman spectra of Al-doped and Ga-doped ZnO ceramics. Curr. Appl. Phys. 2009, 9, 651–657. [Google Scholar] [CrossRef]
- Ivansyah, A.L.; Amelia, S.R.; Rohmatulloh, Y.; Sanusi; Listiani, P.; Ichikawa, Y.; Honda, M.; Sudiarti, T. Insight into novel triple doping (Mg, Cu, N and Mg, Cu, B) on the structural, optical, photocatalytic, and antibacterial properties of ZnO. Colloids Surf. A Physicochem. Eng. Asp. 2023, 678, 132454. [Google Scholar] [CrossRef]
- Keyes, B.M.; Gedvilas, L.M.; Li, X.; Coutts, T.J. Infrared spectroscopy of polycrystalline ZnO and ZnO:N thin films. J. Cryst. Growth 2005, 281, 297–302. [Google Scholar] [CrossRef]
- Pandey, V.; Singh, N.; Haque, F.Z. Enhancement in Structural and Optical Properties of Boron Doped ZnO Nanostructures Synthesized by Simple Aqueous Solution Growth Technique. J. Adv. Phys. 2017, 6, 358–366. [Google Scholar] [CrossRef]
- Kirste, R.; Aksu, Y.; Wagner, M.R.; Khachadorian, S.; Jana, S.; Driess, M.; Thomsen, C.; Hoffmann, A. Raman and photoluminescence spectroscopic detection of surface bound Li+O2− defect sites in Li-doped ZnO nanocrystals derived from molecular precursors. ChemPhysChem 2011, 12, 1189–1195. [Google Scholar] [CrossRef]
- Hjiri, M.; Aida, M.; Lemine, O.; El Mir, L. Study of defects in Li-doped ZnO thin films. Mater. Sci. Semicond. Process. 2019, 89, 149–153. [Google Scholar] [CrossRef]
- Gai, Y.; Tang, G.; Li, J. Formation of Shallow Acceptors in ZnO Doped by Lithium with the Addition of Nitrogen. J. Phys. Chem. Solids 2011, 72, 725–729. [Google Scholar] [CrossRef]
- Hu, Y.M.; Li, J.Y.; Chen, N.Y.; Chen, C.Y.; Han, T.C.; Yu, C.C. Correlation between defect-related photoluminescence emission and anomalous Raman peaks in N-Al co-doped ZnO thin films. Appl. Phys. Lett. 2017, 110, 141903. [Google Scholar] [CrossRef]
- He, H.; Zhuge, F.; Ye, Z.; Zhu, L.; Zhao, B.; Huang, J. Defect-related vibrational and photoluminescence spectroscopy of a codoped ZnO: Al : N. J. Phys. D Appl. Phys. 2006, 39, 2339–2342. [Google Scholar] [CrossRef]
- Cerqueira, M.F.; Rolo, A.G.; Viseu, T.; de Campos, J.A.; de Lacerda-Arôso, T.; Oliveira, F.; Vasilevskiy, M.I.; Alves, E. Raman study of doped-ZnO thin films grown by rf sputtering. Phys. Status Solidi C 2010, 7, 2290. [Google Scholar] [CrossRef]
- Chen, A.; Zhu, H.; Wu, Y.; Chen, M.; Zhu, Y.; Gui, X.; Tang, Z. Beryllium-Assisted p-Type Doping for ZnO Homojunction Light-Emitting Devices. Adv. Funct. Mater. 2016, 26, 3696–3702. [Google Scholar] [CrossRef]
- Sharma, P.; Bhardwaj, R.; Kumar, A.; Mukherjee, S. Trap Assisted Charge Multiplication Enhanced Photo response of Li−P Codoped p-ZnO/n-Si Heterojunction Ultraviolet Photodetectors. J. Phys. D Appl. Phys. 2018, 51, 015103. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, J.; Chen, S.; Pan, X.; Chen, L.; Ye, Z. P-Type Single-Crystalline ZnO Films Obtained by (Na,N) Dual Implantation through Dynamic Annealing Process. J. Cryst. Growth 2018, 483, 236–240. [Google Scholar] [CrossRef]
- Janotti, A.; Van de Walle, C.G. Native Point Defects in ZnO. Phys. Rev. B 2007, 76, 165202. [Google Scholar] [CrossRef]
- Chen, M.; Zhu, Y.; Su, L.; Zhang, Q.; Chen, A.; Ji, X.; Xiang, R.; Gui, X.; Wu, T.; Pan, B.; et al. Formation behavior of BexZn1−xO alloys grown by plasma assisted molecular beam epitaxy. Appl. Phys. Lett. 2013, 102, 202103. [Google Scholar] [CrossRef]
- Cui, Y.; Du, G.; Zhang, Y.; Zhu, H.; Zhang, B. Growth of ZnO(0 0 2) and ZnO(1 0 0) films on GaAs substrates by MOCVD. J. Cryst. Growth 2005, 282, 389–393. [Google Scholar] [CrossRef]
- Bang, K.-H.; Hwang, D.-K.; Lim, S.-W.; Myoung, J.-M. Effects of growth temperature on the properties of ZnO/GaAs prepared by metalorganic chemical vapor deposition. J. Cryst. Growth 2003, 250, 437–443. [Google Scholar] [CrossRef]
- Nicolay, S.; Fay, S.; Ballif, C. Growth Model of MOCVD Polycrystalline ZnO. Cryst. Growth Des. 2009, 9, 4957. [Google Scholar] [CrossRef]
- Zhang, J.; Cui, X.; Shi, Z.; Wu, B.; Zhang, Y.; Zhang, B. Nucleation and growth of ZnO films on Si substrates by LP-MOCVD. Superlattices Microstruct. 2014, 71, 23–29. [Google Scholar] [CrossRef]
- Zheng, Y.; Gu, S.; Ye, J.; Liu, W.; Zhu, S.; Qin, F.; Hu, L.; Zhang, R.; Shi, Y. MOCVD Growth and Properties of ZnO and Znl-x,MgxO Films. In Proceedings of the Sixth Chinese Optoelectronics Symposium (IEEE Cat. No. 03EX701), Hong Kong, China, 14 September 2003; IEEE: Piscataway, NJ, USA, 2003. [Google Scholar]
- Kadhim, G.A. Study of the Structural and Optical Traits of In:ZnO Thin Films Via Spray Pyrolysis Strategy: Influence of laser Radiation Change in Different Periods. AIP Conf. Proc. 2024, 2922, 240006. [Google Scholar] [CrossRef]
- Wei, X.H.; Li, Y.R.; Zhu, J.; Huang, W.; Zhang, Y.; Luo, W.B.; Ji, H. Epitaxial properties of ZnO thin films on Sr Ti O3 substrates grown by laser molecular beam epitaxy. Appl. Phys. Lett. 2007, 90, 151918. [Google Scholar] [CrossRef]
- Opel, M.; Geprags, S.; Althammer, M.; Brenninger, T.; Gross, R. Laser molecular beam epitaxy of ZnO thin films and heterostructures. J. Phys. D Appl. Phys. 2014, 47, 034002. [Google Scholar] [CrossRef]
- Chauveau, J.-M.; Morhain, C.; Teisseire, M.; Laugt, M.; Deparis, C.; Zuniga-Perez, J.; Vinter, B. (Zn, Mg)O/ZnO-based heterostructures grown by molecular beam epitaxy on sapphire: Polar vs. non-polar. Microelectron. J. 2009, 40, 512–516. [Google Scholar] [CrossRef]
- Horio, Y.; Yuhara, J.; Takakuwa, Y.; Ogawa, S.; Abe, K. Polarity identification of ZnO (0001) surface by reflection high-energy electron diffraction. Jpn. J. Appl. Phys. 2018, 57, 045701. [Google Scholar] [CrossRef]
- Chen, Y.; Bagnall, D.; Yao, T. ZnO as a novel photonic material for the UV region. Mater. Sci. Eng. B 2000, 75, 190–198. [Google Scholar] [CrossRef]
- Huang, M.R.S.; Erni, R.; Lin, H.-Y.; Wang, R.-C.; Liu, C.-P. Characterization of wurtzite ZnO using valence electron energy loss spectroscopy. Phys. Rev. B 2011, 84, 155203. [Google Scholar] [CrossRef]
- Kaida, T.; Kamioka, K.; Ida, T.; Kuriyama, K.; Kushida, K.; Kinomura, A. Rutherford backscattering and nuclear reaction analyses of hydrogen ion-implanted ZnO bulk single crystals. Nucl. Instrum. Methods Phys. Res. B 2014, 332, 15–18. [Google Scholar] [CrossRef]
- Ismail, M.A.; Taha, K.K.; Modwi, A.; Khezami, L. ZnO Nanoparticles: Surface and X-ray profile analysis. J. Ovonic Res. 2018, 14, 381–393. [Google Scholar]
- Mohan, A.C.; Renjanadevi, B. Preparation of Zinc Oxide Nanoparticles and its Characterization Using Scanning Electron Microscopy (SEM) and X-Ray Diffraction (XRD). Procedia Technol. 2016, 24, 761–766. [Google Scholar] [CrossRef]
- Martínez-Tomás, M.C.; Hortelano, V.; Jiménez, J.; Wang, B.; Muñoz-Sanjosé, V. High resolution X-ray diffraction, X-ray multiple diffraction and cathodoluminescence as combined tools for the characterization of substrates for epitaxy: The ZnO case. CrystEngComm 2013, 15, 3951–3958. [Google Scholar] [CrossRef]
- Chao, L.-C.; Yang, S.-H. Growth and Auger electron spectroscopy characterization of donut-shaped ZnO nanostructures. Appl. Surf. Sci. 2007, 253, 7162–7165. [Google Scholar] [CrossRef]
- Ni, H.; Li, X. Young’s modulus of ZnO nanobelts measured using atomic force microscopy and nanoindentation techniques. Nanotechnology 2006, 17, 3591. [Google Scholar] [CrossRef]
- Kirmse, H.; Sparenberg, M.; Zykov, A.; Sadofev, S.; Kowarik, S.; Blumstengel, S. Structure of p-Sexiphenyl Nanocrystallites in ZnO Revealed by High Resolution Transmission Electron Microscopy. Cryst. Growth Des. 2016, 16, 2789–2794. [Google Scholar] [CrossRef]
- Li, X.; Cheng, S.; Deng, S.; We, X.; Zhu, J.; Che, Q. Direct Observation of the Layer-by Layer Growth of ZnO Nanopillar by In situ High Resolution Transmission Electron Microscopy. Sci. Rep. 2017, 7, 40911. [Google Scholar] [CrossRef] [PubMed]
- Raouf, D. Synthesis and photoluminescence characterization of ZnO nanoparticles. J. Lumin. 2013, 134, 213–219. [Google Scholar] [CrossRef]
- Saadatkia, P.; Ariyawansa, G.; Leedy, K.D.; Look, D.C.; Boatner, L.A.; Selim, F.A. Fourier Transform Infrared Spectroscopy Measurements of Multi-phonon and Free-Carrier Absorption in ZnO. J. Electron. Mater. 2016, 45, 6329. [Google Scholar] [CrossRef]
- Damen, T.C.; Porto, S.P.S.; Tell, B. Raman Effect in Zinc Oxide. Phys. Rev. 1966, 142, 570. [Google Scholar] [CrossRef]
- Calleja, J.M.; Cardona, M. Resonant raman scattering in ZnO. Phys. Rev. B 1977, 16, 3753. [Google Scholar] [CrossRef]
- Manjon, F.J.; Syassen, K.; Lauck, R. Effect of pressure on phonon modes in wurtzite zinc oxide. High Press. Res. 2002, 22, 299. [Google Scholar] [CrossRef]
- Kokila, M.K.; Reddy, A.J.; Nagabhushana, H.; Rao, J.L.; Shivakumara, C.; Nagabhushana, B.M.; Chakradhar, R.P.S. Combustion synthesis, characterization and Raman studies of ZnO nano powders. Spectrochim. Acta Part A 2011, 81, 53–58. [Google Scholar]
- Serrano, J.; Manjón, F.J.; Romero, A.H.; Ivanov, A.; Cardona, M.; Lauck, R.; Bosak, A.; Krisch, M. Phonon dispersion relations of zinc oxide: Inelastic neutron scattering and ab initio calculations. Phys. Rev. B 2010, 81, 174304. [Google Scholar] [CrossRef]
- Serrano, J.; Romero, A.H.; Manjo’n, F.J.; Lauck, R.; Cardona, M.; Rubio, A. Pressure dependence of the lattice dynamics of ZnO: An ab initio approach. Phys. Rev. B 2004, 69, 094306. [Google Scholar] [CrossRef]
- Santos, A.W.S.; Silveira, I.S.; Meira-Belo, L.C.; Novais, A.L.F.; Souza, D.N. Structural, vibrational, and luminescent properties of pure and Ce-doped magnesium lithium aluminoborate glass. Appl. Radiat. Isot. 2024, 214, 111548. [Google Scholar] [CrossRef]
- Bohórquez, C.; Bakkali, H.; Delgado, J.J.; Blanco, E.; Herrera, M.; Domínguez, M. Spectroscopic Ellipsometry Study on Tuning the Electrical and Optical Properties of Zr-Doped ZnO Thin Films Grown by Atomic Layer Deposition. ACS Appl. Electron. Mater. 2022, 4, 925–935. [Google Scholar] [CrossRef] [PubMed]
- Bhandari, K.P.; Sapkota, D.R.; Ramanujam, B. Spectroscopic-ellipsometry study of the optical properties of ZnO nanoparticle thin films. MRS Commun. 2024, 14, 1085–1089. [Google Scholar] [CrossRef]
- Lyons, J.L.; Varley, J.B.; Steiauf, D.; Janotti, A.; Van de Walle, C.G. First-Principles Characterization of Native-Defect-Related Optical Transitions in ZnO. J. Appl. Phys. 2017, 122, 035704. [Google Scholar] [CrossRef]
- Buckeridge, J.; Catlow, C.R.A.; Farrow, M.R.; Logsdail, A.J.; Scanlon, D.O.; Keal, T.W.; Sherwood, P.; Woodley, S.M.; Sokol, A.A.; Walsh, A. Deep Vs Shallow Nature of Oxygen Vacancies and Consequent N-Type Carrier Concentrations in Transparent Conducting Oxides. Phys. Rev. Mater. 2018, 2, 054604. [Google Scholar] [CrossRef]
- Clark, S.J.; Robertson, J.; Lany, S.; Zunger, A. Intrinsic Defects in ZnO Calculated by Screened Exchange and Hybrid Density Functionals. Phys. Rev. B 2010, 81, 115311. [Google Scholar] [CrossRef]
- Alkauskas, A.; Pasquarello, A. Band-Edge Problem in the Theoretical Determination of Defect Energy Levels: The O Vacancy in ZnO as a Benchmark Case. Phys. Rev. B 2011, 84, 125206. [Google Scholar] [CrossRef]
- Paudel, T.R.; Lambrecht, W.R.L. First-Principles Calculation of the O Vacancy in ZnO: A Self-Consistent Gap-Corrected Approach. Phys. Rev. B 2008, 77, 205202. [Google Scholar] [CrossRef]
- Thienprasert, J.T.; Limpijumnong, S.; Janotti, A.; Van de Walle, C.G.; Zhang, L.; Du, M.-H.; Singh, D.J. Vibrational signatures of OTe and OTe–VCd in CdTe: A first-principles study. Comput. Mater. Sci. 2010, 49, S242–S245. [Google Scholar] [CrossRef]
- Baraff, G.A.; Kane, E.O.; Schluter, M. Enfeebled oxygen bonding and metastability in GaP:O. Phys. Rev. B 1982, 25, 548. [Google Scholar] [CrossRef]
- Pavone, P.; Karch, K.; Schiitt, O.; Windl, W.; Strauch, D.; Giannozzi, P.; Baroni, S. Ab initio lattice dynamics of diamond. Phys. Rev. B 1993, 48, 3156. [Google Scholar] [CrossRef] [PubMed]
- Kern, G.; Kresse, G.; Hafner, J. Ab initio calculation of the lattice dynamics and phase diagram of boron nitride. Phys. Rev. B 1999, 59, 8551. [Google Scholar] [CrossRef]
- Duman, S.; Sütlü, A.; Bağcı, S.; Tütüncü, H.M.; Srivastava, G.P. Structural, elastic, electronic, and phonon properties of zincblende and wurtzite BeO. J. Appl. Phys. 2009, 105, 033719. [Google Scholar] [CrossRef]
- Maradudin, A.A.; Montroll, E.W.; Weiss, G.H.; Ipatova, I.P. Solid State Physics, 2nd ed.; Seitz, F., Turnbull, D., Ehrenreich, H., Eds.; Academic: New York, NY, USA, 1971. [Google Scholar]
- Elliott, R.J.; Krumhansl, J.A.; Leath, P.L. The theory and properties of randomly disordered crystals and related physical systems. Rev. Mod. Phys. 1974, 46, 465. [Google Scholar] [CrossRef]
- Newman, R.C. Semiconductors and Semimetals; Weber, E., Ed.; Academic: New York, NY, USA, 1993; Volume 38, Chapter 4. [Google Scholar]
- Spitzer, W.G. Advances in Solid State Physics; Madelung, O., Ed.; Pergamon Press: Oxford, UK, 1971; Volume XI, p. 1. [Google Scholar]
- Talwar, D.N. Dilute III-V Nitride Semiconductors and Material Systems: Physics and Technology; Erol, A., Ed.; Springer Series in Materials Science; Springer: Berlin, Germany, 2008; Volume 105, Chapter 9. [Google Scholar]
- Talwar, D.N.; Vandevyver, M.; Bajaj, K.K.; Theis, W.M. Gallium-isotope fine structure of impurity modes due to defect complexes in GaAs. Phys. Rev. B 1986, 33, 8525. [Google Scholar] [CrossRef]
- Vandevyver, M.; Plumelle, P. Local force variations due to substitution impurities in nine compounds with the zinc-blende structure. Phys. Rev. B 1978, 17, 675. [Google Scholar] [CrossRef]
- Vandevyver, M.; Talwar, D.N. Green s-function theory of impurity vibrations due to defect complexes in elemental and compound semiconductors. Phys. Rev. 1980, 21, 3405. [Google Scholar] [CrossRef]
- Kunc, K. Dynamique de réseau de composés ANB8-N présentant la structure de la blende. Ann. Phys. 1973, 8, 319. [Google Scholar] [CrossRef]
- Chang, I.F.; Mitra, S.S. Application of a modified random-element-isodisplacement model to long-wavelength optic phonons of mixed crystals. Phys. Rev. 1968, 172, 924. [Google Scholar] [CrossRef]
- Gorska, M.; Nazarewicz, W. Application of the Random-Element Iso-displacement Model to Long-Wavelength Optical Phonons in CdSexTe1−x Mixed Crystals. Phys. Status Solidi B 1974, 65, 193. [Google Scholar] [CrossRef]
- Grimm, A.; Maradudin, A.A.; Ipatova, I.P.; Subashiev, A.V. Impurity vibrations of copper defect complexes in gallium arsenide crystals. J. Phys. Chem. Solids 1972, 33, 775. [Google Scholar] [CrossRef]
- Waugh, J.L.T.; Dolling, G. Crystal Dynamics of Gallium Arsenide. Phys. Rev. 1963, 132, 2410. [Google Scholar] [CrossRef]
- Harrison, W.A. Electronic Structure and the Properties of Solids; Freeman: San Francisco, CA, USA, 1980. [Google Scholar]
- Ludwig, G.W.; Woodbury, H.H. Solid State Physics, 2nd ed.; Seitz, F., Turnbull, D., Ehreneich, H., Eds.; Academic: New York, NY, USA, 1962; Volume 13, p. 223. [Google Scholar]
- Talwar, D.N.; Becla, P. Systematic Simulations of Structural Stability, Phonon Dispersions and Thermal Expansion in Zinc-blende ZnO. Nanomaterials 2025, 15, 308. [Google Scholar] [CrossRef]
- Yıldırım, H. Dispersion relations of interface and quasi-confined phonon modes in ZnO/BeZnO quantum wells. Phys. Lett. A 2021, 385, 126977. [Google Scholar] [CrossRef]
- Talwar, D.N.; Semone, S.; Becla, P. Strain-Dependent Effects on Confinement of Folded Acoustic and Optical Phonons in Short-Period (XC)m/(YC)n with X,Y (≡Si, Ge, Sn) Superlattices. Materials 2024, 17, 3082. [Google Scholar] [CrossRef]
- Talwar, D.N. Composition-Dependent Phonon and Thermodynamic Characteristics of C-Based XxY1−xC (X, Y≡ Si, Ge, Sn) Alloys. Inorganics 2024, 12, 100. [Google Scholar] [CrossRef]
- Talwar, D.N.; Haraldsen, J.T. Simulations of Infrared Reflectivity and Transmission Phonon Spectra for Undoped and Doped GeC/Si (001). Nanomaterials 2024, 14, 1439. [Google Scholar] [CrossRef] [PubMed]
- Talwar, D.N.; Feng, Z.C.; Liu, C.W.; Tin, C.-C. Influence of surface roughness and interfacial layer on the infrared spectra of VCVD grown 3C-SiC/Si (1 0 0) epilayers. Semicond. Sci. Technol. 2012, 27, 115019. [Google Scholar] [CrossRef]



| wz ZnO | zb ZnO | ||
|---|---|---|---|
| 560 (584, 575) | 558 | ||
| 556 (595, 580, 588) | 403 | ||
| 552 | 551 | ||
| 440 (438, 439) | 487 | ||
| 409 (410, 411) | 561 | ||
| 391 (380, 379) | 443 | ||
| 261 | 128 | ||
| 91 (100) | 93 |
| (i) | |||||
|---|---|---|---|---|---|
| BeO | 728 | 1073 | BeO:Zn = 280 | 3.10 | 3.81 |
| ZnO | 403 | 558 | ZnO:Be = 775 | 5.32 | 4.504 |
| 3.10 | |||||
| 5.32 | |||||
| 2.99E+5 dyn/cm | |||||
| 2.40E+5 dyn/cm | |||||
| 5.96E+4 dyn/cm | |||||
| θ | 0.12 | ||||
| System | Impurity Modes (a) | Impurity Modes (Others) (b) | Δf/f |
|---|---|---|---|
| ZnO:Li | 372 cm−1 (GM), 732 cm−1 (LVM) | 735 cm−1 | −0.17 |
| ZnO:Be | 363 cm−1 (GM), 775 cm−1 (LVM) | ~760, ~775 cm−1 | −0.50 |
| ZnO:B | 354 cm−1 (GM), 804 cm−1 (LVM) | 806, 819, 880 cm−1 | −0.82 |
| ZnO:Na | 305 cm−1 (GM), 486, 541 cm−1 | 270, 513 cm−1 | 0.07 |
| ZnO:Mg | 298 cm−1 (GM), 467, 551, 574 cm−1 | 250, 304, 490, 562, 568 cm−1 | −0.25 |
| ZnO:Al | 295 cm−1 (GM), 497, 545, 612 (LVM) cm−1 | 475, 500, 560, 581, 623 cm−1 | −0.55 |
| ZnO:N | 497, 575 cm−1 | 277, 497, 512, 552, 575, 582 cm−1 | −0.1 |
| ZnO:P | 372 cm−1 (GM), 466, 543 cm−1 | 284, 361, 486 cm−1 | −0.14 |
| ZnO:As | 273, 470, 545 cm−1 | 220, 266, 550 cm−1 | −0.17 |
| ZnO:Sb | 235, 470, 545 cm−1 | 235, 534 cm−1 | −0.2 |
| zb ZnO | Modes (cm−1) | Average Impurity Mode | |
|---|---|---|---|
| 627 | −0.55 | ||
| −0.10 | |||
| −0.55 | |||
| −0.08 | |||
| −0.55 | |||
| −0.06 | |||
| −0.55 | |||
| −0.04 | |||
| : | −0.83 | ||
| −0.17 | |||
| : | −0.83 | ||
| −0.17 | |||
| : | −0.55 | ||
| −0.17 | |||
| : | −0.55 | ||
| −0.17 | |||
| : | −0.45 | ||
| −0.17 | |||
| : | −0.45 | ||
| −0.17 | |||
| : | −0.35 | ||
| −0.17 | |||
| : | −0.35 | ||
| −0.17 | |||
| : | 1.00 | ||
| −0.55 | |||
| : | 1.00 | ||
| −0.83 | |||
| : | 1.00 | ||
| −0.1 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Talwar, D.N.; Becla, P. Dynamical Characteristics of Isolated Donors, Acceptors, and Complex Defect Centers in Novel ZnO. Nanomaterials 2025, 15, 749. https://doi.org/10.3390/nano15100749
Talwar DN, Becla P. Dynamical Characteristics of Isolated Donors, Acceptors, and Complex Defect Centers in Novel ZnO. Nanomaterials. 2025; 15(10):749. https://doi.org/10.3390/nano15100749
Chicago/Turabian StyleTalwar, Devki N., and Piotr Becla. 2025. "Dynamical Characteristics of Isolated Donors, Acceptors, and Complex Defect Centers in Novel ZnO" Nanomaterials 15, no. 10: 749. https://doi.org/10.3390/nano15100749
APA StyleTalwar, D. N., & Becla, P. (2025). Dynamical Characteristics of Isolated Donors, Acceptors, and Complex Defect Centers in Novel ZnO. Nanomaterials, 15(10), 749. https://doi.org/10.3390/nano15100749






