Spin Glass State and Griffiths Phase in van der Waals Ferromagnetic Material Fe5GeTe2
Abstract
1. Introduction
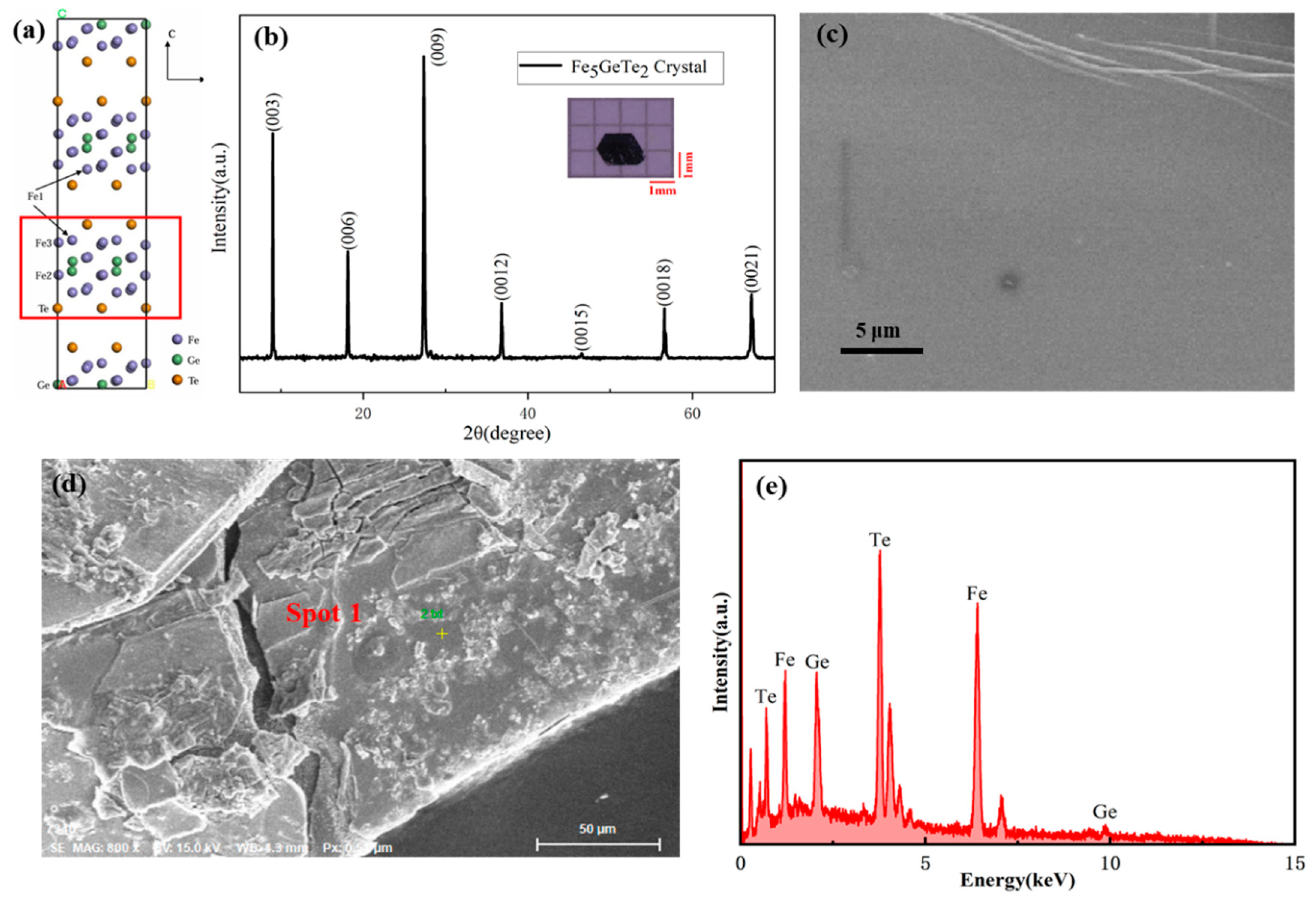
2. Sample Preparation and Characterization
2.1. Single-Crystal Growth
2.2. X-ray Diffraction Measurements
2.3. Scanning Electron Microscope Measurements
2.4. Energy-Dispersive X-ray Spectroscopy Measurements
3. X-ray Photoemission Spectroscopy Measurements
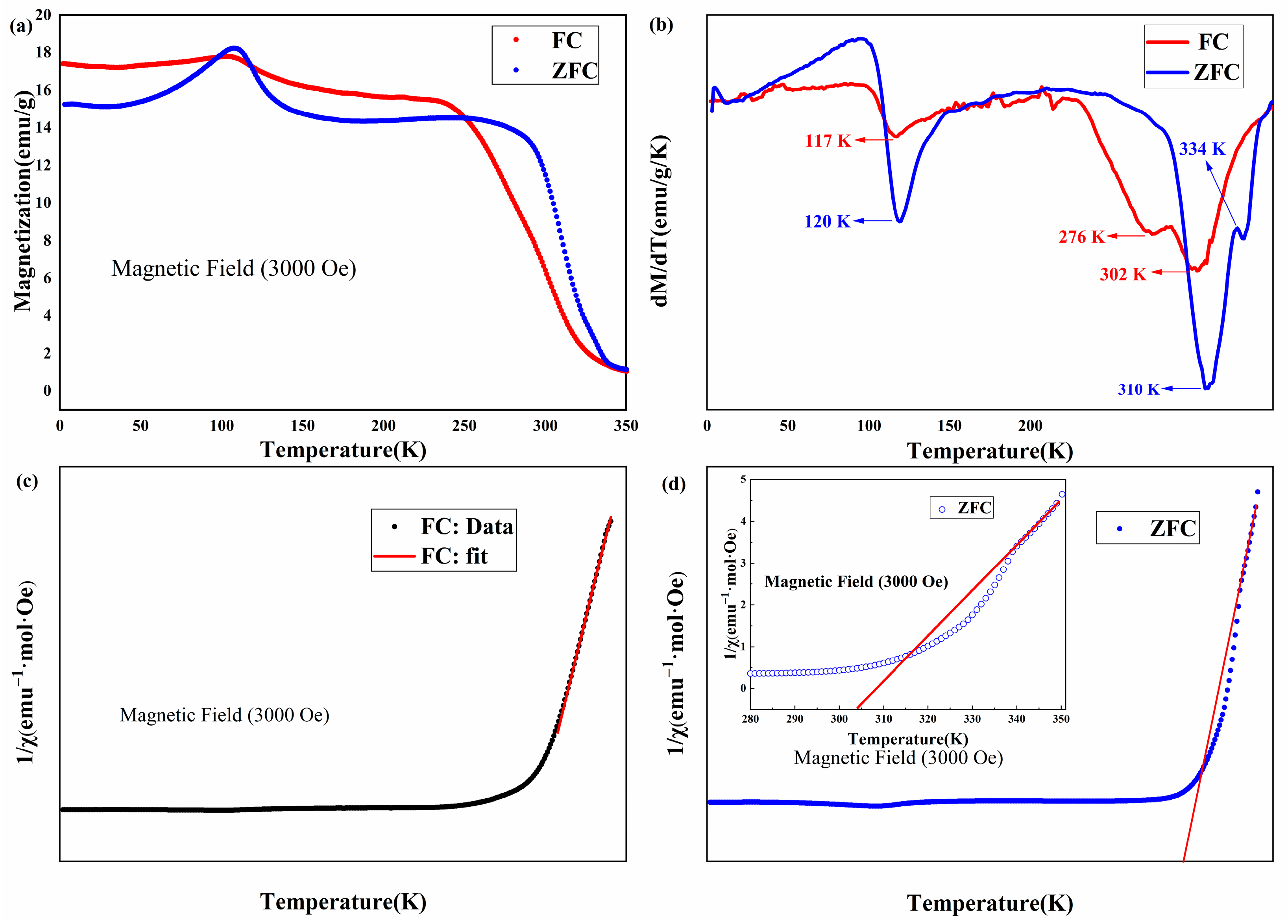
4. Magnetization Measurements
5. Summary
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Khan, K.; Tareen, A.K.; Aslam, M.; Wang, R.; Zhang, Y.; Mahmood, A.; Ouyang, Z.; Zhang, H.; Guo, Z. Recent developments in emerging two-dimensional materials and their applications. J. Mater. Chem. C 2020, 8, 387–440. [Google Scholar] [CrossRef]
- Wang, Q.H.; Bedoya-Pinto, A.; Blei, M.; Dismukes, A.H.; Hamo, A.; Jenkins, S.; Koperski, M.; Liu, Y.; Sun, Q.C.; Telford, E.J.; et al. The magnetic genome of two-dimensional van der Waals materials. ACS Nano 2022, 16, 6960–7079. [Google Scholar] [CrossRef]
- Kumbhakar, P.; Gowda, C.C.; Mahapatra, P.L.; Mukherjee, M.; Malviya, K.D.; Chaker, M.; Chandra, A.; Lahiri, B.; Ajayan, P.; Jariwala, D.; et al. Emerging 2D metal oxides and their applications. Mater. Today 2021, 45, 142–168. [Google Scholar] [CrossRef]
- Chen, Y.; Fan, Z.; Zhang, Z.; Niu, W.; Li, C.; Yang, N.; Chen, B.; Zhang, H. Two-dimensional metal nanomaterials: Synthesis, properties, and applications. Chem. Rev. 2018, 118, 6409–6455. [Google Scholar] [CrossRef] [PubMed]
- Mermin, N.D.; Wagner, H. Absence of ferromagnetism or antiferromagnetism in one-or two-dimensional isotropic Heisenberg models. Phys. Rev. Lett. 1966, 17, 1133. [Google Scholar] [CrossRef]
- Gong, C.; Li, L.; Li, Z.; Ji, H.; Stern, A.; Xia, Y.; Cao, T.; Bao, W.; Wang, C.; Wang, Y.; et al. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature 2017, 546, 265–269. [Google Scholar] [CrossRef]
- Huang, B.; Clark, G.; Navarro-Moratalla, E.; Klein, D.R.; Cheng, R.; Seyler, K.L.; Zhong, D.; Schmidgall, E.; McGuire, M.A.; Cobden, D.H.; et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature 2017, 546, 270–273. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Yang, J.; Wang, H.; Imai, M.; Ohta, H.; Michioka, C.; Yoshimura, K.; Fang, M. Magnetic properties of layered itinerant electron ferromagnet Fe3GeTe2. J. Phys. Soc. Jpn. 2013, 82, 124711. [Google Scholar] [CrossRef]
- Fei, Z.; Huang, B.; Malinowski, P.; Wang, W.; Song, T.; Sanchez, J.; Yao, W.; Xiao, D.; Zhu, X.; May, A.F.; et al. Two-dimensional itinerant ferromagnetism in atomically thin Fe3GeTe2. Nat. Mater. 2018, 17, 778–782. [Google Scholar] [CrossRef]
- Deng, Y.; Yu, Y.; Song, Y.; Zhang, J.; Wang, N.Z.; Sun, Z.; Yi, Y.; Wu, Y.Z.; Wu, S.; Zhu, J.; et al. Gate-tunable room-temperature ferromagnetism in two-dimensional Fe3GeTe2. Nature 2018, 563, 94–99. [Google Scholar] [CrossRef]
- Wang, C.; Zhu, K.; Ma, Y.; Lu, L.; Hu, T.; Li, L.; Kan, X.; Xiong, Y.; Zhang, Y.; Wang, G.; et al. Magnetism control with enhanced hard magnetic temperature in heterostructures based on the van der Waals magnet Fe5GeTe2. Phys. Rev. B 2023, 108, 094408. [Google Scholar] [CrossRef]
- May, A.F.; Ovchinnikov, D.; Zheng, Q.; Hermann, R.; Calder, S.; Huang, B.; Fei, Z.; Liu, Y.; Xu, X.; McGuire, M.A. Ferromagnetism near room temperature in the cleavable van der Waals crystal Fe5GeTe2. ACS Nano 2019, 13, 4436–4442. [Google Scholar] [CrossRef] [PubMed]
- Casas, B.W.; Li, Y.; Moon, A.; Xin, Y.; McKeever, C.; Macy, J.; Petford-Long, A.K.; Phatak, C.M.; Santos, E.J.; Choi, E.S.; et al. Coexistence of merons with skyrmions in the centrosymmetric van der Waals ferromagnet Fe5–xGeTe2. Adv. Mater. 2023, 35, 2212087. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Liu, C.; Zhang, S.; Zhou, B.; Guan, C.; Ma, Y.; Algaidi, H.; Zheng, D.; Li, Y.; He, X.; et al. Magnetic skyrmions with unconventional helicity polarization in a van der Waals ferromagnet. Adv. Mater. 2022, 34, 2204163. [Google Scholar] [CrossRef] [PubMed]
- Tang, M.; Huang, J.; Qin, F.; Zhai, K.; Ideue, T.; Li, Z.; Meng, F.; Nie, A.; Wu, L.; Bi, X.; et al. Continuous manipulation of magnetic anisotropy in a van der Waals ferromagnet via electrical gating. Nat. Electron. 2023, 6, 28–36. [Google Scholar] [CrossRef]
- Bhat, F.; Anjum, G.; Kumar, R.; Malik, M.A.; Choudhary, R.; Shukla, D. XAS and XPS analysis of double magnetic transition, canonical spin glass behavior and magnetoresistance in LaMn1−xCoxO3 (0.1 ≤ x ≤ 0.5) system. Ceram. Int. 2021, 47, 6753–6763. [Google Scholar] [CrossRef]
- Stahl, J.; Shlaen, E.; Johrendt, D. The van der Waals ferromagnets Fe5–δGeTe2 and Fe5–δ–xNixGeTe2–crystal structure, stacking faults, and magnetic pro perties. Z. Anorg. Allg. Chem. 2018, 644, 1923–1929. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, R.; Zhai, K.; Chen, X.; Caretta, L.; Huang, X.; Chopdekar, R.V.; Cao, J.; Sun, J.; Yao, J.; et al. Itinerant ferromagnetism in van der Waals Fe5− xGeTe2 crystals above room temperature. Phys. Rev. B 2020, 102, 064417. [Google Scholar] [CrossRef]
- Saha, R.; Meyerheim, H.L.; Göbel, B.; Hazra, B.K.; Deniz, H.; Mohseni, K.; Antonov, V.; Ernst, A.; Knyazev, D.; Bedoya-Pinto, A.; et al. Observation of Néel-type skyrmions in acentric self-intercalated Cr1+δTe2. Nat. Commun. 2022, 13, 3965. [Google Scholar] [CrossRef] [PubMed]
- Bera, S.; Pradhan, S.K.; Khan, M.S.; Pal, R.; Pal, B.; Kalimuddin, S.; Bera, A.; Das, B.; Pal, A.N.; Mondal, M. Unravelling the nature of spin reorientation transition in quasi-2D vdW magnetic material, Fe4GeTe2. J. Magn. Magn. Mater. 2023, 565, 170257. [Google Scholar] [CrossRef]
- Li, G.; Ma, S.; Li, Z.; Zhang, Y.; Diao, J.; Xia, L.; Zhang, Z.; Huang, Y. High-Quality Ferromagnet Fe3GeTe2 for High-Efficiency Electromagnetic Wave Absorption and Shielding with Wideband Radar Cross Section Reduction. ACS Nano 2022, 16, 7861–7879. [Google Scholar] [CrossRef]
- Angelkort, J.; Wölfel, A.; Schönleber, A.; van Smaalen, S.; Kremer, R.K. Observation of strong magnetoelastic coupling in a first-order phase transition of CrOCl. Phys. Rev. B 2009, 80, 144416. [Google Scholar] [CrossRef]
- Roy, R.; Mondal, R. Anisotropic magnetic, magnetocaloric properties, and critical behavior studies of CVT-grown single-crystalline Fe3−xGeTe2. Phys. Rev. B 2024, 109, 024416. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, H.; Wang, Y.; Tan, W.; Huo, D. Spin glass feature and exchange bias effect in metallic Pt/antiferromagnetic LaMnO3 heterostructure. J. Phys. Condens. Matter 2021, 33, 285802. [Google Scholar] [CrossRef] [PubMed]
- Ali, W.; Chen, X.; Yin, H.; Zheng, Z.; Yuan, S.L. Comparative study on the magnetic properties of Fe-substituted Co2Sn1−xFexO4 spinel oxides and its exchange bias effect. J. Phys. Condens. Matter 2024, 36, 425803. [Google Scholar] [CrossRef]
- Li, S.J.; Zhao, D.; Wang, S.; Cui, S.T.; Wang, N.Z.; Li, J.; Song, D.W.; Kang, B.L.; Zheng, L.X.; Nie, L.P.; et al. Emergent spin-glass state in the doped Hund’s metal CsFe2As2. Phys. Rev. B 2023, 107, 115144. [Google Scholar] [CrossRef]
- Lue, C.S.; Öner, Y.; Naugle, D.G.; Ross, J.H., Jr. Spin glass behavior in FeAl2. Phys. Rev. B 2001, 63, 184405. [Google Scholar] [CrossRef]
- Bao, S.; Wang, W.; Shangguan, Y.; Cai, Z.; Dong, Z.Y.; Huang, Z.; Si, W.; Ma, Z.; Kajimoto, R.; Ikeuchi, K.; et al. Neutron spectroscopy evidence on the dual nature of magnetic excitations in a van der Waals metallic ferromagnet Fe2.72GeTe2. Phys. Rev. X 2022, 12, 011022. [Google Scholar] [CrossRef]
- Binder, K.; Young, A.P. Spin glasses: Experimental facts, theoretical concepts, and open questions. Rev. Mod. Phys. 1986, 58, 801. [Google Scholar] [CrossRef]
- Yang, W.; Kan, X.; Liu, X.; Wang, Z.; Chen, Z.; Wang, Z.; Zhu, R.; Shezad, M. Spin glass behavior in Zn0.8−xNixCu0.2Fe2O4 (0 ≤ x ≤ 0.28) ferrites. Ceram. Int. 2019, 45, 23328–23332. [Google Scholar] [CrossRef]
- May, A.F.; Calder, S.; Cantoni, C.; Cao, H.; McGuire, M.A. Magnetic structure and phase stability of the van der Waals bonded ferromagnet Fe3−xGeTe2. Phys. Rev. B 2016, 93, 014411. [Google Scholar] [CrossRef]
- Seo, J.; Kim, D.Y.; An, E.S.; Kim, K.; Kim, G.Y.; Hwang, S.Y.; Kim, D.W.; Jang, B.G.; Kim, H.; Eom, G.; et al. Nearly room temperature ferromagnetism in a magnetic metal-rich van der Waals metal. Sci. Adv. 2020, 6, eaay8912. [Google Scholar] [CrossRef] [PubMed]
- Magen, C.; Algarabel, P.A.; Morellon, L.; Araújo, J.P.; Ritter, C.; Ibarra, M.R.; Pereira, A.M.; Sousa, J.B. Observation of a Griffiths-like phase in the magnetocaloric compound Tb5Si2Ge2. Phys. Rev. Lett. 2006, 96, 167201. [Google Scholar] [CrossRef] [PubMed]
- Deisenhofer, J.; Braak, D.; Krug von Nidda, H.A.; Hemberger, J.; Eremina, R.M.; Ivanshin, V.A.; Balbashov, A.M.; Jug, G.; Loidl, A.; Kimura, T.; et al. Observation of a griffiths phase in paramagnetic La1−xSrxMnO3. Phys. Rev. Lett. 2005, 95, 257202. [Google Scholar] [CrossRef]
- Liu, Y.; Ivanovski, V.N.; Petrovic, C. Critical behavior of the van der Waals bonded ferromagnet Fe3−xGeTe2. Phys. Rev. B 2017, 96, 144429. [Google Scholar] [CrossRef]
- Banerjee, B.K. On a generalised approach to first and second order magnetic transitions. Phys. Lett. 1964, 12, 16–17. [Google Scholar] [CrossRef]
- Chen, B.; Ohta, H.; Michioka, C.; Yoshimura, K. Intercalation and substitution effects of Si in weak itinerant ferromagnetic Ni3Al. J. Phys. Soc. Jpn. 2010, 79, 064707. [Google Scholar] [CrossRef]
- Shimizu, K.; Maruyama, H.; Yamazaki, H.; Watanabe, H. Effect of spin fluctuations on magnetic properties and thermal expansion in pseudobinary system FexCo1−xSi. J. Phys. Soc. Jpn. 1990, 59, 305–318. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, J.; Cao, Y.; Zou, Y.; Liu, M.; Wang, J.; Zhu, W.; Pan, M. Spin Glass State and Griffiths Phase in van der Waals Ferromagnetic Material Fe5GeTe2. Nanomaterials 2025, 15, 19. https://doi.org/10.3390/nano15010019
He J, Cao Y, Zou Y, Liu M, Wang J, Zhu W, Pan M. Spin Glass State and Griffiths Phase in van der Waals Ferromagnetic Material Fe5GeTe2. Nanomaterials. 2025; 15(1):19. https://doi.org/10.3390/nano15010019
Chicago/Turabian StyleHe, Jiaqi, Yuan Cao, Yu Zou, Mengyuan Liu, Jia Wang, Wenliang Zhu, and Minghu Pan. 2025. "Spin Glass State and Griffiths Phase in van der Waals Ferromagnetic Material Fe5GeTe2" Nanomaterials 15, no. 1: 19. https://doi.org/10.3390/nano15010019
APA StyleHe, J., Cao, Y., Zou, Y., Liu, M., Wang, J., Zhu, W., & Pan, M. (2025). Spin Glass State and Griffiths Phase in van der Waals Ferromagnetic Material Fe5GeTe2. Nanomaterials, 15(1), 19. https://doi.org/10.3390/nano15010019





