Abstract
Topological insulators (TIs) can be widely applied in the fields of ultrafast optical and spintronic devices owing to the existence of topologically protected gapless Dirac surface states. However, the study of ultrafast dynamics of carriers in TIs remains elusive. In this work, the carrier dynamics of Li-doped Bi2−xSe3 single crystals were investigated by femtosecond (fs) transient optical spectroscopy (ΔR/R(t) signals). The temperature dependence for the relaxation rates of the electron–electron interaction and electron–phonon coupling is consistent with the results of electrical transport, which indicates the carrier dynamics of TI is highly related with carrier concentrations. We find that the carrier type and concentration of Bi2Se3 can be tuned by Li doping, leading to a metal-insulation transition at low temperatures (T ≤ 55 K), indicating that electron–electron interactions are dominant at low temperature. For T > 55 K, electron–phonon coupling in the bulk carriers becomes the main electric transport mechanism.
1. Introduction
Bismuth selenide (Bi2Se3) is classified as a three-dimensional (3D) topological insulator (TI) and has attracted intense interest due to its sizable bulk band gap (~0.3 eV) and gapless metallic surface states [1,2,3], topologically protected by time reversal symmetry [4,5,6] and spin–orbit interactions [7,8]. The unique transport properties of the topological surface state (TSS) have broad potential applications in the fields of ultrafast optical and spintronic devices [9,10,11]. These tunable electronic high-speed devices can be designed based on the different mechanisms of electron energy relaxation in 3D and 2D states associated with the electron–phonon interaction and deformation potential/thermoelastic scattering, respectively [12,13,14,15,16]. Previously, the ultrafast dynamics of TIs has been reported. For example, the thickness dependence [16,17,18] and the temperature dependence [19,20,21,22] of ultrafast dynamics in TIs have been studied. Qi et al. [23] found that the ultrafast carrier and phonon dynamics of Bi2Se3 crystals are affected by the environment. As recently reported by Tu et al. [24] and Shi et al. [25], the ultrafast dynamics of Bi2Se3 are sensitive to impurities. These results indicate that the ultrafast dynamics of Bi2Se3 can be effectively tuned by multiple factors, suggesting that the topological insulator Bi2Se3 has broad potential application in the field of tunable optoelectronic devices. Understanding the ultrafast dynamics of Bi2Se3 is essential for future optoelectronic and spintronic applications.
In addition, bulk Bi2Se3 is actually poorly insulating due to the intrinsic Se vacancy. To achieve a bulk-insulating state in Bi2Se3, hole doping to compensate for the residual electrons is a viable strategy. Tremendous research interest in metal-doped TIs has been focused on p doping. For example, Mn doping can change the carrier type from n-type to p-type [26]. Cd doping can suppress the formation of Se vacancies and tune the carrier type and density in Bi2Se3, and achieve insulating behavior [27]. Doping of Nb, Sr, and Cu can induce superconductivity in Bi2Se3 [28]. The Fermi energy of Bi2Se3 can be tuned by 1% Mg doping to realize quantum topological transport [29]. However, with strong metallic properties, the light element of lithium (Li)-doped Bi2Se3 has not yet been reported. In previous studies, Li ions have been injected into layered materials and tuned the material properties [30,31,32]. Therefore, introducing Li into Bi2Se3 is feasible and may lead to change in the properties as well as the ultrafast dynamics of Bi2Se3.
In this work, LixBi2−xSe3 crystals were synthesized by the self-flux method. The crystal structure and surface morphology were characterized. The ultrafast dynamics of the bulk and surface states were investigated by both electrical transport measurements and femtosecond transient optical spectroscopy. The R-T curve and the data of Hall measurements show that the carriers in Bi2Se3 can be tuned by the Li impurities. Femtosecond (fs) transient optical spectroscopy (ΔR/R(t) signals) was measured and analyzed to obtain the ultrafast dynamics parameters. The temperature dependence of the relaxation rate of the electron–electron interaction and electron–phonon coupling is found to be consistent with the results of electrical transport. The results indicate that electron–electron interaction is dominated by surface state carriers at low temperatures (T ≤ 55 K), and electron–phonon coupling is dominated by bulk carriers at T > 55 K.
2. Experimental Section
LixBi2−xSe3 (x = 0, 0.02, 0.05 and 0.08) crystals were synthesized by melting high-purity (99.999%) bismuth, selenium powders, and Li particles (Aladdin, Shanghai, China) in their molar ratio at 850° C in a high-vacuum quartz tube. The evacuated quartz tubes were slowly (3.8° C/h) cooled to 620° C. Finally, the samples were quenched in cold water. The test samples were exfoliated flakes from the LixBi2−xSe3 block, the size ws~3.0 mm × 1.5 mm, and the thickness was about 650 nm (see the Supplementary Materials part S1).
The fresh surfaces for all samples were tested by X-ray diffraction (XRD, X’Pert Panalytical, Almelo, The Netherlands) with Cu Kα emission (λ = 1.5418Å). at room temperature. The microstructure was examined with field emission scanning electron microscopy (FESEM, JSM−7001F, Japan Electron Optics Laboratory Co., Ltd.). Electrical transport properties were examined by a Physical Property Measurement System (PPMS, Quantum Design, USA) at temperatures ranging from 5 K to 300 K using the standard four-probe method.
Using femtosecond (fs) pump-femtosecond (fs) probe spectroscopy (Coherent, USA), the ΔR/R0 (t) measurements were performed using a commercial mode-locked Ti: sapphire laser system (~35 fs pulse duration, 800 nm center wavelength, and 80 MHz repetition rate). Both pump and probe laser beams were focused onto the sample with a spot diameter of ~30 mm2. The pump and probe beam fluence was 10.0 J/cm2 and 1.00 J/cm2, respectively.
3. Results and Discussion
Figure 1a shows the XRD patterns for the LixBi2−xSe3 crystals. All the diffraction peaks are attributed to the (0 0 l) orientation of Bi2Se3 without an obvious impurity phase, which indicates that the samples have a pure c-axis orientation. The lattice constants of the c-axis were calculated, as shown in Figure 1b. With Li contents ranging from 0 to 0.08, the parameter c increases from 28.66 Å, 28.82 Å, 28.63 Å and 28.86 Å. The results indicate that Li atoms are mixed into the Bi2Se3 crystal.
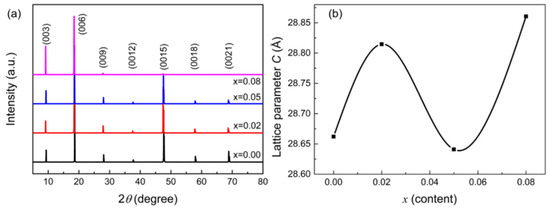
Figure 1.
(a) The crystal structure of LixBi2−xSe3. (b) The lattice parameter c of LixBi2−xSe3.
Simultaneously, we also provided the ICP-OES data in the Supplementary Materials, and the results of ICP-OES indicated that the content of Li was consistent with the stoichiometric ratio in the LixBi2−xSe3 single crystals (see Table S1 of the Supplementary Materials part S2). The Li + ion radius is 0.59 Å, and the Bi3 + ion radius is 0.96 Å. When Li replaces the Bi position in the Bi2Se3 crystal, the lattice parameters of the c axis will decrease. Conversely, the lattice parameters increase for x = 0.02 and 0.08. This result implies that Li may not succeed in replacing Bi and enters the van der Waals layers in between two adjacent quintuple layers (QLs); the larger Li atomic radius (1.54 Å) leads to an increase in the lattice parameters. This result is similar to the c-axis lattice parameters of BS magnetism of Upreti et al. in regulating the changes in the c-axis lattice parameters of FePS3 by Lithium Intercalation [32].
To prove this speculation, the microstructure of the samples was detected by FESEM. The results are shown in Figure 2. Multilayered structures were observed in all samples. Meanwhile, nanoparticles were found to exist in the interlayers of Li-doped samples, as shown in Figure 2b. For the Li (x = 0.02 and 0.08) sample, nanoparticles were abundant. The results implied that Li impurities enter the interlayers of samples, and the Li atomic radius is larger than Bi, resulting in an increase in the lattice in the c direction (see the Figure 1b). With the increase in doping amount of 5%, Li impurities diffuse into QLs, the number of Bi atoms that are replaced increases, and the lattice parameters of the sample are reduced. Further, the impurity of Li continues to increase to 8%, more impurity elements may enter the interlayer and inlayer of the crystal, the van der Waals interlayer once again demonstrates nanoclusters, and the lattice parameters increase. The X-ray photoelectron spectroscopy (XPS) of samples further support this inference. From Figure 2e and f, the peak area of Li + 1s (centered on the 54.9 eV) increases with the increase in doping amount, indicating that the relative content of Li + increases in the samples. This result confirms our prediction based on the XRD data.

Figure 2.
FESEM images of LixBi2−xSe3: (a) x = 0.00; (b) x = 0.02; (c) x = 0.05; (d) x = 0.08; (e) and (f) the XPS spectra of the Li0.02Bi1.98Se3 and Li0.05Bi1.95Se3.
In addition, the carrier type [24], concentration [25], and temperature-dependent characteristics [19,20,21,22] of Bi2Se3 crystals have a significant influence on the ultrafast dynamics. To analyze the influence of Li impurities on different ultrafast relaxation processes of Bi2Se3 crystals, the electric transport properties, carrier type, and concentration were measured, as shown in Figure 3. The temperature dependence of the electrical resistance was measured by a PPMS, which shows a typical metal-insulation transition in the low-temperature region for Li-doped samples, as shown in Figure 3a. The metal-insulation transition temperature is marked by the dotted line at approximately 55 K. For T ≤ 55 K, the resistance decreases with increasing temperature, showing insulating behavior for the LixBi2−xSe3 crystals. For T > 55 K, the resistance of the samples increases with temperature and demonstrates a metallic behavior. It is known that the as-grown crystals of Bi2Se3 display metallic behavior due to the electrons donated by Se vacancies. Chemical doping can drive the Fermi level into the topological gap, leading to nonmetallic behavior [33,34,35]. In Figure 3b, we have obtained Hall coefficients (RH) of samples at different temperatures. When Li impurity is introduced in the Bi2Se3 crystal, RH is changed from negative to positive, indicating that Li impurities provide the holes that compensate for the Se vacancy defects of Bi2Se3, and the Fermi energy sits within the gap. Insulating behavior is observed at T ≤ 55 K in Figure 3a. This phenomenon has been reported in previous studies, which can be explained by the fact that bulk carriers freeze out and surface-state carriers dominate the conductivity in the low-temperature regions, while bulk conductance dominates in the high-temperature regions [36,37,38]. From Figure 3c, the carrier concentration (n) of pristine Bi2Se3 and 2% remained almost constant at T ≤ 55 K. When the Li doping amount increases to 5%, n increases with temperature at T > 50 K. The results indicate that the surface state may be enhanced by Li impurities. According to the previous report by Hong et al., [39] the transport behavior of the Bi2Se3 is dominated by surface-state electrons at low temperatures, and the bulk carrier activity gradually plays a crucial role as the temperature rises. At T ≤ 55 K, the carrier conduction (e.g., phonon) in the bulk carrier is suppressed, and the electron–electron scattering of the materials is dominant in the electric transport behavior [39]. Then, the carriers (e.g., electron) are tuned by Li doping, which leads to the Fermi level adjusting to the gap, and the electrical transport behavior of the material is manifested as an insulating state. For T > 55 K, the bulk phonons activity is gradually enhanced, n increases rapidly with temperature, the electron–phonon coupling of the bulk carrier dominates the electric transport behavior, and the resistance increases with increasing temperature [39].
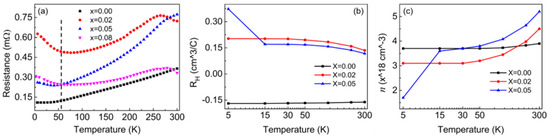
Figure 3.
(a) Temperature-dependent resistance of LixBi2−xSe3 crystals in zero magnetic field (dashed lines are used to indicate the metal-insulation transition temperature of the Li-doped samples, T ~55 K); (b) the Hall coefficient RH and (c) carrier concentration n of LixBi2−xSe3 (x = 0, 0.02, 0.05) at different temperatures.
The special electric transport mechanism of LixBi2−xSe3 is highly related with the dynamic response of nonequilibrium charge carriers in surface states, and it is necessary to further study the ultrafast dynamics of LixBi2−xSe3 crystals. At present, fs transient optical spectroscopy has been widely used to study the ultrafast dynamics of topological insulators [40,41,42]. The ultrafast dynamics of Bi2Se3 has especially been widely studied [14,15,16,17,40,43]. Therefore, femtosecond (fs) transient optical spectroscopy was performed to characterize the LixBi2−xSe3 crystals; Figure 4a shows the evolution of Li0.02Bi1.98Se3 crystals with increasing temperature, and the fs transient optical spectroscopy of other samples (e.g., pure Bi2Se3, 5% Li-doped, and 8% Li-doped) are shown in the Supplementary Materials (see the Supplementary Materials part S3). As shown in Figure 4a, the ΔR/R0 (t) time series was collected from 5 to 280 K, and it is found that the relaxation signal does not return to the equilibrium position at long timescales (1000 ps) below 190 K, which indicates a long relaxation process in the ultrafast response of the samples. And the spectra of all Li-doped samples show similar variation patterns, as shown in Figure S2. However, similar behavior was not observed in Bi2Se3 crystals [43] (see the Supplementary Materials part S4; the relaxation signals have returned to the equilibrium position at 50 ps), which may be due to Li impurities. Meanwhile, the ΔR/R0 (t) traces show a rise and multiple decay behavior in the initial few picoseconds (ps), which is typical for Bi2Se3 crystals [23,43]. The ΔR/R0 (t) experimental data for the samples were fitted by three exponential functions to obtain the decay time constants, and Equation (1) can be written as
where Ai and τi are the amplitude and relaxation time of the decay of hot carriers via different relaxation mechanisms. C is a constant. The three times constants of the three relaxation processes in LixBi2−xSe3 crystals can be fitted by Equation (1), where τ1 is the time constant of electron–electron interaction, τ2 is the time constant of the carrier recombination process, and τ3 is the time constant of electron–phonon coupling.
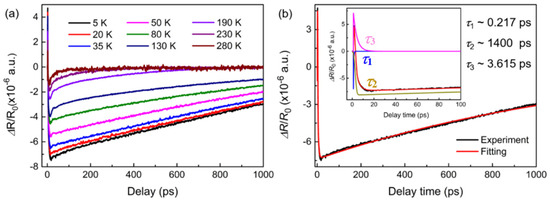
Figure 4.
(a) Femtosecond (fs) transient optical spectroscopy (ΔR/R(t) signals) measured for Li0.02Bi1.98Se3 at various temperatures ranging from 5 K to 280 K. (b) Representative differential reflectivity at 5 K; the red line is a fit to Equation (1). Inset: demonstration of three independent exponential relaxation processes with time constants of τ1 (blue line), τ2 (light brown line), and τ3 (pink line).
The fitting results for Li0.02Bi1.98Se3 at 5 K are shown in Figure 4b. The decay times τ1 and τ3 at 5 K are determined to be approximately 0.217 ps and 3.615 ps, respectively, consistent with the report of Qi et al. [23]. τ2 is approximately equal to 1400 ps; this result is given only for reference due to experimental test limitations. In fact, the relaxation time of τ2 could be longer. As shown in Table 1, the three relaxation times of LixBi2−xSe3 at different characteristic temperatures are presented.

Table 1.
The three relaxation times of the LixBi2−xSe3 at different characteristic temperatures.
From Table 1, compared with the pure Bi2Se3, the ultrafast dynamics of the Li-doped samples is different. For τ1, especially, it has an advantage in terms of the time scale. And τ2 represents a new relaxation process. A similar process in Bi2Se3 thin films has been reported [44,45,46], which was attributed to the carrier recombination process. In this paper, it is speculated that a shallow impurity band exists below the bulk conduction band, which provides a large number of holes to capture hot carriers, the carrier recombination process is slower, and a longer relaxation time is detected. Figure 5b shows a diagram for τ2. With increasing temperature, the defect carrier motion is intensified, and the hot carrier recombination process is promoted. Therefore, the relaxation time of τ2 decreases to 190 ~130 ps at 280K. Luo et al. once observed similar ΔR/R(t) signals in CuxBi2Se3−y samples [47]. Their research results indicated that the negative component in ΔR/R, which is assigned to carrier relaxation in a Dirac cone, is 1.62 ps and 20.5 ps, respectively [47]. The reason for this result might be that different impurity particles are introduced into the Bi2Se3 system by different methods and concentrations, resulting in different ultrafast carrier dynamics processes and different relaxation times. Thus, Bi2Se3 materials doped with different elements can be applied in various fields.
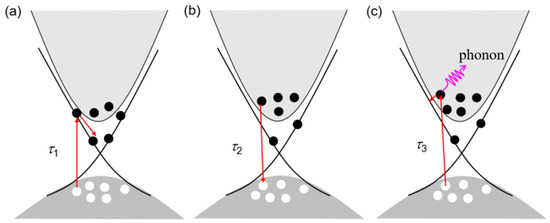
Figure 5.
Schematic diagram of three relaxation processes in LixBi2−xSe3 crystals: (a) τ1 is the time constant of electron–electron interaction (the electrons in the valence band are excited to the surface state by the laser, and relax to equilibrium along the channel provided by the surface state); (b) τ2 is the time constant of carrier recombination process; and (c) τ3 is the time constant of electron–phonon coupling (the electrons in the valence band are excited to the conduction band by the laser, coupling with the phonon, and relax to the equilibrium).
According to previous reports, τ1 and τ3 can be attributed to the electron–electron interaction and electron–phonon coupling of hot carriers [12,13,19,23,48], which is shown in Figure 5a and Figure 5c, respectively. The fitting data for all samples are shown in Figure 6. Figure 6a and Figure 6b show the temperature dependence of τ1 for the LixBi2−xSe3 crystals, where τ1 and τ1−1 are the relaxation time and relaxation rate of the electron–electron interaction, respectively. From Figure 6a,b, we find that the value of τ1 first increases and then decreases with increasing temperature, and the trend for τ1−1 shows the opposite behavior. The temperature dependence of τ1 and τ1−1 is consistent with the R-T and carrier concentration. The results show that the electrical transport properties of the LixBi2−xSe3 crystals are related to the electron–electron relaxation mechanism. At low temperatures (T ≤ 55 K), the electron–electron scattering of the surface state is dominant in the electric transport behavior. However, a large number of impurity carriers are introduced by Li doping, which tune the surface state via hole capture by surface-state electrons. Simultaneously, Li impurities are introduced to regulate the electronic structure and Fermi levels of Bi2Se3 crystals, leading to the closure of partial carrier channels, an increase in the electron–electron relaxation time and a slowdown in the rate. With increasing temperature, the bulk carriers enhance the electron–electron interaction, and the relaxation becomes faster.
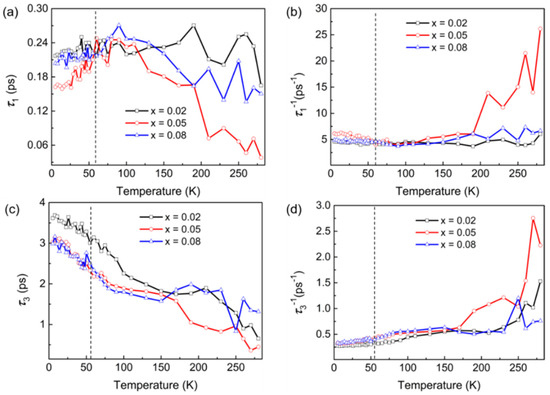
Figure 6.
(a,b) The inverse of the decay time constants (τ1 and τ1−1) at different temperatures for LixBi2−xSe3. (c,d) The inverse of the decay time constants (τ3 and τ3−1) at different temperatures for LixBi2−xSe3.
The relaxation process for τ3 is attributed to electron–phonon coupling, as shown in Figure 6c,d. The relaxation time (τ3) becomes shorter from 5 K to 280 K. In particular, τ3−1 is very slow at low temperatures. The variation in τ3 and τ3−1 is also consistent with the R-T and carrier concentration. The temperature dependence of τ3 and τ3-1 indicates that the electron–phonon coupling is weak at low temperature (T ≤ 55 K).
The result can be explained by the so-called two temperature model (TTM), which is treated as an ultrafast transient of electron–phonon thermalization [18,19,49,50]. The main idea of the TTM is that electron–electron thermalization is much faster than electron–phonon thermalization. However, this basic assumption fails at low temperatures (T ≤ 50 K) [50]. Electrons thermalize with the lattice in a characteristic electron–phonon thermalization time, which in metals is typically in the 100 fs–1 ps range [51]. The relationship between the electron–phonon coupling strength and relaxation time can be deduced from the TTM, which is expressed as follows:
Here, λ is the electron–phonon coupling strength, τe−ph is the electron–phonon coupling relaxation time, w is the phonon vibration frequency, kB is the Boltzmann constant, ℏ = h/2π, h is the Planck constant, and Te is the electron temperature. When T ≤ 55 K, TTM fails, phonons are suppressed by temperature, electron–phonon coupling is weaker, and τe−ph is long, as shown in Figure 6c,d. At higher temperature, phonons soften due to lattice expansion, the electron–phonon coupling strength increases, the relaxation time decreases, and the relaxation rate increases. The results further indicate that the electron–electron scattering of the surface state dominates the conductance of the LixBi2−xSe3 crystals at low temperature (T ≤ 55 K), and the electron–phonon coupling of the bulk carrier dominates the conductance at T > 55 K. This result is consistent with the suggestion that surface phonons are less effective in cooling the electron gas in the conduction band [48].
In addition, at T ≤ 55 K, no obvious dependence of the three relaxation processes on doping is observed. These results may be related to the small amount of Li replacing Bi. Li + replaces Bi3+, and fewer impurity carriers have less effect on the surface states, which cannot be reflected in the relaxation process dominated by the surface state at low temperature. However, the 5% Li-doped samples still showed differences, which further indicated that Li replacing Bi was more favorable for surface-state enhancement. At a higher temperature (T >150 K), the relaxation rate of Li0.05Bi1.95Se3 becomes obviously faster. This result is consistent with the carrier concentration at the different temperature, which suggested the response of τ1 and τ3 may be related to the carrier concentration. Previously, several groups have reported that carrier dynamics of TI can be influenced by carrier concentration [44,46,52,53]. These results indicate that Bi is replaced, which shows an advantage in the ultrafast relaxation process that is dominated by the bulk carrier. Furthermore, it has also been reported that electron–electron scattering and Mott modes coexist at low temperatures. When the Mott range-varying transition mode is dominant, electrons can jump between energy levels that are close in energy but far apart, thereby causing the metal-insulator transition [36,54]. At this point, we speculate that the minor changes in τ1 and τ3 around 55K may also be related to the metal-insulation transition of the material.
4. Conclusions
In this paper, LixBi2−xSe3 crystals were synthesized by the self-flux method. The crystalline structure was characterized by XRD and SEM, and the results showed that Li impurities are introduced into Bi2Se3 crystals. The R-T curve and the data of Hall measurements show that the carriers in Bi2Se3 can be tuned by the Li impurities. Femtosecond (fs) transient optical spectroscopy (ΔR/R(t) signals) was measured and analyzed to obtain the ultrafast dynamics parameters. The temperature dependence for the relaxation rates of the electron–electron interaction and electron–phonon coupling is consistent with the results of electrical transport. The results indicate that electron–electron interaction is dominated by free carriers at low temperatures (T ≤ 55 K), and electron–phonon coupling is dominated by bulk carriers at T > 55 K.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/nano15131010/s1, Figure S1: The samples of LixBi2−xSe3 crystals; Figure S2: (a) and (b) Representative ΔR/R0(t) time series of single crystal LixBi2−xSe3 at 5–280 K. (c) and (d) Representative ΔR/R0(t) time series of single crystal LixBi2−xSe3 within 15 ps; Figure S3: (a) Representative ΔR/R0(t) time series of single crystal Bi2Se3 at 5–280 K. (b) ΔR/R0(t) time series at 5 K and the fitting with Equation (1); Table S1: Li content for all samples [33,55].
Author Contributions
Methodology, Q.L.; software, M.Z.; investigation, Q.L. and M.Z.; writing—original draft preparation, Q.L. and M.Z.; writing—review and editing, M.P.; funding acquisition, X.Y., T.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported by the project of the Science and Technology Department of Sichuan Province (No. 2025ZNSFSC1139, 2023ZYD0175), the Chengdu University of Information Technology Talent Introduction Project (No. KYTZ202248), the Innovation Team Funds of China West Normal University (No. KCXTD2024–4). The authors would like to thank the Analytical and Testing Center of Southwest Jiaotong University for the efficient cooperation. Y. Zhao is grateful to the Fujian Normal University and Chengdu University, China for the financial support of the talent project.
Data Availability Statement
The original contributions presented in this study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Moore, J.E. The birth of topological insulators. Nature 2010, 464, 194–198. [Google Scholar] [CrossRef] [PubMed]
- Xia, Y.; Qian, D.; Hsieh, D.; Wray, L.; Pal, A.; Lin, H.; Bansil, A.; Grauer, D.; Hor, Y.S.; Cava, R.J.; et al. Observation of a large-gap topological-insulator class with a single Dirac cone on the surface. Nat. Phys. 2009, 5, 398–402. [Google Scholar]
- Brahlek, M.; Kim, Y.S.; Bansal., N.; Edrey, E.; Oh, S. Surface versus bulk state in topological insulator Bi2Se3 under environmental disorder. Appl. Phys. Lett 2011, 99, 012109. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, C.X.; Qi, X.L.; Dai, X.; Zhong, F.; Zhang, S.C. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 2009, 5, 438–442. [Google Scholar] [CrossRef]
- Ahmad, F.; Kumar, R.; Kushvaha, S.S.; Kumar, M.; Kumar, P. Charge transfer induced symmetry breaking in GaN/Bi2Se3 topological heterostructure device. npj 2D Mater. Appl. 2022, 6, 12. [Google Scholar] [CrossRef]
- He, P.; Isobe, H.; Zhu, D.; Hsu, C.H.; Fu, L.; Yang, H. Quantum frequency doubling in the topological insulator Bi2Se3. Nat. Commun. 2021, 12, 1–7. [Google Scholar] [CrossRef]
- Jeong, K.; Park, H.; Chae, J.; Sim, K.I.; Yang, W.J.; Kim, J.H.; Hong, S.B.; Kim, J.H.; Cho, M.H. Topological Phase Control of Surface States in Bi2Se3 via Spin−Orbit Coupling Modulation through Interface Engineering between HfO2−x. ACS Appl. Mater. Interfaces 2020, 12, 12215–12226. [Google Scholar] [CrossRef]
- Clark, O.J.; Freyse, F.; Yashina, L.V.; Rader, O.; Sánchez-Barriga, J. Robust behavior and spin-texture stability of the topological surface state in Bi2Se3 upon deposition of gold. Npj Quantum Mater. 2022, 7, 36. [Google Scholar] [CrossRef]
- Steinberg, H.; Gardner, D.R.; Lee, Y.S.; Jarillo-Herrero, P. Surface state transport and ambipolar electric field effect in Bi2Se3 nanodevices. Nano Lett. 2010, 10, 5032–5036. [Google Scholar] [CrossRef]
- Sun, J.; Singh, D.J. Using gapped topological surface states of Bi2Se3 films in a field effect transistor. J. Appl. Phys. 2017, 121, 064301. [Google Scholar] [CrossRef]
- Viti, L.; Coquillat, D.; Politano, A.; Kokh, K.A.; Aliev, Z.S.; Babanly, M.B.; Tereshchenko, O.E.; Knap, W.; Chulkov, E.V.; Vitiello, M.S. Plasma-Wave Terahertz Detection Mediated by Topological Insulators Surface States. Nano Lett. 2016, 16, 80–87. [Google Scholar] [CrossRef] [PubMed]
- Sobota, S.J.A.; Yang, S.L.; Leuenberger, D.; Kemper, A.F.; Analytis, J.G.; Fisher, I.R.; Kirchmann, P.S.; Devereaux, T.P.; Shen, Z.-X. Distinguishing bulk and surface electron-phonon coupling in the topological insulator Bi2Se3 using time-resolved photoemission spectroscopy. Phys. Rev. Lett. 2014, 113, 157401. [Google Scholar] [CrossRef] [PubMed]
- Sadasivam, S.; Chan, M.K.Y.; Darancet, P. Theory of thermal relaxation of electrons in semiconductors. Phys. Rev. Lett. 2017, 119, 136602. [Google Scholar] [CrossRef] [PubMed]
- Glinka, Y.D.; He, T.; Sun, X.W. Dynamic opening of a gap in Dirac surface states of the thin-film 3D topological insulator Bi2Se3 driven by the dynamic Rashba effect. J. Phys. Chem. Lett. 2021, 12, 5593–5600. [Google Scholar] [CrossRef]
- Glinka, Y.D.; Li, J.; He, T.; Sun, X.W. Clarifying ultrafast carrier dynamics in ultrathin films of the topological insulator Bi2Se3 using transient absorption spectroscopy. ACS Photonics 2021, 8, 1191–1205. [Google Scholar] [CrossRef]
- Glinka, Y.D.; Babakiray, S.; Johnson, T.A.; Lederman, D. Thickness tunable quantum interference between surface phonon and Dirac plasmon states in thin films of the topological insulator Bi2Se3. J. Phys.: Condens. Matter. 2015, 27, 052203. [Google Scholar] [CrossRef]
- Kim, S.; Shin, D.H.; Kim, J.H.; Jang, C.W.; Park, J.W.; Lee, H.; Choi, S.-H.; Kim, S.H.; Yee, K.-J.; Bansal, N.; et al. Resonance effects in thickness-dependent ultrafast carrier and phonon dynamics of topological insulator Bi2Se3. Nanotechnology 2015, 27, 045705. [Google Scholar] [CrossRef]
- Zhao, J.; Xu, Z.; Zang, Y.; Gong., Y.; Zheng, X.; He, K.; Cheng, X.A.; Jiang, T. Thickness-dependent carrier and phonon dynamics of topological insulator Bi2Te3 thin films. Opt. Express 2017, 25, 14635–14643. [Google Scholar]
- Lai, Y.P.; Chen, H.J.; Wu, K.H.; Liu, J.M. Temperature-dependent carrier–phonon coupling in topological insulator Bi2Se3. Appl. Phys. Lett. 2014, 105, 232110. [Google Scholar] [CrossRef]
- Kamboj, V.S.; Singh, A.; Ferrus, T. Probing the topological surface state in Bi2Se3 thin films using temperature-dependent terahertz spectroscopy. ACS Photonics 2017, 4, 2711–2718. [Google Scholar] [CrossRef]
- Kamaraju, N.; Kumar, S.; Sood, A.K. Temperature-dependent chirped coherent phonon dynamics in Bi2Te3 using high-intensity femtosecond laser pulses. EPL (Europhys. Lett. ) 2010, 92, 47007. [Google Scholar] [CrossRef]
- Cheng, L.; La-o-Vorakiat, C.; Tang, C.S.; Nair, S.K.; Xia, B.; Wang, L.; Zhu, J.-X.; Chia, E.E.M. Temperature-dependent ultrafast carrier and phonon dynamics of topological insulator Bi1.5Sb0.5Te1.8Se1.2. Appl. Phys. Lett. 2014, 104, 211906. [Google Scholar] [CrossRef]
- Qi, J.; Chen, X.; Yu, W.; Cadden-Zimansky, P.; Smirnov, D.; Tolk, N.H.; Miotkowski, I.; Cao, H.; Chen, Y.P.; Wu, Y.; et al. Ultrafast carrier and phonon dynamics in Bi2Se3 crystals. Appl. Phys. Lett. 2010, 97, 182102. [Google Scholar]
- Tu, J.; Zhao, Y.; Zhang, X.; Nie, Z.; Li, Y.; Zhang, Y.; Turcu, I.C.E.; Poletto, L.; Frassetto, F.; Ruan, X.; et al. Impurity band assisted carrier relaxation in Cr doped topological insulator Bi2Se3. Appl. Phys. Lett. 2021, 118, 081103. [Google Scholar] [CrossRef]
- Shi, T.; Kushnir, K.; Wang, Z.; Law, S.; Titova, L.V. Photoexcited free carrier dynamics in Bi2Se3, (Bi0.75In0.25) 2Se3, and (Bi0.50In0.50)2Se3: From topological to band insulator. ACS Photonics 2020, 7, 2778–2786. [Google Scholar] [CrossRef]
- Choi, Y.H.; Jo, N.H.; Lee, K.J.; Lee, H.W.; Jo, Y.H.; Kajino, J.; Takabatake, T.; Ko, K.T.; Park, J.-H.; Jung, M.H. Simple tuning of carrier type in topological insulator Bi2Se3 by Mn doping. Appl. Phys. Lett. 2012, 101, 152103. [Google Scholar] [CrossRef]
- Wang, Z.; Lin, T.; Wei, P.; Liu, X.; Dumas, R.; Liu, K.; Shi, J. Tuning carrier type and density in Bi2Se3 by Ca-doping. Appl. Phys. Lett. 2010, 97, 042112. [Google Scholar] [CrossRef]
- Sharma, M.M.; Sharma, P.; Karn, N.K.; Awana, V.P.S. Comprehensive review on topological superconducting materials and interfaces. Supercond. Sci. Technol. 2022, 35, 083003. [Google Scholar] [CrossRef]
- Kuroda, K.; Arita, M.; Miyamoto, K.; Ye, M.; Jiang, J.; Kimura, A.; Krasovskii, E.E.; Chulkov, E.V.; Iwasawa, H.; Okuda, T.; et al. Hexagonally deformed Fermi surface of the 3D topological insulator Bi2Se3. Appl. Phys. Lett. 2010, 105, 076802. [Google Scholar] [CrossRef]
- Li, Y.; Li, J.; Ye, M.; Zheng, F.; Zhang, Z.; Fu, J.; Duan, W.; Xu, Y. High-temperature quantum anomalous hall insulators in lithium-decorated iron-based superconductor materials. Phys. Rev. Lett. 2020, 125, 086401. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, Y.; Qi, S.; Chen, J.H. Gate-controlled magnetic transitions in Fe3GeTe2 with lithium ion conducting glass substrate. Chin. Phys. B 2021, 30, 097504. [Google Scholar] [CrossRef]
- Upreti, D.; Basnet, R.; Sharma, M.M.; Chhetri, S.K.; Acharya, G.; Nabi, M.R.U.; Sakon, J.; Da, B.; Mortazavi, M.; Hu., J. Tuning magnetism in ising-type van der waals magnet FePS3 by lithium intercalation. J. Phys. Condens. Matter. 2025, 37, 135805. [Google Scholar] [CrossRef] [PubMed]
- Checkelsky, J.G.; Hor, Y.S.; Cava, R.J.; Ong, N.P. Bulk Band Gap and Surface State Conduction Observed in Voltage-Tuned Crystals of the Topological Insulator Bi2Se3. Phys. Rev. Lett. 2011, 106, 196801. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Ma, Z.; Zhao, Y.; Meenakshi, S.; Wang, J. Transport properties of topological insulators films and nanowires. Chin. Phys. B 2013, 22, 067302. [Google Scholar] [CrossRef]
- Gopal, R.K.; Singh, S.; Mandal, A.; Sarkar, J.; Mitra, C. Topological delocalization and tuning of surface channel separation in Bi2Se2Te Topological Insulator Thin films. Sci. Rep. 2017, 7, 4924. [Google Scholar] [CrossRef]
- He, L.; Xiu, F.; Wang, Y.; Fedorov, A.V.; Huang, G.; Kou, X.; Lang, M.; Beyermann, W.P.; Zou, J.; Wang, K.L. Epitaxial growth of Bi2Se3 topological insulator thin films on Si (111). J. Appl. Phys. 2011, 109, 103702. [Google Scholar] [CrossRef]
- Zhang, M.; Wei, Z.; Jin, R.; Ji, Y.; Yan, Y.; Pu, X.; Yang, X.; Zhao, Y. Electrical transport properties and morphology of topological insulator Bi2Se3 thin films with different thickness prepared by magnetron sputtering. Thin Solid Films 2016, 603, 289–293. [Google Scholar] [CrossRef]
- Checkelsky, J.G.; Hor, Y.S.; Liu, M.H.; Qu, D.X.; Cave, R.J.; Ong, N.P. Quantum interference in macroscopic crystals of nonmetallic Bi2Se3. Phys. Rev. Lett. 2009, 103, 246601. [Google Scholar] [CrossRef]
- Hong, S.S.; Cha, J.J.; Kong, D.; Cui, Y. Ultra-low carrier concentration and surface-dominant transport in antimony-doped Bi2Se3 topological insulator nanoribbons. Nat. Commun. 2012, 3, 757. [Google Scholar] [CrossRef]
- Zhang, J.; Jiang, T.; Zhou, T.; Ouyang, H.; Zhang, C.; Xin, Z.; Wang, Z.; Cheng, X.A. Saturated absorption of different layered Bi2Se3 films in the resonance zone. Photonics Res. 2018, 6, C8–C14. [Google Scholar] [CrossRef]
- Park, D.; Jeong, K.; Maeng, I.H.; Kim, D.; Kwon, H.; Hong, S.-B.; Kim, J.-H.; Kee, C.-S.; Kang, C.; Cho, M.-H. Ultrafast Photo-Response by Surface State-Mediated Optical Transitions in Topological Insulator Bi2Te3 Nanowire. Adv. Opt. Mater. 2019, 7, 1900621. [Google Scholar] [CrossRef]
- Iyer, V.; Chen, Y.P.; Xu, X. Ultrafast surface state spin-carrier dynamics in the topological insulator Bi2Te2Se. Phys. Rev. Lett. 2018, 121, 026807. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Shao, R.; Li, N.; Lang, W.; Yang, X.; Luo, S.N.; Zhao, Y. Anharmonicity of Bi2Se3 revealed by fs transient optical spectroscopy. Appl. Phys. Lett. 2019, 115, 201902. [Google Scholar] [CrossRef]
- Glinka, Y.D.; Babakiray, S.; Johnson, T.A.; Holcomb, M.B.; Lederman, D. Effect of carrier recombination on ultrafast carrier dynamics in thin films of the topological insulator Bi2Se3. Appl. Phys. Lett. 2014, 105, 171905. [Google Scholar] [CrossRef]
- Kim, S.; Kim, Y.; Kim, J.; Choi, S.; Yun, K.; Kim, D.; Lim, S.Y.; Kim, S.; Chun, S.H.; Park, J.; et al. Ultrafast Carrier–Lattice Interactions and Interlayer Modulations of Bi2Se3 by X-ray Free-Electron Laser Diffraction. Nano Lett. 2021, 21, 8554–8562. [Google Scholar] [CrossRef]
- Jnawali, G.; Linser, S.; Shojaei, I.A.; Pournia, S.; Jackson, H.E.; Smith, L.M.; Need, R.F.; Wilson, S.D. Revealing optical transitions and carrier recombination dynamics within the bulk band structure of Bi2Se3. Nano Lett. 2018, 18, 5875–5884. [Google Scholar] [CrossRef]
- Luo, C.W.; Chen, H.-J.; Wang, H.J.; Ku, S.A.; Wu, K.H.; Uen, T.M.; Juang, J.Y.; Lin, J.-Y.; Young, B.L.; Kobayashi, T.; et al. Ultrafast dynamics in topological insulators. In Ultrafast Phenomena and Nanophotonics XVII; SPIE: Bellingham, WA, USA, 2013; Volume 8623, pp. 59–65. [Google Scholar]
- Crepaldi, A.; Ressel, B.; Cilento, F.; Zacchigna, M.; Grazioli, C.; Berger, H.; Bugnon, P.; Kern, K.; Grioni, M.; Parmigiani, F. Ultrafast photodoping and effective Fermi-Dirac distribution of the Dirac particles in Bi2Se3. Phys. Rev. B 2012, 86, 205133. [Google Scholar] [CrossRef]
- Giraud, S.; Egger, R. Electron-phonon scattering in topological insulators. Phys. Rev. B 2011, 83, 245322. [Google Scholar] [CrossRef]
- Hase, M.; Ishioka, K.; Demsar, J.; Ushida, K.; Kitajima, M. Ultrafast dynamics of coherent optical phonons and nonequilibrium electrons in transition metals. Phys. Rev. B 2005, 71, 184301. [Google Scholar] [CrossRef]
- Groeneveld, R.H.M.; Sprik, R.; Lagendijk, A. Femtosecond spectroscopy of electron-electron and electron-phonon energy relaxation in Ag and Au. Phys. Rev. B 1995, 51, 11433. [Google Scholar] [CrossRef]
- Onishi, Y.; Ren, Z.; Segawa, K.; Kaszub, W.; Lorenc, M.; Ando, Y.; Tanaka, K. Ultrafast carrier relaxation through Auger recombination in the topological insulator Bi1.5Sb0.5Te1.7Se1.3. Phys. Rev. B 2015, 91, 085306. [Google Scholar] [CrossRef]
- Glinka, Y.D.; Babakiray, S.; Holcomb, M.B.; Lederman, D. Effect of Mn doping on ultrafast carrier dynamics in thin films of the topological insulator Bi2Se3. J. Phys. Condens. Matter 2016, 28, 165601. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Lv, L.; Zhang, M.; Wei, Z.T.; Yang, L.Q.; Yang, X.S.; Zhao, Y. Enhanced contribution of surface state and modification of magnetoresistance in FexBi2−xSe3 topological insulator crystals. J. Appl. Phys. 2013, 113, 043923. [Google Scholar] [CrossRef]
- Wang, J.L.; Guo, L.; Ling, C.; Song, Y.M.; Xu, X.F.; Ni, Z.H.; Chen, Y.F. Carrier dynamics in femtosecond-laser-excited bismuth telluride. Phys. Rev. B 2016, 93, 155306. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).