Third Harmonic Generation in Thin NbOI2 and TaOI2
Abstract
1. Introduction
2. Materials and Methods
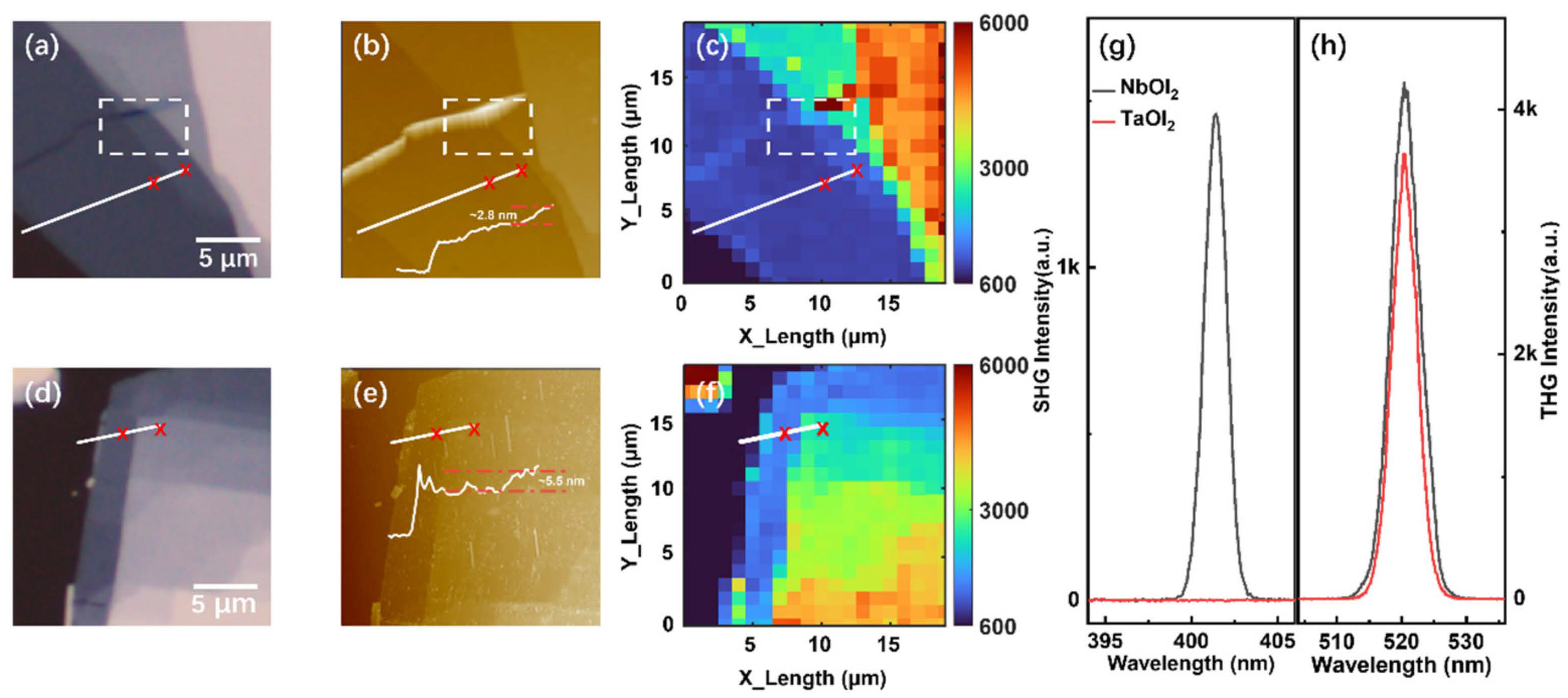
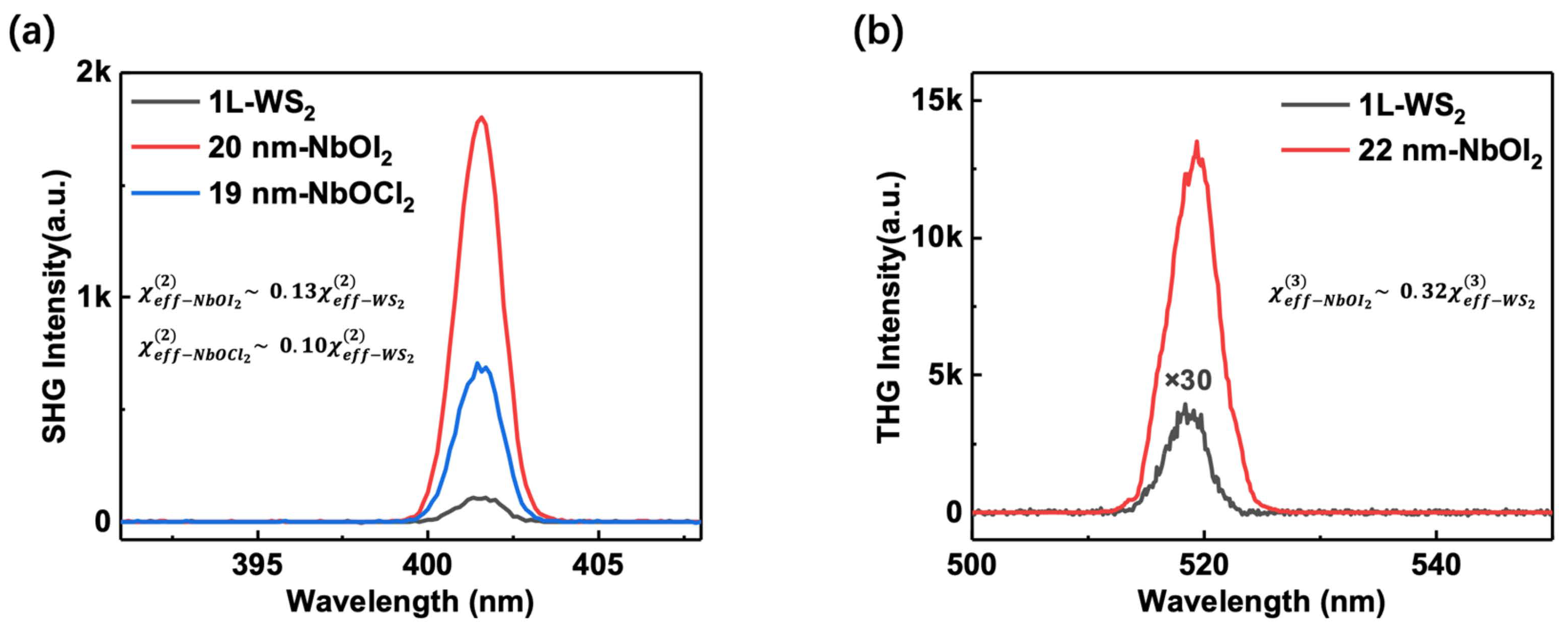
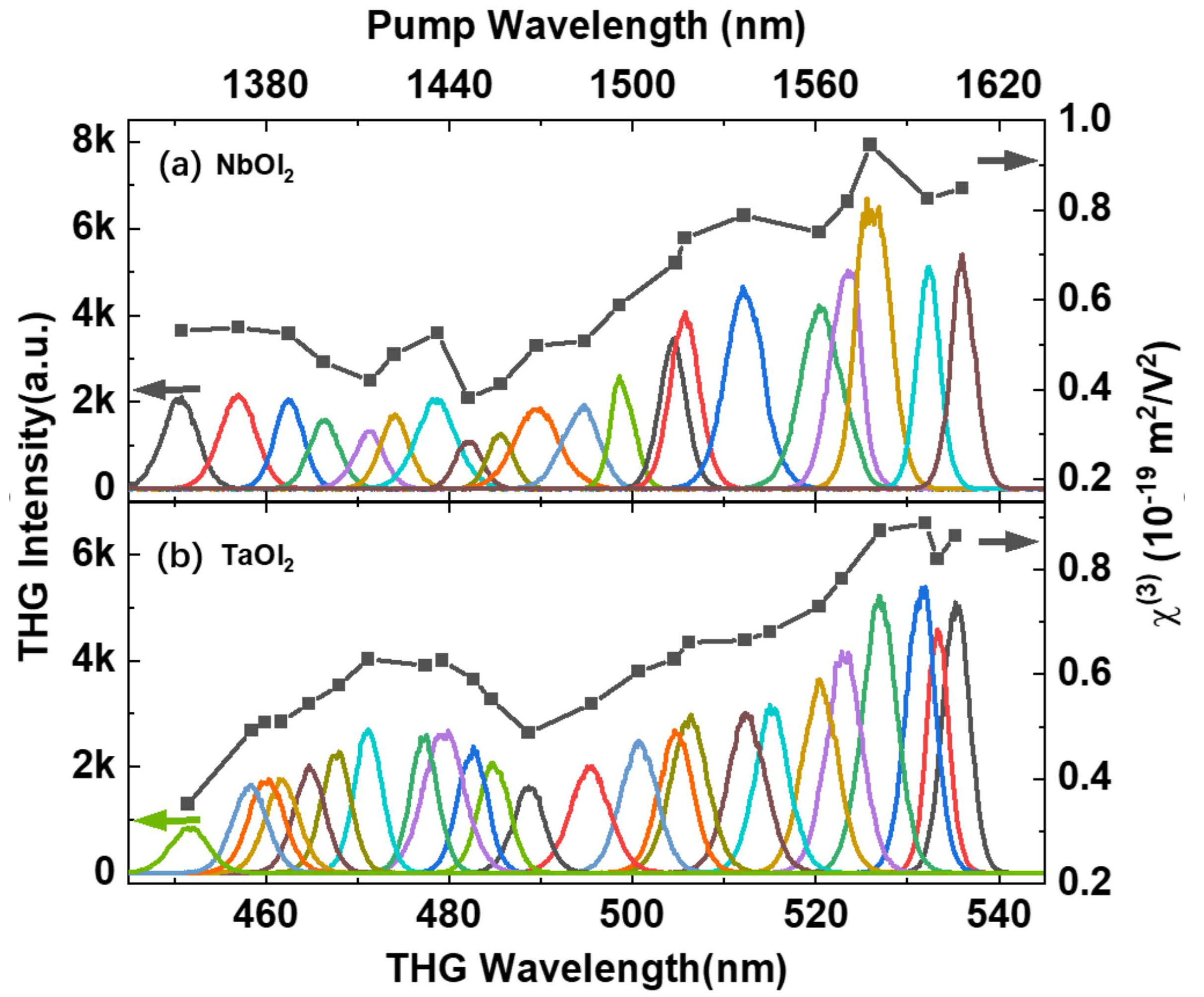
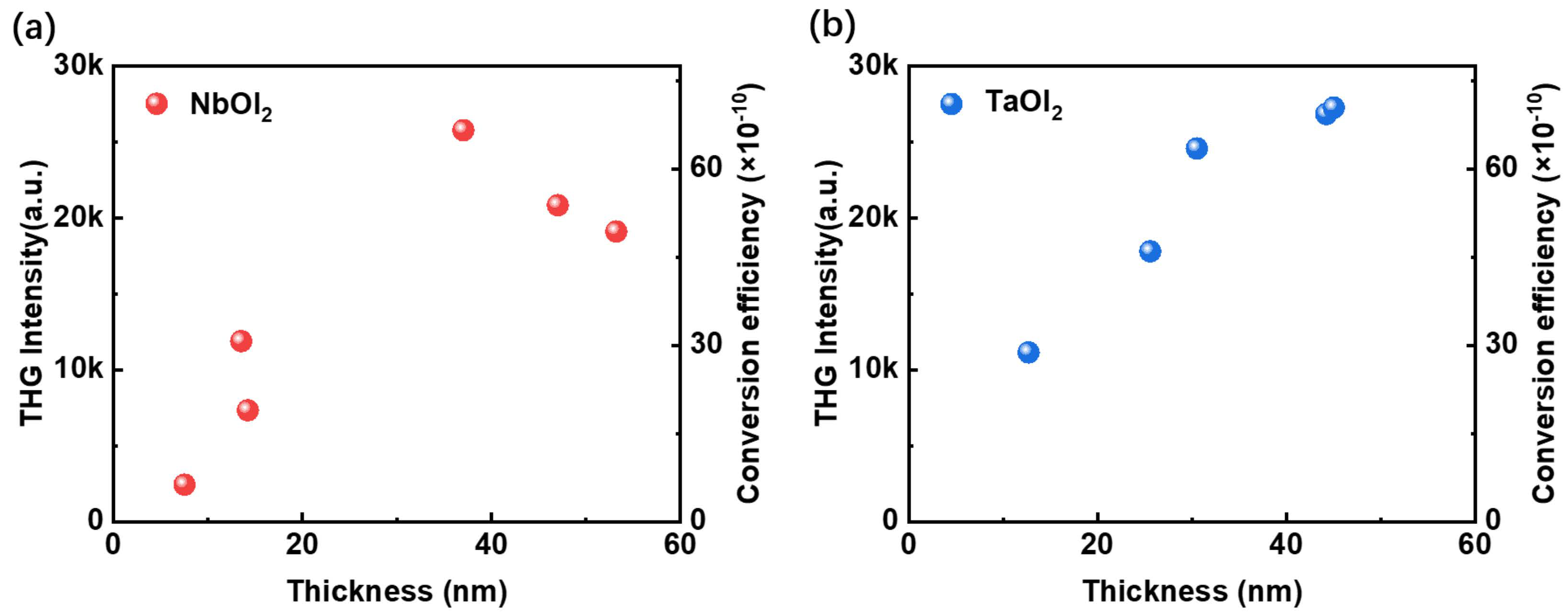
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Seyler, K.L.; Schaibley, J.R.; Gong, P.; Rivera, P.; Jones, A.M.; Wu, S.; Yan, J.; Mandrus, D.G.; Yao, W.; Xu, X. Electrical control of second-harmonic generation in a WSe2 monolayer transistor. Nat. Nanotechnol. 2015, 10, 407–411. [Google Scholar] [CrossRef]
- Preciado, E.; Schülein, F.J.R.; Nguyen, A.E.; Barroso, D.; Isarraraz, M.; von Son, G.; Lu, I.H.; Michailow, W.; Möller, B.; Klee, V.; et al. Scalable fabrication of a hybrid field-effect and acousto-electric device by direct growth of monolayer MoS2/LiNbO3. Nat. Commun. 2015, 6, 8593. [Google Scholar] [CrossRef]
- Sun, Z.; Martinez, A.; Wang, F. Optical modulators with 2D layered materials. Nat. Photon. 2016, 10, 227–238. [Google Scholar] [CrossRef]
- Li, Y.; Rao, Y.; Mak, K.F.; You, Y.; Wang, S.; Dean, C.R.; Heinz, T.F. Probing symmetry properties of few-layer MoS2 and h-BN by optical second-harmonic generation. Nano Lett. 2013, 13, 3329–3333. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.; Jia, B.; Chen, X.; Gu, M. In Situ Third-Order Non-linear Responses during Laser Reduction of Graphene Oxide Thin Films Towards On-Chip Non-linear Photonic Devices. Adv. Mater. 2014, 26, 2699–2703. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Marie, X.; Gerber, I.; Amand, T.; Lagarde, D.; Bouet, L.; Vidal, M.; Balocchi, A.; Urbaszek, B. Giant enhancement of the optical second-harmonic emission of WSe(2) monolayers by laser excitation at exciton resonances. Phys. Rev. Lett. 2015, 114, 097403. [Google Scholar] [CrossRef] [PubMed]
- Shree, S.; Lagarde, D.; Lombez, L.; Robert, C.; Balocchi, A.; Watanabe, K.; Taniguchi, T.; Marie, X.; Gerber, I.C.; Glazov, M.M.; et al. Interlayer exciton mediated second harmonic generation in bilayer MoS2. Nat. Commun. 2021, 12, 6894. [Google Scholar] [CrossRef] [PubMed]
- Lafeta, L.; Corradi, A.; Zhang, T.; Kahn, E.; Bilgin, I.; Carvalho, B.R.; Kar, S.; Terrones, M.; Malard, L.M. Second- and third-order optical susceptibilities across excitons states in 2D monolayer transition metal dichalcogenides. 2D Mater. 2021, 8, 035010. [Google Scholar] [CrossRef]
- Xiao, J.; Ye, Z.; Wang, Y.; Zhu, H.; Wang, Y.; Zhang, X. Nonlinear optical selection rule based on valley-exciton locking in monolayer ws2. Light Sci. Appl. 2015, 4, e366. [Google Scholar] [CrossRef]
- Khan, A.R.; Zhang, L.; Ishfaq, K.; Ikram, A.; Yildrim, T.; Liu, B.; Rahman, S.; Lu, Y. Optical Harmonic Generation in 2D Materials. Adv. Funct. Mater. 2021, 32, 2105259. [Google Scholar] [CrossRef]
- Autere, A.; Jussila, H.; Dai, Y.; Wang, Y.; Lipsanen, H.; Sun, Z. Nonlinear Optics with 2D Layered Materials. Adv. Mater. 2018, 30, e1705963. [Google Scholar] [CrossRef]
- Sun, Z.; Hasan, T.; Ferrari, A.C. Ultrafast lasers mode-locked by nanotubes and graphene. Phys. E Low-Dimens. Syst. Nanostruct. 2012, 44, 1082–1091. [Google Scholar] [CrossRef]
- Martinez, A.; Sun, Z. Nanotube and graphene saturable absorbers for fibre lasers. Nat. Photon. 2013, 7, 842–845. [Google Scholar] [CrossRef]
- Liu, X.; Guo, Q.; Qiu, J. Emerging Low-Dimensional Materials for Nonlinear Optics and Ultrafast Photonics. Adv. Mater. 2017, 29, 1605886. [Google Scholar] [CrossRef]
- Yu, S.; Wu, X.; Wang, Y.; Guo, X.; Tong, L. 2D Materials for Optical Modulation: Challenges and Opportunities. Adv. Mater. 2017, 29, 1606128. [Google Scholar] [CrossRef]
- Low, T.; Chaves, A.; Caldwell, J.D.; Kumar, A.; Fang, N.X.; Avouris, P.; Heinz, T.F.; Guinea, F.; Martin-Moreno, L.; Koppens, F. Polaritons in layered two-dimensional materials. Nat. Mater. 2017, 16, 182–194. [Google Scholar] [CrossRef]
- Malard, L.M.; Alencar, T.V.; Barboza, A.P.M.; Mak, K.F.; de Paula, A.M. Observation of intense second harmonic generation from MoS2 atomic crystals. Phys. Rev. B 2013, 87, 201401. [Google Scholar] [CrossRef]
- Hsu, W.-T.; Zhao, Z.-A.; Li, L.-J.; Chen, C.-H.; Chiu, M.-H.; Chang, P.-S.; Chou, Y.-C.; Chang, W.-H. Second Harmonic Generation from Artificially Stacked Transition Metal Dichalcogenide Twisted Bilayers. ACS Nano 2014, 8, 8. [Google Scholar] [CrossRef] [PubMed]
- Saynatjoki, A.; Karvonen, L.; Rostami, H.; Autere, A.; Mehravar, S.; Lombardo, A.; Norwood, R.A.; Hasan, T.; Peyghambarian, N.; Lipsanen, H.; et al. Ultra-strong nonlinear optical processes and trigonal warping in MoS2 layers. Nat. Commun. 2017, 8, 893. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Li, Y.; You, Y.S.; Ghimire, S.; Heinz, T.F.; Reis, D.A. High-harmonic generation from an atomically thin semiconductor. Nat. Phys. 2016, 13, 262–265. [Google Scholar] [CrossRef]
- Boyd, R. Nonlinear Optics; Academic Press: New York, NY, USA, 2007. [Google Scholar]
- Wen, X.; Gong, Z.; Li, D. Nonlinear optics of two-dimensional transition metal dichalcogenides. InfoMat 2019, 1, 317–337. [Google Scholar] [CrossRef]
- Hendry, E.; Hale, P.J.; Moger, J.; Savchenko, A.K.; Mikhailov, S.A. Coherent Nonlinear Optical Response of Graphene. Phys. Rev. Lett. 2010, 105, 097401. [Google Scholar] [CrossRef] [PubMed]
- Vermeulen, N.; Castelló-Lurbe, D.; Cheng, J.; Pasternak, I.; Krajewska, A.; Ciuk, T.; Strupinski, W.; Thienpont, H.; Van Erps, J. Negative Kerr Nonlinearity of Graphene as seen via Chirped-Pulse-Pumped Self-Phase Modulation. Phys. Rev. Appl. 2016, 6, 044006. [Google Scholar] [CrossRef]
- Kim, J.H.; Yee, K.J.; Lim, Y.S.; Booshehri, L.G.; Hároz, E.H.; Kono, J. Dephasing of G-band phonons in single-wall carbon nanotubes probed via impulsive stimulated Raman scattering. Phys. Rev. B 2012, 86, 161415. [Google Scholar] [CrossRef]
- Fang, Y.; Wang, F.; Wang, R.; Zhai, T.; Huang, F. 2D NbOI(2): A Chiral Semiconductor with Highly In-Plane Anisotropic Electrical and Optical Properties. Adv. Mater. 2021, 33, e2101505. [Google Scholar] [CrossRef]
- Mortazavi, B.; Shahrokhi, M.; Javvaji, B.; Shapeev, A.V.; Zhuang, X. Highly anisotropic mechanical and optical properties of 2D NbOX2 (X = Cl, Br, I) revealed by first-principle. Nanotechnology 2022, 33, 275701. [Google Scholar] [CrossRef]
- Abdelwahab, I.; Tilmann, B.; Wu, Y.; Giovanni, D.; Verzhbitskiy, I.; Zhu, M.; Berté, R.; Xuan, F.; Menezes, L.d.S.; Eda, G.; et al. Giant second-harmonic generation in ferroelectric NbOI2. Nat. Photon. 2022, 16, 644–650. [Google Scholar] [CrossRef]
- Fu, J.; Yang, N.; Liu, Y.; Liu, Q.; Du, J.; Fang, Y.; Wang, J.; Gao, B.; Xu, C.; Zhang, D.; et al. Emission Dipole and Pressure-Driven Tunability of Second Harmonic Generation in vdWs Ferroelectric NbOI2. Adv. Funct. Mater. 2023, 34, 2308207. [Google Scholar] [CrossRef]
- Guo, Q.; Qi, X.Z.; Zhang, L.; Gao, M.; Hu, S.; Zhou, W.; Zang, W.; Zhao, X.; Wang, J.; Yan, B.; et al. Ultrathin quantum light source with van der Waals NbOCl(2) crystal. Nature 2023, 613, 53–59. [Google Scholar] [CrossRef]
- Abdelwahab, I.; Tilmann, B.; Zhao, X.; Verzhbitskiy, I.; Berté, R.; Eda, G.; Wilson, W.L.; Grinblat, G.; Menezes, L.d.S.; Loh, K.P.; et al. Highly Efficient Sum-Frequency Generation in Niobium Oxydichloride NbOCl2 Nanosheets. Adv. Opt. Mater. 2023, 11, 2202833. [Google Scholar] [CrossRef]
- Fu, T.; Bu, K.; Sun, X.; Wang, D.; Feng, X.; Guo, S.; Sun, Z.; Fang, Y.; Hu, Q.; Ding, Y.; et al. Manipulating Peierls Distortion in van der Waals NbOX2 Maximizes Second-Harmonic Generation. J. Am. Chem. Soc. 2023, 145, 16828–16834. [Google Scholar] [CrossRef] [PubMed]
- Ruck, M. TAOI2—A Centrosymmetric Variant of NbOI2 Structure. Acta Crystallogr. C Struct. Commun. 1995, 51, 1960–1962. [Google Scholar] [CrossRef]
- Wu, Y.; Abdelwahab, I.; Kwon, K.C.; Verzhbitskiy, I.; Wang, L.; Liew, W.H.; Yao, K.; Eda, G.; Loh, K.P.; Shen, L.; et al. Data-driven discovery of high performance layered van der Waals piezoelectric NbOI(2). Nat. Commun. 2022, 13, 1884. [Google Scholar] [CrossRef]
- Blake, P.; Hill, E.W.; Castro Neto, A.H.; Novoselov, K.S.; Jiang, D.; Yang, R.; Booth, T.J.; Geim, A.K. Making graphene visible. Appl. Phys. Lett. 2007, 91, 063124. [Google Scholar] [CrossRef]
- Yin, X.; Ye, Z.; Chenet, D.A.; Ye, Y.; O’Brien, K.; Hone, J.C.; Zhang, X. Edge Nonlinear Optics on a MoS2 Atomic Monolayer. Science 2014, 344, 488–491. [Google Scholar] [CrossRef] [PubMed]
- Lin, K.I.; Ho, Y.H.; Liu, S.B.; Ciou, J.J.; Huang, B.T.; Chen, C.; Chang, H.C.; Tu, C.L.; Chen, C.H. Atom-Dependent Edge-Enhanced Second-Harmonic Generation on MoS2 Monolayers. Nano Lett. 2018, 18, 793–797. [Google Scholar] [CrossRef]
- Karvonen, L.; Saynatjoki, A.; Huttunen, M.J.; Autere, A.; Amirsolaimani, B.; Li, S.; Norwood, R.A.; Peyghambarian, N.; Lipsanen, H.; Eda, G.; et al. Rapid visualization of grain boundaries in monolayer MoS2 by multiphoton microscopy. Nat. Commun. 2017, 8, 15714. [Google Scholar] [CrossRef]
- Woodward, R.I.; Murray, R.T.; Phelan, C.F.; Oliveira, R.E.P.d.; Runcorn, T.H.; Kelleher, E.J.R.; Li, S.; Oliveira, E.C.d.; Fechine, G.J.M.; Eda, G.; et al. Characterization of the second- and third-order nonlinear optical susceptibilities of monolayer MoS2 using multiphoton microscopy. 2D Mater. 2017, 4, 011006. [Google Scholar] [CrossRef]
- Autere, A.; Jussila, H.; Marini, A.; Saavedra, J.R.M.; Dai, Y.; Säynätjoki, A.; Karvonen, L.; Yang, H.; Amirsolaimani, B.; Norwood, R.A.; et al. Optical harmonic generation in monolayer group-VI transition metal dichalcogenides. Phys. Rev. B 2018, 98, 115426. [Google Scholar] [CrossRef]
- Xia, M.J.; Xu, B.; Li, R.K. Growth and nonlinear optical properties of K3B6O10Br crystal. J. Cryst. Growth 2014, 404, 65–68. [Google Scholar] [CrossRef]
- Li, R.; Nie, W.; Shang, Z.; Cheng, C.; Akhmadaliev, S.; Zhou, S.; Lu, Q.; Chen, F. Guided-wave second harmonics in Nd:YCOB ridge waveguides produced by combination of carbon ion irradiation and precise diamond blade dicing. Opt. Mater. 2016, 57, 153–157. [Google Scholar] [CrossRef]
- Zhou, Y.; Yue, Y.; Wang, J.; Yang, F.; Cheng, X.; Cui, D.; Peng, Q.; Hu, Z.; Xu, Z. Nonlinear optical properties of BaAlBO3F2 crystal. Opt. Express 2009, 17, 20033–20038. [Google Scholar] [CrossRef] [PubMed]
- Popkova, A.A.; Antropov, I.M.; Fröch, J.E.; Kim, S.; Aharonovich, I.; Bessonov, V.O.; Solntsev, A.S.; Fedyanin, A.A. Optical Third-Harmonic Generation in Hexagonal Boron Nitride Thin Films. ACS Photon. 2021, 8, 824–831. [Google Scholar] [CrossRef]
- Youngblood, N.; Peng, R.; Nemilentsau, A.; Low, T.; Li, M. Layer-Tunable Third-Harmonic Generation in Multilayer Black Phosphorus. ACS Photon. 2016, 4, 8–14. [Google Scholar] [CrossRef]
- Ning, T.Y.; Hyvärinen, O.; Pietarinen, H.; Kaplas, T.; Kauranen, M.; Genty, G. Third-harmonic UV generation in silicon nitride nanostructures. Opt. Express 2013, 21, 2012–2017. [Google Scholar] [CrossRef] [PubMed]
- Lafrentz, M.; Brunne, D.; Rodina, A.V.; Pavlov, V.V.; Pisarev, R.V.; Yakovlev, D.R.; Bakin, A.; Bayer, M. Second-harmonic generation spectroscopy of excitons in ZnO. Phys. Rev. B 2013, 88, 235207. [Google Scholar] [CrossRef]
- Qian, C.; Villafañe, V.; Soubelet, P.; Ji, P.; Stier, A.V.; Finley, J.J. Probing the Dark Exciton in Monolayer MoS2 by Quantum Interference in Second Harmonic Generation Spectroscopy. arXiv 2023, arXiv:2309.02303v1. [Google Scholar]
- Soavi, G.; Wang, G.; Rostami, H.; Purdie, D.G.; De Fazio, D.; Ma, T.; Luo, B.; Wang, J.; Ott, A.K.; Yoon, D.; et al. Broadband, electrically tunable third-harmonic generation in graphene. Nat. Nanotechnol. 2018, 13, 583–588. [Google Scholar] [CrossRef]
- Jiang, T.; Huang, D.; Cheng, J.; Fan, X.; Zhang, Z.; Shan, Y.; Yi, Y.; Dai, Y.; Shi, L.; Liu, K.; et al. Gate-tunable third-order nonlinear optical response of massless Dirac fermions in graphene. Nat. Photon. 2018, 12, 430–436. [Google Scholar] [CrossRef]
- Alexander, K.; Savostianova, N.A.; Mikhailov, S.A.; Kuyken, B.; Van Thourhout, D. Electrically Tunable Optical Nonlinearities in Graphene-Covered SiN Waveguides Characterized by Four-Wave Mixing. ACS Photon. 2017, 4, 3039–3044. [Google Scholar] [CrossRef]
- Burns, W.K.; Bloembergen, N. Third-Harmonic Generation in Absorbing Media of Cubic or Isotropic Symmetry. Phys. Rev. B 1971, 4, 3437–3450. [Google Scholar] [CrossRef]
- Mishina, E.; Sherstyuk, N.; Lavrov, S.; Sigov, A.; Mitioglu, A.; Anghel, S.; Kulyuk, L. Observation of two polytypes of MoS2 ultrathin layers studied by second harmonic generation microscopy and photoluminescence. Appl. Phys. Lett. 2015, 106, 131901. [Google Scholar] [CrossRef]

| Material | THG Wavelength (nm) | Thickness | Substrate | Reference | ||
|---|---|---|---|---|---|---|
| NbOI2 | 450–535 | 0.4–0.9 | 22.9–114 (0.75) | 22 nm | SiO2/Si | This work |
| TaOI2 | 450–535 | 0.3–0.9 | 9.5–94.7 (0.75) | 20 nm | SiO2/Si | This work |
| WS2 | 520 | 3.2 | 1.4 (0.75) | ML | SiO2/Si | This work |
| WS2 | 520 | 2.4 | 28 (2.7) | ML | SiO2/Si | [40] |
| hBN | 360 | 0.084 | 5.3 (3.6) | 37 nm | Fused silica | [44] |
| BP | 519 | 1.4 | 6 (8.1) | 14.5 nm | SiO2/Si | [45] |
| Graphene | 520 | 1 | 5.4 (1.6) | ML | Glass | [39] |
| Silicon nitride | 355 | 0.28 | 0.2 (143) | 200 nm | Fused silica | [46] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, T.; Hu, D.; Lin, D.; Yang, L.; Shen, Z.; Yang, W.; Liu, H.; Li, H.; Fan, X.; Wang, Z.; et al. Third Harmonic Generation in Thin NbOI2 and TaOI2. Nanomaterials 2024, 14, 412. https://doi.org/10.3390/nano14050412
Tang T, Hu D, Lin D, Yang L, Shen Z, Yang W, Liu H, Li H, Fan X, Wang Z, et al. Third Harmonic Generation in Thin NbOI2 and TaOI2. Nanomaterials. 2024; 14(5):412. https://doi.org/10.3390/nano14050412
Chicago/Turabian StyleTang, Tianhong, Deng Hu, Di Lin, Liu Yang, Ziling Shen, Wenchen Yang, Haiyang Liu, Hanting Li, Xiaoyue Fan, Zhiwei Wang, and et al. 2024. "Third Harmonic Generation in Thin NbOI2 and TaOI2" Nanomaterials 14, no. 5: 412. https://doi.org/10.3390/nano14050412
APA StyleTang, T., Hu, D., Lin, D., Yang, L., Shen, Z., Yang, W., Liu, H., Li, H., Fan, X., Wang, Z., & Wang, G. (2024). Third Harmonic Generation in Thin NbOI2 and TaOI2. Nanomaterials, 14(5), 412. https://doi.org/10.3390/nano14050412







