Haptic-Based Real-Time Platform for Microswarm Steering in a Multi-Bifurcation Vascular Network
Abstract
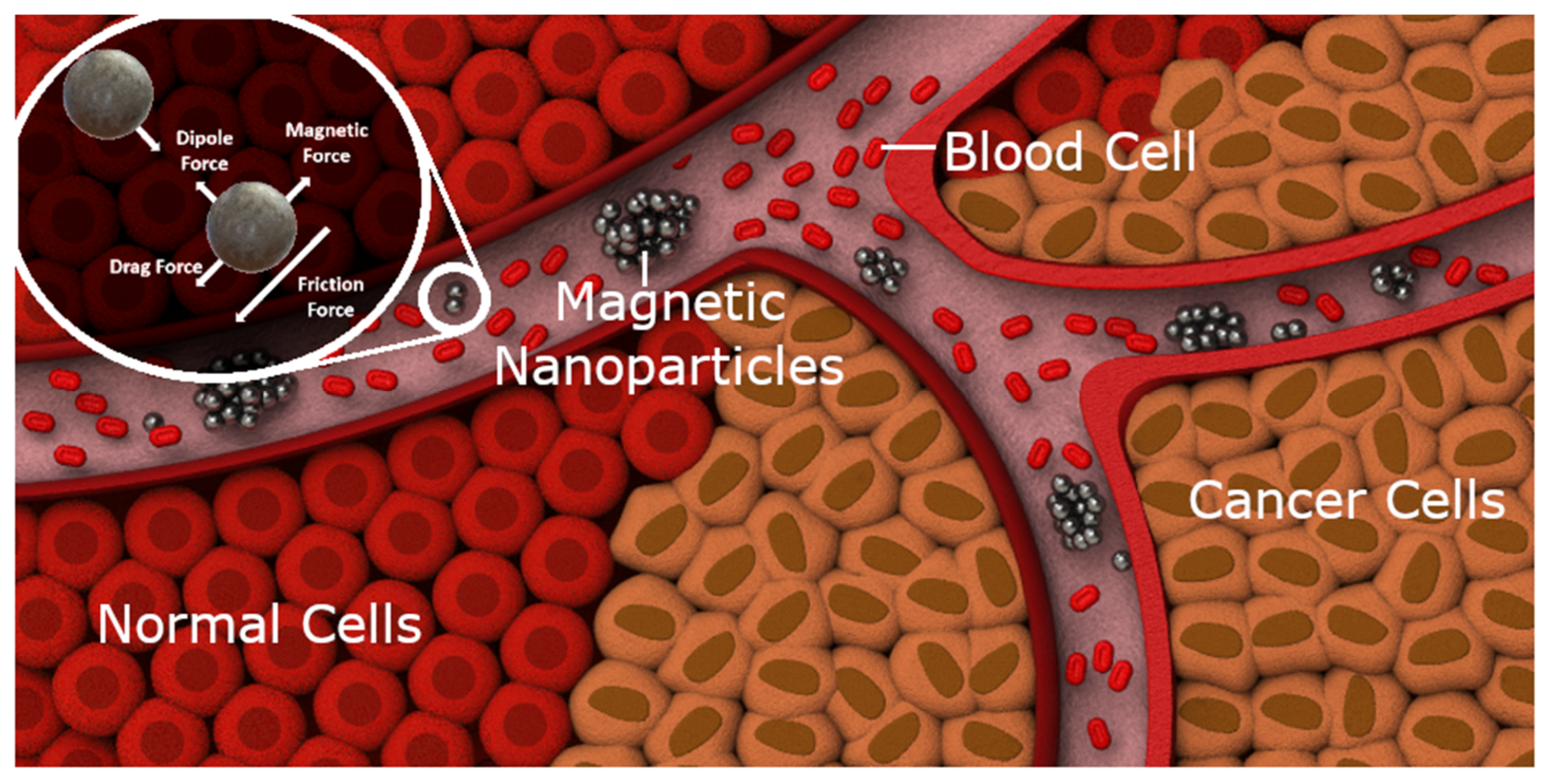
:1. Introduction
2. Materials and Methods
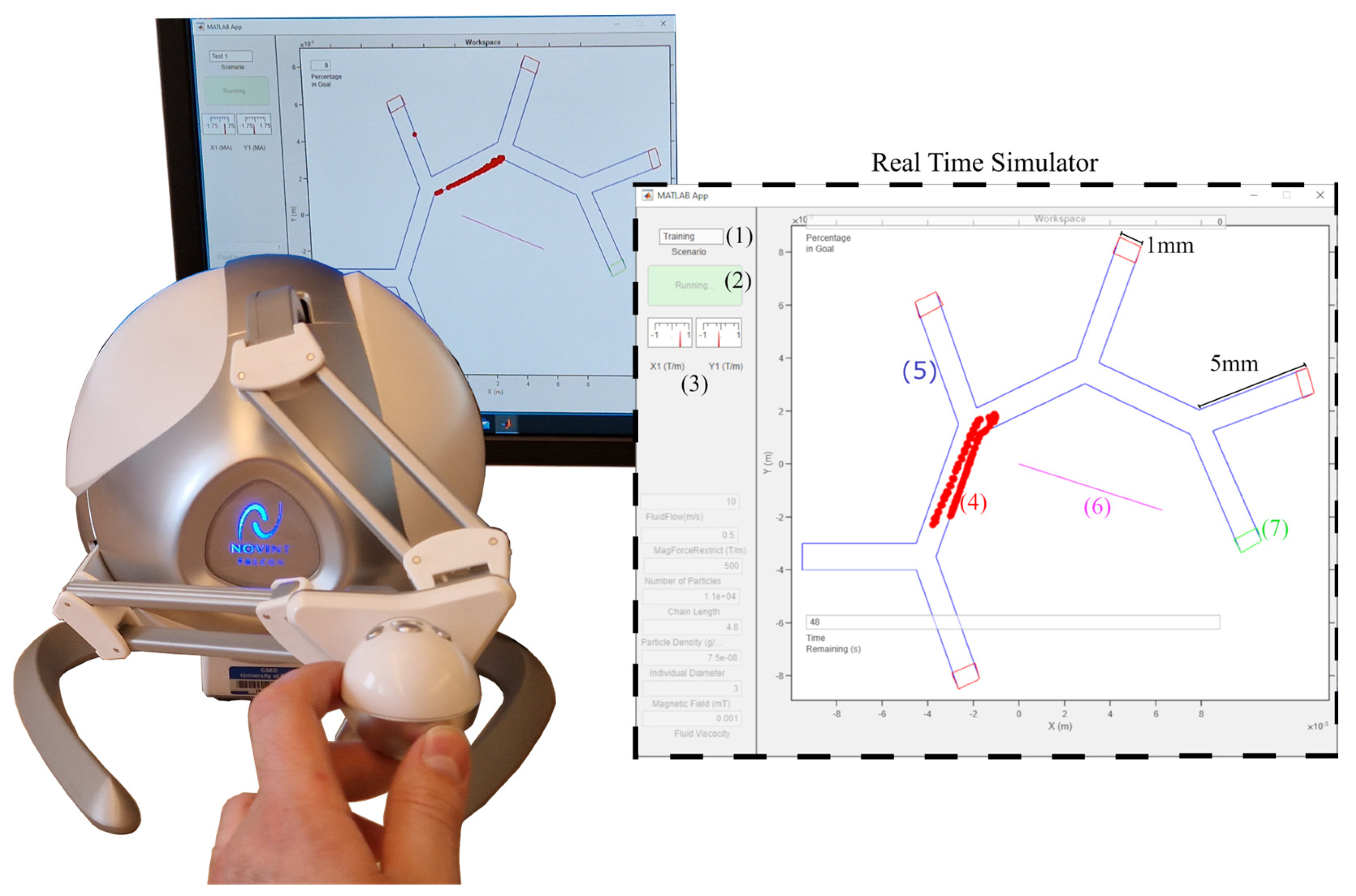
2.1. Design and Implementation
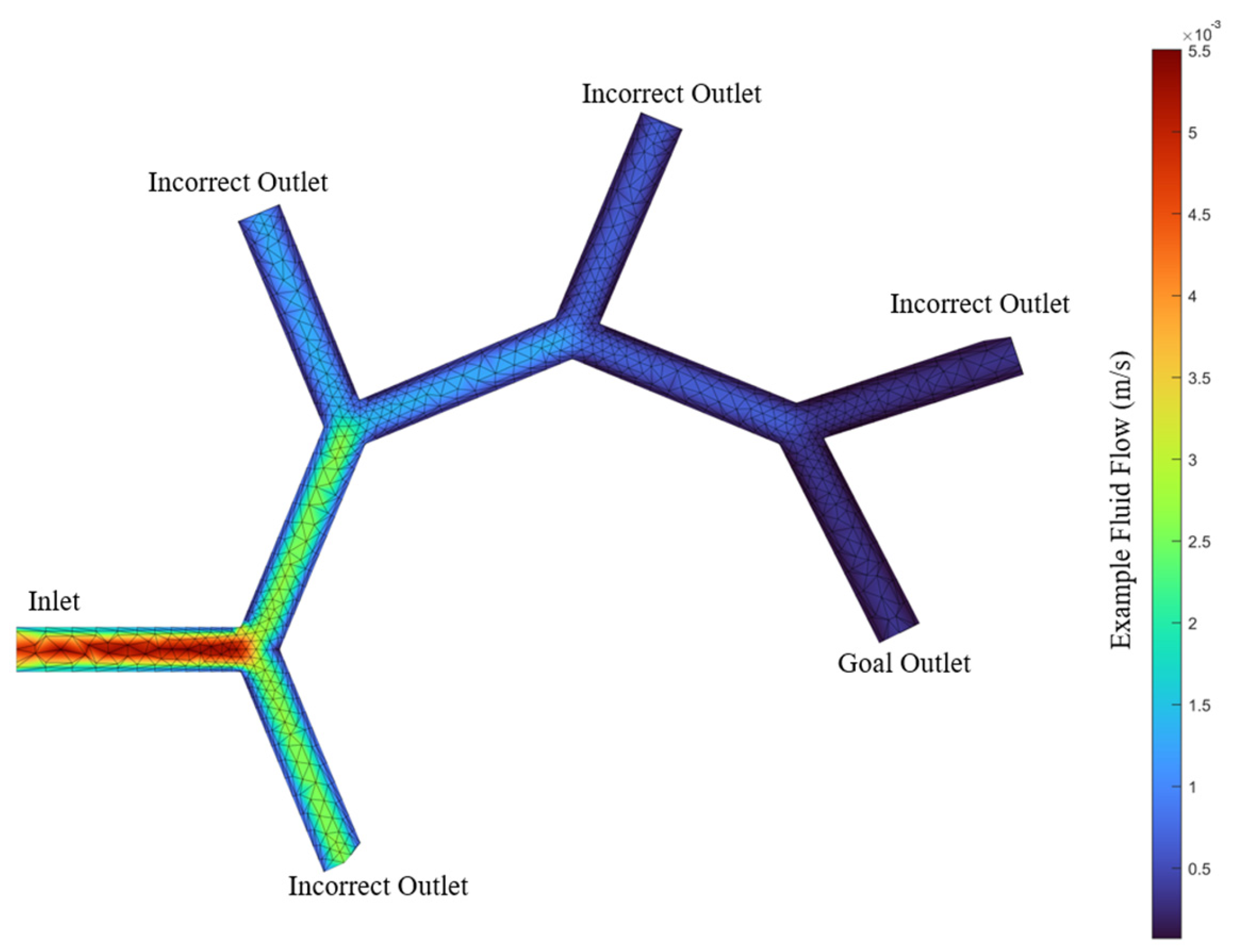
2.2. Mathematical Model for the Steering Platform
2.3. Experimental Study to Validate Simulator
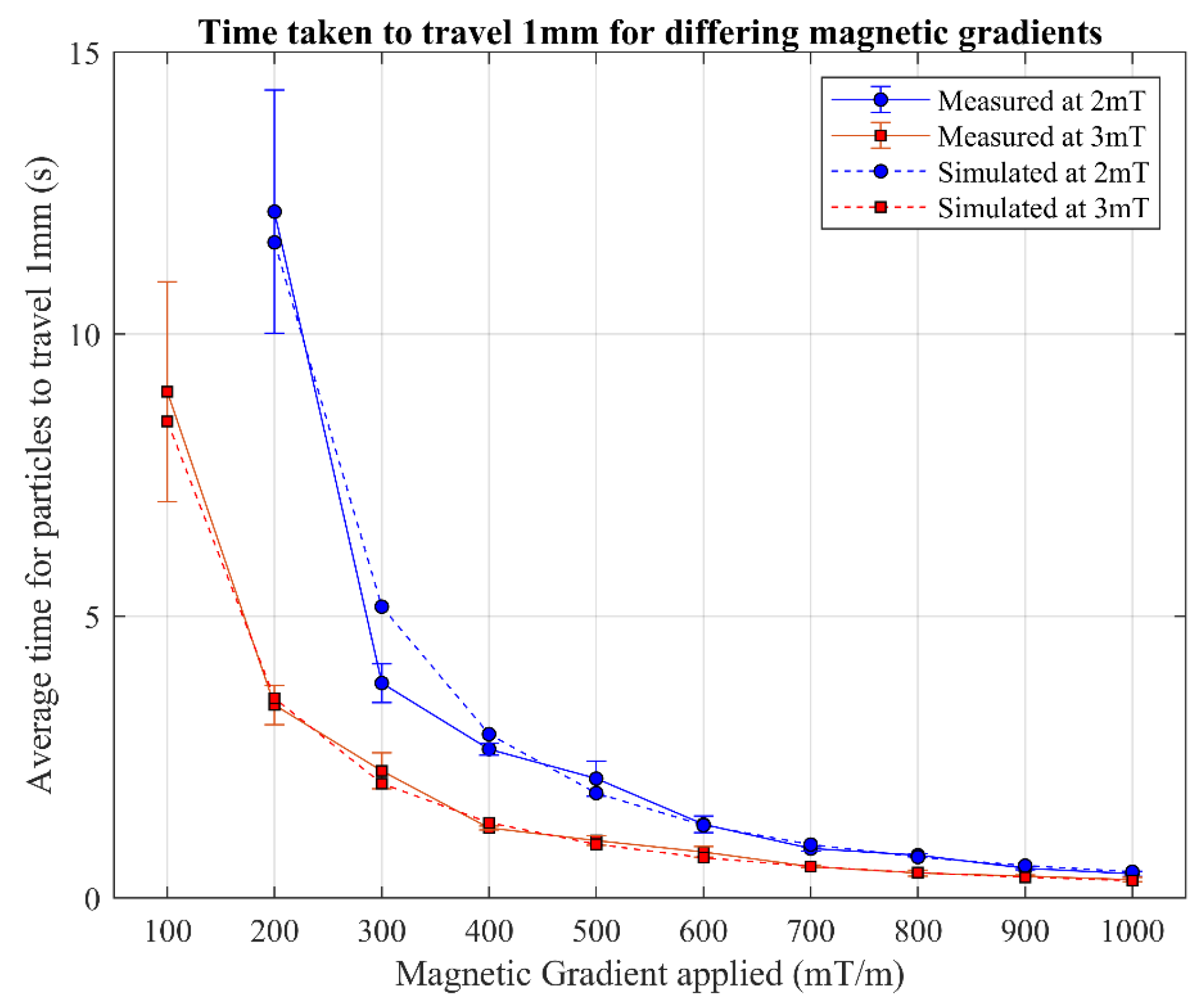
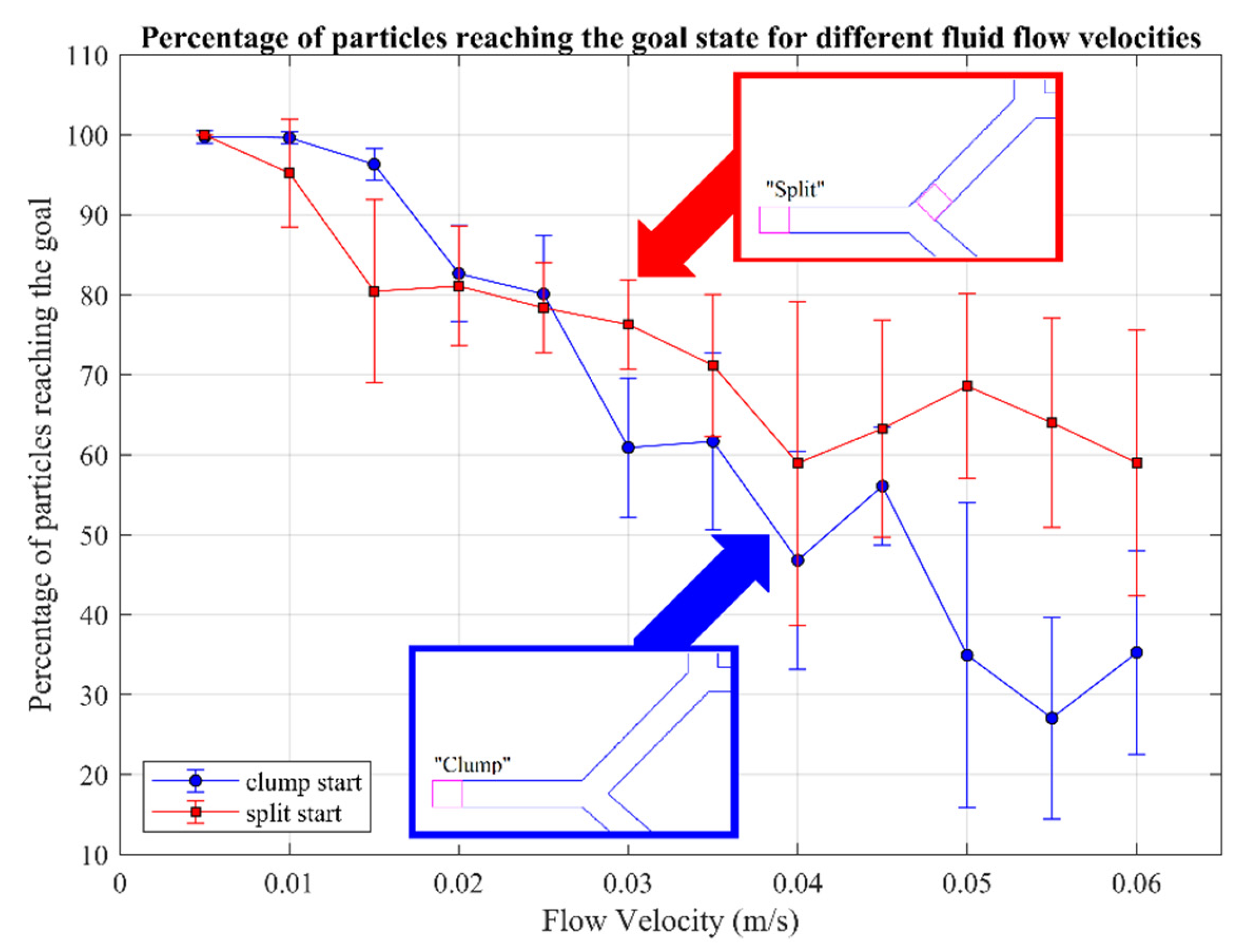
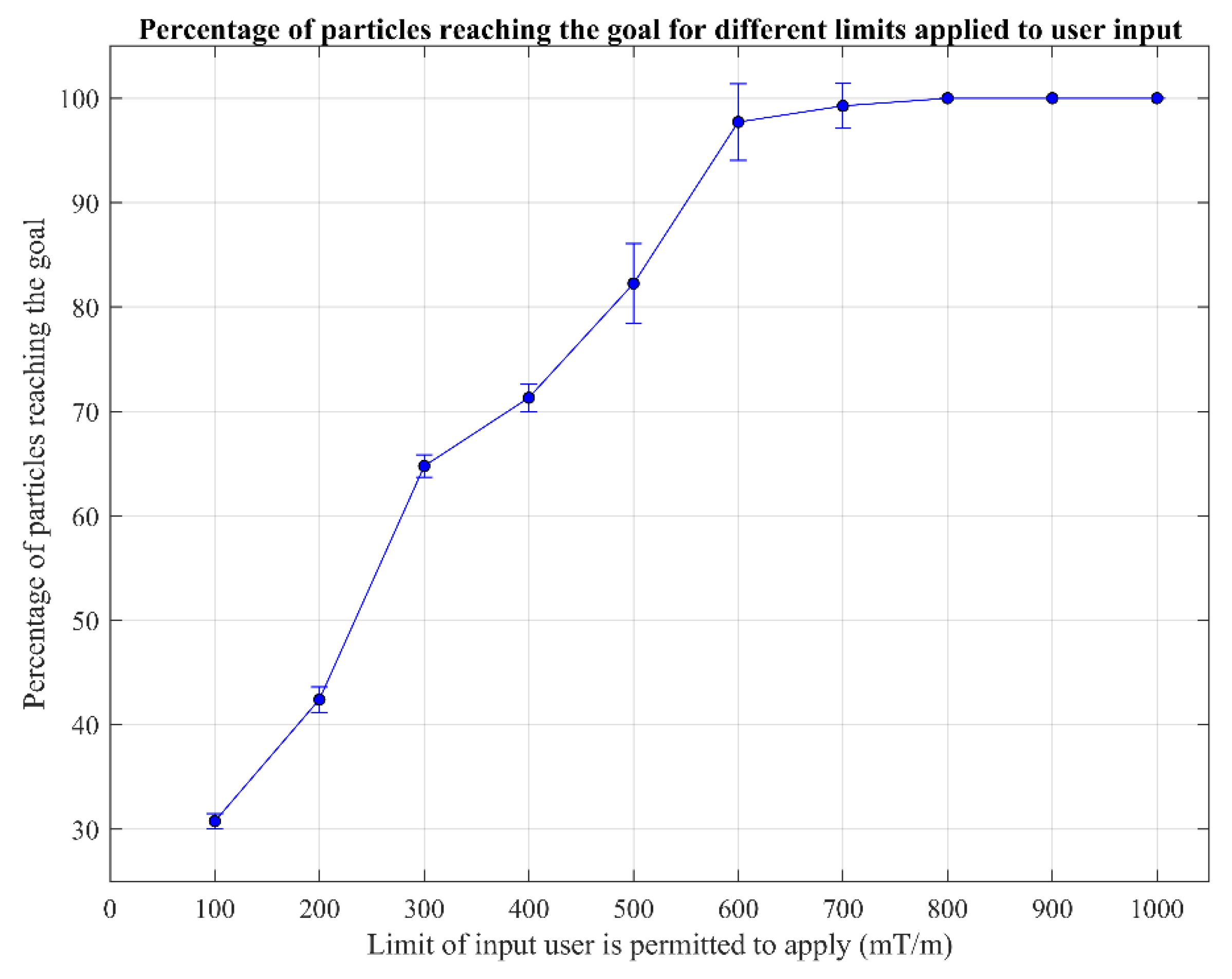
3. Results and Discussion
4. Conclusions and Future Work
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Staub, B.N.; Sadrameli, S.S. The use of robotics in minimally invasive spine surgery. J. Spine Surg. 2019, 5, S31. [Google Scholar] [CrossRef] [PubMed]
- Diaz-Aguilar, L.D.; Brown, N.J.; Bui, N.; Alvandi, B.; Pennington, Z.; Gendreau, J.; Jeswani, S.P.; Pham, M.H.; Santiago-Dieppa, D.R.; Nguyen, A.D. The Use of Robot-Assisted Surgery for the Unstable Traumatic Spine: A Retrospective Cohort Study. N. Am. Spine Soc. J. (NASSJ) 2023, 15, 100234. [Google Scholar] [CrossRef]
- Nelson, B.J.; Kaliakatsos, I.K.; Abbott, J.J. Microrobots for Minimally Invasive Medicine. Annu. Rev. Biomed. Eng. 2010, 12, 55–85. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Zhang, L. Motion control in magnetic microrobotics: From individual and multiple robots to swarms. Annu. Rev. Control Robot. Auton. Syst. 2021, 4, 509–534. [Google Scholar] [CrossRef]
- Sitti, M. Voyage of the microrobots. Nature 2009, 458, 1121–1122. [Google Scholar] [CrossRef]
- Xu, T.; Yu, J.; Yan, X.; Choi, H.; Zhang, L. Magnetic actuation based motion control for microrobots: An overview. Micromachines 2015, 6, 1346–1364. [Google Scholar] [CrossRef]
- Zhang, L.; Abbott, J.J.; Dong, L.; Kratochvil, B.E.; Bell, D.; Nelson, B.J. Artificial bacterial flagella: Fabrication and magnetic control. Appl. Phys. Lett. 2009, 94, 064107. [Google Scholar] [CrossRef]
- Hoshiar, A.K.; Le, T.-A.; Faiz, A.U.; Myeong, K.O.; Yoon, J. Studies of aggregated nanoparticles steering during magnetic-guided drug delivery in the blood vessels. J. Magn. Magn. Mater. 2017, 427, 181–187. [Google Scholar] [CrossRef]
- Choi, J.; Hwang, J.; Kim, J.y.; Choi, H. Recent progress in magnetically actuated microrobots for targeted delivery of therapeutic agents. Adv. Healthc. Mater. 2021, 10, 2001596. [Google Scholar] [CrossRef] [PubMed]
- Ye, M.; Zhou, Y.; Zhao, H.; Wang, X. Magnetic microrobots with folate targeting for drug delivery. Cyborg Bionic Syst. 2023, 4, 0019. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Chan, K.F.; Yu, J.; Wang, Q.; Yang, L.; Chiu, P.W.Y.; Zhang, L. Reconfigurable Swarms of Ferromagnetic Colloids for Enhanced Local Hyperthermia. Adv. Funct. Mater. 2018, 28, 1705701. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, Y.; Jin, D.; Jiang, Z.; Liu, Y.; Knoll, A.; Jiang, H.; Ying, Y.; Zhou, M. Magnetic Soft Microrobot Design for Cell Grasping and Transportation. Cyborg Bionic Syst. 2024, 5, 0109. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.; Chen, Z.; Deng, Y.; Liu, D.; Liu, X.; Huang, Q.; Arai, T. Field-controlled microrobots fabricated by photopolymerization. Cyborg Bionic Syst. 2023, 4, 0009. [Google Scholar] [CrossRef] [PubMed]
- Peyer, K.E.; Tottori, S.; Qiu, F.; Zhang, L.; Nelson, B.J. Magnetic helical micromachines. Chem.–A Eur. J. 2013, 19, 28–38. [Google Scholar] [CrossRef]
- Martel, S.; Mohammadi, M.; Felfoul, O.; Lu, Z.; Pouponneau, P. Flagellated magnetotactic bacteria as controlled MRI-trackable propulsion and steering systems for medical nanorobots operating in the human microvasculature. Int. J. Robot. Res. 2009, 28, 571–582. [Google Scholar] [CrossRef]
- Behkam, B.; Sitti, M. Bacterial flagella-based propulsion and on/off motion control of microscale objects. Appl. Phys. Lett. 2007, 90, 023902. [Google Scholar] [CrossRef]
- Abolfathi, K.; Yazdi, M.R.H.; Hoshiar, K.A. Studies of Different Swarm Modes for the MNPs under the Rotating Magnetic Field. IEEE Trans. Nanotechnol. 2020, 19, 849–855. [Google Scholar] [CrossRef]
- Le, T.-A.; Hadadian, Y.; Yoon, J. A prediction model for magnetic particle imaging–based magnetic hyperthermia applied to a brain tumor model. Comput. Methods Programs Biomed. 2023, 235, 107546. [Google Scholar] [CrossRef] [PubMed]
- Hoshiar, A.K.; Le, T.-A.; Valdastri, P.; Jungwon, Y. Swarm of magnetic nanoparticles steering in multi-bifurcation vessels under fluid flow. J. Micro-Bio Robot. 2020, 16, 137–145. [Google Scholar] [CrossRef]
- Amin, F.U.; Hoshiar, A.K.; Do, T.D.; Noh, Y.; Shah, S.A.; Khan, M.S.; Yoon, J.; Kim, O.M. Osmotin-loaded magnetic nanoparticles with electromagnetic guidance for the treatment of Alzheimer’s disease. Nanoscale 2017, 9, 10619–10632. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Jin, D.; Chan, K.-F.; Wang, Q.; Yuan, K.; Zhang, L. Active generation and magnetic actuation of microrobotic swarms in bio-fluids. Nat. Commun. 2019, 10, 5631. [Google Scholar] [CrossRef]
- Park, M.; Le, T.-A.; Yoon, J. Offline programming guidance for swarm steering of micro-/nano magnetic particles in a dynamic multichannel vascular model. IEEE Robot. Autom. Lett. 2022, 7, 3977–3984. [Google Scholar] [CrossRef]
- Park, M.; Le, T.-A.; Eizad, A.; Jungwon, Y. A Novel Shared Guidance Scheme for Intelligent Haptic Interaction Based Swarm Control of Magnetic Nanoparticles in Blood Vessels. IEEE Access 2020, 8, 106714–106725. [Google Scholar] [CrossRef]
- Hamdipoor, V.; Afzal, M.R.; Le, T.-A.; Yoon, J. Haptic-based manipulation scheme of magnetic nanoparticles in a multi-branch blood vessel for targeted drug delivery. Micromachines 2018, 9, 14. [Google Scholar] [CrossRef] [PubMed]
- Park, M.; Yoon, J. User-interfaced guidance scheme for steering swarm of magnetic nanoparticles. In Proceedings of the 2021 21st International Conference on Control, Automation and Systems (ICCAS), Jeju, Republic of Korea, 12–15 October 2021; pp. 1716–1719. [Google Scholar]
- Jarvis, B.W.; Poli, R.; Hoshiar, A.K. Online real-time platform for microrobot steering in a multi-bifurcation. In Proceedings of the 2022 International Conference on Manipulation, Automation and Robotics at Small Scales (MARSS), Toronto, ON, Canada, 25–29 July 2022; pp. 1–6. [Google Scholar]
- Von Helmholtz, H. Treatise on Physiological Optics, Volume III; Courier Corporation: Washington, DC, USA, 2013; Volume 3. [Google Scholar]
- Cullity, B.D.; Graham, C.D. Introduction to Magnetic Materials; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Chen, Y.-T.; Medhi, R.; Nekrashevich, I.; Litvinov, D.; Xu, S.; Lee, T.R. Specific detection of proteins using exceptionally responsive magnetic particles. Anal. Chem. 2018, 90, 6749–6756. [Google Scholar] [CrossRef] [PubMed]
- Kabir, A.M.R.; Inoue, D.; Kishimoto, Y.; Hotta, J.-i.; Sasaki, K.; Kitamura, N.; Gong, J.P.; Mayama, H.; Kakugo, A. Drag force on micron-sized objects with different surface morphologies in a flow with a small Reynolds number. Polym. J. 2015, 47, 564–570. [Google Scholar] [CrossRef]
- Klarhöfer, M.; Csapo, B.; Balassy, C.; Szeles, J.; Moser, E. High-resolution blood flow velocity measurements in the human finger. Magn. Reson. Med. Off. J. Int. Soc. Magn. Reson. Med. 2001, 45, 716–719. [Google Scholar] [CrossRef] [PubMed]


| Parameter | Symbol Used | Simulation Value |
|---|---|---|
| Magnetic field (mT) | B | 3 |
| Permeability of free space (N/A2) | µ0 | 4π × 10−7 |
| Magnetization (emu/g) | Mm | 33.74 |
| Magnetic gradient (mT/m) | ∇H | 1000 |
| Equivalent volume (m3) | Veq | 7.95 × 10−18 |
| Actual particle diameter (m) | d | 75 × 10−9 |
| Actual particle density (kg/m3) | ρ | 4800 |
| Average chain length (particles) | n | 12,000 |
| Equivalent diameter (m) | Deq | 2.48 × 10−6 |
| Fluid flow (m/s) | νf | 0.005 |
| Particle velocity(m/s) | νp | - |
| Fluid viscosity (Pa.S) | η | 0.001 |
| Number of particles | N | 500 |
| Parameter | Range |
|---|---|
| COMSOL fluid flow (m/s) | 0.005–0.06 |
| Real-world fluid flow (m/s) | 0.015–0.071 |
| COMSOL vessel diameter (m) | 0.001 |
| Real-world vessel diameter (m) | 0.0008–0.0018 |
| COMSOL temperature (K) | 293.15 |
| Parameter | Default Value | Variation Range |
|---|---|---|
| Magnetic gradient (mT/m) | 500 | 100–1000 |
| Limit of magnetic gradient (mT/m) | 500 | 100–1000 |
| Fluid flow (m/s) | 0.005 | 0.005–0.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jarvis, B.W.; Abolfathi, K.; Poli, R.; Kafash Hoshiar, A. Haptic-Based Real-Time Platform for Microswarm Steering in a Multi-Bifurcation Vascular Network. Nanomaterials 2024, 14, 1917. https://doi.org/10.3390/nano14231917
Jarvis BW, Abolfathi K, Poli R, Kafash Hoshiar A. Haptic-Based Real-Time Platform for Microswarm Steering in a Multi-Bifurcation Vascular Network. Nanomaterials. 2024; 14(23):1917. https://doi.org/10.3390/nano14231917
Chicago/Turabian StyleJarvis, Benjamin W., Kiana Abolfathi, Riccardo Poli, and Ali Kafash Hoshiar. 2024. "Haptic-Based Real-Time Platform for Microswarm Steering in a Multi-Bifurcation Vascular Network" Nanomaterials 14, no. 23: 1917. https://doi.org/10.3390/nano14231917
APA StyleJarvis, B. W., Abolfathi, K., Poli, R., & Kafash Hoshiar, A. (2024). Haptic-Based Real-Time Platform for Microswarm Steering in a Multi-Bifurcation Vascular Network. Nanomaterials, 14(23), 1917. https://doi.org/10.3390/nano14231917





