Retention and Transport of Nanoplastics with Different Surface Functionalities in a Sand Filtration System
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. Z-Average Hydrodynamic Diameter and Zeta (ζ) Potential Measurements
2.2.2. Turbidity Measurements
2.2.3. Scanning Electron Microscopy (SEM) and Transmission Electron Microscopy (TEM) Imaging
2.2.4. UV-Vis Spectrophotometry
2.2.5. Column Experiments
2.2.6. Aggregate Assessment with Fractal Dimension
3. Results
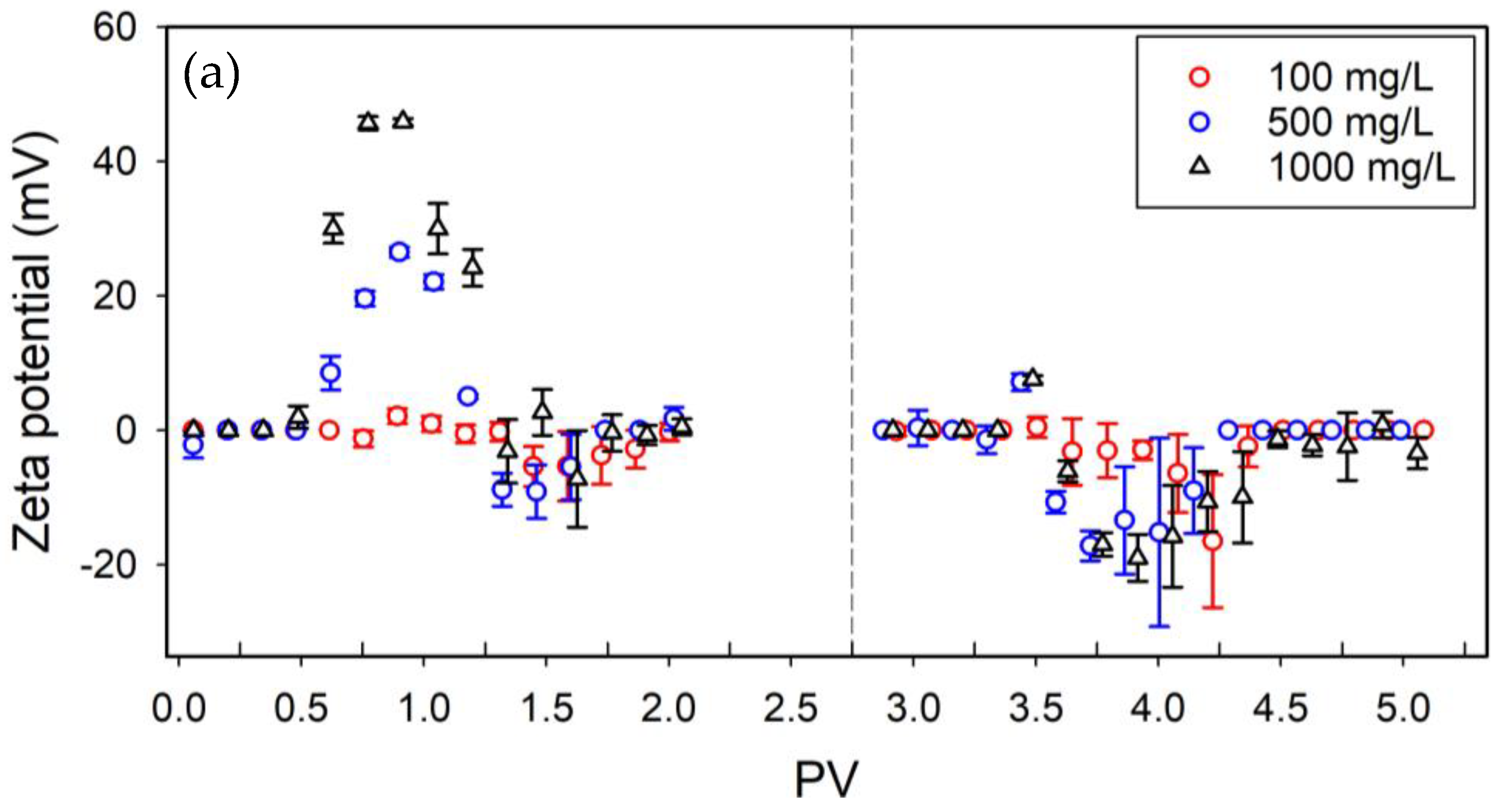
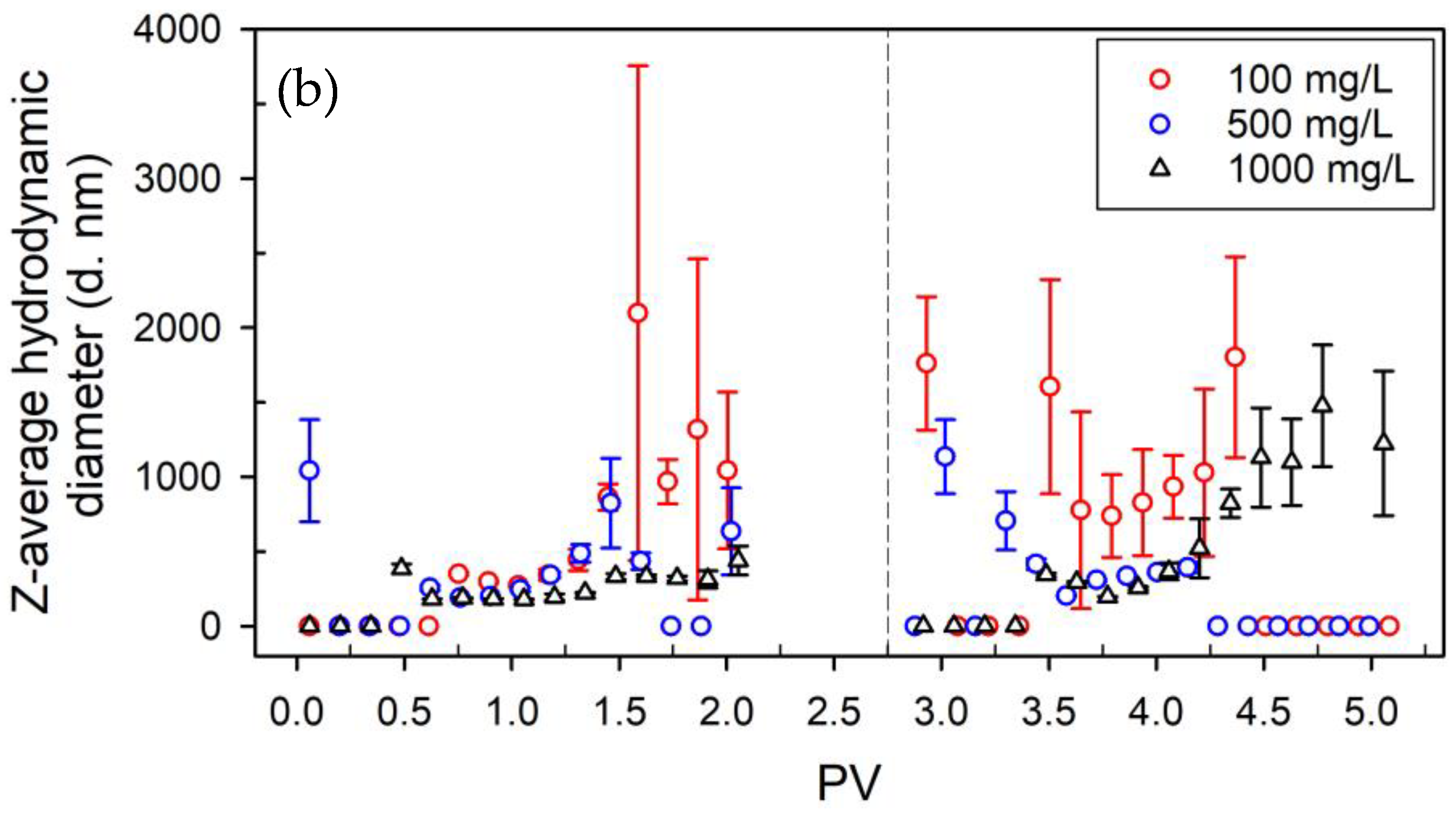
3.1. Characterization of NPLs with Different Surface Functionalities
3.2. NPLs Transport and Retention Behavior in Sand Filter
3.2.1. Effects of Injection Concentration
3.2.2. Effect of the NPLs Surface Properties
3.3. Effects of Surfactant Coating
3.4. Remobilization
3.5. Aggregate Properties
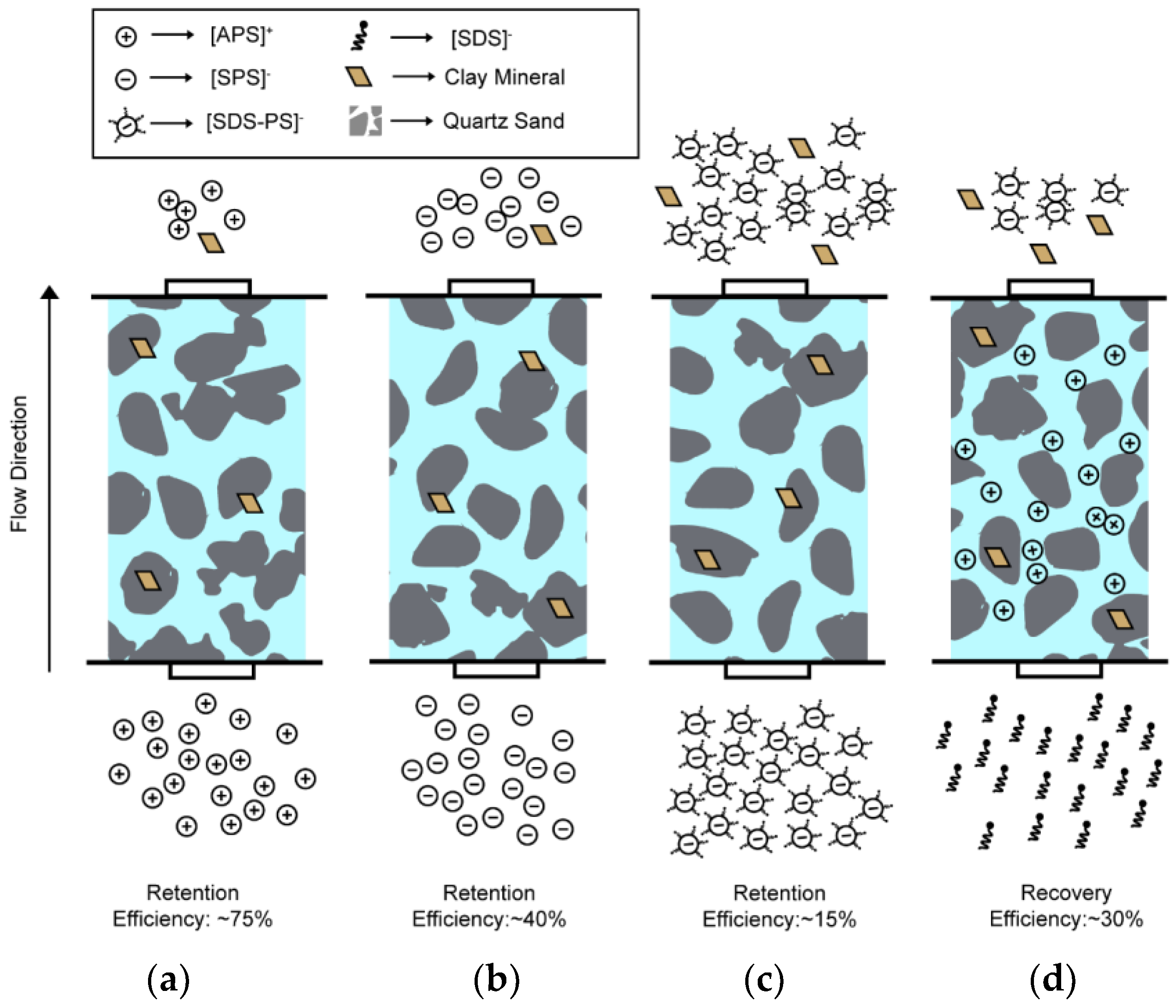
3.6. Summary of Mechanism
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Geyer, R.; Jambeck, J.R.; Law, K.L. Production, use, and fate of all plastics ever made. Sci. Adv. 2017, 3, 25–29. [Google Scholar] [CrossRef] [PubMed]
- Mintenig, S.M.; Int-Veen, I.; Löder, M.G.J.; Primpke, S.; Gerdts, G. Identification of microplastic in effluents of waste water treatment plants using focal plane array-based micro-Fourier-transform infrared imaging. Water Res. 2017, 108, 365–372. [Google Scholar] [CrossRef] [PubMed]
- Koelmans, A.A.; Mohamed Nor, N.H.; Hermsen, E.; Kooi, M.; Mintenig, S.M.; De France, J. Microplastics in freshwaters and drinking water: Critical review and assessment of data quality. Water Res. 2019, 155, 410–422. [Google Scholar] [CrossRef] [PubMed]
- Velasco, A.d.J.N.; Rard, L.; Blois, W.; Lebrun, D.; Lebrun, F.; Pothe, F.; Stoll, S. Microplastic and fibre contamination in a remote Mountain lake in Switzerland. Water 2020, 12, 2410. [Google Scholar] [CrossRef]
- Birch, Q.T.; Potter, P.M.; Pinto, P.X.; Dionysiou, D.D.; Al-Abed, S.R. Sources, transport, measurement and impact of nano and microplastics in urban watersheds. Rev. Environ. Sci. Bio/Technol. 2020, 19, 275–336. [Google Scholar] [CrossRef]
- da Costa, J.P.; Santos, P.S.M.; Duarte, A.C.; Rocha-Santos, T. (Nano)plastics in the environment—Sources, fates and effects. Sci. Total Environ. 2016, 566–567, 15–26. [Google Scholar] [CrossRef]
- Zhang, Y.; Diehl, A.; Lewandowski, A.; Gopalakrishnan, K.; Baker, T. Removal efficiency of micro- and nanoplastics (180 nm–125 μm) during drinking water treatment. Sci. Total Environ. 2020, 720, 137383. [Google Scholar] [CrossRef]
- Negrete Velasco, A.; Ramseier Gentile, S.; Zimmermann, S.; Stoll, S. Contamination and Removal Efficiency of Microplastics and Synthetic Fibres in a Conventional Drinking Water Treatment Plant. Front. Water 2022, 4, 835451. [Google Scholar] [CrossRef]
- Li, Y.; Li, J.; Ding, J.; Song, Z.; Yang, B.; Zhang, C.; Guan, B. Degradation of nano-sized polystyrene plastics by ozonation or chlorination in drinking water disinfection processes. Chem. Eng. J. 2022, 427, 131690. [Google Scholar] [CrossRef]
- Ramirez Arenas, L.; Ramseier Gentile, S.; Zimmermann, S.; Stoll, S. Coagulation of TiO2, CeO2 nanoparticles, and polystyrene nanoplastics in bottled mineral and surface waters. Effect of water properties, coagulant type, and dosage. Water Environ. Res. 2020, 92, 1184–1194. [Google Scholar] [CrossRef]
- Ramirez Arenas, L.; Ramseier Gentile, S.; Zimmermann, S.; Stoll, S. Fate and removal efficiency of polystyrene nanoplastics in a pilot drinking water treatment plant. Sci. Total Environ. 2022, 813, 152623. [Google Scholar] [CrossRef] [PubMed]
- Pulido-Reyes, G.; Magherini, L.; Bianco, C.; Sethi, R.; Von Gunten, U.; Kaegi, R.; Mitrano, D.M. Nanoplastics removal during drinking water treatment: Laboratory- and pilot-scale experiments and modeling. J. Hazard. Mater. 2022, 436, 129011. [Google Scholar] [CrossRef] [PubMed]
- Xing, X.; Zhang, Y.; Zhou, G.; Zhang, Y.; Yue, J.; Wang, X.; Yang, Z. Mechanisms of polystyrene nanoplastics adsorption onto activated carbon modified by ZnCl2. Sci. Total Environ. 2023, 876, 162763. [Google Scholar] [CrossRef] [PubMed]
- Pivokonsky, M.; Cermakova, L.; Novotna, K.; Peer, P.; Cajthaml, T.; Janda, V. Occurrence of microplastics in raw and treated drinking water. Sci. Total Environ. 2018, 643, 1644–1651. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Murphy, M.J.; Yu, H.; Bagaria, H.G.; Yoon, K.Y.; Neilson, B.M.; Bielawski, C.W.; Johnston, K.P.; Huh, C.; Bryant, S.L. Investigation of Nanoparticle Adsorption during Transport in Porous Media. SPE J. 2015, 20, 667–677. [Google Scholar] [CrossRef]
- Compère, F.; Porel, G.; Delay, F. Transport and retention of clay particles in saturated porous media. Influence of ionic strength and pore velocity. J. Contam. Hydrol. 2001, 49, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Dong, Z.; Qiu, Y.; Zhang, W.; Yang, Z.; Wei, L. Size-dependent transport and retention of micron-sized plastic spheres in natural sand saturated with seawater. Water Res. 2018, 143, 518–526. [Google Scholar] [CrossRef]
- Hul, G.; Martignier, A.; Gentile, S.R.; Zimmermann, S.; Ramaciotti, P.; Perdaems, P.; Stoll, S. Insights into polystyrene nanoplastics adsorption mechanisms onto quartz sand used in drinking water treatment plants. Sci. Total Environ. 2024, 908, 168076. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, Y.; Fan, W.; Yang, Z.; Tan, W.; Huo, M.; Huo, Y. Environment Mechanism comparisons of transport-deposition-reentrainment between microplastics and natural mineral particles in porous media: A theoretical and experimental study. Sci. Total Environ. 2022, 850, 157998. [Google Scholar] [CrossRef]
- Ling, X.; Yan, Z.; Liu, Y.; Lu, G. Transport of nanoparticles in porous media and its effects on the co-existing pollutants *. Environ. Pollut. 2021, 283, 117098. [Google Scholar] [CrossRef]
- Lu, T.; Gilfedder, B.S.; Peng, H.; Niu, G.; Frei, S. Effects of clay minerals on the transport of nanoplastics through water-saturated porous media. Sci. Total Environ. 2021, 796, 148982. [Google Scholar] [CrossRef] [PubMed]
- Liang, Y.; Luo, Y.; Shen, C.; Bradford, S.A. Micro- and nanoplastics retention in porous media exhibits different dependence on grain surface roughness and clay coating with particle size. Water Res. 2022, 221, 118717. [Google Scholar] [CrossRef]
- Peng, L.; Wang, Y. Sediment organic carbon dominates the heteroaggregation of suspended sediment and nanoplastics in natural and surfactant-polluted aquatic environments. J. Hazard. Mater. 2022, 440, 129802. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Zhou, S.; Fei, J.; Qin, Z.; Yin, X.; Sun, H.; Sun, Y. Transport of different microplastics in porous media: Effect of the adhesion of surfactants on microplastics. Water Res. 2022, 215, 118262. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Yin, X.; Xi, X.; Guan, D.; Sun, H.; Wang, N. Effect of surfactants on the transport of polyethylene and polypropylene microplastics in porous media. Water Res. 2021, 196, 117016. [Google Scholar] [CrossRef] [PubMed]
- Praetorius, A.; Badetti, E.; Brunelli, A.; Clavier, A.; Gallego-Urrea, J.A.; Gondikas, A.; Hassellöv, M.; Hofmann, T.; Mackevica, A.; Marcomini, A.; et al. Strategies for determining heteroaggregation attachment efficiencies of engineered nanoparticles in aquatic environments. Environ. Sci. Nano 2020, 7, 351–367. [Google Scholar] [CrossRef]
- Kanniah, V.; Wu, P.; Mandzy, N.; Grulke, E.A. Fractal analysis as a complimentary technique for characterizing nanoparticle size distributions. Powder Technol. 2012, 226, 189–198. [Google Scholar] [CrossRef]
- Chakraborti, R.K.; Gardner, K.H.; Atkinson, J.F.; Van Benschoten, J.E. Changes in fractal dimension during aggregation. Water Res. 2003, 37, 873–883. [Google Scholar] [CrossRef] [PubMed]
- Hul, G.; Ramseier Gentile, S.; Zimmermann, S.; Stoll, S. Towards a better understanding of CeO2 manufactured nanoparticles adsorption onto sand grains used in drinking water treatment plants. Colloids Surfaces A Physicochem. Eng. Asp. 2022, 646, 129000. [Google Scholar] [CrossRef]
- Einstein, A. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann. Phys. 1905, 322, 549–560. [Google Scholar] [CrossRef]
- Smoluchowski, M. Elektrische Endosmose und Strömungsströme; Polska Akademia Umiejętności: Krakow, Poland, 1921. [Google Scholar]
- Goldscheider, N.; Drew, D. Methods in Karst Hydrogeology: IAH: International Contributions to Hydrogeology, 26, 1st ed.; CRC Press: Boca Raton, FL, USA, 2007; ISBN 9780429153419. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W.H. Freeman and Co.: San Francisco, CA, USA, 1982. [Google Scholar]
- Karperien, A. FracLac for ImageJ. Available online: http://rsb.info.nih.gov/ij/plugins/fraclac/FLHelp/Introduction.htm (accessed on 29 June 2023).
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Preibisch, S.; Rueden, C.; Saalfeld, S.; Schmid, B.; et al. Fiji: An open-source platform for biological-image analysis. Nature Methods 2012, 9, 676–682. [Google Scholar] [CrossRef] [PubMed]
- Landini, G. Fractals in microscopy. J. Microsc. 2011, 241, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Karperien, A. FracLac Advanced User’s Manual. 2004. Available online: http://rsbweb.nih.gov/ij/plugins/fraclac/FLHelp/Introduction.htm (accessed on 1 November 2023).
- Torre, I.G.; Heck, R.J.; Tarquis, A.M. MULTIFRAC: An ImageJ plugin for multiscale characterization of 2D and 3D stack images. SoftwareX 2020, 12, 100574. [Google Scholar] [CrossRef]
- Molnar, I.L.; Johnson, W.P.; Gerhard, J.I.; Willson, C.S.; O’Carroll, D.M. Predicting colloid transport through saturated porous media: A critical review. Water Resour. Res. 2015, 51, 6804–6845. [Google Scholar] [CrossRef]
- Tufenkji, N.; Elimelech, M. Deviation from the Classical Colloid Filtration Theory in the Presence of Repulsive DLVO Interactions. Langmuir 2004, 20, 10818–10828. [Google Scholar] [CrossRef] [PubMed]
- Hou, J.; Zhang, M.; Wang, P.; Wang, C.; Miao, L.; Xu, Y.; You, G.; Lv, B.; Yang, Y.; Liu, Z. Transport and long-term release behavior of polymer-coated silver nanoparticles in saturated quartz sand: The impacts of input concentration, grain size and flow rate. Water Res. 2017, 127, 86–95. [Google Scholar] [CrossRef] [PubMed]
- Sun, P.; Shijirbaatar, A.; Fang, J.; Owens, G.; Lin, D.; Zhang, K. Distinguishable Transport Behavior of Zinc Oxide Nanoparticles in Silica Sand and Soil Columns. Sci. Total Environ. 2015, 505, 189–198. [Google Scholar] [CrossRef] [PubMed]
- Hou, J.; Xu, X.; Lan, L.; Miao, L.; Xu, Y.; You, G.; Liu, Z. Transport behavior of micro polyethylene particles in saturated quartz sand: Impacts of input concentration and physicochemical factors. Environ. Pollut. 2020, 263, 114499. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Gao, B.; Bradford, S.A.; Wu, L.; Chen, H.; Shi, X.; Wu, J. Transport, retention, and size perturbation of graphene oxide in saturated porous media: Effects of input concentration and grain size. Water Res. 2015, 68, 24–33. [Google Scholar] [CrossRef]
- Bradford, S.A.; Bettahar, M. Concentration dependent transport of colloids in saturated porous media. J. Contam. Hydrol. 2006, 82, 99–117. [Google Scholar] [CrossRef]
- Bradford, S.A.; Yates, S.R.; Bettahar, M.; Simunek, J. Physical factors affecting the transport and fate of colloids in saturated porous media. Water Resour. Res. 2002, 38, 63-1–63-12. [Google Scholar] [CrossRef]
- Zhang, M.; Hou, J.; Wu, J.; Miao, L.; Zeng, Y. Effects of input concentration, media particle size, and flow rate on fate of polystyrene nanoplastics in saturated porous media. Sci. Total Environ. 2023, 881, 163237. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Zhang, X.; Yi, K.; He, L.; Han, P.; Tong, M. Transport and deposition of microplastic particles in saturated porous media: Co-effects of clay particles and natural organic matter. Environ. Pollut. 2021, 287, 117585. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wang, X.; Fu, W.; Xia, X.; Liu, C.; Min, J.; Zhang, W.; Crittenden, J.C. Interactions between nano/micro plastics and suspended sediment in water: Implications on aggregation and settling. Water Res. 2019, 161, 486–495. [Google Scholar] [CrossRef] [PubMed]
- Farrokhbin, M.; Stojimirović, B.; Galli, M.; Khajeh Aminian, M.; Hallez, Y.; Trefalt, G. Surfactant mediated particle aggregation in nonpolar solvents. Phys. Chem. Chem. Phys. 2019, 21, 18866–18876. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhao, X.; Wu, A.; Tang, Z.; Niu, L.; Wu, F.; Wang, F.; Zhao, T.; Fu, Z. Aggregation and stability of sulfate-modified polystyrene nanoplastics in synthetic and natural waters. Environ. Pollut. 2021, 268, 114240. [Google Scholar] [CrossRef] [PubMed]
- Jódar-Reyes, A.B.; Martín-Rodríguez, A.; Ortega-Vinuesa, J.L. Effect of the ionic surfactant concentration on the stabilization/destabilization of polystyrene colloidal particles. J. Colloid Interface Sci. 2006, 298, 248–257. [Google Scholar] [CrossRef]
- Hul, G.; Seijo, M.; Carnal, F.; Cornelis, G.; Stoll, S. Effect of deposition, detachment and aggregation processes on nanoparticle transport in porous media using Monte Carlo simulations. Environ. Sci. Nano 2021, 8, 2223–2234. [Google Scholar] [CrossRef]
- Maloszewski, P.; Harum, T.; Benischke, R. Mathematical modelling of tracer experiments in the karst of Lurbach system. Hydrogeologie 1992, 43, 116–136. [Google Scholar]
- Kreft, A.; Zuber, A. On the physical meaning of the dispersion equation and its solutions for different initial and boundary conditions. Chem. Eng. Sci. 1978, 33, 1471–1480. [Google Scholar] [CrossRef]
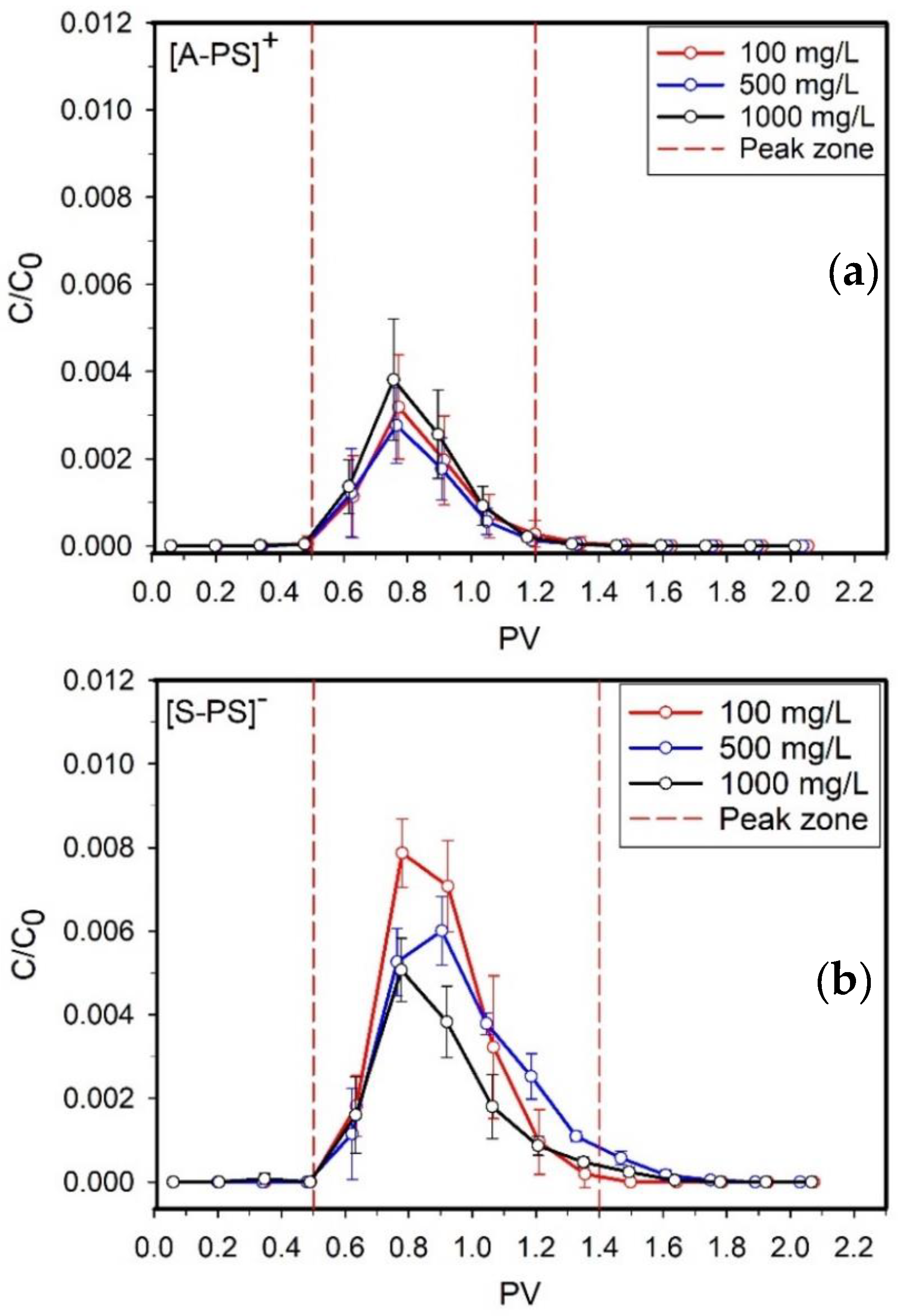
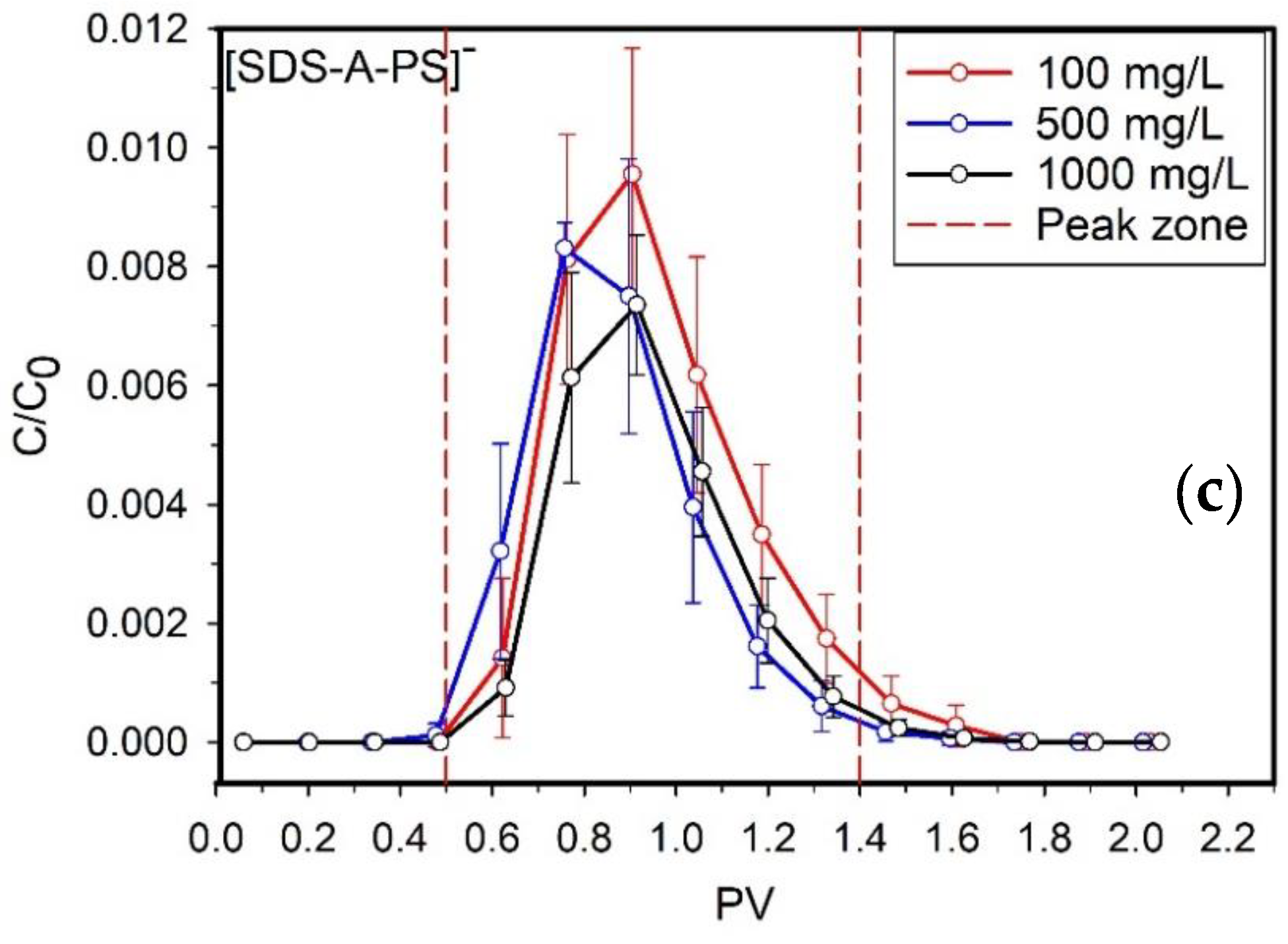
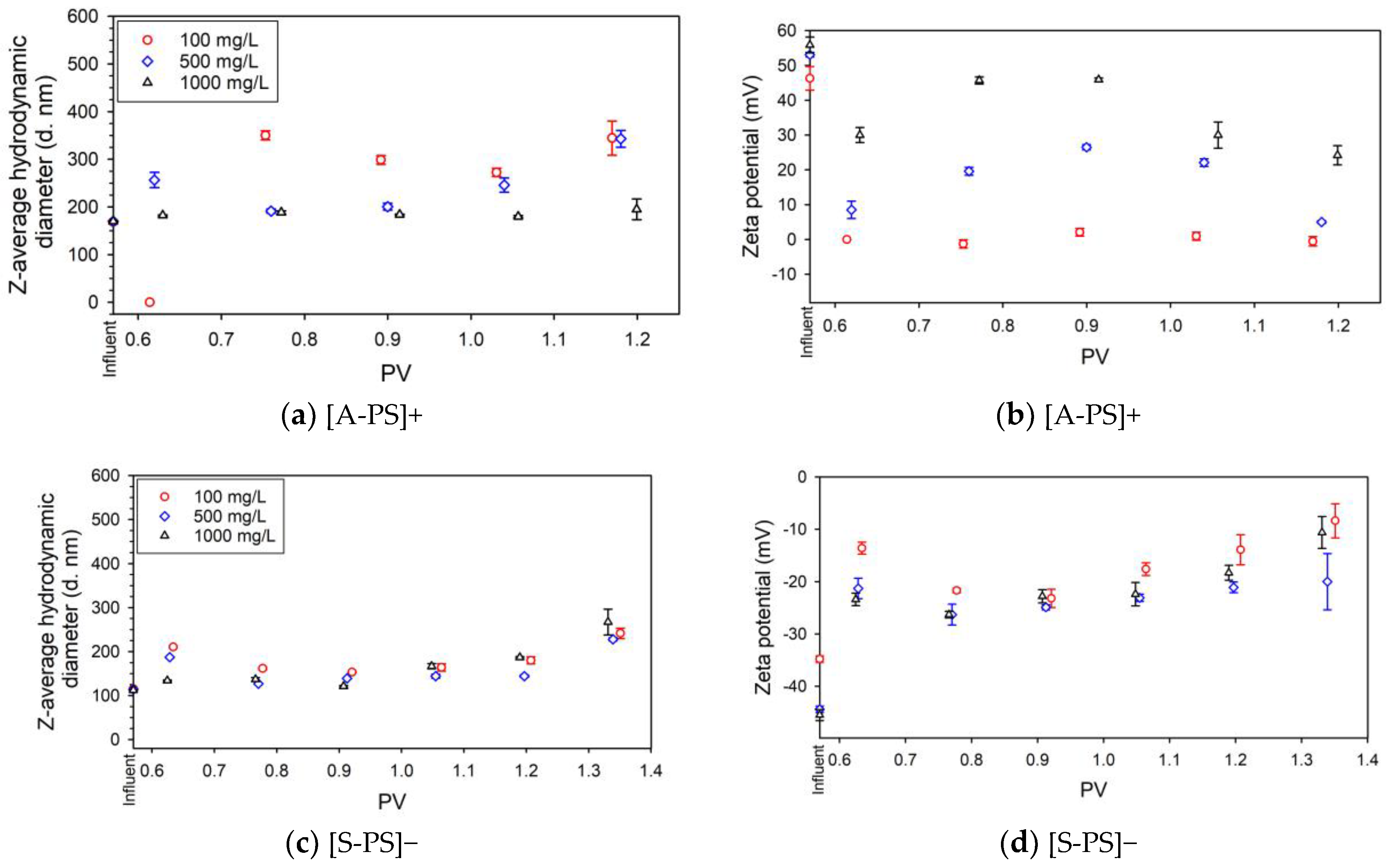
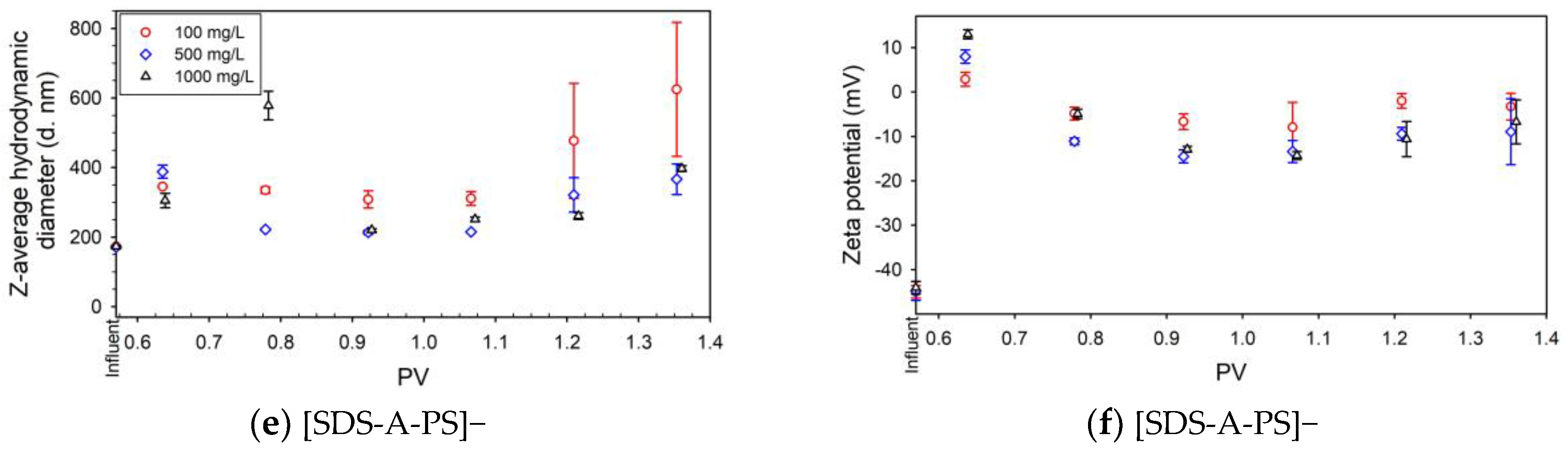


| Type | Injection Concentration (mg/L) | MEC (mg/L) | Retention Efficiency (%) |
|---|---|---|---|
| [A-PS]+ | 100 | 0.4 ± 0.2 | 76 ± 9 |
| 500 | 1.4 ± 0.4 | 79 ± 6 | |
| 1000 | 3.8 ± 1.2 | 71 ± 9 | |
| [S-PS]− | 100 | 0.8 ± 0.1 | 32 ± 4 |
| 500 | 3.1 ± 0.2 | 34 ± 2 | |
| 1000 | 5.1 ± 0.6 | 55 ± 3 | |
| [SDS-A-PS]− | 1000 | 1.0 ± 0.1 | 3 ± 11 |
| 100 | 4.4 ± 0.4 | 9 ± 10 | |
| 500 | 7.4 ± 1.0 | 30 ± 13 |
| Injected NPL Concentration (mg/L) | Recovered Mass 1 * (%) | Recovered Mass 2 ** (%) | Total Recovered Mass (%) |
|---|---|---|---|
| 100 | 31 ± 6 | 16 ± 4 | 47 ± 8 |
| 500 | 20 ± 6 | 10 ± 2 | 30 ± 5 |
| 1000 | 34 ± 8 | 7 ± 2 | 42 ± 6 |
| Type | Injection Concentrations | Fractal Dimension, Df | Retention Efficiency, % |
|---|---|---|---|
| [A-PS]+ | 100 | 1.885 ± 0.017 | 76 ± 9 |
| [A-PS]+ | 500 | 1.889 ± 0.019 | 79 ± 6 |
| [A-PS]+ | 1000 | 1.904 ± 0.003 | 71 ± 9 |
| [S-PS]− | 100 | 1.894 ± 0.026 | 32 ± 4 |
| [S-PS]− | 500 | 1.887 ± 0.012 | 34 ± 2 |
| [S-PS]− | 1000 | 1.846 ± 0.005 | 55 ± 3 |
| [SDS-A-PS]− | 100 | 1.892 ± 0.005 | 3 ± 11 |
| [SDS-A-PS]− | 500 | 1.878 ± 0.015 | 9 ± 10 |
| [SDS-A-PS]− | 1000 | 1.848 ± 0.017 | 30 ± 13 |
| Desorption | 100 | 1.889 ± 0.022 | 52 ± 8 |
| Desorption | 500 | 1.881 ± 0.014 | 70 ± 5 |
| Desorption | 1000 | 1.882 ± 0.015 | 58 ± 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Okutan, H.; Hul, G.; Stoll, S.; Le Coustumer, P. Retention and Transport of Nanoplastics with Different Surface Functionalities in a Sand Filtration System. Nanomaterials 2024, 14, 32. https://doi.org/10.3390/nano14010032
Okutan H, Hul G, Stoll S, Le Coustumer P. Retention and Transport of Nanoplastics with Different Surface Functionalities in a Sand Filtration System. Nanomaterials. 2024; 14(1):32. https://doi.org/10.3390/nano14010032
Chicago/Turabian StyleOkutan, Hande, Gabriela Hul, Serge Stoll, and Philippe Le Coustumer. 2024. "Retention and Transport of Nanoplastics with Different Surface Functionalities in a Sand Filtration System" Nanomaterials 14, no. 1: 32. https://doi.org/10.3390/nano14010032
APA StyleOkutan, H., Hul, G., Stoll, S., & Le Coustumer, P. (2024). Retention and Transport of Nanoplastics with Different Surface Functionalities in a Sand Filtration System. Nanomaterials, 14(1), 32. https://doi.org/10.3390/nano14010032








