Polarization-Dependent Metasurface Enables Near-Infrared Dual-Modal Single-Pixel Sensing
Abstract
1. Introduction
2. Principle
2.1. Principle of the Device
2.2. Fourier Modulation
2.3. Hadamard Modulation
2.4. Binary Random Modulation
3. Simulations and Analysis
3.1. Design of Metasurface
3.2. Full-Process Simulations
3.3. Generalization Analysis
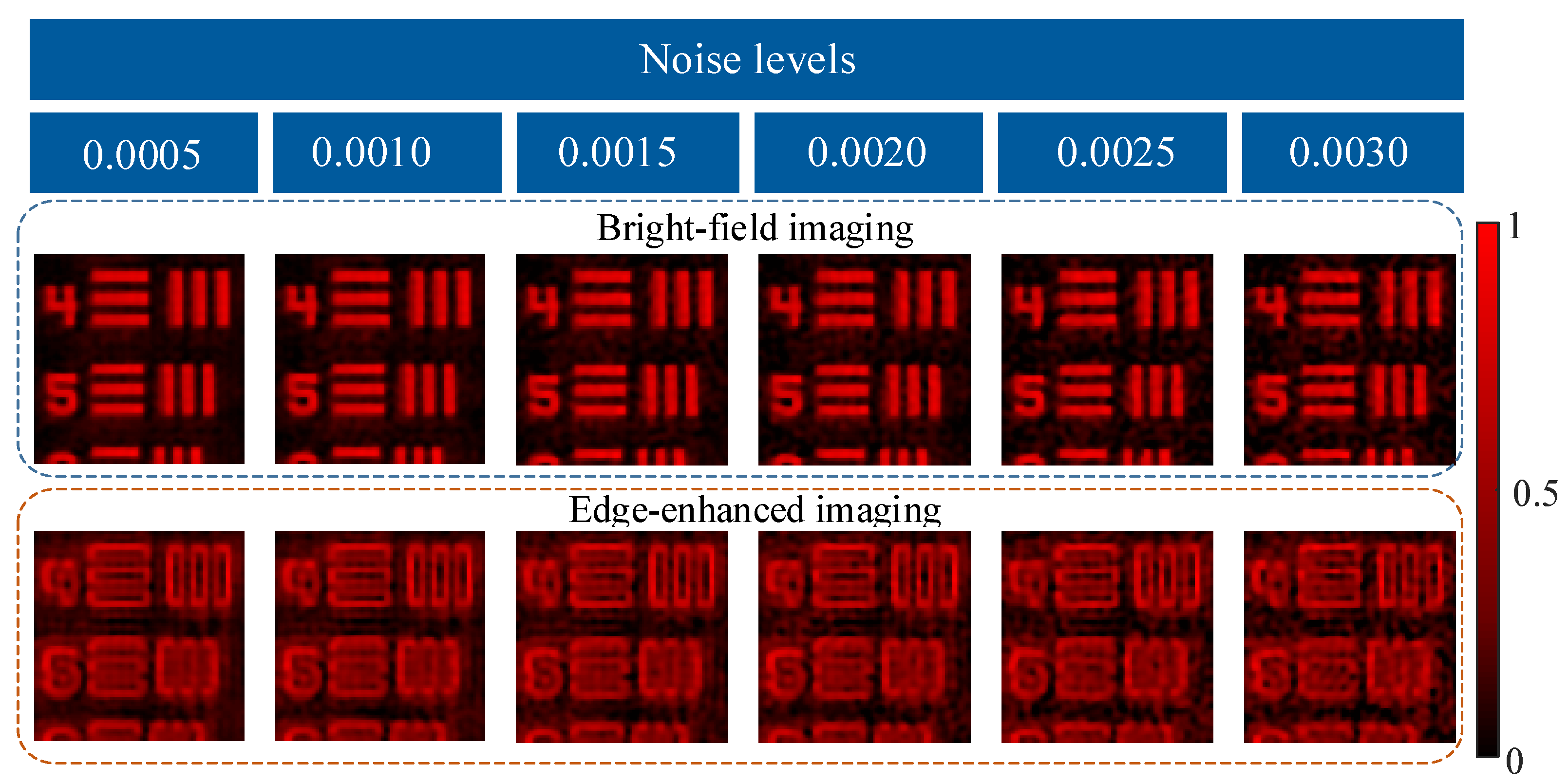
3.4. Robustness Analysis
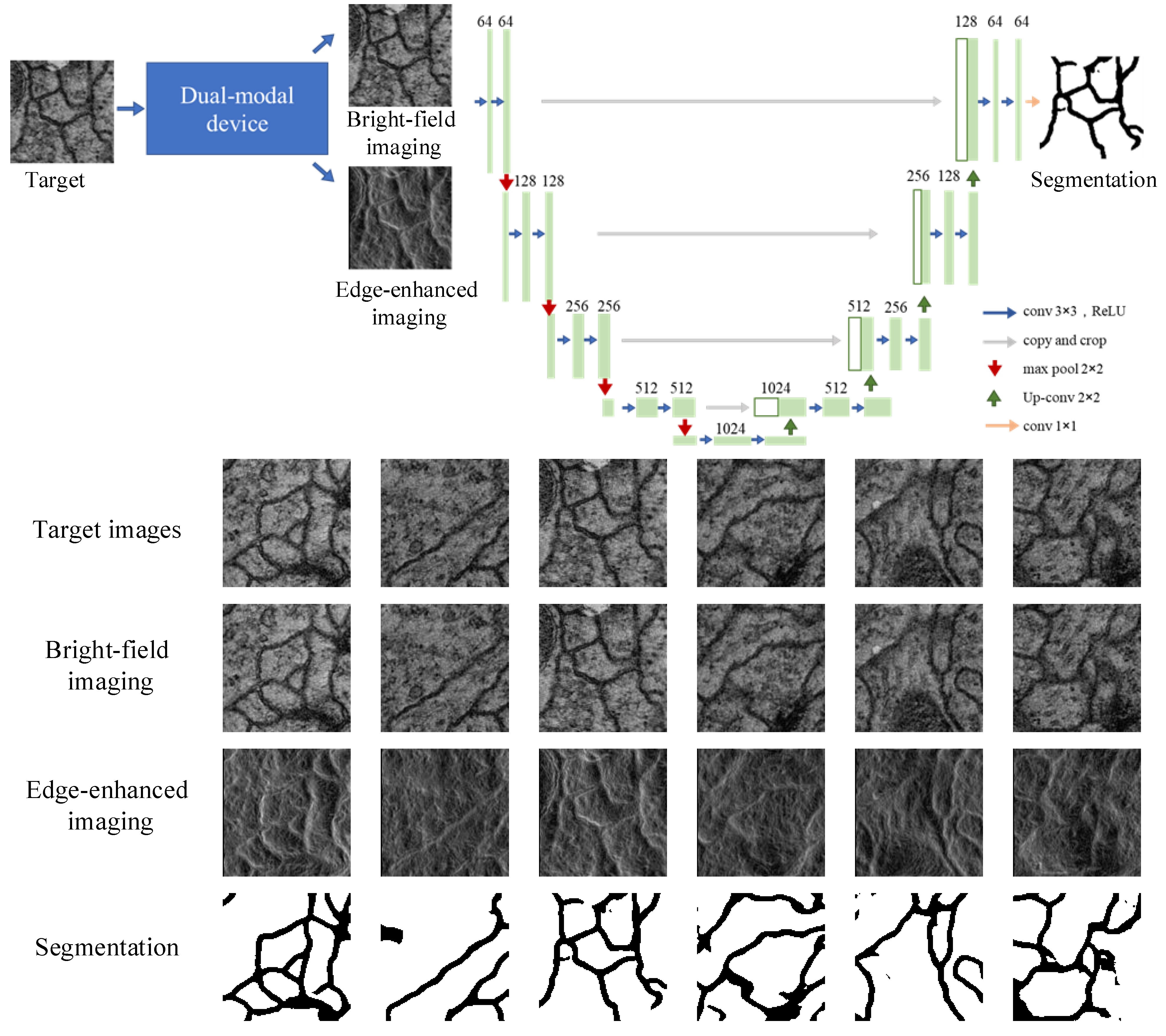
4. Biomedical Applications
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Huang, K.; Fang, J.; Yan, M.; Wu, E.; Zeng, H. Wide-field mid-infrared single-photon upconversion imaging. Nat. Commun. 2022, 13, 1077. [Google Scholar] [CrossRef]
- Chen, C.P.; Li, H.; Wei, Y.; Xia, T.; Tang, Y.Y. A local contrast method for small infrared target detection. IEEE Trans. Geosci. Remote Sens. 2013, 52, 574–581. [Google Scholar] [CrossRef]
- Radwell, N.; Mitchell, K.J.; Gibson, G.M.; Edgar, M.P.; Bowman, R.; Padgett, M.J. Single-pixel infrared and visible microscope. Optica 2014, 1, 285–289. [Google Scholar] [CrossRef]
- d’Acremont, A.; Fablet, R.; Baussard, A.; Quin, G. CNN-based target recognition and identification for infrared imaging in defense systems. Sensors 2019, 19, 2040. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.C.; Yang, B.; Guo, Q.; Shi, J.; Guan, C.; Zheng, G.; Mühlenbernd, H.; Li, G.; Zentgraf, T.; Zhang, S. Single-pixel computational ghost imaging with helicity-dependent metasurface hologram. Sci. Adv. 2017, 3, e1701477. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Huang, K.; Fang, J.; Yan, M.; Wu, E.; Zeng, H. Mid-infrared single-pixel imaging at the single-photon level. Nat. Commun. 2023, 14, 1073. [Google Scholar] [CrossRef]
- Vodopyanov, K.L. Laser-Based Mid-Infrared Sources and Applications; John Wiley & Sons: New York, NY, USA, 2020. [Google Scholar]
- Hermes, M.; Morrish, R.B.; Huot, L.; Meng, L.; Junaid, S.; Tomko, J.; Lloyd, G.R.; Masselink, W.T.; Tidemand-Lichtenberg, P.; Pedersen, C.; et al. Mid-IR hyperspectral imaging for label-free histopathology and cytology. J. Opt. 2018, 20, 023002. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Z.; Zheng, Y.; Chuang, Y.Y.; Satoh, S. Learning to Reduce Dual-Level Discrepancy for Infrared-Visible Person Re-Identification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Solli, D.R.; Jalali, B. Analog optical computing. Nat. Photonics 2015, 9, 704–706. [Google Scholar] [CrossRef]
- Yang, H.; Xie, Z.; He, H.; Zhang, Q.; Li, J.; Zhang, Y.; Yuan, X. Switchable imaging between edge-enhanced and bright-field based on a phase-change metasurface. Opt. Lett. 2021, 46, 3741–3744. [Google Scholar] [CrossRef]
- Badri, S.H.; Gilarlue, M.; SaeidNahaei, S.; Kim, J.S. Narrowband-to-broadband switchable and polarization-insensitive terahertz metasurface absorber enabled by phase-change material. J. Opt. 2022, 24, 025101. [Google Scholar] [CrossRef]
- Badri, S.H.; SaeidNahaei, S.; Kim, J.S. Polarization-sensitive tunable extraordinary terahertz transmission based on a hybrid metal–vanadium dioxide metasurface. Appl. Opt. 2022, 61, 5972–5979. [Google Scholar] [CrossRef]
- Li, Y.B.; Li, L.L.; Cai, B.G.; Cheng, Q.; Cui, T.J. Holographic leaky-wave metasurfaces for dual-sensor imaging. Sci. Rep. 2015, 5, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Ye, W.; Zeuner, F.; Li, X.; Reineke, B.; He, S.; Qiu, C.W.; Liu, J.; Wang, Y.; Zhang, S.; Zentgraf, T. Spin and wavelength multiplexed nonlinear metasurface holography. Nat. Commun. 2016, 7, 11930. [Google Scholar] [CrossRef]
- Wang, Z.; Li, T.; Soman, A.; Mao, D.; Kananen, T.; Gu, T. On-chip wavefront shaping with dielectric metasurface. Nat. Commun. 2019, 10, 3547. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Liu, W.; Li, Z.; Cheng, H.; Tian, J. Metasurface-empowered optical multiplexing and multifunction. Adv. Mater. 2020, 32, 1805912. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, X.; Luo, X.; Ou, X.; Li, L.; Chen, Y.; Yang, P.; Wang, S.; Duan, H. All-dielectric metasurfaces for polarization manipulation: Principles and emerging applications. Nanophotonics 2020, 9, 3755–3780. [Google Scholar] [CrossRef]
- Rubin, N.A.; Chevalier, P.; Juhl, M.; Tamagnone, M.; Chipman, R.; Capasso, F. Imaging polarimetry through metasurface polarization gratings. Opt. Express 2022, 30, 9389–9412. [Google Scholar] [CrossRef]
- Deng, Y.; Cai, Z.; Ding, Y.; Bozhevolnyi, S.I.; Ding, F. Recent progress in metasurface-enabled optical waveplates. Nanophotonics 2022. [Google Scholar] [CrossRef]
- Joseph, S.; Sarkar, S.; Joseph, J. Grating-coupled surface plasmon-polariton sensing at a flat metal–analyte interface in a hybrid-configuration. ACS Appl. Mater. Interfaces 2020, 12, 46519–46529. [Google Scholar] [CrossRef]
- Lio, G.E.; Ferraro, A.; Kowerdziej, R.; Govorov, A.O.; Wang, Z.; Caputo, R. Engineering Fano-Resonant Hybrid Metastructures with Ultra-High Sensing Performances. Adv. Opt. Mater. 2022, 2203123. [Google Scholar] [CrossRef]
- Abdollahramezani, S.; Hemmatyar, O.; Adibi, A. Meta-optics for spatial optical analog computing. Nanophotonics 2020, 9, 4075–4095. [Google Scholar] [CrossRef]
- Zangeneh-Nejad, F.; Sounas, D.L.; Alù, A.; Fleury, R. Analogue computing with metamaterials. Nat. Rev. Mater. 2021, 6, 207–225. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, Y.; Ding, X.; Li, H.; Fu, J.; Zhang, K.; Burokur, S.N.; Wu, Q. Compact logic operator utilizing a single-layer metasurface. Photonics Res. 2022, 10, 316–322. [Google Scholar] [CrossRef]
- He, S.; Wang, R.; Luo, H. Computing metasurfaces for all-optical image processing: A brief review. Nanophotonics 2022. [Google Scholar] [CrossRef]
- Badloe, T.; Lee, S.; Rho, J. Computation at the speed of light: Metamaterials for all-optical calculations and neural networks. Adv. Photonics 2022, 4, 064002. [Google Scholar] [CrossRef]
- Huo, P.; Zhang, C.; Zhu, W.; Liu, M.; Zhang, S.; Zhang, S.; Chen, L.; Lezec, H.J.; Agrawal, A.; Lu, Y.; et al. Photonic Spin-Multiplexing Metasurface for Switchable Spiral Phase Contrast Imaging. Nano Lett. 2020, 20, 2791–2798. [Google Scholar] [CrossRef]
- Xiao, T.; Yang, H.; Yang, Q.; Xu, D.; Wang, R.; Chen, S.; Luo, H. Realization of tunable edge-enhanced images based on computing metasurfaces. Opt. Lett. 2022, 47, 925–928. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, Q.; He, S.; Wang, R.; Luo, H. Computing Metasurfaces Enabled Broad-Band Vectorial Differential Interference Contrast Microscopy. ACS Photonics 2022. [Google Scholar] [CrossRef]
- Zeng, B.; Huang, Z.; Singh, A.; Yao, Y.; Azad, A.K.; Mohite, A.D.; Taylor, A.J.; Smith, D.R.; Chen, H.T. Hybrid graphene metasurfaces for high-speed mid-infrared light modulation and single-pixel imaging. Light Sci. Appl. 2018, 7, 51. [Google Scholar] [CrossRef]
- Yan, J.; Wang, Y.; Liu, Y.; Wei, Q.; Zhang, X.; Li, X.; Huang, L. Single pixel imaging based on large capacity spatial multiplexing metasurface. Nanophotonics 2022, 11, 3071–3080. [Google Scholar] [CrossRef]
- Yan, J.; Wei, Q.; Liu, Y.; Geng, G.; Li, J.; Li, X.; Li, X.; Wang, Y.; Huang, L. Single pixel imaging key for holographic encryption based on spatial multiplexing metasurface. Small 2022, 18, 2203197. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Ma, X.; Zhong, J. Single-pixel imaging by means of Fourier spectrum acquisition. Nat. Commun. 2015, 6, 6225. [Google Scholar] [CrossRef] [PubMed]
- Duarte, M.F.; Davenport, M.A.; Takhar, D.; Laska, J.N.; Sun, T.; Kelly, K.F.; Baraniuk, R.G. Single-pixel imaging via compressive sampling. IEEE Signal Process. Mag. 2008, 25, 83–91. [Google Scholar] [CrossRef]
- Watts, C.M.; Shrekenhamer, D.; Montoya, J.; Lipworth, G.; Hunt, J.; Sleasman, T.; Krishna, S.; Smith, D.R.; Padilla, W.J. Terahertz compressive imaging with metamaterial spatial light modulators. Nat. Photonics 2014, 8, 605–609. [Google Scholar] [CrossRef]
- Sun, B.; Edgar, M.P.; Bowman, R.; Vittert, L.E.; Welsh, S.; Bowman, A.; Padgett, M.J. 3D computational imaging with single-pixel detectors. Science 2013, 340, 844–847. [Google Scholar] [CrossRef]
- St-Charles, P.; Bilodeau, G.; Bergevin, R. Online Mutual Foreground Segmentation for Multispectral Stereo Videos. 2019. Available online: https://www.polymtl.ca/litiv/codes-et-bases-de-donnees (accessed on 1 December 2022).
- Seo, H.; Badiei Khuzani, M.; Vasudevan, V.; Huang, C.; Ren, H.; Xiao, R.; Jia, X.; Xing, L. Machine learning techniques for biomedical image segmentation: An overview of technical aspects and introduction to state-of-art applications. Med. Phys. 2020, 47, e148–e167. [Google Scholar] [CrossRef]
- Zhang, Z.; Fu, H.; Dai, H.; Shen, J.; Pang, Y.; Shao, L. Et-net: A generic edge-attention guidance network for medical image segmentation. In Proceedings of the Medical Image Computing and Computer Assisted Intervention–MICCAI, Shenzhen, China, 13–17 October 2019; Springer: Cham, Switzerland, 2019; pp. 442–450. [Google Scholar]
- Valanarasu, J.M.J.; Sindagi, V.A.; Hacihaliloglu, I.; Patel, V.M. Kiu-net: Towards accurate segmentation of biomedical images using over-complete representations. In Proceedings of the Medical Image Computing and Computer Assisted Intervention–MICCAI: 23rd International Conference, Lima, Peru, 4–8 October 2020; Springer International Publishing: Cham, Switzerland, 2020; pp. 363–373. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention (MICCAI), Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland, 2015; Volume 9351, pp. 234–241. [Google Scholar]
- WWW: Web Page of the Em Segmentation Challenge. Available online: http://brainiac2.mit.edu/isbi_challenge/ (accessed on 1 March 2023).








| NUM | a(nm) | b(nm) | ||||
|---|---|---|---|---|---|---|
| 1 | 78 | 160 | 3.07 | 0.85 | 0.62 | 0.4 |
| 2 | 82 | 156 | −2.81 | 0.83 | 0.32 | 0.74 |
| 3 | 86 | 152 | −2.32 | 0.83 | 0.36 | 0.68 |
| 4 | 88 | 150 | −2.11 | 0.88 | 0.44 | 0.53 |
| 5 | 92 | 160 | −1.46 | 0.92 | 0.23 | 0.95 |
| 6 | 96 | 160 | −1.10 | 1 | 0.38 | 0.94 |
| 7 | 104 | 40 | 1.48 | 0.96 | 0.69 | 0.98 |
| 8 | 104 | 158 | −0.60 | 0.96 | 0.53 | 0.91 |
| 9 | 112 | 152 | −0.24 | 0.99 | 0.49 | 0.91 |
| 10 | 116 | 40 | 1.86 | 0.95 | 0.72 | 0.98 |
| 11 | 126 | 144 | 0.18 | 0.98 | 0.50 | 0.92 |
| 12 | 130 | 40 | 2.33 | 0.97 | 0.76 | 0.98 |
| 13 | 140 | 40 | 2.73 | 0.9 | 0.79 | 0.98 |
| 14 | 144 | 136 | 0.62 | 0.96 | 0.50 | 0.92 |
| 15 | 152 | 40 | −3.14 | 0.78 | 0.82 | 0.98 |
| 16 | 160 | 130 | 1.03 | 0.85 | 0.47 | 0.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, R.; Wang, W.; Hu, Y.; Hao, Q.; Bian, L. Polarization-Dependent Metasurface Enables Near-Infrared Dual-Modal Single-Pixel Sensing. Nanomaterials 2023, 13, 1542. https://doi.org/10.3390/nano13091542
Yan R, Wang W, Hu Y, Hao Q, Bian L. Polarization-Dependent Metasurface Enables Near-Infrared Dual-Modal Single-Pixel Sensing. Nanomaterials. 2023; 13(9):1542. https://doi.org/10.3390/nano13091542
Chicago/Turabian StyleYan, Rong, Wenli Wang, Yao Hu, Qun Hao, and Liheng Bian. 2023. "Polarization-Dependent Metasurface Enables Near-Infrared Dual-Modal Single-Pixel Sensing" Nanomaterials 13, no. 9: 1542. https://doi.org/10.3390/nano13091542
APA StyleYan, R., Wang, W., Hu, Y., Hao, Q., & Bian, L. (2023). Polarization-Dependent Metasurface Enables Near-Infrared Dual-Modal Single-Pixel Sensing. Nanomaterials, 13(9), 1542. https://doi.org/10.3390/nano13091542







