Electrical and Recombination Properties of Polar Orthorhombic κ-Ga2O3 Films Prepared by Halide Vapor Phase Epitaxy
Abstract
1. Introduction
2. Materials and Methods
2.1. Growth
2.2. Characterization of Electrical Properties, Deep Trap Spectra, Photocurrent and Photocapacitance Spectra, and Recombination Properties
3. Results and Discussion
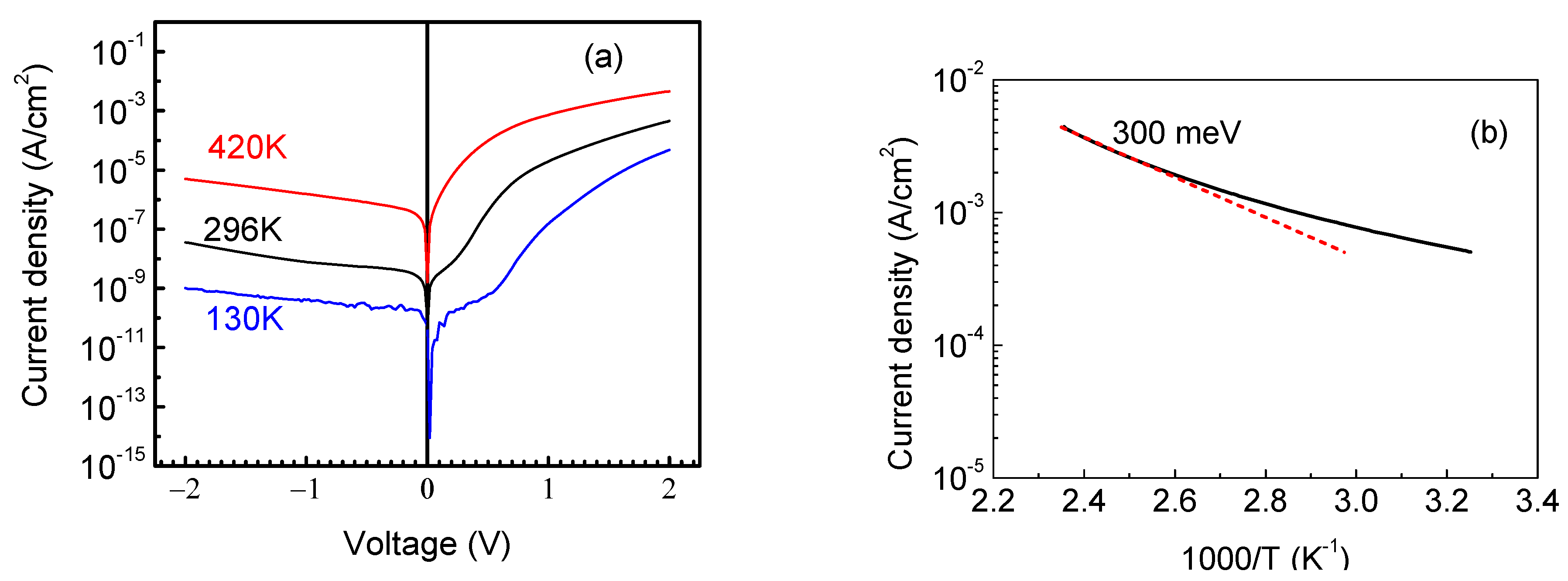
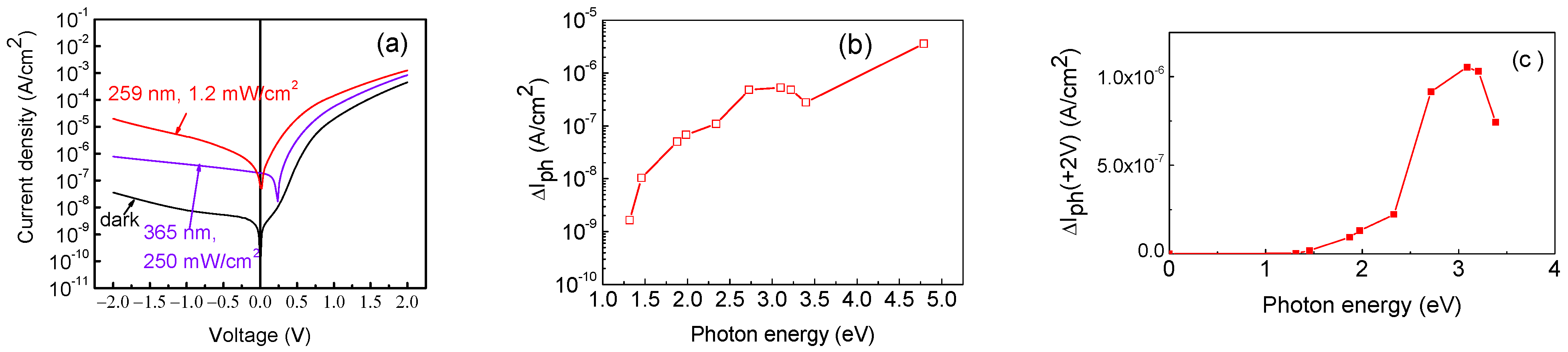
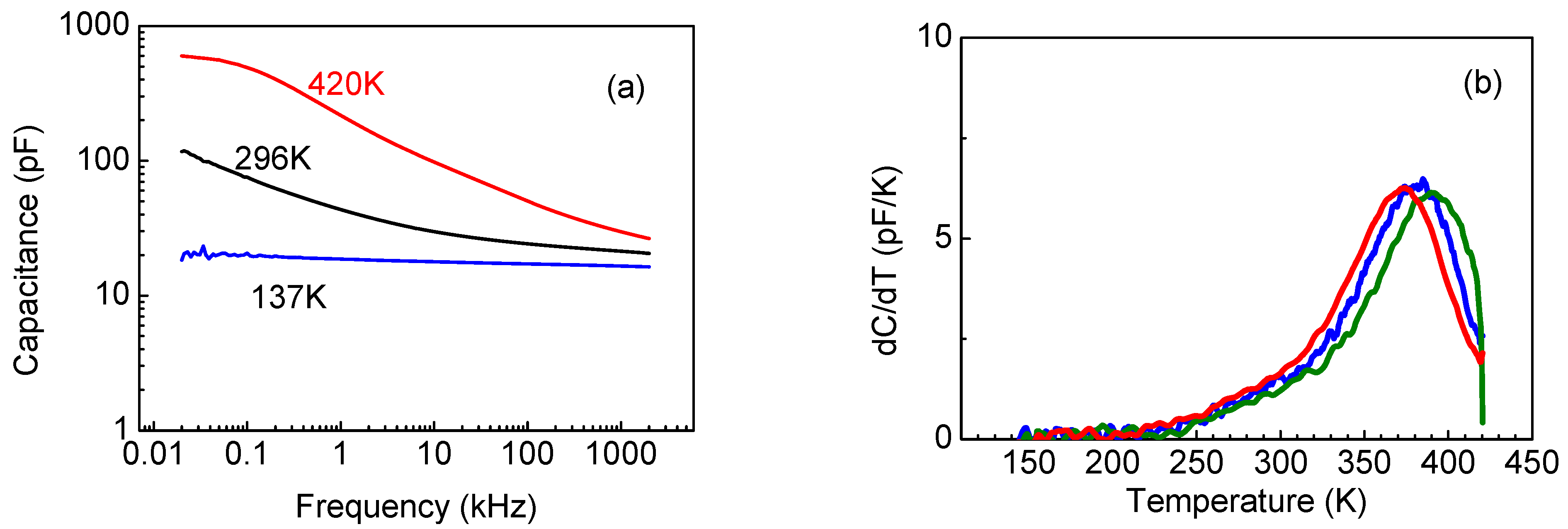
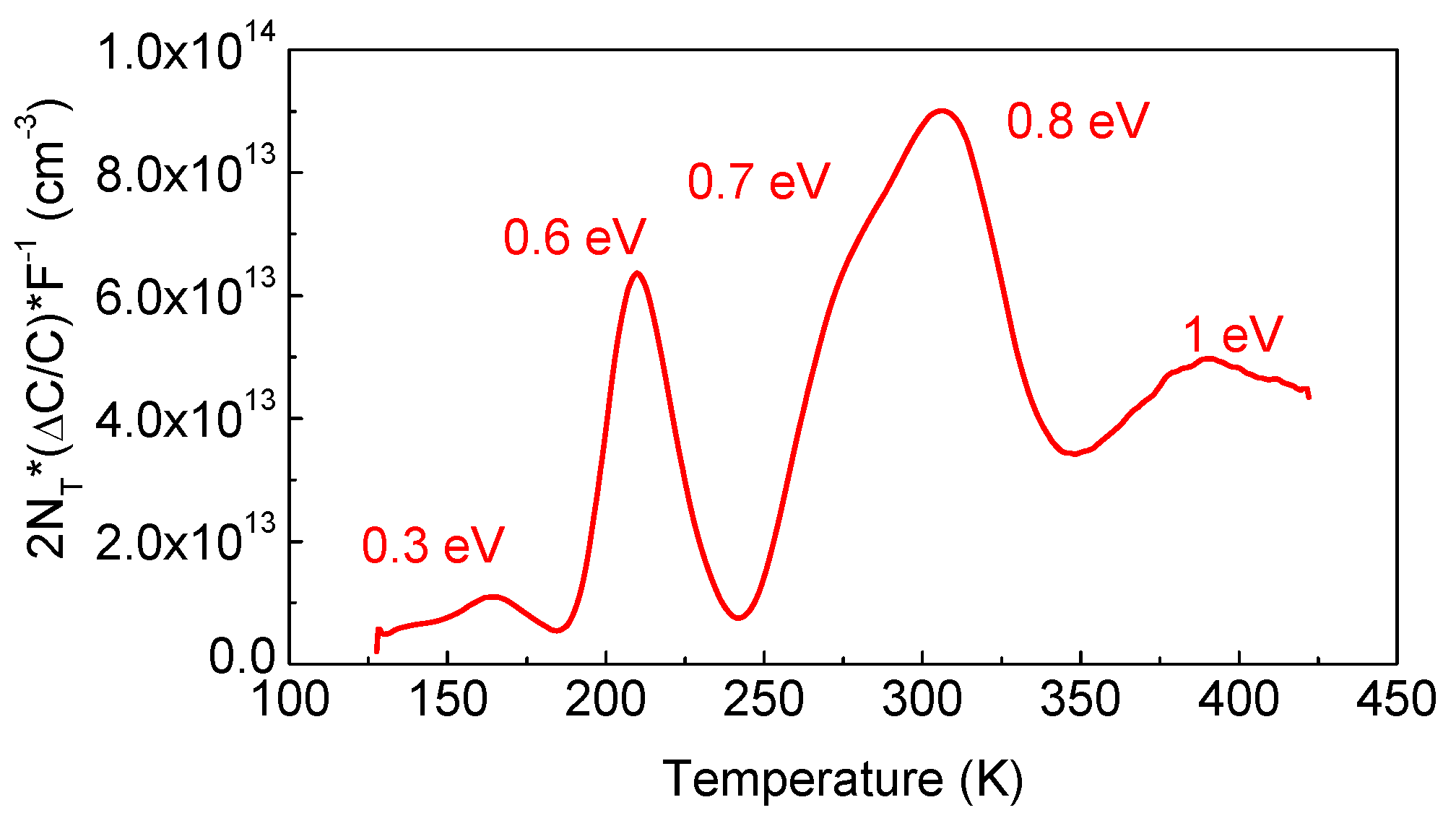
3.1. Thin κ-Ga2O3 Films on AlN/Si Templates: Electrical Properties and Deep Traps
3.2. κ-Ga2O3 Films on n-GaN/Sapphire Templates: Structural Characteristics, Electrical Properties and Deep Traps, Recombination Properties
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pearton, S.J.; Ren, F.; Tadjer, M.; Kim, J. Perspective: Ga2O3 for ultra-high power rectifiers and MOSFETS. J. Appl. Phys. 2018, 124, 220901. [Google Scholar] [CrossRef]
- Higashiwaki, M.; Fujita, S. (Eds.) Gallium Oxide: Materials Properties, Crystal Growth, and Devices; Springer Series in Materials Science; Springer Nature: Cham, Switzerland, 2020; Volume 293. [Google Scholar]
- Xu, J.; Zheng, W.; Huang, F. Gallium oxide solar-blind ultraviolet photodetectors: A review. J. Mater. Chem. C 2019, 7, 8753–8770. [Google Scholar] [CrossRef]
- Cora, I.; Fogarassy, Z.; Fornari, R.; Bosi, M.; Recnik, A.; Pécz, B. In situ TEM study of κ→ β and κ→ γ phase transformations in Ga2O3. Acta Mater. 2020, 183, 216–227. [Google Scholar] [CrossRef]
- García-Fernández, J.; Kjeldby, S.B.; Nguyen, P.D.; Karlsen, O.B.; Vines, L.; Prytz, Ø. Formation of γ-Ga2O3 by ion implantation: Polymorphic phase transformation of β-Ga2O3. Appl. Phys. Lett. 2022, 121, 191601. [Google Scholar] [CrossRef]
- Shivani; Kaur, D.; Ghosh, A.; Kumar, M. A strategic review on gallium oxide based power electronics: Recent progress and future prospects. Mater. Today Commun. 2022, 33, 104244. [Google Scholar] [CrossRef]
- Ingebrigtsen, M.E.; Kuznetsov, A.Y.; Svensson, B.G.; Alfieri, G.; Mihaila, A.; Badstübner, U.; Perron, A.; Vines, L.; Varley, J.B. Impact of proton irradiation on conductivity and deep level defects in β-Ga2O3. APL Mater. 2019, 7, 022510. [Google Scholar] [CrossRef]
- Deák, P.; Ho, Q.D.; Seemann, F.; Aradi, B.; Lorke, M.; Frauenheim, T. Choosing the correct hybrid for defect calculations: A case study on intrinsic carrier trapping in β-Ga2O3. Phys. Rev. B 2017, 95, 075208. [Google Scholar] [CrossRef]
- Polyakov, A.Y.; Nikolaev, V.I.; Yakimov, E.B.; Ren, F.; Pearton, S.J.; Kim, J. Deep level defect states in β-, α-, and ε-Ga2O3 crystals and films: Impact on device performance. J. Vac. Sci. Technol. A 2022, 40, 020804. [Google Scholar] [CrossRef]
- Kim, J.; Pearton, S.J.; Fares, C.; Yang, J.; Ren, F.; Kim, S.; Polyakov, A.Y. Radiation damage effects in Ga2O3 materials and devices. J. Mater. Chem. C 2018, 7, 10–24. [Google Scholar] [CrossRef]
- Tamura Products. Available online: www.tamura-ss.co.jp/en/products (accessed on 1 March 2023).
- Kaneko, K.; Fujita, S.; Hitora, T. A power device material of corundum-structured α-Ga2O3 fabricated by MIST EPITAXY technique. Jpn. J. Appl. Phys. 2018, 57, 02CB18. [Google Scholar] [CrossRef]
- Polyakov, A.Y.; Smirnov, N.B.; Shchemerov, I.V.; Yakimov, E.B.; Nikolaev, V.I.; Stepanov, S.I.; Pechnikov, A.I.; Chernykh, A.V.; Shcherbachev, K.D.; Shikoh, A.S.; et al. Deep trap spectra of Sn-doped α-Ga2O3 grown by halide vapor phase epitaxy on sapphire. APL Mater. 2019, 7, 051103. [Google Scholar] [CrossRef]
- Polyakov, A.Y.; Nikolaev, V.I.; Stepanov, S.I.; Pechnikov, A.I.; Yakimov, E.B.; Smirnov, N.B.; Shchemerov, I.V.; Vasilev, A.A.; Kochkova, A.I.; Chernykh, A.V.; et al. Editors’ Choice—Electrical Properties and Deep Traps in α-Ga2O3:Sn Films Grown on Sapphire by Halide Vapor Phase Epitaxy. ECS J. Solid State Sci. Technol. 2020, 9, 045003. [Google Scholar] [CrossRef]
- Ahmadi, E.; Oshima, Y. Materials issues and devices of α- and β-Ga2O3. J. Appl. Phys. 2019, 126, 160901. [Google Scholar] [CrossRef]
- Jinno, R.; Uchida, T.; Kaneko, K.; Fujita, S. Reduction in edge dislocation density in corundum-structured α-Ga2O3 layers on sapphire substrates with quasi-graded α-(Al,Ga)2O3 buffer layers. Appl. Phys. Express 2016, 9, 071101. [Google Scholar] [CrossRef]
- Stepanov, S.I.; Nikolaev, V.I.; Almaev, A.V.; Pechnikov, A.I.; Scheglov, M.P.; Chikiryaka, A.V.; Kushnarev, B.O.; Polyakov, A.Y. HVPE growth of corundum-structured α-Ga2O3 on sapphire substrates with α-Cr2O3 buffer layer. Mater. Phys. Mech. 2021, 47, 577–581. [Google Scholar] [CrossRef]
- Polyakov, A.; Nikolaev, V.; Stepanov, S.; Almaev, A.; Pechnikov, A.; Yakimov, E.; Kushnarev, B.O.; Shchemerov, I.; Scheglov, M.; Chernykh, A.; et al. Electrical properties of α-Ga2O3 films grown by halide vapor phase epitaxy on sapphire with α-Cr2O3 buffers. J. Appl. Phys. 2022, 131, 215701. [Google Scholar] [CrossRef]
- Oshima, Y.; Kawara, K.; Shinohe, T.; Hitora, T.; Kasu, M.; Fujita, S. Epitaxial lateral overgrowth of α-Ga2O3 by halide vapor phase epitaxy. APL Mater. 2019, 7, 022503. [Google Scholar] [CrossRef]
- McCandless, J.P.; Chang, C.S.; Nomoto, K.; Casamento, J.; Protasenko, V.; Vogt, P.; Rowe, D.; Gann, K.; Ho, S.T.; Li, W.; et al. Thermal stability of epitaxial a-Ga2O3 and (Al,Ga)2O3 layers on m-plane sapphire. Appl. Phys. Lett. 2021, 119, 062102. [Google Scholar] [CrossRef]
- Kobayashi, T.; Gake, T.; Kumagai, Y.; Oba, F.; Matsushita, Y. Energetics and electronic structure of native point defects in α-Ga2O3. Appl. Phys. Express 2019, 12, 091001. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, X.; Ren, F.-F.; Gu, S.; Ye, J. Deep-level defects in gallium oxide. J. Phys. D Appl. Phys. 2021, 54, 043002. [Google Scholar] [CrossRef]
- Biswas, M.; Nishinaka, H. Thermodynamically metastable α-, ε- (or κ-), and γ-Ga2O3: From material growth to device applications. APL Mater. 2022, 10, 060701. [Google Scholar] [CrossRef]
- Bae, J.; Park, J.-H.; Jeon, D.-W.; Kim, J. Self-powered solar-blind α-Ga2O3 thin-film UV-C photodiode grown by halide vapor-phase epitaxy. APL Mater. 2021, 9, 101108. [Google Scholar] [CrossRef]
- Parisini, A.; Bosio, A.; Montedoro, V.; Gorreri, A.; Lamperti, A.; Bosi, M.; Garulli, G.; Vantaggio, S.; Fornari, R. Si and Sn doping of ε-Ga2O3 layers. APL Mater. 2019, 7, 031114. [Google Scholar] [CrossRef]
- Mezzadri, F.; Calestani, G.; Boschi, F.; Delmonte, D.; Bosi, M.; Fornari, R. Crystal Structure and Ferroelectric Properties of ε-Ga2O3 Films Grown on (0001)-Sapphire. Inorg. Chem. 2016, 55, 12079–12084. [Google Scholar] [CrossRef]
- von Wenckstern, H. Group-III Sesquioxides: Growth, physical properties and devices. Adv. Electron. Mater. 2017, 3, 1600350. [Google Scholar] [CrossRef]
- Wang, J.; Guo, H.; Zhu, C.-Z.; Cai, Q.; Yang, G.-F.; Xue, J.-J.; Chen, D.-J.; Tong, Y.; Liu, B.; Lu, H.; et al. ε-Ga2O3: A Promising Candidate for High-Electron-Mobility Transistors. IEEE Electr. Dev. Lett. 2017, 38, 1052–1055. [Google Scholar] [CrossRef]
- Cho, S.B.; Mishra, R. Epitaxial Engineering of polar ε-Ga2O3 for tunable two-dimensional electron gas at the heterointerface. Appl. Phys. Lett. 2018, 112, 162101. [Google Scholar] [CrossRef]
- Polyakov, A.Y.; Nikolaev, V.I.; Pechnikov, A.I.; Yakimov, E.B.; Karpov, S.Y.; Stepanov, S.I.; Shchemerov, I.V.; Vasilev, A.A.; Chernykh, A.V.; Kuznetsov, A.; et al. Two-dimensional hole gas formation at the κ-Ga2O3/AlN heterojunction interface. J. Alloys Compd. 2023, 936, 168315. [Google Scholar] [CrossRef]
- Chen, Z.; Lu, X.; Tu, Y.; Chen, W.; Zhang, Z.; Cheng, S.; Chen, S.; Luo, H.; He, Z.; Pei, Y.; et al. 𝝐-Ga2O3: An Emerging Wide Bandgap Piezoelectric Semiconductor for Application in Radio Frequency Resonators. Adv. Sci. 2022, 9, 2203927. [Google Scholar] [CrossRef]
- Nishinaka, H.; Komai, H.; Tahara, D.; Arata, Y.; Yoshimoto, M. Microstructures and rotational domains in orthorhombic ε-Ga2O3 thin films. Jpn. J. Appl. Phys. 2018, 57, 115601. [Google Scholar] [CrossRef]
- Cora, I.; Mezzadri, F.; Boschi, F.; Bosi, M.; Čaplovičova, M.; Calestani, G.; Dódony, I.; Pécz, B.; Fornari, R. The real structure of ε-Ga2O3 and its relation to κ-phase. CrystEngComm 2017, 19, 1509–1516. [Google Scholar] [CrossRef]
- Nishinaka, H.; Ueda, O.; Ito, Y.; Ikenaga, N.; Hasuike, N.; Yoshimoto, M. Plan-view TEM observation of a single-domain κ-Ga2O3 thin film grown on ε-GaFeO3 substrate using GaCl3 precursor by mist chemical vapor deposition. Jpn J. Appl. Phys. 2022, 61, 018002. [Google Scholar] [CrossRef]
- Kneiß, M.; Splith, D.; Schlupp, P.; Hassa, A.; von Wenckstern, H.; Lorenz, M.; Grundmann, M. Realization of highly rectifying Schottky barrier diodes and pn heterojunctions on κ-Ga2O3 by overcoming the conductivity anisotropy. J. Appl. Phys. 2021, 130, 084502. [Google Scholar] [CrossRef]
- Hassa, A.; Wouters, C.; Kneiß, M.; Splith, D.; Sturm, C.; von Wenckstern, H.; Albrecht, M.; Lorenz, M.; Grundmann, M. Control of phase formation of (AlxGa1−x)2O3 thin films on c-plane Al2O3. J. Phys. D Appl. Phys. 2020, 53, 485105. [Google Scholar] [CrossRef]
- Nikolaev, V.I.; Stepanov, S.I.; Pechnikov, A.I.; Shapenkov, S.V.; Scheglov, M.P.; Chikiryaka, A.V.; Vyvenko, O.F. HVPE Growth and Characterization of ε-Ga2O3 Films on Various Substrates. ECS J. Solid State Sci. Technol. 2020, 9, 045014. [Google Scholar] [CrossRef]
- Azarov, A.; Bazioti, C.; Venkatachalapathy, V.; Vajeeston, P.; Monakhov, E.; Kuznetsov, A. Disorder-Induced Ordering in Gallium Oxide Polymorphs. Phys. Rev. Lett. 2022, 128, 015704. [Google Scholar] [CrossRef] [PubMed]
- Anber, E.A.; Foley, D.; Lang, A.C.; Nathaniel, J.; Hart, J.L.; Tadjer, M.J.; Hobart, K.D.; Pearton, S.; Taheri, M.L. Structural transition and recovery of Ge implanted β-Ga2O3. Appl. Phys. Lett. 2020, 117, 152101. [Google Scholar] [CrossRef]
- Petkov, A.; Cherns, D.; Chen, W.-Y.; Liu, J.; Blevins, J.; Gambin, V.; Li, M.; Liu, D.; Kuball, M. Structural stability of β-Ga2O3 under ion irradiation. Appl. Phys. Lett. 2022, 121, 171903. [Google Scholar] [CrossRef]
- Polyakov, A.Y.; Nikolaev, V.I.; Pechnikov, A.I.; Stepanov, S.I.; Yakimov, E.B.; Scheglov, M.P.; Shchemerov, I.V.; Vasilev, A.A.; Kochkova, A.I.; Chernykh, A.V.; et al. Structural and electrical properties of thick κ-Ga2O3 grown on GaN/sapphire templates. APL Mater. 2022, 10, 061102. [Google Scholar] [CrossRef]
- Stepanov, S.I.; Nikolaev, V.I.; Polyakov, A.Y.; Pechnikov, A.I.; Yakimov, E.B.; Scheglov, M.P.; Shchemerov, I.V.; Vasilev, A.A.; Kochkova, A.I.; Chernykh, A.V.; et al. HVPE Growth and Characterization of Thick κ-Ga2O3 layers on GaN/Sapphire Templates. ECS J. Solid State Sci. Technol. 2023, 12, 015002. [Google Scholar] [CrossRef]
- Nikolaev, V.I.; Polyakov, A.Y.; Stepanov, S.I.; Pechnikov, A.I.; Yakimov, E.B.; Chernykh, A.V.; Vasilev, A.A.; Shchemerov, I.V.; Kochkova, A.I.; Guzilova, L.; et al. Electrical and Structural Properties of Two-Inch Diameter (0001) α-Ga2O3 Films Doped with Sn and Grown by Halide Epitaxy. ECS J. Solid State Sci. Technol. 2022, 11, 115002. [Google Scholar] [CrossRef]
- Polyakov, A.Y.; Smirnov, N.B.; Shchemerov, I.V.; Pearton, S.J.; Ren, F.; Chernykh, A.V.; Lagov, P.B.; Kulevoy, T.V. Hole traps and persistent photocapacitance in proton irradiated β-Ga2O3 films doped with Si. APL Mater. 2018, 6, 096102. [Google Scholar] [CrossRef]
- Polyakov, A.Y.; Smirnov, N.B.; Yakimov, E.B.; Tarelkin, S.A.; Turutin, A.V.; Shemerov, I.V.; Pearton, S.J.; Lee, I.-H. Deep traps determining the non-radiative lifetime and defect band yellow luminescence in n-GaN. J. Alloys Compd. 2016, 686, 1044–1052. [Google Scholar] [CrossRef]
- Schroder, D.K. Semiconductor Material and Device Characterization, 3rd ed.; Wiley-Interscience: New York, NY, USA, 2006. [Google Scholar]
- Li, J.V.; Ferrari, G. (Eds.) Capacitance Spectroscopy of Semiconductors; Pan Stanford Publishing Pte Ltd.: Singapore, 2018. [Google Scholar]
- Polyakov, A.Y.; Smirnov, N.B.; Lee, I.-H.; Pearton, S.J. Deep level transient spectroscopy in III-Nitrides: Decreasing the effects of series resistance. J. Vacuum Sci. Technol. B 2015, 33, 061203. [Google Scholar] [CrossRef]
- Zhang, Z.; Farzana, E.; Arehart, A.R.; Ringel, S.A. Deep level defects throughout the bandgap of (010) β-Ga2O3 detected by optically and thermally stimulated defect spectroscopy. Appl. Phys. Lett. 2016, 108, 052105. [Google Scholar] [CrossRef]
- Yakimov, E.B. What is the real value of diffusion length in GaN? J. Alloys Compd. 2015, 627, 344–351. [Google Scholar] [CrossRef]
- Yakimov, E.B.; Polyakov, A.Y.; Smirnov, N.B.; Shchemerov, I.V.; Yang, J.; Ren, F.; Yang, G.; Kim, J.; Pearton, S.J. Diffusion length of non-equilibrium minority charge carriers in β-Ga2O3 measured by electron beam induced current. J. Appl. Phys. 2018, 123, 185704. [Google Scholar] [CrossRef]
- Donolato, C. A reciprocity theorem for charge collection. Appl. Phys. Lett. 1985, 46, 270–272. [Google Scholar] [CrossRef]
- Yakimov, E.B.; Polyakov, A.Y.; Shchemerov, I.V.; Smirnov, N.B.; Vasilev, A.A.; Vergeles, P.S.; Yakimov, E.E.; Chernykh, A.V.; Ren, F.; Pearton, S.J. Experimental estimation of electron–hole pair creation energy in β-Ga2O3. Appl. Phys. Lett. 2021, 118, 202106. [Google Scholar] [CrossRef]
- Peelaers, H.; Lyons, J.L.; Varley, J.B.; Van de Walle, C.G. Deep acceptors and their diffusion in Ga2O3. APL Mater. 2019, 7, 022519. [Google Scholar] [CrossRef]
- Field Effect Transistor Integrated Simulator (FETIS). Available online: https://str-soft.com/devices/fetis/ (accessed on 1 March 2023).
- Lukin, G.; Schneider, T.; Förste, M.; Barchuk, M.; Schimpf, C.; Röder, C.; Zimmermann, F.; Niederschlag, E.; Pätzold, O.; Beyer, F.C.; et al. Heteroepitaxial growth of GaN on sapphire substrates by high temperature vapor phase epitaxy. J. Crystal Growth 2019, 524, 125185. [Google Scholar] [CrossRef]
- Yakimov, E.B. Study of Wide-Gap Semiconductors Using Electron-Beam Induced Current Method. Crystallogr. Rep. 2021, 66, 581–593. [Google Scholar] [CrossRef]
- Borelli, C.; Bosio, A.; Parisini, A.; Pavesi, M.; Vantaggio, S.; Fornari, R. Electronic properties and photo-gain of UV-C photodetectors based on high-resistivity orthorhombic κ-Ga2O3 epilayers. Mater. Sci. Eng. B 2022, 286, 116056. [Google Scholar] [CrossRef]
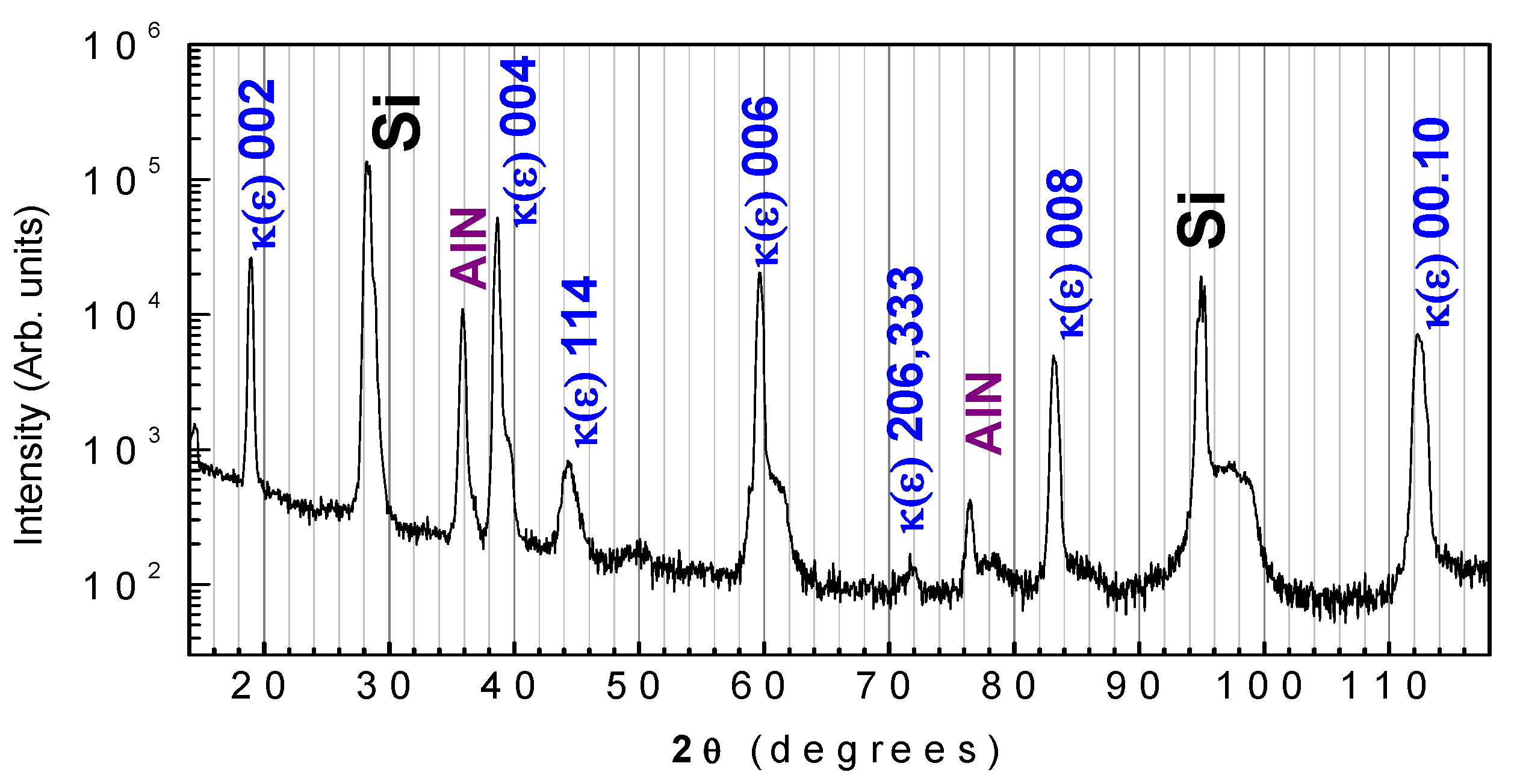


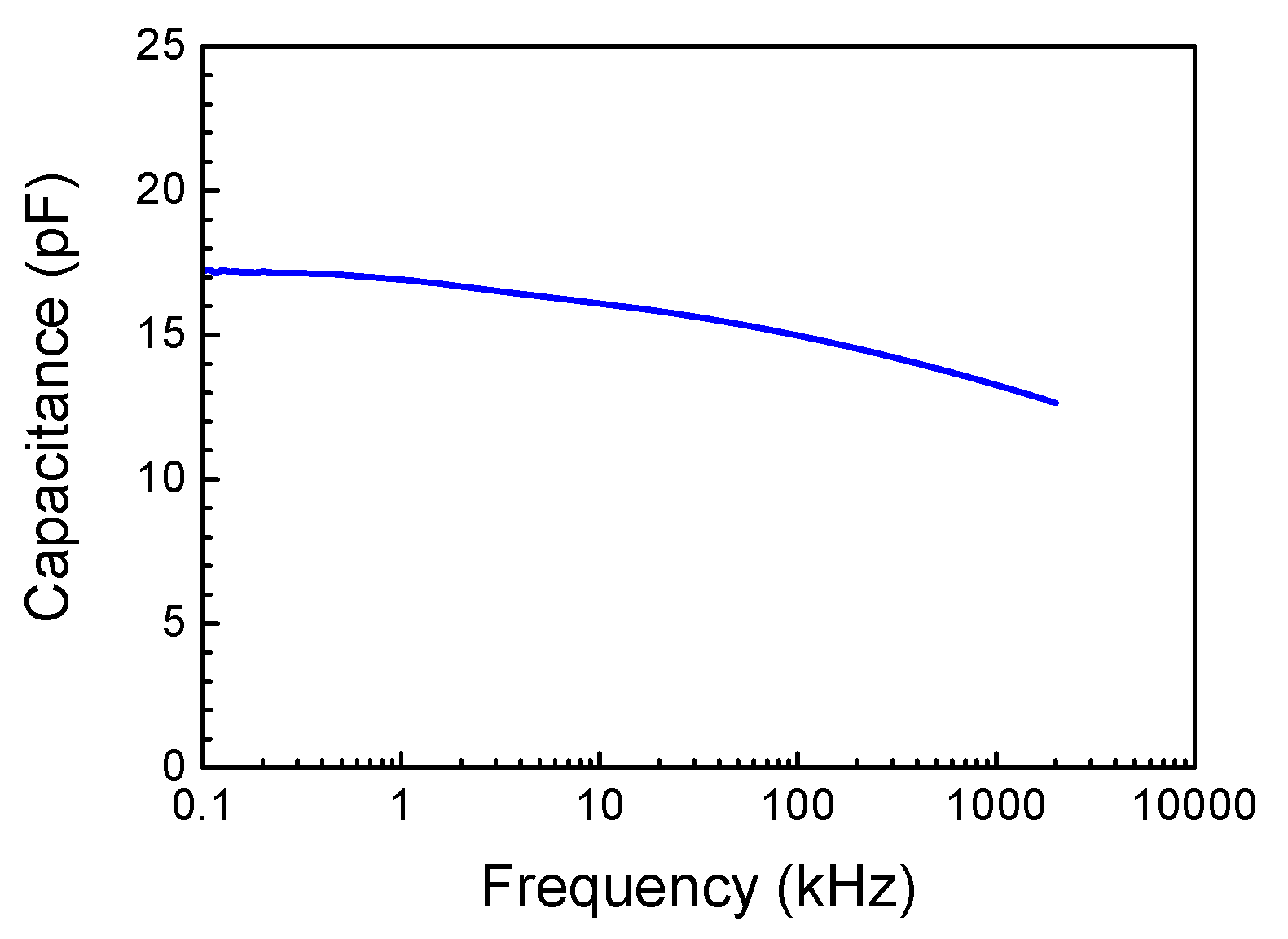
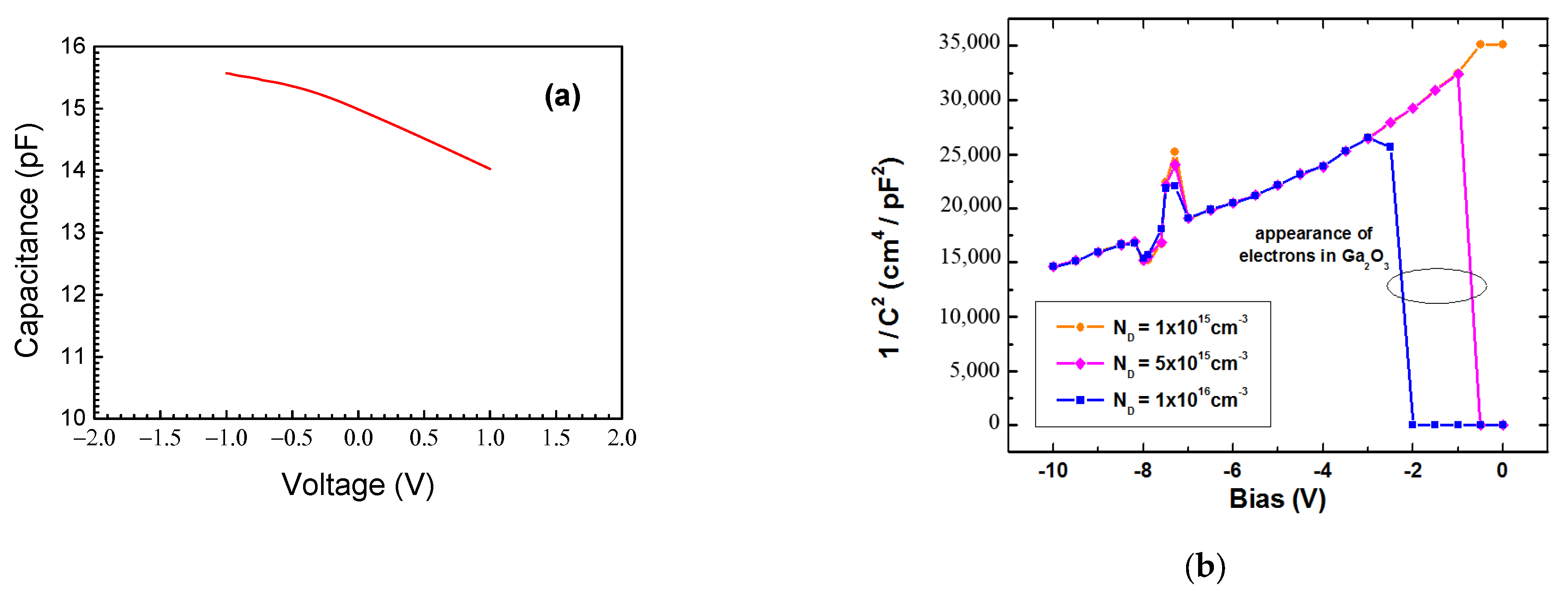
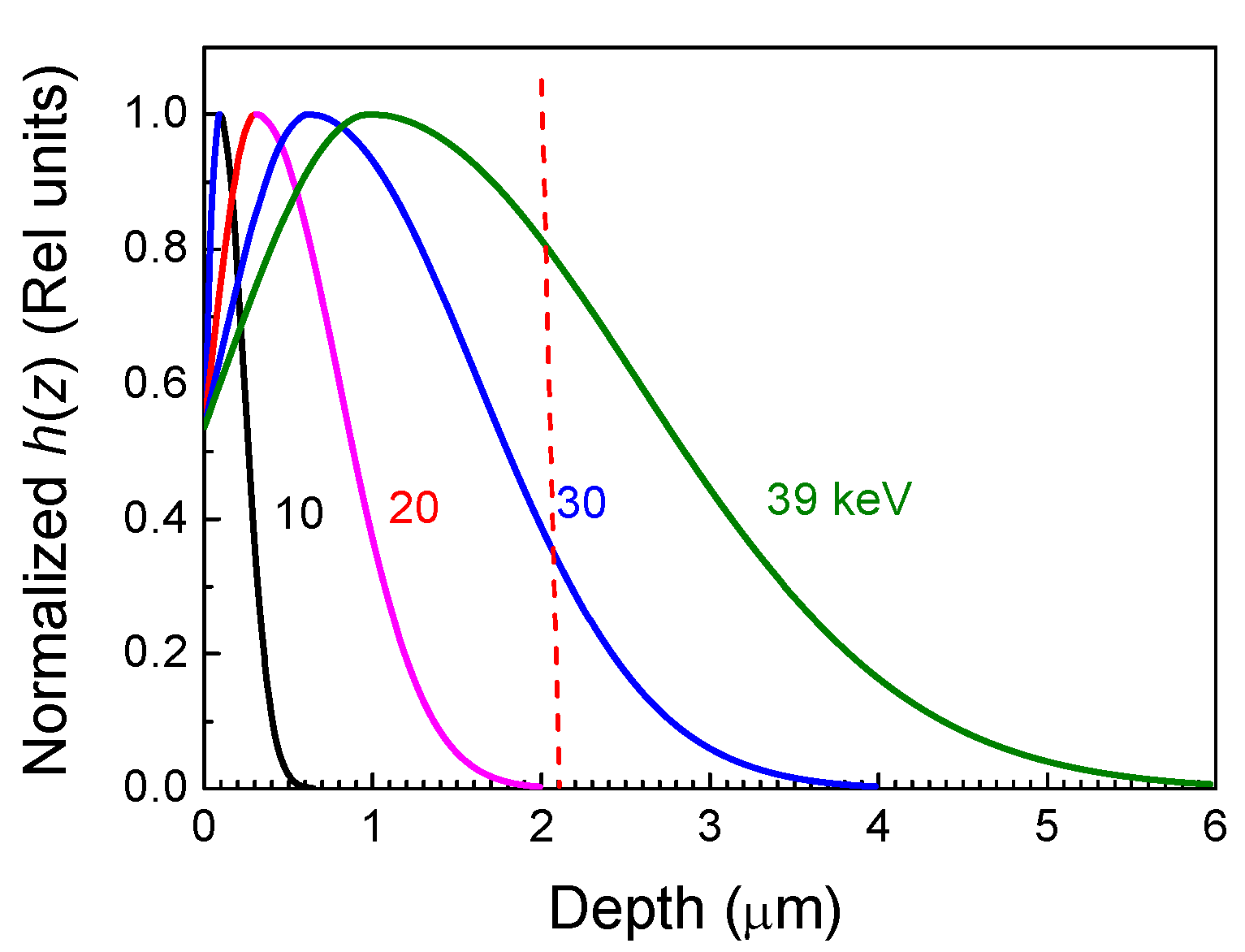

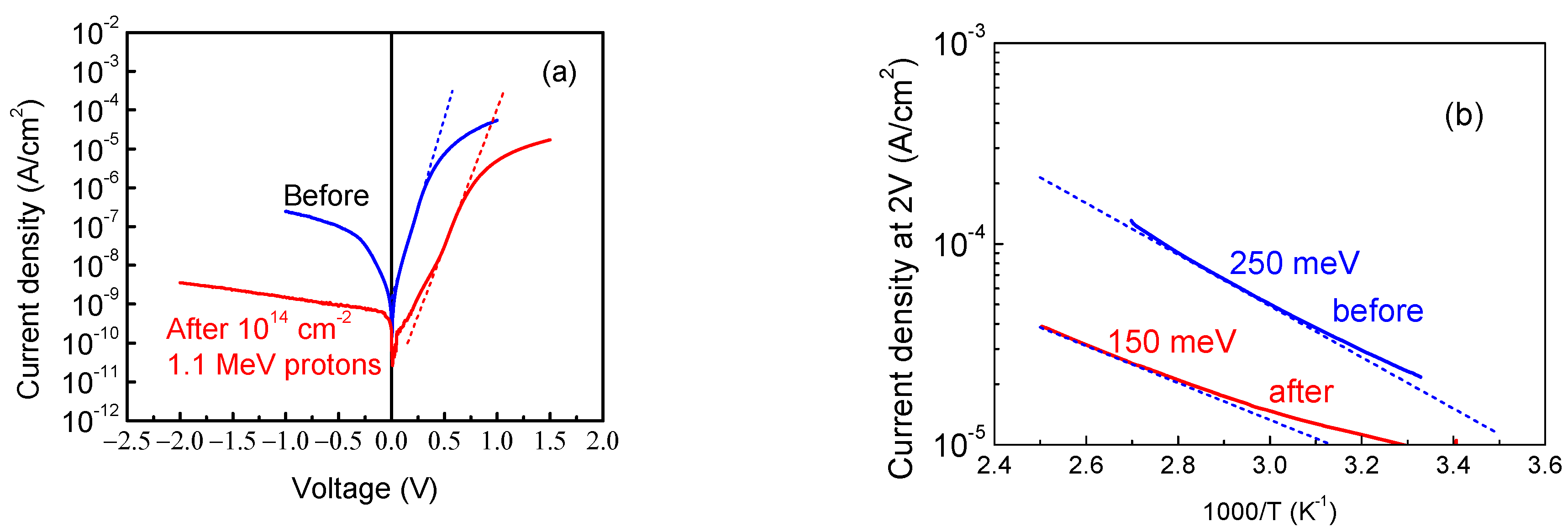
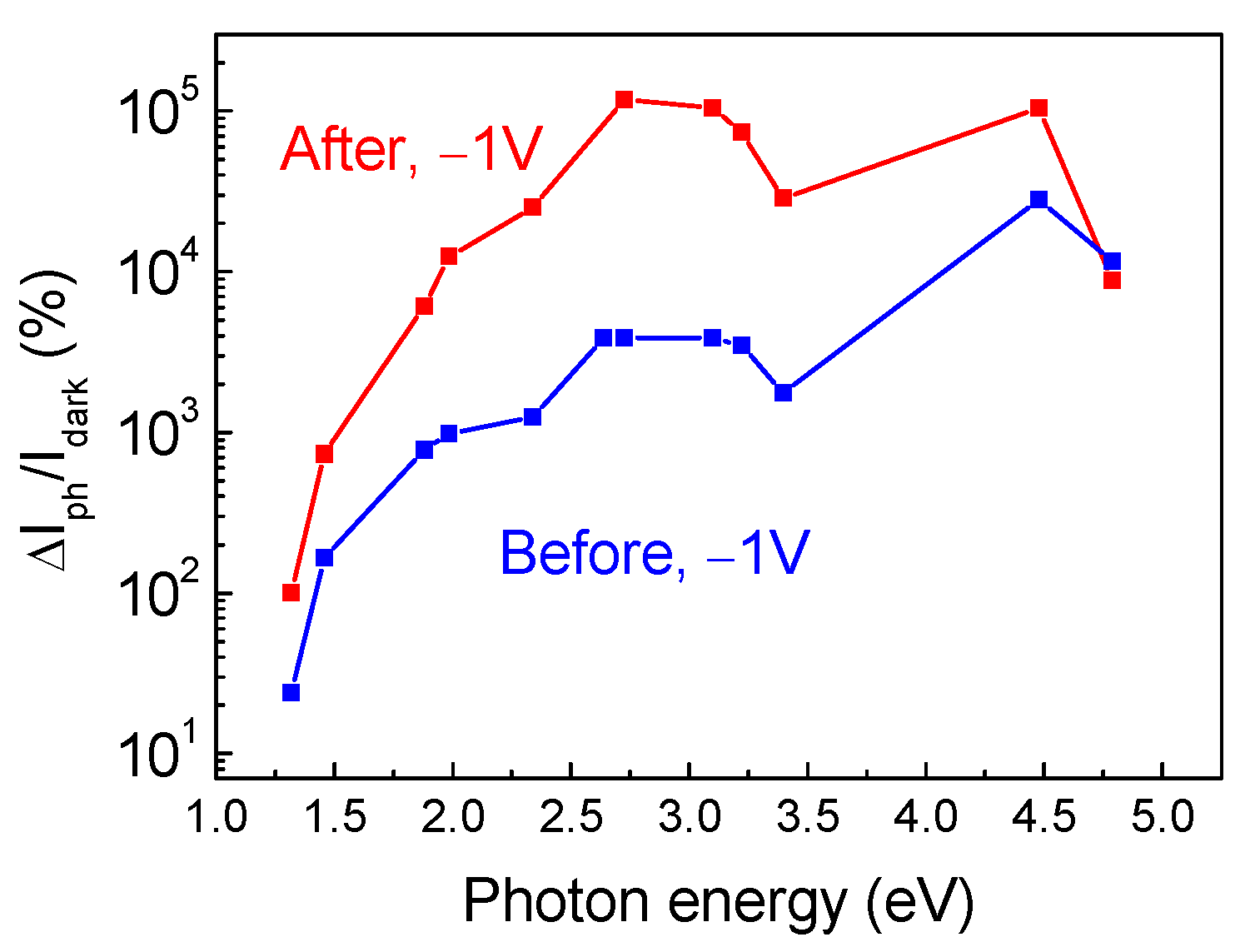
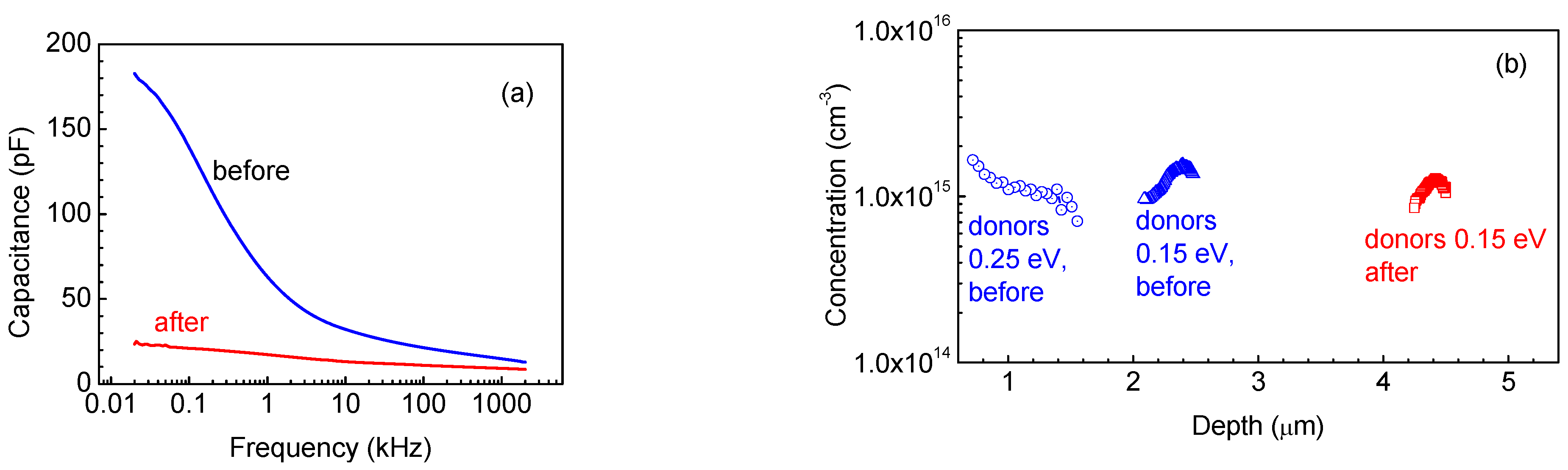

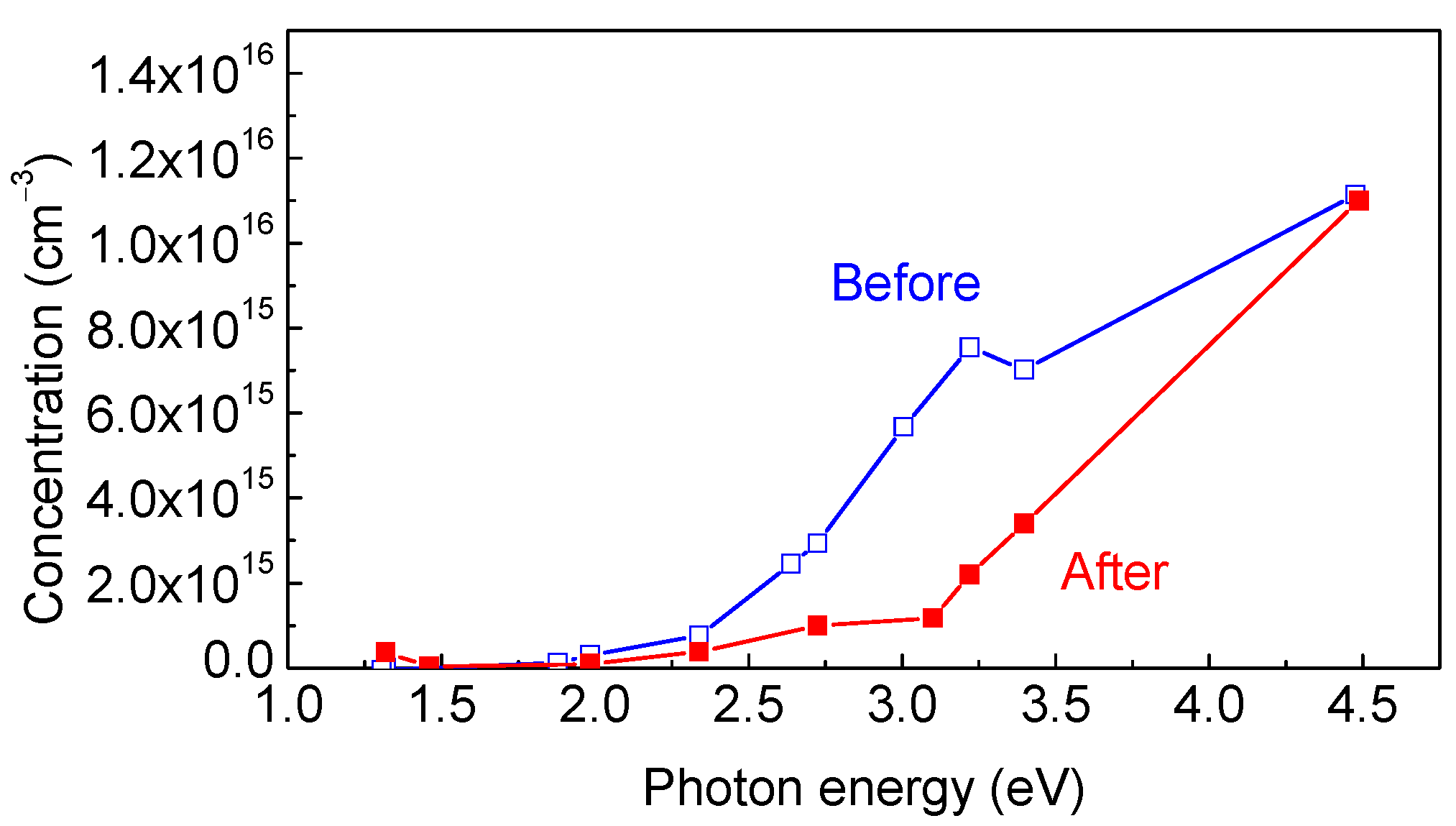

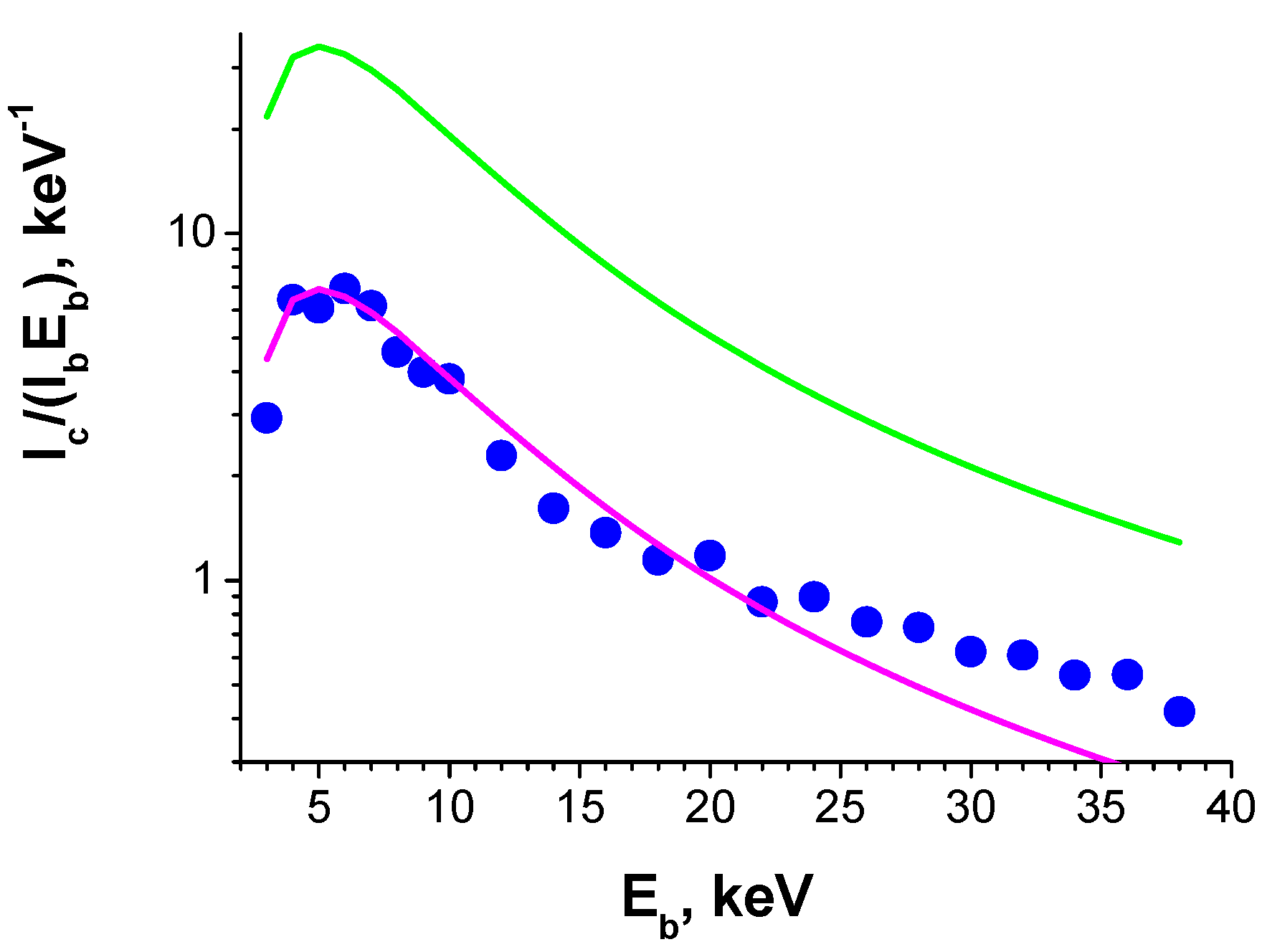
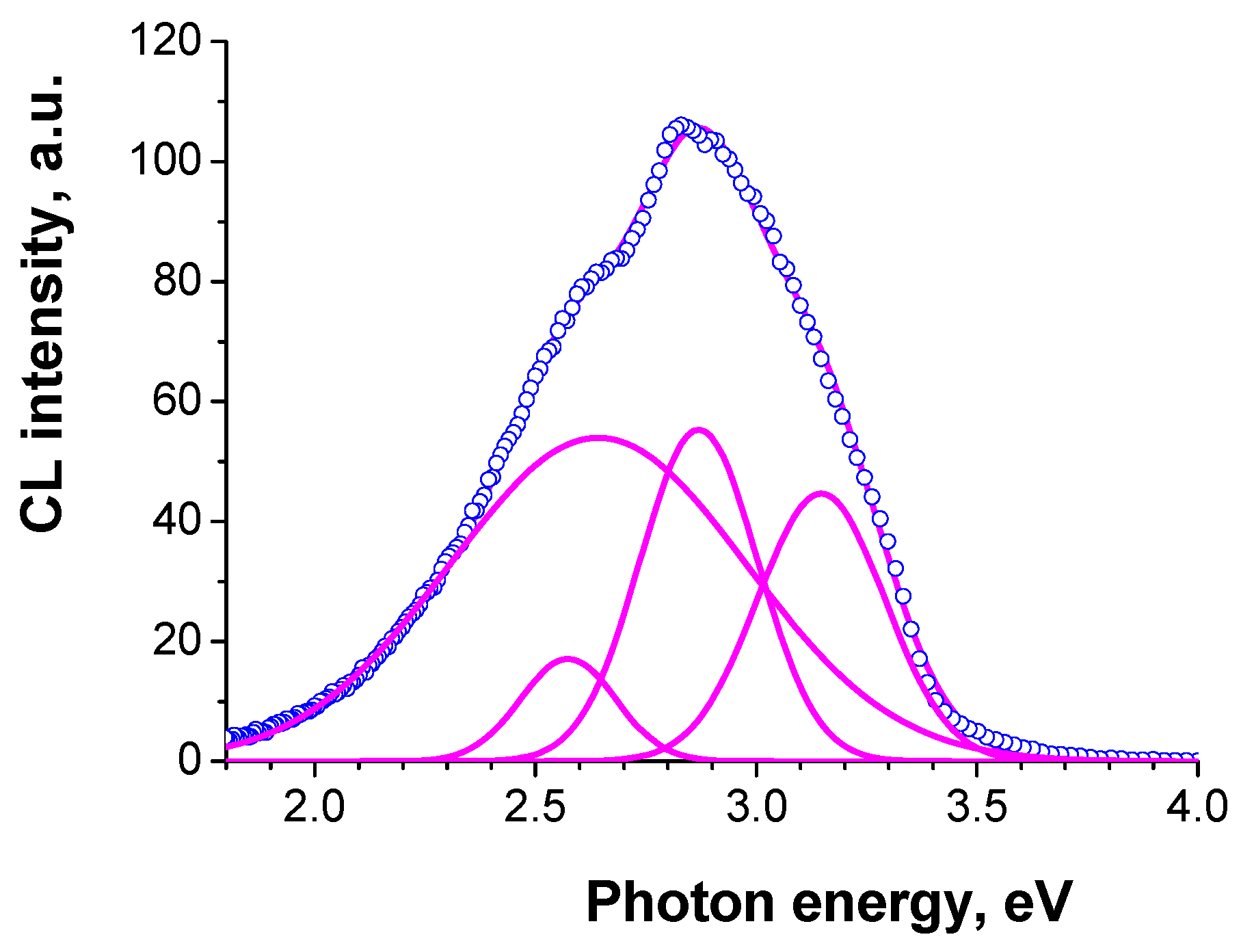
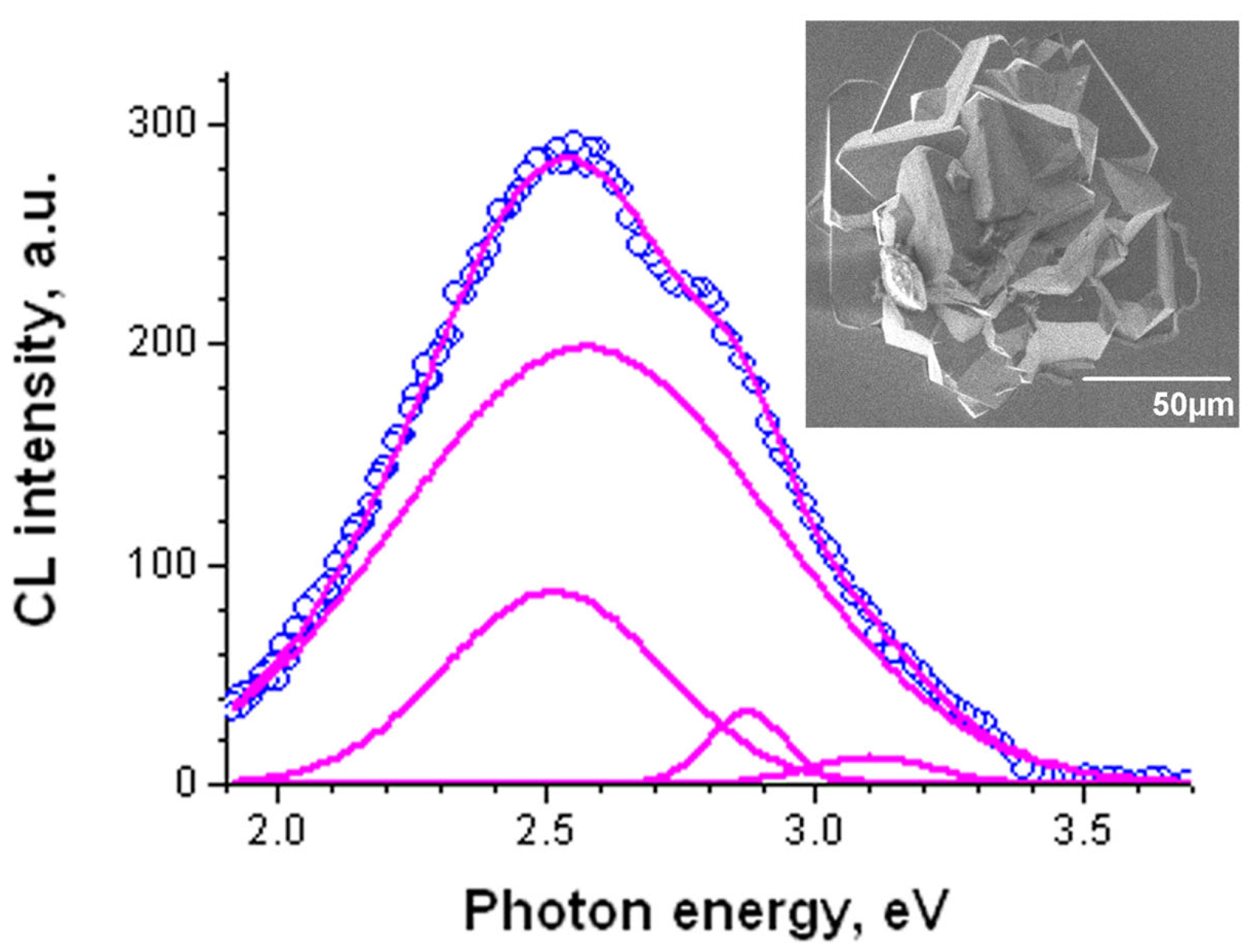
| Sample No | Number of Growth Runs | Thickness (μm) | FWHM (arcMin) | ρs Screw, cm−2 | ρe Edge, cm−2 | ρ Total, cm−2 | ||
|---|---|---|---|---|---|---|---|---|
| 004 | 206 | 206 (twist) | 004 | 206 (twist) | ||||
| S1 | 1 | 10 | 24′ | 18′ | 36′ | 4 × 109 | 4 × 1010 | 4.4 × 1010 |
| S2 | 1 | 13 | 9′ | 12′ | 28′ | 1.7 × 109 | 3 × 1010 | 4.7 × 1010 |
| S3 | 2 | 20 | 12′ | 12′ | 24′ | 2 × 109 | 2.6 × 1010 | 2.8 × 1010 |
| S4 | 2 | 23 | 16′ | 14′ | 26′ | 2.1 × 109 | 2.8 × 1010 | 3 × 1010 |
| S5 | 4 | 60 | 20′ | 34′ | 48’ | 3.3 × 109 | 7 × 1010 | 7.3 × 1010 |
| S6 | 6 | 86 | 60′ | 60′ | 90′ | 1 × 1010 | 13 × 1010 | 14 × 1010 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yakimov, E.B.; Polyakov, A.Y.; Nikolaev, V.I.; Pechnikov, A.I.; Scheglov, M.P.; Yakimov, E.E.; Pearton, S.J. Electrical and Recombination Properties of Polar Orthorhombic κ-Ga2O3 Films Prepared by Halide Vapor Phase Epitaxy. Nanomaterials 2023, 13, 1214. https://doi.org/10.3390/nano13071214
Yakimov EB, Polyakov AY, Nikolaev VI, Pechnikov AI, Scheglov MP, Yakimov EE, Pearton SJ. Electrical and Recombination Properties of Polar Orthorhombic κ-Ga2O3 Films Prepared by Halide Vapor Phase Epitaxy. Nanomaterials. 2023; 13(7):1214. https://doi.org/10.3390/nano13071214
Chicago/Turabian StyleYakimov, Eugene B., Alexander Y. Polyakov, Vladimir I. Nikolaev, Alexei I. Pechnikov, Mikhail P. Scheglov, Eugene E. Yakimov, and Stephen J. Pearton. 2023. "Electrical and Recombination Properties of Polar Orthorhombic κ-Ga2O3 Films Prepared by Halide Vapor Phase Epitaxy" Nanomaterials 13, no. 7: 1214. https://doi.org/10.3390/nano13071214
APA StyleYakimov, E. B., Polyakov, A. Y., Nikolaev, V. I., Pechnikov, A. I., Scheglov, M. P., Yakimov, E. E., & Pearton, S. J. (2023). Electrical and Recombination Properties of Polar Orthorhombic κ-Ga2O3 Films Prepared by Halide Vapor Phase Epitaxy. Nanomaterials, 13(7), 1214. https://doi.org/10.3390/nano13071214







