Asymmetrical Plasmon Distribution in Hybrid AuAg Hollow/Solid Coded Nanotubes
Abstract
1. Introduction
2. Methods
2.1. Synthesis of 1D AuAg Nanostructures
2.2. EELS Acquisition and Data Processing
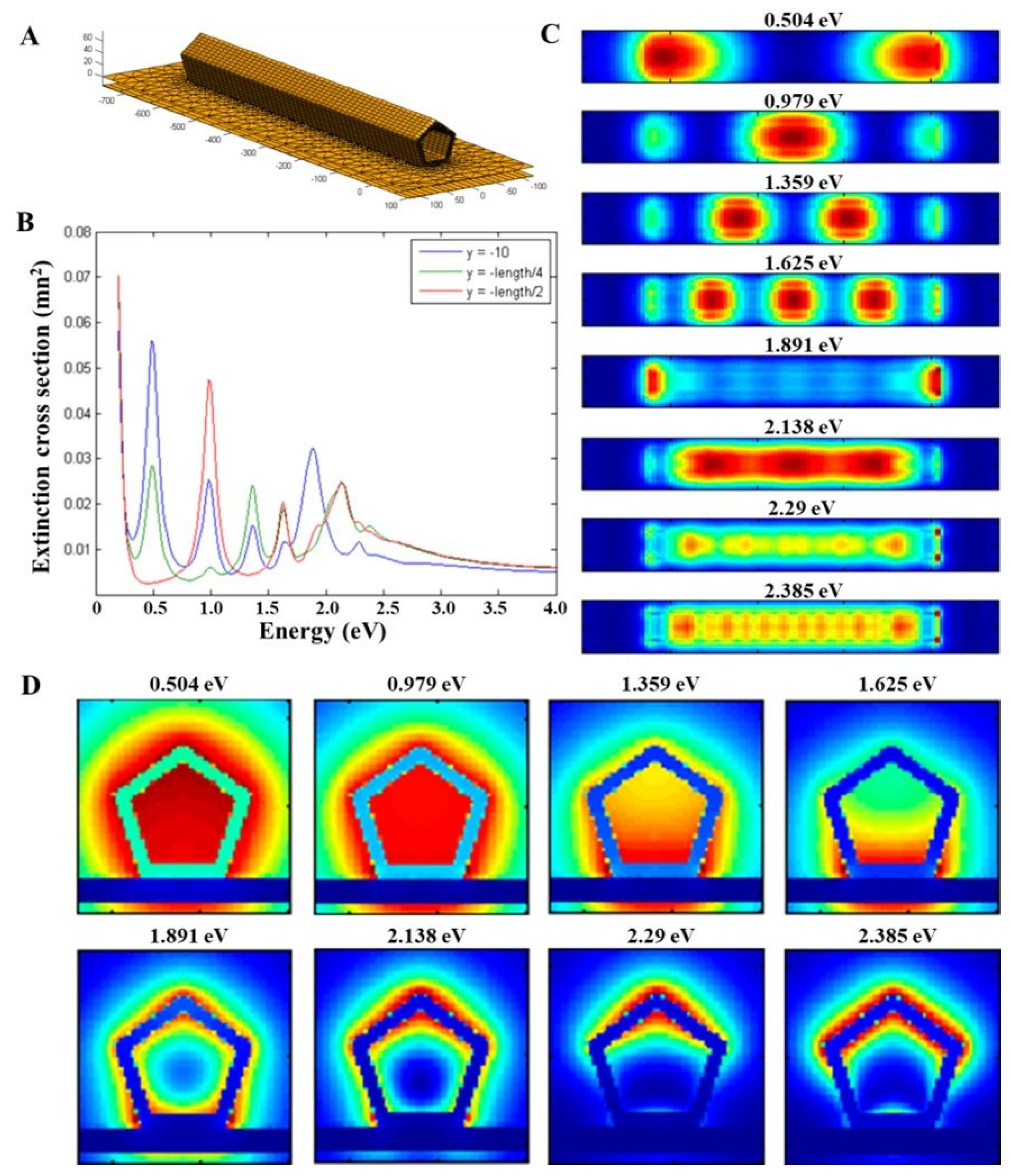
2.3. Simulations
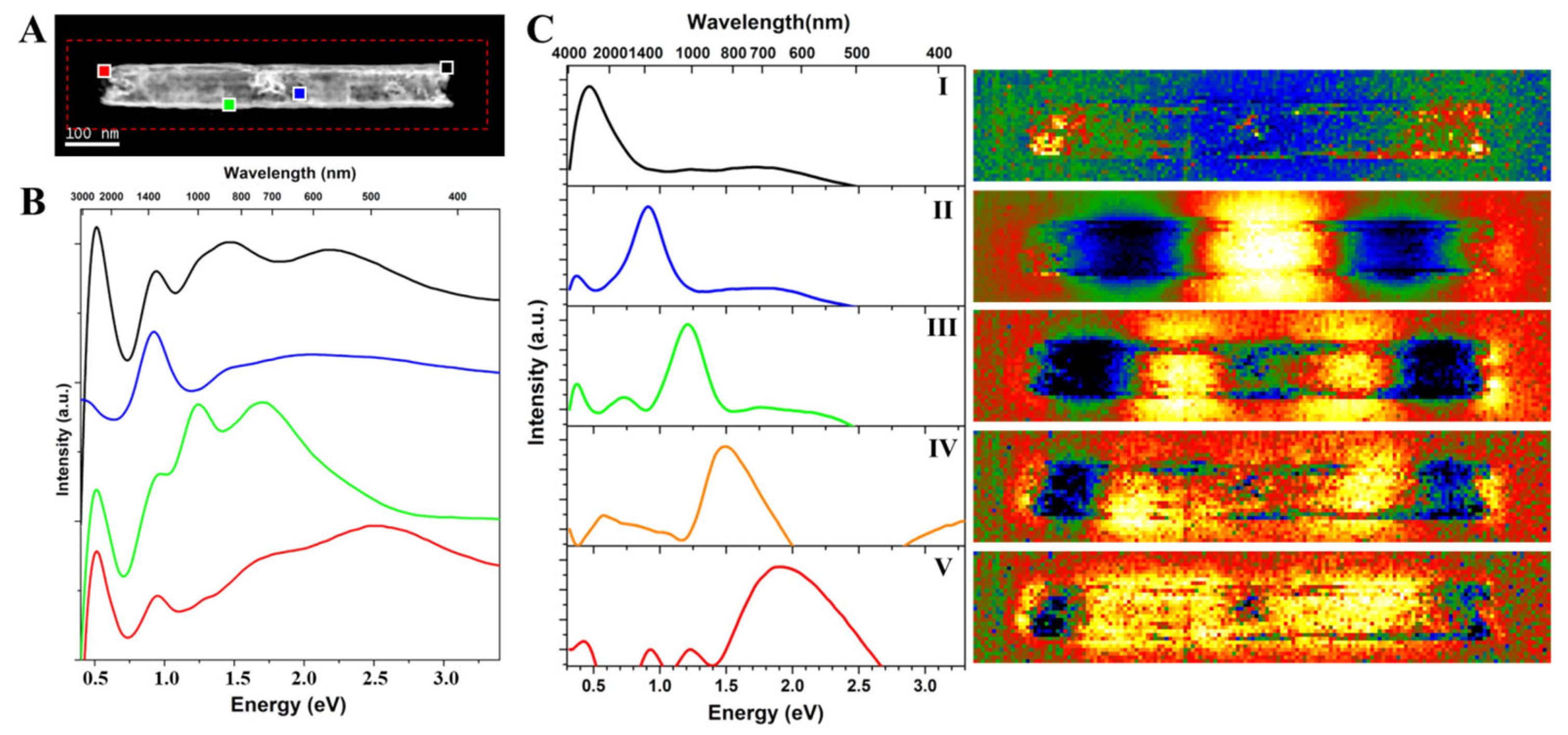
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Barnes, W.L.; Dereux, A.; Ebbesen, T.W. Surface plasmon subwavelength optics. Nature 2003, 424, 824–830. [Google Scholar] [CrossRef]
- Mayer, K.M.; Hafner, J.H. Localized surface plasmon resonance sensors. Chem. Rev. 2011, 111, 3828–3857. [Google Scholar] [CrossRef]
- Xu, Y.; Bai, P.; Zhou, X.; Akimov, Y.; Png, C.E.; Ang, L.K.; Knoll, W.; Wu, L. Optical Refractive Index Sensors with Plasmonic and Photonic Structures: Promising and Inconvenient Truth. Adv. Opt. Mater. 2019, 7, 1801433. [Google Scholar] [CrossRef]
- Haes, A.J.; Haynes, C.L.; McFarland, A.D.; Schatz, G.C.; Van Duyne, R.P.; Zou, S. Plasmonic Materials for Surface-Enhanced Sensing and Spectroscopy. MRS Bull. 2005, 30, 368–375. [Google Scholar] [CrossRef]
- Wang, J.; Koo, K.M.; Wang, Y.; Trau, M. Engineering State-of-the-Art Plasmonic Nanomaterials for SERS-Based Clinical Liquid Biopsy Applications. Adv. Sci. 2019, 6, 1900730. [Google Scholar] [CrossRef]
- Huang, Y.; Huang, P.; Lin, J. Plasmonic Gold Nanovesicles for Biomedical Applications. Small Methods 2019, 3, 1800394. [Google Scholar] [CrossRef]
- Atwater, H.A.; Polman, A. Plasmonics for improved photovoltaic devices. Nat. Mater. 2010, 9, 205–213. [Google Scholar] [CrossRef]
- Mendes, M.J.; Morawiec, S.; Simone, F.; Priolo, F.; Crupi, I. Colloidal plasmonic back reflectors for light trapping in solar cells. Nanoscale 2014, 6, 4796–4805. [Google Scholar] [CrossRef]
- Gramotnev, D.K.; Bozhevolnyi, S.I. Plasmonics beyond the diffraction limit. Nat. Photonics 2010, 4, 83–91. [Google Scholar] [CrossRef]
- Schuller, J.A.; Barnard, E.S.; Cai, W.; Jun, Y.C.; White, J.S.; Brongersma, M.L. Plasmonics for extreme light concentration and manipulation. Nat. Mater. 2010, 9, 193–204. [Google Scholar] [CrossRef]
- Bharadwaj, P.; Deutsch, B.; Novotny, L. Optical Antennas. Adv. Opt. Photonics 2009, 1, 438–483. [Google Scholar] [CrossRef]
- Novotny, L.; van Hulst, N. Antennas for light. Nat. Photonics 2011, 5, 83–90. [Google Scholar] [CrossRef]
- Rusak, E.; Straubel, J.; Gladysz, P.; Göddel, M.; Kedziorski, A.; Kühn, M.; Weigend, F.; Rockstuhl, C.; Slowik, K. Enhancement of and interference among higher-order multipole transitions in molecules near a plasmonic nanoantenna. Nat. Commun. 2019, 10, 5775. [Google Scholar] [CrossRef]
- Giannini, V.; Fernandez-Dominguez, A.I.; Heck, S.C.; Maier, S.A. Plasmonic nanoantennas: Fundamentals and their use in controlling the radiative properties of nanoemitters. Chem. Rev. 2011, 111, 3888–3912. [Google Scholar] [CrossRef]
- Hanke, T.; Cesar, J.; Knittel, V.; Trugler, A.; Hohenester, U.; Leitenstorfer, A.; Bratschitsch, R. Tailoring spatiotemporal light confinement in single plasmonic nanoantennas. Nano Lett. 2012, 12, 992–996. [Google Scholar] [CrossRef]
- Coenen, T.; Vesseur, E.J.R.; Polman, A. Deep subwavelength spatial characterization of angular emission from single-crystal au plasmonic ridge nanoantennas. ACS Nano 2012, 6, 1742–1750. [Google Scholar] [CrossRef]
- Pelaez-Fernandez, M.; Majerus, B.; Funes, D.; Dufour, R.; Duvail, J.L.; Henrard, L.; Arenal, R. Toward laser-induced tuning of plasmonic response in high aspect ratio gold nanostructures. Nanophotonics 2022, 11, 3719–3728. [Google Scholar] [CrossRef]
- Knight, M.W.; Sobhani, H.; Nordlander, P.; Halas, N.J. Photodetection with active optical nanoantennas. Science 2011, 332, 702–704. [Google Scholar] [CrossRef]
- Habib, A.; Zhu, X.; Can, U.I.; McLanahan, M.L.; Zorlutuna, P.; Yanik, A.A. Electro-plasmonic nanoantenna: A nonfluorescent optical probe for ultrasensitive label-free detection of electrophysiological signals. Sci. Adv. 2019, 5, eaav9786. [Google Scholar] [CrossRef]
- Alu, A.; Engheta, N. Tuning the scattering response of optical nanoantennas with nanocircuit loads. Nat. Photonics 2008, 2, 307–310. [Google Scholar] [CrossRef]
- Hayat, O.; Geng, J.; Liang, X.; Jin, R.; Hayat, K.; He, C. Subwavelength plasmonic nanoantenna as a Plasmonic Induced Polarization Rotator (PI-PR). Sci. Rep. 2020, 10, 2809. [Google Scholar] [CrossRef]
- Huang, K.C.Y.; Seo, M.K.; Sarmiento, T.; Huo, Y.; Harris, J.S.; Brongersma, M.L. Electrically driven subwavelength optical nanocircuits. Nat. Photonics 2014, 8, 244–249. [Google Scholar] [CrossRef]
- Colliex, C.; Kociak, M.; Stephan, O. Electron Energy Loss Spectroscopy imaging of surface plasmons at the nanometer scale. Ultramicroscopy 2016, 162, 1–24. [Google Scholar] [CrossRef]
- Wu, Y.; Li, G.; Camden, J.P. Probing nanoparticle plasmons with electron energy loss spectroscopy. Chem. Rev. 2018, 118, 2994–3031. [Google Scholar] [CrossRef]
- Martí-Sánchez, S.; Botifoll, M.; Oksenberg, E.; Koch, C.; Borja, C.; Spadaro, M.C.; Di Giulio, V.; Ramasse, Q.; García de Abajo, F.J.; Joselevich, E.; et al. Sub-nanometer mapping of strain-induced band structure variations in planar nanowire core-shell heterostructures. Nat. Commun. 2022, 13, 4089. [Google Scholar] [CrossRef]
- Nicoletti, O.; Wubs, M.; Mortensen, N.A.; Sigle, W.; van Aken, P.A.; Midgley, P.A. Surface plasmon modes of a single silver nanorod: An electron energy loss study. Opt. Express 2011, 19, 15371–15379. [Google Scholar] [CrossRef]
- Guiton, B.S.; Iberi, V.; Li, S.; Leonard, D.N.; Parish, C.M.; Kotula, P.G.; Varela, M.; Schatz, G.C.; Pennycook, S.J.; Camden, J.P. Correlated optical measurements and plasmon mapping of silver nanorods. Nano Lett. 2011, 11, 3482–3488. [Google Scholar] [CrossRef]
- Rossouw, D.; Couillard, M.; Vickery, J.; Kumacheva, E.; Botton, G.A. Multipolar plasmonic resonances in silver nanowire antennas imaged with a subnanometer electron probe. Nano Lett. 2011, 11, 1499–1504. [Google Scholar] [CrossRef]
- Bigelow, N.W.; Vaschillo, A.; Iberi, V.; Camden, J.P.; Masiello, D.J. Characterization of the electron- and photon-driven plasmonic excitations of metal nanorods. ACS Nano 2012, 6, 7497–7504. [Google Scholar] [CrossRef]
- Bellido, E.P.; Rossouw, D.; Botton, G.A. Toward 10 meV Electron Energy-Loss Spectroscopy Resolution for Plasmonics. Microsc. Microanal. 2014, 20, 767–778. [Google Scholar] [CrossRef]
- Alber, I.; Sigle, W.; Muller, S.; Neumann, R.; Picht, O.; Rauber, M.; van Aken, P.A.; Toimil-Molares, M.E. Visualization of multipolar longitudinal and transversal surface plasmon modes in nanowire dimers. ACS Nano 2011, 5, 9845–9853. [Google Scholar] [CrossRef]
- Genç, A.; Patarroyo, J.; Sancho-Parramon, J.; Arenal, R.; Duchamp, M.; Gonzalez, E.E.; Henrard, L.; Bastus, N.G.; Dunin-Borkowski, R.E.; Puntes, V.; et al. Tuning the plasmonic response up: Hollow cuboid metal nanostructures. ACS Photonics 2016, 3, 770–779. [Google Scholar] [CrossRef]
- Genç, A.; Patarroyo, J.; Sancho-Parramon, J.; Bastús, N.G.; Puntes, V.; Arbiol, J. Hollow metal nanostructures for enhanced plasmonics: Synthesis, local plasmonic properties and applications. Nanophotonics 2017, 6, 193–213. [Google Scholar] [CrossRef]
- Russo, L.; Sánchez-Purrà, M.; Rodriguez-Quijada, C.; Leonardo, B.M.; Puntes, V.; Hamad-Schifferli, K. Detection of resistance protein A (MxA) in paper-based immunoassays with surface enhanced Raman spectroscopy with AuAg nanoshells. Nanoscale 2019, 11, 10819. [Google Scholar] [CrossRef]
- Prieto, M.; Arenal, R.; Henrard, L.; Gomez, L.; Sebastian, V.; Arruebo, M. Morphological tunability of the plasmonic response: From hollow gold nanoparticles to gold nanorings. J. Phys. Chem. C 2014, 118, 28804–28811. [Google Scholar] [CrossRef]
- Prodan, E.; Radloff, C.; Halas, N.J.; Nordlander, P. A hybridization model for the plasmon response of complex nanostructures. Science 2003, 302, 419–422. [Google Scholar] [CrossRef]
- Yazdi, S.; Daniel, J.R.; Large, N.; Schatz, G.C.; Boudreau, D.; Ringe, E. Reversible Shape and Plasmon Tuning in Hollow AgAu Nanorods. Nano Lett. 2016, 16, 6939–6945. [Google Scholar] [CrossRef]
- Wu, K.; Chen, Y.; Cheng, J.; Xu, K. Use of carrier injection engineering to increase the light intensity of a polycrystalline silicon avalanche mode light-emitting device. J. Appl. Phys. 2020, 128, 173104. [Google Scholar] [CrossRef]
- Gonzalez, E.; Arbiol, J.; Puntes, V.F. Carving at the nanoscale: Sequential galvanic exchange and Kirkendall growth at room temperature. Science 2011, 334, 1377–1380. [Google Scholar] [CrossRef]
- Sun, Y.; Yin, Y.; Mayers, B.T.; Herricks, T.; Xia, Y. Uniform Silver Nanowires Synthesis by Reducing AgNO3 with Ethylene Glycol in the Presence of Seeds and Poly (Vinyl Pyrrolidone). Chem. Mater. 2002, 14, 4736–4745. [Google Scholar] [CrossRef]
- Garcia de Abajo, F.J. Optical excitations in electron microscopy. Rev. Mod. Phys. 2010, 82, 209–275. [Google Scholar] [CrossRef]
- Jeanguillaume, C.; Colliex, C. Spectrum-image: The next step in EELS digital acquisition and processing. Ultramicroscopy 1989, 28, 252–257. [Google Scholar] [CrossRef]
- Arenal, R.; de la Pena, F.; Stephan, O.; Walls, M.; Tence, M.; Loiseau, A.; Colliex, C. Extending the analysis of EELS spectrum-imaging data, from elemental to bond mapping in complex nanostructures. Ultramicroscopy 2008, 109, 32–38. [Google Scholar] [CrossRef]
- Nascimento, J.M.P.; Bioucas-Dias, J. Vertex component analysis: A fast algorithm to unmix hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 898–910. [Google Scholar] [CrossRef]
- Dobigeon, N.; Brun, N. Spectral mixture analysis of EELS spectrum-images. Ultramicroscopy 2012, 120, 25–34. [Google Scholar] [CrossRef]
- Duchamp, M.; Lachmann, M.; Boothroyd, C.B.; Kovacs, A.; Haug, F.J.; Ballif, C.; Dunin-Borkowski, R.E. Compositional study of defects in microcrystalline silicon solar cells using spectral decomposition in the scanning transmission electron microscope. Appl. Phys. Lett. 2013, 102, 133902. [Google Scholar] [CrossRef]
- De la Peña, F.; Burdet, P.; Ostasevicius, T.; Sarahan, M.; Nord, M.; Fauske, V.T.; Taillon, J.; Eljarrat, A.; Mazzucco, S.; Donval, G.; et al. hyperspy: HyperSpy, version 0.8.2; Zenodo: Geneve, Switzerland, 2015. [Google Scholar] [CrossRef]
- Garcia de Abajo, F.J.; Howie, A. Relativistic Electron Energy Loss and Electron-Induced Photon Emission in Inhomogeneous Dielectrics. Phys. Rev. Lett. 1998, 80, 5180–5183. [Google Scholar] [CrossRef]
- Garcia de Abajo, F.J.; Howie, A. Retarded field calculation of electron energy loss in inhomogeneous dielectrics. Phys. Rev. B 2002, 65, 1–17. [Google Scholar] [CrossRef]
- Hohenester, U. Simulating electron energy loss spectroscopy with the MNPBEM toolbox. Comput. Phys. Commun. 2014, 185, 1177–1187. [Google Scholar] [CrossRef]
- Johnson, J.B.; Christy, R.W. Optical Constants of the Noble Metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar] [CrossRef]
- Pena-Rodriguez, O.; Caro, M.; Rivera, A.; Olivares, J.; Perlado, J.M.; Caro, A. Optical properties of Au-Ag alloys: An ellipsometric study. Opt. Mater. Express 2014, 4, 403–410. [Google Scholar] [CrossRef]
- Hovel, H.; Fritz, S.; Hilger, A.; Kreibig, U. Width of cluster plasmon resonances: Bulk dielectric functions and chemical interface damping. Phys. Rev. B 1993, 48, 18178–18188. [Google Scholar] [CrossRef]
- Canepa, S.; Yesibolati, M.N.; Schiøtz, J.; Kadkhodazadeh, S.; Huang, W.; Sun, H.; Mølhave, K. Initiation and Progression of Anisotropic Galvanic Replacement Reactions in a Single Ag Nanowire: Implications for Nanostructure Synthesis. ACS Appl. Nano Mater. 2021, 4, 12346–12355. [Google Scholar] [CrossRef]
- Egerton, R.F. Electron Energy-Loss Spectroscopy in the Electron Microscope, 3rd ed.; Springer: Cham, Switzerland, 2011. [Google Scholar]
- Dorfmuller, J.; Vogelgesang, R.; Weitz, R.T.; Rockstuhl, C.; Etrich, C.; Pertsch, T.; Lederer, F.; Kern, K. Fabry-Perot Resonances in One-Dimensional Plasmonic Nanostructures. Nano Lett. 2009, 9, 2372–2377. [Google Scholar] [CrossRef]
- Amendola, V.; Bakr, O.M.; Stellacci, F. A study of the surface plasmon resonance of silver nanoparticles by the discrete dipole approximation method: Effect of shape, size, structure, and assembly. Plasmonics 2010, 5, 85–97. [Google Scholar] [CrossRef]
- Noguez, C. Surface Plasmons on Metal Nanoparticles: The Influence of Shape and Physical Environment. J. Phys. Chem. C 2007, 111, 3806–3819. [Google Scholar] [CrossRef]
- Nicoletti, O.; de la Pena, F.; Leary, R.K.; Holland, D.J.; Ducati, C.; Midgley, P.A. Three-dimensional imaging of localized surface plasmon resonances of metal nanoparticles. Nature 2013, 502, 80–84. [Google Scholar] [CrossRef]
- Das, P.; Chini, T.K. Substrate Induced Symmetry Breaking in Penta-twinned Gold Nanorod Probed by Free Electron Impact. J. Phys. Chem. C 2014, 118, 26284–26291. [Google Scholar] [CrossRef]
- Zhang, S.; Bao, K.; Halas, N.J.; Xu, H.; Nordlander, P. Substrate-induced Fano resonances of a plasmonic nanocube: A route to increased-sensitivity localized surface plasmon resonance sensors revealed. Nano Lett. 2011, 11, 1657–1663. [Google Scholar] [CrossRef]
- Liang, H.; Rossouw, D.; Zhao, H.; Cushing, S.K.; Shi, H.; Korinek, A.; Xu, H.; Rosei, F.; Wang, W.; Wu, N.; et al. Asymmetric Silver “Nanocarrot” Structures: Solution Synthesis and Their Asymmetric Plasmonic Resonances. J. Am. Chem. Soc. 2013, 135, 9616–9619. [Google Scholar] [CrossRef]
- Schubert, I.; Sigle, W.; van Aken, P.A.; Trautmann, C.; Toimil-Molares, M.E. STEM-EELS analysis of multipole surface plasmon modes in symmetry-broken AuAg nanowire dimers. Nanoscale 2015, 7, 4935–4941. [Google Scholar] [CrossRef]
- Bellido, E.P.; Zhang, Y.; Manjavacas, A.; Nordlander, P.; Botton, G.A. Plasmonic Coupling of Multipolar Edge Modes and the Formation of Gap Modes. ACS Photonics 2017, 4, 1558–1565. [Google Scholar] [CrossRef]
- Pakeltis, G.; Rotunno, E.; Khorassani, S.; Garfinkel, D.A.; Collette, R.; West, C.A.; Retterer, S.T.; Idrobo, J.C.; Masiello, D.J.; Rack, P.D. High spatial and energy resolution electron energy loss spectroscopy of the magnetic and electric excitations in plasmonic nanorod oligomers. Opt. Express 2021, 29, 4661–4671. [Google Scholar] [CrossRef]
- Xi, M.; Ding, S.; Li, N.; Wang, Z. Angular Scattered Light Intensity of Dipole−Multipole Plasmonic Hybridization. J. Phys. Chem. C 2021, 125, 23231–23239. [Google Scholar] [CrossRef]
- Xu, K. Silicon electro-optic micro-modulator fabricated in standard CMOS technology as components for all silicon monolithic integrated optoelectronic systems. J. Micromech. Microeng. 2021, 31, 054001. [Google Scholar] [CrossRef]
- González-Rubio, G.; de Oliveira, T.M.; Albrecht, W.; Díaz-Núñez, P.; Castro-Palacio, J.C.; Prada, A.; González, R.I.; Scarabelli, L.; Bañares, L.; Rivera, A.; et al. Formation of Hollow Gold Nanocrystals by Nanosecond Lazer Irradiation. J. Phys. Chem. Lett. 2020, 11, 670–677. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Genç, A.; Patarroyo, J.; Sancho-Parramon, J.; Arenal, R.; Bastús, N.G.; Puntes, V.; Arbiol, J. Asymmetrical Plasmon Distribution in Hybrid AuAg Hollow/Solid Coded Nanotubes. Nanomaterials 2023, 13, 992. https://doi.org/10.3390/nano13060992
Genç A, Patarroyo J, Sancho-Parramon J, Arenal R, Bastús NG, Puntes V, Arbiol J. Asymmetrical Plasmon Distribution in Hybrid AuAg Hollow/Solid Coded Nanotubes. Nanomaterials. 2023; 13(6):992. https://doi.org/10.3390/nano13060992
Chicago/Turabian StyleGenç, Aziz, Javier Patarroyo, Jordi Sancho-Parramon, Raul Arenal, Neus G. Bastús, Victor Puntes, and Jordi Arbiol. 2023. "Asymmetrical Plasmon Distribution in Hybrid AuAg Hollow/Solid Coded Nanotubes" Nanomaterials 13, no. 6: 992. https://doi.org/10.3390/nano13060992
APA StyleGenç, A., Patarroyo, J., Sancho-Parramon, J., Arenal, R., Bastús, N. G., Puntes, V., & Arbiol, J. (2023). Asymmetrical Plasmon Distribution in Hybrid AuAg Hollow/Solid Coded Nanotubes. Nanomaterials, 13(6), 992. https://doi.org/10.3390/nano13060992








