Fine Structure Splitting of Phonon-Assisted Excitonic Transition in (PEA)2PbI4 Two-Dimensional Perovskites
Abstract
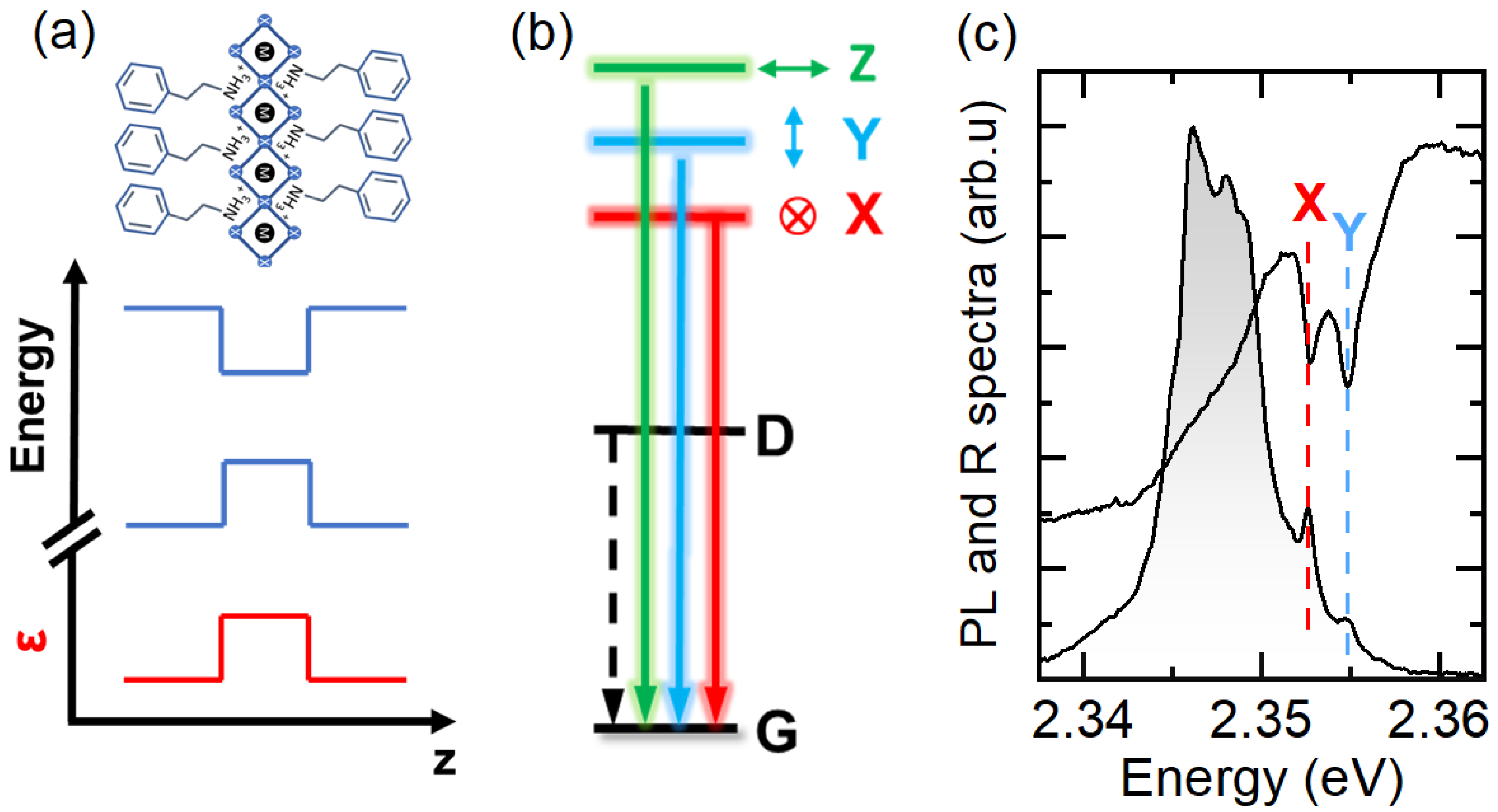
1. Introduction
2. Materials and Methods
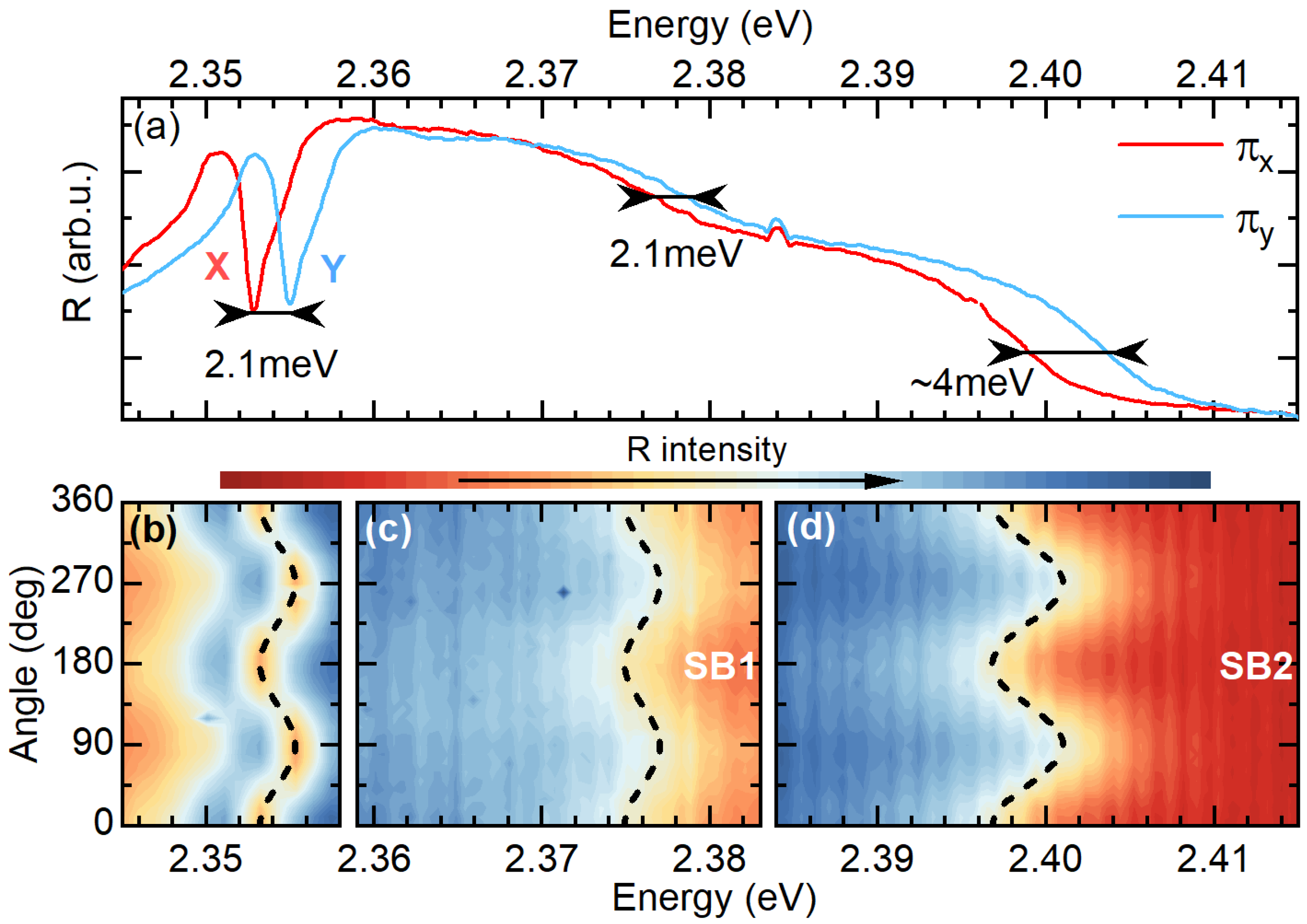
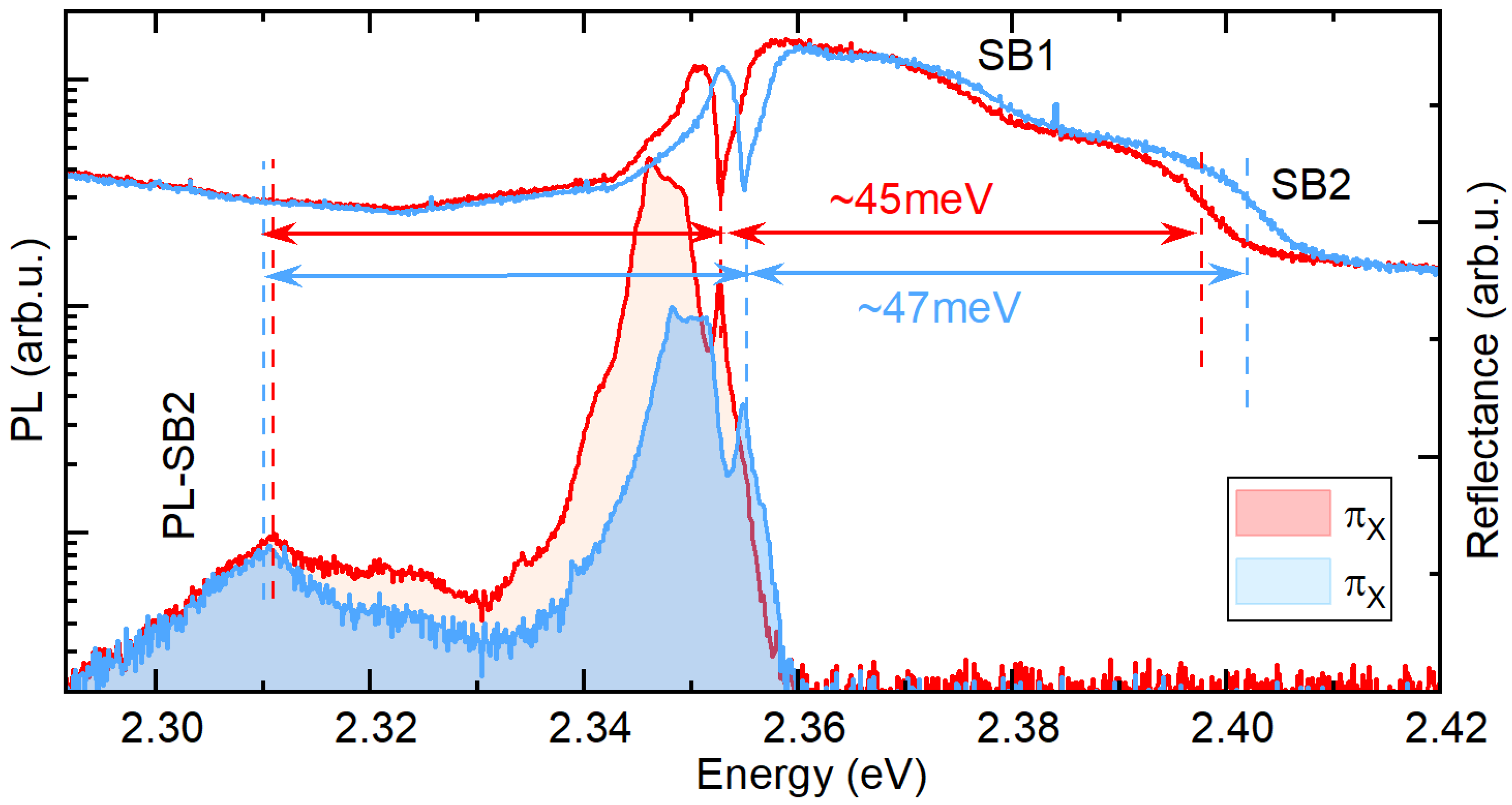
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, Y.; Sun, Y.; Peng, J.; Tang, J.; Zheng, K.; Liang, Z. 2D Ruddlesden–Popper perovskites for optoelectronics. Adv. Mater. 2018, 30, 1703487. [Google Scholar] [CrossRef]
- Straus, D.B.; Kagan, C.R. Electrons, excitons, and phonons in two-dimensional hybrid perovskites: Connecting structural, optical, and electronic properties. J. Phys. Chem. Lett. 2018, 9, 1434–1447. [Google Scholar] [CrossRef]
- Manser, J.S.; Christians, J.A.; Kamat, P.V. Intriguing optoelectronic properties of metal halide perovskites. Chem. Rev. 2016, 116, 12956–13008. [Google Scholar] [CrossRef] [PubMed]
- Stranks, S.D.; Snaith, H.J. Metal-halide perovskites for photovoltaic and light-emitting devices. Nat. Nanotechnol. 2015, 10, 391–402. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.K.; Xu, W.; Bai, S.; Jin, Y.; Wang, J.; Friend, R.H.; Gao, F. Metal halide perovskites for light-emitting diodes. Nat. Mater. 2021, 20, 10–21. [Google Scholar] [CrossRef] [PubMed]
- Tan, C.; Cao, X.; Wu, X.J.; He, Q.; Yang, J.; Zhang, X.; Chen, J.; Zhao, W.; Han, S.; Nam, G.H.; et al. Recent advances in ultrathin two-dimensional nanomaterials. Chem. Rev. 2017, 117, 6225–6331. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Mishchenko, A.; Carvalho, o.A.; Castro Neto, A. 2D materials and van der Waals heterostructures. Science 2016, 353, aac9439. [Google Scholar] [CrossRef]
- Egger, D.A.; Bera, A.; Cahen, D.; Hodes, G.; Kirchartz, T.; Kronik, L.; Lovrincic, R.; Rappe, A.M.; Reichman, D.R.; Yaffe, O. What remains unexplained about the properties of halide perovskites? Adv. Mater. 2018, 30, 1800691. [Google Scholar] [CrossRef]
- Tao, W.; Zhang, C.; Zhou, Q.; Zhao, Y.; Zhu, H. Momentarily trapped exciton polaron in two-dimensional lead halide perovskites. Nat. Commun. 2021, 12, 1400. [Google Scholar] [CrossRef]
- Blancon, J.C.; Stier, A.V.; Tsai, H.; Nie, W.; Stoumpos, C.C.; Traore, B.; Pedesseau, L.; Kepenekian, M.; Katsutani, F.; Noe, G.; et al. Scaling law for excitons in 2D perovskite quantum wells. Nat. Commun. 2018, 9, 2254. [Google Scholar] [CrossRef]
- Dyksik, M.; Wang, S.; Paritmongkol, W.; Maude, D.K.; Tisdale, W.A.; Baranowski, M.; Plochocka, P. Tuning the Excitonic Properties of the 2D (PEA)2 (MA)n-1PbnI3n+1 Perovskite Family via Quantum Confinement. J. Phys. Chem. Lett. 2021, 12, 1638–1643. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Chernikov, A.; Glazov, M.M.; Heinz, T.F.; Marie, X.; Amand, T.; Urbaszek, B. Colloquium: Excitons in atomically thin transition metal dichalcogenides. Rev. Mod. Phys. 2018, 90, 021001. [Google Scholar] [CrossRef]
- Yu, Z. Effective-mass model and magneto-optical properties in hybrid perovskites. Sci. Rep. 2016, 6, 28576. [Google Scholar] [CrossRef]
- Fu, M.; Tamarat, P.; Huang, H.; Even, J.; Rogach, A.L.; Lounis, B. Neutral and charged exciton fine structure in single lead halide perovskite nanocrystals revealed by magneto-optical spectroscopy. Nano Lett. 2017, 17, 2895–2901. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, K.; Takahashi, T.; Kondo, T.; Umeda, K.; Ema, K.; Umebayashi, T.; Asai, K.; Uchida, K.; Miura, N. Electronic and excitonic structures of inorganic–organic perovskite-type quantum-well crystal (C4H9NH3)2PbBr4. Jpn. J. Appl. Phys. 2005, 44, 5923. [Google Scholar] [CrossRef]
- Do, T.T.H.; Granados del Aguila, A.; Zhang, D.; Xing, J.; Liu, S.; Prosnikov, M.; Gao, W.; Chang, K.; Christianen, P.C.; Xiong, Q. Bright exciton fine-structure in two-dimensional lead halide perovskites. Nano Lett. 2020, 20, 5141–5148. [Google Scholar] [CrossRef]
- Posmyk, K.; Zawadzka, N.; Dyksik, M.; Surrente, A.; Maude, D.K.; Kazimierczuk, T.; Babinski, A.; Molas, M.R.; Paritmongkol, W.; Maczka, M.; et al. Quantification of Exciton Fine Structure Splitting in a Two-Dimensional Perovskite Compound. J. Phys. Chem. Lett. 2022, 13, 4463–4469. [Google Scholar] [CrossRef]
- Dyksik, M.; Duim, H.; Maude, D.K.; Baranowski, M.; Loi, M.A.; Plochocka, P. Brightening of dark excitons in 2D perovskites. Sci. Adv. 2021, 7, eabk0904. [Google Scholar] [CrossRef]
- Canet-Albiach, R.; Krecmarova, M.; Bailach, J.B.; Gualdrón-Reyes, A.F.; Rodríguez-Romero, J.; Gorji, S.; Pashaei-Adl, H.; Mora-Seró, I.; Martinez Pastor, J.P.; Sánchez-Royo, J.F.; et al. Revealing giant exciton fine-structure splitting in two-dimensional perovskites using van der Waals passivation. Nano Lett. 2022, 22, 7621–7627. [Google Scholar] [CrossRef]
- Wang, S.; Dyksik, M.; Lampe, C.; Gramlich, M.; Maude, D.K.; Baranowski, M.; Urban, A.S.; Plochocka, P.; Surrente, A. Thickness-Dependent Dark-Bright Exciton Splitting and Phonon Bottleneck in CsPbBr3-Based Nanoplatelets Revealed via Magneto-Optical Spectroscopy. Nano Lett. 2022, 22, 7011–7019. [Google Scholar] [CrossRef]
- Ema, K.; Umeda, K.; Toda, M.; Yajima, C.; Arai, Y.; Kunugita, H.; Wolverson, D.; Davies, J. Huge exchange energy and fine structure of excitons in an organic-inorganic quantum well material. Phys. Rev. B 2006, 73, 241310. [Google Scholar] [CrossRef]
- Kataoka, T.; Kondo, T.; Ito, R.; Sasaki, S.; Uchida, K.; Miura, N. Magneto-optical study on the excitonic spectrum of (C6H13NH3)2PbI4. Phys. B Condens. Matter 1993, 184, 132–136. [Google Scholar] [CrossRef]
- Fang, H.h.; Yang, J.; Adjokatse, S.; Tekelenburg, E.; Kamminga, M.E.; Duim, H.; Ye, J.; Blake, G.R.; Even, J.; Loi, M.A. Band-edge exciton fine structure and exciton recombination dynamics in single crystals of layered hybrid perovskites. Adv. Funct. Mater. 2020, 30, 1907979. [Google Scholar] [CrossRef]
- Folpini, G.; Cortecchia, D.; Petrozza, A.; Kandada, A.R.S. The role of a dark exciton reservoir in the luminescence efficiency of two-dimensional tin iodide perovskites. J. Mater. Chem. C 2020, 8, 10889–10896. [Google Scholar] [CrossRef]
- Bayer, M.; Ortner, G.; Stern, O.; Kuther, A.; Gorbunov, A.; Forchel, A.; Hawrylak, P.; Fafard, S.; Hinzer, K.; Reinecke, T.; et al. Fine structure of neutral and charged excitons in self-assembled In (Ga) As/(Al) GaAs quantum dots. Phys. Rev. B 2002, 65, 195315. [Google Scholar] [CrossRef]
- Blackwood, E.; Snelling, M.; Harley, R.; Andrews, S.; Foxon, C. Exchange interaction of excitons in GaAs heterostructures. Phys. Rev. B 1994, 50, 14246. [Google Scholar] [CrossRef]
- Straus, D.B.; Hurtado Parra, S.; Iotov, N.; Gebhardt, J.; Rappe, A.M.; Subotnik, J.E.; Kikkawa, J.M.; Kagan, C.R. Direct observation of electron–phonon coupling and slow vibrational relaxation in organic–inorganic hybrid perovskites. J. Am. Chem. Soc. 2016, 138, 13798–13801. [Google Scholar] [CrossRef]
- Urban, J.M.; Chehade, G.; Dyksik, M.; Menahem, M.; Surrente, A.; Trippé-Allard, G.; Maude, D.K.; Garrot, D.; Yaffe, O.; Deleporte, E.; et al. Revealing Excitonic Phonon Coupling in (PEA)2 (MA)n-1PbnI3n+1 2D Layered Perovskites. J. Phys. Chem. Lett. 2020, 11, 5830–5835. [Google Scholar] [CrossRef]
- Neutzner, S.; Thouin, F.; Cortecchia, D.; Petrozza, A.; Silva, C.; Kandada, A.R.S. Exciton-polaron spectral structures in two-dimensional hybrid lead-halide perovskites. Phys. Rev. Mater. 2018, 2, 064605. [Google Scholar] [CrossRef]
- Baranowski, M.; Zelewski, S.J.; Kepenekian, M.; Traoré, B.; Urban, J.M.; Surrente, A.; Galkowski, K.; Maude, D.K.; Kuc, A.; Booker, E.P.; et al. Phase-transition-induced carrier mass enhancement in 2D Ruddlesden–Popper perovskites. ACS Energy Lett. 2019, 4, 2386–2392. [Google Scholar] [CrossRef]
- Thouin, F.; Valverde-Chávez, D.A.; Quarti, C.; Cortecchia, D.; Bargigia, I.; Beljonne, D.; Petrozza, A.; Silva, C.; Srimath Kandada, A.R. Phonon coherences reveal the polaronic character of excitons in two-dimensional lead halide perovskites. Nat. Mater. 2019, 18, 349–356. [Google Scholar] [CrossRef] [PubMed]
- Srimath Kandada, A.R.; Silva, C. Exciton polarons in two-dimensional hybrid metal-halide perovskites. J. Phys. Chem. Lett. 2020, 11, 3173–3184. [Google Scholar] [CrossRef] [PubMed]
- Paritmongkol, W.; Dahod, N.S.; Stollmann, A.; Mao, N.; Settens, C.; Zheng, S.L.; Tisdale, W.A. Synthetic variation and structural trends in layered two-dimensional alkylammonium lead halide perovskites. Chem. Mater. 2019, 31, 5592–5607. [Google Scholar] [CrossRef]
- Paritmongkol, W.; Powers, E.R.; Dahod, N.S.; Tisdale, W.A. Two origins of broadband emission in multilayered 2D lead iodide perovskites. J. Phys. Chem. Lett. 2020, 11, 8565–8572. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Surrente, A.; Galkowski, K.; Bruyant, N.; Maude, D.K.; Haghighirad, A.A.; Snaith, H.J.; Plochocka, P.; Nicholas, R.J. Unraveling the exciton binding energy and the dielectric constant in single-crystal methylammonium lead triiodide perovskite. J. Phys. Chem. Lett. 2017, 8, 1851–1855. [Google Scholar] [CrossRef] [PubMed]
- Pelant, I.; Valenta, J. Luminescence Spectroscopy of Semiconductors; OUP Oxford: Oxford, PA, USA, 2012. [Google Scholar]
- de Jong, M.; Seijo, L.; Meijerink, A.; Rabouw, F.T. Resolving the ambiguity in the relation between Stokes shift and Huang–Rhys parameter. Phys. Chem. Chem. Phys. 2015, 17, 16959–16969. [Google Scholar] [CrossRef]
- Fang, H.H.; Yang, J.; Tao, S.; Adjokatse, S.; Kamminga, M.E.; Ye, J.; Blake, G.R.; Even, J.; Loi, M.A. Unravelling Light-Induced Degradation of Layered Perovskite Crystals and Design of Efficient Encapsulation for Improved Photostability. Adv. Funct. Mater. 2018, 28, 1800305. [Google Scholar] [CrossRef]
- Dhanabalan, B.; Leng, Y.C.; Biffi, G.; Lin, M.L.; Tan, P.H.; Infante, I.; Manna, L.; Arciniegas, M.P.; Krahne, R. Directional anisotropy of the vibrational modes in 2D-layered perovskites. ACS Nano 2020, 14, 4689–4697. [Google Scholar] [CrossRef]
- Menahem, M.; Dai, Z.; Aharon, S.; Sharma, R.; Asher, M.; Diskin-Posner, Y.; Korobko, R.; Rappe, A.M.; Yaffe, O. Strongly anharmonic octahedral tilting in two-dimensional hybrid halide perovskites. ACS Nano 2021, 15, 10153–10162. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Posmyk, K.; Dyksik, M.; Surrente, A.; Zalewska, K.; Śmiertka, M.; Cybula, E.; Paritmongkol, W.; Tisdale, W.A.; Plochocka, P.; Baranowski, M. Fine Structure Splitting of Phonon-Assisted Excitonic Transition in (PEA)2PbI4 Two-Dimensional Perovskites. Nanomaterials 2023, 13, 1119. https://doi.org/10.3390/nano13061119
Posmyk K, Dyksik M, Surrente A, Zalewska K, Śmiertka M, Cybula E, Paritmongkol W, Tisdale WA, Plochocka P, Baranowski M. Fine Structure Splitting of Phonon-Assisted Excitonic Transition in (PEA)2PbI4 Two-Dimensional Perovskites. Nanomaterials. 2023; 13(6):1119. https://doi.org/10.3390/nano13061119
Chicago/Turabian StylePosmyk, Katarzyna, Mateusz Dyksik, Alessandro Surrente, Katarzyna Zalewska, Maciej Śmiertka, Ewelina Cybula, Watcharaphol Paritmongkol, William A. Tisdale, Paulina Plochocka, and Michał Baranowski. 2023. "Fine Structure Splitting of Phonon-Assisted Excitonic Transition in (PEA)2PbI4 Two-Dimensional Perovskites" Nanomaterials 13, no. 6: 1119. https://doi.org/10.3390/nano13061119
APA StylePosmyk, K., Dyksik, M., Surrente, A., Zalewska, K., Śmiertka, M., Cybula, E., Paritmongkol, W., Tisdale, W. A., Plochocka, P., & Baranowski, M. (2023). Fine Structure Splitting of Phonon-Assisted Excitonic Transition in (PEA)2PbI4 Two-Dimensional Perovskites. Nanomaterials, 13(6), 1119. https://doi.org/10.3390/nano13061119





