CNT-PUFs: Highly Robust and Heat-Tolerant Carbon-Nanotube-Based Physical Unclonable Functions †
Abstract
:1. Introduction
1.1. Contributions
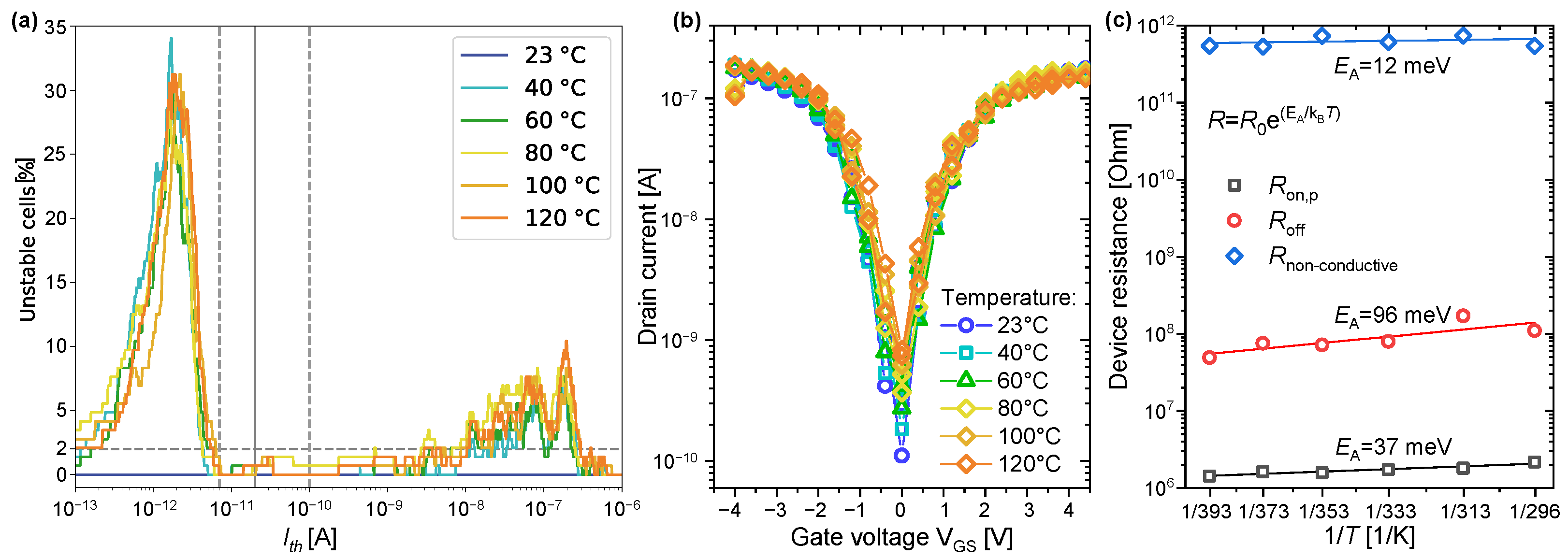
- We conducted an additional temperature analysis of our CNT-PUFs, extending the application area of the CNT-PUFs to include even harsh environments. The investigated CNT-PUFs demonstrated very high stability with at most 2% unstable cells in the temperature range from to .
- We performed a more-extensive security analysis of the raw CNT-PUF measurements. An analysis of the unpredictability of the raw PUF responses through an evaluation of the measurements by the statistical randomness tests of the National Institute of Standards and Technology (NIST) SP 800-22 test suite [24] was conducted. Our PUFs passed all applicable statistical randomness tests of the NIST SP 800-22 test suite [24], confirming the ability to use our CNT-PUFs as strong cryptographic primitives within cryptographic protocols.
- Finally, we present a very lightweight and efficient post-processing method that ranks all cells according to their stability and selects the most-stable cells for further use. By using this method, our CNT-PUFs are able to produce fully stable PUF responses.
1.2. Paper Organisation
2. Related Work
3. Preliminaries: PUF Metrics
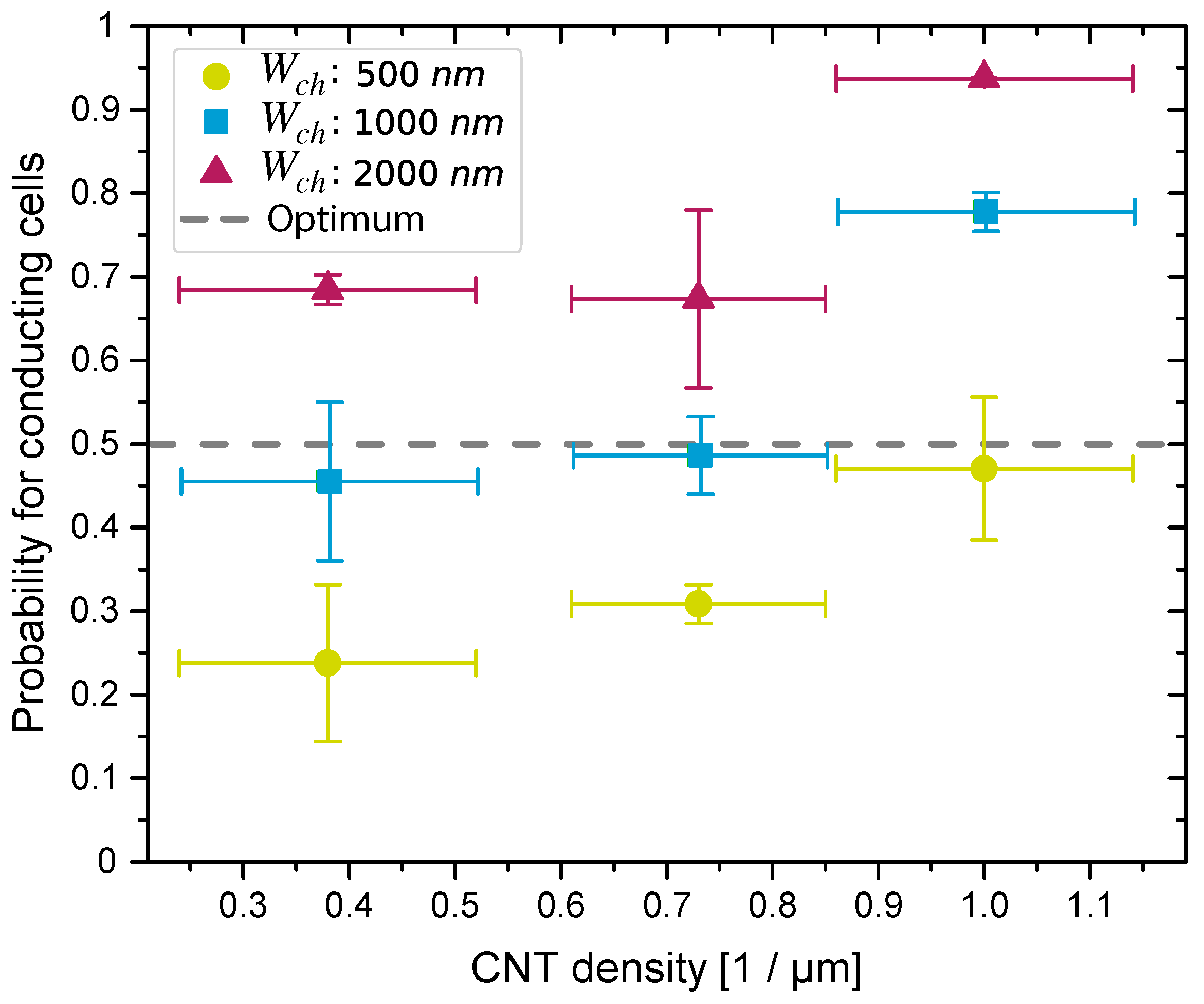
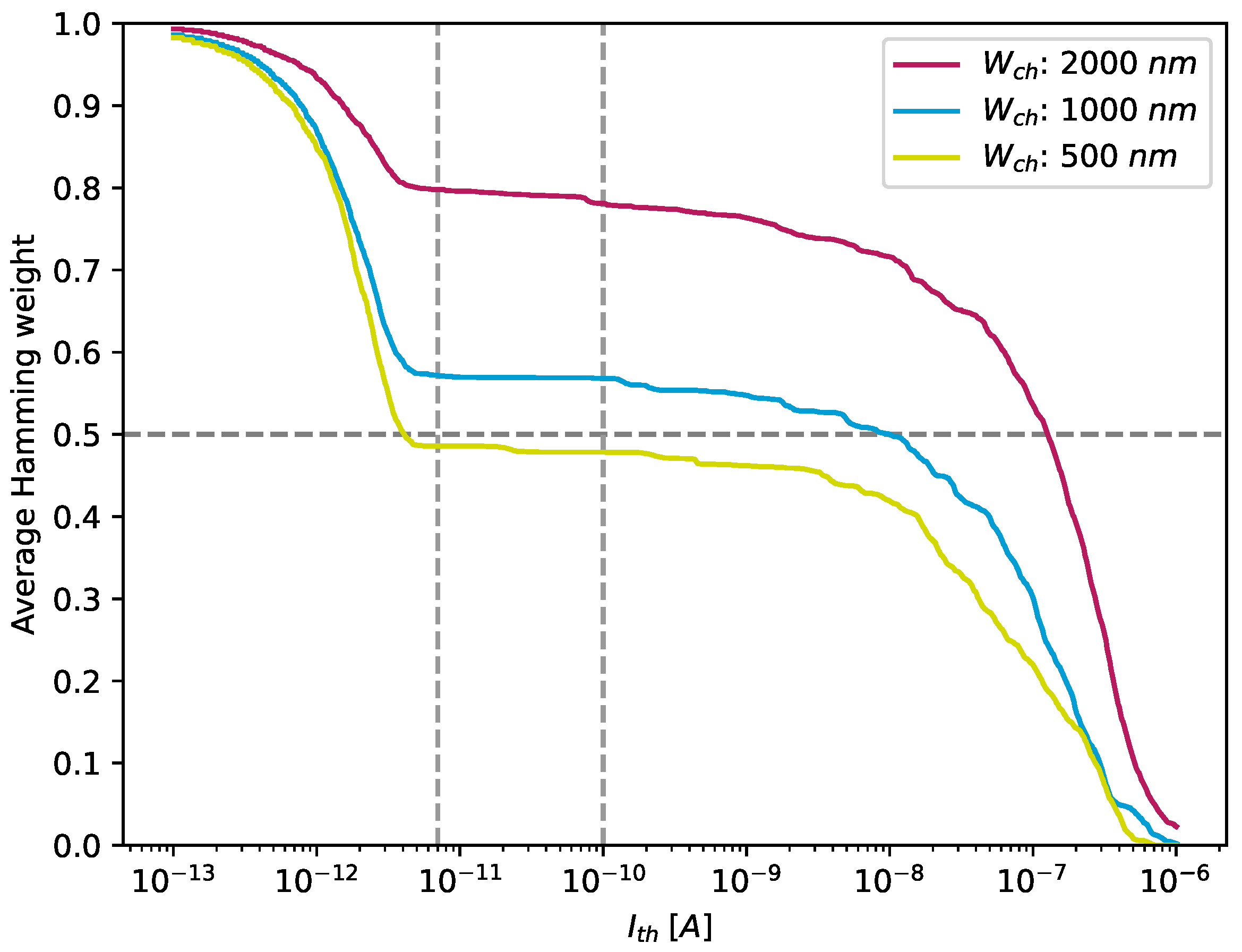
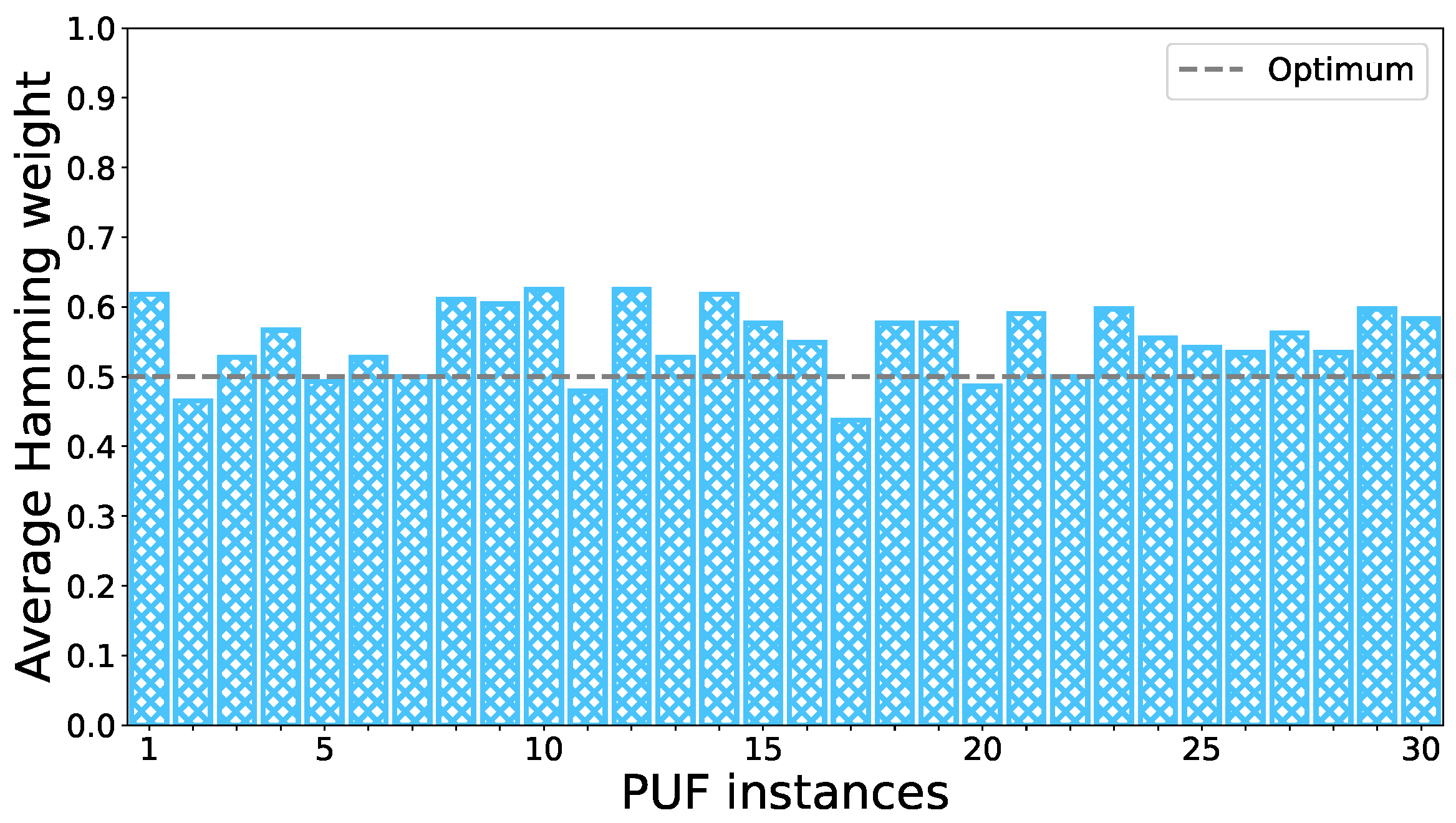
- Uniformity describes how the bits of an individual PUF response are distributed. It is favourable to achieve an equal distribution of zeros and ones. A bias towards one of the values leads to higher predictability of the responses, compromising the overall security of the resulting response. Uniformity is evaluated by the Hamming weight , which measures the number of ones in a binary PUF response of PUF instance i to challenge C that has been received at normalised time x. The normalised average for a PUF i is calculated as follows:where l is the number of responses collected for a challenge C at all normalised time values and the length of the PUF responses of PUF i. The ideal value of signifies, on average, a perfectly balanced distribution of zeros and ones within the PUF responses of PUF i.
- Uniqueness measures the independence of responses originating from different PUFs for the same challenge C. This property is typically evaluated by the average fractional inter-device Hamming distance , which specifies the normalised average number of bit positions that differ in the responses of all different PUF instances, with response being the response of PUF i to challenge C at normalised time x and response being the response of PUF j to challenge C at normalised time y. Essentially, the Hamming distance between and , denoted by , is equal to , counting the number of different bit positions when comparing the two binary vectors and . For PUF responses of equal length (if the PUF responses differ in their length, the length of the shorter response is chosen for their comparison, and the number of bits remaining from the longer response is added to the comparison result, to calculate the overall ), with k being the number of devices measured, m the number of responses collected from device i for a response C at all normalised times, and n the number of responses collected from device j for the response C at all normalised times; is given by:A value of , meaning that, on average, half of the bits of the response of one PUF instance have a different value from the bits of all other instances, indicates the highest possible degree of uniqueness.
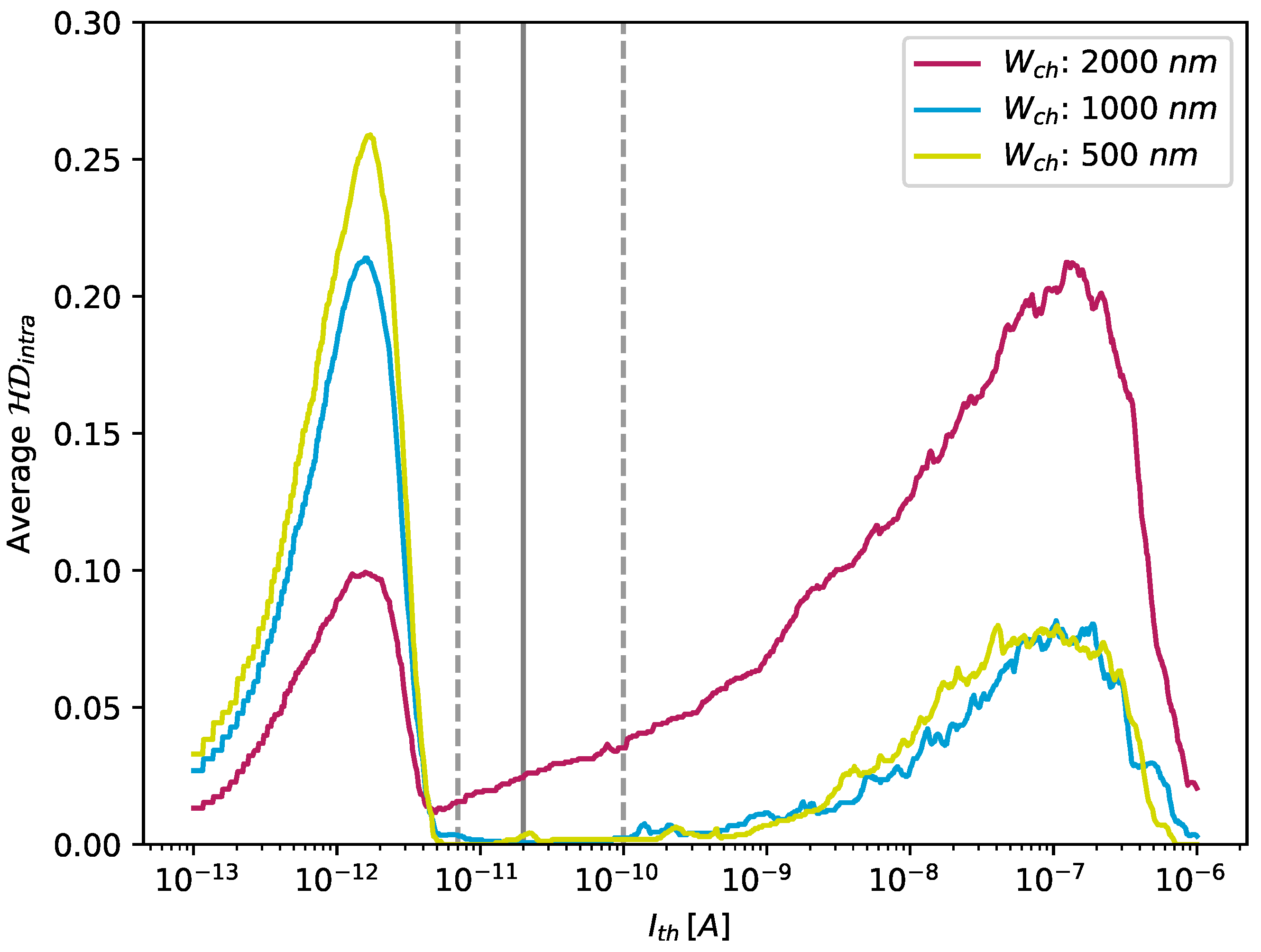
- The property of robustness describes the stability of PUF responses originating from the same PUF, for a given challenge C, under repeated PUF measurements. This property is evaluated using the average fractional intra-device Hamming distance , which measures the normalised average number of bit positions that differ between each two responses and stemming from the same device i produced using the same challenge C and captured at different normalised times x and y. is given by:where l is the number of responses collected for a challenge C at all normalised time values and the length of the PUF responses of PUF i. A value of , meaning that all of the bits are identical in all responses, indicates the highest possible degree of stability and, hence, robustness.
- Another important property is the unpredictability of the generated responses. One pre-condition for high unpredictability is a uniform distribution of logical ones and zeros as explained previously. In addition, single bits of the PUF response should be free of correlations. Unpredictability is typically evaluated by a collection of statistical tests for randomness performed on the PUF responses. This paper used the well-known NIST SP 800-22 test suite [24]. This test suite consists of various statistical tests applied to presumably random strings, to check if they meet the entropy requirements to be used as primitives in cryptographic protocols.
4. Fabrication and Implementation of CNT-PUFs
4.1. Wafer-Level Fabrication Process
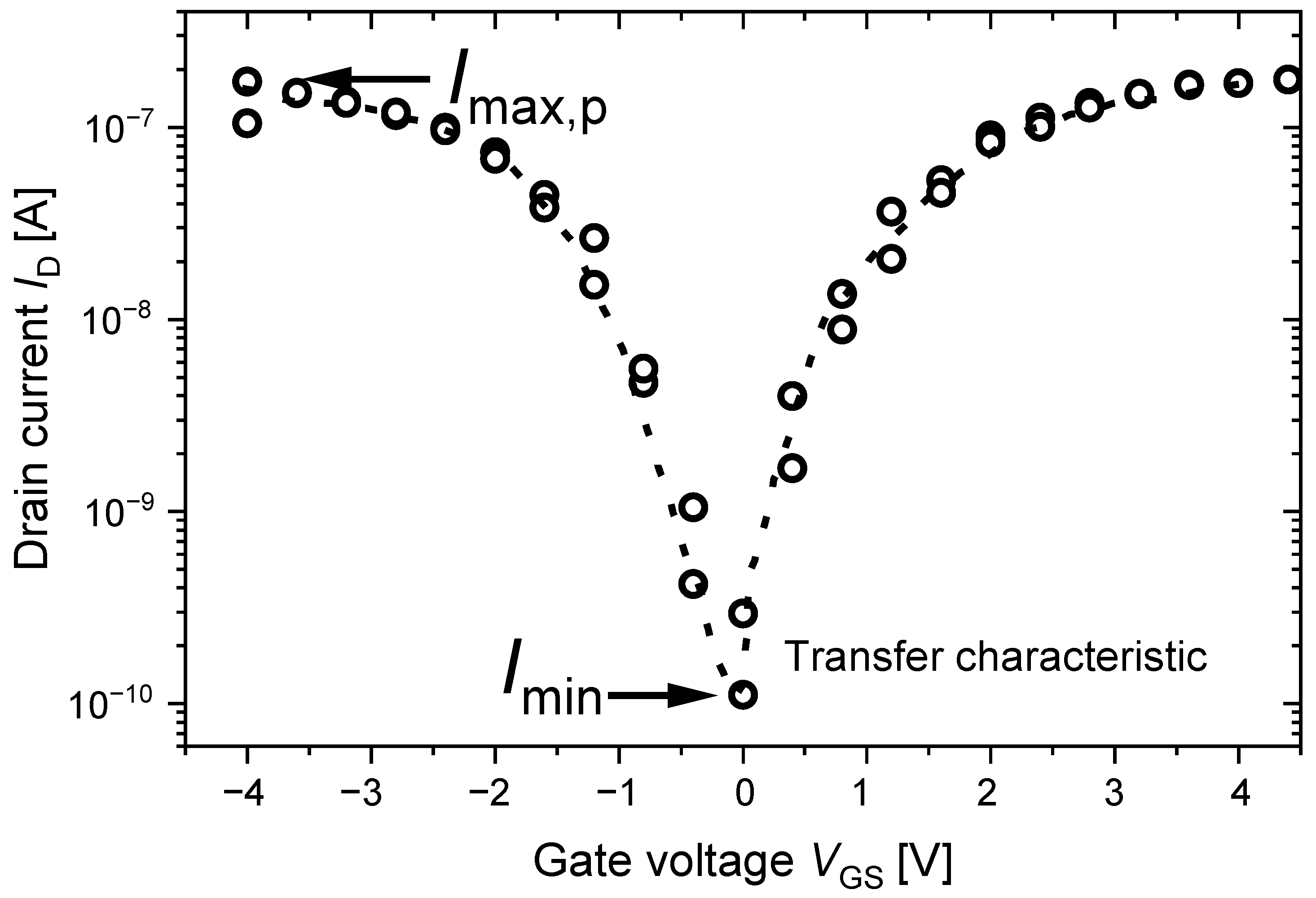
4.2. CNT-PUF Characterisation
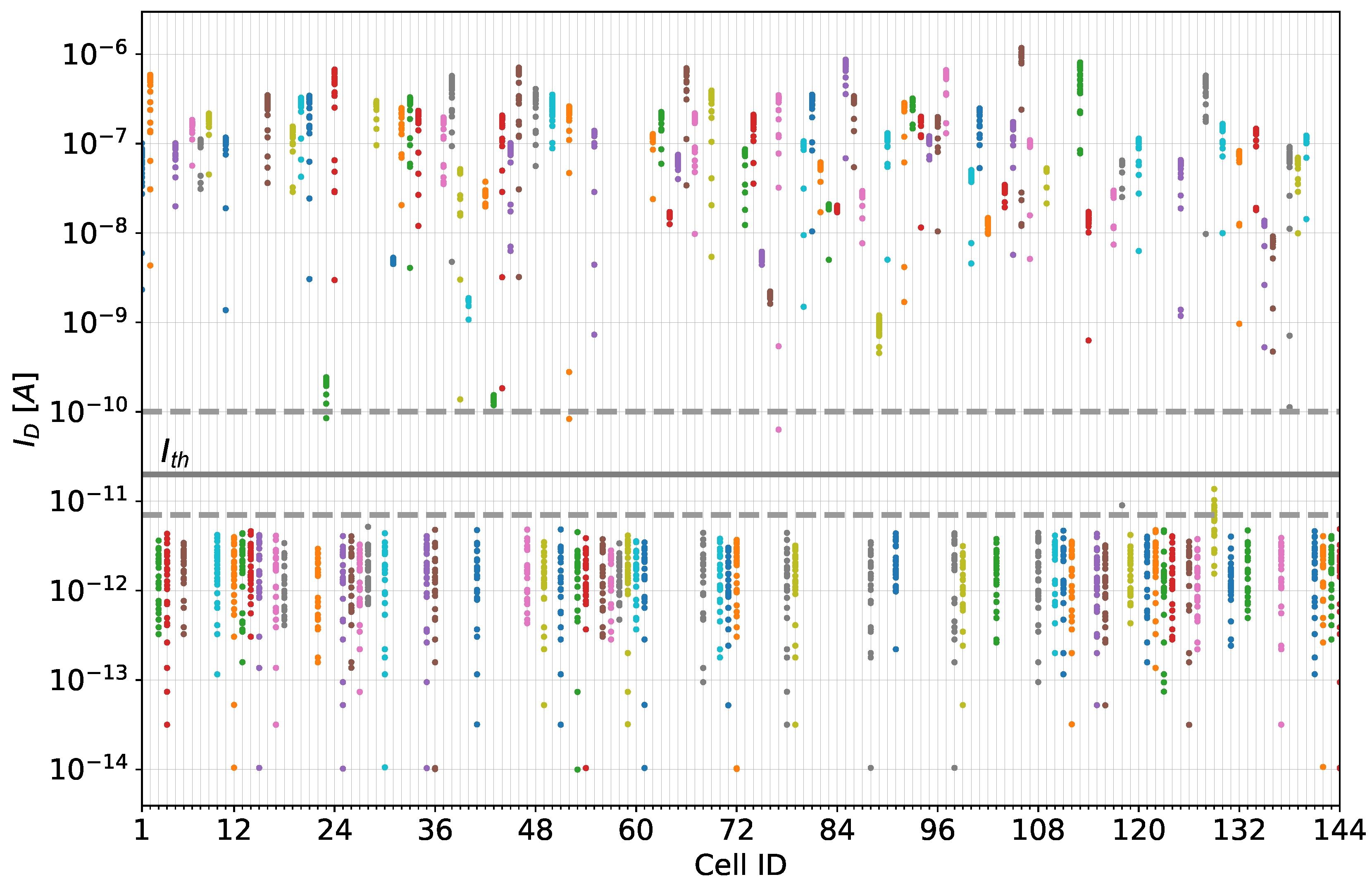
4.3. CNT-PUF Quantisation
5. Evaluation of the Fabricated CNT-PUFs
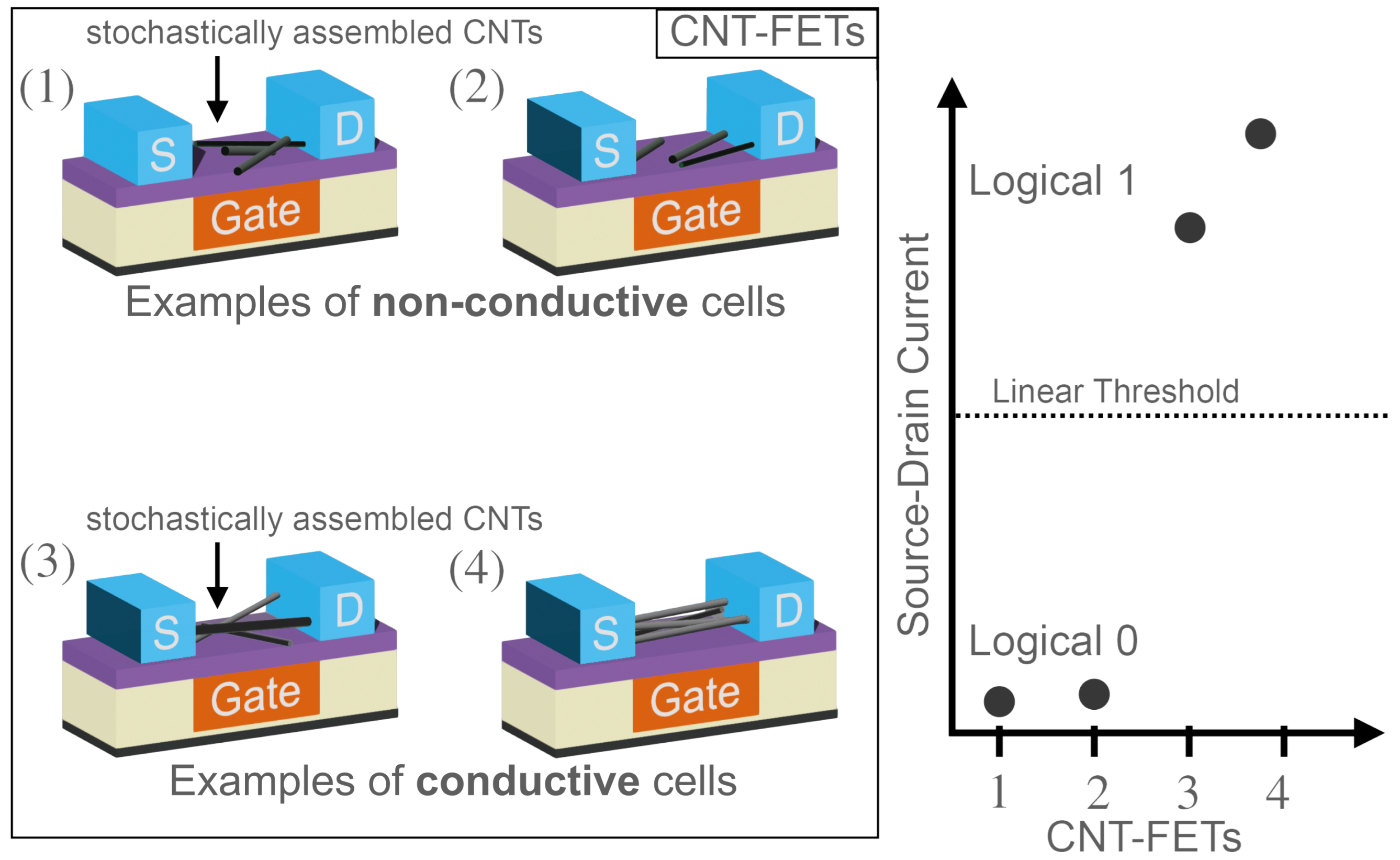
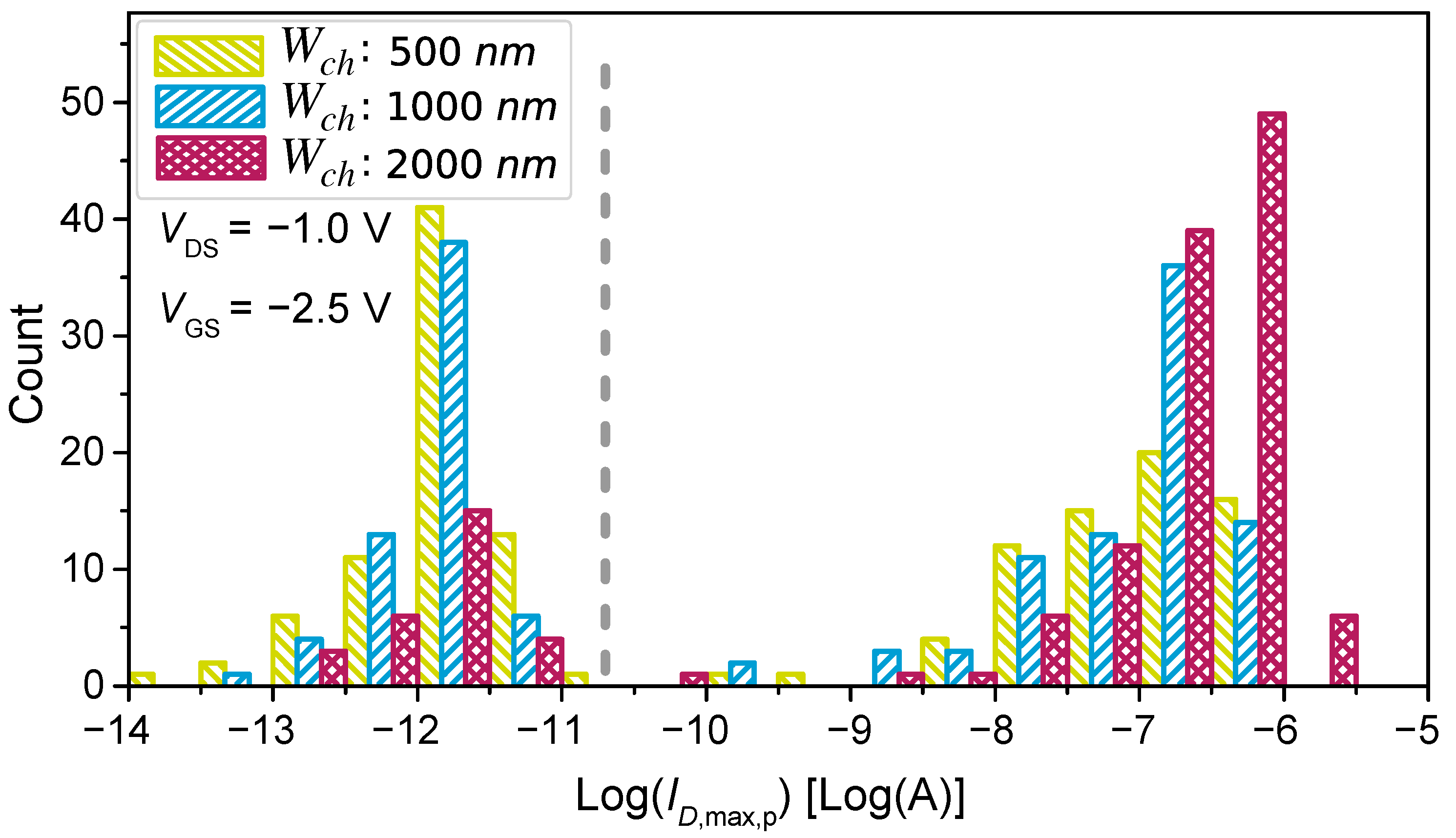
5.1. CNT-PUF Design with Highly Distinguishable Responses
5.2. Evaluation of CNT-PUFs under Normal Conditions
5.2.1. Uniformity
5.2.2. Uniqueness
5.2.3. Unpredictability
5.2.4. Robustness
5.3. Heat-Tolerant CNT-PUFs
6. Stable Key Extraction from CNT-PUFs
6.1. Enrolment
| Algorithm 1 Retrieving a challenge as a list of cell indices of stable cells of a CNT-PUF p. |
|
| Algorithm 2 Selection of random PUF cells using a Random Number Generator (RNG). |
|
6.2. Reconstruction
| Algorithm 3 Algorithm describing the reconstruction phase of a CNT-PUF p. |
|
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AFM | Atomic Force Microscopy |
| ALD | Atomic Layer Deposition |
| ASIC | Application-Specific Integrated Circuit |
| CMOS | Complementary Metal–Oxide–Semiconductor |
| CNT | Carbon NanoTube |
| CNT-FET | Carbon NanoTube Field-Effect Transistor |
| CNT-PUF | Carbon NanoTube-based Physical Unclonable Function |
| CVD | Chemical Vapour Deposition |
| EBL | Electron-Beam Lithography |
| FET | Field-Effect Transistor |
| IoT | Internet of Things |
| NIST | National Institute of Standards and Technology |
| PUF | Physical Unclonable Function |
| RNG | Random Number Generator |
| SoC | System on a Chip |
References
- Suh, G.E.; O’Donnell, C.W.; Sachdev, I.; Devadas, S. Design and implementation of the AEGIS single-chip secure processor using physical random functions. In Proceedings of the 32nd International Symposium on Computer Architecture (ISCA’05), Madison, WI, USA, 4–8 June 2005; pp. 25–36. [Google Scholar] [CrossRef]
- Lee, J.W.; Lim, D.; Gassend, B.; Suh, G.E.; van Dijk, M.; Devadas, S. A technique to build a secret key in integrated circuits for identification and authentication applications. In Proceedings of the 2004 Symposium on VLSI Circuits. Digest of Technical Papers (IEEE Cat. No.04CH37525), Honolulu, HI, USA, 17–19 June 2004; pp. 176–179. [Google Scholar] [CrossRef]
- Devadas, S.; Suh, E.; Paral, S.; Sowell, R.; Ziola, T.; Khandelwal, V. Design and Implementation of PUF-Based “Unclonable” RFID ICs for Anti-Counterfeiting and Security Applications. In Proceedings of the 2008 IEEE International Conference on RFID, Las Vegas, NV, USA, 16–17 April 2008; pp. 58–64. [Google Scholar] [CrossRef]
- Gassend, B.; Lim, D.; Clarke, D.; van Dijk, M.; Devadas, S. Identification and authentication of integrated circuits. Concurr. Comput. Pract. Exp. 2004, 16, 1077–1098. [Google Scholar] [CrossRef]
- Škorić, B.; Schrijen, G.J.; Tuyls, P.; Ignatenko, T.; Willems, F. Secure Key Storage with PUFs. In Security with Noisy Data: On Private Biometrics, Secure Key Storage and Anti-Counterfeiting; Springer: London, UK, 2007; pp. 269–292. [Google Scholar] [CrossRef]
- Yu, M.D.M.; M’Raihi, D.; Sowell, R.; Devadas, S. Lightweight and Secure PUF Key Storage Using Limits of Machine Learning. In Lecture Notes in Computer Science, Proceedings of the Cryptographic Hardware and Embedded Systems—CHES, Nara, Japan, 28 September–1 October 2011; Preneel, B., Takagi, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6917, pp. 358–373. [Google Scholar] [CrossRef]
- Maes, R.; Van Herrewege, A.; Verbauwhede, I. PUFKY: A Fully Functional PUF-Based Cryptographic Key Generator. In Lecture Notes in Computer Science, Proceedings of the Cryptographic Hardware and Embedded Systems—CHES, Leuven, Belgium, 9–12 September 2012; Prouff, E., Schaumont, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7428, pp. 302–319. [Google Scholar] [CrossRef]
- Kong, J.; Koushanfar, F.; Pendyala, P.K.; Sadeghi, A.R.; Wachsmann, C. PUFatt: Embedded Platform Attestation Based on Novel Processor-Based PUFs. In Proceedings of the 51st Annual Design Automation Conference. Association for Computing Machinery, 2014, DAC ’14, San Francisco, CA, USA, 1–5 June 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Schulz, S.; Sadeghi, A.R.; Wachsmann, C. Short Paper: Lightweight Remote Attestation Using Physical Functions. In Proceedings of the Fourth ACM Conference on Wireless Network Security. Association for Computing Machinery, 2011, WiSec ’11, Hamburg, Germany, 14–17 June 2011; pp. 109–114. [Google Scholar] [CrossRef]
- Hartmann, M.; Hermann, S.; Marsh, P.F.; Rutherglen, C.; Wang, D.; Ding, L.; Peng, L.M.; Claus, M.; Schröter, M. CNTFET Technology for RF Applications: Review and Future Perspective. IEEE J. Microwaves 2021, 1, 275–287. [Google Scholar] [CrossRef]
- Zaporotskova, I.V.; Boroznina, N.P.; Parkhomenko, Y.N.; Kozhitov, L.V. Carbon nanotubes: Sensor properties. A review. Mod. Electron. Mater. 2016, 2, 95–105. [Google Scholar] [CrossRef]
- Dürkop, T.; Getty, S.A.; Cobas, E.; Fuhrer, M.S. Extraordinary Mobility in Semiconducting Carbon Nanotubes. Nano Lett. 2004, 4, 35–39. [Google Scholar] [CrossRef]
- Javey, A.; Guo, J.; Paulsson, M.; Wang, Q.; Mann, D.; Lundstrom, M.; Dai, H. High-Field Quasiballistic Transport in Short Carbon Nanotubes. Phys. Rev. Lett. 2004, 92, 106804. [Google Scholar] [CrossRef]
- Zeng, Z.; Wang, C.; Siqueira, G.; Han, D.; Huch, A.; Abdolhosseinzadeh, S.; Heier, J.; Nüesch, F.; Zhang, C.J.; Nyström, G. Nanocellulose-MXene Biomimetic Aerogels with Orientation-Tunable Electromagnetic Interference Shielding Performance. Adv. Sci. 2020, 7, 2000979. [Google Scholar] [CrossRef]
- Zeng, Z.; Wu, T.; Han, D.; Ren, Q.; Siqueira, G.; Nyström, G. Ultralight, Flexible, and Biomimetic Nanocellulose/Silver Nanowire Aerogels for Electromagnetic Interference Shielding. ACS Nano 2020, 14, 2927–2938. [Google Scholar] [CrossRef]
- Yang, Y.; Han, M.; Liu, W.; Wu, N.; Liu, J. Hydrogel-based composites beyond the porous architectures for electromagnetic interference shielding. Nano Res. 2022, 15, 9614–9630. [Google Scholar] [CrossRef]
- Qiu, C.; Zhang, Z.; Xiao, M.; Yang, Y.; Zhong, D.; Peng, L.M. Scaling carbon nanotube complementary transistors to 5-nm gate lengths. Science 2017, 355, 271–276. [Google Scholar] [CrossRef]
- Rosendale, G.; Kianian, S.; Manning, M.; Hamilton, D.; Huang, X.M.H.; Robinson, K.; Kim, Y.W.; Rueckes, T. A 4 Megabit Carbon Nanotube-based Nonvolatile Memory (NRAM). In Proceedings of the 2010 ESSCIRC, Seville, Spain, 14–16 September 2010; pp. 478–481. [Google Scholar] [CrossRef]
- Böttger, S.; Frank, F.; Anagnostopoulos, N.A.; Mohamed, A.; Hartmann, M.; Arul, T.; Hermann, S.; Katzenbeisser, S. CNT-PUFs: Highly Robust Physical Unclonable Functions Based on Carbon Nanotubes. In Proceedings of the 2023 IEEE 23rd International Conference on Nanotechnology (NANO), Jeju City, Republic of Korea, 2–5 July 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Katzenbeisser, S.; Kocabaş, Ü.; Rožić, V.; Sadeghi, A.R.; Verbauwhede, I.; Wachsmann, C. PUFs: Myth, Fact or Busted? A Security Evaluation of Physically Unclonable Functions (PUFs) Cast in Silicon. In Proceedings of the Cryptographic Hardware and Embedded Systems—CHES, Leuven, Belgium, 9–12 September 2012; Prouff, E., Schaumont, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 283–301. [Google Scholar] [CrossRef]
- Frank, F.; Xiong, W.; Anagnostopoulos, N.A.; Schaller, A.; Arul, T.; Koushanfar, F.; Katzenbeisser, S.; Rührmair, U.; Szefer, J. Abusing Commodity DRAMs in IoT Devices to Remotely Spy on Temperature. IEEE Trans. Inf. Forensics Secur. 2023, 18, 2991–3005. [Google Scholar] [CrossRef]
- Hesselbarth, R.; Wilde, F.; Gu, C.; Hanley, N. Large scale RO PUF analysis over slice type, evaluation time and temperature on 28 nm Xilinx FPGAs. In Proceedings of the 2018 IEEE International Symposium on Hardware Oriented Security and Trust (HOST), Washington, DC, USA, 30 April–4 May 2018; pp. 126–133. [Google Scholar] [CrossRef]
- Böttger, S.; Dietz, F.; Hartmann, M.; Dahra, N.; Kaulfersch, E.; Hermann, S. Functional CMOS extension with integrated carbon nano devices. In Proceedings of the 2022 Smart Systems Integration (SSI), Grenoble, France, 27–28 April 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Rukhin, A.; Soto, J.; Nechvatal, J.; Smid, M.; Barker, E.; Leigh, S.; Levenson, M.; Vangel, M.; Banks, D.; Heckert, A.; et al. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications; National Institute of Standards and Technology (NIST): Gaithersburg, MD, USA, 2010; Special Publication 800-22. [Google Scholar] [CrossRef]
- Konigsmark, S.T.C.; Hwang, L.K.; Chen, D.; Wong, M.D.F. CNPUF: A Carbon Nanotube-based Physically Unclonable Function for Secure Low-Energy Hardware Design. In Proceedings of the 2014 19th Asia and South Pacific Design Automation Conference (ASP-DAC), Singapore, 20–23 January 2014; pp. 73–78. [Google Scholar] [CrossRef]
- Hu, Z.; Comeras, J.M.M.L.; Park, H.; Tang, J.; Afzali, A.; Tulevski, G.S.; Hannon, J.B.; Liehr, M.; Han, S.J. Physically unclonable cryptographic primitives using self-assembled carbon nanotubes. Nat. Nanotechnol. 2016, 11, 559–565. [Google Scholar] [CrossRef] [PubMed]
- Moradi, M.; Tao, S.; Mirzaee, R.F. Physical Unclonable Functions Based on Carbon Nanotube FETs. In Proceedings of the 2017 IEEE 47th International Symposium on Multiple-Valued Logic (ISMVL), Novi Sad, Serbia, 22–24 May 2017; pp. 124–129. [Google Scholar] [CrossRef]
- Liu, L.; Huang, H.; Hu, S. Lorenz Chaotic System-Based Carbon Nanotube Physical Unclonable Functions. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2018, 37, 1408–1421. [Google Scholar] [CrossRef]
- Kumar, N.; Chen, J.; Kar, M.; Sitaraman, S.K.; Mukhopadhyay, S.; Kumar, S. Multigated Carbon Nanotube Field Effect Transistors-Based Physically Unclonable Functions as Security Keys. IEEE IoT J. 2019, 6, 325–334. [Google Scholar] [CrossRef]
- Moon, D.I.; Rukhin, A.; Gandhiraman, R.P.; Kim, B.; Kim, S.; Seol, M.L.; Yoon, K.J.; Lee, D.; Koehne, J.; Han, J.W.; et al. Physically Unclonable Function by an All-Printed Carbon Nanotube Network. ACS Appl. Electron. Mater. 2019, 1, 1162–1168. [Google Scholar] [CrossRef]
- Burzurí, E.; Granados, D.; Pérez, E.M. Physically Unclonable Functions Based on Single-Walled Carbon Nanotubes: A Scalable and Inexpensive Method toward Unique Identifiers. ACS Appl. Nano Mater. 2019, 2, 1796–1801. [Google Scholar] [CrossRef]
- Srinivasu, B.; Chattopadhyay, A. Cycle PUF: A Cycle operator based PUF in Carbon Nanotube FET Technology. In Proceedings of the 2021 IEEE 21st International Conference on Nanotechnology (NANO), Montreal, QC, Canada, 28–30 July 2021; pp. 13–16. [Google Scholar] [CrossRef]
- Zhong, D.; Liu, J.; Xiao, M.; Xie, Y.; Shi, H.; Liu, L.; Zhao, C.; Ding, L.; Peng, L.M.; Zhang, Z. Twin physically unclonable functions based on aligned carbon nanotube arrays. Nat. Electron. 2022, 5, 424–432. [Google Scholar] [CrossRef]
- Jeon, D.; Baek, J.H.; Kim, Y.D.; Lee, J.; Kim, D.K.; Choi, B.D. A Physical Unclonable Function with Bit Error Rate < 2.3 × 10−8 Based on Contact Formation Probability Without Error Correction Code. IEEE J. Solid State Circuits 2020, 55, 805–816. [Google Scholar] [CrossRef]
- Marakis, E.; Rührmair, U.; Lachner, M.; Uppu, R.; Škorić, B.; Pinkse, P.W.H. Clones of the Unclonable: Nanoduplicating Optical PUFs and Applications. arXiv 2022, arXiv:2212.12495. [Google Scholar] [CrossRef]
- Mizutani, T.; Iwatsuki, S.; Ohno, Y.; Kishimoto, S. Effects of Fabrication Process on Current–Voltage Characteristics of Carbon Nanotube Field Effect Transistors. Jpn. J. Appl. Phys. 2005, 44, 1599. [Google Scholar] [CrossRef]
- Derycke, V.; Martel, R.; Appenzeller, J.; Avouris, P. Controlling doping and carrier injection in carbon nanotube transistors. Appl. Phys. Lett. 2002, 80, 2773–2775. [Google Scholar] [CrossRef]
- Collins, P.G.; Bradley, K.; Ishigami, M.; Zettl, A. Extreme Oxygen Sensitivity of Electronic Properties of Carbon Nanotubes. Science 2000, 287, 1801–1804. [Google Scholar] [CrossRef]
- Kang, D.; Park, N.; hye Ko, J.; Bae, E.; Park, W. Oxygen-induced p-type doping of a long individual single-walled carbon nanotube. Nanotechnology 2005, 16, 1048. [Google Scholar] [CrossRef]
- Nanointegris Technologies Inc. IsoSol-S100® Polymer-Wrapped Nanotubes Technical Data Sheet. Available online: https://nanointegris.com/our-products/isosol-s100-polymer-wrapped-nanotubes/ (accessed on 26 October 2023).
- Anagnostopoulos, N.A.; Mexis, N.; Böttger, S.; Hartmann, M.; Mohamed, A.; Hermann, S.; Katzenbeisser, S.; Stavrinides, S.; Arul, T. A Method to Construct Efficient Carbon-Nanotube-Based Physical Unclonable Functions and True Random Number Generators. In Proceedings of the 2023 26th Euromicro Conference on Digital System Design (DSD), Durrës, Albania, 6–8 September 2023. Accepted for publication. [Google Scholar]
- Mexis, N.; Arul, T.; Anagnostopoulos, N.A.; Frank, F.; Böttger, S.; Hartmann, M.; Hermann, S.; Kavun, E.B.; Katzenbeisser, S. Spatial Correlation in Weak Physical Unclonable Functions: A Comprehensive Overview. In Proceedings of the 2023 26th Euromicro Conference on Digital System Design (DSD), Durrës, Albania, 6–8 September 2023. Accepted for publication. [Google Scholar]
- Das, D.; Pendse, N.; Wilkinson, C.; Pecht, M. Parameter recharacterization: A method of thermal uprating. IEEE Trans. Components Packag. Technol. 2001, 24, 729–737. [Google Scholar] [CrossRef]
- Lukas, S.; Hartwig, O.; Prechtl, M.; Capraro, G.; Bolten, J.; Meledin, A.; Mayer, J.; Neumaier, D.; Kataria, S.; Duesberg, G.S.; et al. Correlating Nanocrystalline Structure with Electronic Properties in 2D Platinum Diselenide. Adv. Funct. Mater. 2021, 31, 2102929. [Google Scholar] [CrossRef]
- Shawkat, M.S.; Gil, J.; Han, S.S.; Ko, T.J.; Wang, M.; Dev, D.; Kwon, J.; Lee, G.H.; Oh, K.H.; Chung, H.S.; et al. Thickness-Independent Semiconducting-to-Metallic Conversion in Wafer-Scale Two-Dimensional PtSe2 Layers by Plasma-Driven Chalcogen Defect Engineering. ACS Appl. Mater. Interfaces 2020, 12, 14341–14351. [Google Scholar] [CrossRef] [PubMed]
- Ansari, L.; Monaghan, S.; McEvoy, N.; Ó Coileáin, C.; Cullen, C.P.; Lin, J.; Siris, R.; Stimpel-Lindner, T.; Burke, K.F.; Mirabelli, G.; et al. Quantum confinement-induced semimetal-to-semiconductor evolution in large-area ultra-thin PtSe2 films grown at 400 ∘C. NPJ 2D Mater. Appl. 2019, 3, 33. [Google Scholar] [CrossRef]
- Hu, S.; Gopinadhan, K.; Rakowski, A.; Neek-Amal, M.; Heine, T.; Grigorieva, I.V.; Haigh, S.J.; Peeters, F.M.; Geim, A.K.; Lozada-Hidalgo, M. Transport of hydrogen isotopes through interlayer spacing in van der Waals crystals. Nat. Nanotechnol. 2018, 13, 468–472. [Google Scholar] [CrossRef]
- Ramanujam, S.; Karuppiah, M. Designing an algorithm with high avalanche effect. Int. J. Comput. Sci. Netw. Secur. (IJCSNS) 2011, 11, 106–111. [Google Scholar]


| Statistical Test | Average p-Value | Passed/Total | Input Length Recommendation Test Parameters |
|---|---|---|---|
| Frequency (Monobit) | 0.28 | 25/30 | 100 bits |
| Frequency Test within a Block | 0.32 | 28/30 | 100 bits M = 20 bits (block length) |
| Runs Test | 0.43 | 30/30 | 100 bits |
| Test for the Longest Run of Ones in a Block | 0.41 | 27/30 | 128 bits m = 8 bits (block length) |
| Binary Matrix Rank Test | / | / | ≥ 38,912 bits |
| Discrete Fourier Transform (Spectral) Test | / | / | ≥ 1000 bits |
| Non-overlapping Template Matching Test | 0.86 | 30/30 | m = 9 bits (template size) |
| Overlapping Template Matching Test | / | / | ≥ bits |
| Maurer’s “Universal Statistical” Test | / | / | ≥ 387,840 bits |
| Linear Complexity Test | / | / | ≥ bits |
| Serial Test | 0.36 | 30/30 | m = 4 bits (block length) |
| Approximate Entropy Test | 0.33 | 27/30 | m = 2 bits (block length) |
| Cumulative Sums (Cusum) Test | 0.30 | 26/30 | bits |
| Random Excursions Test | / | / | ≥ bits |
| Random Excursions Variant Test | / | / | ≥ bits |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frank, F.; Böttger, S.; Mexis, N.; Anagnostopoulos, N.A.; Mohamed, A.; Hartmann, M.; Kuhn, H.; Helke, C.; Arul, T.; Katzenbeisser, S.; et al. CNT-PUFs: Highly Robust and Heat-Tolerant Carbon-Nanotube-Based Physical Unclonable Functions. Nanomaterials 2023, 13, 2930. https://doi.org/10.3390/nano13222930
Frank F, Böttger S, Mexis N, Anagnostopoulos NA, Mohamed A, Hartmann M, Kuhn H, Helke C, Arul T, Katzenbeisser S, et al. CNT-PUFs: Highly Robust and Heat-Tolerant Carbon-Nanotube-Based Physical Unclonable Functions. Nanomaterials. 2023; 13(22):2930. https://doi.org/10.3390/nano13222930
Chicago/Turabian StyleFrank, Florian, Simon Böttger, Nico Mexis, Nikolaos Athanasios Anagnostopoulos, Ali Mohamed, Martin Hartmann, Harald Kuhn, Christian Helke, Tolga Arul, Stefan Katzenbeisser, and et al. 2023. "CNT-PUFs: Highly Robust and Heat-Tolerant Carbon-Nanotube-Based Physical Unclonable Functions" Nanomaterials 13, no. 22: 2930. https://doi.org/10.3390/nano13222930
APA StyleFrank, F., Böttger, S., Mexis, N., Anagnostopoulos, N. A., Mohamed, A., Hartmann, M., Kuhn, H., Helke, C., Arul, T., Katzenbeisser, S., & Hermann, S. (2023). CNT-PUFs: Highly Robust and Heat-Tolerant Carbon-Nanotube-Based Physical Unclonable Functions. Nanomaterials, 13(22), 2930. https://doi.org/10.3390/nano13222930









