Determination of the Primary Excitation Spectra in XPS and AES
Abstract
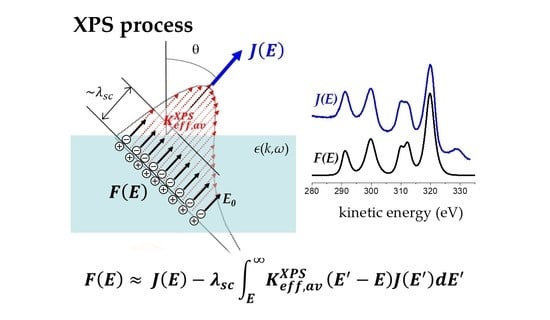
1. Introduction
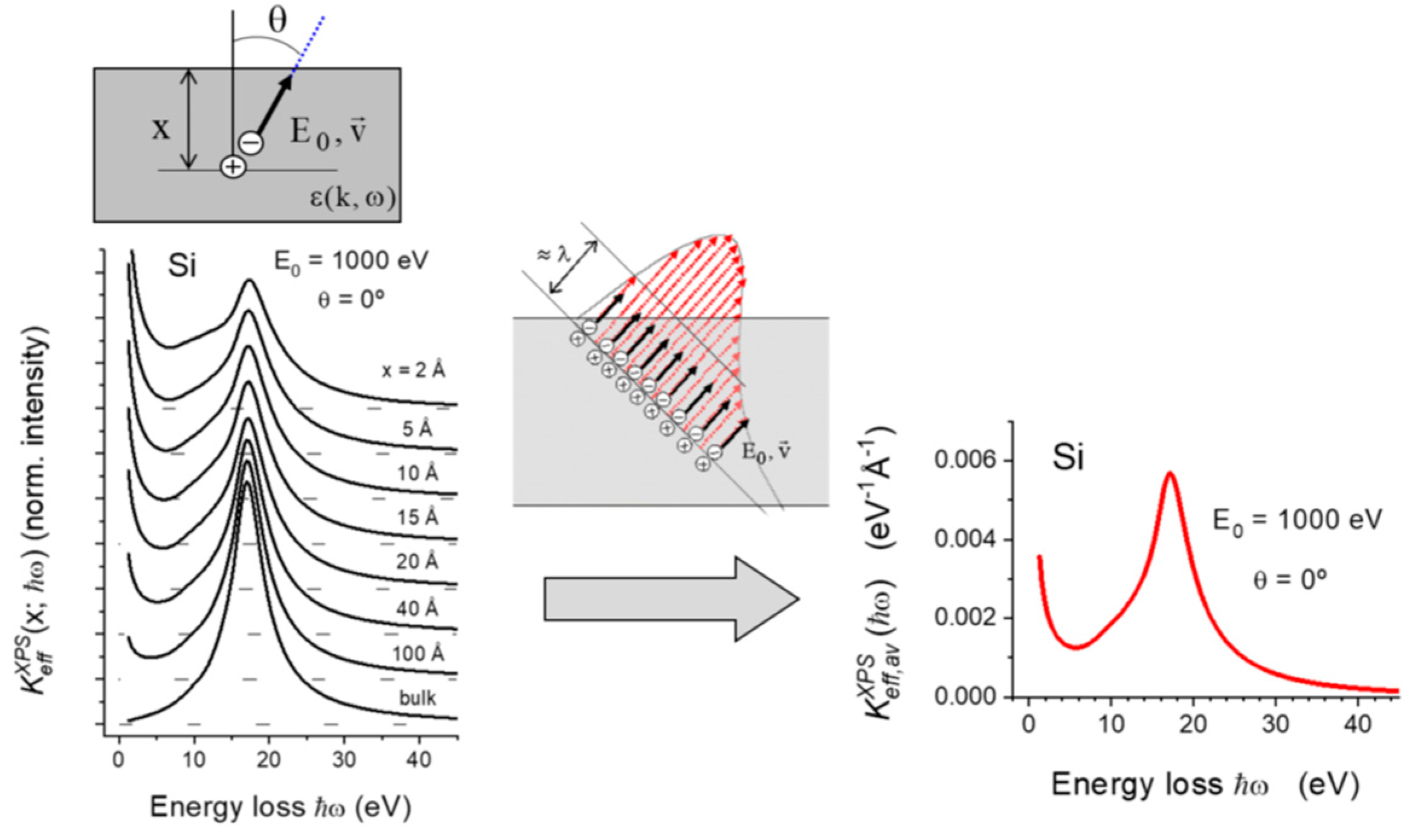
2. Theoretical Model
- (a)
- A non-local dielectric description of the material response [9]. This allows for a straightforward analytical evaluation of the energy loss probability of swift emitted electrons in presence of a positive stationary charge;
- (b)
- Elastic scattering is neglected. This is justified by the fact that it is of minor importance for the description of energy losses lower than ~30 eV [13], which are mostly considered here.
3. Case Studies
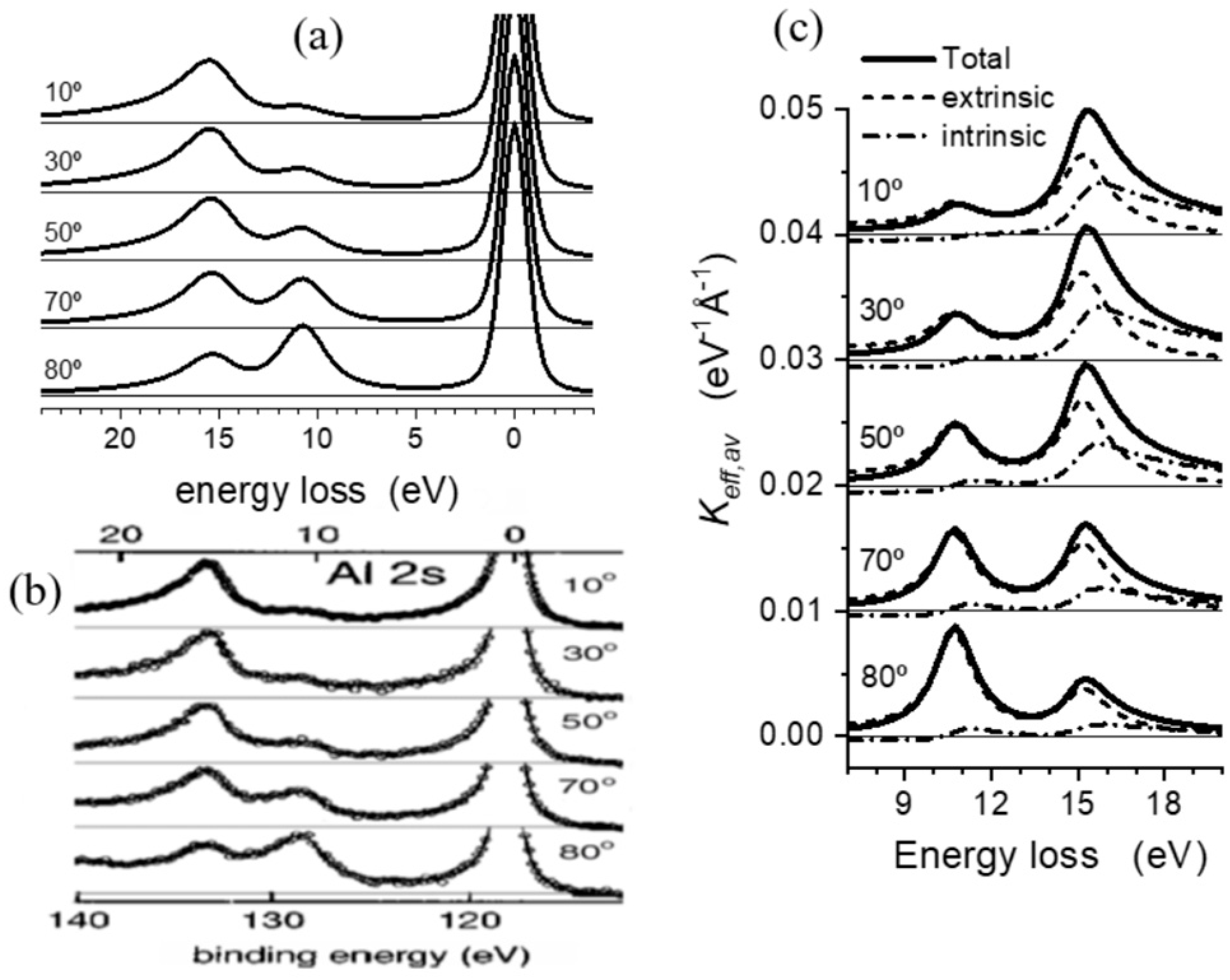
3.1. Angular Dependence of Al 2s Photoelectron Emission from Aluminum
3.2. Ag 3d Photoelectron Emission from Silver
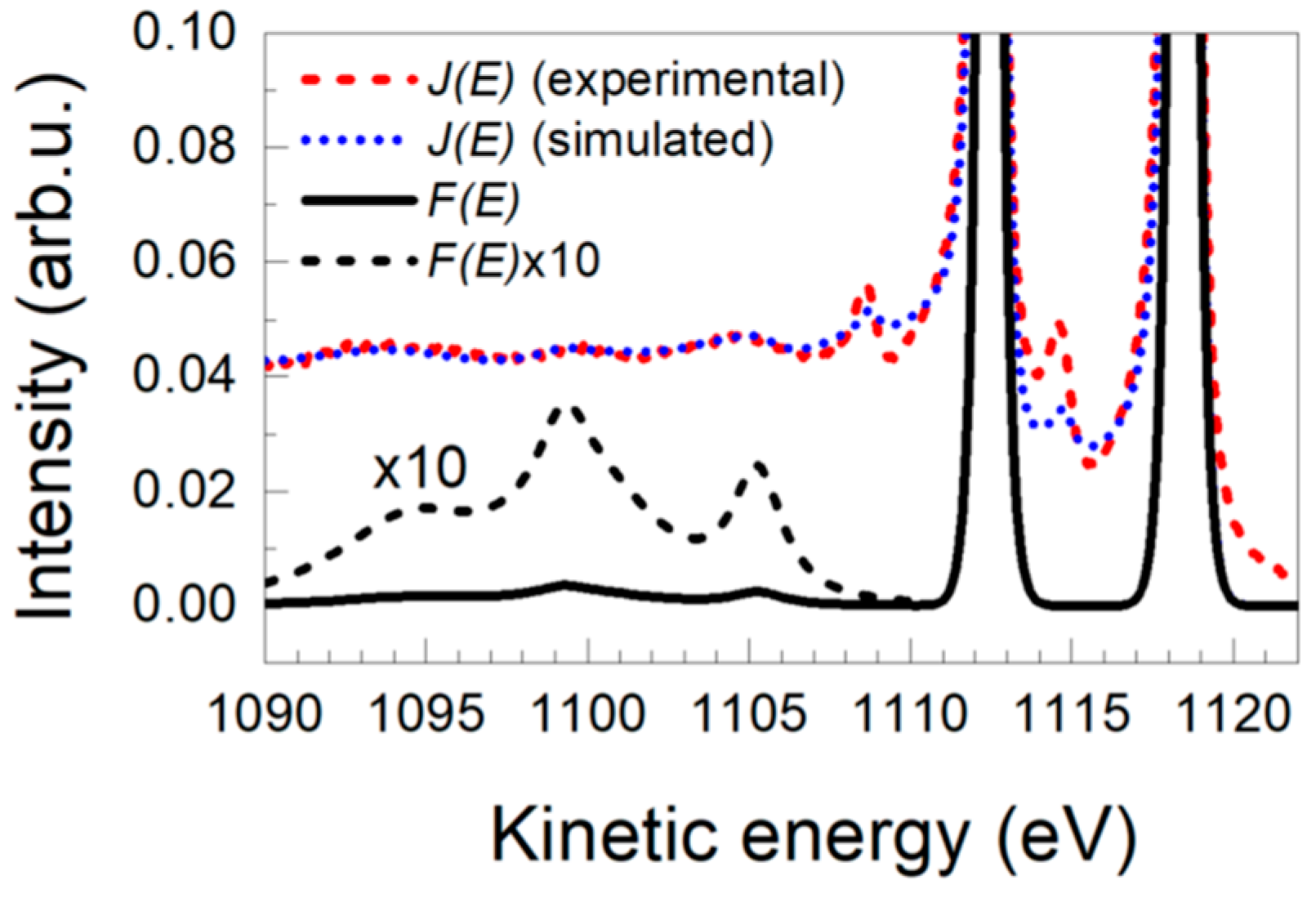
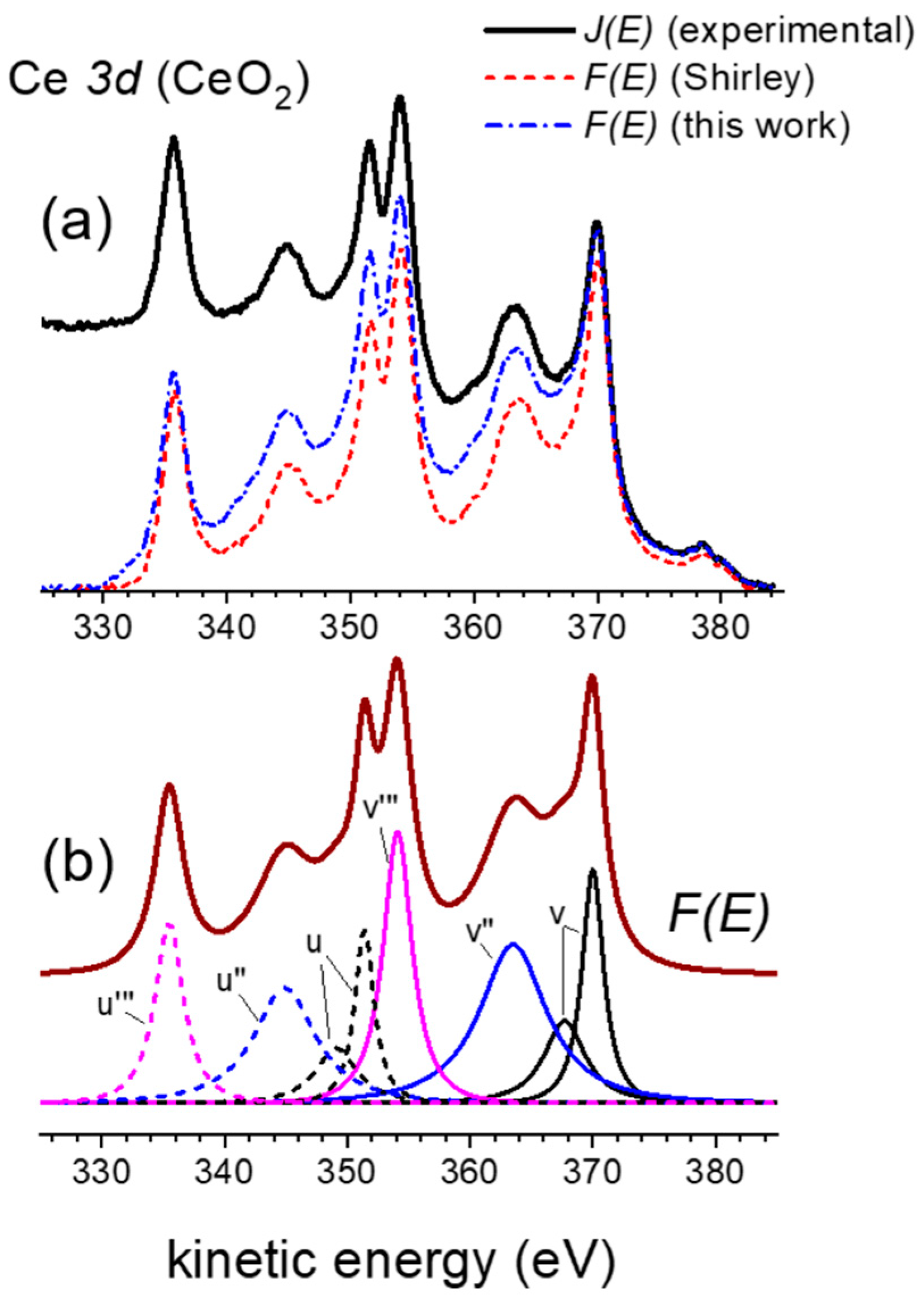
3.3. Ce 3d Photoelectron Emission from CeO2
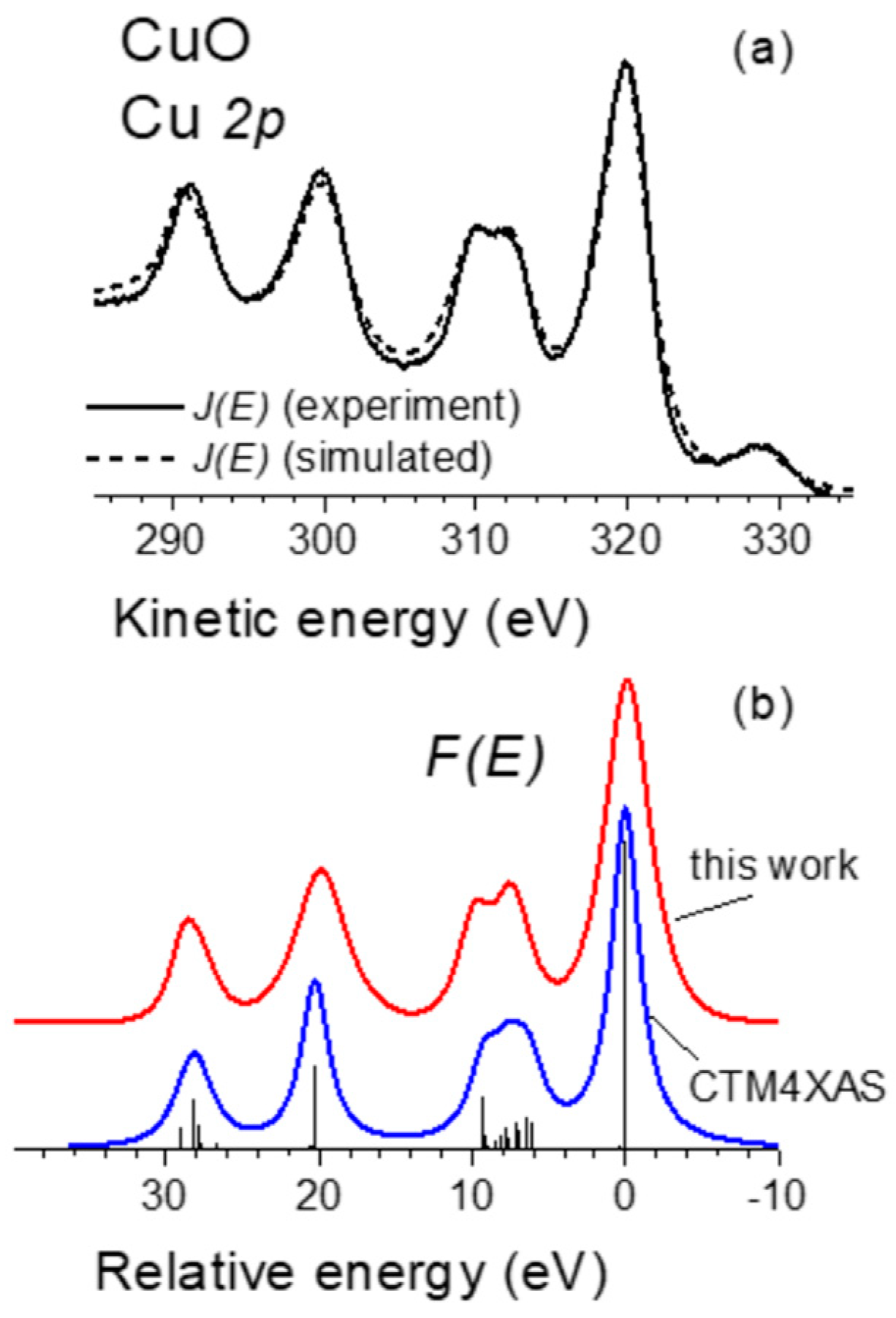
3.4. Cu 2p Photoelectron Emission from CuO
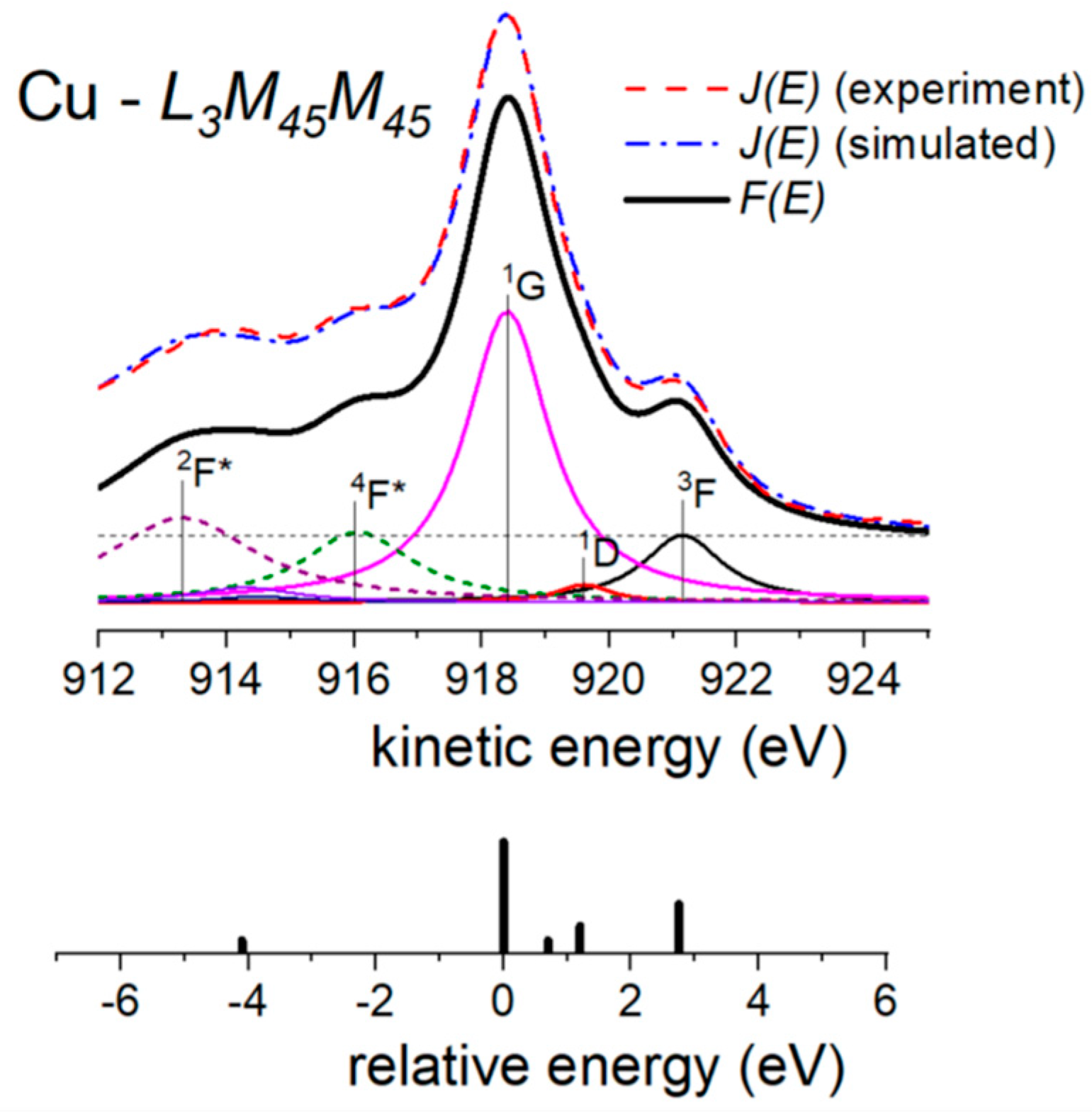
3.5. L3M45M45 Auger Emission from Copper
4. Summary and Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Briggs, D.; Grant, J.T. Surface Analysis by Auger and X-ray Photoelectron Spectroscopy; IM-Publications: Chichester, UK, 2003; 900p. [Google Scholar]
- Watts, J.F.; Wolstenholme, J. An Introduction to Surface Analysis by XPS and AES, 2nd ed.; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2020. [Google Scholar]
- Franklin, T. Applications of Near Ambient Pressure XPS in Heterogeneous Catalysis; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2022. [Google Scholar]
- Woicik, J.C. Hard X-ray Photoelectron Spectroscopy (HAXPES); Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Berglund, C.N.; Spicer, W.E. Photoemission studies of copper and silver, theory. Phy. Rev. 1964, 136, A1030–A1044. [Google Scholar] [CrossRef]
- Citrin, P.H.; Wertheim, G.K.; Baer, Y. Many-body processes in x-ray photoemission line shapes from Li, Na, Mg, and Al metals. Phys. Rev B 1977, 16, 4256–4282. [Google Scholar] [CrossRef]
- Tougaard, S. Energy loss in XPS: Fundamental processes and applications for quantification, non-destructive depth profiling and 3D imaging. J. Electron. Spectrosc. Relat Phenom. 2010, 178, 128–153. [Google Scholar] [CrossRef]
- Stavitski, E.; de Groot, F.M.F. The CTM4XAS program for EELS and XAS spectral shape analysis of transition metal L edges. Micron 2010, 41, 687–694. [Google Scholar] [CrossRef] [PubMed]
- Simonsen, A.C.; Yubero, F.; Tougaard, S. Quantitative model of electron energy loss in XPS. Phys Rev B 1997, 56, 1612–1619. [Google Scholar] [CrossRef]
- Tougaard, S.; Yubero, F. QUEELS-XPS: Quantitative Analysis of Electron Energy Loss in XPS Spectra. Version 2.1. 2011. Available online: http://www.quases.com/ (accessed on 13 June 2022). [CrossRef]
- Shirley, D.A. High-resolution X-ray photoemission spectrum of the valence bands of gold. Phys Rev B 1972, 5, 4709–4714. [Google Scholar] [CrossRef]
- Weightman, P.; Roberts, E.D.; Johnson, C.E. L2,3MM Auger processes in selenium. J. Phys. C Solid St. Phys. 1975, 8, 550–566. [Google Scholar] [CrossRef]
- Pauly, N.; Tougaard, S.; Yubero, F. Modeling of X-ray photoelectron spectra: Surface and core-hole effects. Surf. Interface Anal. 2014, 46, 920–923. [Google Scholar] [CrossRef]
- Tougaard, S. Inelastic background removal in X-ray excited photoelectron spectra from homogeneous and inhomogeneous solids. J. Vac. Sci. Technol. A 1987, 5, 1230–1234. [Google Scholar] [CrossRef]
- Tougaard, S. QUASES: Software Packages to Characterize Surface Nano-Structures by Analysis of Electron Spectra. Version 5.1. 2005. Available online: http://www.quases.com/ (accessed on 13 June 2022).
- Palik, E.D. Handbook of Optical Constants of Solids; Academic Press: Orlando, FL, USA, 1998; 2000p. [Google Scholar]
- Pauly, N.; Yubero, F.; Tougaard, S. ELF Dielectric Functions for Various Materials. (1.0) [Data Set]. Zenodo. Available online: https://doi.org/10.5281/zenodo.6024064 (accessed on 13 June 2022).
- Tougaard, S.; Pauly, N.; Yubero, F. QUEELS: Software to calculate the energy loss processes in TEELS, REELS, XPS and AES including effects of the core hole. Surf. Interface Anal. 2022, 54, 820–833. [Google Scholar] [CrossRef]
- Tougaard, S.; Yubero, F. Software package to calculate the effects of the core hole and surface excitations on XPS and AES. Surf. Interface Anal. 2012, 44, 1114–1118. [Google Scholar] [CrossRef]
- Doniach, S.; Sunjíc, M. Many-electron singularity in X-ray photoemission and X-ray line spectra from metals. J. Phys. C Solid State Phys. 1970, 3, 285–291. [Google Scholar] [CrossRef]
- Tougaard, S.; Sigmund, P. Influence of elastic and inelastic scattering on energy spectra of electrons emitted from solids. Phys. Rev. B. 1982, 25, 4452–4466. [Google Scholar] [CrossRef]
- Yubero, F.; Tougaard, S. Quantification of plasmon excitations in core-level photoemission. Phys. Rev. B. 2005, 71, 045414. [Google Scholar] [CrossRef]
- Pauly, N.; Yubero, F.; Tougaard, S. Quantitative analysis of satellite structures in XPS spectra of gold and silver. Appl. Surf. Sci. 2016, 383, 317–323. [Google Scholar] [CrossRef]
- Pauly, N.; Tougaard, S.; Yubero, F. Determination of the Cu 2p primary excitation spectra for Cu, Cu2O and CuO. Surf. Sci. 2014, 620, 17–22. [Google Scholar] [CrossRef]
- Pauly, N.; Yubero, F.; Tougaard, S. XPS primary excitation spectra of Zn 2p, Fe 2p, and Ce 3d from ZnO, 𝛼-Fe2O3, and CeO2. Surf. Interface Anal. 2019, 51, 353–360. [Google Scholar] [CrossRef]
- Pauly, N.; Tougaard, S.; Yubero, F. LMM Auger primary excitation spectra of copper. Surf. Sci. 2014, 630, 294–299. [Google Scholar] [CrossRef]
- Biswas, C.; Shukla, A.K.; Banik, S.; Ahire, V.K.; Barman, S.R. Plasmons in core-level photoemission spectra of Al(111). Phys. Rev. B 2003, 67, 165416. [Google Scholar] [CrossRef]
- Mårtensson, N.; Nyholm, R.; Johansson, B. New observation of two-hole core-level satellites in copper, silver, and gold. Phys. Rev. B 1984, 29, 4800–4802. [Google Scholar] [CrossRef]
- Eckardt, H.; Fritsche, L. Theoretical explanation of the XPS satellite structure of elementary metals: Application to Ag. Solid State Commun. 1985, 54, 405–407. [Google Scholar] [CrossRef]
- Romeo, M.; Bak, K.; El Fallah, J.; Le Normand, F.; Hilaire, L. XPS Study of the reduction of cerium dioxide. Surf. Interface Anal. 1993, 20, 508–512. [Google Scholar] [CrossRef]
- Pfau, A.; Schierbaum, K.D. The electronic structure of stoichiometric and reduced CeO2 surfaces: An XPS, UPS and HREELS study. Surf. Sci. 1994, 321, 71–80. [Google Scholar] [CrossRef]
- Zhu, Y.; Jain, N.; Hudait, M.K.; Maurya, D.; Varghese, R.; Priya, S. X-ray photoelectron spectroscopy analysis and band offset determination of CeO2 deposited on epitaxial (100), (110), and (111)Ge. J. Vac. Sci. Technol. B 2014, 32, 011217. [Google Scholar] [CrossRef]
- Skála, T.; Sutara, F.; Prince, K.C.; Matolín, V. Cerium oxide stoichiometry alteration via Sn deposition: Influence of temperature. J. Electron. Spectrosc. Relat. Phenom. 2009, 169, 20–25. [Google Scholar] [CrossRef]
- Végh, J. On analyzing the intrinsic processes through the Shirley background correction procedure. Surf. Sci. 2005, 577, 220–228. [Google Scholar] [CrossRef]
- Nelin, C.J.; Bagus, P.S.; Ilton, E.S.; Chambers, S.A.; Kuhlenbeck, H.; Freund, H.J. Freund, Relationships between complex core level spectra and materials properties. Int. J. Quantum Chem. 2010, 110, 2752–2764. [Google Scholar] [CrossRef]
- Ghijsen, J.; Tjeng, L.H.; van Elp, J.; Eskes, H.; Westerink, J.; Sawatzky, G.A. Electronic structure of Cu2O and CuO. Phys. Rev. B. 1988, 38, 11322–11330. [Google Scholar] [CrossRef]
- Okada, K.; Kotani, A. Multiplet structure in core-level XPS of high-Tc material La2CuO4 and related Cu-compounds. J. Electron. Spectr. Relat. Phenom. 1990, 52, 313–322. [Google Scholar] [CrossRef]
- Antonides, E.; Janse, E.C.; Sawatzky, G.A. LMM Auger spectra of Cu, Zn, Ga, and Ge. I. Transition probabilities, term splittings, and effective Coulomb interaction. Phys. Rev. B 1977, 15, 1669–1979. [Google Scholar] [CrossRef]
- Antonides, E.; Janse, E.C.; Sawatzky, G.A. LMM Auger spectra of Cu, Zn, Ga, and Ge, II. Relationship with the L23 photoelectron spectra via the L2L3M45 Coster-Kronig process. Phys. Rev. B 1977, 15, 4596–4601. [Google Scholar] [CrossRef]
- Roberts, E.D.; Weightman, P.; Johnson, C.E. Auger vacancy satellite structure in the L3M4,5M4,5 Auger spectra of copper. J. Phys. C Solid State Phys. 1975, 8, L301–L304. [Google Scholar] [CrossRef]
- Fuggle, J.C.; Bennett, P.; Hillebrecht, F.U.; Lenselink, A.; Sawatzky, G.A. Influence of Multiplet Splittings in High-Polarity States on Magnetism in Transition Metals. Phys. Rev. Lett. 1982, 49, 1787–1790. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pauly, N.; Yubero, F.; Tougaard, S. Determination of the Primary Excitation Spectra in XPS and AES. Nanomaterials 2023, 13, 339. https://doi.org/10.3390/nano13020339
Pauly N, Yubero F, Tougaard S. Determination of the Primary Excitation Spectra in XPS and AES. Nanomaterials. 2023; 13(2):339. https://doi.org/10.3390/nano13020339
Chicago/Turabian StylePauly, Nicolas, Francisco Yubero, and Sven Tougaard. 2023. "Determination of the Primary Excitation Spectra in XPS and AES" Nanomaterials 13, no. 2: 339. https://doi.org/10.3390/nano13020339
APA StylePauly, N., Yubero, F., & Tougaard, S. (2023). Determination of the Primary Excitation Spectra in XPS and AES. Nanomaterials, 13(2), 339. https://doi.org/10.3390/nano13020339