Cationic Pollutant Removal from Aqueous Solution Using Reduced Graphene Oxide
Abstract
:1. Introduction
2. Materials and Method
2.1. Materials
- Graphite powder (<150 μm, 99.99%, Sigma-Aldrich, Burlington, MA, USA);
- Sulfuric acid (H2SO4, 95.0–98.0%, Sigma-Aldrich, Burlington, MA, USA);
- Potassium permanganate (KMnO4, ≥99.0%, Sigma-Aldrich, Burlington, MA, USA);
- Hydrochloric acid (HCl, 37%, Sigma-Aldrich, Burlington, MA, USA);
- Citric acid (C6H8O7, ≥99.5%, Sigma-Aldrich, Burlington, MA, USA);
- Methyl blue (MB, C16H18N3ClS, Sigma-Aldrich, Burlington, MA, USA);
- Hydrogen peroxide (H2O2, 30%, Merk, Darmstadt, Germany);
- Sodium hydroxide (NaOH, 1310-73-2, 40.00 g/mol, Merk, Darmstadt, Germany);
- Mercury (II) oxide (HgO, 21908-53-2, 219.59 g/mol, Merk, Darmstadt, Germany).
2.2. Preparation of Oxidized Graphenes
2.3. Characterization of GO and rGO
2.4. Preparation of MB Solutions and Experimental Set-Up of MB Adsorption on rGO
2.5. Preparation of Hg(II) Solutions and Experimental Set-Up of Hg(II) Adsorption on rGO
3. Results and Discussion
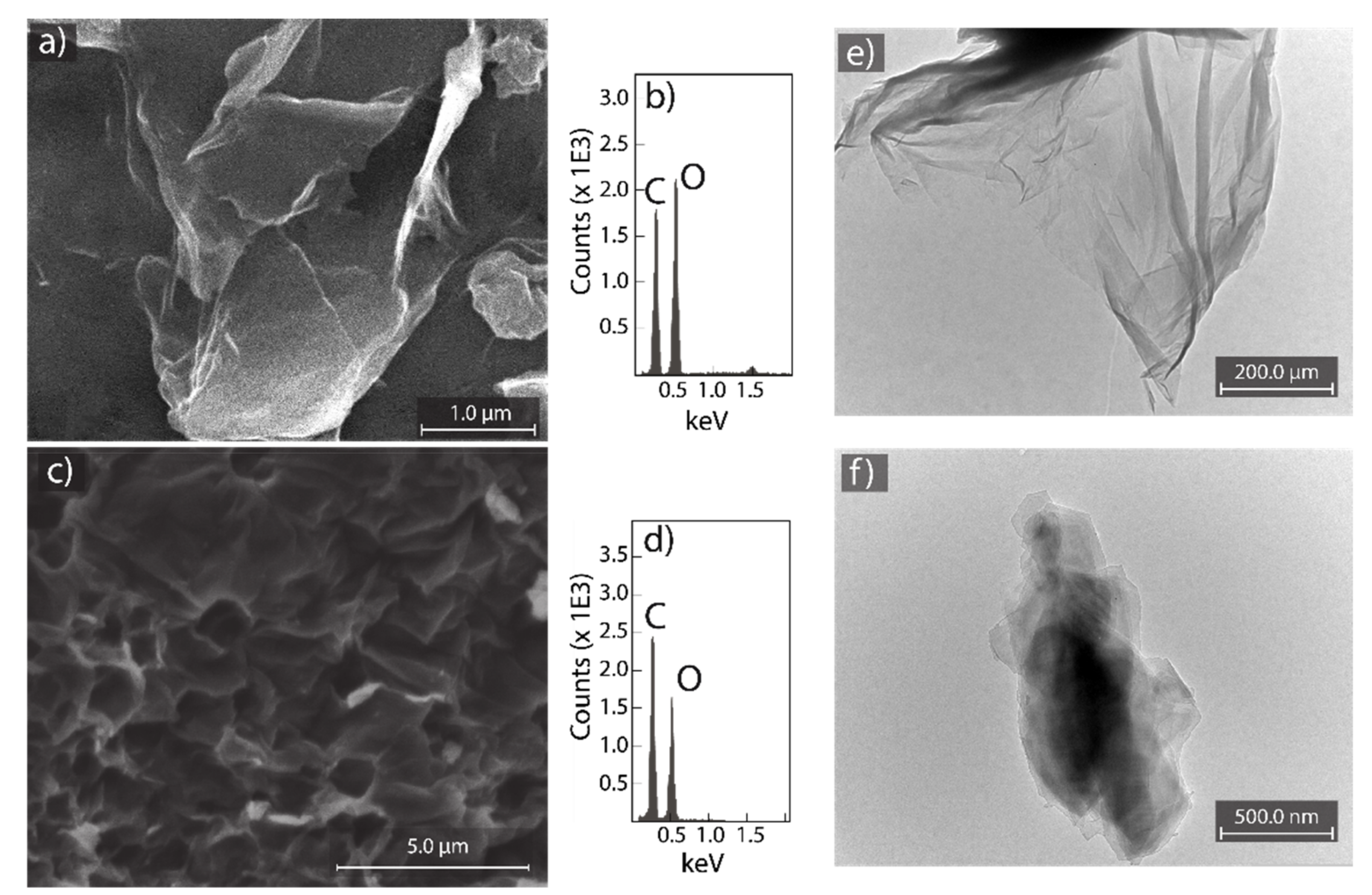
3.1. Characterization of Graphite
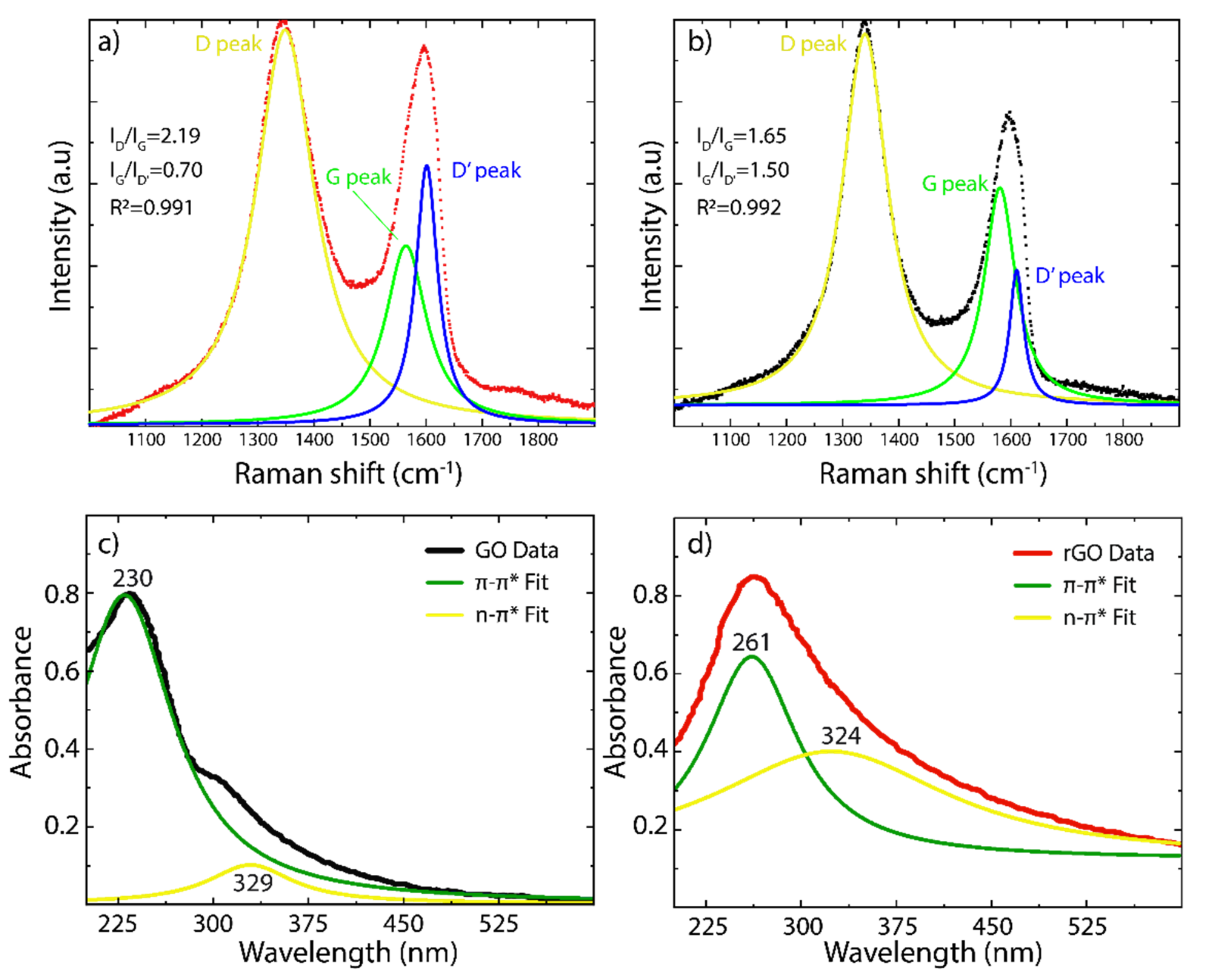
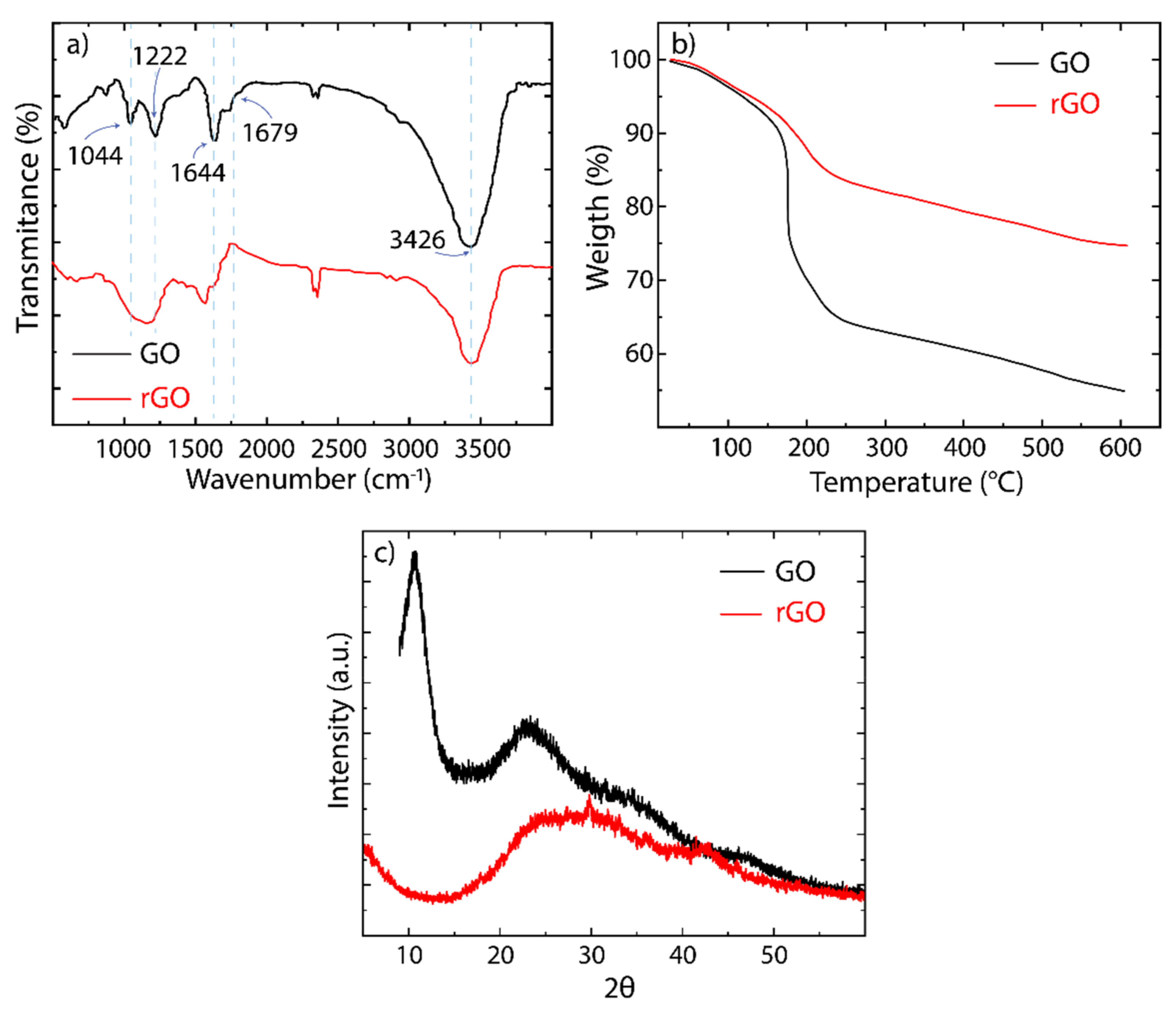
3.2. Characterization of GO and rGO
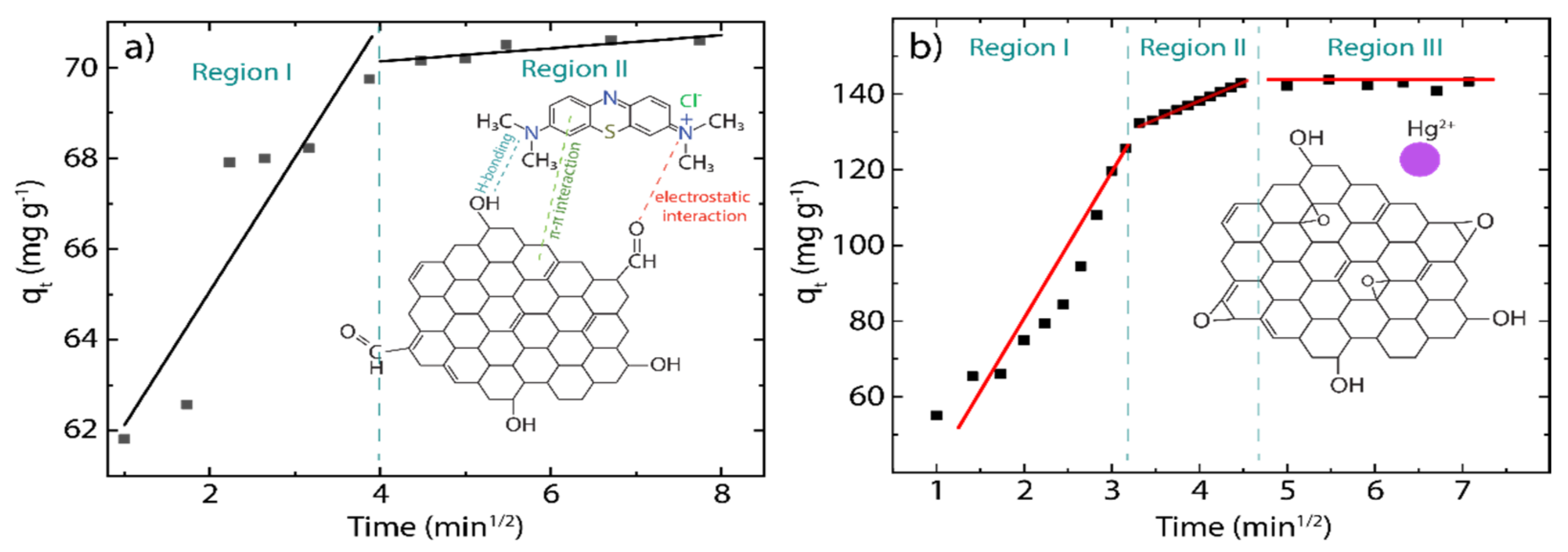
3.3. Adsorption Kinetics
3.4. Intraparticle Diffusion Study
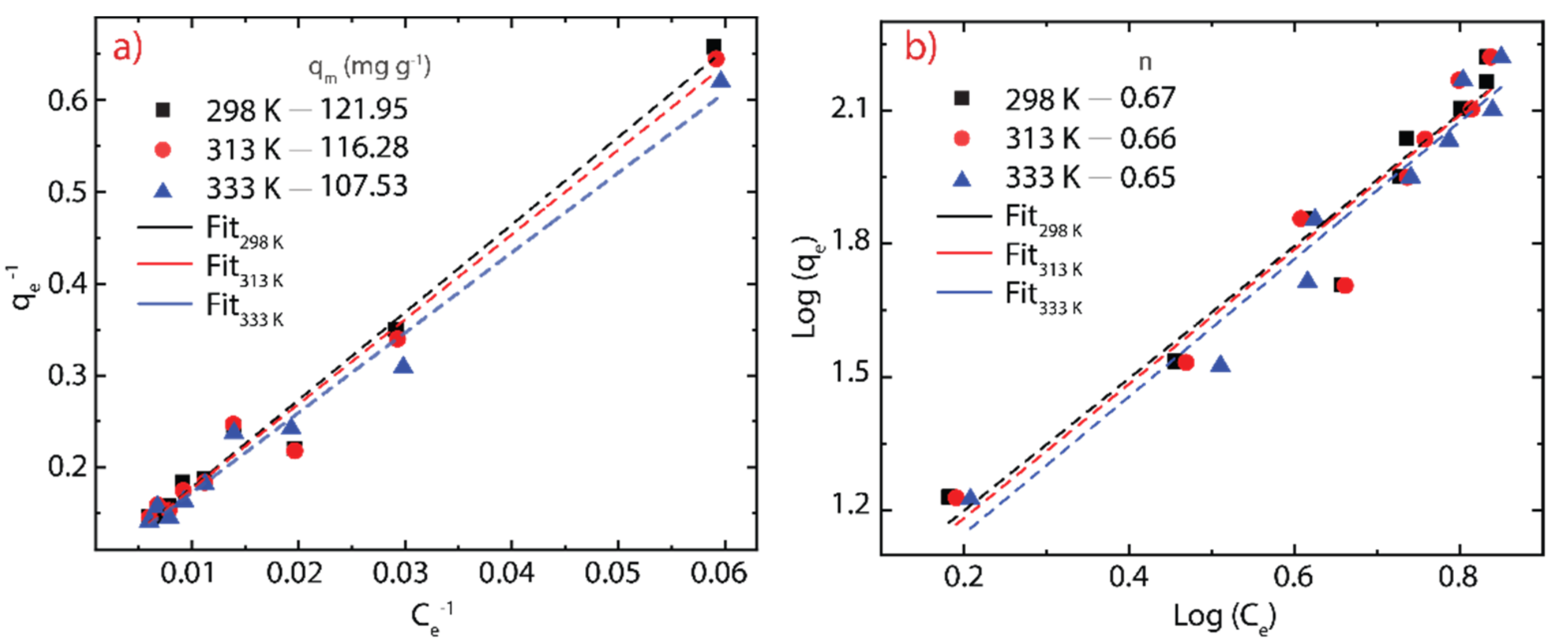
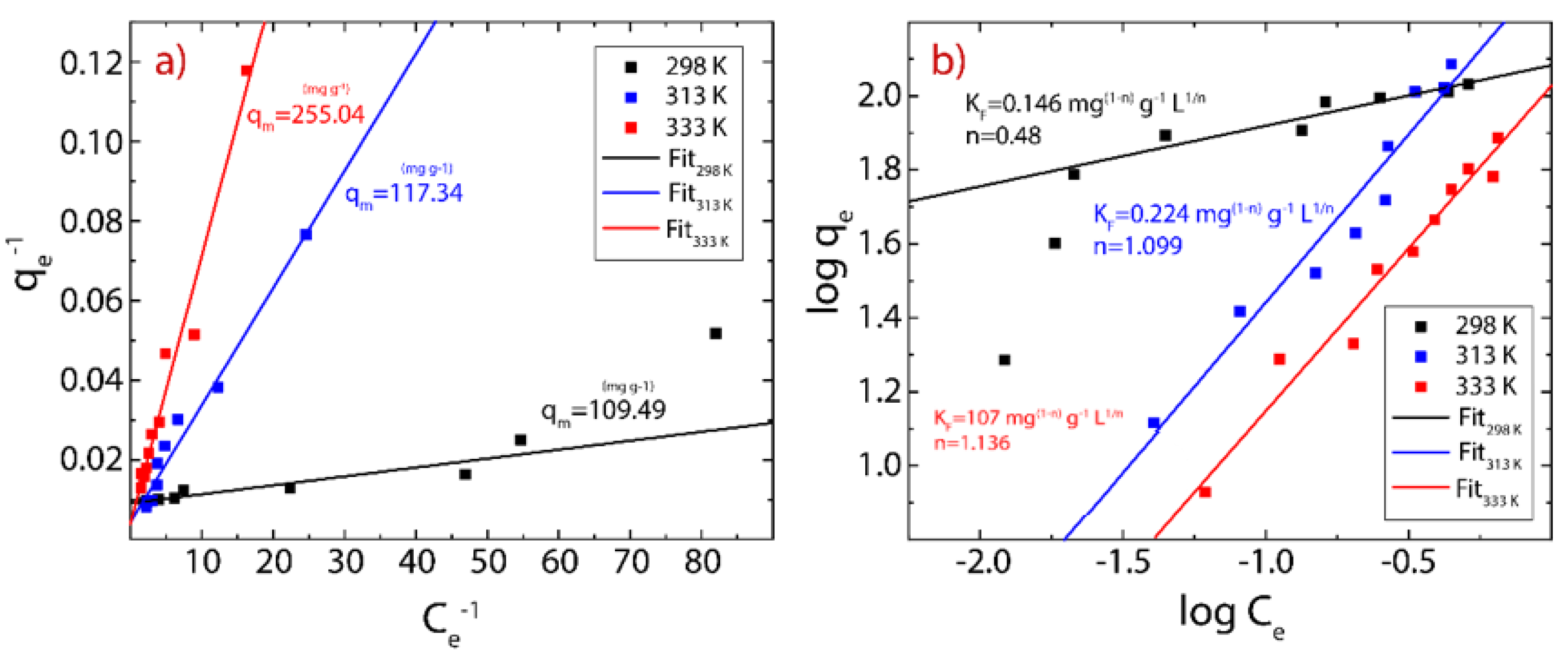
3.5. Adsorption Isotherms
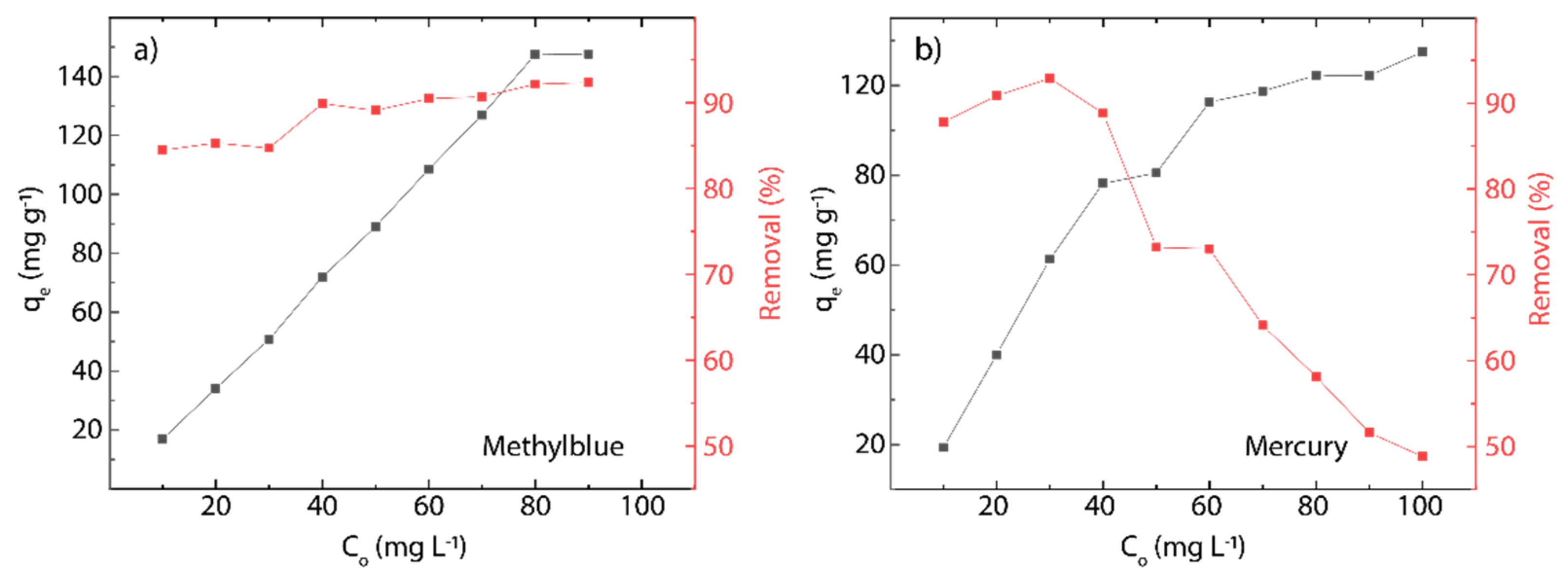
3.6. Effect of pH and Initial Concentration
3.7. Adsorption Thermodynamics
3.8. Final Remarks
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hairom, N.H.H.; Soon, C.F.; Mohamed, R.M.S.R.; Morsin, M.; Zainal, N.; Nayan, N.; Zulkifli, C.Z.; Harun, N.H. A review of nanotechnological applications to detect and control surface water pollution. Environ. Technol. Innov. 2021, 24, 102032. [Google Scholar] [CrossRef]
- Zamora-Ledezma, C.; Negrete-Bolagay, D.; Figueroa, F.; Zamora-Ledezma, E.; Ni, M.; Alexis, F.; Guerrero, V.H. Heavy metal water pollution: A fresh look about hazards, novel and conventional remediation methods. Environ. Technol. Innov. 2021, 22, 101504. [Google Scholar] [CrossRef]
- Benkhaya, S.; M’rabet, S.; El Harfi, A. Classifications, properties, recent synthesis and applications of azo dyes. Heliyon 2020, 6, e03271. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Lu, J.; Zhou, Y.; Liu, Y. Recent advances for dyes removal using novel adsorbents: A review. Environ. Pollut. 2019, 252, 352–365. [Google Scholar] [CrossRef] [PubMed]
- Ayodhya, D.; Venkatesham, M.; Santoshi Kumari, A.; Reddy, G.B.; Ramakrishna, D.; Veerabhadram, G. Photocatalytic degradation of dye pollutants under solar, visible and UV lights using green synthesised CuS nanoparticles. J. Exp. Nanosci. 2016, 11, 418–432. [Google Scholar] [CrossRef]
- Tang, A.Y.L.; Lo, C.K.Y.; Kan, C. Textile dyes and human health: A systematic and citation network analysis review. Color. Technol. 2018, 134, 245–257. [Google Scholar] [CrossRef]
- Zhang, D.; Tong, Z.; Zheng, W. Does designed financial regulation policy work efficiently in pollution control? Evidence from manufacturing sector in China. J. Clean. Prod. 2021, 289, 125611. [Google Scholar] [CrossRef]
- Fu, Z.; Xi, S. The effects of heavy metals on human metabolism. Toxicol. Mech. Methods 2020, 30, 167–176. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; Massey, I.Y.; Al Osman, M. Exposure routes and health effects of heavy metals on children. Biometals 2019, 32, 563–573. [Google Scholar]
- Efome, J.E.; Rana, D.; Matsuura, T.; Lan, C.Q. Experiment and modeling for flux and permeate concentration of heavy metal ion in adsorptive membrane filtration using a metal-organic framework incorporated nanofibrous membrane. Chem. Eng. J. 2018, 352, 737–744. [Google Scholar] [CrossRef]
- Da̧browski, A.; Hubicki, Z.; Podkościelny, P.; Robens, E. Selective removal of the heavy metal ions from waters and industrial wastewaters by ion-exchange method. Chemosphere 2004, 56, 91–106. [Google Scholar] [CrossRef] [PubMed]
- Arias, F.E.A.; Beneduci, A.; Chidichimo, F.; Furia, E.; Straface, S. Study of the adsorption of mercury (II) on lignocellulosic materials under static and dynamic conditions. Chemosphere 2017, 180, 11–23. [Google Scholar] [CrossRef]
- Al-Shannag, M.; Al-Qodah, Z.; Bani-Melhem, K.; Qtaishat, M.R.; Alkasrawi, M. Heavy metal ions removal from metal plating wastewater using electrocoagulation: Kinetic study and process performance. Chem. Eng. J. 2015, 260, 749–756. [Google Scholar] [CrossRef]
- Belkacem, M.; Khodir, M.; Abdelkrim, S. Treatment characteristics of textile wastewater and removal of heavy metals using the electroflotation technique. Desalination 2008, 228, 245–254. [Google Scholar] [CrossRef]
- Rajamani, A.R.; Ragula, U.B.R.; Kothurkar, N.; Rangarajan, M. Nano-and micro-hexagons of bismuth on polycrystalline copper: Electrodeposition and heavy metal sensing. Cryst. Eng. Comm. 2014, 16, 2032–2038. [Google Scholar] [CrossRef]
- Umapathi, R.; Ghoreishian, S.M.; Sonwal, S.; Rani, G.M.; Huh, Y.S. Portable electrochemical sensing methodologies for on-site detection of pesticide residues in fruits and vegetables. Coord. Chem. Rev. 2022, 453, 214305. [Google Scholar] [CrossRef]
- Umapathi, R.; Sonwal, S.; Lee, M.J.; Rani, G.M.; Lee, E.S.; Jeon, T.J.; Kang, S.M.; Oh, M.-H.; Huh, Y.S. Colorimetric based on-site sensing strategies for the rapid detection of pesticides in agricultural foods: New horizons, perspectives, and challenges. Coord. Chem. Rev. 2021, 446, 214061. [Google Scholar] [CrossRef]
- Cheng, T.-H.; Sankaran, R.; Show, P.L.; Ooi, C.W.; Liu, B.-L.; Chai, W.S.; Chang, Y.-K. Removal of protein wastes by cylinder-shaped NaY zeolite adsorbents decorated with heavy metal wastes. Int. J. Biol. Macromol. 2021, 185, 761–772. [Google Scholar] [CrossRef]
- Joo, G.; Lee, W.; Choi, Y. Heavy metal adsorption capacity of powdered Chlorella vulgaris biosorbent: Effect of chemical modification and growth media. Environ. Sci. Pollut. Res. 2021, 28, 25390–25399. [Google Scholar] [CrossRef]
- Sabir, A.; Altaf, F.; Batool, R.; Shafiq, M.; Khan, R.U.; Jacob, K.I. Agricultural Waste Absorbents for Heavy Metal Removal. In Green Adsorbents to Remove Metals, Dyes and Boron from Polluted Water; Springer: Berlin/Heidelberg, Germany, 2021; pp. 195–228. [Google Scholar]
- Penido, E.S.; de Oliveira, M.A.; Sales, A.L.R.; Ferrazani, J.C.; Magalhães, F.; Bianchi, M.L.; Melo, L.C.A. Biochars produced from various agro-industrial by-products applied in Cr (VI) adsorption-reduction processes. J. Environ. Sci. Health Part A 2021, 1–10. [Google Scholar] [CrossRef]
- Mariana, M.; HPS, A.K.; Mistar, E.M.; Yahya, E.B.; Alfatah, T.; Danish, M.; Amayreh, M. Recent advances in activated carbon modification techniques for enhanced heavy metal adsorption. J. Water Process Eng. 2021, 43, 102221. [Google Scholar] [CrossRef]
- Hoang, A.T.; Nižetić, S.; Cheng, C.K.; Luque, R.; Thomas, S.; Banh, T.L.; Pham, V.V.; Nguyen, X.P. Heavy metal removal by biomass-derived carbon nanotubes as a greener environmental remediation: A comprehensive review. Chemosphere 2021, 287, 131959. [Google Scholar] [CrossRef] [PubMed]
- Velusamy, S.; Roy, A.; Sundaram, S.; Kumar Mallick, T. A Review on Heavy Metal Ions and Containing Dyes Removal Through Graphene Oxide-Based Adsorption Strategies for Textile Wastewater Treatment. Chem. Rec. 2021, 21, 1570. [Google Scholar] [CrossRef] [PubMed]
- Arias Arias, F.; Guevara, M.; Tene, T.; Angamarca, P.; Molina, R.; Valarezo, A.; Salguero, O.; Vacacela Gomez, C.; Arias, M.; Caputi, L.S. The adsorption of methylene blue on eco-friendly reduced graphene oxide. Nanomaterials 2020, 10, 681. [Google Scholar] [CrossRef] [Green Version]
- Sindona, A.; Pisarra, M.; Gomez, C.V.; Riccardi, P.; Falcone, G.; Bellucci, S. Calibration of the fine-structure constant of graphene by time-dependent density-functional theory. Phys. Rev. B 2017, 96, 201408. [Google Scholar] [CrossRef]
- Villamagua, L.; Carini, M.; Stashans, A.; Gomez, C.V. Band gap engineering of graphene through quantum confinement and edge distortions. Ric. Mat. 2016, 65, 579–584. [Google Scholar] [CrossRef]
- Sindona, A.; Pisarra, M.; Bellucci, S.; Tene, T.; Guevara, M.; Gomez, C.V. Plasmon oscillations in two-dimensional arrays of ultranarrow graphene nanoribbons. Phys. Rev. B 2019, 100, 235422. [Google Scholar] [CrossRef]
- Gomez, C.V.; Pisarra, M.; Gravina, M.; Riccardi, P.; Sindona, A. Plasmon properties and hybridization effects in silicene. Phys. Rev. B 2017, 95, 85419. [Google Scholar] [CrossRef] [Green Version]
- Han, C.; Wang, X.; Peng, J.; Xia, Q.; Chou, S.; Cheng, G.; Huang, Z.; Li, W. Recent Progress on Two-Dimensional Carbon Materials for Emerging Post-Lithium (Na+, K+, Zn2+) Hybrid Supercapacitors. Polymers 2021, 13, 2137. [Google Scholar] [CrossRef]
- Fossum, J.; Lindholm, F.; Shibib, M. The importance of surface recombination and energy-bandgap arrowing in p-n-junction silicon solar cells. IEEE Trans. Electron Devices 1979, 26, 1294–1298. [Google Scholar] [CrossRef]
- Tene, T.; Guevara, M.; Valarezo, A.; Salguero, O.; Arias Arias, F.; Arias, M.; Scarcello, A.; Caputi, L.S.; Vacacela Gomez, C. Drying-Time Study in Graphene Oxide. Nanomaterials 2021, 11, 1035. [Google Scholar] [CrossRef] [PubMed]
- Tene, T.; Tubon Usca, G.; Guevara, M.; Molina, R.; Veltri, F.; Arias, M.; Caputi, L.S.; Vacacela Gomez, C. Toward Large-Scale Production of Oxidized Graphene. Nanomaterials 2020, 10, 279. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fiallos, D.C.; Gómez, C.V.; Tubon Usca, G.; Pérez, D.C.; Tavolaro, P.; Martino, G.; Caputi, L.S.; Tavolaro, A. Removal of acridine orange from water by graphene oxide. AIP Conf. Proc. 2015, 1646, 38–45. [Google Scholar]
- Sadeghi, M.H.; Tofighy, M.A.; Mohammadi, T. One-dimensional graphene for efficient aqueous heavy metal adsorption: Rapid removal of arsenic and mercury ions by graphene oxide nanoribbons (GONRs). Chemosphere 2020, 253, 126647. [Google Scholar] [CrossRef]
- Bao, S.; Wang, Y.; Yu, Y.; Yang, W.; Sun, Y. Cross-linked sulfydryl-functionalized graphene oxide as ultra-high capacity adsorbent for high selectivity and ppb level removal of mercury from water under wide pH range. Environ. Pollut. 2021, 271, 116378. [Google Scholar] [CrossRef]
- Sitko, R.; Musielak, M.; Serda, M.; Talik, E.; Zawisza, B.; Gagor, A.; Malecka, M. Thiosemicarbazide-grafted graphene oxide as superior adsorbent for highly efficient and selective removal of mercury ions from water. Sep. Purif. Technol. 2021, 254, 117606. [Google Scholar] [CrossRef]
- Li, M.; Wang, B.; Yang, M.; Li, Q.; Calatayud, D.G.; Zhang, S.; Wang, H.; Wang, L.; Mao, B. Promoting mercury removal from desulfurization slurry via S-doped carbon nitride/graphene oxide 3D hierarchical framework. Sep. Purif. Technol. 2020, 239, 116515. [Google Scholar] [CrossRef]
- Khorshidi, P.; Shirazi, R.H.S.M.; Miralinaghi, M.; Moniri, E.; Saadi, S. Adsorptive removal of mercury (II), copper (II), and lead (II) ions from aqueous solutions using glutathione-functionalized NiFe2O4/graphene oxide composite. Res. Chem. Intermed. 2020, 46, 3607–3627. [Google Scholar] [CrossRef]
- Yap, P.L.; Tung, T.T.; Kabiri, S.; Matulick, N.; Tran, D.N.H.; Losic, D. Polyamine-modified reduced graphene oxide: A new and cost-effective adsorbent for efficient removal of mercury in waters. Sep. Purif. Technol. 2020, 238, 116441. [Google Scholar] [CrossRef]
- Golden, P.J.; Weinstein, R. Treatment of high-risk, refractory acquired methemoglobinemia with automated red blood cell exchange. J. Clin. Apher. Off. J. Am. Soc. Apher. 1998, 13, 28–31. [Google Scholar] [CrossRef]
- Al-Saleh, I.; Moncari, L.; Jomaa, A.; Elkhatib, R.; Al-Rouqi, R.; Eltabache, C.; Al-Rajudi, T.; Alnuwaysir, H.; Nester, M.; Aldhalaan, H. Effects of early and recent mercury and lead exposure on the neurodevelopment of children with elevated mercury and/or developmental delays during lactation: A follow-up study. Int. J. Hyg. Environ. Health 2020, 230, 113629. [Google Scholar] [CrossRef]
- Gomez, C.V.; Guevara, M.; Tene, T.; Villamagua, L.; Usca, G.T.; Maldonado, F.; Tapia, C.; Cataldo, A.; Bellucci, S.; Caputi, L.S. The liquid exfoliation of graphene in polar solvents. Appl. Surf. Sci. 2021, 546, 149046. [Google Scholar] [CrossRef]
- Cayambe, M.; Zambrano, C.; Tene, T.; Guevara, M.; Usca, G.T.; Brito, H.; Molina, R.; Coello-Fiallos, D.; Caputi, L.S.; Gomez, C.V. Dispersion of graphene in ethanol by sonication. Mater. Today Proc. 2020, 37, 4027–4030. [Google Scholar] [CrossRef]
- Tubon Usca, G.; Vacacela Gomez, C.; Guevara, M.; Tene, T.; Hernandez, J.; Molina, R.; Tavolaro, A.; Miriello, D.; Caputi, L.S. Zeolite-Assisted Shear Exfoliation of Graphite into Few-Layer Graphene. Crystals 2019, 9, 377. [Google Scholar] [CrossRef] [Green Version]
- Vacacela Gomez, C.; Tene, T.; Guevara, M.; Tubon Usca, G.; Colcha, D.; Brito, H.; Molina, R.; Bellucci, S.; Tavolaro, A. Preparation of Few-Layer Graphene Dispersions from Hydrothermally Expanded Graphite. Appl. Sci. 2019, 9, 2539. [Google Scholar] [CrossRef] [Green Version]
- Pierantoni, L.; Mencarelli, D.; Bozzi, M.; Moro, R.; Moscato, S.; Perregrini, L.; Micciulla, F.; Cataldo, A.; Bellucci, S. Broadband microwave attenuator based on few layer graphene flakes. IEEE Trans. Microw. Theory Tech. 2015, 63, 2491–2497. [Google Scholar] [CrossRef]
- Maffucci, A.; Micciulla, F.; Cataldo, A.; Miano, G.; Bellucci, S. Bottom-up realization and electrical characterization of a graphene-based device. Nanotechnology 2016, 27, 095204. [Google Scholar] [CrossRef]
- Ivanov, E.; Velichkova, H.; Kotsilkova, R.; Bistarelli, S.; Cataldo, A.; Micciulla, F.; Bellucci, S. Rheological behavior of gra-phene/epoxy nanodispersions. Appl. Rheol. 2017, 27, 1–9. [Google Scholar]
- Bellucci, S.; Maffucci, A.; Maksimenko, S.; Micciulla, F.; Migliore, M.D.; Paddubskaya, A.; Pinchera, D.; Schettino, F. Electrical permittivity and conductivity of a graphene nanoplatelet contact in the microwave range. Materials 2018, 11, 2519. [Google Scholar] [CrossRef] [Green Version]
- Bellucci, S.; Bovesecchi, G.; Cataldo, A.; Coppa, P.; Corasaniti, S.; Potenza, M. Transmittance and reflectance effects during thermal diffusivity measurements of GNP samples with the flash method. Materials 2019, 12, 696. [Google Scholar] [CrossRef] [Green Version]
- Cataldo, A.; Biagetti, G.; Mencarelli, D.; Micciulla, F.; Crippa, P.; Turchetti, C.; Pierantoni, L.; Bellucci, S. Modeling and Electrochemical Characterization of Electrodes Based on Epoxy Composite with Functionalized Nanocarbon Fillers at High Concentration. Nanomaterials 2020, 10, 850. [Google Scholar] [CrossRef]
- Cabrera, H.; Korte, D.; Budasheva, H.; Abbasgholi, N.A.B.; Bellucci, S. Through-Plane and In-Plane Thermal Diffusivity Determination of Graphene Nanoplatelets by Photothermal Beam Deflection Spectrometry. Materials 2021, 14, 7273. [Google Scholar] [CrossRef]
- Gomez, C.V.; Robalino, E.; Haro, D.; Tene, T.; Escudero, P.; Haro, A.; Orbe, J. Structural and electronic properties of graphene oxide for different degree of oxidation. Mater. Today Proc. 2016, 3, 796–802. [Google Scholar] [CrossRef]
- Ofomaja, A.E.; Naidoo, E.B.; Pholosi, A. Intraparticle diffusion of Cr (VI) through biomass and magnetite coated biomass: A comparative kinetic and diffusion study. S. Afr. J. Chem. Eng. 2020, 32, 39–55. [Google Scholar]
- Oliva, J.; Martinez, A.I.; Oliva, A.I.; Garcia, C.R.; Martinez-Luevanos, A.; Garcia-Lobato, M.; Ochoa-Valiente, R.; Berlanga, A. Flexible graphene composites for removal of methylene blue dye-contaminant from water. Appl. Surf. Sci. 2018, 436, 739–746. [Google Scholar] [CrossRef]
- Ma, Y.-X.; Shao, W.-J.; Sun, W.; Kou, Y.-L.; Li, X.; Yang, H.-P. One-step fabrication of $β$-cyclodextrin modified magnetic graphene oxide nanohybrids for adsorption of Pb (II), Cu (II) and methylene blue in aqueous solutions. Appl. Surf. Sci. 2018, 459, 544–553. [Google Scholar] [CrossRef]
- Zhu, B.; Xia, P.; Ho, W.; Yu, J. Isoelectric point and adsorption activity of porous g-C3N4. Appl. Surf. Sci. 2015, 344, 188–195. [Google Scholar] [CrossRef]
- Su, H.; Li, W.; Han, Y.; Liu, N. Magnetic carboxyl functional nanoporous polymer: Synthesis, characterization and its application for methylene blue adsorption. Sci. Rep. 2018, 8, 6506. [Google Scholar] [CrossRef] [Green Version]
- Wu, M.; Li, Y.; Yue, R.; Zhang, X.; Huang, Y. Removal of silver nanoparticles by mussel-inspired Fe3O4@polydopamine core-shell microspheres and its use as efficient catalyst for methylene blue reduction. Sci. Rep. 2017, 7, 42773. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wijaya, R.; Andersan, G.; Santoso, S.P.; Irawaty, W. Green reduction of graphene oxide using kaffir lime peel extract (Citrus hystrix) and its application as adsorbent for methylene blue. Sci. Rep. 2020, 10, 667. [Google Scholar] [CrossRef]




| Parameters | MB | Hg(II) |
|---|---|---|
| qe(exp) (mg g−1) | 68.21 | 142.26 |
| Pseudo-first-order model | ||
| qe (mg g−1) | 69.82 ± 0.05 | 143.70 ± 5.70 |
| k1 (min−1) | 2.166 ± 0.03 | 0.19 ± 0.03 |
| SSE | 13.38 | 1826 |
| R2 | 0.997 | 0.949 |
| RMSE | 1.157 | 8.546 |
| Pseudo-second-order model | ||
| qe (mg g−1) | 70.72 ± 0.08 | 158.30 ± 9.45 |
| k2 (g mg−1 min−1) | 0.075 ± 0.005 | 0.002 ± 0.001 |
| SSE | 5.239 | 2480 |
| R2 | 0.999 | 0.931 |
| RMSE | 0.724 | 9.960 |
| MB | Hg(II) | |
|---|---|---|
| Parameters | Value | Value |
| Kp (mg g−1 min−1/2) | 2.95 ± 0.67 | 7.82 ± 1.25 |
| C (mg g−1) | 59.17 ± 1.75 | 44.28 ± 7.75 |
| Ri | 0.132 | 0.69 |
| R2 | 0.829 | 0.963 |
| T (K) | Langmuir Model | Freundlich Model | ||||
|---|---|---|---|---|---|---|
| KL (L g−1) | qm(cal) (mg g−1) | R2 | KF (mg(1-n) g−1 L1/n) | n | R2 | |
| 298 | 0.079 | 121.95 | 0.982 | 7.956 | 0.671 | 0.945 |
| 313 | 0.081 | 116.28 | 0.980 | 7.568 | 0.661 | 0.936 |
| 333 | 0.082 | 107.53 | 0.984 | 6.869 | 0.646 | 0.955 |
| T (K) | Langmuir Model | Freundlich Model | ||||
|---|---|---|---|---|---|---|
| KL (L g−1) | qm(cal) (mg g−1) | R2 | KF (mg(1-n) g−1 L1/n) | n | R2 | |
| 298 | 0.047 | 109.493 | 0.934 | 0.146 | 0.480 | 0.918 |
| 313 | 0.017 | 217.344 | 0.973 | 0.224 | 1.099 | 0.947 |
| 333 | 0.006 | 255.037 | 0.968 | 0.107 | 1.136 | 0.956 |
| T (K) | |||
|---|---|---|---|
| MB | |||
| 298 | −22.75 | −2.20 | 0.069 |
| 313 | −23.81 | ||
| 333 | −25.16 | ||
| Hg(II) | |||
| 298 | −39.84 | −0.14 | 0.079 |
| 313 | −31.55 | ||
| 333 | −32.97 | ||
| MB | Hg(II) | ||
|---|---|---|---|
| Adsorbents | Adsorption Capacity (mg g−1) | Adsorbents | Adsorption Capacity (mg g−1) |
| Graphene/SrAl2O3:Bi3+ [56] | 42.93 | GONR [35] | 33.02 |
| ß-cyclodextrin/MGO [57] | 93.97 | S-GO [36] | 3490 |
| g-C3N4 (Urea) [58] | 2.51 | GO-TSC [37] | 231 |
| Magnetic carboxyl functional nanoporous polymer [59] | 57.74 | S-doped g-C3N4/LGO [38] | 46 |
| Ag-Fe3O4-polydopamine [60] | 45.00 | GSH-NiFe2O4/GO [39] | 272.94 |
| Citrus hystrix-rGO [61] | 276.06 | HT-rGO-N [40] | 75.8 |
| This work | 121.95 | This work | 109.49 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tene, T.; Bellucci, S.; Guevara, M.; Viteri, E.; Arias Polanco, M.; Salguero, O.; Vera-Guzmán, E.; Valladares, S.; Scarcello, A.; Alessandro, F.; et al. Cationic Pollutant Removal from Aqueous Solution Using Reduced Graphene Oxide. Nanomaterials 2022, 12, 309. https://doi.org/10.3390/nano12030309
Tene T, Bellucci S, Guevara M, Viteri E, Arias Polanco M, Salguero O, Vera-Guzmán E, Valladares S, Scarcello A, Alessandro F, et al. Cationic Pollutant Removal from Aqueous Solution Using Reduced Graphene Oxide. Nanomaterials. 2022; 12(3):309. https://doi.org/10.3390/nano12030309
Chicago/Turabian StyleTene, Talia, Stefano Bellucci, Marco Guevara, Edwin Viteri, Malvin Arias Polanco, Orlando Salguero, Eder Vera-Guzmán, Sebastián Valladares, Andrea Scarcello, Francesca Alessandro, and et al. 2022. "Cationic Pollutant Removal from Aqueous Solution Using Reduced Graphene Oxide" Nanomaterials 12, no. 3: 309. https://doi.org/10.3390/nano12030309
APA StyleTene, T., Bellucci, S., Guevara, M., Viteri, E., Arias Polanco, M., Salguero, O., Vera-Guzmán, E., Valladares, S., Scarcello, A., Alessandro, F., Caputi, L. S., & Vacacela Gomez, C. (2022). Cationic Pollutant Removal from Aqueous Solution Using Reduced Graphene Oxide. Nanomaterials, 12(3), 309. https://doi.org/10.3390/nano12030309












