EMHD Nanofluid Flow with Radiation and Variable Heat Flux Effects along a Slandering Stretching Sheet
Abstract
1. Introduction
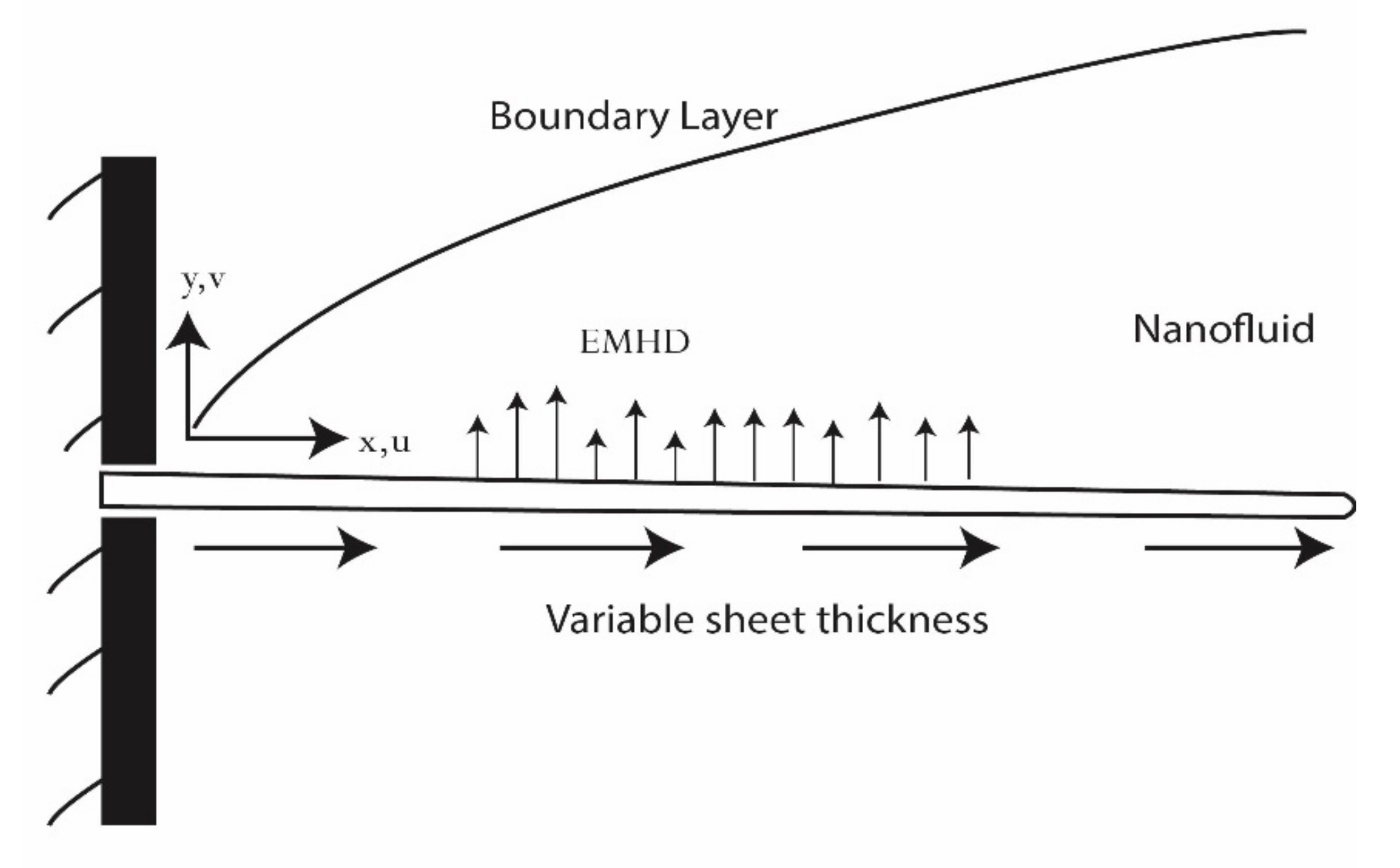
2. Problem Formulation
3. Thermo-Physical Properties
4. Physical Quantities
5. Numerical Method
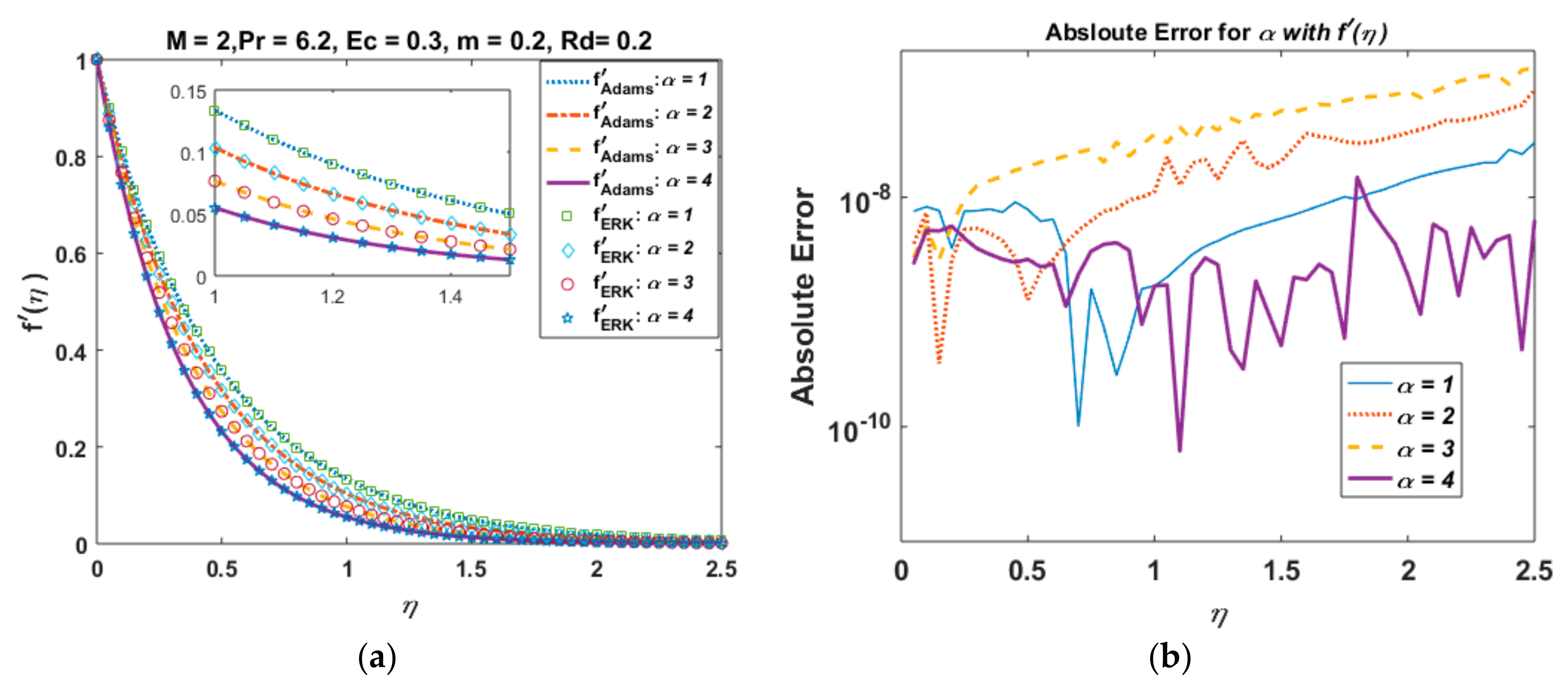
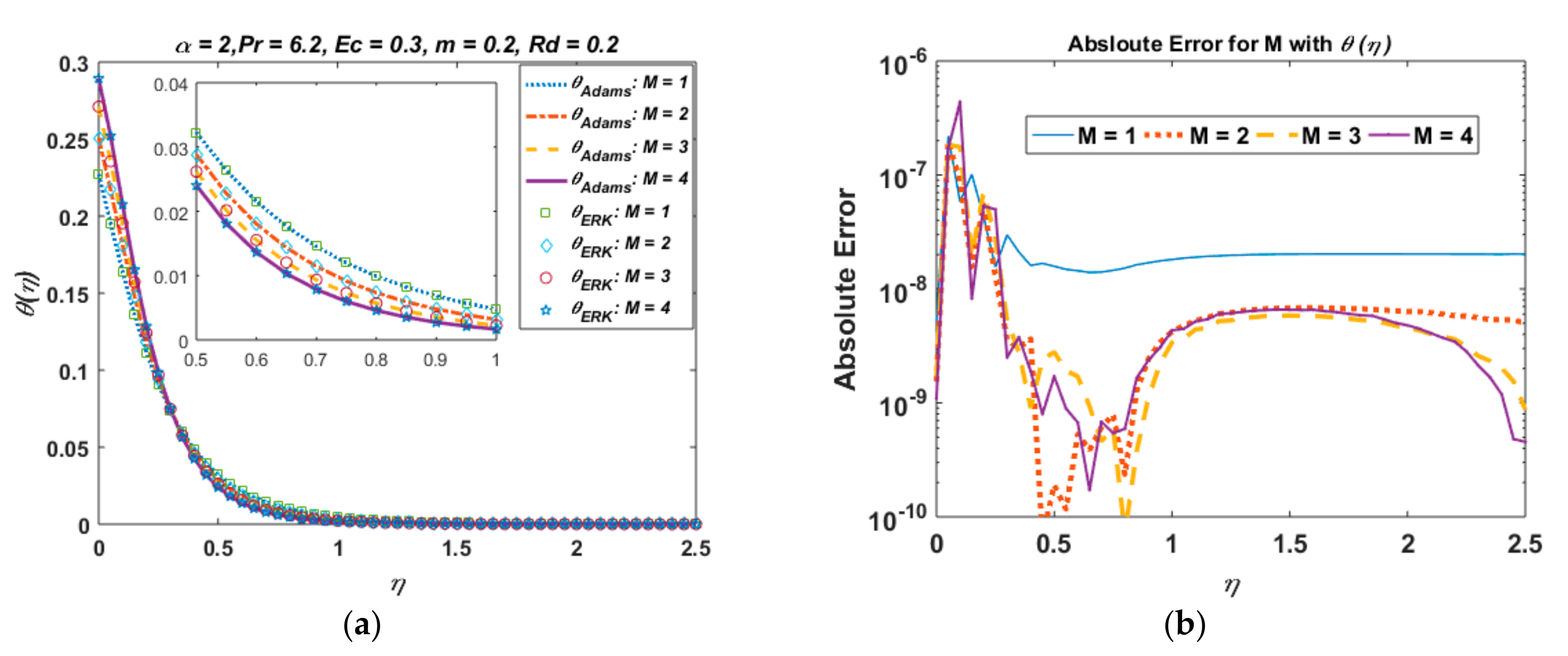
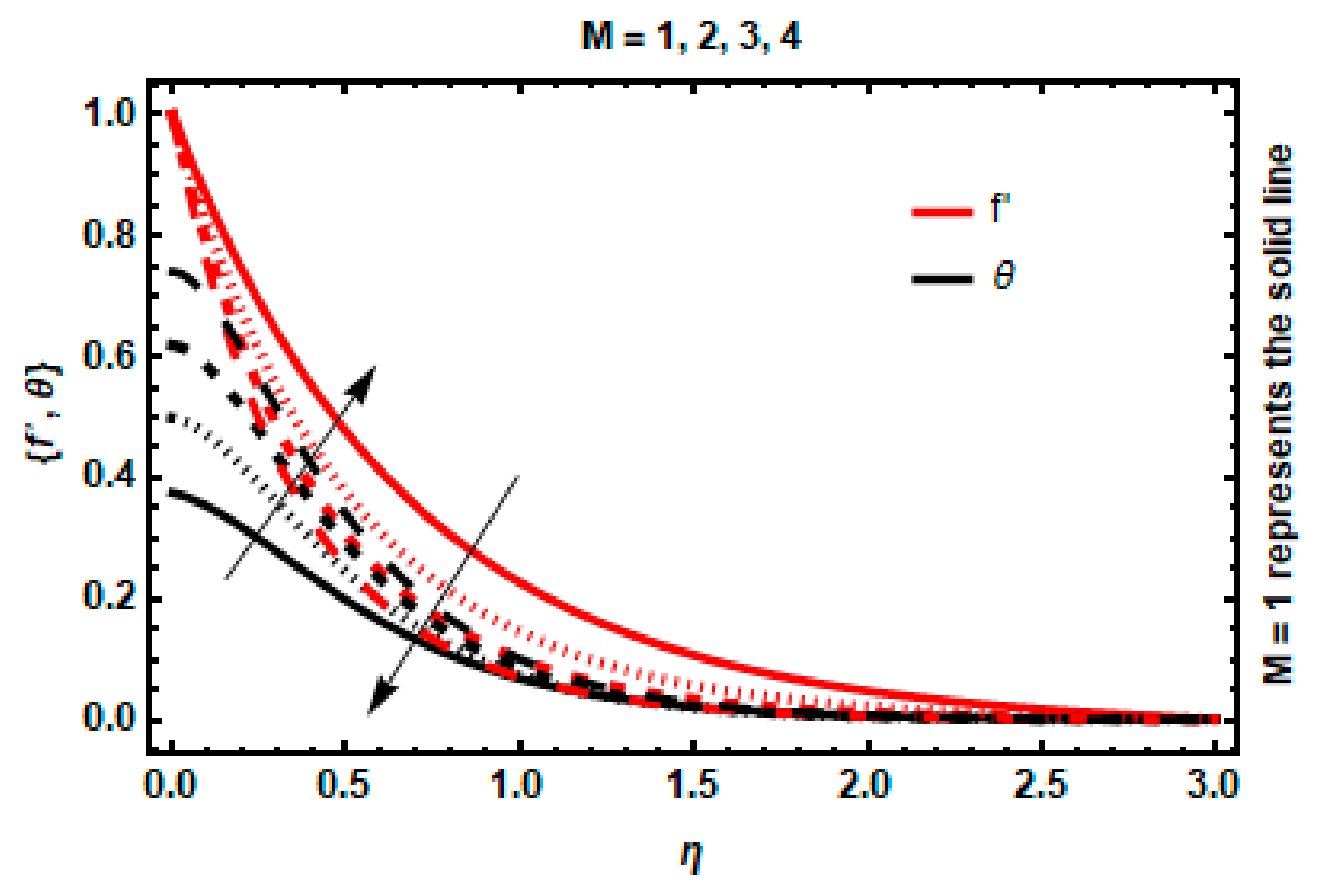
6. Graphical Analysis
7. Conclusions
- The fluid’s velocity, as well as the temperature of the nanofluid, increase when the velocity power index increases.
- By increasing the wall thickness parameter, the fluid’s velocity and temperature are reduced.
- As the temperature rises, both the fluid velocity decreases and the Hartmann number decrease.
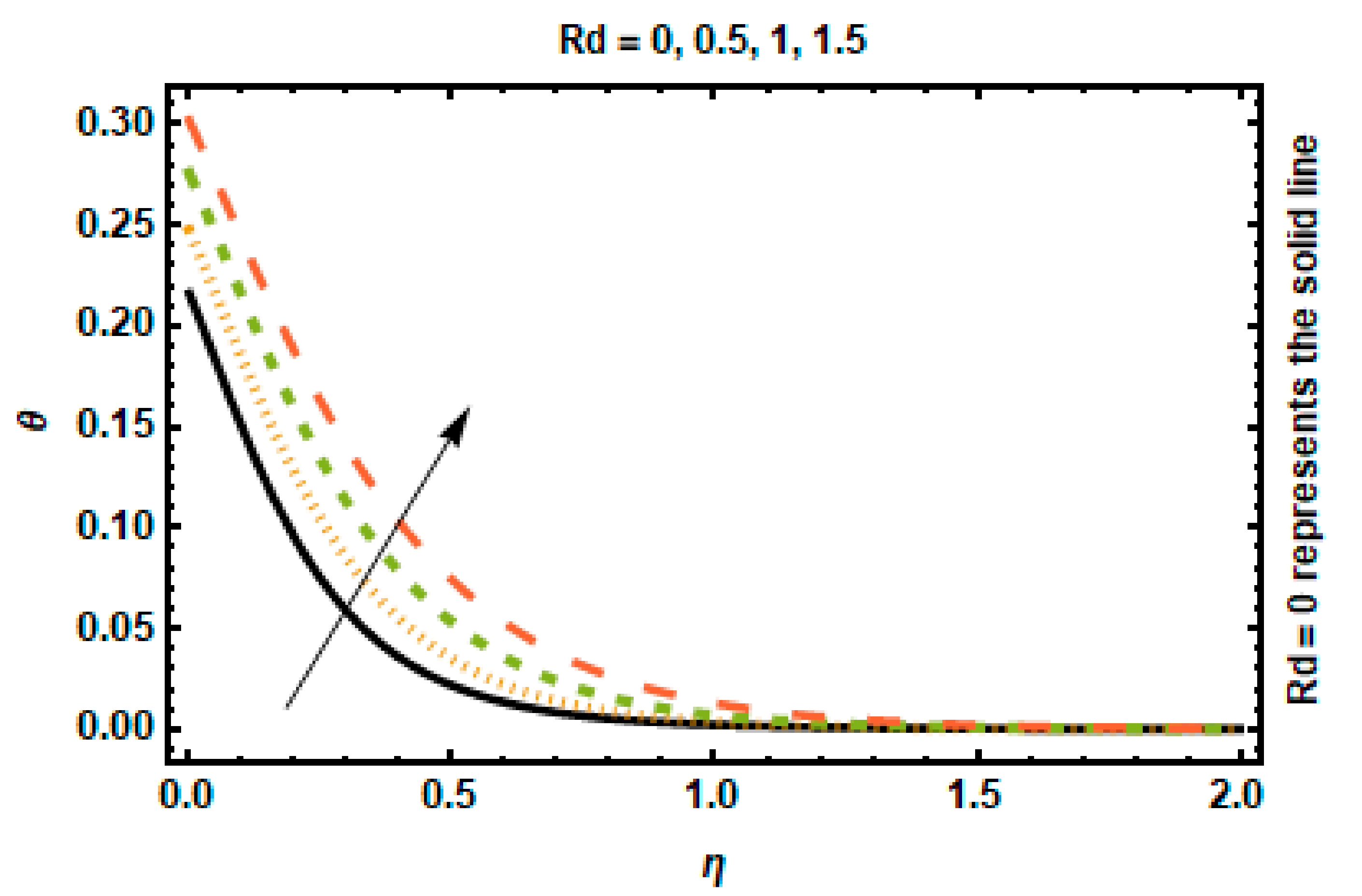
- By raising the heat transfer Biot number, thermal radiation parameter, and viscous dissipation parameter, the fluid’s temperature rises.
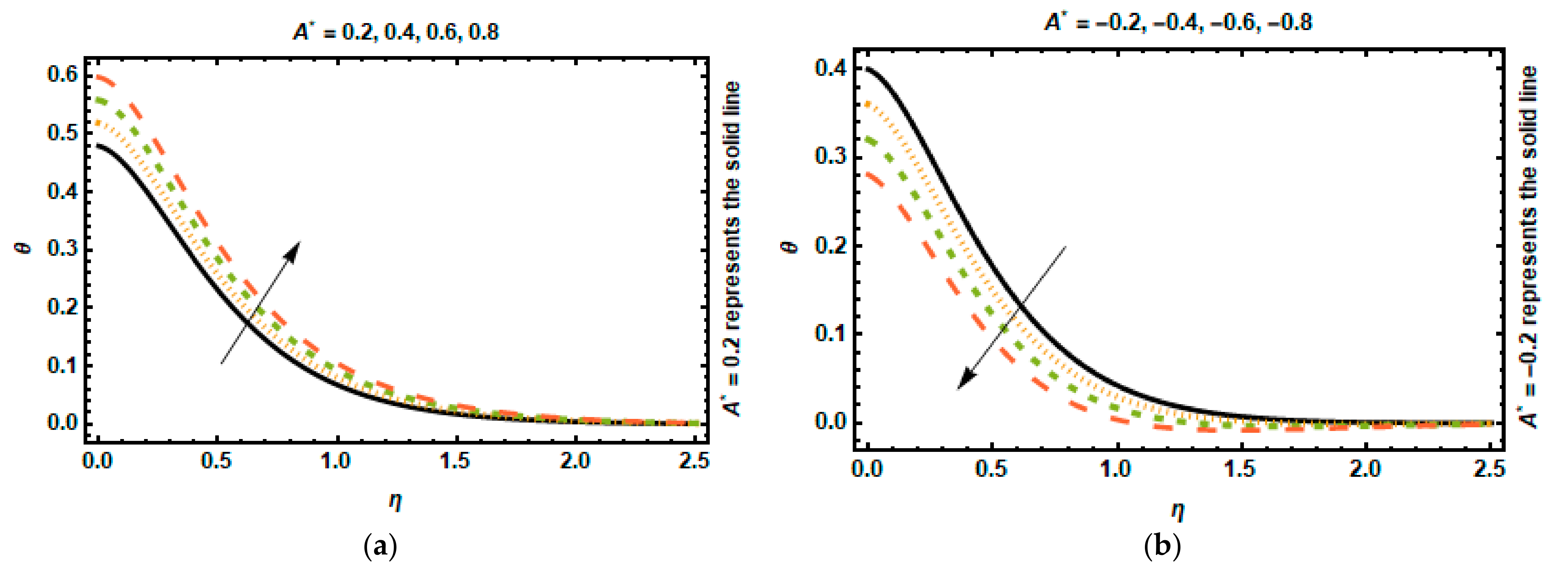
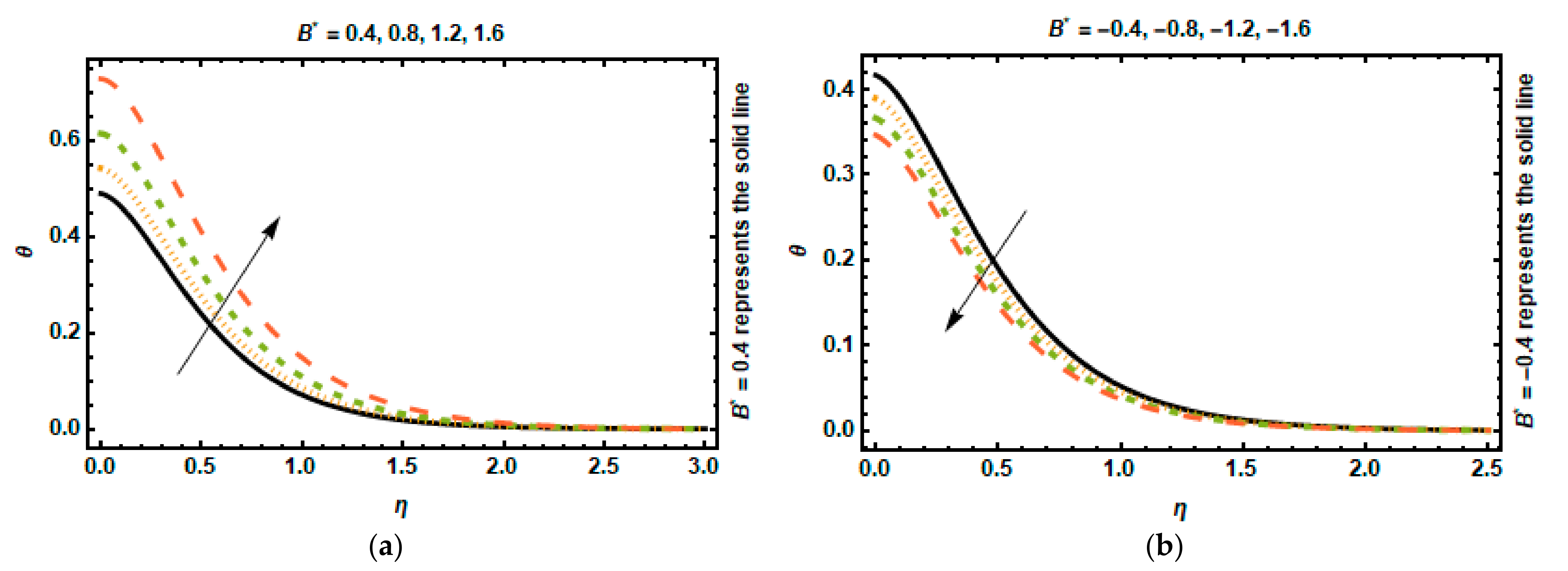
- When the positive values increase, the impact of the space-dependent and time-dependent heat generation and absorption parameters generates heat and absorbs temperature when the negative values decrease.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Magnetic field strength () | |
| Electric field strength () | |
| M | Magnetic field parameter |
| Electric field parameter | |
| Fluid temperature () | |
| Surface temperature () | |
| Free stream temperature () | |
| Heat capacity () | |
| Rd | Radiation parameter |
| Prandtl number | |
| Biot number | |
| Eckert number | |
| Wall thickness parameter | |
| Radiative heat flux () | |
| Mean absorption coefficient | |
| n | Velocity power index parameter |
| Variable viscosity parameter | |
| Components of velocity () | |
| N | Co-efficient related to stretching sheet |
| Space-dependent co-efficient | |
| Time-dependent co-efficient | |
| Greek symbol | |
| Dimensionless temperature () | |
| Density () | |
| Kinematic viscosity () | |
| Dynamic viscosity () | |
| Electric conductivity () | |
| Stefan–Boltzmann constant () | |
| Thermal conductivity () | |
| Non-dimensional similarity variable | |
| Stretching velocity () | |
| Subscript | |
| Nanofluid | |
| Base fluid |
References
- Sakiadis, B.C. Boundary layer behavior on a continuous solid surface: I. Boundary layer equations for two-dimensional and asymmetric flow. Am. Inst. Chem. Eng. (AIChE) J. 1961, 7, 26–28. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. Z. Für Angew. Math. Und Phys. (ZAMP) 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Vajravelu, K.; Rollins, D. Heat transfer in a viscoelastic fluid over a stretching sheet. J. Math. Anal. Appl. 1991, 158, 241–255. [Google Scholar] [CrossRef]
- Vajravelu, K.; Cannon, J.R. Fluid flow over a nonlinear stretching sheet. Appl. Math. Comput. 2006, 181, 609–618. [Google Scholar]
- Lee, L.L. Boundary layer over a thin needle. Phys. Fluids 1967, 10, 820. [Google Scholar] [CrossRef]
- Gupta, P.S.; Gupta, A.S. Heat and mass transfer on a stretching sheet with suction or blowing. Can. J. Chem. Eng. 1977, 55, 744–746. [Google Scholar] [CrossRef]
- Cortell, R. Viscous flow and heat transfer over a nonlinearly stretching sheet. Appl. Math. Comput. 2007, 184, 864–873. [Google Scholar] [CrossRef]
- Fang, T.; Zhang, J.; Zhong, Y. Boundary layer flow over a stretching sheet with variable thickness. Appl. Math. Comput. 2012, 218, 7241–7252. [Google Scholar] [CrossRef]
- Khader, M.M.; Megahed, A.M. Numerical solution for boundary layer flow due to a nonlinearly stretching sheet with variable thickness and slip velocity. Eur. Phys. J. Plus 2013, 128, 100. [Google Scholar] [CrossRef]
- Elbashbeshy, E.M.A.; Asker, H.G.; Abdelgaberc, K.M.; Sayed, E.A. Heat transfer over a stretching surface with variable thickness embedded in porous medium in the presence of Maxwell fluid. J. Appl. Mech. Eng. 2018, 7, 307. [Google Scholar] [CrossRef]
- Ali, A.; Maqsood, M.; Anjum, H.J.; Awais, M.; Sulaiman, M. Analysis of heat transfer on MHD Jeffrey nanofluid flow over nonlinear elongating surface of variable thickness. Z. Für Angew. Math. Und Mech. (ZAMM) 2022, 102, e202100250. [Google Scholar] [CrossRef]
- Choi, S.U.S. Enhancing thermal conductivity of fluids with nanoparticles. In Proceedings of the 1995 ASME International Mechanical Engineering Congress and Exposition, San Francisco, CA, USA, 12–17 November 1995; Volume 66, pp. 99–105. [Google Scholar]
- Khan, W.A.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Nadeem, S.; Lee, C. Boundary layer flow of nanofluid over an exponentially stretching surface. Nanoscale Res. Lett. 2012, 7, 94. [Google Scholar] [CrossRef] [PubMed]
- Malvandi, A.; Hedayati, F.; Ganji, D. Slip effects on unsteady stagnation point flow of a nanofluid over a stretching sheet. Powder Technol. 2014, 253, 377–384. [Google Scholar] [CrossRef]
- Khan, J.A.; Mustafa, M.; Hayat, T.; Sheikholeslami, M.; Alsaedi, A. Three-Dimensional Flow of Nanofluid Induced by an Exponentially Stretching Sheet: An Application to Solar Energy. PLoS ONE 2015, 10, e0116603. [Google Scholar] [CrossRef]
- Ali, A.; Shehzadi, K.; Sulaiman, M.; Asghar, S. Heat and mass transfer analysis of 3D Maxwell nanofluid over an exponentially stretching surface. Phys. Scr. 2019, 94, 065206. [Google Scholar] [CrossRef]
- Bognár, G.; Klazly, M.; Hriczó, K. Nanofluid flow past a stretching plate. Processes 2020, 8, 827. [Google Scholar] [CrossRef]
- Ali, A.; Akhtar, J.; Anjum, H.; Awais, M.; Shah, Z.; Kumam, P. 3D nanofluid flow over exponentially expanding surface of Oldroyd-B fluid. Ain Shams Eng. J. 2021, 12, 3939–3946. [Google Scholar]
- Alazwari, M.A.; Abu-Hamdeh, N.H.; Goodarzi, M. Entropy Optimization of First-Grade Viscoelastic Nanofluid Flow over a Stretching Sheet by Using Classical Keller-Box Scheme. Mathematics 2021, 9, 2563. [Google Scholar] [CrossRef]
- Aouinet, H.; Dhahri, M.; Safaei, M.R.; Sammouda, H.; Anqi, A.E. Turbulent boundary layers and hydrodynamic flow analysis of nanofluids over a plate. J. Cent. South Univ. 2021, 28, 3340–3353. [Google Scholar] [CrossRef]
- Waqas, H.; Farooq, U.; Alshehri, H.M.; Goodarzi, M. Marangoni-bioconvectional flow of Reiner–Philippoff nanofluid with melting phenomenon and nonuniform heat source/sink in the presence of a swimming microorganisms. Math. Methods Appl. Sci. 2021. [Google Scholar] [CrossRef]
- Imran, M.; Farooq, U.; Waqas, H.; Anqi, A.E.; Safaei, M.R. Numerical performance of thermal conductivity in Bioconvection flow of cross nanofluid containing swimming microorganisms over a cylinder with melting phenomenon. Case Stud. Therm. Eng. 2021, 26, 101181. [Google Scholar] [CrossRef]
- Maleki, H.; Safaei, M.R.; Alrashed, A.A.A.A.; Kasaeian, A. Flow and heat transfer in non-Newtonian nanofluids over porous surfaces. J. Therm. Anal. Calorim. 2019, 135, 1655–1666. [Google Scholar] [CrossRef]
- Rasool, G.; Wakif, A. Numerical spectral examination of EMHD mixed convective flow of second-grade nanofluid towards a vertical Riga plate using an advanced version of the revised Buongiorno’s nanofluid model. J. Therm. Anal. Calorim. 2021, 143, 2379–2393. [Google Scholar] [CrossRef]
- Lacobazzi, F.; Milanese, M.; Colangelo, G.; Risi, A.D. A critical analysis of clustering phenomenon in Al2O3 nanofluids. J. Therm. Anal. Calorim. 2019, 135, 371–377. [Google Scholar] [CrossRef]
- Colangelo, G.; Diamante, N.F.; Milanese, M.; Starace, G.; Risi, A.D. Critical Review of Experimental Investigations about Convective Heat Transfer Characteristics of Nanofluids under Turbulent and Laminar Regimes with a Focus on the Experimental Setup. Energies 2021, 14, 6004. [Google Scholar] [CrossRef]
- Colangelo, G.; Favale, E.; Milanese, M.; Starace, G.; De Risi, A. Experimental Measurements of Al2O3 and CuO Nanofluids Interaction with Microwaves. J. Energy Eng. 2017, 143, 04016045. [Google Scholar] [CrossRef]
- Alfven, H. Existence of electromagnetic-hydrodynamic waves. Nature 1942, 150, 405–406. [Google Scholar] [CrossRef]
- Ishak, A.; Nazar, R.; Pop, I. Hydromagnetic flow and heat transfer adjacent to a stretching vertical sheet. Heat Mass Transf. 2008, 44, 921. [Google Scholar] [CrossRef]
- Ibrahim, W.; Shankar, B. MHD boundary layer flow and heat transfer of a nanofluid past a permeable stretching sheet with velocity, thermal and solutal slip boundary conditions. Comput. Fluids 2013, 75, 1–10. [Google Scholar] [CrossRef]
- Babu, M.J.; Sandeep, N. MHD non-Newtonian fluid flow over a slandering stretching sheet in the presence of cross diffusion effects. Alex. Eng. J. 2016, 55, 2193–2201. [Google Scholar] [CrossRef]
- Daniel, Y.S.; Aziz, Z.A.; Ismail, Z.; Salah, F. Impact of thermal radiation on electrical MHD flow of nanofluid over nonlinear stretching sheet with variable thickness. Alex. Eng. J. 2018, 57, 2187–2197. [Google Scholar] [CrossRef]
- Adem, G.A. Analytic treatment for Electrical MHD Non-Newtonian fluid flow over a stretching sheet through a porous medium. Adv. Math. Phys. 2020, 2020, 8879264. [Google Scholar] [CrossRef]
- Ali, L.; Ali, B.; Ghori, M.B. Melting effect on Cattaneo-Christov and thermal radiation features for aligned MHD nanofluid flow comprising microorganisms to leading edge: FEM approach. Comput. Math. Appl. 2022, 109, 260–269. [Google Scholar] [CrossRef]
- Souayeh, B.; Ramesh, K.; Hdhiri, N.; Tasin, E.; Alam, M.W.; Alfares, K.; Yasin, A. Heat Transfer Attributes of Gold–Silver–Blood Hybrid Nanomaterial Flow in an EMHD Peristaltic Channel with Activation Energy. Nanomaterials 2022, 12, 1615. [Google Scholar] [CrossRef]
- Abel, M.S.; Mahesha, N. Heat transfer in MHD viscoelastic fluid flow over a stretching sheet with variable thermal conductivity, non-uniform heat source and radiation. Appl. Math. Model. 2008, 32, 1965–1983. [Google Scholar] [CrossRef]
- Mukhopadhyay, S. Slip effects on MHD boundary layer flow over an exponentially stretching sheet with suction/blowing and thermal radiation. Ain Shams Eng. J. 2013, 4, 485–491. [Google Scholar] [CrossRef]
- Ahmad, I.; Sajid, M.; Awan, W.; Rafique, M.; Aziz, W.; Ahmed, M.; Abbasi, A.; Taj, M. MHD flow of a viscous fluid over an exponentially stretching sheet in a porous medium. J. Appl. Math. 2014, 2014, 256761. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D.; Javed, M.Y.; Ellahi, R. Effect of thermal radiation on magnetohydrodynamics nanofluid flow and heat transfer by means of two phase model. J. Magn. Magn. Mater. 2015, 374, 36–43. [Google Scholar] [CrossRef]
- Krishna, P.M.; Sandeep, N.; Sharma, R.P.; Makinde, O.D. Thermal radiation effect on 3D slip motion of Alcu-Water and Cu-Water nanofluids over a variable thickness stretched surface. Defect Diffus. Forum 2017, 377, 141–154. [Google Scholar] [CrossRef]
- Khan, H.; Haneef, M.; Shah, Z.; Islam, S.; Khan, W.; Muhammad, S. The combined magneto hydrodynamic and electric field effect on an unsteady Maxwell nanofluid flow over a stretching surface under the influence of variable heat and thermal radiation. Appl. Sci. 2018, 8, 160. [Google Scholar] [CrossRef]
- Jamshed, W.; Devi, S.U.; Goodarzi, M.; Prakash, M.; Nisar, K.S.; Zakarya, M.; Abdel-Aty, A.H. Evaluating the unsteady Casson nanofluid over a stretching sheet with solar thermal radiation: An optimal case study. Case Stud. Therm. Eng. 2021, 26, 101160. [Google Scholar] [CrossRef]
- Waqas, H.; Farooq, U.; Khan, S.A.; Alshehri, H.M.; Goodarzi, M. Numerical analysis of dual variable of conductivity in bioconvection flow of Carreau–Yasuda nanofluid containing gyrotactic motile microorganisms over a porous medium. J. Therm. Anal. Calorim. 2021, 145, 2033–2044. [Google Scholar] [CrossRef]
- Kumar, P.; Poonia, H.; Ali, L.; Areekara, S. The numerical simulation of nanoparticle size and thermal radiation with the magnetic field effect based on tangent hyperbolic nanofluid flow. Case Stud. Therm. Eng. 2022, 37, 102247. [Google Scholar] [CrossRef]
- Hsiao, K.L. Stagnation electrical MHD nanofluid mixed convection with slip boundary on a stretching sheet. Appl. Therm. Eng. 2016, 98, 850–861. [Google Scholar] [CrossRef]
- Sharma, K.; Gupta, S. Viscous dissipation and thermal radiation effects in MHD flow of Jeffery nanofluid through impermeable surface with heat generation/absorption. Nonlinear Eng. 2017, 6, 153–166. [Google Scholar] [CrossRef]
- Shahzad, F.; Sagheer, M.; Hussain, S. Numerical simulation of magnetohydrodynamic Jeffrey nanofluid flow and heat transfer over a stretching sheet considering Joule heating and viscous dissipation. AIP Adv. 2018, 8, 065316. [Google Scholar] [CrossRef]
- Kumar, K.G.; Ramesh, G.K.; Gireesha, B.J.; Gorla, R.S.R. Characteristics of Joule heating and viscous dissipation on three-dimensional flow of Oldroyd B nanofluid with thermal radiation. Alex. Eng. J. 2018, 57, 2139–2149. [Google Scholar] [CrossRef]
- Muhammad, T.; Hayat, T.; Shehzad, S.A.; Alsaedi, A. Viscous dissipation and Joule heating effects in MHD 3D flow with heat and mass fluxes. Results Phys. 2018, 8, 365–371. [Google Scholar] [CrossRef]
- Maleki, H.; Alsarraf, J.; Moghanizadeh, A.; Hajabdollahi, H.; Safai, M.R. Heat transfer and nanofluid flow over a porous plate with radiation and slip boundary conditions. J. Cent. South Univ. 2019, 26, 1099–1115. [Google Scholar] [CrossRef]
- Maleki, H.; Safaei, M.R.; Togun, H.; Dahari, M. Heat transfer and fluid flow of pseudo-plastic nanofluid over a moving permeable plate with viscous dissipation and heat absorption/generation. J. Therm. Anal. Calorim. 2019, 135, 1643–1654. [Google Scholar] [CrossRef]
- Zeeshan, A.; Shehzad, N.; Abbas, T.; Ellahi, R. Effects of radiative electro-magnetohydrodynamics diminishing internal energy of pressure-driven flow of titanium dioxide-water nanofluid due to entropy generation. Entropy 2019, 21, 236. [Google Scholar] [CrossRef] [PubMed]
- Thiagarajan, M.; Kumar, M.D. Heat source/sink and chemical reaction effects on MHD and heat transfer flow of radiative nanofluid over a porous exponentially stretching sheet with viscous dissipation and ohmic heating. Int. J. Basic Sci. Appl. Comput. 2019, 2, 5–12. [Google Scholar]
- Swain, B.K.; Parida, B.C.; Kar, S.; Senapati, N. Viscous dissipation and joule heating effect on MHD flow and heat transfer past a stretching sheet embedded in a porous medium. Heliyon 2020, 6, e05338. [Google Scholar] [CrossRef] [PubMed]
- Thumma, T.; Mishra, S.R. Effect of nonuniform heat source/sink, and viscous and Joule dissipation on 3D Eyring–Powell nanofluid flow over a stretching sheet. J. Comput. Des. Eng. 2020, 7, 412–426. [Google Scholar] [CrossRef]
- Sharma, R.P.; Ibrahim, S.M.; Mishra, S.R.; Tinker, S. Impact of dissipative heat and radiative heat on MHD viscous flow through a slandering stretching sheet with temperature- dependent variable viscosity. Heat Transf.–Asian Res. 2021, 50, 7568–7587. [Google Scholar] [CrossRef]
- Sajid, T.; Jamshed, W.; Shahzad, F.; Eid, M.R.; Alshehri, H.M.; Goodarzi, M.; Akgul, E.K.; Nisar, K.S. Micropolar fluid past a convectively heated surface embedded with nth order chemical reaction and heat source/sink. Phys. Scr. 2021, 96, 104010. [Google Scholar] [CrossRef]
- Abu-Hamdeh, N.H.; Alsulami, R.A.; Rawa, M.J.H.; Alazwari, M.A.; Goodarzi, M.; Safaei, M.R. A Significant Solar Energy Note on Powell-Eyring Nanofluid with Thermal Jump Conditions: Implementing Cattaneo-Christov Heat Flux Model. Mathematics 2021, 9, 2669. [Google Scholar] [CrossRef]
- Nazeer, M.; Saleem, S.; Hussain, F.; Al-Mubaddel, F.S.; Ali, A.; Saleem, A.; Saleem, M. Mathematical modeling and numerical solution of Cross-flow of Non-Newtonian fluid: Effects of viscous dissipation and slip boundary conditions. Z. Für Angew. Math. Und Mech. (ZAMM) 2022, 102, e202100130. [Google Scholar]
- Hamilton, R.L.; Crosser, O.K. Thermal conductivity of heterogeneous two component systems. Ind. Eng. Chem. Fundam. 1962, 1, 187–191. [Google Scholar] [CrossRef]
- Raza, J.; Rohni, A.M.; Omar, Z. MHD flow and heat transfer of Cu-water nanofluid in a semi porous channel with stretching walls. Int. J. Heat Mass Transf. 2016, 103, 336–340. [Google Scholar] [CrossRef]




| Properties | Nanofluid |
|---|---|
| Density | |
| Viscosity | |
| Heat capacity | |
| Thermal conductivity | |
| Electric conductivity |
| Physical Properties | Base Fluid (H2O) | Copper (Cu) |
|---|---|---|
| 997.1 | 8933 | |
| 4179 | 385 | |
| 0.613 | 401 | |
| 0.05 |
| Daniel et al. [33] | Present Result | |
|---|---|---|
| 10 | 1.143316 | 1.143220 |
| 9 | 1.140388 | 1.140575 |
| 7 | 1.132281 | 1.132588 |
| 5 | 1.118587 | 1.118767 |
| 3 | 1.090490 | 1.090916 |
| 1 | 1.000001 | 1.000019 |
| 0.5 | 0.933828 | 0.933556 |
| 0 | 0.784284 | 0.784312 |
| −1/3 | 0.500000 | 0.500003 |
| −0.5 | 0.083289 | 0.083242 |
| −0.51 | 0.038484 | 0.038349 |
| −0.55 | −0.197647 | −0.197772 |
| −0.60 | −0.850207 | −0.850697 |
| −0.61 | −1.224426 | −1.22459 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, A.; Khan, H.S.; Saleem, S.; Hussan, M. EMHD Nanofluid Flow with Radiation and Variable Heat Flux Effects along a Slandering Stretching Sheet. Nanomaterials 2022, 12, 3872. https://doi.org/10.3390/nano12213872
Ali A, Khan HS, Saleem S, Hussan M. EMHD Nanofluid Flow with Radiation and Variable Heat Flux Effects along a Slandering Stretching Sheet. Nanomaterials. 2022; 12(21):3872. https://doi.org/10.3390/nano12213872
Chicago/Turabian StyleAli, Aamir, Hajra Safdar Khan, Salman Saleem, and Muhammad Hussan. 2022. "EMHD Nanofluid Flow with Radiation and Variable Heat Flux Effects along a Slandering Stretching Sheet" Nanomaterials 12, no. 21: 3872. https://doi.org/10.3390/nano12213872
APA StyleAli, A., Khan, H. S., Saleem, S., & Hussan, M. (2022). EMHD Nanofluid Flow with Radiation and Variable Heat Flux Effects along a Slandering Stretching Sheet. Nanomaterials, 12(21), 3872. https://doi.org/10.3390/nano12213872






