Optimization of N-PERT Solar Cell under Atacama Desert Solar Spectrum
Abstract
1. Introduction
2. Materials and Methods
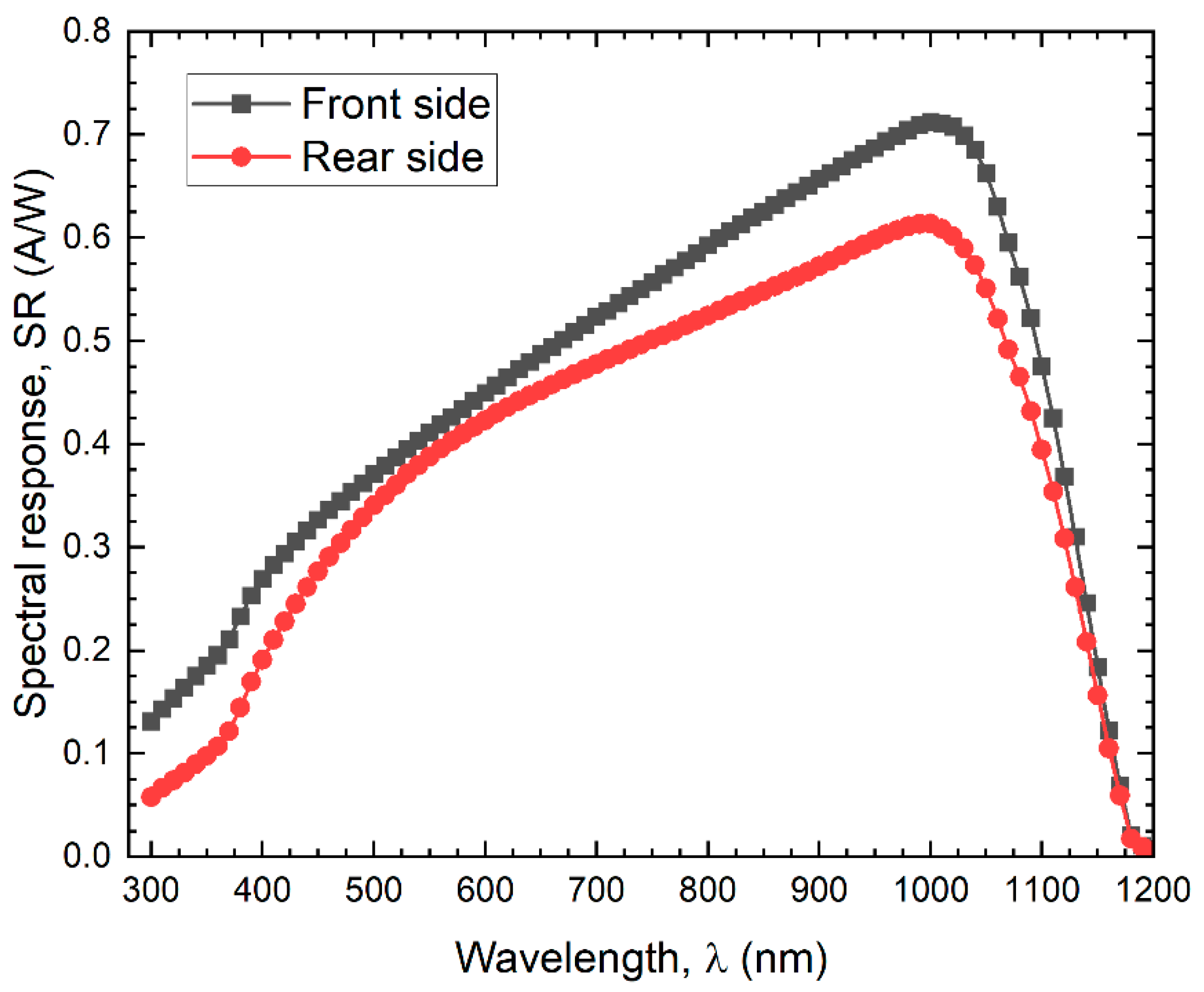
2.1. Model Validation at STC
- (1)
- The model assumes flat surfaces; thus, a correction factor must be introduced to match the short current density. However, the increase in surface area is accompanied by an increment in the saturation current density due to recombination. Fell et al. [1] considered both issues and defined correction factors () for different solar cells. In this work, the calculated short current density under STC conditions, , was multiplied by for comparison with the measured short current density, .
- (2)
- The model does not consider metal induced recombination. Therefore, the open circuit voltage may be higher than the experimental result. These differences were quantified and fully described by Edler et al. [29]. They quantified the reduction in the open circuit voltage of n-PERT solar cells by varying the metal fraction and quantifying the dark saturation current density at the metal/semiconductor interfaces. For the metal fraction of n-PERT solar cells in this work (0.099 and 0.052 for the front and rear side, respectively), the estimation indicates that the can decrease 45 mV due to the front side metallization and 35 mV due to the rear side metallization. It is pointed out that the effect of series and shunt resistances, and , is observable in the shape of the IV curve, and thus, on the and [30]. Based on the referenced experimental work, metal induced recombination can be applied after the model is solved, by subtracting for the corresponding metal fraction. In addition, ohmic losses will affect and . For power, , where is the power without resistance effects. For the fill factor, , where is the fill factor without resistive effects, is the normalized series resistance to the characteristic resistance ( and ) [31].
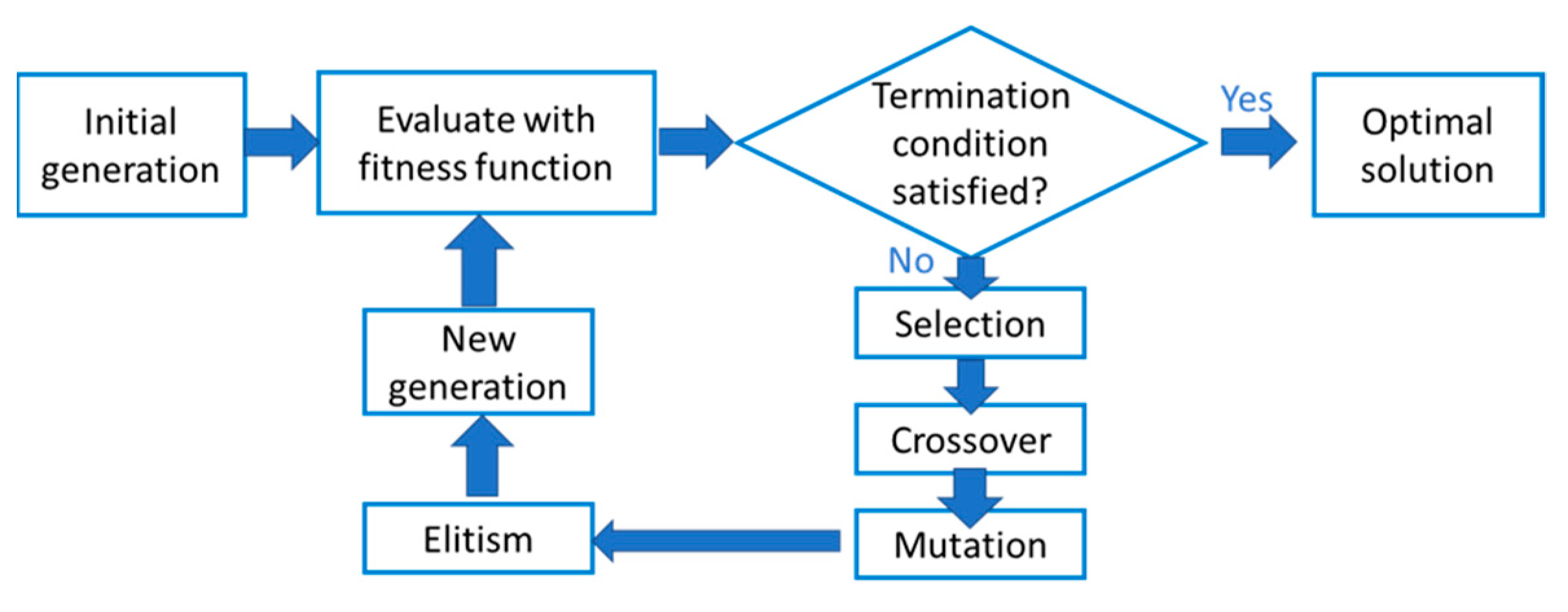
2.2. Determination of the Optimal Solar Cell Parameters
- Selection: We calculated the value of the cost function of all points , and it was denoted as , with . For each , a probability to be selected, was assigned. The probability can be written in terms of the cost function, . Once the probability was computed, elements called parents were randomly chosen, and they were denoted as , with . This procedure assumed that the region of the points with the lowest value of is explored with a larger frequency.
- Crossover: We created elements called children and denoted as , with , from the values of the parents by considering a random point included in the segment defined by two parents. This step was intended to explore a zone included between two parents’ points and determine if there was a better element.
- Mutation: We modified randomly some components of the elements. The goal was to explore some areas of the search space randomly. In addition, this step allowed for escape from possible local minima, which may attract too many elements of the population.
- Elitism: We aimed to ensure that the convergence of the GA was always decreasing, that is, the value of of the best element from each generation was decreasing from one generation to another. Thus, we directly copied the best element from the previous generation and it was denoted as .
3. Theory
- i.
- Net charge density relation
- ii.
- Transport equations
- iii.
- Continuity equations
4. Results
4.1. Measurements and Simulation of the Solar Cell at Standard Conditions
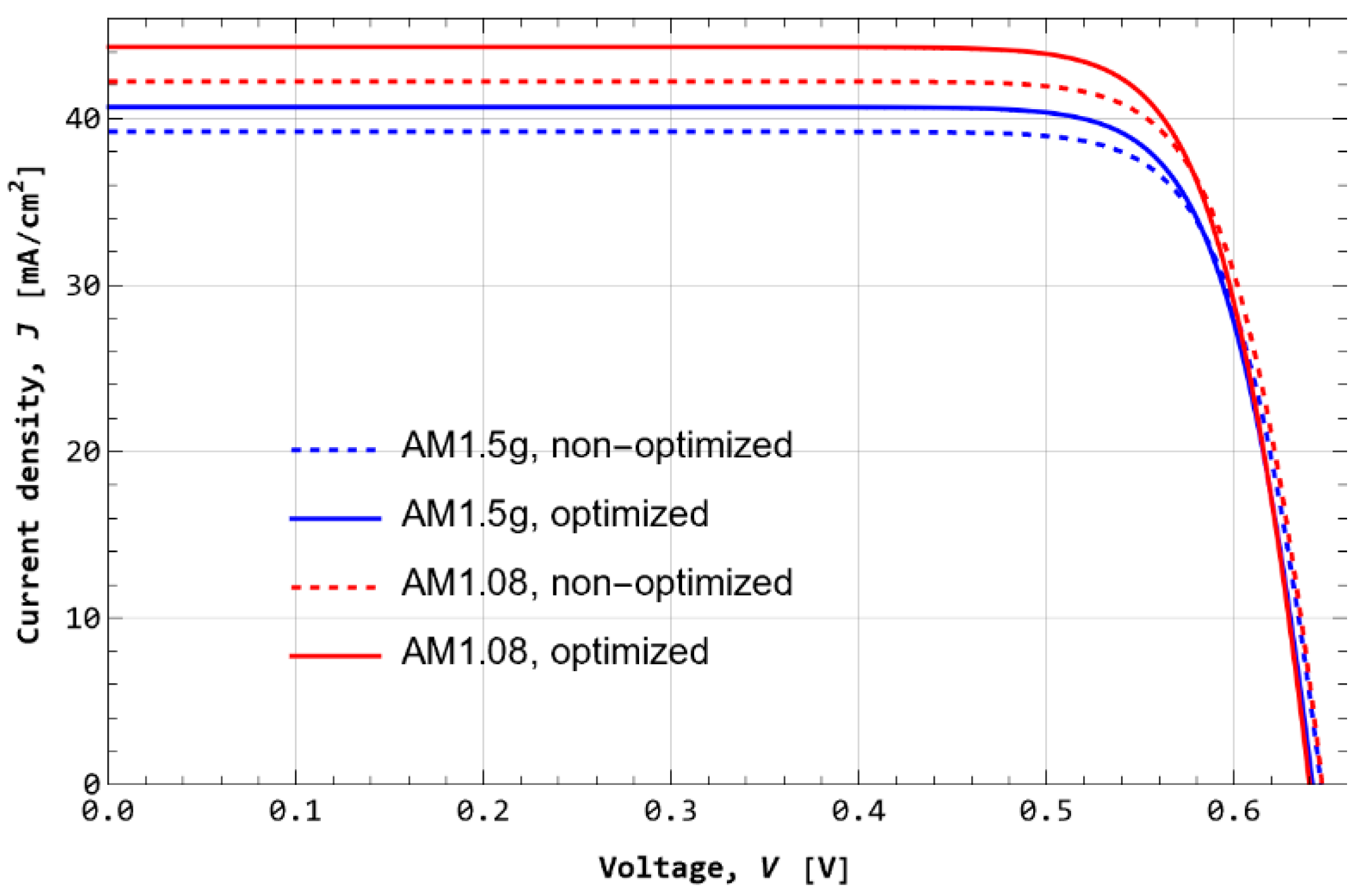
4.2. Optimal Solar Cell Parameters
5. Discussion
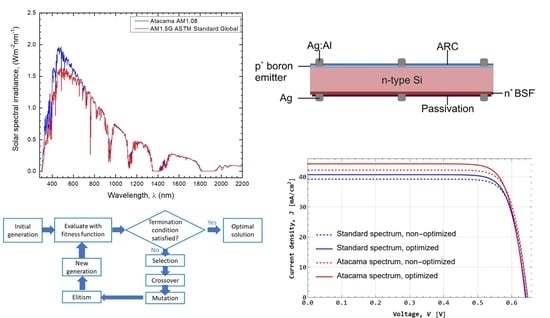
5.1. Solar Spectrum
5.2. Metallization
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Input Parameter | Value |
|---|---|
| Emitter thickness, (nm) | 650 |
| Wafer thickness, (µm) | 180 × 103 |
| BSF thickness, (nm) | 450 |
| Simulated area, (cm2) | 1 |
| Relative dielectric constant, | 11.7 |
| Electron affinity, (eV) | 4.05 |
| Bandgap, (eV) | 1.12 |
| Effective conduction band density, (cm−3) | (T/300[K]) 3/2 × 1.04 × 1019 [cm−3] |
| Effective valence band density, (cm−3) | (T/300[K])3/2 × 2.8 × 1019 [cm−3] |
| Electron mobility, (cm2V−1s−1) | Arora model |
| Hole mobility, (cm2V−1s−1) | Arora model |
| Front-side surface doping, (cm−3) | 2.44 × 1019 |
| Base doping concentration, (cm−3) | 8.44 × 1014 |
| Rear-side surface doping, (cm−3) | 6.17 × 1019 |
| c-Si density, (kg/m3) | 2329 |
| Auger Recombination coefficient for electrons, (cm6s−1) | 2.80 × 10−31 |
| Auger Recombination coefficient for holes, (cm6s−1) | 9.90 × 10−32 |
| Direct band-to-band recombination coefficient, (cm3s−1) | 4.73 × 10−15 |
| Tau trap for electrons and holes, (ms) | 1 |
| Input Parameter | Value |
|---|---|
| Electron mobility reference, (cm2/(Vs) | 1252 |
| Hole mobility reference, (cm2/(Vs) | 407 |
| Electron mobility reference minimum, (cm2/(Vs) | 88 |
| Hole mobility reference minimum, (cm2/(Vs) | 54.3 |
| Electron reference impurity concentration, (1/cm3]) | 1.26 × 1017 |
| Hole reference impurity concentration, (1/cm3) | 2.35 × 1017 |
| Alpha coefficient, | 0.88 |
| Mobility reference minimum exponent, | −0.57 |
| Mobility reference exponent, | −2.33 |
| Impurity concentration reference exponent, | −2.33 |
| Alpha coefficient exponent, | −0.146 |
| Reference temperature, (K) | 300 |
References
- Fell, A.; McIntosh, K.R.; Altermatt, P.P.; Janssen, G.J.M.; Stangl, R.A.; Ho-Baillie, H.; Steinkemper, J.; Greulich, M.; Muller, B.; Min, B.; et al. Input Parameters for the Simulation of Silicon Solar Cells in 2014. IEEE J. Photovoltaics 2015, 5, 1250–1263. [Google Scholar] [CrossRef]
- Peng, Z.-W.; Koduvelikulathu, L.J.; Kopecek, R. The impact of bulk resistivity on bifacial n-PERT rear junction solar cells. In Proceedings of the Conference Record of the Photovoltaic Specialists Conference, Calgary, AB, Canada, 15 June–21 August 2020; pp. 1606–1610. [Google Scholar] [CrossRef]
- Ferrada, P.; Marzo, A.; Cabrera, E.; Chu, H.; del Campo, V.; Rabanal, J.; Diaz-Almeida, D.; Schneider, A.; Kopecek, R. Potential for photogenerated current for silicon based photovoltaic modules in the Atacama Desert. Sol. Energy 2017, 144, 580–593. [Google Scholar] [CrossRef]
- Dehghanzadeh, A.; Farahani, G.; Maboodi, M. A novel approximate explicit double-diode model of solar cells for use in simulation studies. Renew. Energy 2017, 103, 468–477. [Google Scholar] [CrossRef]
- Boussaid, M.; Belghachi, A.; Agroui, K.; Abdelaoui, M.; Otmani, M. Solar cell degradation under open circuit condition in out-doors-in desert region. Results Phys. 2016, 6, 837–842. [Google Scholar] [CrossRef]
- Vincent, P.; Sergio, G.C.; Jang, J.; Kang, I.M.; Park, J.; Kim, H.; Lee, M.; Bae, J.-H. Application of Genetic Algorithm for More Efficient Multi-Layer Thickness Optimization in Solar Cells. Energies 2020, 13, 1726. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef] [PubMed]
- Razzaq, A.; Mayer, A.; Depauw, V.; Gordon, I.; Hajjiah, A.; Poortmans, J. Application of a Genetic Algorithm in Four-Terminal Perovskite/Crystalline-Silicon Tandem Devices. IEEE J. Photovolt. 2020, 10, 1689–1700. [Google Scholar] [CrossRef]
- Attari, K.; Amhaimar, L.; El Yaakoubi, A.; Asselman, A.; Bassou, M. The Design and Optimization of GaAs Single Solar Cells Using the Genetic Algorithm and Silvaco ATLAS. Int. J. Photoenergy 2017, 2017, 1–7. [Google Scholar] [CrossRef]
- Fertig, F.; Nold, S.; Wöhrle, N.; Greulich, J.; Hädrich, I.; Krauß, K.; Mittag, M.; Biro, D.; Rein, S.; Preu, R. Economic feasibility of bifacial silicon solar cells. Prog. Photovolt. Res. Appl. 2016, 24, 800–817. [Google Scholar] [CrossRef]
- Phillips, A.B.; Subedi, K.K.; Liyanage, G.K.; Alfadhili, F.K.; Ellingson, R.J.; Heben, M.J. Understanding and Advancing Bifacial Thin Film Solar Cells. ACS Appl. Energy Mater. 2020, 3, 6072–6078. [Google Scholar] [CrossRef]
- Rodriguez, J.; Wang, E.-C.; Chen, N.; Ho, J.W.; Li, M.; Buatis, J.K.; Nagarajan, B.; Xu, L.; Choy, W.L.; Shanmugam, V.; et al. Towards 22% efficient screen-printed bifacial n-type silicon solar cells. Sol. Energy Mater. Sol. Cells 2018, 187, 91–96. [Google Scholar] [CrossRef]
- Marzo, A.; Ferrada, P.; Beiza, F.; Besson, P.; Alonso-Montesinos, J.; Ballestrín, J.; Román, R.; Portillo, C.; Escobar, R.; Fuentealba, E. Standard or local solar spectrum? Implications for solar technologies studies in the Atacama desert. Renew. Energy 2018, 127, 871–882. [Google Scholar] [CrossRef]
- Polo, J.; Alonso-Abella, M.; Chivelet, N.M.; Alonso-Montesinos, J.; López, G.; Marzo, A.; Nofuentes, G.; Vela-Barrionuevo, N. Typical Meteorological Year methodologies applied to solar spectral irradiance for PV applications. Energy 2019, 190, 116453. [Google Scholar] [CrossRef]
- Jessen, W.; Wilbert, S.; Gueymard, C.A.; Polo, J.; Bian, Z.; Driesse, A.; Habte, A.; Marzo, A.; Armstrong, P.R.; Vignola, F.; et al. Proposal and evaluation of subordinate standard solar irradiance spectra for applications in solar energy systems. Sol. Energy 2018, 168, 30–43. [Google Scholar] [CrossRef]
- Wilbert, S.; Jessen, W.; Gueymard, C.; Polo, J.; Bian, Z.; Driesse, A.; Habte, A.; Marzo, A.; Armstrong, P.; Vignola, F.; et al. Proposal and Evaluation of Subordinate Standard Solar Irradiance Spectra with a Focus on Air Mass Effects; International Solar Energy Society: Freiburg im Breisgau, Germany, 2017; pp. 1372–1384. [Google Scholar] [CrossRef][Green Version]
- Marzo, A.; Ballestrín, J.; Alonso-Montesinos, J.; Ferrada, P.; Polo, J.; López, G.; Barbero, J. Field Quality Control of Spectral Solar Irradiance Measurements by Comparison with Broadband Measurements. Sustainability 2021, 13, 10585. [Google Scholar] [CrossRef]
- Gueymard, C.A. Parameterized transmittance model for direct beam and circumsolar spectral irradiance. Sol. Energy 2001, 71, 325–346. [Google Scholar] [CrossRef]
- Gueymard, C. SMARTS: Simple Model of the Atmospheric Radiative Transfer of Sunshine | Grid Modernization | NREL. 1995. Available online: https://www.nrel.gov/grid/solar-resource/smarts.html (accessed on 23 March 2019).
- Kato, S.; Rose, F.G.; Sun-Mack, S.; Miller, W.F.; Chen, Y.; Rutan, D.A.; Stephens, G.L.; Loeb, N.G.; Minnis, P.; Wielicki, B.A.; et al. Improvements of top-of-atmosphere and surface irradiance computations with CALIPSO-, CloudSat-, and MODIS-derived cloud and aerosol properties. J. Geophys. Res. Atmos. 2011, 116, 1–21. [Google Scholar] [CrossRef]
- Bellouin, N.; Quaas, J.; Morcrette, J.-J.; Boucher, O. Estimates of aerosol radiative forcing from the MACC re-analysis. Atmospheric Chem. Phys. 2013, 13, 2045–2062. [Google Scholar] [CrossRef]
- Remer, L.A.; Kaufman, Y.J.; Tanré, D.; Mattoo, S.; Chu, D.A.; Martins, J.V.; Li, R.R.; Ichoku, C.; Levy, R.C.; Kleidman, R.G.; et al. The MODIS Aerosol Algorithm, Products, and Validation. J. Atmos. Sci. 2005, 62, 947–973. [Google Scholar] [CrossRef]
- Wang, H.; Zou, X.; Li, G. An Improved Quality Control for AIRS Total Column Ozone Observations within and around Hurricanes. J. Atmos. Ocean. Technol. 2012, 29, 417–432. [Google Scholar] [CrossRef]
- ECMWF | ERA Interim, Daily. 2022. Available online: https://apps.ecmwf.int/datasets/data/interim-full-daily/levtype=sfc/ (accessed on 12 April 2022).
- Berrisford, P.; Dee, D.; Fielding, K.; Fuentes, M.; Kallberg, P.; Kobayashi, S.S. Uppala, The ERA-Interim Archive. 2009. Available online: https://www.ecmwf.int/en/elibrary/8173-era-interim-archive (accessed on 7 September 2022).
- Giovanni. 2022. Available online: https://giovanni.gsfc.nasa.gov/giovanni/ (accessed on 12 April 2022).
- Ferrada, P.; Rudolph, D.; Portillo, C.; Adrian, A.; Correa-Puerta, J.; Sierpe, R.; Del Campo, V.; Flores, M.; Corrales, T.P.; Henriquez, R.; et al. Interface analysis of Ag/n-type Si contacts in n-type PERT solar cells. Prog. Photovoltaics Res. Appl. 2020, 28, 358–371. [Google Scholar] [CrossRef]
- Edler, A. Development of Bifacial n-Type Solar Cells for Industrial Application. Universität Konstanz. 2014. Available online: http://nbn-resolving.de/urn:nbn:de:bsz:352-275017 (accessed on 7 September 2022).
- Edler, A.; Mihailetchi, V.D.; Koduvelikulathu, L.J.; Comparotto, C.; Kopecek, R.; Harney, R. Metallization-induced recombination losses of bifacial silicon solar cells. Prog. Photovolt. Res. Appl. 2015, 23, 620–627. [Google Scholar] [CrossRef]
- Slooff, L.; Brockholz, B.; Verhees, W.; Veenstra, S.; Cobussen-Pool, E.; Kroon, J.; Bende, E. Determination of the Intrinsic Diode Parameters of Polymer Solar Cells. Energy Procedia 2012, 31, 11–20. [Google Scholar] [CrossRef]
- Green, M.A. Solar cell fill factors: General graph and empirical expressions. Solid-state Electron. 1981, 24, 788–789. [Google Scholar] [CrossRef]
- Vasconcelos, J.; Saldanha, R.; Krähenbühl, L.; Nicolas, A. Genetic algorithm coupled with a deterministic method for optimization in electromagnetics. IEEE Trans. Magn. 1997, 33, 1860–1863. [Google Scholar] [CrossRef]
- Altermatt, P.P. Models for numerical device simulations of crystalline silicon solar cells—A review. J. Comput. Electron. 2011, 10, 314–330. [Google Scholar] [CrossRef]
- Arora, N.; Hauser, J.; Roulston, D. Electron and hole mobilities in silicon as a function of concentration and temperature. IEEE Trans. Electron Devices 1982, 29, 292–295. [Google Scholar] [CrossRef]
- Semiconductor Module User’s Guide. COMSOL Multiphysics® v. 6.0. COMSOL AB, Stockholm, Sweden. 2021. Available online: https://doc.comsol.com/6.0/doc/com.comsol.help.semicond/SemiconductorModuleUsersGuide.pdf (accessed on 7 September 2022).
- Chowdhury, M.M.; Debnath, B. Approximation of carrier generation rate in common solar cells and studies for optimization of n+p silicon solar cell for AM1.5G and AM1.5D. In Proceedings of the 2012 7th International Conference of Electronic and Computer Engineering ICECE, Dhaka, Bangladesh, 20–22 December 2012; pp. 327–330. [Google Scholar] [CrossRef]
- Cuevas, A.; Yan, D. Misconceptions and Misnomers in Solar Cells. IEEE J. Photovolt. 2013, 3, 916–923. [Google Scholar] [CrossRef]
- Mahajan, S.; SreeHarsha, K.S. Principles of Growth and Processing of Semiconductors, 1st ed.; McGraw-Hill Science: New York, NY, USA, 1998. [Google Scholar]
- Sai, H.; Sato, Y.; Oku, T.; Matsui, T. Very thin crystalline silicon cells: A way to improve the photovoltaic performance at elevated temperatures. Prog. Photovoltaics: Res. Appl. 2021, 29, 1093–1104. [Google Scholar] [CrossRef]
- Brendel, R.; Queisser, H. On the thickness dependence of open circuit voltages of p-n junction solar cells. Sol. Energy Mater. Sol. Cells 1993, 29, 397–401. [Google Scholar] [CrossRef]
- Sinton, R.A.; Swanson, R.M. Recombination in highly injected silicon. IEEE Trans. Electron Dev. 1987, 34, 1380–1389. [Google Scholar] [CrossRef]
- Dhariwal, S.; Kulshreshtha, A.P. Theory of back surface field silicon solar cells. Solid-State Electron. 1981, 24, 1161–1165. [Google Scholar] [CrossRef]
- Stem, N.; Cid, M. Studies of phosphorus Gaussian profile emitter silicon solar cells. Mater. Res. 2001, 4, 143–148. [Google Scholar] [CrossRef]
- Almeida, D.D.; Ferrada, P.; Marzo, A.; Cabrera, E.; Urrejola, E.; Espinoza, D.; Castillo, R.; Llanos, J.; Portillo, C. Theoretical Calculation of the Photo-generated Current Density by Using Optical Path-length Enhancement Factor for Si-based PV Devices in the Atacama Desert. In Proceedings of the 2018 IEEE 7th World Conference on Photovoltaic Energy Conversion, WCPEC, Honolulu, HI, USA, 10–15 June 2018; pp. 3237–3242. [Google Scholar] [CrossRef]
- Diaz Almeida, D.F.; Araya, P.; Ferrada, A.; Sanz Martinez, N.; Yurrita Zubillaga, O. Evaluation of Antireflection and Antisoiling Coatings for PV Modules in the Atacama Desert. In Proceedings of the 33rd European Photovoltaic Solar Energy Conference and Exhibition, Amsterdam, The Netherlands, 25–29 September 2017; pp. 1391–1395. [Google Scholar] [CrossRef]
- Cabrera, E.; Olibet, S.; Rudolph, D.; Glatz-Reichenbach, J.; Kopecek, R.; Reinke, D.; Gotz, A.; Schubert, G. Impact of Si surface topography on the glass layer resulting from screen printed Ag-paste solar cell contacts. In Proceedings of the Conference Record of the IEEE Photovoltaic Specialists Conference, Austin, TX, USA, 3–8 June 2012; pp. 204–208. [Google Scholar] [CrossRef]
- Koduvelikulathu, L.J.; Mihailetchi, V.D.; Olibet, S.; Rudolph, D.; Cabrera, E. Two-Dimensional Modeling of the Metallization-Induced Recombination Losses of Screen-Printed Solar Cells. IEEE J. Photovolt. 2015, 5, 159–165. [Google Scholar] [CrossRef]
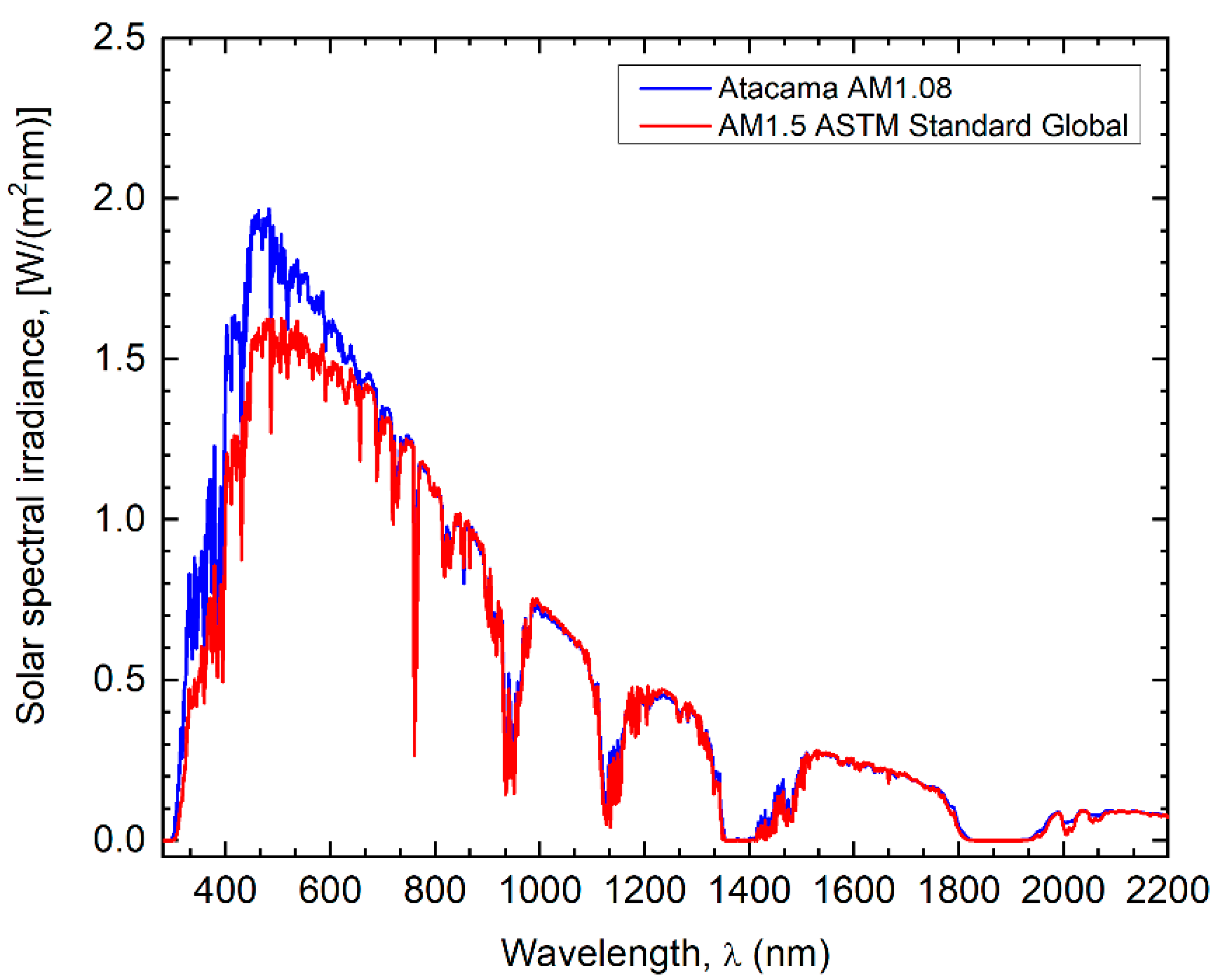



| Name | Value | Description |
|---|---|---|
| 180 µm | Solar cell thickness | |
| 0.65 µm | Emitter depth | |
| 0.45 µm | Thickness of BSF | |
| 2.44 × 1019 cm−3 | Emitter surface conc. | |
| 8.436 × 1014 cm−3 | Base doping | |
| 6.17 × 1019 cm−3 | BSF surface conc. | |
| 1.5 ms | SRH Carrier lifetime | |
| 1.5 ms | SRH Carrier lifetime | |
| 0.052 | Metal fraction front side |
| JV Measurement | JV Simulation | |||
|---|---|---|---|---|
| Parameter | Front | Rear | Front | Rear |
| 39.2 ± 0.03 | 34.6 ± 0.03 | 39.2 | 34.2 | |
| 653.1 ± 2 | 649.7 ± 2 | 646.4 | 654.6 | |
| 4.9 ± 0.02 | 4.3 ± 0.09 | 5.3 | 4.6 | |
| 78.3 ± 0.2 | 78.2 ± 0.16 | 78.7 | 78.7 | |
| 20 ± 0.08 | 17.6 ± 0.1 | 20.0 | 18.0 | |
| Solar Cell Parameters | Initial Values | Range |
|---|---|---|
| (nm) | 650 | 50–750 |
| (nm) | 180 × 103 | 150 × 103–200 × 103 |
| (nm) | 450 | 50–750 |
| (cm−3) | 2.44 × 1019 | 1 × 1019–1 × 1020 |
| (cm−3) | 8.44 × 1014 | 1 × 1014–5 × 1015 |
| (cm−3) | 6.16 × 1019 | 1 × 1019–5 × 1020 |
| GA Parameters | Value |
|---|---|
| Population size | 70 |
| Generations | 110 |
| Stopping criterium | 10 |
| Mutation probability | 10% |
| Non-Optimized | Optimized | Increment | ||||
|---|---|---|---|---|---|---|
| Parameter | STC AM1.5G | ATA AM1.08 | STC AM1.5G | ATA AM1.08 | STC AM1.5g | ATA AM1.08 |
| 39.2 | 42.2 | 40.7 | 44.3 | 3.7% | 4.9% | |
| 646.4 | 647.0 | 641.7 | 640.1 | −0.7% | −1.1% | |
| 5.3 | 5.7 | 5.5 | 6.1 | 4.3% | 5.7% | |
| 78.7 | 78.9 | 79.1 | 80.1 | 0.5% | 1.5% | |
| 20.0 | 21.6 | 20.8 | 22.7 | 4.3% | 5.4% | |
| Description | Parameter | Exp. Values | AM1.5G | AM1.08 |
|---|---|---|---|---|
| Emitter thickness | dE (nm) | 650 | 200.2 | 201 |
| Cell thickness | dcell (nm) | 180 × 103 | 154.2 × 103 | 165.1 × 103 |
| BSF thickness | dBSF (nm) | 450 | 330 | 250 |
| Emitter doping | NE (cm−3) | 2.44 × 1019 | 9.89 × 1019 | 9.36 × 1019 |
| Base doping | NB (cm−3) | 8.44 × 1014 | 9.83 × 1014 | 9.81 × 1014 |
| BSF doping | NBSF (cm−3) | 6.16 × 1019 | 3.87 × 1020 | 4.92 × 1020 |
| n-PERT Front (AM 1.5G) | n-PERT Rear (AM 1.5G) | n-PERT Front (AM 1.08) | n-PERT Rear (AM 1.08) | |
|---|---|---|---|---|
| Measured Jsc (mA/cm2) | 39.2 | 34.6 | X | X |
| Calculated Jsc via COMSOL (mA/cm2) | 39.2 | 34.2 | 44.3 | X |
| Calculated Jph (mA/cm2) | 38.9 | 34.3 | 42.2 | 37.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferrada, P.; Marzo, A.; Ferrández, M.R.; Reina, E.R.; Ivorra, B.; Correa-Puerta, J.; Campo, V.d. Optimization of N-PERT Solar Cell under Atacama Desert Solar Spectrum. Nanomaterials 2022, 12, 3554. https://doi.org/10.3390/nano12203554
Ferrada P, Marzo A, Ferrández MR, Reina ER, Ivorra B, Correa-Puerta J, Campo Vd. Optimization of N-PERT Solar Cell under Atacama Desert Solar Spectrum. Nanomaterials. 2022; 12(20):3554. https://doi.org/10.3390/nano12203554
Chicago/Turabian StyleFerrada, Pablo, Aitor Marzo, Miriam Ruiz Ferrández, Emilio Ruiz Reina, Benjamin Ivorra, Jonathan Correa-Puerta, and Valeria del Campo. 2022. "Optimization of N-PERT Solar Cell under Atacama Desert Solar Spectrum" Nanomaterials 12, no. 20: 3554. https://doi.org/10.3390/nano12203554
APA StyleFerrada, P., Marzo, A., Ferrández, M. R., Reina, E. R., Ivorra, B., Correa-Puerta, J., & Campo, V. d. (2022). Optimization of N-PERT Solar Cell under Atacama Desert Solar Spectrum. Nanomaterials, 12(20), 3554. https://doi.org/10.3390/nano12203554