Multi-Scale Modelling of Aggregation of TiO2 Nanoparticle Suspensions in Water
Abstract
:1. Introduction
2. Materials and Methods
2.1. Molecular Models and Strategy
2.2. Ab Initio DFT Calculations
2.3. Classical Molecular Dynamics Simulations
2.4. Brownian Dynamics Simulations
3. Results
3.1. Ab Initio DFT Characterization
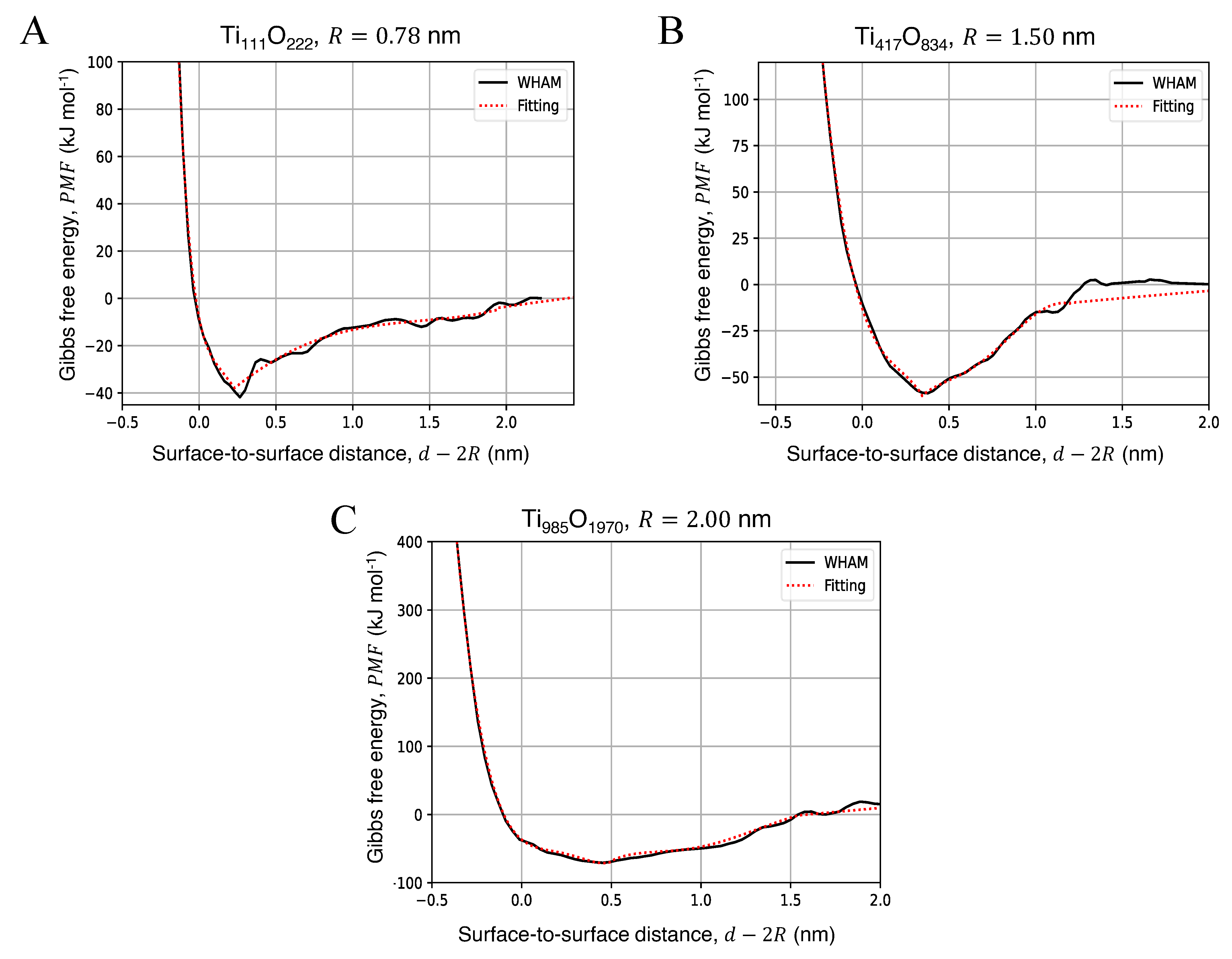
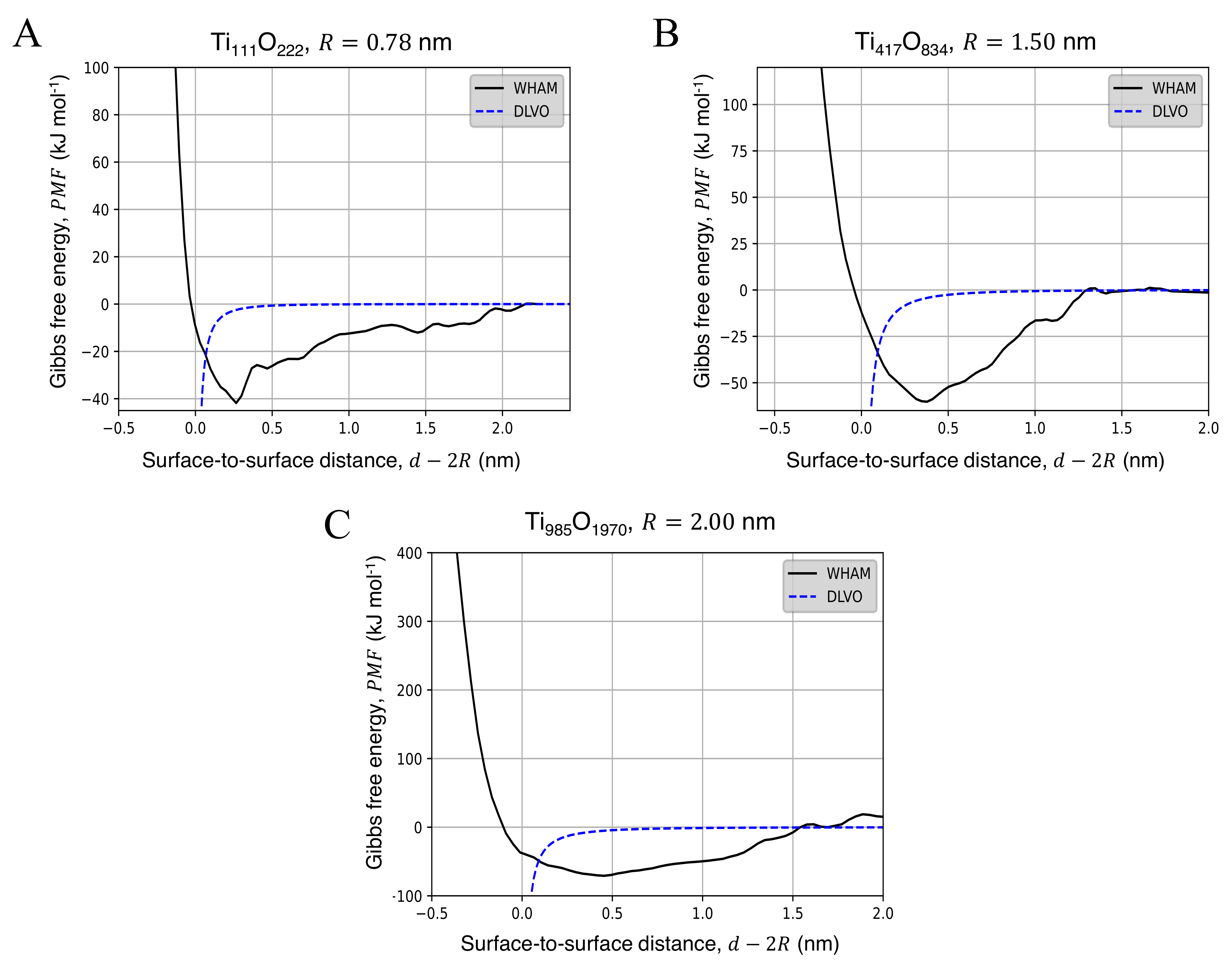
3.2. Potential of Mean Force for the Approach of Two Identical Titanium Dioxide Anatase Nanoparticles in Water
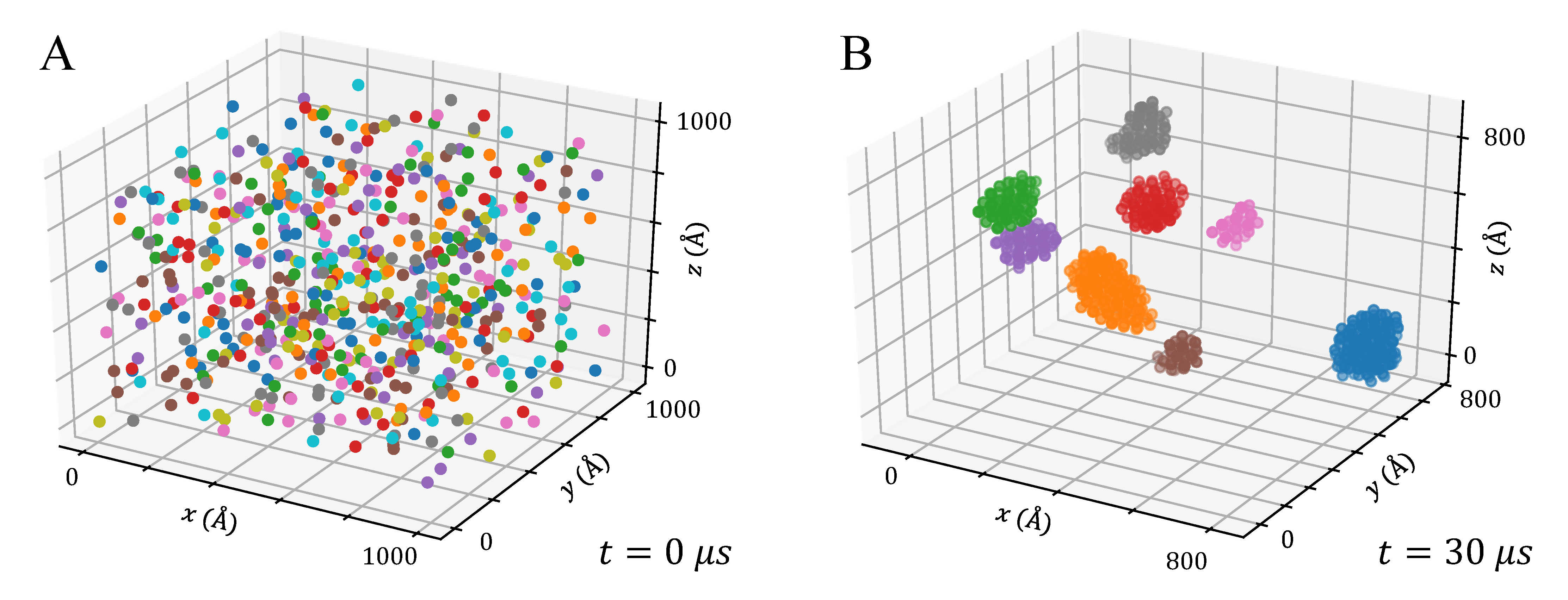
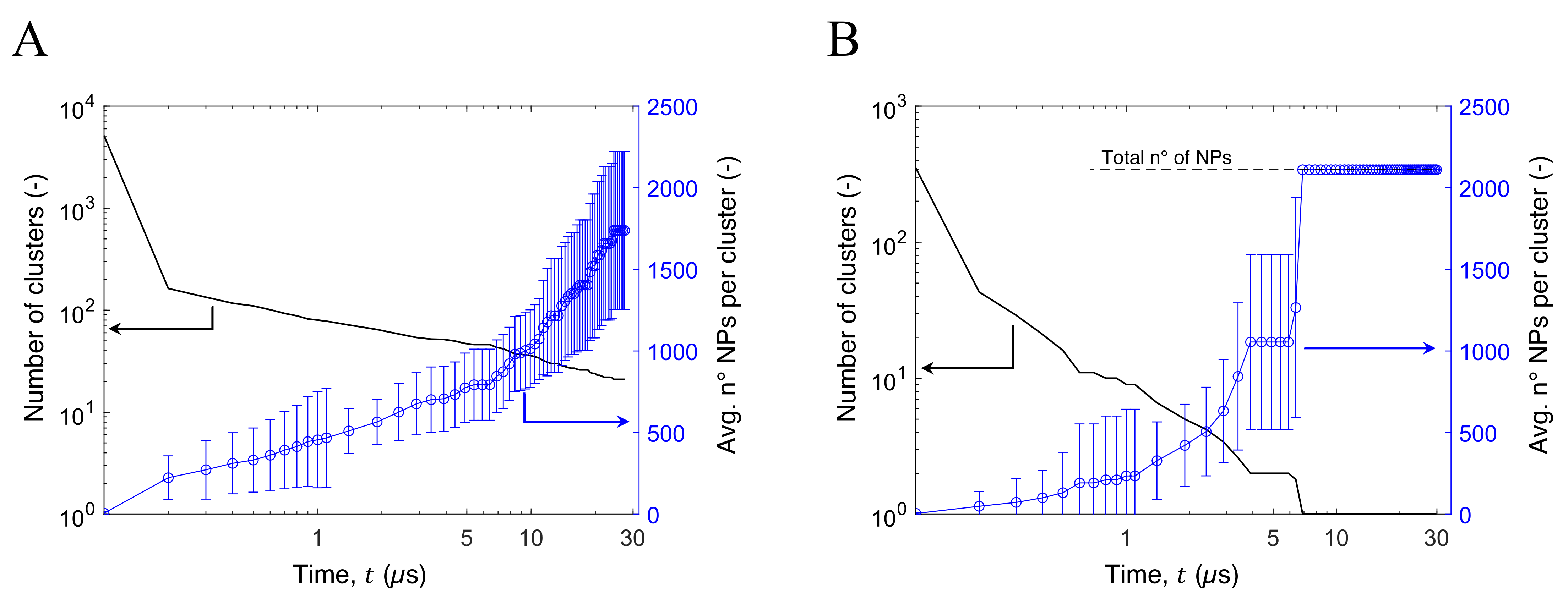
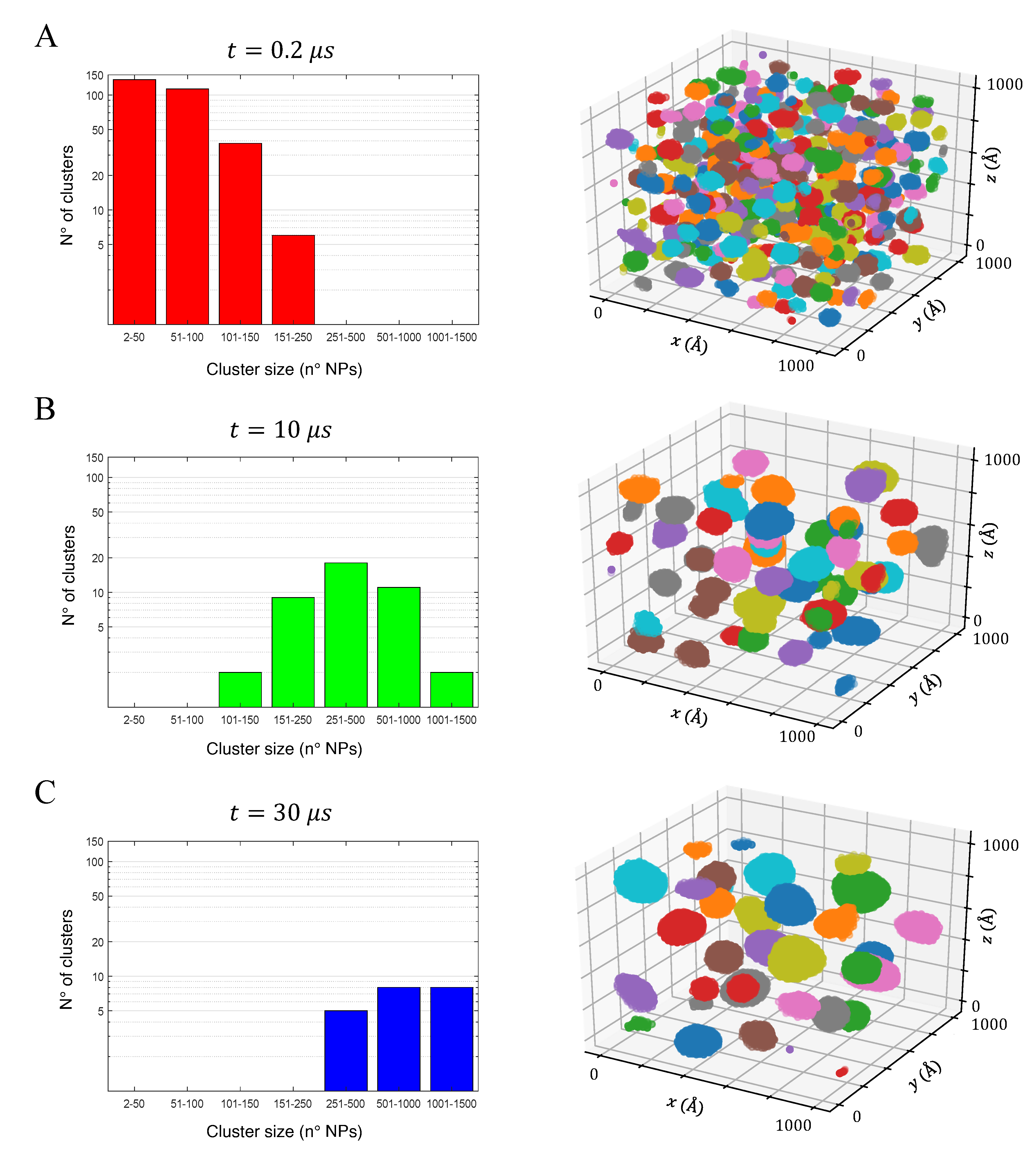
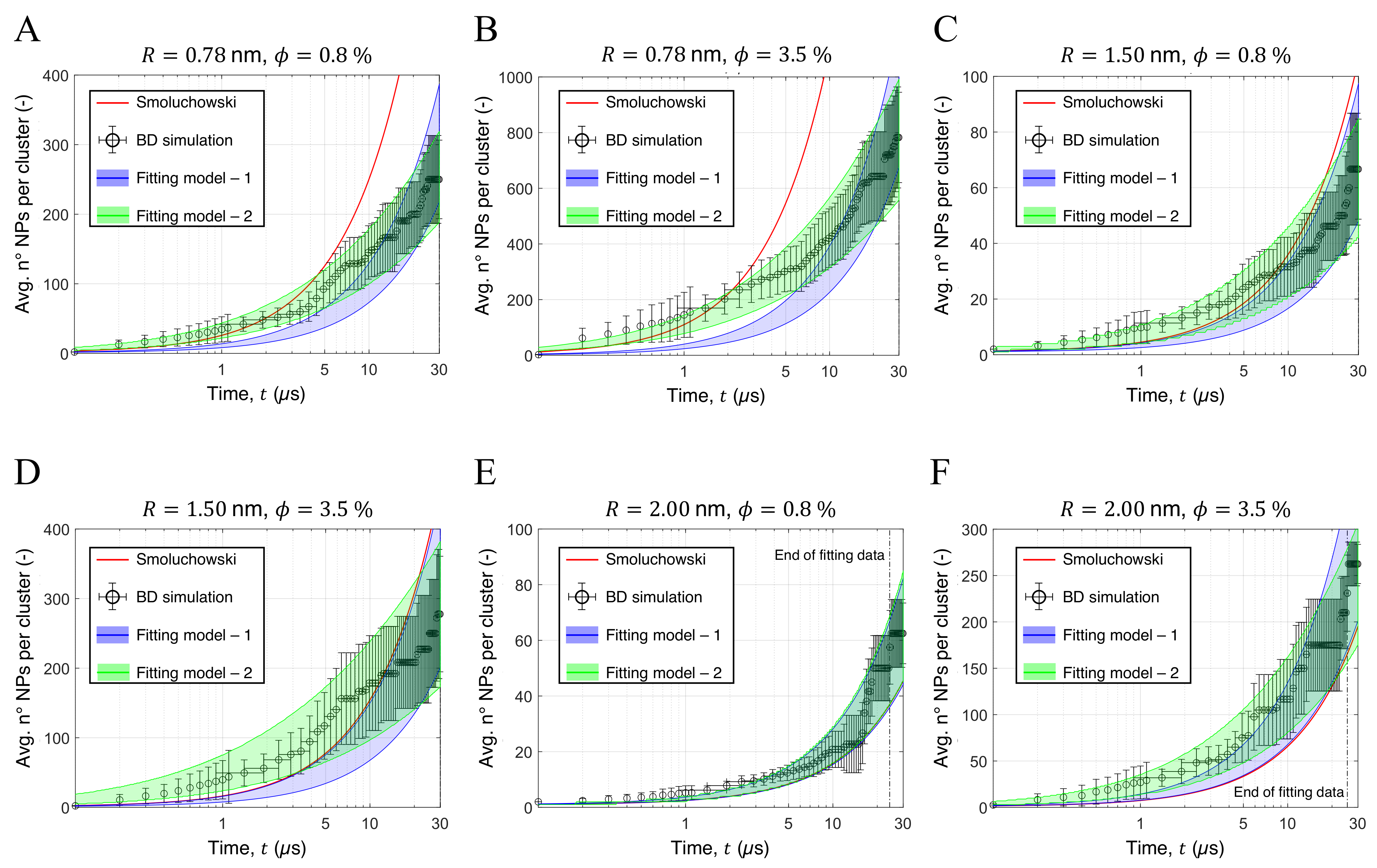
3.3. Aggregation of Titanium Dioxide Anatase Nanoparticles Using Brownian Dynamics
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AFE | Aggregation Free Energy |
| BD | Brownian Dynamics |
| DFT | Density Functional Theory |
| EFSA | European Food Safety Authority |
| MD | Molcular Dynamics |
| NP | Nanoparticle |
| PMF | Potential of Mean Force |
| QSAR | Quantitative Structure Activity relationship |
| US | Umbrella Sampling |
| WHAM | Weighted Histogram Analysis |
References
- Chiavazzo, E.; Asinari, P. Enhancing surface heat transfer by carbon nanofins: Towards an alternative to nanofluids? Nanoscale Res. Lett. 2011, 6, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Chiavazzo, E.; Asinari, P. Reconstruction and modeling of 3D percolation networks of carbon fillers in a polymer matrix. Int. J. Therm. Sci. 2010, 49, 2272–2281. [Google Scholar] [CrossRef] [Green Version]
- Sangermano, M.; Calvara, L.; Chiavazzo, E.; Ventola, L.; Asinari, P.; Mittal, V.; Rizzoli, R.; Ortolani, L.; Morandi, V. Enhancement of electrical and thermal conductivity of Su-8 photocrosslinked coatings containing graphene. Prog. Org. Coatings 2015, 86, 143–146. [Google Scholar] [CrossRef]
- Hubbell, J.A.; Chilkoti, A. Nanomaterials for drug delivery. Science 2012, 337, 303–305. [Google Scholar] [CrossRef] [PubMed]
- Gizzatov, A.; Key, J.; Aryal, S.; Ananta, J.; Cervadoro, A.; Palange, A.L.; Fasano, M.; Stigliano, C.; Zhong, M.; Di Mascolo, D.; et al. Hierarchically Structured Magnetic Nanoconstructs with Enhanced Relaxivity and Cooperative Tumor Accumulation. Adv. Funct. Mater. 2014, 24, 4584–4594. [Google Scholar] [CrossRef] [Green Version]
- Gomes, S.I.; Amorim, M.J.; Pokhrel, S.; Mädler, L.; Fasano, M.; Chiavazzo, E.; Asinari, P.; Jänes, J.; Tämm, K.; Burk, J.; et al. Machine learning and materials modelling interpretation of: In vivo toxicological response to TiO2 nanoparticles library (UV and non-UV exposure). Nanoscale 2021, 13, 14666–14678. [Google Scholar] [CrossRef] [PubMed]
- NanoInformaTIX Horizon 2020 Project. Available online: https://cordis.europa.eu/project/id/814426 (accessed on 10 November 2021).
- NanoSolveIT Horizon 2020 Project. Available online: https://cordis.europa.eu/project/id/814572 (accessed on 10 November 2021).
- Puzyn, T.; Rasulev, B.; Gajewicz, A.; Hu, X.; Dasari, T.P.; Michalkova, A.; Hwang, H.M.; Toropov, A.; Leszczynska, D.; Leszczynski, J. Using nano-QSAR to predict the cytotoxicity of metal oxide nanoparticles. Nat. Nanotechnol. 2011, 6, 175–178. [Google Scholar] [CrossRef]
- Mikolajczyk, A.; Gajewicz, A.; Mulkiewicz, E.; Rasulev, B.; Marchelek, M.; Diak, M.; Hirano, S.; Zaleska-Medynska, A.; Puzyn, T. Nano-QSAR modeling for ecosafe design of heterogeneous TiO2-based nano-photocatalysts. Environ. Sci. Nano 2018, 5, 1150–1160. [Google Scholar] [CrossRef]
- Rybińska-Fryca, A.; Mikolajczyk, A.; Puzyn, T. Structure-activity prediction networks (SAPNets): A step beyond Nano-QSAR for effective implementation of the safe-by-design concept. Nanoscale 2020, 12, 20669–20676. [Google Scholar] [CrossRef]
- Tämm, K.; Sikk, L.; Burk, J.; Rallo, R.; Pokhrel, S.; Mädler, L.; Scott-Fordsmand, J.J.; Burk, P.; Tamm, T. Parametrization of nanoparticles: Development of full-particle nanodescriptors. Nanoscale 2016, 8, 16243–16250. [Google Scholar] [CrossRef]
- Okuda-Shimazaki, J.; Takaku, S.; Kanehira, K.; Sonezaki, S.; Taniguchi, A. Effects of titanium dioxide nanoparticle aggregate size on gene expression. Int. J. Mol. Sci. 2010, 11, 2383–2392. [Google Scholar] [CrossRef] [Green Version]
- Murugadoss, S.; Brassinne, F.; Sebaihi, N.; Petry, J.; Cokic, S.M.; Van Landuyt, K.L.; Godderis, L.; Mast, J.; Lison, D.; Hoet, P.H.; et al. Agglomeration of titanium dioxide nanoparticles increases toxicological responses in vitro and in vivo. Part. Fibre Toxicol. 2020, 17, 10. [Google Scholar] [CrossRef]
- Dar, M.I.; Chandiran, A.K.; Grätzel, M.; Nazeeruddin, M.K.; Shivashankar, S.A. Controlled synthesis of TiO2 nanoparticles and nanospheres using a microwave assisted approach for their application in dye-sensitized solar cells. J. Mater. Chem. A 2014, 2, 1662–1667. [Google Scholar] [CrossRef]
- Luttrell, T.; Halpegamage, S.; Tao, J.; Kramer, A.; Sutter, E.; Batzill, M. Why is anatase a better photocatalyst than rutile?—Model studies on epitaxial TiO2 films. Sci. Rep. 2015, 4, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Chandren, S.; Zulfemi, N.H. Titania nanoparticles coated on polycarbonate car headlights for self-cleaning purpose. J. Phys. Conf. Ser. 2019, 1321, 022032. [Google Scholar] [CrossRef] [Green Version]
- Younes, M.; Aquilina, G.; Castle, L.; Engel, K.H.; Fowler, P.; Frutos Fernandez, M.J.; Fürst, P.; Gundert-Remy, U.; Gürtler, R.; Husøy, T.; et al. Safety assessment of titanium dioxide (E171) as a food additive. EFSA J. 2021, 19, e06585. [Google Scholar] [PubMed]
- Geiss, O.; Bianchi, I.; Senaldi, C.; Bucher, G.; Verleysen, E.; Waegeneers, N.; Brassinne, F.; Mast, J.; Loeschner, K.; Vidmar, J.; et al. Particle size analysis of pristine food-grade titanium dioxide and E 171 in confectionery products: Interlaboratory testing of a single-particle inductively coupled plasma mass spectrometry screening method and confirmation with transmission electron micr. Food Control 2021, 120, 107550. [Google Scholar] [CrossRef]
- Dréno, B.; Alexis, A.; Chuberre, B.; Marinovich, M. Safety of titanium dioxide nanoparticles in cosmetics. J. Eur. Acad. Dermatol. Venereol. 2019, 33, 34–46. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Treacy, J.P.; Hussain, H.; Torrelles, X.; Grinter, D.C.; Cabailh, G.; Bikondoa, O.; Nicklin, C.; Selcuk, S.; Selloni, A.; Lindsay, R.; et al. Geometric structure of anatase TiO2(101). Phys. Rev. B 2017, 95, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Balajka, J.; Aschauer, U.; Mertens, S.F.; Selloni, A.; Schmid, M.; Diebold, U. Surface Structure of TiO2 Rutile (011) Exposed to Liquid Water. J. Phys. Chem. C 2017, 121, 26424–26431. [Google Scholar] [CrossRef] [PubMed]
- Fazio, G.; Ferrighi, L.; Di Valentin, C. Spherical versus Faceted Anatase TiO2 Nanoparticles: A Model Study of Structural and Electronic Properties. J. Phys. Chem. C 2015, 119, 20735–20746. [Google Scholar] [CrossRef]
- Huang, L.; Gubbins, K.E.; Li, L.; Lu, X. Water on titanium dioxide surface: A revisiting by reactive molecular dynamics simulations. Langmuir 2014, 30, 14832–14840. [Google Scholar] [CrossRef] [PubMed]
- Petersen, T.; Klüner, T. Water Adsorption on Ideal Anatase-TiO2(101)—An Embedded Cluster Model for Accurate Adsorption Energetics and Excited State Properties. Z. Phys. Chem. 2020, 234, 813–834. [Google Scholar] [CrossRef] [Green Version]
- Rouse, I.; Power, D.; Brandt, E.G.; Schneemilch, M.; Kotsis, K.; Quirke, N.; Lyubartsev, A.P.; Lobaskin, V. First principles characterisation of bio-nano interface. Phys. Chem. Chem. Phys. 2021, 23, 13473–13482. [Google Scholar] [CrossRef]
- Chatzigoulas, A.; Karathanou, K.; Dellis, D.; Cournia, Z. NanoCrystal: A Web-Based Crystallographic Tool for the Construction of Nanoparticles Based on Their Crystal Habit. J. Chem. Inf. Model. 2018, 58, 2380–2386. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. Sartorius products. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metalamorphous- semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Mathew, K.; Sundararaman, R.; Letchworth-Weaver, K.; Arias, T.A.; Hennig, R.G. Implicit solvation model for density-functional study of nanocrystal surfaces and reaction pathways. J. Chem. Phys. 2014, 140, 084106. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Todorov, I.T.; Smith, W.; Trachenko, K.; Dove, M.T. DL_POLY_3: New dimensions in molecular dynamics simulations via massive parallelism. J. Mater. Chem. 2006, 16, 1911–1918. [Google Scholar] [CrossRef] [Green Version]
- Colón-Ramos, D.A.; La Riviere, P.; Shroff, H.; Oldenbourg, R. Transforming the development and dissemination of cutting-edge microscopy and computation. Nat. Methods 2019, 16, 667–669. [Google Scholar] [CrossRef]
- Bonomi, M.; Branduardi, D.; Bussi, G.; Camilloni, C.; Provasi, D.; Raiteri, P.; Donadio, D.; Marinelli, F.; Pietrucci, F.; Broglia, R.A.; et al. PLUMED: A portable plugin for free-energy calculations with molecular dynamics. Comput. Phys. Commun. 2009, 180, 1961–1972. [Google Scholar] [CrossRef] [Green Version]
- Tribello, G.A.; Bonomi, M.; Branduardi, D.; Camilloni, C.; Bussi, G. PLUMED 2: New feathers for an old bird. Comput. Phys. Commun. 2014, 185, 604–613. [Google Scholar] [CrossRef] [Green Version]
- Almora-Barrios, N.; De Leeuw, N.H. Modelling the interaction of a Hyp-Pro-Gly peptide with hydroxyapatite surfaces in aqueous environment. CrystEngComm 2010, 12, 960–967. [Google Scholar] [CrossRef]
- Jiang, Y.; Dehghan, S.; Karimipour, A.; Toghraie, D.; Li, Z.; Tlili, I. Effect of copper nanoparticles on thermal behavior of water flow in a zig-zag nanochannel using molecular dynamics simulation. Int. Commun. Heat Mass Transf. 2020, 116, 104652. [Google Scholar] [CrossRef]
- Tang, C.; Li, X.; Tang, Y.; Zeng, J.; Xie, J.; Xiong, B. Agglomeration mechanism and restraint measures of SiO2 nanoparticles in meta-aramid fibers doping modification via molecular dynamics simulations. Nanotechnology 2020, 31, 165702. [Google Scholar] [CrossRef]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef] [Green Version]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Matsui, M.; Akaogi, M. Molecular dynamics simulation of the structural and physical properties of the four polymorphs of TiO2. Mol. Simul. 1991, 6, 239–244. [Google Scholar] [CrossRef]
- Alimohammadi, M.; Fichthorn, K.A. A force field for the interaction of water with TiO2 surfaces. J. Phys. Chem. C 2011, 115, 24206–24214. [Google Scholar] [CrossRef]
- Mancardi, G.; Hernandez Tamargo, C.; Terranova, U.; De Leeuw, N. Calcium Phosphate Deposition on Planar and Stepped (101) Surfaces of Anatase TiO2: Introducing an Interatomic Potential for the TiO2/Ca-PO4/Water Interface. Langmuir 2018, 34, 10144–10152. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Torrie, G.M.; Valleau, J.P. Nonphysical Sampling Distributions in Monte Carlo Free-Energy Estimation: Umbrella Sampling. J. Comput. Phys. 1977, 23, 187–199. [Google Scholar] [CrossRef]
- Grossfield, A. WHAM: The Weighted Histogram Analysis Method, Version 2.0.10. 2020. Available online: http://membrane.urmc.rochester.edu/wordpress/?page_id=126 (accessed on 10 November 2021).
- Kumar, S.; Bouzida, D.; Swendsen, R.H.; Kollman, P.A.; Rosenberg, J.M. The weighted histogram analysis method for free-energy calculations on biomolecules. J. Comput. Chem. 1992, 13, 1011–1021. [Google Scholar] [CrossRef]
- Kumar, S.; Rosenberg, J.M.; Bouzida, D.; Swendsen, R.H.; Kollman, P.A. Multidimensional Free—Energy Calculations Using the Weighted Histogram Analysis Method. J. Comput. Chem. 1995, 16, 1339–1350. [Google Scholar] [CrossRef]
- GROMACS 2019.6 Manual. 2019. Available online: https://zenodo.org/record/3685925#.YdwL72jMKUk (accessed on 10 November 2021).
- Cardellini, A.; Alberghini, M.; Govind Rajan, A.; Misra, R.P.; Blankschtein, D.; Asinari, P. Multi-scale approach for modeling stability, aggregation, and network formation of nanoparticles suspended in aqueous solutions. Nanoscale 2019, 11, 3925–3932. [Google Scholar] [CrossRef] [Green Version]
- Berendsen, H.J.C. Simulating the Physical World; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Kubo, R. The fluctuation-dissipation theorem The fluctuation-dissipation theorem. Rep. Prog. Phys. 1966, 29, 255. [Google Scholar] [CrossRef] [Green Version]
- Goga, N.; Rzepiela, A.J.; De Vries, A.H.; Marrink, S.J.; Berendsen, H.J. Efficient algorithms for langevin and DPD dynamics. J. Chem. Theory Comput. 2012, 8, 3637–3649. [Google Scholar] [CrossRef] [Green Version]
- Lide, D.R. CRC Handbook of Chemistry and Physics; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Murshed, S.M.; Leong, K.C.; Yang, C. Enhanced thermal conductivity of TiO2—Water based nanofluids. Int. J. Therm. Sci. 2005, 44, 367–373. [Google Scholar] [CrossRef]
- Israelachvili, J. Intermolecular and Surface Forces; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Derjaguin, B.; Landau, L. Theory of the Stability of Strongly Charged Lyophobic Sols and of the Adhesion of Strongly Charged Particles in Solutions of Electrolytes. Acta Physicochim. URSS 1941, 14, 633–652. [Google Scholar] [CrossRef]
- Verwey, E.; Overbeek, J.T.G. Theory of the stability of lyophobic colloids. J. Colloid Sci. 1955, 10, 224–225. [Google Scholar] [CrossRef] [Green Version]
- Butt, H.J.; Graf, K.; Kappl, M. Physiscs and Chemistry of Interfaces; WILEY-VCH GmbH & Co. KGaA: Weinheim, Germany, 2003; p. 86. [Google Scholar]
- Schmoluchowski, M. Grundriß der Koagulationskinetik kolloider Lösungen. Kolloid-Zeitschrift 1917, 21, 98–104. [Google Scholar] [CrossRef]
- Prasher, R.; Phelan, P.E.; Bhattacharya, P. Effect of aggregation kinetics on the thermal conductivity of nanoscale colloidal solutions (nanofluid). Nano Lett. 2006, 6, 1529–1534. [Google Scholar] [CrossRef] [PubMed]
- Hanus, L.H.; Hartzler, R.U.; Wagner, N.J. Electrolyte-induced aggregation of acrylic latex. 1: Dilute particle concentrations. Langmuir 2001, 17, 3136–3147. [Google Scholar] [CrossRef]
- Schudel, M.; Behrens, S.H.; Holthoff, H.; Kretzschmar, R.; Borkovec, M. Absolute aggregation rate constants of hematite particles in aqueous suspensions: A comparison of two different surface morphologies. J. Colloid Interface Sci. 1997, 196, 241–253. [Google Scholar] [CrossRef]
- Honig, E.P.; Roebersen, G.J.; Wiersema, P.H. Effect of hydrodynamic interaction on the coagulation rate of hydrophobic colloids. J. Colloid Interface Sci. 1971, 36, 97–109. [Google Scholar] [CrossRef]
- Veshchunov, M.S.; Tarasov, V.I. Extension of the smoluchowski theory to transitions from dilute to dense regime of brownian coagulation: Triple collisions. Aerosol Sci. Technol. 2014, 48, 813–821. [Google Scholar] [CrossRef] [Green Version]
- Clogston, J.D.; Patri, A.K. Zeta Potential Measurement. In Characterization of Nanoparticles Intended for Drug Delivery; McNeil, S.E., Ed.; Humana Press: Totowa, NJ, USA, 2011; pp. 63–70. [Google Scholar]
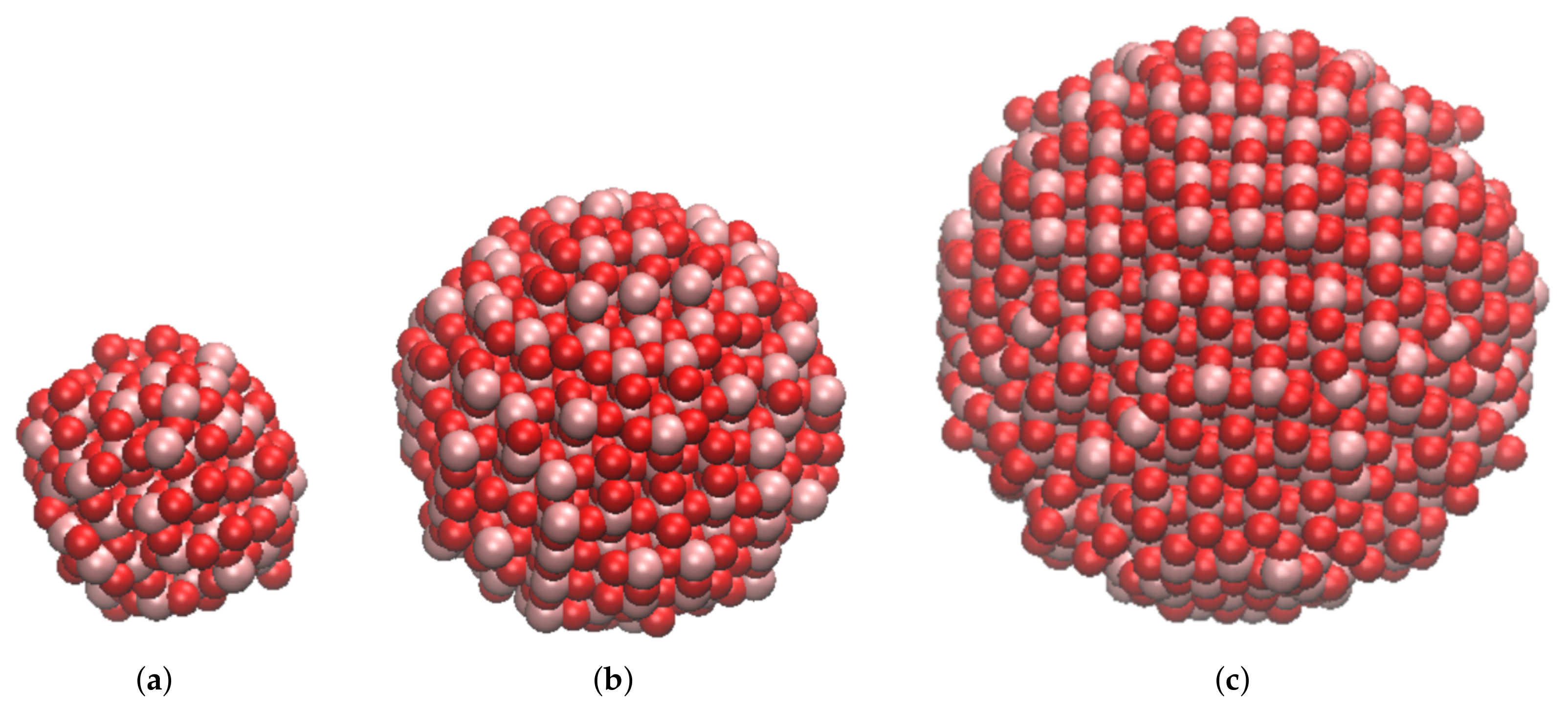
| Property | 0.78 nm | 1.5 nm | 2.0 nm | Bulk |
|---|---|---|---|---|
| TiO2 unit formula | 111 | 417 | 985 | 4 |
| SASA × (m) | 2.15 | 4.44 | 7.14 | - |
| E (eV) | −2808.98 | −10,623.23 | −25,498.99 | −105.93 |
| /TiO (eV) | −8.28 | −8.45 | −8.86 | −9.46 |
| E (eV) | −0.42 | −0.34 | - | - |
| NP Radius, R (nm) | AFE (kJ mol) | (nm) |
|---|---|---|
| 0.78 | 44.18 | 0.23 |
| 1.50 | 54.35 | 0.35 |
| 2.00 | 75.56 | 0.46 |
| R (nm) | |||
|---|---|---|---|
| 0.8% | 0.101 | 0.221 | |
| 1.8% | 0.101 | 0.362 | |
| 3.5% | 0.134 | 0.221 | |
| 7.0% | 0.148 | 0.101 | |
| 0.8% | 0.141 | 0.181 | |
| 1.8% | 0.134 | 0.161 | |
| 3.5% | 0.268 | 0.027 | |
| 7.0% | 0.027 | 0.094 | |
| 0.8% | 0.0 | 0.698 | |
| 1.8% | 0.162 | 0.114 | |
| 3.5% | 0.169 | 0.067 | |
| 7.0% | 0.040 | 0.034 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mancardi, G.; Alberghini, M.; Aguilera-Porta, N.; Calatayud, M.; Asinari, P.; Chiavazzo, E. Multi-Scale Modelling of Aggregation of TiO2 Nanoparticle Suspensions in Water. Nanomaterials 2022, 12, 217. https://doi.org/10.3390/nano12020217
Mancardi G, Alberghini M, Aguilera-Porta N, Calatayud M, Asinari P, Chiavazzo E. Multi-Scale Modelling of Aggregation of TiO2 Nanoparticle Suspensions in Water. Nanomaterials. 2022; 12(2):217. https://doi.org/10.3390/nano12020217
Chicago/Turabian StyleMancardi, Giulia, Matteo Alberghini, Neus Aguilera-Porta, Monica Calatayud, Pietro Asinari, and Eliodoro Chiavazzo. 2022. "Multi-Scale Modelling of Aggregation of TiO2 Nanoparticle Suspensions in Water" Nanomaterials 12, no. 2: 217. https://doi.org/10.3390/nano12020217
APA StyleMancardi, G., Alberghini, M., Aguilera-Porta, N., Calatayud, M., Asinari, P., & Chiavazzo, E. (2022). Multi-Scale Modelling of Aggregation of TiO2 Nanoparticle Suspensions in Water. Nanomaterials, 12(2), 217. https://doi.org/10.3390/nano12020217








