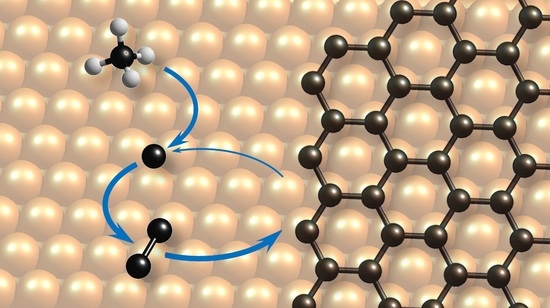
Analytical Model of CVD Growth of Graphene on Cu(111) Surface
Abstract
:1. Introduction
- The surface-catalyzed pyrolysis of hydrocarbons that lead to numerous carbon species on the surface;
- The aggregation and nucleation of these species on the metal surface, which produces graphene nuclei;
- The growth of the nuclei due to the attachment of feeding species;
- The coalescence of the flakes when high coverage is reached.
- Simulations are performed in the range of up to several hundred nanometers, whereas the typical sizes of the nuclei observed in experiments are in the micrometer scale [30];
- kMC calculations are usually limited to the steady growth of a single graphene nucleus, so there is no information on the nucleation step included. Consequently, no size distribution or nuclei density can be obtained, which are known to be crucial characteristics of CVD graphene;
- Simulations on the hexagonal kMC lattice are complicated by the formation of the pentagon edge (the pairwise closing of the Klein edge of graphene on the Cu(111) surface) and its opening by the next attaching particle.
2. Theory and Computational Details
- and adparticles which have high mobility on the surface and play the role of feeding species for nucleation and growth;
- Small clusters of various geometries which cannot yet be associated with the solid crystalline graphene phase;
- Well-defined graphene nuclei which are immobile on the surface and grow due to the attachments of and particles.
2.1. Growth Rate
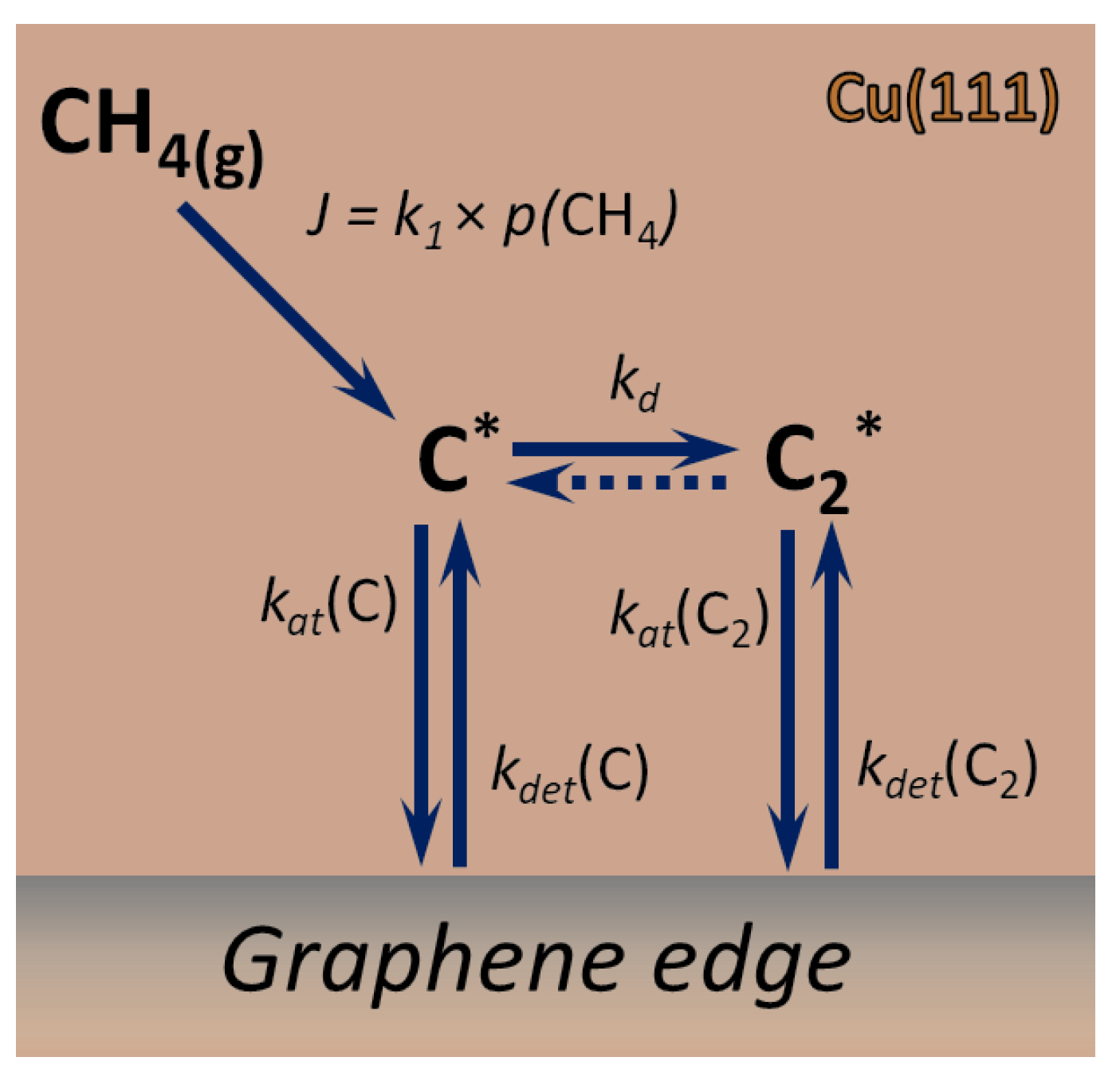
2.2. Kinetic Model of Growth
2.3. Nucleation Rate
2.4. Details of DFT Calculations
3. Results and Discussion
3.1. DFT Calculations
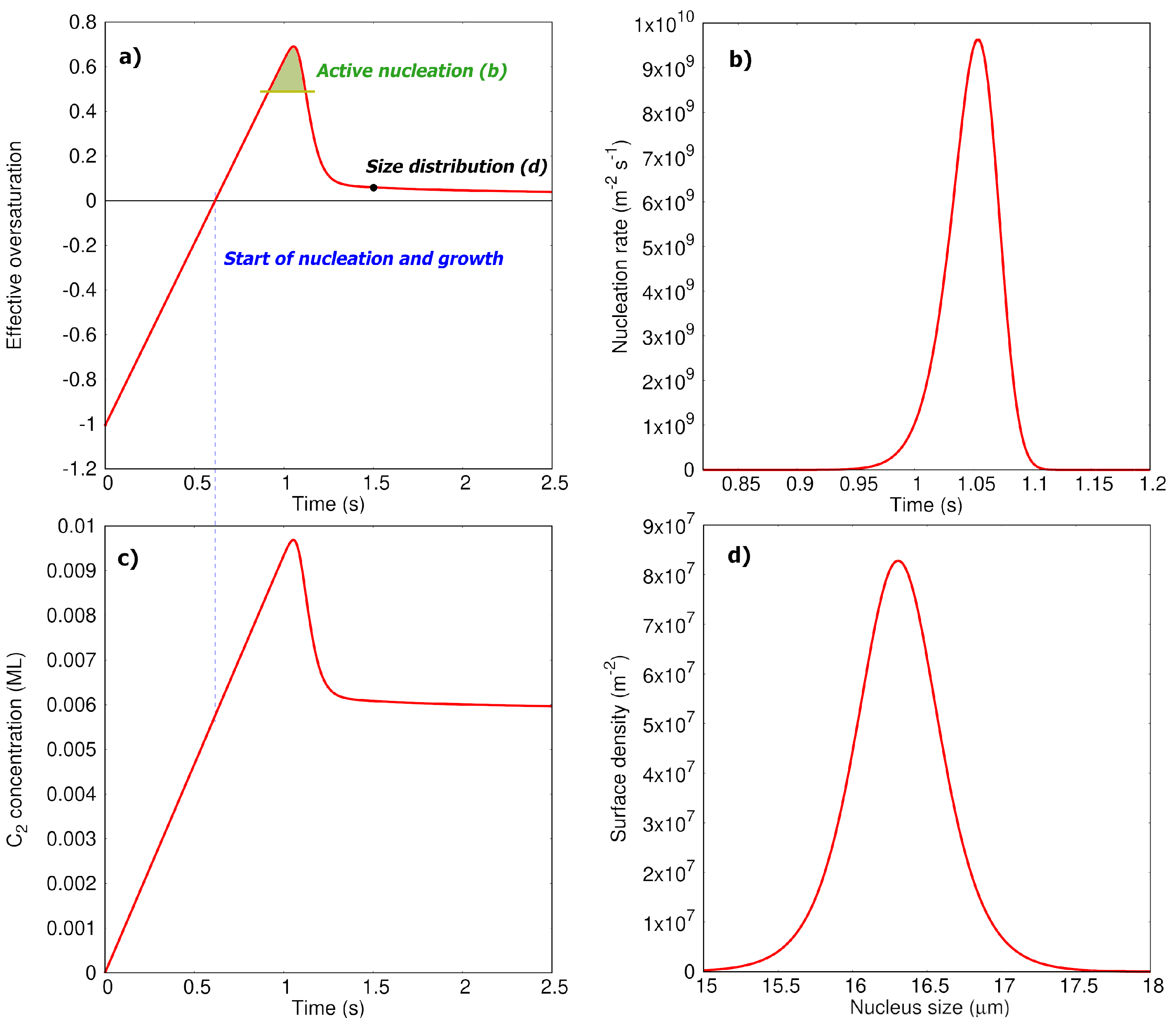
3.2. Analytical Kinetic Model
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CVD | chemical vapor deposition |
| BEEF–vdW | Bayesian error estimation functional with van der Waals correlation |
| DFT | density functional theory |
| D2 / D3 | D2 / D3 dispersion correction of Grimme |
| kMC | kinetic Monte Carlo |
| ML | monolayer (unit of the surface concentration) |
| PBE | Perdew–Burke–Ernzerhof functional |
Appendix A. Expressions for the Rate Constants
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef]
- Akinwande, D.; Tao, L.; Yu, Q.; Lou, X.; Peng, P.; Kuzum, D. Large-Area Graphene Electrodes: Using CVD to facilitate applications in commercial touchscreens, flexible nanoelectronics, and neural interfaces. IEEE Nanotechnol. Mag. 2015, 9, 6–14. [Google Scholar] [CrossRef]
- Zhong, M.; Xu, D.; Yu, X.; Huang, K.; Liu, X.; Qu, Y.; Xu, Y.; Yang, D. Interface coupling in graphene/fluorographene heterostructure for high-performance graphene/silicon solar cells. Nano Energy 2016, 28, 12–18. [Google Scholar] [CrossRef]
- Graphene Applications & Uses. Available online: https://www.graphenea.com/pages/graphene-uses-applications (accessed on 4 August 2022).
- Dong, J.; Zhang, L.; Wu, B.; Ding, F.; Liu, Y. Theoretical Study of Chemical Vapor Deposition Synthesis of Graphene and Beyond: Challenges and Perspectives. J. Phys. Chem. Lett. 2021, 12, 7942–7963. [Google Scholar] [CrossRef] [PubMed]
- Paton, K.R.; Varrla, E.; Backes, C.; Smith, R.J.; Khan, U.; O’Neill, A.; Boland, C.; Lotya, M.; Istrate, O.M.; King, P.; et al. Scalable production of large quantities of defect-free few-layer graphene by shear exfoliation in liquids. Nat. Mater. 2014, 13, 624–630. [Google Scholar] [CrossRef]
- Sadri, R.; Kamali, K.Z.; Hosseini, M.; Zubir, N.; Kazi, S.N.; Ahmadi, G.; Dahari, M.; Huang, N.M.; Golsheikh, A.M. Experimental study on thermo-physical and rheological properties of stable and green reduced graphene oxide nanofluids: Hydrothermal assisted technique. J. Dispers. Sci. Technol. 2017, 38, 1302–1310. [Google Scholar] [CrossRef]
- Chakrabarti, A.; Lu, J.; Skrabutenas, J.C.; Xu, T.; Xiao, Z.; Maguire, J.A.; Hosmane, N.S. Conversion of carbon dioxide to few-layer graphene. J. Mater. Chem. 2011, 21, 9491–9493. [Google Scholar] [CrossRef]
- Liu, W.; Li, H.; Xu, C.; Khatami, Y.; Banerjee, K. Synthesis of high-quality monolayer and bilayer graphene on copper using chemical vapor deposition. Carbon 2011, 49, 4122–4130. [Google Scholar] [CrossRef]
- Melero, C.; Rincón, R.; Muñoz, J.; Zhang, G.; Sun, S.; Perez, A.; Royuela, O.; González-Gago, C.; Calzada, M.D. Scalable graphene production from ethanol decomposition by microwave argon plasma torch. Plasma Phys. Control. Fusion 2017, 60, 014009. [Google Scholar] [CrossRef]
- Bonaccorso, F.; Lombardo, A.; Hasan, T.; Sun, Z.; Colombo, L.; Ferrari, A.C. Production and processing of graphene and 2d crystals. Mater. Today 2012, 15, 564–589. [Google Scholar] [CrossRef]
- Raccichini, R.; Varzi, A.; Passerini, S.; Scrosati, B. The role of graphene for electrochemical energy storage. Nat. Mater. 2015, 14, 271–279. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Fal’ko, V.I.; Colombo, L.; Gellert, P.R.; Schwab, M.G.; Kim, K. A roadmap for graphene. Nature 2012, 490, 192–200. [Google Scholar] [CrossRef]
- Xu, Y.; Cao, H.; Xue, Y.; Li, B.; Cai, W. Liquid-Phase Exfoliation of Graphene: An Overview on Exfoliation Media, Techniques, and Challenges. Nanomaterials 2018, 8, 942. [Google Scholar] [CrossRef]
- Ron Mertens, General Graphene Launched Its New High-Capacity CVD Graphene Roll-to-Roll Production Line. 2021. Available online: https://www.graphene-info.com/general-graphene-launched-its-new-high-capacity-cvd-graphene-roll-roll (accessed on 4 August 2022).
- Liu, H.; Liu, Y. Controlled Chemical Synthesis in CVD Graphene. Phys. Sci. Rev. 2017, 2, 20160107. [Google Scholar]
- Lyding, J.; Wood, J.; Pop, E. Growing better graphene by finding the best copper surface. SPIE Newsroom 2012, 10, 004110. [Google Scholar] [CrossRef]
- Zhao, L.; Rim, K.; Zhou, H.; He, R.; Heinz, T.; Pinczuk, A.; Flynn, G.; Pasupathy, A. Influence of copper crystal surface on the CVD growth of large area monolayer graphene. Solid State Commun. 2011, 151, 509–513. [Google Scholar] [CrossRef]
- Li, P.; Li, Z.; Yang, J. Dominant Kinetic Pathways of Graphene Growth in Chemical Vapor Deposition: The Role of Hydrogen. J. Phys. Chem. C 2017, 121, 25949–25955. [Google Scholar] [CrossRef]
- Qiu, Z.; Li, P.; Li, Z.; Yang, J. Atomistic Simulations of Graphene Growth: From Kinetics to Mechanism. Accounts Chem. Res. 2018, 51, 728–735. [Google Scholar] [CrossRef]
- Chen, S.; Gao, J.; Srinivasan, B.M.; Zhang, G.; Sorkin, V.; Hariharaputran, R.; Zhang, Y.-W. An all-atom kinetic Monte Carlo model for chemical vapor deposition growth of graphene on Cu(1 1 1) substrate. J. Phys. Condens. Matter 2020, 32, 155401. [Google Scholar] [CrossRef]
- Gaillard, P.; Chanier, T.; Henrard, L.; Moskovkin, P.; Lucas, S. Multiscale simulations of the early stages of the growth of graphene on copper. Surf. Sci. 2015, 637–638, 11–18. [Google Scholar] [CrossRef]
- Dong, J.; Zhang, L.; Ding, F. Kinetics of Graphene and 2D Materials Growth. Adv. Mater. 2019, 31, 1801583. [Google Scholar] [CrossRef] [PubMed]
- Seah, C.-M.; Chai, S.-P.; Mohamed, A.R. Mechanisms of graphene growth by chemical vapour deposition on transition metals. Carbon 2014, 70, 1–21. [Google Scholar] [CrossRef]
- Saeed, M.; Alshammari, Y.; Majeed, S.A.; Al-Nasrallah, E. Chemical Vapour Deposition of Graphene-Synthesis, Characterisation, and Applications: A Review. Molecules 2020, 25, 3856. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhang, L.; Zhou, C. Review of Chemical Vapor Deposition of Graphene and Related Applications. Accounts Chem. Res. 2013, 46, 2329–2339. [Google Scholar] [CrossRef] [PubMed]
- Balerba, A.K.; Kotanidis, A.; Paraskeuas, A.; Gialampouki, M.; Gutiérrez Moreno, J.J.; Papageorgiou, D.G.; Evangelakis, G.A.; Lekka, C.E. Chapter 9—Graphene nano-flakes on Cu low-index surfaces by density functional theory and molecular dynamics simulations. Front. Nanosci. 2020, 17, 141–159. [Google Scholar]
- Lee, J.; Varshney, V.; Park, J.; Farmer, B.L.; Roy, A.K. In silico carbon molecular beam epitaxial growth of graphene on the h-BN substrate: Carbon source effect on van der Waals epitaxy. Nanoscale 2016, 8, 9704–9713. [Google Scholar] [CrossRef]
- Wu, P.; Zhang, Y.; Cui, P.; Li, Z.; Yang, J.; Zhang, Z. Carbon Dimers as the Dominant Feeding Species in Epitaxial Growth and Morphological Phase Transition of Graphene on Different Cu Substrates. Phys. Rev. Lett. 2015, 114, 216102. [Google Scholar] [CrossRef]
- Kim, H.; Mattevi, C.; Calvo, M.R.; Oberg, J.C.; Artiglia, L.; Agnoli, S.; Hirjibehedin, C.F.; Chhowalla, M.; Saiz, E. Activation Energy Paths for Graphene Nucleation and Growth on Cu. ACS Nano 2012, 6, 3614–3623. [Google Scholar] [CrossRef]
- Leidinger, P.; Kraus, J.; Günther, S. Predicting Graphene Growth on Cu: Universal Kinetic Growth Model and Its Experimental Verification. ACS Nano 2021, 15, 12201–12212. [Google Scholar] [CrossRef]
- Volmer, M. (Ed.) Kinetics of Formation of a New Phase. In Die Chemische Reaktion. Bd. IV. Kinetik der Phasenbildung; Translation to Russian of Volmer; M. Nauka: Moscow, Russia, 1939. [Google Scholar]
- Osipov, A.V. Kinetic model of vapour-deposited thin film condensation: Nucleation stage. Thin Solid Film. 1993, 227, 111–118. [Google Scholar] [CrossRef]
- Lifshitz, I.; Slyozov, V. The kinetics of precipitation from supersaturated solid solutions. J. Phys. Chem. Solids 1961, 19, 35–50. [Google Scholar] [CrossRef]
- Desai, R.C.; Kapral, R. Lifshitz–Slyozov–Wagner theory. In Dynamics of Self-Organized and Self-Assembled Structures; Cambridge University Press: Cambridge, UK, 2009; pp. 87–95. [Google Scholar]
- Becker, R.; Döring, W. Kinetische Behandlung der Keimbildung in übersättigten Dämpfen. Ann. Der Phys. 1935, 416, 719–752. [Google Scholar] [CrossRef]
- Yuan, Q.; Gao, J.; Shu, H.; Zhao, J.; Chen, X.; Ding, F. Magic Carbon Clusters in the Chemical Vapor Deposition Growth of Graphene. J. Am. Chem. Soc. 2012, 134, 2970–2975. [Google Scholar] [CrossRef]
- Ma, T.; Ren, W.; Zhang, X.; Liu, Z.; Gao, Y.; Yin, L.C.; Ma, X.L.; Ding, F.; Cheng, H.M. Edge-controlled growth and kinetics of single-crystal graphene domains by chemical vapor deposition. Proc. Natl. Acad. Sci. USA 2013, 110, 20386–20391. [Google Scholar] [CrossRef]
- Xing, S.; Wu, W.; Wang, Y.; Bao, J.; Pei, S.S. Kinetic study of graphene growth: Temperature perspective on growth rate and film thickness by chemical vapor deposition. Chem. Phys. Lett. 2013, 580, 62–66. [Google Scholar] [CrossRef]
- Wu, B.; Geng, D.; Xu, Z.; Guo, Y.; Huang, L.; Xue, Y.; Chen, J.; Yu, G.; Liu, Y. Self-organized graphene crystal patterns. NPG Asia Mater. 2013, 5, e36. [Google Scholar] [CrossRef]
- Cho, S.Y.; Kim, M.S.; Kim, M.; Kim, K.J.; Kim, H.M.; Lee, D.J.; Lee, S.H.; Kim, K.B. Self-assembly and continuous growth of hexagonal graphene flakes on liquid Cu. Nanoscale 2015, 7, 12820–12827. [Google Scholar] [CrossRef]
- Reckinger, N.; Tang, X.; Joucken, F.; Lajaunie, L.; Arenal, R.; Dubois, E.; Hackens, B.; Henrard, L.; Colomer, J.F. Oxidation-assisted graphene heteroepitaxy on copper foil. Nanoscale 2016, 8, 18751–18759. [Google Scholar] [CrossRef]
- Grebenko, A.K.; Krasnikov, D.V.; Bubis, A.V.; Stolyarov, V.S.; Vyalikh, D.V.; Makarova, A.A.; Fedorov, A.; Aitkulova, A.; Alekseeva, A.A.; Gilshtein, E.; et al. High-Quality Graphene Using Boudouard Reaction. Adv. Sci. 2022, 9, 2200217. [Google Scholar] [CrossRef]
- Wellendorff, J.; Lundgaard, K.T.; Møgelhøj, A.; Petzold, V.; Landis, D.D.; Nørskov, J.K.; Bligaard, T.; Jacobsen, K.W. Density functionals for surface science: Exchange-correlation model development with Bayesian error estimation. Phys. Rev. B 2012, 85, 235149. [Google Scholar] [CrossRef]
- Dirac, P.A.M.; Fowler, R.H. Quantum mechanics of many-electron systems. Proc. R. Soc. Lond. A. Math. Phys. Sci. 1929, 123, 714–733. [Google Scholar]
- Slater, J.C. A Simplification of the Hartree-Fock Method. Phys. Rev. 1951, 81, 385–390. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Wellendorff, J.; Silbaugh, T.L.; Garcia-Pintos, D.; Nørskov, J.K.; Bligaard, T.; Studt, F.; Campbell, C.T. A benchmark database for adsorption bond energies to transition metal surfaces and comparison to selected DFT functionals. Surf. Sci. 2015, 640, 36–44. [Google Scholar] [CrossRef]
- Sharada, S.M.; Bligaard, T.; Luntz, A.C.; Kroes, G.J.; Nørskov, J.K. SBH10: A Benchmark Database of Barrier Heights on Transition Metal Surfaces. J. Phys. Chem. C 2017, 121, 19807–19815. [Google Scholar] [CrossRef]
- Lundgaard, K.T.; Wellendorff, J.; Voss, J.; Jacobsen, K.W.; Bligaard, T. mBEEF-vdW: Robust fitting of error estimation density functionals. Phys. Rev. B 2016, 93, 235162. [Google Scholar] [CrossRef]
- Studt, F.; Abild-Pedersen, F.; Varley, J.B.; Nørskov, J.K. CO and CO2 Hydrogenation to Methanol Calculated Using the BEEF-vdW Functional. Catal. Lett. 2012, 143, 71–73. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Annalen der Physik 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Jónsson, H.; Mills, G.; Jacobsen, K.W. Nudged elastic band method for finding minimum energy paths of transitions. In Classical and Quantum Dynamics in Condensed Phase Simulations; World Scientific: Singapore, 1998; pp. 385–404. [Google Scholar]
- Chakraverty, B. Grain size distribution in thin films—1. Conservative systems. J. Phys. Chem. Solids 1967, 28, 2401–2412. [Google Scholar] [CrossRef]

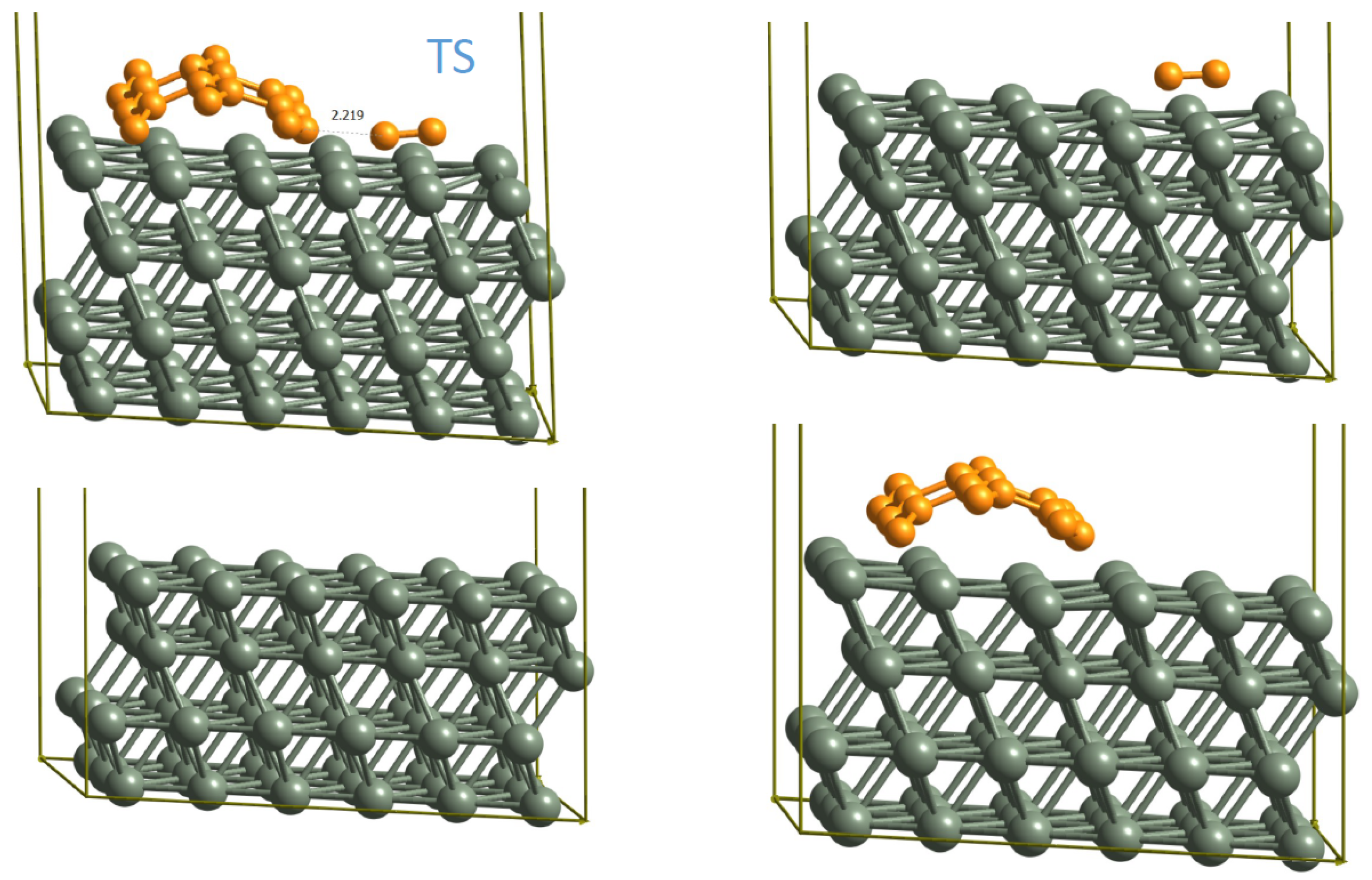
| Reaction | BEEF-vdW | PBE-D3 | Ref. [19] |
|---|---|---|---|
| 1.94 | 1.48 | 1.63 | |
| 0.25 | 0.55 | 0.25 | |
| 3.97 | 3.62 | 2.75 | |
| 0.57 | 0.68 | 1.27 | |
| 1.76 | 1.36 | 1.57 | |
| 1.21 | 1.32 | 0.58 | |
| 2.31 | 2.30 | 2.19 |
| Ribbon Width | Attachment Barrier (eV) | Detachment Barrier (eV) |
|---|---|---|
| two-ring | 1.21 | 2.40 |
| three-ring | 1.32 | 2.38 |
| four-ring | 1.25 | 2.28 |
| five-ring | 1.21 | 2.31 |
| Kinetic Parameter | Units | Value | Physical Meaning |
|---|---|---|---|
| J | Rate of production | ||
| Rate constant of dimerization | |||
| Rate constant of attachment to a flake | |||
| Rate constant of detachment from a flake | |||
| Rate constant of attachment to a flake | |||
| Rate constant of detachment from a flake | |||
| A | Rate of nucleation assuming zero nucleation barrier | ||
| U | - | 15 | Value of - defines nucleation barrier for the given effective oversaturation |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Popov, I.; Bügel, P.; Kozlowska, M.; Fink, K.; Studt, F.; Sharapa, D.I. Analytical Model of CVD Growth of Graphene on Cu(111) Surface. Nanomaterials 2022, 12, 2963. https://doi.org/10.3390/nano12172963
Popov I, Bügel P, Kozlowska M, Fink K, Studt F, Sharapa DI. Analytical Model of CVD Growth of Graphene on Cu(111) Surface. Nanomaterials. 2022; 12(17):2963. https://doi.org/10.3390/nano12172963
Chicago/Turabian StylePopov, Ilya, Patrick Bügel, Mariana Kozlowska, Karin Fink, Felix Studt, and Dmitry I. Sharapa. 2022. "Analytical Model of CVD Growth of Graphene on Cu(111) Surface" Nanomaterials 12, no. 17: 2963. https://doi.org/10.3390/nano12172963
APA StylePopov, I., Bügel, P., Kozlowska, M., Fink, K., Studt, F., & Sharapa, D. I. (2022). Analytical Model of CVD Growth of Graphene on Cu(111) Surface. Nanomaterials, 12(17), 2963. https://doi.org/10.3390/nano12172963