Photonic Materials Cloud: An Online Interactive Open Tool for Creating, Comparing, and Testing Photonic Materials
Abstract
:1. Introduction
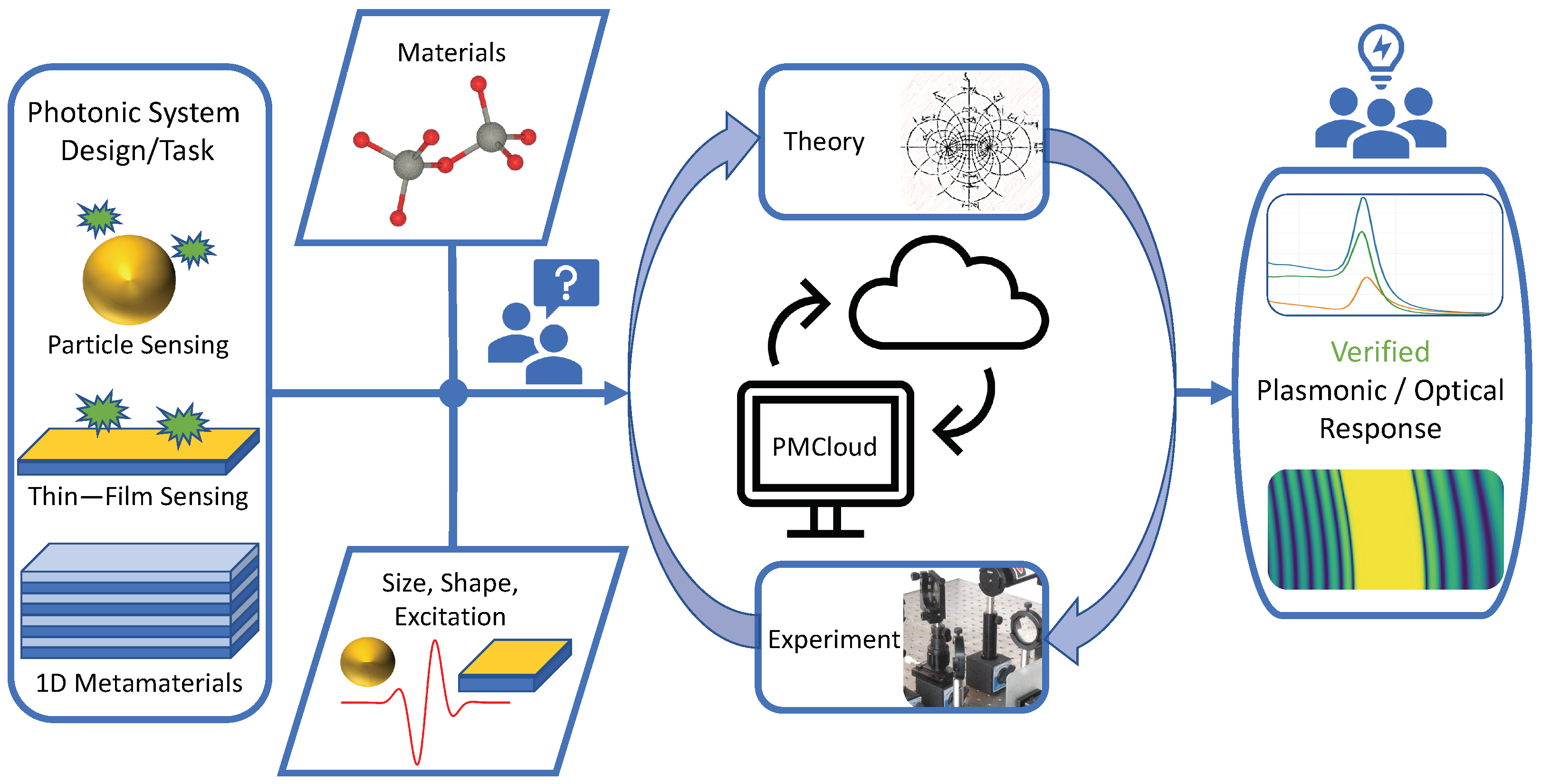
2. Use Cases—What can the PMCloud Help with?
2.1. Plasmonic Bio-Sensing
2.2. Material Development
2.3. Thin Films
2.4. Teaching
3. Methods
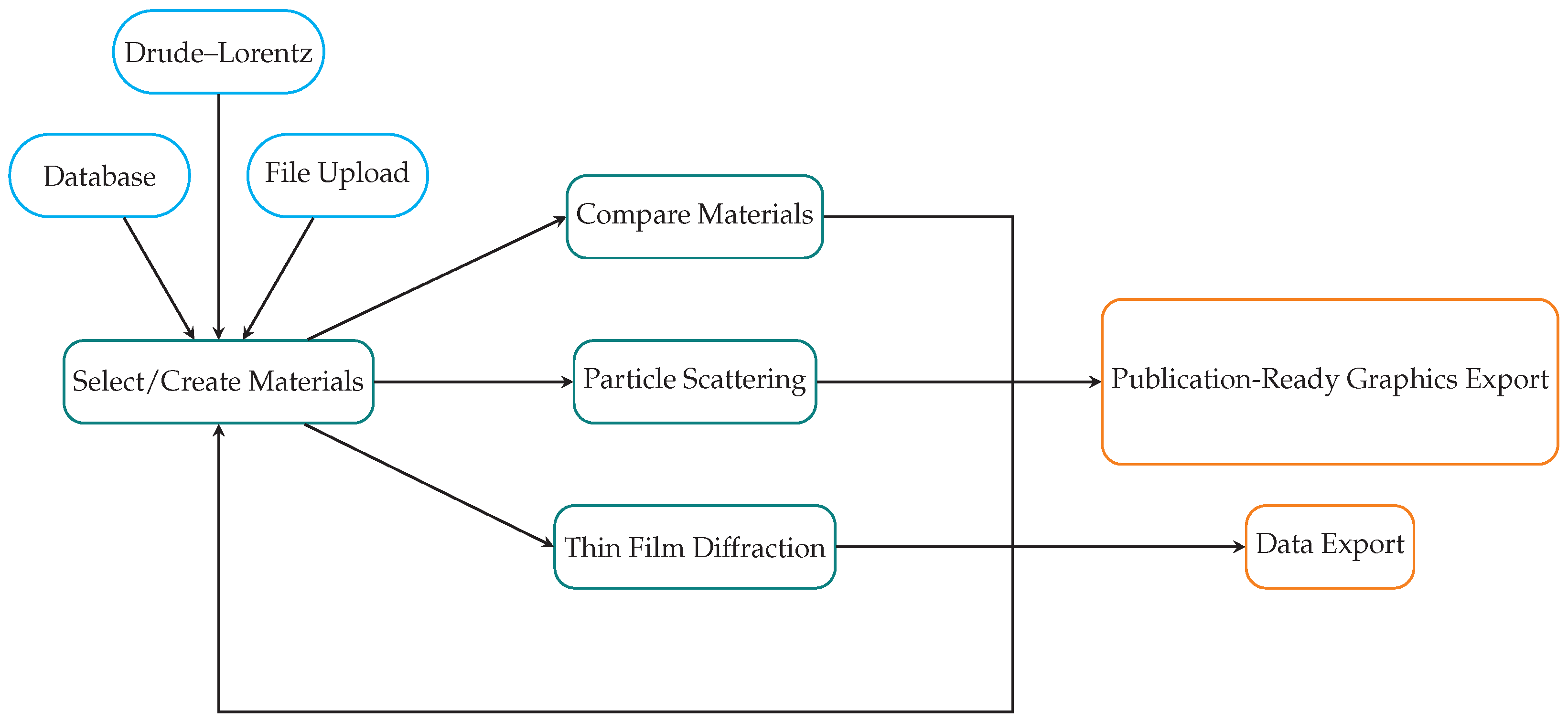
3.1. Materials Tool
- Uploading a .txt file from experimental data, simulation, or other source.
- Pulling the material model from the refractive index database [22].
- Generating a material using Drude–Lorentz parameters.
- Generating a simple constant refractive index material by entering the n and k values.
Drude–Lorentz Material Model
3.2. Comparison Tool
3.3. Particle Scattering through Mie Theory
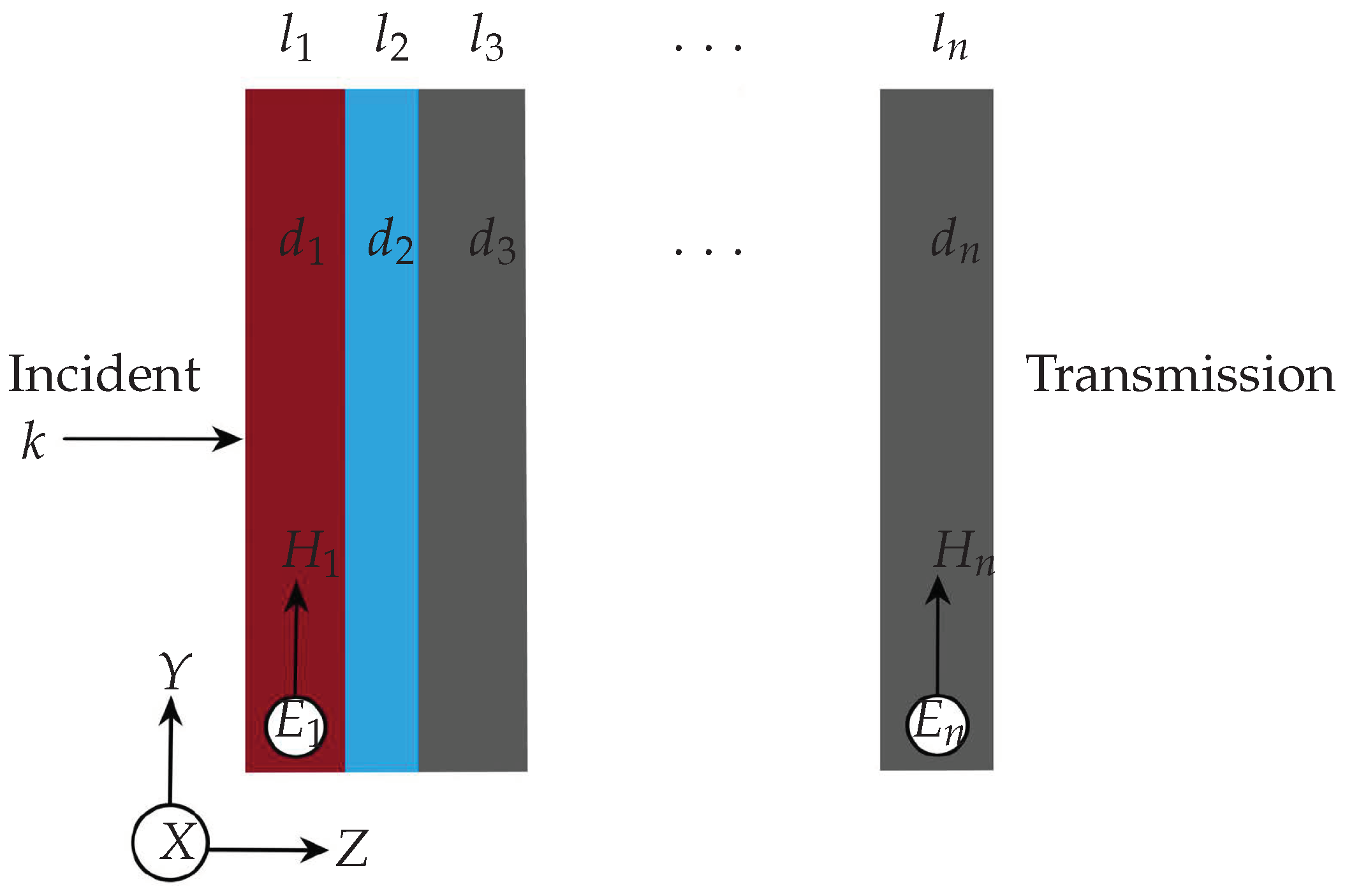
3.4. Thin-Film Tool
4. Numerical Results and Discussion
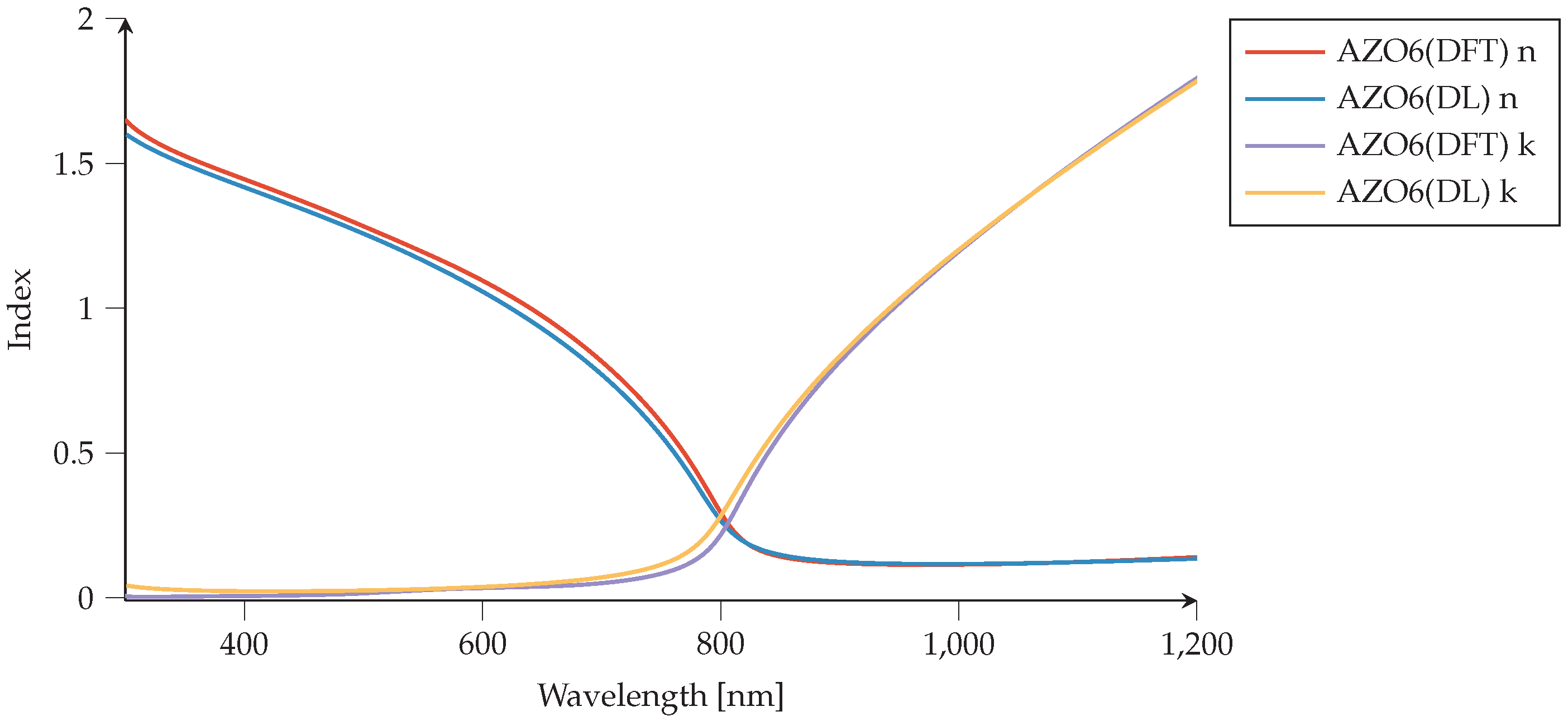
4.1. Materials Tool: Drude–Lorentz Parameters
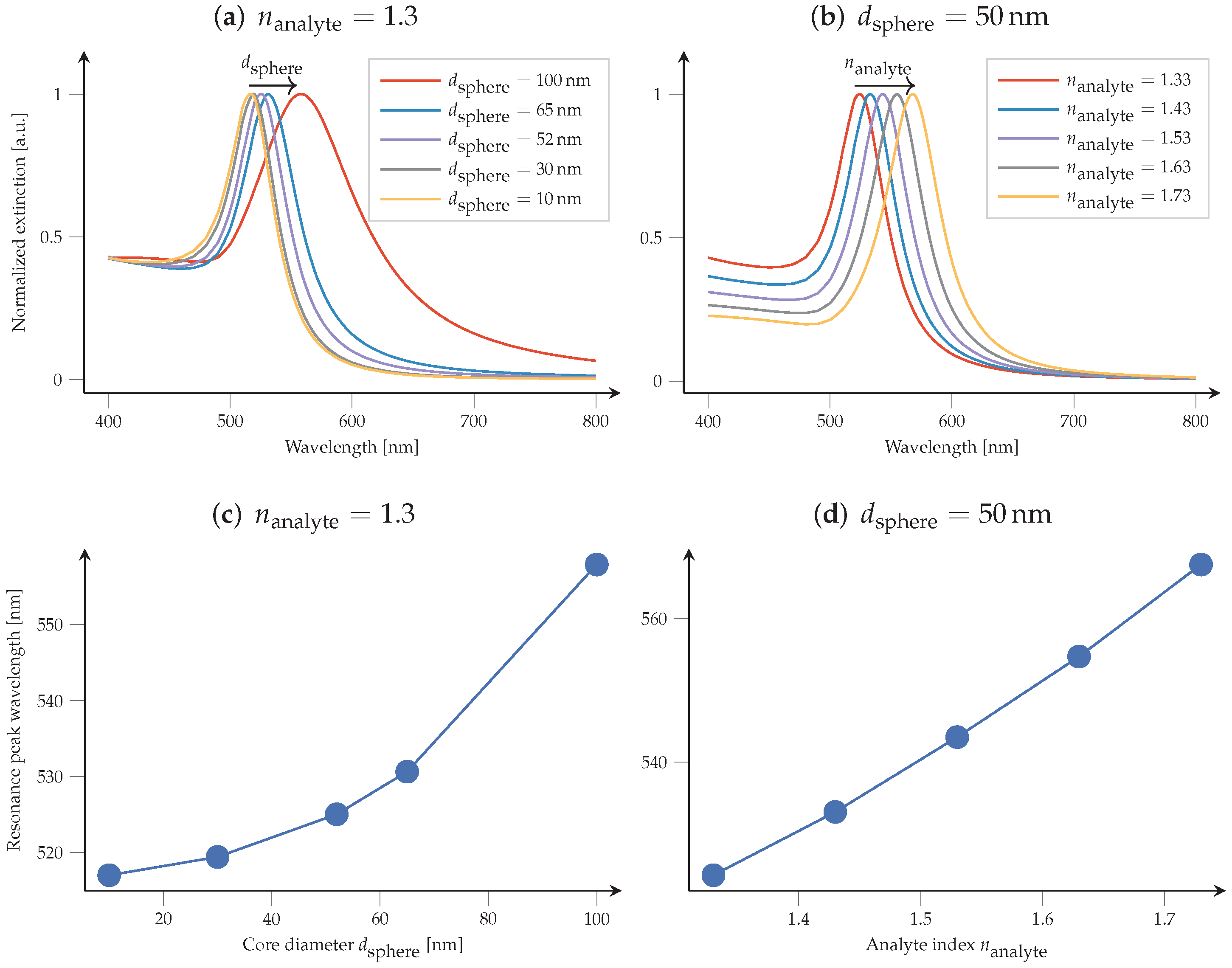
4.2. Particle Scattering
4.2.1. Light Scattering from a Gold Sphere for Sensing Applications
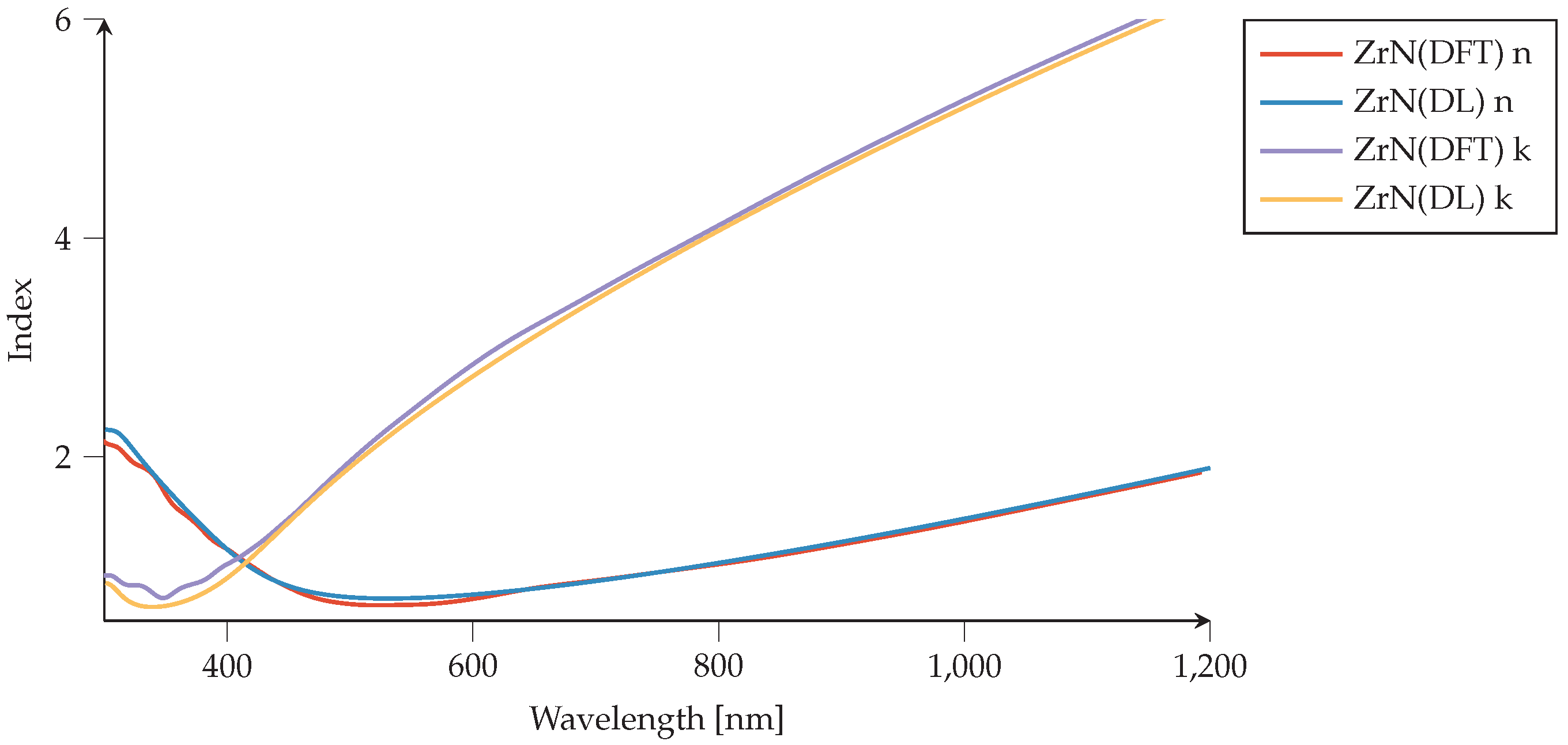
4.2.2. Light Scattering from AZO and ZrN Spheres
4.3. Kretschmann Configuration for AZO6
4.4. An AlAs/GaAs Thin-Film Bragg Reflector
5. Conclusions and Future Plans
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kasani, S.; Curtin, K.; Wu, N. A review of 2D and 3D plasmonic nanostructure array patterns: Fabrication, light management and sensing applications. Nanophotonics 2019, 8, 2065–2089. [Google Scholar] [CrossRef]
- de Aberasturi, D.J.; Serrano-Montes, A.B.; Liz-Marzán, L.M. Modern Applications of Plasmonic Nanoparticles: From Energy to Health. Adv. Opt. Mater. 2015, 3, 602–617. [Google Scholar] [CrossRef]
- Thraskias, C.A.; Lallas, E.N.; Neumann, N.; Schares, L.; Offrein, B.J.; Henker, R.; Plettemeier, D.; Ellinger, F.; Leuthold, J.; Tomkos, I. Survey of Photonic and Plasmonic Interconnect Technologies for Intra-Datacenter and High-Performance Computing Communications. IEEE Commun. Surv. Tutor. 2018, 20, 2758–2783. [Google Scholar] [CrossRef] [Green Version]
- Anttu, N.; Mäntynen, H.; Sorokina, A.; Turunen, J.; Sadi, T.; Lipsanen, H. Applied electromagnetic optics simulations for nanophotonics. J. Appl. Phys. 2021, 129, 131102. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; Wiley: New York, NY, USA; Chichester, UK, 2004. [Google Scholar]
- Khurgin, J.B. How to deal with the loss in plasmonics and metamaterials. Nat. Nanotechnol. 2015, 10, 2–6. [Google Scholar] [CrossRef]
- Khlebtsov, N.G.; Dykman, L.A. Optical properties and biomedical applications of plasmonic nanoparticles. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 1–35. [Google Scholar] [CrossRef]
- Otto, A. Excitation of nonradiative surface plasma waves in silver by the method of frustrated total reflection. Z. Phys. A Hadrons Nucl. 1968, 216, 398–410. [Google Scholar] [CrossRef]
- Kretschmann, E.; Raether, H. Radiative Decay of Non Radiative Surface Plasmons Excited by Light. Z. Naturforsch. A Phys. Sci. 1968, 23, 2135–2136. [Google Scholar] [CrossRef]
- Chen, T.; Li, S.; Sun, H. Metamaterials application in sensing. Sensors 2012, 12, 2742–2765. [Google Scholar] [CrossRef] [PubMed]
- Yao, K.; Liu, Y. Plasmonic metamaterials. Nanotechnol. Rev. 2014, 3, 177–210. [Google Scholar] [CrossRef] [Green Version]
- Jang, Y.H.; Jang, Y.J.; Kim, S.; Quan, L.N.; Chung, K.; Kim, D.H. Plasmonic Solar Cells: From Rational Design to Mechanism Overview. Chem. Rev. 2016, 116, 14982–15034. [Google Scholar] [CrossRef] [PubMed]
- Stewart, M.E.; Anderton, C.R.; Thompson, L.B.; Maria, J.; Gray, S.K.; Rogers, J.A.; Nuzzo, R.G. Nanostructured plasmonic sensors. Chem. Rev. 2008, 108, 494–521. [Google Scholar] [CrossRef] [PubMed]
- Fang, Y.; Sun, M. Nanoplasmonic waveguides: Towards applications in integrated nanophotonic circuits. Light Sci. Appl. 2015, 4, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Baig, N.; Kammakakam, I.; Falath, W. Nanomaterials: A review of synthesis methods, properties, recent progress, and challenges. Mater. Adv. 2021, 2, 1821–1871. [Google Scholar] [CrossRef]
- Lock, J.A.; Gouesbet, G. Generalized Lorenz-Mie theory and applications. J. Quant. Spectrosc. Radiat. Transf. 2009, 110, 800–807. [Google Scholar] [CrossRef]
- Gouesbet, G.; Grehan, G.; Maheu, B. Scattering of a Gaussian beam by a Mie scatter center using a Bromwich formalism. J. Opt. 1985, 16, 83–93. [Google Scholar] [CrossRef]
- Walder, C.; Lacombe, J.; von Maydell, K.; Agert, C. Optical modeling of thin film silicon solar cells by combination of the transfer-matrix method and the Raytracer algorithm. Opt. Model. Des. II 2012, 8429, 84290K. [Google Scholar] [CrossRef]
- Yu, S.G.; Kim, K.W.; Stroscio, M.A.; Iafrate, G.J.; Sun, J.P.; Haddad, G.I. Transfer matrix method for interface optical-phonon modes in multiple-interface heterostructure systems. J. Appl. Phys. 1997, 82, 3363–3367. [Google Scholar] [CrossRef]
- Poncelet, O.; Kotipalli, R.; Vermang, B.; Macleod, A.; Francis, L.A.; Flandre, D. Optimisation of rear reflectance in ultra-thin CIGS solar cells towards >20% efficiency. Sol. Energy 2017, 146, 443–452. [Google Scholar] [CrossRef] [Green Version]
- The Photonic Materials Cloud. Available online: http://photonicmaterials.eu (accessed on 4 July 2022).
- Refractive Index Database. Available online: https://refractiveindex.info (accessed on 4 July 2022).
- Mie Scattering Calculator. Available online: https://omlc.org/calc/mie_calc.html (accessed on 4 July 2022).
- Mayer, K.M.; Hafner, J.H. Localized Surface Plasmon Resonance Sensors. Chem. Rev. 2011, 111, 3828–3857. [Google Scholar] [CrossRef]
- Yesudasu, V.; Pradhan, H.S.; Pandya, R.J. Recent progress in surface plasmon resonance based sensors: A comprehensive review. Heliyon 2021, 7, e06321. [Google Scholar] [CrossRef]
- Shrivastav, A.M.; Cvelbar, U.; Abdulhalim, I. A comprehensive review on plasmonic-based biosensors used in viral diagnostics. Commun. Biol. 2021, 4, 70. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.; Liu, W.; Cai, C.; Liu, H. Comparative investigation of infrared optical absorption properties of silicon oxide, oxynitride and nitride films. Seventh Int. Conf. Thin Film. Phys. Appl. 2010, 7995, 79950T. [Google Scholar] [CrossRef]
- Patsalas, P.; Kalfagiannis, N.; Kassavetis, S. Optical properties and plasmonic performance of titanium nitride. Materials 2015, 8, 3128–3154. [Google Scholar] [CrossRef] [Green Version]
- Adams, D.C.; Inampudi, S.; Ribaudo, T.; Slocum, D.; Vangala, S.; Kuhta, N.A.; Goodhue, W.D.; Podolskiy, V.A.; Wasserman, D. Funneling light through a subwavelength aperture with epsilon-near-zero materials. Phys. Rev. Lett. 2011, 107, 1090–1099. [Google Scholar] [CrossRef] [PubMed]
- Naik, G.V.; Shalaev, V.M.; Boltasseva, A. Alternative plasmonic materials: Beyond gold and silver. Adv. Mater. 2013, 25, 3264–3294. [Google Scholar] [CrossRef]
- Lu, J.; Ueda, K.I.; Yagi, H.; Yanagitani, T.; Akiyama, Y.; Kaminskii, A.A. Neodymium doped yttrium aluminum garnet (Y3Al5O 12) nanocrystalline ceramics—A new generation of solid state laser and optical materials. J. Alloys Compd. 2002, 341, 220–225. [Google Scholar] [CrossRef]
- Haw, C.; Chiu, W.; Abdul Rahman, S.; Khiew, P.; Radiman, S.; Abdul Shukor, R.; Hamid, M.A.A.; Ghazali, N. The design of new magnetic-photocatalyst nanocomposites (CoFe2O4-TiO2) as smart nanomaterials for recyclable-photocatalysis applications. New J. Chem. 2016, 40, 1124–1136. [Google Scholar] [CrossRef]
- Liu, X.; Zhu, G.; Wang, X.; Yuan, X.; Lin, T.; Huang, F. Progress in Black Titania: A New Material for Advanced Photocatalysis. Adv. Energy Mater. 2016, 6, 1600452. [Google Scholar] [CrossRef]
- Oreski, G.; Stein, J.S.; Eder, G.C.; Berger, K.; Bruckman, L.; French, R.; Vedde, J.; Weiß, K.A. Motivation, benefits, and challenges for new photovoltaic material & module developments. Prog. Energy 2022, 4, 032003. [Google Scholar] [CrossRef]
- Gaskins, J.T.; Hopkins, P.E.; Merrill, D.R.; Bauers, S.R.; Hadland, E.; Johnson, D.C.; Koh, D.; Yum, J.H.; Banerjee, S.; Nordell, B.J.; et al. Review—Investigation and Review of the Thermal, Mechanical, Electrical, Optical, and Structural Properties of Atomic Layer Deposited High- k Dielectrics: Beryllium Oxide, Aluminum Oxide, Hafnium Oxide, and Aluminum Nitride. ECS J. Solid State Sci. Technol. 2017, 6, N189–N208. [Google Scholar] [CrossRef] [Green Version]
- Hsieh, W.T.; Wu, P.C.; Khurgin, J.B.; Tsai, D.P.; Liu, N.; Sun, G. Comparative Analysis of Metals and Alternative Infrared Plasmonic Materials. ACS Photonics 2018, 5, 2541–2548. [Google Scholar] [CrossRef] [Green Version]
- Chopra, K.L.; Paulson, P.D.; Dutta, V. Thin-film solar cells: An overview. Prog. Photovolt. 2004, 12, 69–92. [Google Scholar] [CrossRef]
- Malureanu, R.; Lavrinenko, A. Ultra-thin films for plasmonics: A technology overview. Nanotechnol. Rev. 2015, 4, 259–275. [Google Scholar] [CrossRef]
- Korkmaz, S.; Kariper, A. Glass formation, production and superior properties of Zr-based thin film metallic glasses (TFMGs): A status review. J. Non-Cryst. Solids 2020, 527, 119753. [Google Scholar] [CrossRef]
- Sharma, S.; Vyas, S.; Periasamy, C.; Chakrabarti, P. Structural and optical characterization of ZnO thin films for optoelectronic device applications by RF sputtering technique. Superlattices Microstruct. 2014, 75, 378–389. [Google Scholar] [CrossRef]
- Müllerová, J.; Jurečka, S.; Šutta, P. Optical characterization of polysilicon thin films for solar applications. Sol. Energy 2006, 80, 667–674. [Google Scholar] [CrossRef]
- Mustafa, H.; Hunter, D.; Pradhan, A.K.; Roy, U.N.; Cui, Y.; Burger, A. Synthesis and characterization of AgInSe2 for application in thin film solar cells. Thin Solid Films 2007, 515, 7001–7004. [Google Scholar] [CrossRef]
- Paraguay, D.F.; Estrada, L.W.; Acosta, N.D.R.; Andrade, E.; Miki-Yoshida, M. Growth, structure and optical characterization of high quality ZnO thin films obtained by spray pyrolysis. Thin Solid Films 1999, 350, 192–202. [Google Scholar] [CrossRef]
- Vinogradov, A.P.; Dorofeenko, A.V.; Pukhov, A.A.; Lisyansky, A.A. Exciting surface plasmon polaritons in the Kretschmann configuration by a light beam. Phys. Rev. B 2018, 97, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Lambert, A.S.; Valiulis, S.N.; Malinick, A.S.; Tanabe, I.; Cheng, Q. Plasmonic Biosensing with Aluminum Thin Films under the Kretschmann Configuration. Anal. Chem. 2020, 92, 8654–8659. [Google Scholar] [CrossRef] [PubMed]
- Diyatmika, W.; Chu, J.P.; Kacha, B.T.; Yu, C.C.; Lee, C.M. Thin film metallic glasses in optoelectronic, magnetic, and electronic applications: A recent update. Curr. Opin. Solid State Mater. Sci. 2015, 19, 95–106. [Google Scholar] [CrossRef]
- Shabani, A.; Nezhad, M.K.; Rahmani, N.; Mishra, Y.K.; Sanyal, B.; Adam, J. Revisiting the Optical Dispersion of Aluminium-Doped Zinc Oxide: New Perspectives for Plasmonics and Metamaterials. Adv. Photonics Res. 2020, 2, 2000086. [Google Scholar] [CrossRef]
- Van Rossum, G.; Drake, F.L. Python 3 Reference Manual; CreateSpace: Scotts Valley, CA, USA, 2009. [Google Scholar]
- Dash Python User Guide. Available online: https://dash.plotly.com/ (accessed on 4 July 2022).
- Mie, G. Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen. Ann. Phys. 1908, 330, 377–445. [Google Scholar] [CrossRef]
- Wriedt, T. Mie Theory: A Review. In The Mie Theory: Basics and Applications; Springer: Berlin/Heidelberg, Germany, 2012; pp. 53–71. [Google Scholar] [CrossRef]
- Sumlin, B.J.; Heinson, W.R.; Chakrabarty, R.K. Retrieving the aerosol complex refractive index using PyMieScatt: A Mie computational package with visualization capabilities. J. Quant. Spectrosc. Radiat. Transf. 2018, 205, 127–134. [Google Scholar] [CrossRef] [Green Version]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light, 2nd ed.; MacMillan Publishing Company: New York, NY, USA, 1964; pp. xxviii + 808. [Google Scholar]
- Anemogiannis, E.; Glytsis, E.N. Multilayer Waveguides: Efficient Numerical Analysis of General Structures. J. Light. Technol. 1992, 10, 1344–1351. [Google Scholar] [CrossRef]
- Shabani, A.; Korsa, M.T.; Petersen, S.; Nezhad, M.K.; Mishra, Y.K.; Adam, J. Zirconium Nitride: Optical Properties of an Emerging Intermetallic for Plasmonic Applications. Adv. Photonics Res. 2021, 2, 202100178. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.W. Optical Constants of the Noble Metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar] [CrossRef]
- Tang, Y.; Zeng, X.; Liang, J. Surface Plasmon Resonance: An Introduction to a Surface Spectroscopy Technique. J. Chem. Educ. 2010, 87, 742–746. [Google Scholar] [CrossRef] [Green Version]
- Fink, Y.; Winn, J.N.; Fan, S.; Chen, C.; Michel, J.; Joannopoulos, J.D.; Thomas, E.L. A Dielectric Omnidirectional Reflector. Science 1998, 282, 1679–1682. [Google Scholar] [CrossRef] [Green Version]
- Bikbaev, R.G.; Vetrov, S.Y.; Timofeev, I.V. Two Types of Localized States in a Photonic Crystal Bounded by an Epsilon near Zero Nanocomposite. Photonics 2018, 5, 22. [Google Scholar] [CrossRef] [Green Version]
- Wu, F.; Wu, X.; Xiao, S.; Liu, G.; Li, H. Broadband wide-angle multilayer absorber based on a broadband omnidirectional optical Tamm state. Opt. Express 2021, 29, 23976–23987. [Google Scholar] [CrossRef] [PubMed]
- Fu, A.; Gao, H.; Petrov, P.; Yang, P. Widely Tunable Distributed Bragg Reflectors Integrated into Nanowire Waveguides. Nano Lett. 2015, 15, 6909–6913. [Google Scholar] [CrossRef] [PubMed]
- Evans, P.W.; Wierer, J.J.; Holonyak, N. AlxGa1-xAs native-oxide-based distributed Bragg reflectors for vertical cavity surface emitting lasers. J. Appl. Phys. 1998, 84, 5436–5440. [Google Scholar] [CrossRef]
- Schubert, M.F.; Xi, J.Q.; Kim, J.K.; Schubert, E.F. Distributed Bragg reflector consisting of high- and low-refractive-index thin film layers made of the same material. Appl. Phys. Lett. 2007, 90, 141115. [Google Scholar] [CrossRef] [Green Version]
- Sheppard, C.J.R. Approximate calculation of the reflection coefficient from a stratified medium. J. Eur. Opt. Soc. A 1995, 4, 665–669. [Google Scholar] [CrossRef]
- Gao, B.; George, J.P.; Beeckman, J.; Neyts, K. Design, fabrication and characterization of a distributed Bragg reflector for reducing the étendue of a wavelength converting system. Opt. Express 2020, 28, 12837. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, P.; Zhang, Y.; Chen, L.; Yu, Y.; Han, X.; Yan, L.; Deng, G.; Zhang, B. Optimization design and preparation of near ultraviolet AlGaN/GaN distributed Bragg reflectors. Superlattices Microstruct. 2018, 122, 661–666. [Google Scholar] [CrossRef]
- Adachi, S. GaAs, AlAs, and AlxGa1-xAs: Material parameters for use in research and device applications. J. Appl. Phys. 1985, 58, R1–R29. [Google Scholar] [CrossRef]




| Resonance j | [eV] | [eV] | |
|---|---|---|---|
| 1 | 0 | 0.05 | 1 |
| 2 | 0.294 | 0.213 | 0.243 |
| 3 | 4.810 | 0.286 | 0.186 |
| 4 | 5.258 | 0.433 | 0.351 |
| 5 | 5.863 | 0.613 | 0.597 |
| 6 | 6.607 | 0.741 | 0.890 |
| 7 | 7.449 | 0.816 | 1.237 |
| 8 | 8.159 | 0.772 | 1.281 |
| 9 | 8.790 | 0.791 | 2.728 |
| Resonance j | [eV] | [eV] | |
|---|---|---|---|
| 1 | 0 | 0.2 | 1 |
| 2 | 0.269 | 0.216 | 0.088 |
| 3 | 3.986 | 0.240 | 0.148 |
| 4 | 4.280 | 0.352 | 0.284 |
| 5 | 4.634 | 0.527 | 0.519 |
| 6 | 5.098 | 0.742 | 0.819 |
| 7 | 5.712 | 0.998 | 1.204 |
| 8 | 6.489 | 1.317 | 1.882 |
| 9 | 7.495 | 1.724 | 3.508 |
| 10 | 8.879 | 1.697 | 12.81 |
| Resonance j | [eV] | [eV] | |
|---|---|---|---|
| 1 | 0 | 0.62 | 1 |
| 2 | 0.18 | 0.24 | 0.03 |
| 3 | 4.06 | 0.35 | 0.02 |
| 4 | 4.75 | 0.76 | 0.17 |
| 5 | 5.29 | 1.26 | 0.48 |
| 6 | 5.72 | 0.45 | 0.09 |
| 7 | 6.62 | 2.27 | 1.34 |
| 8 | 7.25 | 0.40 | 0.12 |
| 9 | 8.01 | 1.05 | 0.55 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Korsa, M.T.; Petersen, S.; Rahmani, N.; Shabani, A.; Mishra, Y.K.; Adam, J. Photonic Materials Cloud: An Online Interactive Open Tool for Creating, Comparing, and Testing Photonic Materials. Nanomaterials 2022, 12, 2585. https://doi.org/10.3390/nano12152585
Korsa MT, Petersen S, Rahmani N, Shabani A, Mishra YK, Adam J. Photonic Materials Cloud: An Online Interactive Open Tool for Creating, Comparing, and Testing Photonic Materials. Nanomaterials. 2022; 12(15):2585. https://doi.org/10.3390/nano12152585
Chicago/Turabian StyleKorsa, Matiyas Tsegay, Søren Petersen, Neda Rahmani, Alireza Shabani, Yogendra Kumar Mishra, and Jost Adam. 2022. "Photonic Materials Cloud: An Online Interactive Open Tool for Creating, Comparing, and Testing Photonic Materials" Nanomaterials 12, no. 15: 2585. https://doi.org/10.3390/nano12152585
APA StyleKorsa, M. T., Petersen, S., Rahmani, N., Shabani, A., Mishra, Y. K., & Adam, J. (2022). Photonic Materials Cloud: An Online Interactive Open Tool for Creating, Comparing, and Testing Photonic Materials. Nanomaterials, 12(15), 2585. https://doi.org/10.3390/nano12152585








