Sodium-Based Cylindrical Plasmonic Waveguides in the Near-Infrared
Abstract
:1. Introduction
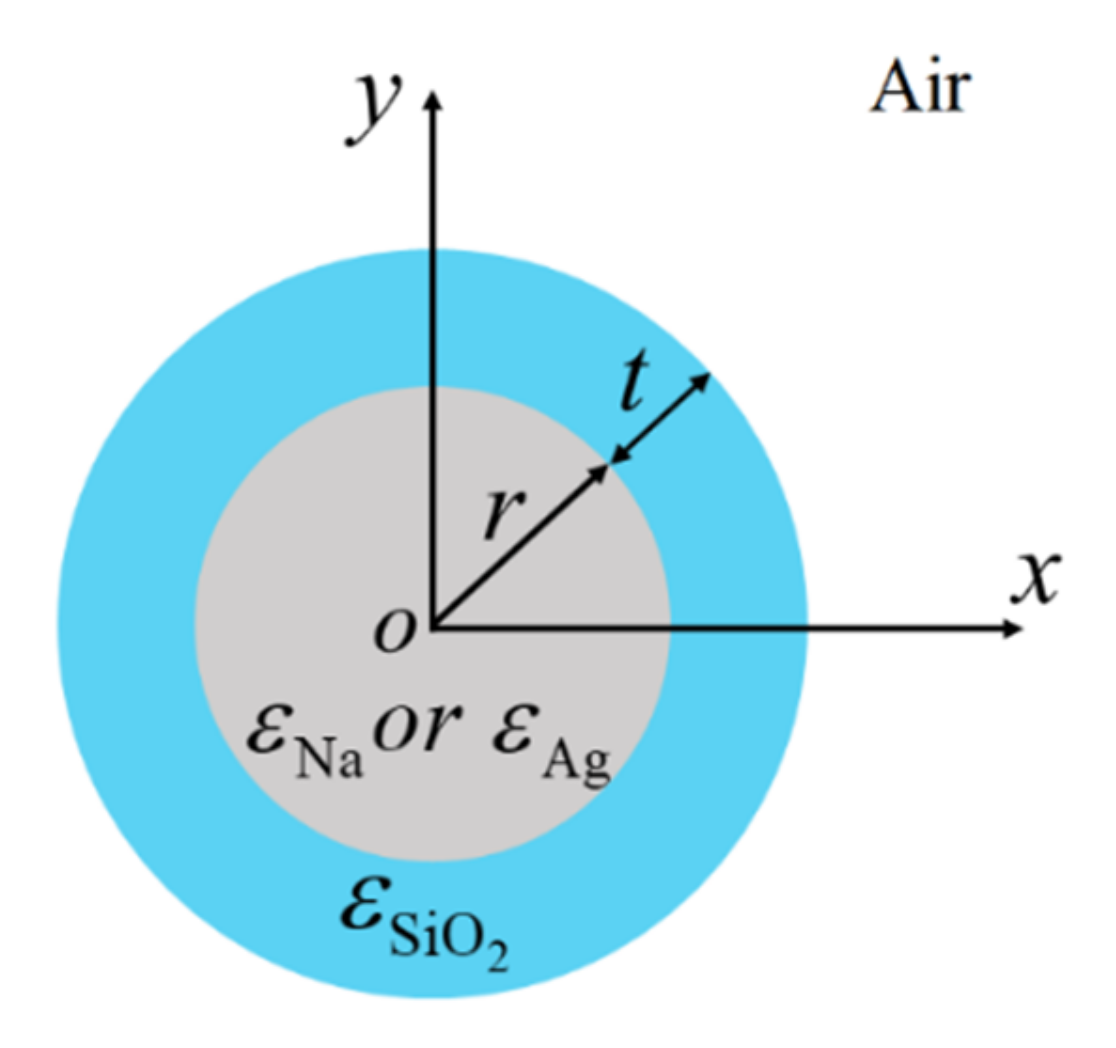
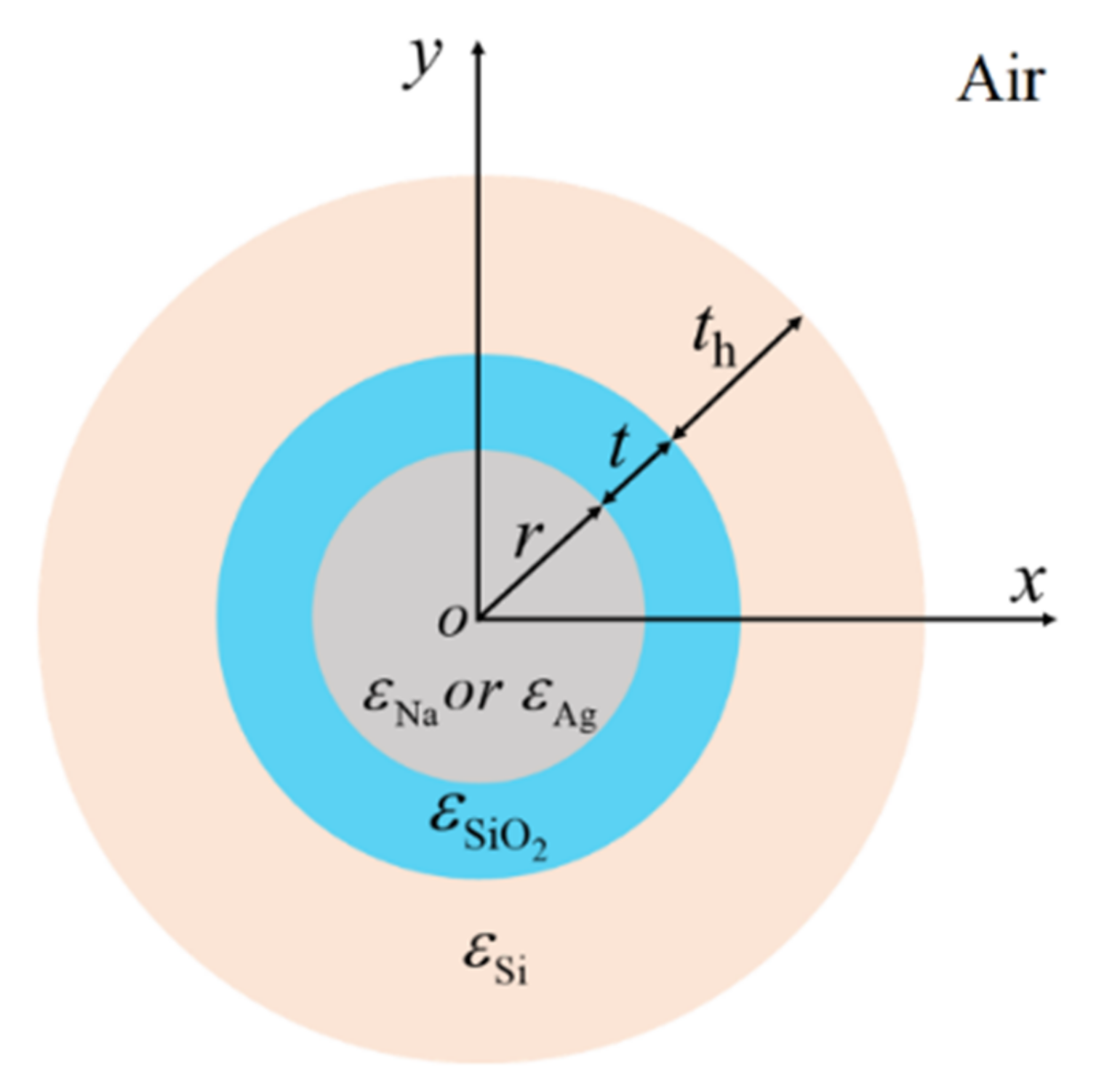
2. Theory
3. Results and Discussion
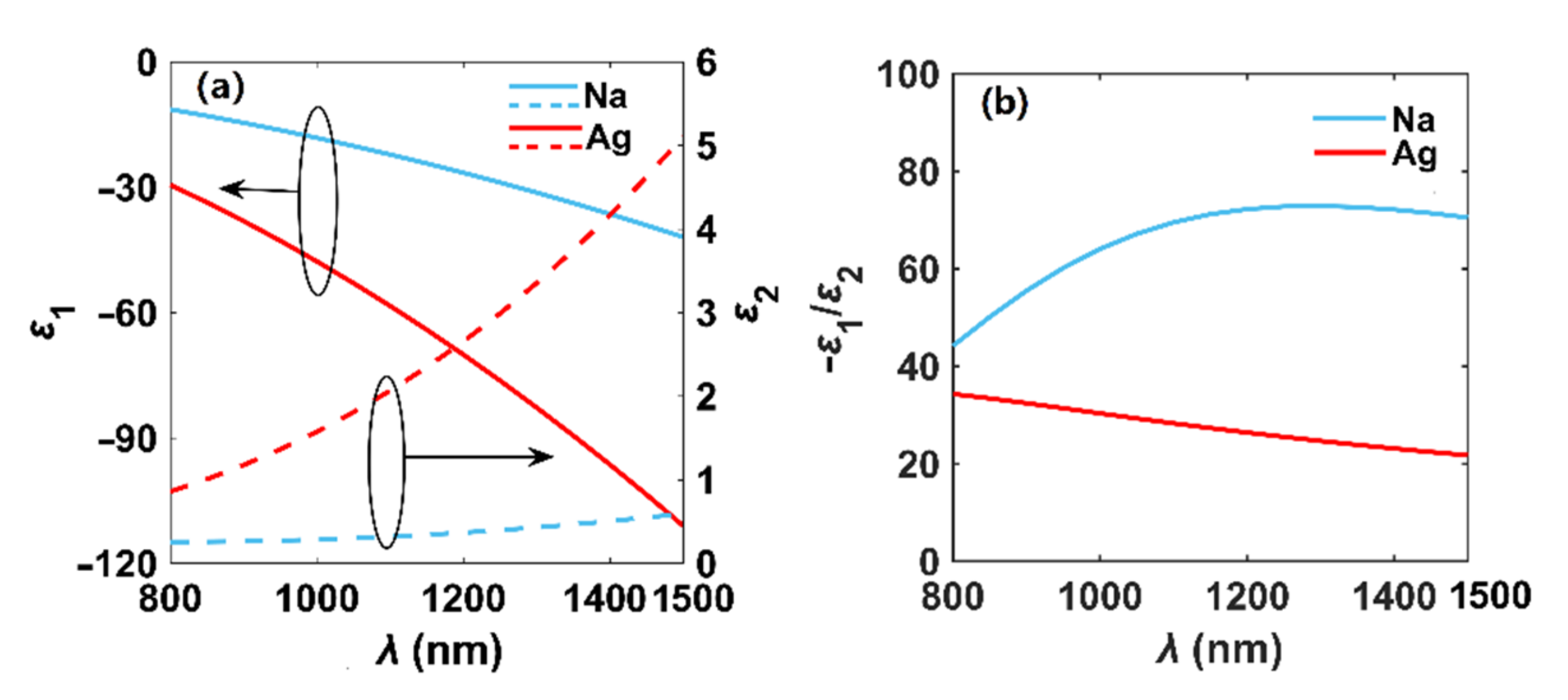
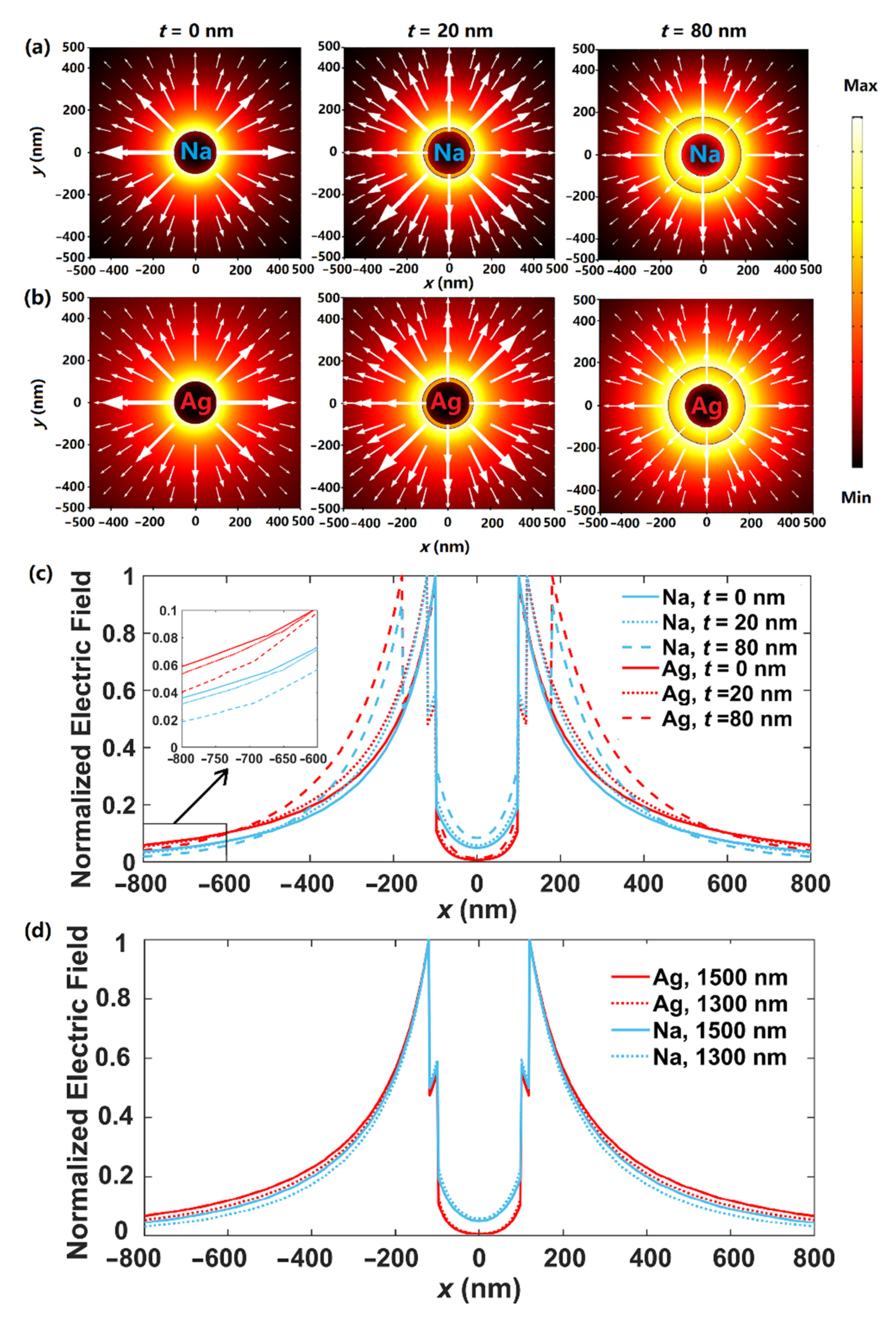
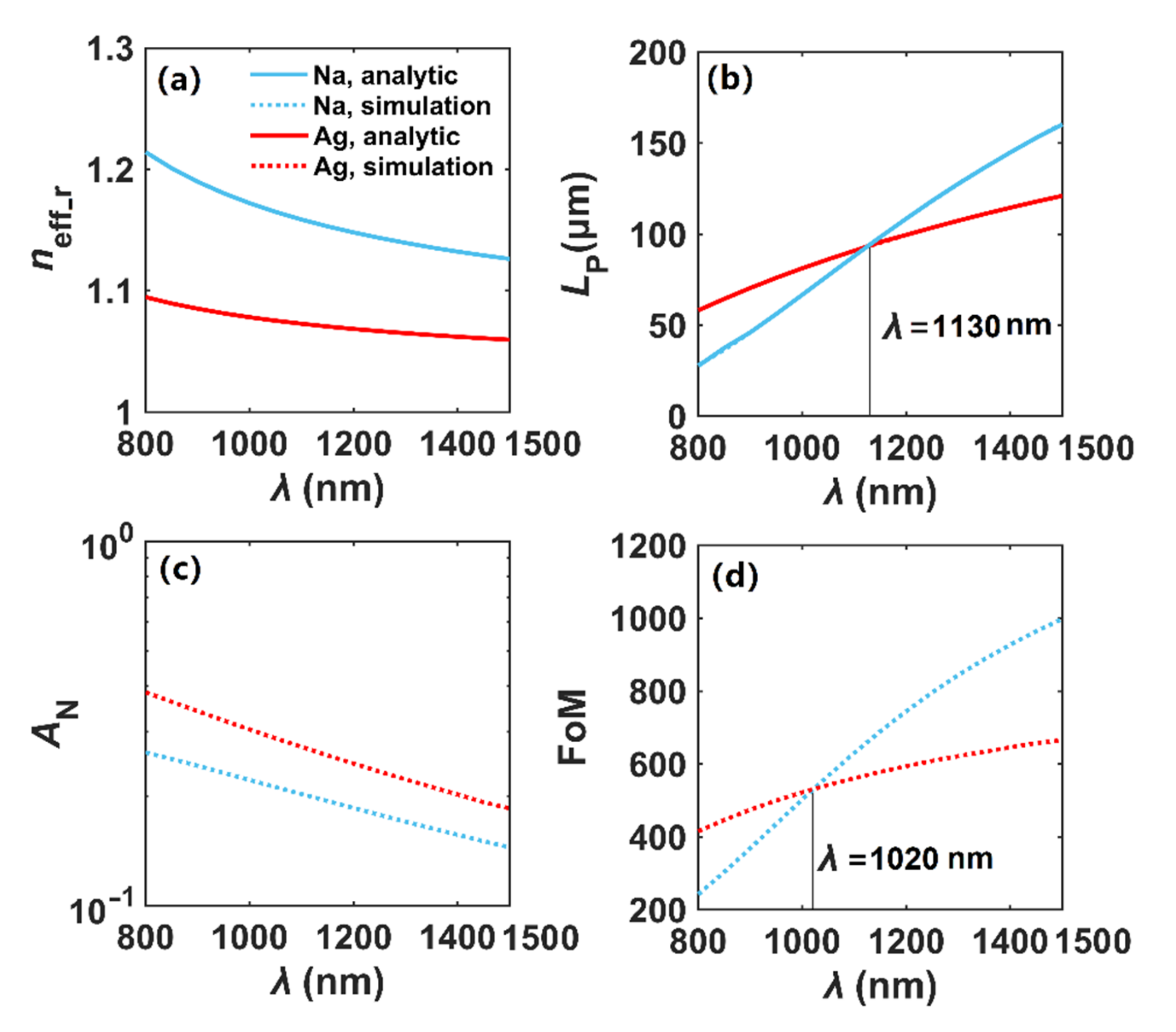
3.1. Modal Properties in Dielectric-Coated Metallic Nanowires (DCMNW)
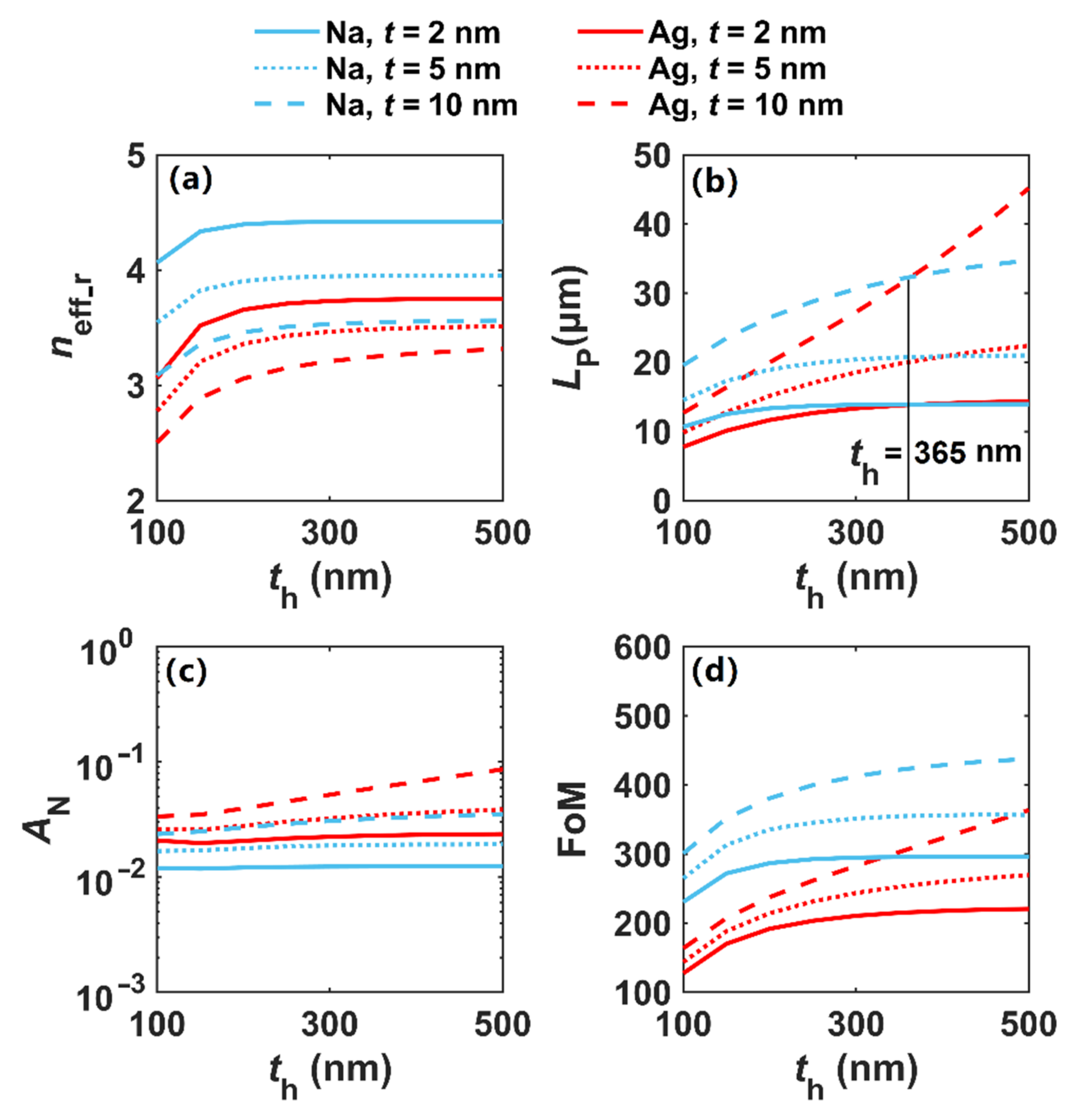
3.2. Modal Properties in Double Dielectric-Coated Metallic Nanowires (DDCMNWs)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Achanta, V.G. Surface waves at metal-dielectric interfaces: Material science perspective. Rev. Phys. 2020, 5, 100041. [Google Scholar] [CrossRef]
- Li, S.; Zuo, G.; Wu, N.; Yang, Z.; Zhao, B.; Xia, L.; Li, W. Hybrid plasmonic nanofocusing waveguide for on-chip SERS tweezer. Opt. Laser Technol. 2021, 143, 107259. [Google Scholar] [CrossRef]
- Gramotnev, D.K.; Bozhevolnyi, S.I. Plasmonics beyond the diffraction limit. Nat. Photon. 2010, 4, 83–91. [Google Scholar] [CrossRef]
- Stockman, M.I. Nanofocusing of optical energy in tapered plasmonic waveguides. Phys. Rev. Lett. 2004, 93, 137404. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wei, H.; Pan, D.; Zhang, S.; Li, Z.; Li, Q.; Liu, N.; Wang, W.; Xu, H. Plasmon waveguiding in nanowires. Chem. Rev. 2018, 118, 2882–2926. [Google Scholar] [CrossRef]
- Liaw, J.W.; Mao, S.Y.; Luo, J.Y.; Ku, Y.C.; Kuo, M.K. Surface plasmon polaritons of higher-order mode and standing waves in metallic nanowires. Opt. Express 2021, 29, 18876–18888. [Google Scholar] [CrossRef]
- Teng, D.; Cao, Q.; Li, S.; Gao, H. Tapered dual elliptical plasmon waveguides as highly efficient terahertz connectors between approximate plate waveguides and two-wire waveguides. J. Opt. Soc. Am. A 2014, 31, 268–273. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Zhao, S.; You, B.; Jhuo, S.; Lu, J.; Chou, S.; Hattori, T. Tuning transmission properties of 3D printed metal rod arrays by breaking the structural symmetry. Opt. Express 2021, 29, 538–551. [Google Scholar] [CrossRef]
- Choo, H.; Kim, M.; Staffaroni, M.; Seok, T.J.; Bokor, J.; Cabrini, S.; Schuck, P.J.; Wu, M.C.; Yablonovitch, E. Nanofocusing in a metal–insulator–metal gap plasmon waveguide with a three-dimensional linear taper. Nat. Photon. 2012, 6, 838–844. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Xie, X.; Yang, J.; Xue, M.; Wu, S.; Xiao, S.; Song, F.; Dang, J.; Sun, S.; Zuo, Z.; et al. Strong light–matter interactions between gap plasmons and two-dimensional excitons under ambient conditions in a deterministic way. Nano Lett. 2022, 22, 2177–2186. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.E.; Hsu, W.H.; Huang, C.C. Highly confined dielectric guiding mode in nanoridges embedded in a conventional slot waveguide. Opt. Express 2021, 29, 16284–16298. [Google Scholar] [CrossRef]
- Han, Z.; Radko, I.P.; Mazurski, N.; Desiatov, B.; Beermann, J.; Albrektsen, O.; Levy, U.; Bozhevolnyi, S.I. On-chip detection of radiation guided by dielectric-loaded plasmonic waveguides. Nano Lett. 2015, 15, 476–480. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pierre, B. Long-range surface plasmon polaritons. Adv. Opt. Photon. 2009, 1, 484–588. [Google Scholar]
- Moreno, E.; Rodrigo, S.G.; Bozhevolnyi, S.I.; Martín-Moreno, L.; García-Vidal, F.J. Guiding and focusing of electromagnetic fields with wedge plasmon polaritons. Phys. Rev. Lett. 2008, 100, 023901. [Google Scholar] [CrossRef] [Green Version]
- Oulton, R.F.; Sorger, V.J.; Genov, D.A.; Pile, D.F.P.; Zhang, X. A hybrid plasmonic waveguide for subwavelength confinement and long-range propagation. Nat. Photon. 2008, 2, 496–500. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Li, J.; Cada, M.; Bian, Y.; Han, Z.; Ma, Y.; Iqbal, M.; Pištora, J. Plasmon generation and routing in nanowire-based hybrid plasmonic coupling systems with incorporated nanodisk antennas. IEEE J. Sel. Top. Quantum Electron. 2021, 27, 1–7. [Google Scholar] [CrossRef]
- Bian, Y.; Zheng, Z.; Zhao, X.; Zhu, J.; Zhou, T. Symmetric hybrid surface plasmon polariton waveguides for 3D photonic integration. Opt. Express 2009, 17, 21320–21325. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Zhang, T.; Li, X.; Huang, W. Novel hybrid plasmonic waveguide consisting of two identical dielectric nanowires symmetrically placed on each side of a thin metal film. Opt. Express 2012, 20, 20535–20544. [Google Scholar] [CrossRef]
- Teng, D.; Wang, Y.; Xu, T.; Wang, H.; Shao, Q.; Tang, Y. Symmetric graphene dielectric nanowaveguides as ultra-compact photonic structures. Nanomaterials 2021, 11, 1281. [Google Scholar] [CrossRef]
- Teng, D.; Cao, Q.; Gao, H.; Wang, K.; Zhu, M. Three-wave approximation for the modal field inside high-index dielectric rods of hybrid plasmonic waveguides. J. Mod. Opt. 2016, 63, 1451–1456. [Google Scholar] [CrossRef]
- Alam, M.Z.; Aitchison, J.S.; Mojahedi, M. A marriage of convenience: Hybridization of surface plasmon and dielectric waveguide modes. Laser Photon Rev. 2014, 8, 1863–8899. [Google Scholar] [CrossRef]
- Dai, D.; He, S. A silicon-based hybrid plasmonic waveguide with a metal cap for a nano-scale light confinement. Opt. Express 2009, 17, 16646–16653. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, P.; Ranjan, R. A metal-cap wedge shape hybrid plasmonic waveguide for nano-scale light confinement and long propagation range. Plasmonics 2022, 17, 95–105. [Google Scholar] [CrossRef]
- Zhang, Q.; Pan, J.; Wang, S.; Du, Y.; Wu, J. A triangle hybrid plasmonic waveguide with long propagation length for ultradeep subwavelength confinement. Crystals 2022, 12, 64. [Google Scholar] [CrossRef]
- Huang, C.C.; Chang, R.J.; Huang, C.C. Nanostructured hybrid plasmonic waveguide in a slot structure for high-performance light transmission. Opt. Express 2021, 29, 29341–29356. [Google Scholar] [CrossRef]
- Sun, P.; Xu, P.; Zhu, K.; Zhou, Z. Silicon-based optoelectronics enhanced by hybrid plasmon polaritons: Bridging dielectric photonics and nanoplasmonics. Photonics 2021, 8, 482. [Google Scholar] [CrossRef]
- Sun, M.; Tian, J.; Li, L. Mode properties of a coaxial multi-layer hybrid surface plasmon waveguide. Phys. Status Solidi B 2015, 252, 1884–1889. [Google Scholar] [CrossRef]
- Teng, D.; Cao, Q.; Wang, K. An extension of the generalized nonlocal theory for the mode analysis of plasmonic waveguides at telecommunication frequency. J. Opt. 2017, 19, 055003. [Google Scholar] [CrossRef] [Green Version]
- West, P.; Ishii, S.; Naik, G.; Emani, N.; Shalaev, V.M.; Boltasseva, A. Searching for better plasmonic materials. Laser Photon. Rev. 2010, 4, 795–808. [Google Scholar] [CrossRef] [Green Version]
- Naik, G.V.; Shalaev, V.M.; Boltasseva, A. Alternative plasmonic materials: Beyond gold and silver. Adv. Mater. 2013, 25, 3264–3294. [Google Scholar] [CrossRef]
- Boltasseva, A.; Atwater, H.A. Low-loss plasmonic metamaterials. Science 2011, 331, 290–291. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, Y.; Xue, T.; Su, H.; Zhang, J. Direct evidence of visible surface plasmon excitation in ITO film coated on LiNbO3 slabs. Opt. Express 2017, 25, 6227–6233. [Google Scholar] [CrossRef]
- Kim, J.T.; Choe, J.-H.; Kim, J.-S.; Seo, D.; Kim, Y.D.; Chung, K.H. Graphene-based plasmonic waveguide devices for electronic-photonic integrated circuit. Opt. Laser Technol. 2018, 106, 76–86. [Google Scholar] [CrossRef]
- Vakil, A.; Engheta, N. Transformation optics using graphene. Science 2011, 332, 1291–1294. [Google Scholar] [CrossRef] [Green Version]
- Teng, D.; Wang, K. Theoretical analysis of terahertz dielectric-loaded graphene waveguide. Nanomaterials 2021, 11, 210. [Google Scholar] [CrossRef]
- Grigorenko, N.; Polini, M.; Novoselov, K.S. Graphene plasmonics. Nat. Photon. 2012, 6, 749–758. [Google Scholar] [CrossRef]
- Teng, D.; Wang, K.; Huan, Q.; Chen, W.; Li, Z. High-performance light transmission based on graphene plasmonic waveguides. J. Mater. Chem. C 2020, 8, 6832–6838. [Google Scholar] [CrossRef]
- Teng, D.; Wang, K.; Li, Z.; Zhao, Y. Graphene-coated nanowire dimers for deep subwavelength waveguiding in mid-infrared range. Opt. Express 2019, 27, 12458–12469. [Google Scholar] [CrossRef]
- Wu, F.; Liu, D.; Xiao, S. Bandwidth-tunable near-infrared perfect absorption of graphene in a compound grating waveguide structure supporting quasi-bound states in the continuum. Opt. Express 2021, 29, 41975–41989. [Google Scholar] [CrossRef]
- Teng, D.; Wang, K.; Li, Z. Graphene-coated nanowire waveguides and their applications. Nanomaterials 2020, 10, 229. [Google Scholar] [CrossRef] [Green Version]
- Tu, P.Y.; Huang, C.C. Analysis of hybrid plasmon-phonon-polariton modes in hBN/graphene/hBN stacks for mid-infrared waveguiding. Opt. Express 2022, 30, 2863–2876. [Google Scholar] [CrossRef]
- Zheng, K.; Song, J.; Qu, J. Hybrid low-permittivity slot-rib plasmonic waveguide based on monolayer two dimensional transition metal dichalcogenide with ultra-high energy confinement. Opt. Express 2018, 26, 15819–15824. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Hong, Q.; Zou, J.; Meng, Q.; Qin, S.; Zhu, Z. Ultra-narrowband visible light absorption in a monolayer MoS2 based resonant nanostructure. Opt. Express 2020, 28, 27608–27614. [Google Scholar] [CrossRef]
- Sun, J.; Li, Y.; Hu, H.; Chen, W.; Zheng, D.; Zhang, S.; Xu, H. Strong plasmon–exciton coupling in transition metal dichalcogenides and plasmonic nanostructures. Nanoscale 2021, 13, 4408–4419. [Google Scholar] [CrossRef]
- Timusk, T.; Carbotte, J.P.; Homes, C.C.; Basov, D.N. Dielectric response and novel electromagnetic modes in three-dimensional Dirac semimetal films. Phys. Rev. B 2016, 93, 235417. [Google Scholar]
- He, X.; Liu, F.; Lin, F.; Shi, W. Tunable 3D Dirac-semimetals supported mid-IR hybrid plasmonic waveguides. Opt. Lett. 2021, 46, 472–475. [Google Scholar] [CrossRef]
- He, X.; Lin, F.; Liu, F.; Shi, W. Tunable terahertz Dirac-semimetal hybrid plasmonic waveguides. Opt. Mater. Express 2022, 12, 73–84. [Google Scholar] [CrossRef]
- Liu, T.; Zhou, C.; Xiao, S. Tailoring anisotropic absorption in a borophene-based structure via critical coupling. Opt. Express 2021, 29, 8941–8950. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Z.; Song, X.; Zhang, H.; Yang, J. Infrared plasmonic sensing with anisotropic two-dimensional material borophene. Nanomaterials 2021, 11, 1165. [Google Scholar] [CrossRef] [PubMed]
- Dereshgi, S.A.; Liu, Z.; Aydin, K. Anisotropic localized surface plasmons in borophene. Opt. Express 2020, 28, 16725–16739. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, J.; Mao, Y.F.; Chen, J.; Zhu, J. Stable, high-performance sodium-based plasmonic devices in the near infrared. Nature 2020, 581, 401–405. [Google Scholar] [CrossRef] [PubMed]
- Gao, J.; Hou, C.; Wang, F.; Liu, H.; Ma, T. A directional coupler based on graphene-enhanced Na-loaded plasmonic rib waveguide. Opt. Commun. 2021, 499, 127316. [Google Scholar] [CrossRef]
- Ma, T.; Ma, J.; Liu, H.; Tian, Y.; Liu, S.; Wang, F. Electro-optic tunable directional coupler based on a LiNbO3/Na surface plasmonic waveguide. Acta Phys. Sin. 2022, 71, 054205. [Google Scholar] [CrossRef]
- Rawashdeh, A.; Lupa, S.; Welch, W.; Yang, A. Sodium surface lattice plasmons. J. Phys. Chem. C 2021, 125, 25148–25154. [Google Scholar] [CrossRef]
- Akbar, J.; Bin, X.; Hou, L.; Marsh, J.H.; Liu, X. Surface plasmon polaritons excitation at the interface of graphene and sodium media. Eur. Phys. J. Plus 2022, 137, 291. [Google Scholar] [CrossRef]
- Yang, H.U.; Archangel, J.D.; Sundheimer, M.L.; Tucker, E.; Boreman, G.D.; Raschke, M.B. Optical dielectric function of silver. Phys. Rev. B 2015, 91, 235137. [Google Scholar] [CrossRef] [Green Version]
- Buckley, R.; Berini, P. Figures of merit for 2D surface plasmon waveguides and application to metal stripes. Opt. Express 2007, 15, 12174–12182. [Google Scholar] [CrossRef]
- Teng, D.; Wang, Z.; Huan, Q.; Wang, H.; Wang, K. A low loss platform for subwavelength terahertz graphene plasmon propagation. Opt. Mater. 2022, 128, 112436. [Google Scholar] [CrossRef]
- Said, A.; Atia, K.S.R.; Obayya, S.S.A. On modeling of plasmonic devices: Overview. J. Opt. Soc. Am. B 2020, 37, A163–A174. [Google Scholar] [CrossRef]
- Gerislioglu, B.; Dong, L.; Ahmadivand, A.; Hu, H.; Nordlander, P.; Halas, N.J. Monolithic metal dimer-on-film structure: New plasmonic properties introduced by the underlying metal. Nano Lett. 2020, 20, 2087–2093. [Google Scholar] [CrossRef]
- Gerislioglu, B.; Ahmadivand, A.; Pala, N. Single-and multimode beam propagation through an optothermally controllable Fano clusters-mediated waveguide. J. Lightwave Technol. 2017, 35, 4961–4966. [Google Scholar] [CrossRef]
- Teng, D.; Wang, K.; Huan, Q.; Zhao, Y.; Tang, Y. High-performance transmission of surface plasmons in graphene-covered nanowire pairs with substrate. Nanomaterials 2019, 9, 1594. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schinke, C.; Christian Peest, P.; Schmidt, J.; Brendel, R.; Bothe, K.; Vogt, M.R.; Kröger, I.; Winter, S.; Schirmacher, A.; Lim, S.; et al. Uncertainty analysis for the coefficient of band-to-band absorption of crystalline silicon. AIP Adv. 2015, 5, 067168. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Xu, Q.; Xia, L.; Li, Y.; Gu, J.; Tian, Z.; Ouyang, C.; Han, J.; Zhang, W. Terahertz surface plasmonic waves: A review. Adv. Photon. 2020, 2, 014001. [Google Scholar] [CrossRef]
- Knight, M.W.; King, N.S.; Liu, L.F.; Everitt, H.O.; Nordlander, P.; Halas, N.J. Aluminum for plasmonics. ACS Nano 2014, 8, 834–840. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teng, D.; Tian, Y.; Hu, X.; Guan, Z.; Gao, W.; Li, P.; Fang, H.; Yan, J.; Wang, Z.; Wang, K. Sodium-Based Cylindrical Plasmonic Waveguides in the Near-Infrared. Nanomaterials 2022, 12, 1950. https://doi.org/10.3390/nano12121950
Teng D, Tian Y, Hu X, Guan Z, Gao W, Li P, Fang H, Yan J, Wang Z, Wang K. Sodium-Based Cylindrical Plasmonic Waveguides in the Near-Infrared. Nanomaterials. 2022; 12(12):1950. https://doi.org/10.3390/nano12121950
Chicago/Turabian StyleTeng, Da, Yuanming Tian, Xuemei Hu, Ziyi Guan, Wencang Gao, Pengyuan Li, Hongli Fang, Jianjun Yan, Zhiwen Wang, and Kai Wang. 2022. "Sodium-Based Cylindrical Plasmonic Waveguides in the Near-Infrared" Nanomaterials 12, no. 12: 1950. https://doi.org/10.3390/nano12121950
APA StyleTeng, D., Tian, Y., Hu, X., Guan, Z., Gao, W., Li, P., Fang, H., Yan, J., Wang, Z., & Wang, K. (2022). Sodium-Based Cylindrical Plasmonic Waveguides in the Near-Infrared. Nanomaterials, 12(12), 1950. https://doi.org/10.3390/nano12121950






