Design of a High-Efficiency Multilayer Dielectric Diffraction Grating with Enhanced Laser Damage Threshold
Abstract
:1. Introduction
2. Materials and Methods
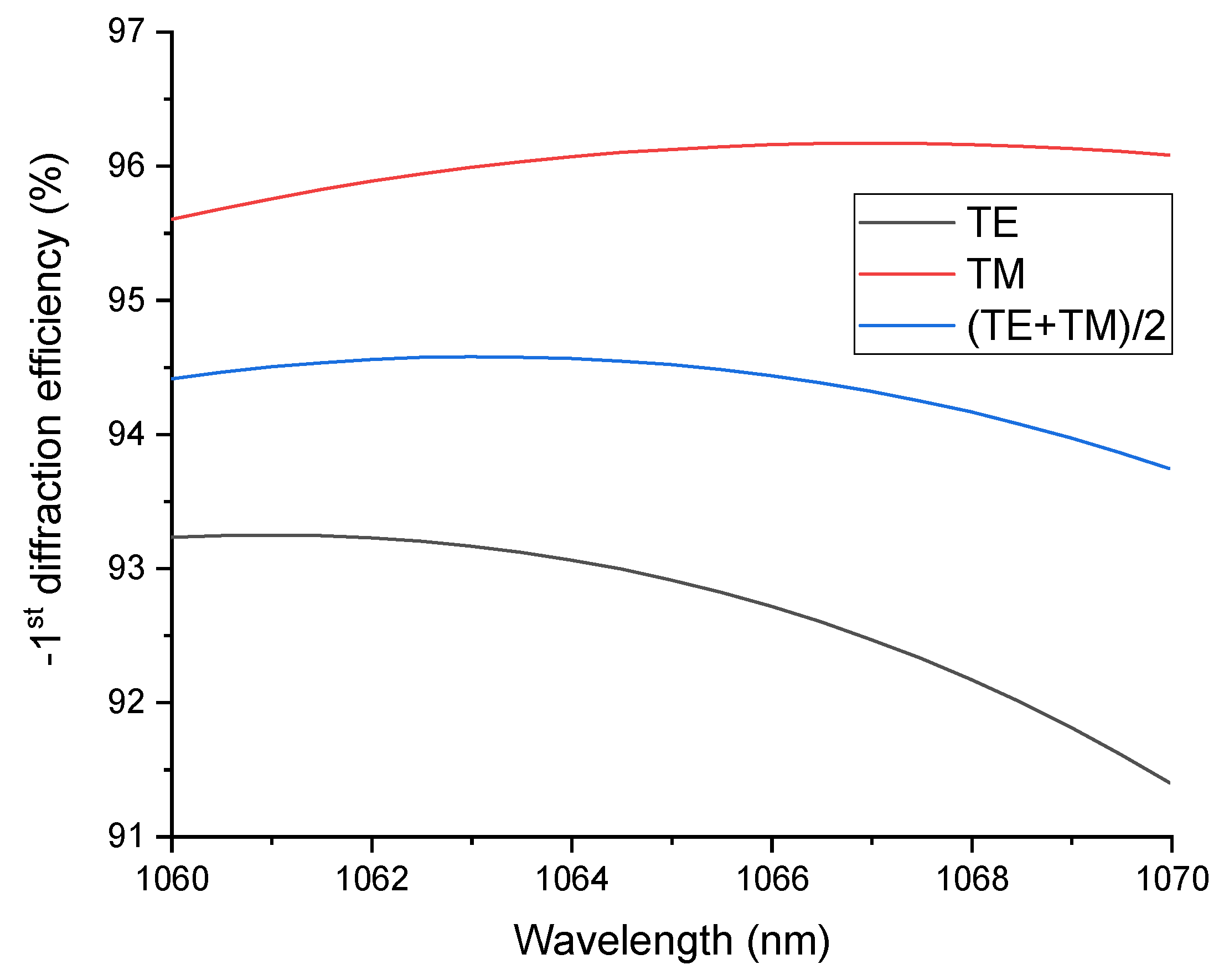
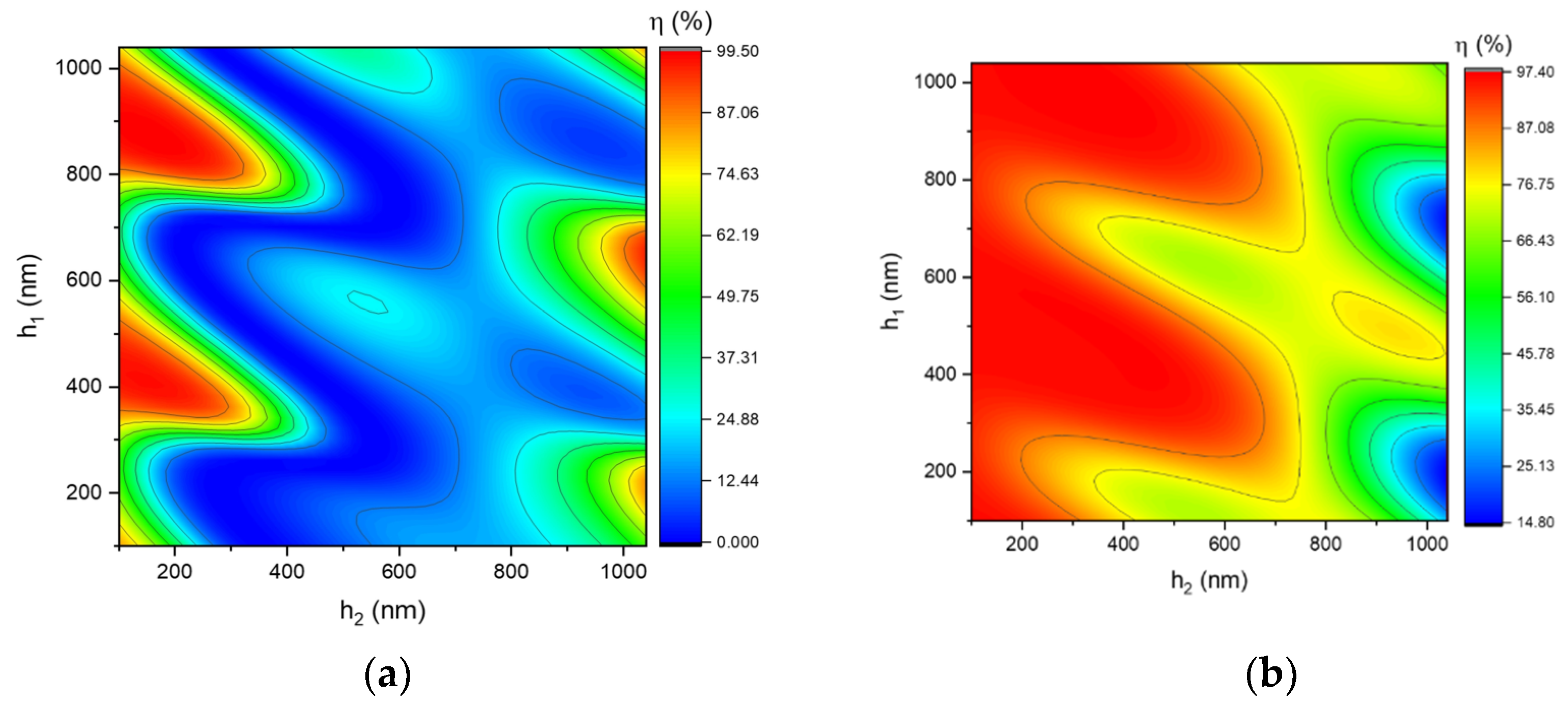
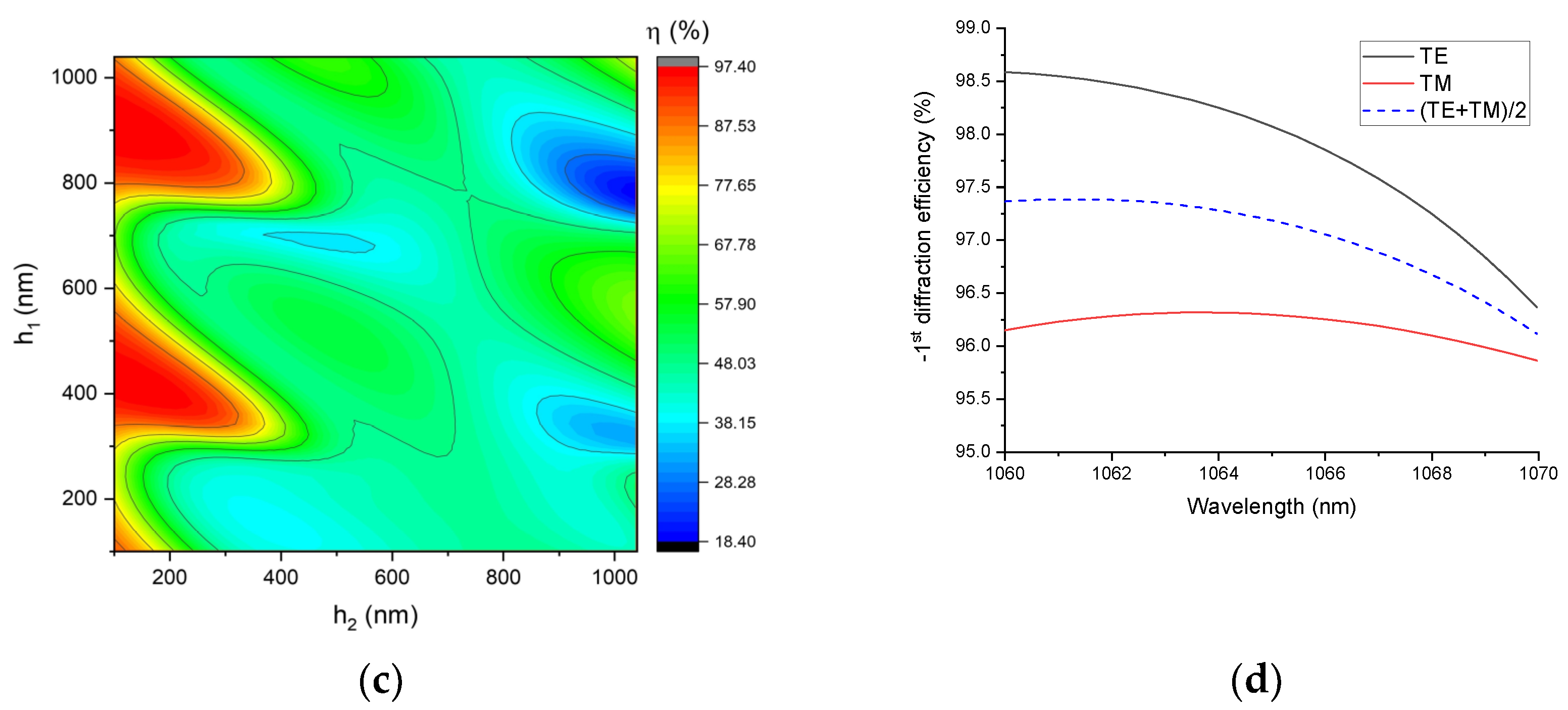
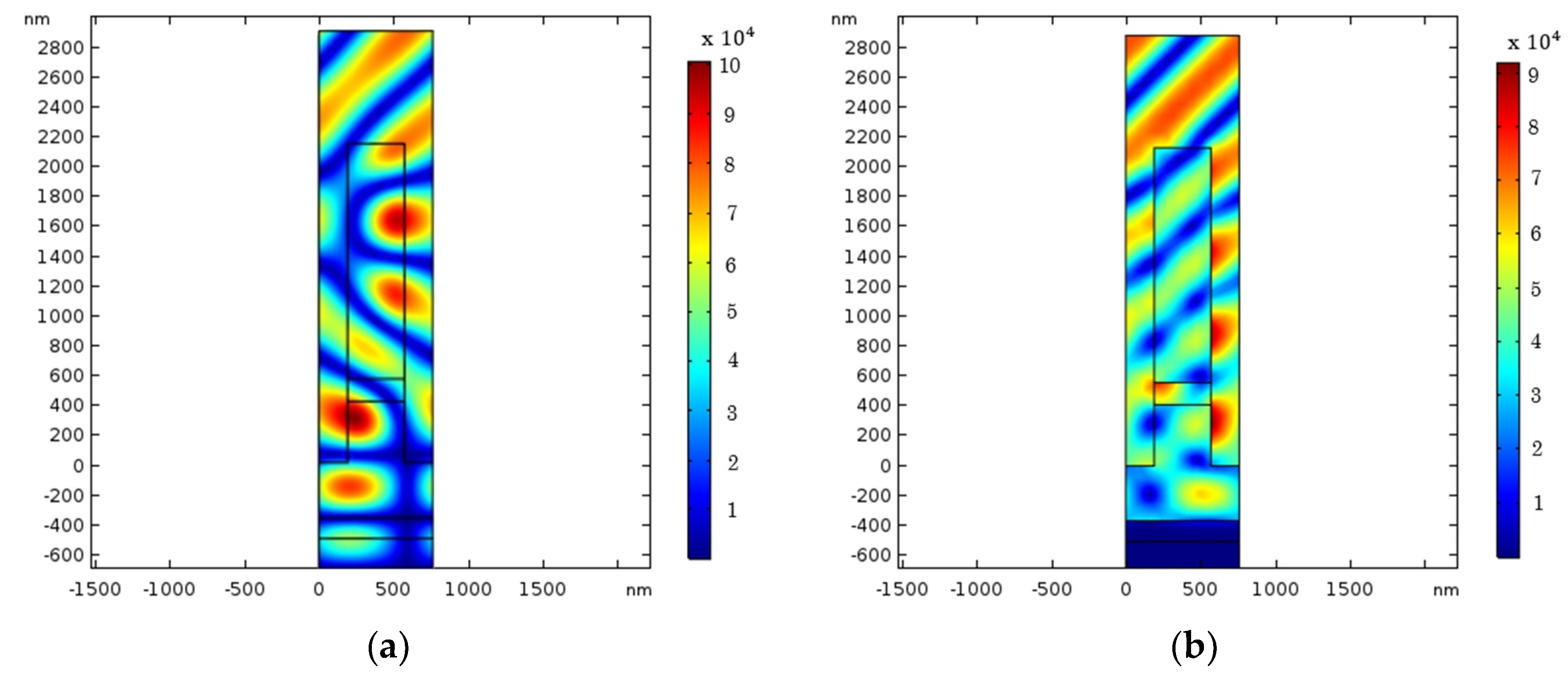
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Madasamy, P.; Jander, D.R.; Brooks, C.D.; Loftus, T.H.; Thomas, A.M.; Jones, P.; Honea, E.C. Dual-Grating Spectral Beam Combination of High-Power Fiber Lasers. IEEE J. Sel. Top. Quantum Electron. 2009, 15, 337–343. [Google Scholar] [CrossRef]
- Zhao, Y.; Sun, F.; Tong, C.; Shu, S.; Hou, G.; Lu, H.; Zhang, X.; Wang, L.; Tian, S.; Wang, L. Going beyond the Beam Quality Limit of Spectral Beam Combining of Diode Lasers in a V-Shaped External Cavity. Opt. Express 2018, 26, 14058. [Google Scholar] [CrossRef]
- Lubatsch, A.; Frank, R. Coherent Transport and Symmetry Breaking—Laser Dynamics of Constrained Granular Matter. New J. Phys. 2014, 16, 083043. [Google Scholar] [CrossRef] [Green Version]
- El-Agmy, R.M.; Al-Hosiny, N. Power Scaling of End-Pumped Nd:YLF Lasers, Modeling and Experiments. Optik 2017, 140, 584–591. [Google Scholar] [CrossRef]
- Huang, X.; Lan, J.; Lin, Z.; Cui, S.; Wang, Y.; Xu, B.; Xu, H.; Cai, Z.; Xu, X.; Xu, J. Power Scaling and Wavelength Tuning of Diode-Pumped Nd:LSO Laser at 1.35 mm. Opt. Mater. 2016, 58, 102–106. [Google Scholar] [CrossRef]
- Zhang, W.S.; Duan, X.M.; Li, L.J. High Power Ho:SSO Laser Resonantly Pumped by a FBG-Locked Tm Fiber Laser at 1940.3 nm. Optik 2018, 175, 340–343. [Google Scholar] [CrossRef]
- Luo, S.; Yan, X.; Cui, Q.; Xu, B.; Xu, H.; Cai, Z. Power Scaling of Blue-Diode-Pumped Pr:YLF Lasers at 523.0, 604.1, 606.9, 639.4, 697.8 and 720.9 nm. Opt. Commun. 2016, 380, 357–360. [Google Scholar] [CrossRef]
- Du, J.; Yu, Y.; An, X.; Shang, J.; Lei, J.; Jiang, J.; Jiang, L.; Lv, W.; Fan, G.; Gao, Q. 60 mm-Aperture High Average Output Power Nd:YAG Composite Ceramic Disk Laser. Optik 2018, 172, 197–202. [Google Scholar] [CrossRef]
- Lubatsch, A.; Frank, R. Tuning the Quantum Efficiency of Random Lasers—Intrinsic Stokes-Shift and Gain. Sci. Rep. 2015, 5, 17000. [Google Scholar] [CrossRef] [Green Version]
- Chen, F.; Ma, J.; Wei, C.; Zhu, R.; Zhou, W.; Yuan, Q.; Pan, S.; Zhang, J.; Wen, Y.; Dou, J. 10 KW-Level Spectral Beam Combination of Two High Power Broad-Linewidth Fiber Lasers by Means of Edge Filters. Opt. Express 2017, 25, 32783. [Google Scholar] [CrossRef]
- Chen, F.; Ma, J.; Zhu, R.; Yuan, Q.; Zhou, W.; Su, J.; Xu, J.; Pan, S. Coupling Efficiency Model for Spectral Beam Combining of High-Power Fiber Lasers Calculated from Spectrum. Appl. Opt. 2017, 56, 2574. [Google Scholar] [CrossRef]
- Loftus, T.H.; Thomas, A.M.; Hoffman, P.R.; Norsen, M.; Royse, R.; Liu, A.; Honea, E.C. Spectrally Beam-Combined Fiber Lasers for High-Average-Power Applications. IEEE J. Sel. Top. Quantum Electron. 2007, 13, 487–497. [Google Scholar] [CrossRef]
- Hu, M.; Zheng, Y.; Yang, Y.; Chen, X.; Liu, K.; Zhao, C.; Wang, J.; Qi, Y.; He, B.; Zhou, J. Nanosecond Double-Pulse Fiber Laser with Arbitrary Sub-Pulse Combined Based on a Spectral Beam Combining System. Opt. Laser Technol. 2017, 90, 22–26. [Google Scholar] [CrossRef]
- Cho, H.J.; Lee, K.H.; Kim, S.I.; Lee, J.H.; Kim, H.T.; Kim, W.S.; Kim, D.H.; Lee, Y.S.; Kim, S.; Kim, T.Y.; et al. Analysis on Design and Fabrication of High-Diffraction-Efficiency Multilayer Dielectric Gratings. Curr. Opt. Photonics 2018, 2, 125–133. [Google Scholar]
- Zhan, S.; Wu, Z.; Hu, J.; Zhang, J.; Wang, P.; You, J.; Wen, J. Investigation on Ultimate Efficiency of Spectral Beam Combining Based on an External Cavity. Optik 2018, 158, 1519–1532. [Google Scholar] [CrossRef]
- Li, H.; Wang, B. Three-Layer Grating with the Enhanced Efficiency and Angular Bandwidth. IEEE Photonics J. 2017, 9, 1–7. [Google Scholar] [CrossRef]
- Vial, B.; Zolla, F.; Nicolet, A.; Commandré, M.; Tisserand, S. Adaptive Perfectly Matched Layer for Wood’s Anomalies in Diffraction Gratings. Opt. Express 2012, 20, 28094. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bao, G.; Chen, Z.; Wu, H. Adaptive Finite-Element Method for Diffraction Gratings. J. Opt. Soc. Am. A 2005, 22, 1106. [Google Scholar] [CrossRef]
- Alessi, D.A.; Rosso, P.A.; Nguyen, H.T.; Aasen, M.D.; Britten, J.A.; Haefner, C. Active Cooling of Pulse Compression Diffraction Gratings for High Energy, High Average Power Ultrafast Lasers. Opt. Express 2016, 24, 30015. [Google Scholar] [CrossRef]
- Huang, H.; Kong, F.; Xia, Z.; Jin, Y.; Li, L.; Wang, L.; Chen, J.; Cui, Y.; Shao, J. Femtosecond-Laser-Induced Damage Initiation Mechanism on Metal Multilayer Dielectric Gratings for Pulse Compression. Opt. Mater. 2018, 75, 727–732. [Google Scholar] [CrossRef]
- Guan, H.; Jin, Y.; Liu, S.; Kong, F.; Du, Y.; He, K.; Yi, K.; Shao, J. Broadband Trapeziform Multilayer Dielectric Grating for Femtosecond Pulse Compressor: Design, Fabrication, and Analysis. Laser Phys. 2013, 23, 115301. [Google Scholar] [CrossRef]
- Gallais, L.; Commandré, M. Laser-Induced Damage Thresholds of Bulk and Coating Optical Materials at 1030 nm, 500 fs. Appl. Opt. 2014, 53, A186. [Google Scholar] [CrossRef]
- Ma, M.; Meyaard, D.S.; Shan, Q.; Cho, J.; Schubert, E.F.; Kim, G.B.; Kim, M.-H.; Sone, C. Polarized Light Emission from GaInN Light-Emitting Diodes Embedded with Subwavelength Aluminum Wire-Grid Polarizers. Appl. Phys. Lett. 2012, 101, 061103. [Google Scholar] [CrossRef] [Green Version]
- Saleem, M.R.; Zheng, D.; Bai, B.; Stenberg, P.; Kuittinen, M.; Honkanen, S.; Turunen, J. Replicable One-Dimensional Non-Polarizing Guided Mode Resonance Gratings under Normal Incidence. Opt. Express 2012, 20, 16974. [Google Scholar] [CrossRef]
- Tan, X.; Jiao, Q.B.; Qi, X.D.; Bayan, H. Fabrication of High-Efficiency and Low-Stray-Light Grating by Inductively Coupled Plasma (ICP) Etching-Polishing Method. Opt. Express 2016, 24, 5896. [Google Scholar] [CrossRef]
- Palmer, C.; Loewen, E. Diffraction Grating Handbook, 6th ed.; Newport Corporation: Irvine, CA, USA, 2005. [Google Scholar]
- Hehl, K.; Bischoff, J.; Mohaupt, U.; Palme, M.; Schnabel, B.; Wenke, L.; Bödefeld, R.; Theobald, W.; Welsch, E.; Sauerbrey, R.; et al. High-Efficiency Dielectric Reflection Gratings: Design, Fabrication, and Analysis. Appl. Opt. 1999, 38, 6257. [Google Scholar] [CrossRef]
- Clausnitzer, T.; Kämpfe, T.; Kley, E.-B.; Tünnermann, A.; Peschel, U.; Tishchenko, A.V.; Parriaux, O. An Intelligible Explanation of Highly-Efficient Diffraction in Deep Dielectric Rectangular Transmission Gratings. Opt. Express 2005, 13, 10448. [Google Scholar] [CrossRef]
- Clausnitzer, T.; Kämpfe, T.; Kley, E.-B.; Tünnermann, A.; Tishchenko, A.; Parriaux, O. Investigation of the Polarization-Dependent Diffraction of Deep Dielectric Rectangular Transmission Gratings Illuminated in Littrow Mounting. Appl. Opt. 2007, 46, 819. [Google Scholar] [CrossRef]
- Cao, H.; Wu, J.; Yu, J.; Ma, J. High-Efficiency Polarization-Independent Wideband Multilayer Dielectric Reflective Bullet-Alike Cross-Section Fused-Silica Beam Combining Grating. Appl. Opt. 2018, 57, 900. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Qiang, Y.; Zhu, Y.; Shao, J.; Fan, Z.; Han, J. Effects of Deposition Parameters on Laser-Induced Damage Threshold of Ta2O5 Films. Opt. Laser Technol. 2010, 42, 497–502. [Google Scholar] [CrossRef]
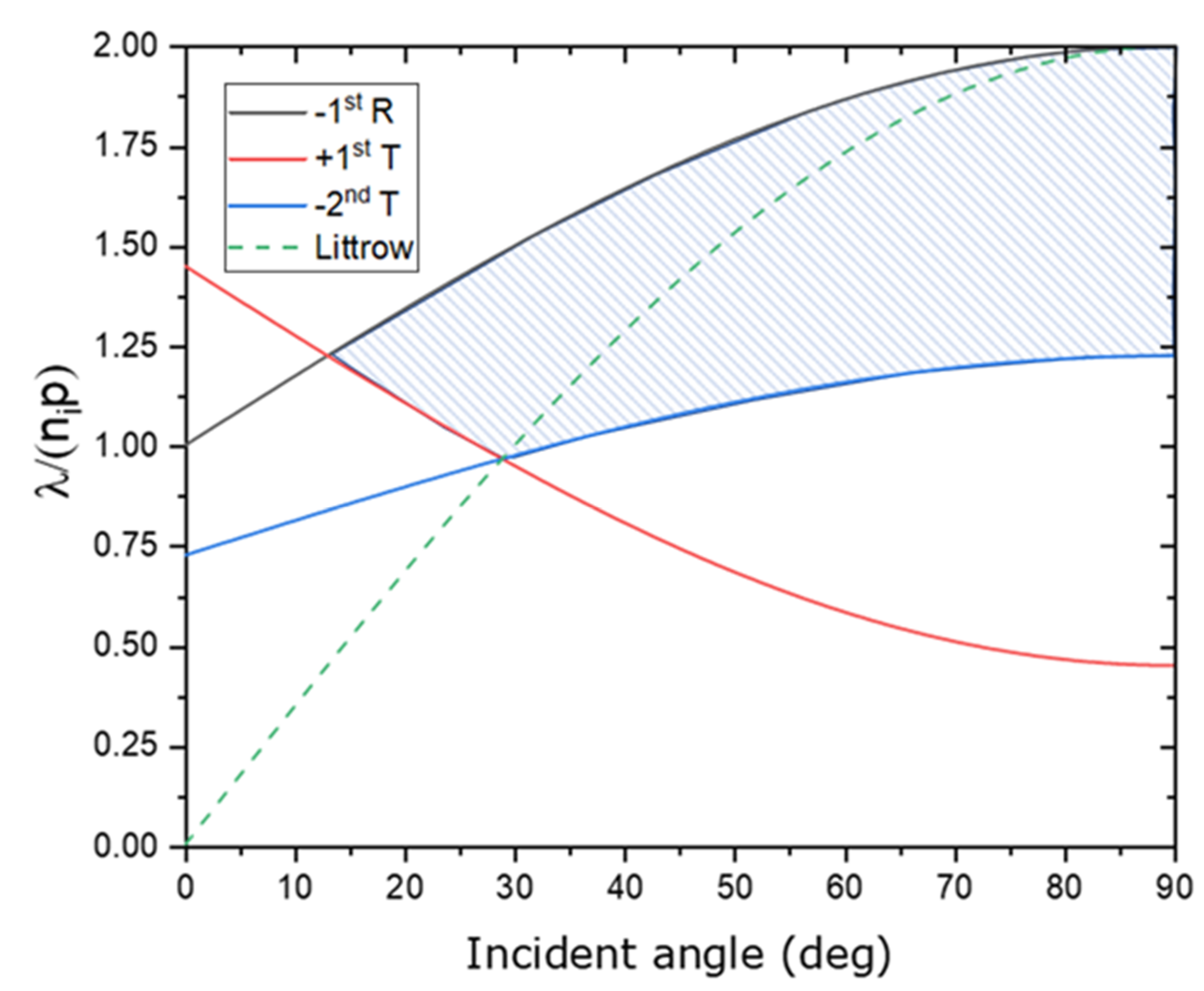
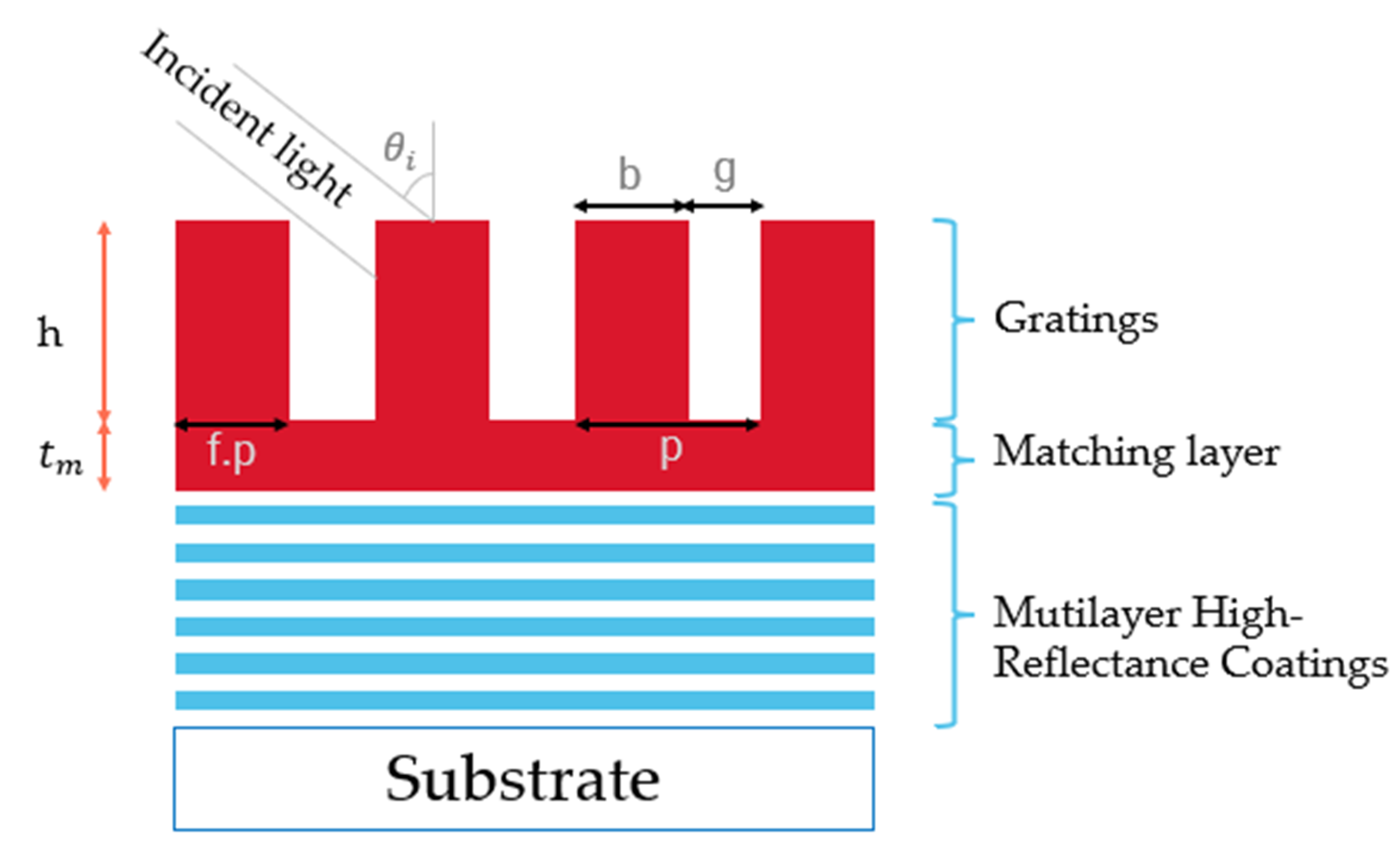
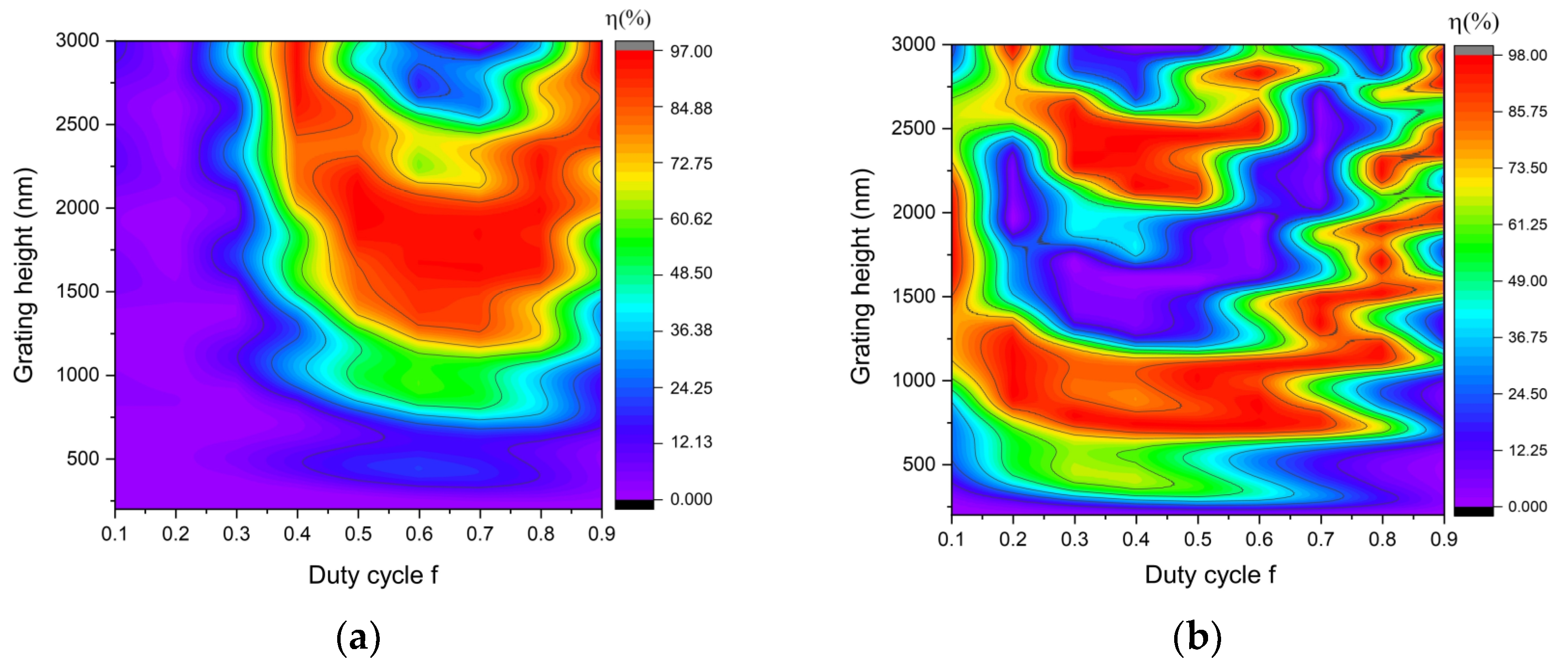
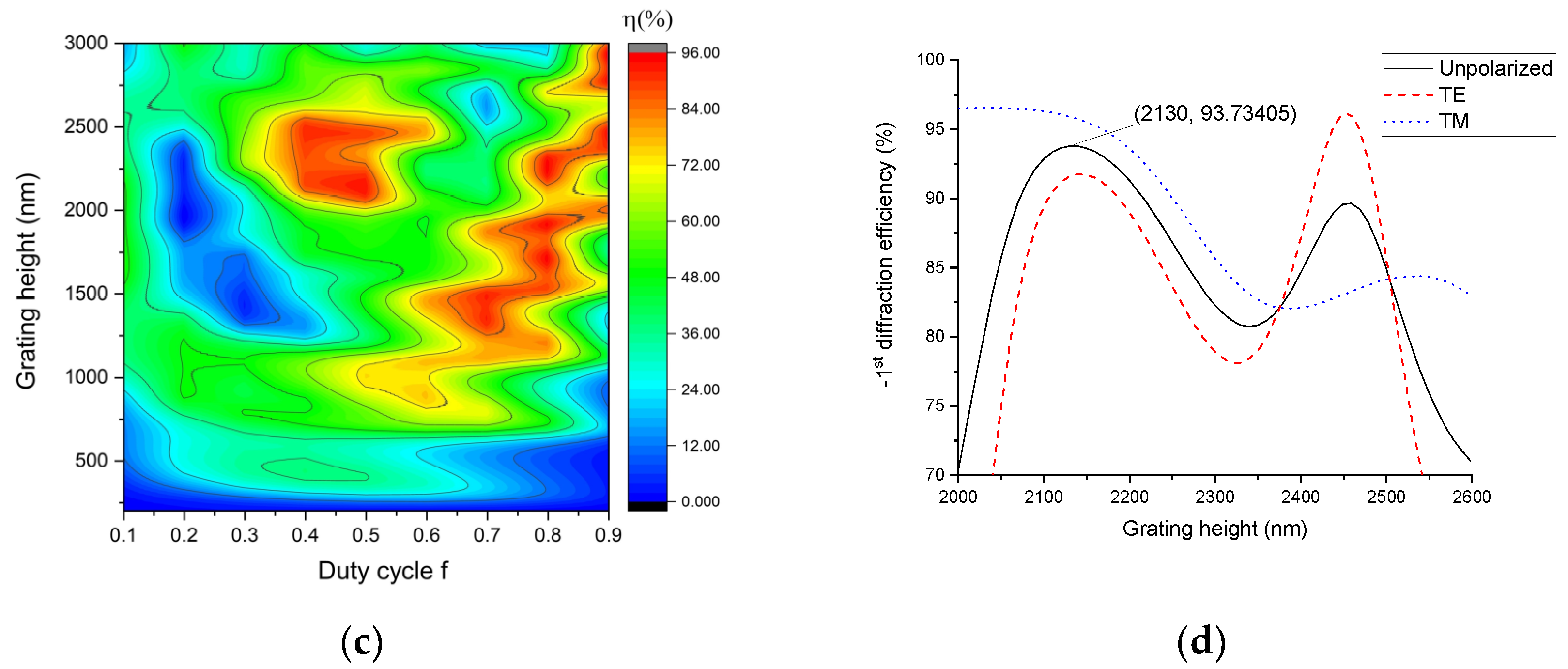


| Parameters | Value |
|---|---|
| Incident wavelength | 1064 nm |
| Period | 760 nm |
| Incident angle | 44.43° |
| Duty cycle | 0.5 |
| Grating’s height | 2130 nm |
| Reflective layer | Gold |
| The thickness of the matching layer (SiO2) | |
| Refractive index of the substrate (Glass) | 1.50664 |
| Refractive index of SiO2 | 1.44964 |
| Parameters | Value |
|---|---|
| Grating’s shape | Rectangular |
| Incident wavelength | 1064 nm |
| Period | 760 nm |
| Incident angle | 44.43° |
| Duty cycle | 0.5 |
| Grating’s depth/height | 2130 nm (409, 150, 1571) |
| The thickness of the matching layer (SiO2) | |
| Refractive index of the substrate (Glass) | 1.50664 |
| Refractive index of SiO2 | 1.44964 |
| Refractive index of Al2O3 | 1.6509 |
| Refractive index of Ta2O5 | 2.10000 |
| Reference wavelength | 1164 nm |
| Reflective multilayer layer structure | Substrate| (HL)^13 H|Air H: Ta2O5 L: SiO2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cu, D.T.; Pham, T.D.; Le, V.T.H.; Li, M.C.; Chen, H.P.; Kuo, C.C. Design of a High-Efficiency Multilayer Dielectric Diffraction Grating with Enhanced Laser Damage Threshold. Nanomaterials 2022, 12, 1952. https://doi.org/10.3390/nano12121952
Cu DT, Pham TD, Le VTH, Li MC, Chen HP, Kuo CC. Design of a High-Efficiency Multilayer Dielectric Diffraction Grating with Enhanced Laser Damage Threshold. Nanomaterials. 2022; 12(12):1952. https://doi.org/10.3390/nano12121952
Chicago/Turabian StyleCu, Duy Thanh, Tien Dat Pham, Vu Tuan Hung Le, Meng Chi Li, Hung Pin Chen, and Chien Cheng Kuo. 2022. "Design of a High-Efficiency Multilayer Dielectric Diffraction Grating with Enhanced Laser Damage Threshold" Nanomaterials 12, no. 12: 1952. https://doi.org/10.3390/nano12121952
APA StyleCu, D. T., Pham, T. D., Le, V. T. H., Li, M. C., Chen, H. P., & Kuo, C. C. (2022). Design of a High-Efficiency Multilayer Dielectric Diffraction Grating with Enhanced Laser Damage Threshold. Nanomaterials, 12(12), 1952. https://doi.org/10.3390/nano12121952








