Next Article in Journal
Nanoarchitectonics for High Adsorption Capacity Carboxymethyl Cellulose Nanofibrils-Based Adsorbents for Efficient Cu2+ Removal
Next Article in Special Issue
A Facile and General Approach to Enhance Water Resistance of Metal-Organic Frameworks by the Post-Modification with Aminopropyltriethoxylsilane
Previous Article in Journal
A Water-Stable 2-Fold Interpenetrating cds Net as a Bifunctional Fluorescence-Responsive Sensor for Selective Detection of Cr(III) and Cr(VI) Ions
Previous Article in Special Issue
The Synthesis and Properties of TIPA-Dominated Porous Metal-Organic Frameworks
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Nanomaterials
Volume 12
Issue 1
10.3390/nano12010159
nanomaterials-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Machine Learning-Assisted Computational Screening of Metal-Organic Frameworks for Atmospheric Water Harvesting

by
Lifeng Li
1,†,
Zenan Shi
1,†,
Hong Liang
1,*,
Jie Liu
2,* and
Zhiwei Qiao
1,*
1
Guangzhou Key Laboratory for New Energy and Green Catalysis, School of Chemistry and Chemical Engineering, Guangzhou University, Guangzhou 510006, China
2
Key Laboratory for Green Chemical Process of Ministry of Education, School of Chemical Engineering and Pharmacy, Wuhan Institute of Technology, Wuhan 430073, China
*
Authors to whom correspondence should be addressed.
†
These authors contributed equally to this work.
Nanomaterials 2022, 12(1), 159; https://doi.org/10.3390/nano12010159
Submission received: 7 November 2021 / Revised: 29 December 2021 / Accepted: 31 December 2021 / Published: 3 January 2022
(This article belongs to the Special Issue Advanced Metal-Organic Frameworks)
Browse Figures
Versions Notes

Abstract

Atmospheric water harvesting by strong adsorbents is a feasible method of solving the shortage of water resources, especially for arid regions. In this study, a machine learning (ML)-assisted high-throughput computational screening is employed to calculate the capture of H2O from N2 and O2 for 6013 computation-ready, experimental metal-organic frameworks (CoRE-MOFs) and 137,953 hypothetical MOFs (hMOFs). Through the univariate analysis of MOF structure-performance relationships, Qst is shown to be a key descriptor. Moreover, three ML algorithms (random forest, gradient boosted regression trees, and neighbor component analysis (NCA)) are applied to hunt for the complicated interrelation between six descriptors and performance. After the optimizing strategy of grid search and five-fold cross-validation is performed, three ML can effectively build the predictive model for CoRE-MOFs, and the accuracy R2 of NCA can reach 0.97. In addition, based on the relative importance of the descriptors by ML, it can be quantitatively concluded that the Qst is dominant in governing the capture of H2O. Besides, the NCA model trained by 6013 CoRE-MOFs can predict the selectivity of hMOFs with a R2 of 0.86, which is more universal than other models. Finally, 10 CoRE-MOFs and 10 hMOFs with high performance are identified. The computational screening and prediction of ML could provide guidance and inspiration for the development of materials for water harvesting in the atmosphere.

Graphical Abstract

1. Induction

As we all know, 71% of the earth’s surface is covered by water, and the remaining 29% is land. At first glance, we have a lot of water resources; in fact, the water we use is mainly fresh water, and fresh water only accounts for 2.5% of all water resources on the earth [1]. Among them, approximately 69% of the fresh water is enclosed in the ice layer of Antarctica and Greenland, and the remaining 30% is stored in the ground, so the fresh water (such as river water and fresh water lakes) that humans can directly use accounts for only 0.4% of all water resources [1]. As population growth and living standards improve, water resources are becoming increasingly scarce, especially daily water for residents of arid regions. Currently, one third of the world’s population live in regions with medium and high water shortages. It is estimated that two thirds of the world will face water shortages by 2050 [2]. Therefore, the lack of fresh water has become one of the major crises to be resolved. At present, several technologies are being used to address this issue. Desalination is one of the main ways to develop new fresh water resources, but the construction of this infrastructure requires a lot of money and the production process is highly energy intensive [3]. In addition, since the main arid and water-scarce areas are far inland, there are never sea water resources available in these places. It is therefore especially important to develop a fresh water technology that can be used in arid areas.
The atmosphere of our planet contains a lot of water, which exists in the form of droplets and vapor. It accounts for about 10% of all fresh water [4]. Therefore, if atmospheric water can be efficiently harvested and used, water shortages can be greatly alleviated. At present, the two main methods for collecting water vapor from the air are vapor condensation and adsorption–desorption technology [5]. Condensation conditions are relatively harsh, usually requiring very high amounts of water vapor from the air (relative humidity, RH = 100%) and a large amount of energy, which is unrealistic when the relative humidity is less than 50% [4]. On the contrary, the adsorption–desorption technology can adsorb the water vapor from the air at low temperature, then, using low-grade energy such as natural sunlight or waste heat, it can desorb and condense it into liquid water. The entire process does not require additional energy. Obviously, adsorption–desorption technology is more convenient and energy-saving, and can be used in relatively low humidity regions.
The key to adsorption–desorption technology is to select a suitable adsorbent. Currently, the main adsorbents are polymers, zeolites, and silica gels. Unfortunately, these adsorbents have some shortcomings that cannot be ignored, such as low adsorption capacity and the fact that regeneration requires a lot of energy [6]. AMetal-organic frameworks (MOFs), a porous crystalline material, is self-assembled from metal ions and organic ligands [7]. Due to its characteristics of high porosity, large specific surface area and adjustable structure, it is regarded as a candidate for traditional adsorption. Although MOFs have long been used in the fields of gas adsorption [8], separation [9,10], storage [11,12], catalysis [13], and heat pumps [14,15], the use of MOFs to harvest water vapor from the atmosphere has only been proposed in recent years [1,16,17]. This is because structural stability of MOFs may deteriorate after absorbing water. As more MOFs with good water stability join the MOF family, the use of MOFs for atmospheric water harvesting has received widespread attention. Furukawa et al. [16] studied and evaluated the water adsorption properties of 23 materials including six newly synthesized zirconium-based MOFs and determined that MOF-841 can be used as a candidate for atmospheric water harvesting in arid regions. In 2017, Kim et al. [4] developed a heat pump system using the MOF as an adsorbent to collect water from the atmosphere. The principle is that the heat pump absorbs water at night, and uses low-grade energy such as natural sunlight to desorb and condense liquid water during the day. The system harvested 2.8 L of water per kilogram of MOF (MOF-801) per day at room temperature with relative humidity below 20%. Recently, Hanikel et al. [18] summarized the progress of atmospheric water harvesting and the use of MOF-designed water-collection equipment. Therefore, it is feasible to use MOFs to capture water vapor from the atmosphere. We need to screen out some super-hydrophilic MOFs in a huge MOF database. The water vapor in the atmosphere is extremely small compared to N2 and O2, so we need super-hydrophilic and highly selective MOFs to efficiently capture water from the atmosphere. It is very difficult to select suitable MOFs from so huge a database by experimental verification.
The emergence of high-throughput computational screening (HTCS) provides a possibility for solving the problem. Qiao et al. [19] used HTCS to select MOFs suitable for separating CO2/N2 and CO2/CH4 from 4764 computation-ready, experimental MOF (CoRE-MOF) databases. In fact, HTCS includes Monte Carlo simulations (MC) and machine learning (ML) [20], and previous studies on HTCS have usually relied on molecular simulation. In recent years, ML has been widely applied to various fields, including image recognition [21], natural language processing [22], data classification and mining [23,24], and material performance prediction [25]. In our previous work, Shi et al. [26] combined MS and ML to screen MOFs with good performance that can be used for adsorption heat pumps. In addition, according to two ML methods with good prediction effects, we determined that the heat of adsorption is the key descriptor that determines the performance of the heat pump. In the work of Dureckova et al. [27], a gradient boosting regression tree (GBRT) model was applied to predict the CO2 working capacity and CO2/H2 adsorption selectivity of carbon capture. It was found that the R2 values of predictive CO2 working capacity and CO2/H2 selectivity were 0.944 and 0.872, respectively. Hypothetical MOFs (hMOFs) can be automatically generated by different metals, linkers. and topologies in computer software. Wilmer et al. [28] generated 137,953 hMOFs from a library of 102 building blocks and screened 300 hMOFs with a higher capacity for methane storage than known CoRE-MOFs. Wu et al. [29] formed a new data set with 130,397 hMOFs and 37 feature descriptors including Henry’s coefficient, atomic number density, and functional group number density. They found that the hMOFs with optimal methane-storage capacities exhibit ϕ of 0.65–0.88, VSA of ~2250 m2·cm–3, etc.
The combination of machine learning and molecular simulation of HTCS has greatly increased the speed of discovering new materials [27,30], because ML suitable for specific systems will reduce the number of simulated materials, especially for the updated database of material. Recently, Pardakhti et al. [31] used the trained random forest (RF) of the ML model to predict the methane adsorption of ~130,000 hMOFs. The results showed that the speed of ML was several orders of magnitude faster than traditional MS. The combination of MS and ML has developed into the current main method of screening materials. In Shi et al.’s review [7], several ML methods were considered to possess better prediction performance, such as back propagation neural network and random forest. Therefore, in this work, we selected these methods, as well as gradient boosting regression tree and neighbor component analysis, on the basis that they have good predictive performance for water harvesting on MOFs.
In the present work, we apply MC and three ML models to study the performance of water harvesting on MOFs. Based on the established structure-performance relationship, all three types of machine learning achieve a relatively good predictive effect. Then we obtained the main descriptors that played an important role in the performance of MOFs for the capture of water, and finally obtained super hydrophilic MOFs. This may provide guidance for experimental workers to synthesize available MOFs.

2. Models and Methods

2.1. Molecular Models

The crystal structures of the version 2017 of 6013 CoRE-MOFs were collected and established by Chung et al. [32,33] removing the free and coordinated solvent molecules. A large crystallographic dataset of 137,953 hMOFs was designed by Wilmer et al. [28] using 102 building blocks and six different topologies. Five structural descriptors including the largest cavity diameter (LCD), pore-limiting diameter (PLD), volumetric surface area (VSA), void fraction (ϕ), density (ρ), and an energy descriptor of heat of adsorption (Qst), were used to quantitatively describe the structure of the MOF. The reasons for the selection of these six descriptors are as follows: (1) they possessed the strong structure-performance relationships between gas and MOFs, confirmed by many previous works [28,32,34,35] of high-throughput calculation of MOFs, which means that these six MOF descriptors have a greater possibility of achieving the accuracy prediction in ML models than the thousands of other descriptors that could have been used; (2) these six descriptors could be applied in accuracy prediction of ML, which coincide with many ML works [36,37,38,39]; (3) these descriptors are relatively easy to measure in the experiment, and they can be used directly to guide the synthesis and application of MOF. The LCD and PLD in each CoRE-MOF were estimated using Zeo++ [40]. The VSA and ϕ were determined using the diameter of 0.364 nm and 0.258 nm of N2 and He as a probe under the RASPA package, respectively [41]. The Qst was calculated by the NVT-Monte Carlo (MC) with the Widom method in RASPA under infinite dilution conditions, where N, V, and T are the number of particles, the volume of system, and the temperature of the system, respectively [41].
The partial atomic charges of MOFs were rapidly estimated and evaluated using the new MEPO-Qeq [42] method trained to reproduce density function theory (DFT), the extended electrostatic potential fitted charges using the Repeating Electrostatic Potential Extracted Atomic (REPEAT) method [43]. The LJ potential parameters of all CoRE-MOFs were obtained from the universal force field (UFF) [44], as listed in Table S1. In our previous work, it was shown that combining the force fields and MEPO-Qeq method can accurately and quickly predict the adsorption and capture of gases in various MOFs [26,45]. The force field parameters of N2 and O2 molecules were described by the transferable potentials for phase equilibria (TraPPE) force field [46], as demonstrated in Table S2. The TIP4P-Ew [47] model was used to simulate H2O molecules with LJ sites on the O and H atoms, along with the partial charges on H atoms and a dummy atom. A three-site model was applied to mimic a CO2 molecule, which has a C-O bond length of 0.116 nm and a bond angle ∠OCO of 180° [48]. Similarly, an N2 molecule was modeled as a three-site model with the N-N bond length of 0.110 nm.

2.2. Monte Carlo Simulations

To capture water from the air, the Henry’s constants of H2O, N2, and O2 were calculated at 298 K using the Widom particle insertion method [49], and then the selectivity S0[H2O/(N2+O2)] was calculated by the Henry’s constant of three gas molecules. In this study, the MOF with the larger Henry’s constant of H2O (KH2O) and higher S0[H2O/(N2+O2)] is regarded as excellent candidate. Notice that Henry’s constant of water is calculated based on the interaction of a water molecule with the framework, which is mainly designed to simulate the extremely low water-molecule content in extreme environments such as deserts (it can be regarded as only one molecule of water in the air). It is noteworthy that, although grand canonical MC (GCMC) is an accurate estimation for the adsorption performance of MOFs, it is difficult to accurately calculate the adsorption loading of H2O. This is because although the structure of a water molecule is very simple, a molecular H-O-H hydrogen bond angle and dipole moment can change continuously during the adsorption process, which further complicates the adsorption [50]. Thus, the H2O adsorption isotherm in most adsorbing has a jump in a narrow range of vapor pressure. This jump is very difficult to calculate during the GCMC simulation. Currently, there was still not a suitable force field or H2O model, which could be used to screen the adsorption loading of H2O in most CoRE-MOFs by GCMC. After the GCMC simulation was repeatedly tested, only several MOFs could be accurately predicted with a relatively good level of agreement with the experimental isotherm [46,50,51,52] Therefore, for a large scale of screening of CoRE-MOFs, the Ki was used to calculate the adsorption selectivity of H2O in this work. For further explanation, see the supporting information (SI).
The simulation unit cell extended to at least 2.4 nm along each dimension, and periodic boundary conditions were applied in the three dimensions. It was assumed that the framework atoms of MOFs were rigid and fixed during the simulations. To calculate the LJ interaction, the long-range corrected spherical cut-off radius was set to 1.2 nm. The Ewald summation [53] method was used to estimate the electrostatic interaction between the frameworks and gas molecules as well as between the gas molecules. The number of MC cycles was 100,000; the first 50,000 cycles were performed to the simulation of the equilibrium system, and the last 50,000 cycles were run for ensemble averages. After testing, it was shown that the effect of increasing the MC cycle on the adsorption results was negligible. All simulations were carried out under the RASPA package [41].

2.3. Machine Learning Method

To find out which of the machine-learning (ML) models is suitable for predicting the relationship between the six descriptors (LCD, ϕ, VSA, PLD, ρ, Qst) and the selectivity S0[H2O/(N2+O2)] of MOFs, further information was sought by ML models. The three kinds of ML employed for the prediction of S0[H2O/(N2+O2)] were random forest (RF), gradient boosting regression tree (GBRT), and neighbor component analysis (NCA), which were run in Statistics and Machine Toolbox Learning under Matlab2019a software. Because the magnitude of the selectivity data span was very large and cannot be predicted directly, it needed to be pre-processed first; that is, the value of S0[H2O/(N2+O2)] was taken by the logarithm (log10(S0[H2O/(N2+O2)])) to narrow the enormous difference in the various data. In this work, after the five-fold cross-validation evaluated all possible values of each parameter, three ML algorithms programmatically selected the optimal parameter values for the final calculation and prediction, in which the six descriptors were regarded as the input variable and log10(S0[H2O/(N2+O2)]) as output variable of ML. The key parameters were optimized by five-fold cross-validation and grid-search, as listed in Table S3. All data were divided into five folds. For each cycle, four-fifths of the data were selected randomly as a training set, and one-fifth of the data as a test set. The ML model was run five times for each group value of key parameters by the five-fold cross-validation. The average determinate coefficient (R2) of test sets in five-fold cross-validation was adopted to indicate the performance of the model built by different parameter groups.
R 2 = 1 − ∑ i = 1 n ( y i − f i ) 2 ∑ i = 1 n ( y i − f ¯ i ) 2
where n, yi, fi, and f i – refer to the number of MOFs, simulated value, ML predicted value, and average ML predicted value, respectively.
In view of the maximum average R2, the optimal parameters could be automatically obtained by the strategy of parameter optimization. Except the optimized parameters, the other parameters were the default values, as listed in Table S4. Secondly, the entire data set of 6013 CoRE-MOFs was adopted to train the model with optimal parameter values. Finally, the data of 10,000 hMOFs were tested.
Among them, NCA [54,55] is a supervised learning algorithm that learns the feature weights using a diagonal adaptation. RF is made of multiple decision trees to achieve comparatively higher robustness, and its output is the average of the prediction results of multiple trees [31]. Similarly, GBRT is also an aggregation method by decision tree, which creates the optimal split criterion by continuously minimizing the least squares-regression error for the reduction of computing residual last time. More details of the three MLs are listed in the SI.

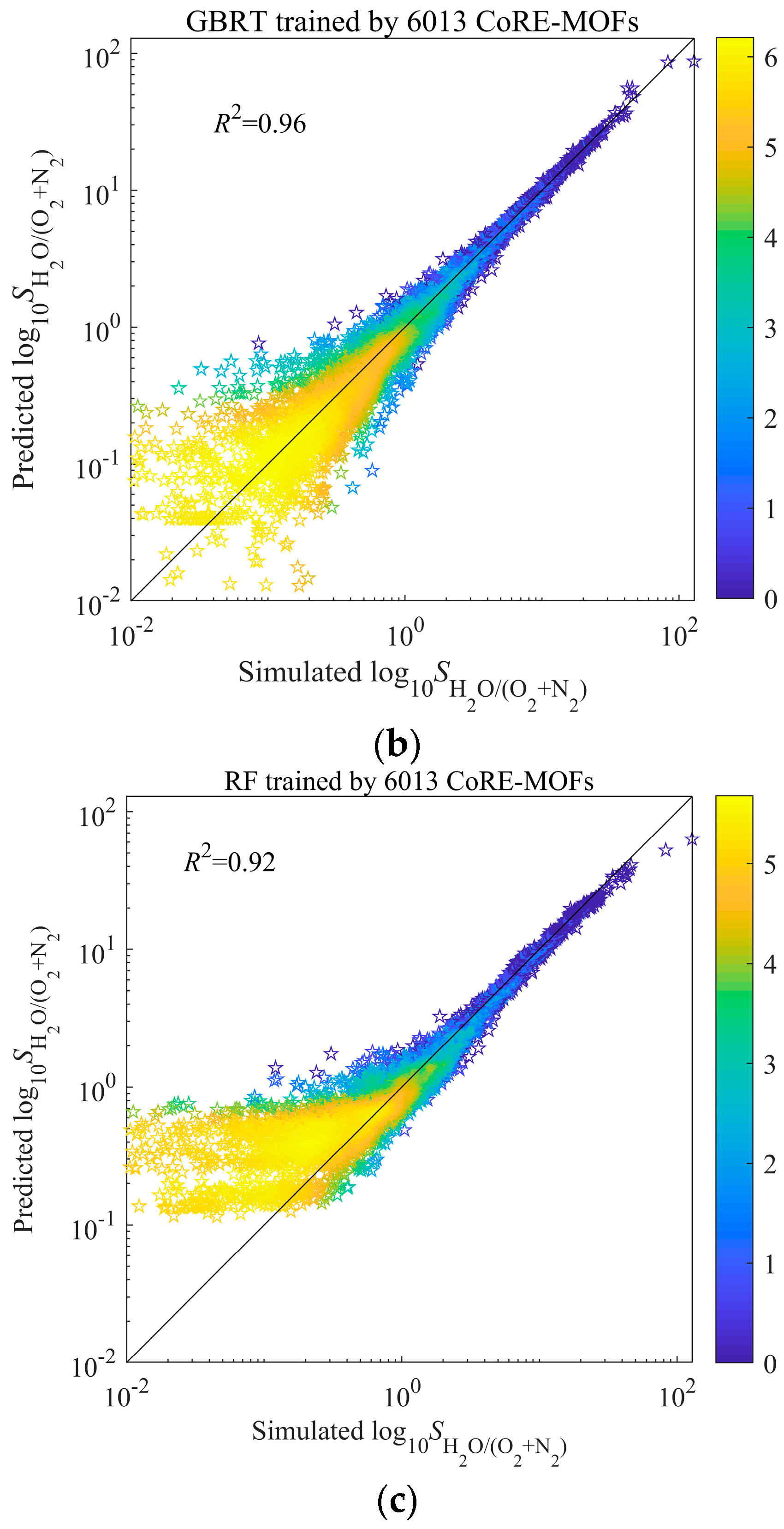
3. Results and Discussion

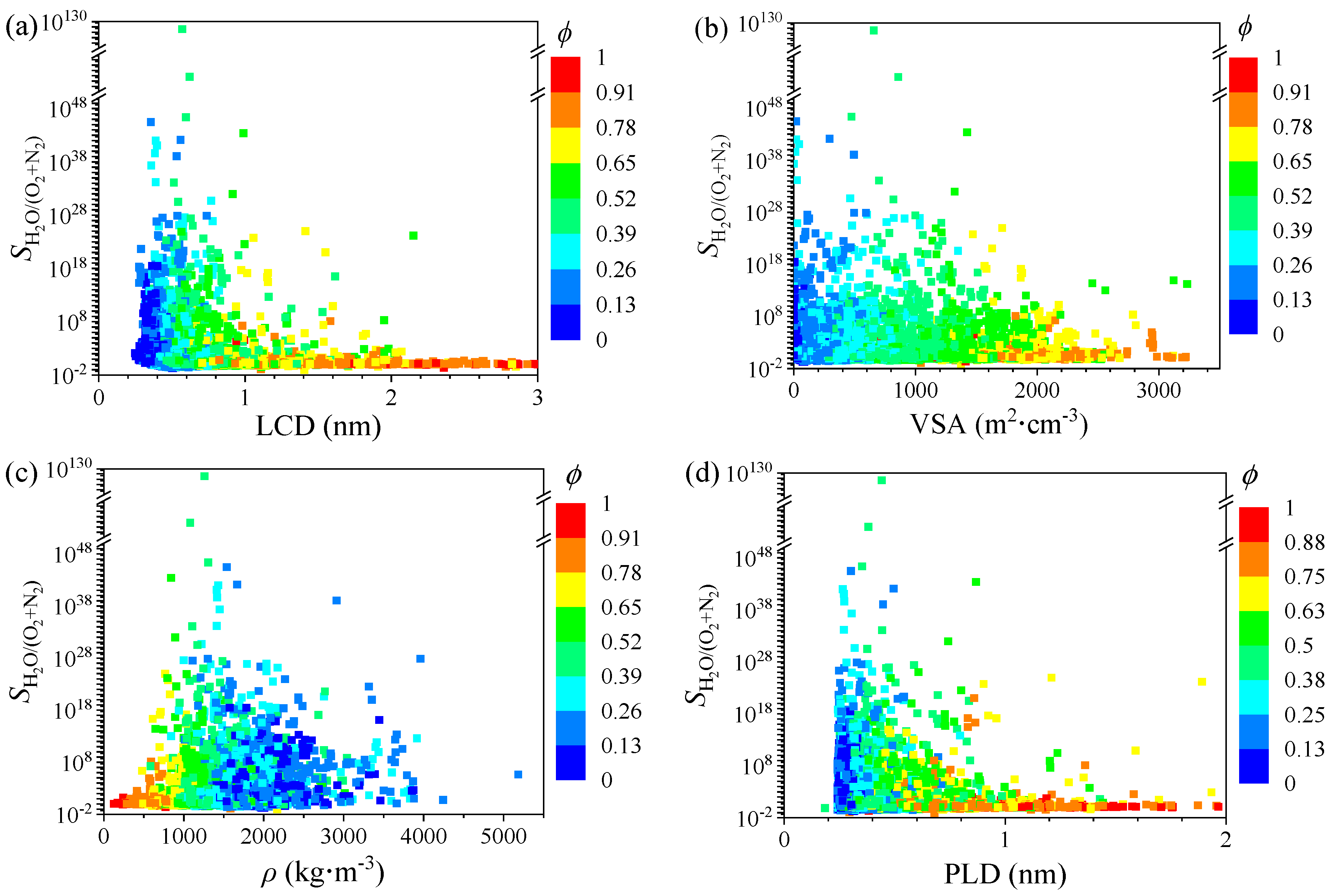
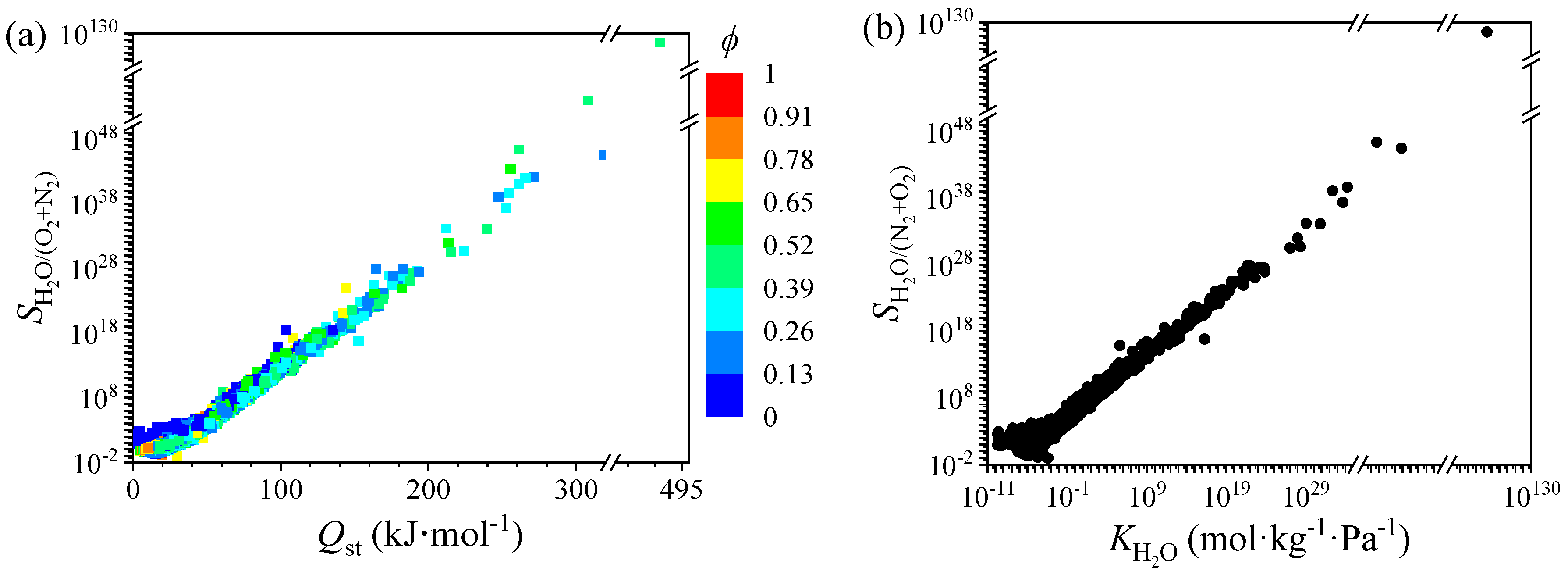
3.1. Univariate Analysis

To explore the effect of the six MOF descriptors on water harvesting performance, we used univariate analysis to understand the relationship between each descriptor (LCD, ϕ, VSA, ρ, PLD, and Qst) and the selectivity S0[H2O/(N2+O2)]. In Figure 1, the scale of S0[H2O/(N2+O2)] is very large, because the adsorption behavior of vapor water is very special; it is different from most gases. It is a typical multilayer adsorption. The adsorption of vapor water in MOFs can be divided into two stages. Firstly, based on the interaction between vapor water and MOFs, the water molecules are gradually adsorbed in the pore wall of MOFs. Second, with the increasing of water molecules entering into the framework, strong hydrogen bonds are formed between water and water molecules, leading to remarkable multilayer adsorption. Thus, it is extremely important in the adsorption process of vapor water that the first layer of water is successfully adsorbed in MOFs. Therefore, the difference in selectivity of H2O between hydrophilic and hydrophobic MOFs is extremely large, leading to the data with very high value. In addition, the content of water vapor in the atmosphere is very small, especially in desert areas. The V-shaped adsorption isotherm and very high selectivity of water could be helpful to achieve the capture of H2O in these extreme environments. Figure 1a shows the relationship of the S0[H2O/(N2+O2)] and LCD. The selectivity is close to 0 in the range of LCD less than 0.27 nm, which may be because the molecules of H2O with the dynamic diameter of 0.264 nm cannot enter the pores of the MOF. As the LCD continues to increase, the S0[H2O/(N2+O2)] gradually decreases and eventually stabilizes at less than 1 (approximately 0.01). The S0[H2O/(N2+O2)] is less than 1, indicating that the MOF does not have the ability to selectively adsorb H2O vapor, but preferentially adsorbs N2 and O2 in the atmosphere. This process reflects the change from shape selective to inverse-shape selective adsorption. The relationship of the S0[H2O/(N2+O2)] and VSA is shown in Figure 1b. In the region where VSA is close to 0, it shows a higher selectivity. When VSA continues to increase, the selectivity reaches its highest point, then gradually decreases. This is because when the VSA is small, the pores of the MOF can accommodate H2O molecules, and when the VSA is too large, the accessible surface of all molecules in the MOF increases, so the contact probability of the N2 and O2 with their optimal adsorption sites increases. Therefore, the selectivity will decrease; that is, the selective separation of H2O vapor cannot be achieved. The super hydrophilic MOFs with high selectivity and high Henry’s constants have a VSA of less than 1000 m2·cm−3, except that the VSA of HUZSUR01 is 1422.66 m2·cm−3.
Figure 1c shows the relationship of the S0[H2O/(N2+O2)] and density ρ. Density and void fraction are correlated descriptors. It is worth noting that as the selectivity increases, the density and void fraction change in opposite directions. This is not difficult to understand. The larger the porosity, the larger the pore volume of the MOF and the lower its density. When the ρ is less than 1260 kg·m−3, the S0[H2O/(N2+O2)] increases as the density increases, and then the selectivity decreases with the increase of the ρ. In Figure 1, the void fraction ϕ is mapped in the subplots as color codes. The MOFs with high selectivity have a medium-range of ϕ (0.20–0.62), except for MOF HEWFUL (ϕ = 0.16). This is because too large and too small pores are not suitable for selective separation. The pore is too small to prevent the molecule of H2O from entering, thus hindering the adsorption. Conversely, if the pore is too large, the interaction between the adsorbed molecules and the MOF will be weakened, which is not conducive to selective separation. The S0[H2O/(N2+O2)] versus PLD is shown in Figure 1d. This trend is similar to the relationship of the S0[H2O/(N2+O2)] and LCD. The highest S0[H2O/(N2+O2)] are observed at PLD with 0.4 nm, which is approximately equaled to the kinetic diameter of N2 and O2 (0.364 nm and 0.346 nm, respectively). Although the PLD of some MOFs is smaller than the dynamic diameter of H2O, it is still possible for water molecules to enter these MOF channels. On the one hand, MOF pores are not regular, H2O molecules may enter from other larger pores; on the other hand, the kinetic diameter of H2O is estimated by empirical estimation, which is usually larger than the actual size [56], so the molecule of adsorbate may be adsorbed in the MOF.
Figure 2a shows that the selectivity increases with the heat of adsorption, which shows a monotonic upward trend. The trend is almost linear, indicating that the isosteric heat of adsorption and the selectivity are strongly correlated variables. When the range of Qst is 270–480 kJ·mol−1, the MOF has its highest S0[H2O/(N2+O2)]. Since we simulated the adsorption of a single H2O molecule in MOF at infinite dilution, so the heat of adsorption can characterize the strength of the adsorption. Therefore, Qst may be a key descriptor for determining S0[H2O/(N2+O2)]. This phenomenon also appeared in the CO2 [57] adsorption and thiol capture [45] from the air in our previous works. Figure 2b plots the relationship of the S0[H2O/(N2+O2)] and the Henry’s constants of water KH2O [58]. On a logarithmic scale, the scatter plot of the S0[H2O/(N2+O2)] and the KH2O shows an upward trend. The Henry’s constant is a parameter that measures the affinity between the optimal adsorption site of the adsorbent and the adsorbate. The larger Henry’s constant indicates that the interaction between adsorbent and adsorbate molecule is stronger, making adsorption-based separation achievable. Thus, it is necessary that the MOF with large KH2O is required to harvest H2O vapor from the air in arid areas (RH ≈ 20%). From Figure 1 and Figure 2, the Qst seems to be the most important descriptor, and its relationship with selectivity is the most obvious. After linear, binomial, and trinomial fitting for S0[H2O/(N2+O2)]~Qst, the R2 of binomial fitting could achieve 0.97 and remain stable by using the trinomial fitting, as is shown in Figure S2. The deviation of two points with highest S in the linear fitting makes a relatively lower R2 than both the binomial and trinomial fitting. In fact, the R2 for linear fitting is only 0.93, and it has no accuracy prediction for data in the range of log S > 47. In view of the fitting, we can simply estimate and understand the structure-property relationships of MOFs for the atmospheric water harvesting. Therefore, Qst is very worthy of attention during the screening process.

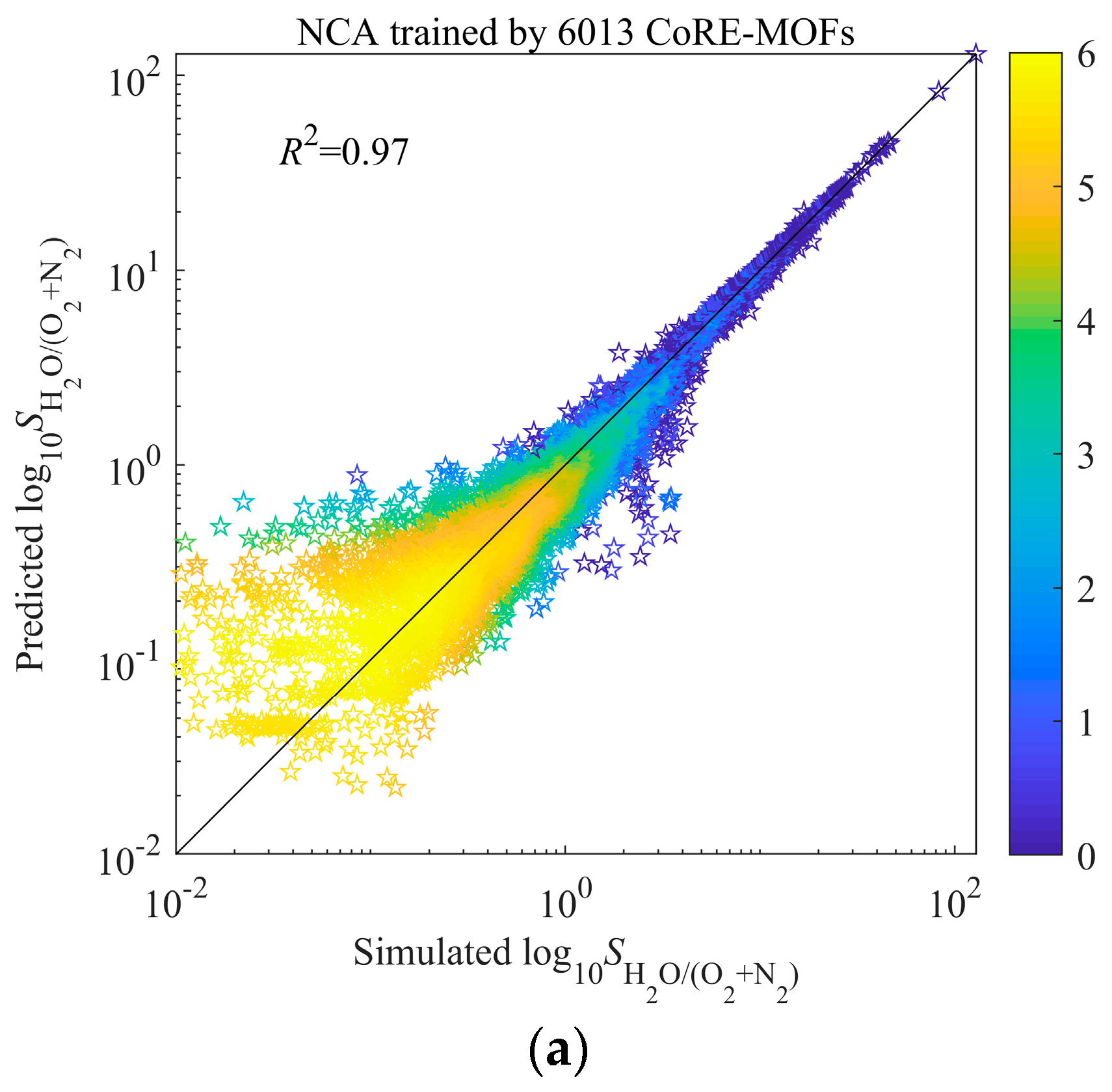
3.2. Machine Learning

At present, ML has been widely used to predict the performance of materials. Through univariate analysis, only the influence of a single descriptor can be obtained, and ML can not only predict the relationship of structure-performance, but also obtain the common impact of multiple descriptors on performance. In our study, the optimal parameters were obtained by five-fold cross-validation and grid-search. The average R2 of test sets in five-fold cross-validation was adopted to indicate the performance of the model built by different parameter groups. The final model trained by all 6013 pieces of data and optimal parameters. The results are showed in Figure 3a–c. The order of three ML is NCA > GBRT > RF. Compared to GBRT, NCA performs better in the range of high log10(S0[H2O/(N2+O2)]), while compared to RF, NCA performs better in the range of both low and high log10(S0[H2O/(N2+O2)]). The reason for this may be the different learning styles of the model, such as feature learning.
To further understand the relative importance of the six descriptors for the S0[H2O/(N2+O2)], we calculated the weight of each descriptor by three MLs. The weight of the descriptors was calculated while the model was being constructed. The value of relative importance was computed by the normalization of the weight of the six descriptors, as shown in Figure 4 and Table S5. Due to the different characteristics of models, ML shows the relative importance of the descriptors in different ways. However, they all have a point of comparison, which is that the proportion of Qst is more than 50%, especially for GBRT almost only built by a variable (Qst). The order of the six descriptors is Qst > ϕ > ρ > LCD ≈ VSA > PLD. Qst seems to govern the MOF performance in this work, because the concentration of vapor water in air is close to the condition of infinite dilution. The result shows that Qst holds an absolute advantage importance relative to others, as in Section 3.1, which provides a guide for designing the best MOFs of adsorption of water vapor in the experiment.
Furthermore, the predictive ML model should be used to accelerate the new HTCS for the other MOF database. Of course, both the simple binomial/trinomial fitting and ML model could achieve this H2O-MOF system, because of the strong relativity of Qst, but ML model would possess higher universality for the other gas-MOF system. Thus, we have added the prediction of a new MOF database (137,953 hMOFs) [28] by ML model, which was trained by 6013 CoRE-MOF datasets. First, Qst was calculated for all 137,953 hMOFs, and then we selected 10,000 hMOFs with the highest Qst for the new prediction, because Qst has the highest importance. As shown in Figure 5a–c, after the predicted results were compared with simulated results by molecular simulation, R2 of the prediction in NCA could reach 0.86. The reasons for the differences of performance between training and predicting are that there exist some differences between the CoRE-MOF and hMOF databases. For examples, there are more than 350 topologies in the CoRE-MOFs database, while there are only six topologies in the hMOFs database, which leads to a diversity gap in those databases; CoRE-MOFs contain much more open metal sites or non-skeleton ions than hMOFs [28]. In this work, the establishment and evaluation of models are finished by 6013 CoRE-MOFs. Ten thousand hMOFs are the extra data, which are different from CoRE-MOFs in some aspects and do not participate in the establishment and evaluation of models. The difference between NCA and GBRT/RF could be that GBRT overemphasizes the importance of Qst (relative importance ≈ 97% in Figure 4); that is, the GBRT model is almost only built by a variable (Qst) and RF may fail to grasp the importance of features other than Qst. Therefore, GBRT and RF may be suitable for the prediction of CoRE-MOFs but not hMOFs, which also means NCA is more universal. Nevertheless, the prediction of NCA for 10,000 hMOFs still shows the sufficient predictive ability of the model, but it is usually not as effective as the original dataset [59]. Moreover, it can be found that, when a hMOF possesses high selectivity (log10S > 5.3), the model performs very well. Thus, the ML model obtained by the CoRE-MOF database can pre-screen out low-performance MOFs to greatly reduce the running time of molecular simulation. Based on the ML algorithm, 80 hMOFs with high performance (log10S > 5.3) could be precisely screened out, and then only the selected 80 hMOFs would have to have their simulated adsorption behavior calculated, as opposed to 137,953 hMOFs, saving a considerable amount of time and computing resource. Finally, the optimal hMOFs were listed in Table S6.

4. Best CoRE-MOFs

According to the principle that both the Henry’s constants of H2O and the selectivity of excellent MOFs are large, we selected 10 optimal CoRE-MOFs for harvesting water from the air based on the order of the selectivity of MOFs from high to low, as listed in Table 1. Among them, the best MOF is QUTHAP, whose KH2O and S0[H2O/(N2+O2)] are 2.78 × 10124 and 4.14 × 10128, respectively. The range of LCD, ϕ, VSA, PLD, ρ, and Qst of 10 MOFs is 0.035–0.988 nm, 0.16–0.62, 10.46–1422.66 m2·cm−3, 0.264–0.867 nm, 842.16–2912.23 kg·m−3, and 261.01–479.91 kJ·mol−1, respectively. The range of Qst, VSA, and ϕ shows significant agreement with the analysis of Section 3, while the others show less because the relationships between them and selectivity are less obvious. Obviously, the Henry’s constants and selectivity show a proportional trend, which is consistent with our univariate analysis. Moreover, we give more excellent hydrophilic MOFs for the further test. The top 200 CoRE-MOFs and top 200 hMOFs were listed in the Excel file of SI.

5. Conclusions

In summary, we simulated the adsorption behaviors of H2O, N2, and O2 on 6013 CoRE-MOFs and 137,953 hMOFs by HTCS and ML. Then, after the relationships between selectivity and six MOF descriptors (LCD, ϕ, VSA, ρ, PLD and Qst) were analyzed, respectively, Qst of H2O was shown to possess a strong correlation with the MOF ability for the capture of H2O. Furthermore, three ML algorithms were employed to predict the adsorption performance for each CoRE-MOF, indicating that NCA with a five-fold cross-validation accuracy of R2 = 0.97 is the best algorithm for the prediction of selectivity and that the rank of their predictive ability is NCA > GBRT> RF. Continuously, the relative importance of the six descriptors by MLs could demonstrate that the Qst took the absolute predominance for designing MOFs with optimal selectivity of H2O/air. In addition, from the three models applied to predict the selectivity of hMOFs, it was found that the predicted R2 of NCA can reach 0.86; NCA is more universal for gas-MOFs systems than other models. Finally, the ten MOFs with the best performance were screened out by the statistical methods. They were potential candidates for the capture of H2O from air, especially for QUTHAP. The bottom-up microscopic insights obtained from this study offer experimentalists the guidelines for the development of MOFs with high performance for atmospheric water harvesting.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/nano12010159/s1, Table S1: Lennard-Jones parameters of MOFs; Figure S1: Models of N2 and O2; Table S2: Lennard-Jones parameters and charges of adsorbates; Explanation about calculation approach; Figure S2: Linear, binomial and trinomial fitting; Figures S3–S5: Details of three ML algorithms; Table S3: Type and the range of key parameters in the optimization; Table S4: Parameters of 4 ML; Table S5: Predictive importance of six descriptor by four ML algorithms; Table S6: Details of top ten hMOFs with optimal performance of water harvesting; Excel file: Top 200 CoRE-MOFs and hMOFs.

Author Contributions

Conceptualization, Z.Q. and J.L.; methodology, Z.Q. and L.L.; software, Z.Q.; validation, L.L., Z.S. and Z.Q.; formal analysis, Z.S.; investigation, H.L.; resources, Z.Q.; data curation, Z.Q.; writing—original draft preparation, L.L. and Z.S.; writing—review and editing, Z.Q., H.L. and J.L.; visualization, L.L.; supervision, H.L.; project administration, H.L.; funding acquisition, Z.Q. All authors have read and agreed to the published version of the manuscript.

Funding

We gratefully thank the National Natural Science Foundation of China (Nos. 21978058, 21706197 and 21676094), the Pearl River Talent Recruitment Program (2019QN01L255), the Natural Science Foundation of Guangdong Province (2020A1515010800) and Science and Technology Planning Project of Guangzhou (202102020875) for financial support.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

Nomenclature

LCDlargest cavity diameter, nm
PLDpore-limiting diameter, nm
VSAvolumetric surface area, m2·cm−3
ϕvoid fraction
ρdensity, kg·m−3
Qstan energy descriptor of heat of adsorption, kJ·mol−1
KH2OHenry’s constant of H2O, mol·kg−1·Pa−1
S0[H2O/(N2+O2)]The initial selectivity of water molecules relative to nitrogen and oxygen adsorbed by MOFs.

References

  1. Kalmutzki, M.J.; Diercks, C.S.; Yaghi, O.M. Metal-Organic Frameworks for Water Harvesting from Air. Adv. Mater. 2018, 30, 1704304.1–1704304.26. [Google Scholar] [CrossRef] [Scilit] [PubMed]
  2. Elimelech, M.; Phillip, W.A. The future of seawater desalination: Energy, technology, and the environment. Science 2011, 333, 712–717. [Google Scholar] [CrossRef] [Scilit]
  3. Ghaffour, N.; Missimer, T.M.; Amy, G.L. Technical review and evaluation of the economics of water desalination: Current and future challenges for better water supply sustainability. Desalination 2013, 309, 197–207. [Google Scholar] [CrossRef] [Scilit]
  4. Kim, H.; Yang, S.; Rao, S.R.; Narayanan, S.; Kapustin, E.A.; Furukawa, H.; Umans, A.S.; Yaghi, O.M.; Wang, E.N. Water harvesting from air with metal-organic frameworks powered by natural sunlight. Science 2017, 356, 430–432. [Google Scholar] [CrossRef] [Scilit]
  5. Gordeeva, L.G.; Solovyeva, M.V.; Sapienza, A.; Aristov, Y.I. Potable water extraction from the atmosphere: Potential of MOFs. Renew. Energ. 2020, 148, 72–80. [Google Scholar] [CrossRef] [Scilit]
  6. Zhang, Y.Z.; He, T.; Kong, X.J.; Lv, X.L.; Wu, X.Q.; Li, J.R. Tuning Water Sorption in Highly Stable Zr(IV)-Metal-Organic Frameworks through Local Functionalization of Metal Clusters. ACS Appl. Mater. Interfaces 2018, 10, 27868–27874. [Google Scholar] [CrossRef] [Scilit]
  7. Shi, Z.N.; Yang, W.Y.; Deng, X.M.; Cai, C.Z.; Yan, Y.L.; Liang, H.; Liu, Z.L.; Qiao, Z.W. Machine-learning-assisted high-throughput computational screening of high performance metal–organic frameworks. Mol. Syst. Des. Eng. 2020, 5, 725–742. [Google Scholar] [CrossRef] [Scilit]
  8. Li, W.; Li, S. CO2 adsorption performance of functionalized metal-organic frameworks of varying topologies by molecular simulations. Chem. Eng. Sci. 2018, 189, 65–74. [Google Scholar] [CrossRef] [Scilit]
  9. Cui, W.G.; Hu, T.L.; Bu, X.H. Metal-Organic Framework Materials for the Separation and Purification of Light Hydrocarbons. Adv. Mater. 2020, 32, 1806445. [Google Scholar] [CrossRef] [Scilit] [PubMed]
  10. Budhathoki, S.; Ajayi, O.; Steckel, J.A.; Wilmer, C.E. High-throughput computational prediction of the cost of carbon capture using mixed matrix membranes. Energy Environ. Sci. 2019, 12, 1255–1264. [Google Scholar] [CrossRef] [Scilit]
  11. Yaghi, O.M. Hydrogen Storage in Metal-Organic Frameworks. Acta Crystallogr. Sect. A Found. Crystallogr. 2005, 61, C69. [Google Scholar] [CrossRef] [Scilit]
  12. Gandara, F.; Furukawa, H.; Lee, S.; Yaghi, O.M. High Methane Storage Capacity in Aluminum Metal-Organic Frameworks. J. Am. Chem. Soc. 2014, 136, 5271–5274. [Google Scholar] [CrossRef] [Scilit]
  13. Zhou, H.-C.; Long, J.R.; Yaghi, O.M. Introduction to Metal-Organic Frameworks. Chem. Rev. 2012, 112, 673–674. [Google Scholar] [CrossRef] [Scilit]
  14. Li, W.; Xia, X.X.; Cao, M.; Li, S. Structure-property relationship of metal-organic frameworks for alcohol-based adsorption-driven heat pumps via high-throughput computational screening. J. Mater. Chem. A 2019, 7, 7470–7479. [Google Scholar] [CrossRef] [Scilit]
  15. de Lange, M.F.; Verouden, K.J.F.M.; Vlugt, T.J.H.; Gascon, J.; Kapteijn, F. Adsorption-Driven Heat Pumps: The Potential of Metal-Organic Frameworks. Chem. Rev. 2015, 115, 12205–12250. [Google Scholar] [CrossRef] [Scilit]
  16. Furukawa, H.; Gandara, F.; Zhang, Y.B.; Jiang, J.; Queen, W.L.; Hudson, M.R.; Yaghi, O.M. Water Adsorption in Porous Metal-Organic Frameworks and Related Materials. J. Am. Chem. Soc. 2014, 136, 4369–4381. [Google Scholar] [CrossRef] [Scilit]
  17. Pan, T.T.; Yang, K.J.; Han, Y. Recent Progress of Atmospheric Water Harvesting Using Metal-Organic Frameworks. Chem. Res. Chin. Univ. 2020, 36, 33–40. [Google Scholar] [CrossRef] [Scilit]
  18. Hanikel, N.; Prévot, M.S.; Yaghi, O.M. MOF water harvesters. Nat. Nanotechnol. 2020, 15, 348–355. [Google Scholar] [CrossRef] [Scilit]
  19. Qiao, Z.W.; Zhang, K.; Jiang, J.W. In silico screening of 4764 computation-ready, experimental metal-organic frameworks for CO2 separation. J. Mater. Chem. A 2016, 4, 2105–2114. [Google Scholar] [CrossRef] [Scilit]
  20. Liu, Z.L.; Li, W.; Liu, H.; Zhuang, X.D.; Li, S. Research Progress of High-throughput Computational Screening of Metal-Organic Frameworks. Acta Chim. Sin. 2019, 77, 323–339. [Google Scholar] [CrossRef] [Scilit]
  21. Song, G.; Dai, Q.; Han, X.M.; Guo, L. Two novel ELM-based stacking deep models focused on image recognition. Appl. Intell. 2020, 50, 1345–1366. [Google Scholar] [CrossRef] [Scilit]
  22. Liu, H.T.; Xu, C.S.; Liang, J.Y. Dependency distance: A new perspective on syntactic patterns in natural languages. Phys. Life Rev. 2017, 21, 171–193. [Google Scholar] [CrossRef] [Scilit]
  23. Cully, A.; Clune, J.; Tarapore, D.; Mouret, J.-B. Robots that can adapt like animals. Nature 2015, 521, 503–507. [Google Scholar] [CrossRef] [Scilit]
  24. Van-Tho, N.; Constant, T.; Kerautret, B.; Debled-Rennesson, I.; Colin, F. A machine-learning approach for classifying defects on tree trunks using terrestrial LiDAR. Comput. Electron. Agric. 2020, 171, 105332. [Google Scholar]
  25. Fanourgakis, G.S.; Gkagkas, K.; Tylianakis, E.; Froudakis, G. A Generic Machine Learning Algorithm for the Prediction of Gas Adsorption in Nanoporous Materials. J. Phys. Chem. C 2020, 124, 7117–7126. [Google Scholar] [CrossRef] [Scilit]
  26. Shi, Z.N.; Liang, H.; Yang, W.Y.; Liu, J.; Liu, Z.L.; Qiao, Z.W. Machine learning and in silico discovery of metal-organic frameworks: Methanol as a working fluid in adsorption-driven heat pumps and chillers. Chem. Eng. Sci. 2020, 214, 115430. [Google Scholar] [CrossRef] [Scilit]
  27. Dureckova, H.; Krykunov, M.; Aghaji, M.Z.; Woo, T.K. Robust Machine Learning Models for Predicting High CO2 Working Capacity and CO2/H−2 Selectivity of Gas Adsorption in Metal Organic Frameworks for Precombustion Carbon Capture. J. Phys. Chem. C 2019, 123, 4133–4139. [Google Scholar] [CrossRef] [Scilit]
  28. Wilmer, C.E.; Leaf, M.; Lee, C.Y.; Farha, O.K.; Hauser, B.G.; Hupp, J.T.; Snurr, R.Q. Large-scale screening of hypothetical metal–organic frameworks. Nat. Chem. 2012, 4, 83–89. [Google Scholar] [CrossRef] [Scilit]
  29. Wu, X.J.; Xiang, S.C.; Su, J.Q.; Cai, W.Q. Understanding Quantitative Relationship between Methane Storage Capacities and Characteristic Properties of Metal–Organic Frameworks Based on Machine Learning. J. Phys. Chem. C 2019, 123, 8550–8559. [Google Scholar] [CrossRef] [Scilit]
  30. Tabor, D.P.; Roch, L.M.; Saikin, S.K.; Kreisbeck, C.; Sheberla, D.; Montoya, J.H.; Dwaraknath, S.; Aykol, M.; Ortiz, C.; Tribukait, H.; et al. Accelerating the discovery of materials for clean energy in the era of smart automation. Nat. Rev. Mater. 2018, 3, 5–20. [Google Scholar] [CrossRef] [Scilit]
  31. Pardakhti, M.; Moharreri, E.; Wanik, D.; Suib, S.L.; Srivastava, R. Machine Learning Using Combined Structural and Chemical Descriptors for Prediction of Methane Adsorption Performance of Metal Organic Frameworks (MOFs). ACS Comb. Sci. 2017, 19, 640–645. [Google Scholar] [CrossRef] [Scilit]
  32. Chung, Y.G.; Camp, J.; Haranczyk, M.; Sikora, B.J.; Bury, W.; Krungleviciute, V.; Yildirim, T.; Farha, O.K.; Sholl, D.S.; Snurr, R.Q. Computation-Ready, Experimental Metal-Organic Frameworks: A Tool To Enable High-Throughput Screening of Nanoporous Crystals. Chem. Mater. 2014, 26, 6185–6192. [Google Scholar] [CrossRef] [Scilit]
  33. Chung, Y.G. CoRE-MOFs. Available online: https://github.com/gregchung/gregchung.github.io/blob/master/CoRE-MOFs/structure-doi-CoRE-MOFsV2.0.csv (accessed on 7 May 2020).
  34. Bobbitt, N.S.; Chen, J.; Snurr, R.Q. High-Throughput Screening of Metal-Organic Frameworks for Hydrogen Storage at Cryogenic Temperature. J. Phys. Chem. C 2016, 120, 27328–27341. [Google Scholar] [CrossRef] [Scilit]
  35. Tang, H.J.; Jiang, J.W. In silico screening and design strategies of ethane-selective metal–organic frameworks for ethane/ethylene separation. AlChE J. 2021, 67, e17025. [Google Scholar] [CrossRef] [Scilit]
  36. Long, R.; Xia, X.; Zhao, Y.; Li, S.; Liu, Z.; Liu, W. Screening metal-organic frameworks for adsorption-driven osmotic heat engines via grand canonical Monte Carlo simulations and machine learning. iScience 2020, 24, 101914. [Google Scholar] [CrossRef] [Scilit]
  37. Aghaji, M.Z.; Fernandez, M.; Boyd, P.G.; Daff, T.D.; Woo, T.K. Quantitative Structure–Property Relationship Models for Recognizing Metal Organic Frameworks (MOFs) with High CO2 Working Capacity and CO2/CH4 Selectivity for Methane Purification. Eur. J. Inorg. Chem. 2016, 2016, 4505–4511. [Google Scholar] [CrossRef] [Scilit]
  38. Fernandez, M.; Woo, T.K.; Wilmer, C.E.; Snurr, R.Q. Large-Scale Quantitative Structure–Property Relationship (QSPR) Analysis of Methane Storage in Metal–Organic Frameworks. J. Phys. Chem. C 2013, 117, 7681–7689. [Google Scholar] [CrossRef] [Scilit]
  39. Li, W.; Xia, X.X.; Li, S. Screening of Covalent–Organic Frameworks for Adsorption Heat Pumps. ACS Appl. Mater. Interfaces 2020, 12, 3265–3273. [Google Scholar] [CrossRef] [Scilit]
  40. Willems, T.F.; Rycroft, C.; Kazi, M.; Meza, J.C.; Haranczyk, M. Algorithms and tools for high-throughput geometry-based analysis of crystalline porous materials. Microporous Mesoporous Mater. 2012, 149, 134–141. [Google Scholar] [CrossRef] [Scilit]
  41. Dubbeldam, D.; Calero, S.; Ellis, D.E.; Snurr, R.Q. RASPA: Molecular simulation software for adsorption and diffusion in flexible nanoporous materials. Mol. Simul. 2016, 42, 81–101. [Google Scholar] [CrossRef] [Scilit]
  42. Kadantsev, E.S.; Boyd, P.G.; Daff, T.D.; Woo, T.K. Fast and Accurate Electrostatics in Metal Organic Frameworks with a Robust Charge Equilibration Parameterization for High-Throughput Virtual Screening of Gas Adsorption. J. Phys. Chem. Lett. 2013, 4, 3056–3061. [Google Scholar] [CrossRef] [Scilit]
  43. Campana, C.; Mussard, B.; Woo, T.K. Electrostatic Potential Derived Atomic Charges for Periodic Systems Using a Modified Error Functional. J. Chem. Theory Comput. 2009, 5, 2866–2878. [Google Scholar] [CrossRef] [Scilit]
  44. Rappe, A.K.; Casewit, C.J.; Colwell, K.S.; Goddard, W.A.; Skiff, W.M. UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. [Google Scholar] [CrossRef] [Scilit]
  45. Qiao, Z.W.; Xu, Q.S.; Cheetham, A.K.; Jiang, J.W. High-Throughput Computational Screening of Metal-Organic Frameworks for Thiol Capture. J. Phys. Chem. C 2017, 121, 22208–22215. [Google Scholar] [CrossRef] [Scilit]
  46. Ghosh, P.; Kim, K.C.; Snurr, R.Q. Modeling Water and Ammonia Adsorption in Hydrophobic Metal-Organic Frameworks: Single Components and Mixtures. J. Phys. Chem. C 2014, 118, 1102–1110. [Google Scholar] [CrossRef] [Scilit]
  47. Horn, H.W.; Swope, W.C.; Pitera, J.W.; Madura, J.D.; Dick, T.J.; Hura, G.L.; Head-Gordon, T. Development of an improved four-site water model for biomolecular simulations: TIP4P-Ew. J. Chem. Phys. 2004, 120, 9665–9678. [Google Scholar] [CrossRef] [Scilit]
  48. Qiao, Z.W.; Xu, Q.S.; Jiang, J.W. Computational screening of hydrophobic metal-organic frameworks for the separation of H2S and CO2 from natural gas. J. Mater. Chem. A 2018, 6, 18898–18905. [Google Scholar] [CrossRef] [Scilit]
  49. Widom, B. Some Topics in the Theory of Fluids. J. Chem. Phys. 1963, 39, 2808–2812. [Google Scholar] [CrossRef] [Scilit]
  50. Zhang, H.; Snurr, R.Q. Computational Study of Water Adsorption in the Hydrophobic Metal–Organic Framework ZIF-8: Adsorption Mechanism and Acceleration of the Simulations. J. Phys. Chem. C 2017, 121, 24000–24010. [Google Scholar] [CrossRef] [Scilit]
  51. Ghosh, P.; Colón, Y.J.; Snurr, R.Q. Water adsorption in UiO-66: The importance of defects. Chem. Commun. 2014, 50, 11329–11331. [Google Scholar] [CrossRef] [Scilit]
  52. Moghadam, P.Z.; Ghosh, P.; Snurr, R.Q. Understanding the Effects of Preadsorbed Perfluoroalkanes on the Adsorption of Water and Ammonia in MOFs. J. Phys. Chem. C 2015, 119, 3163–3170. [Google Scholar] [CrossRef] [Scilit]
  53. Ewald, P.P. Die Berechnung optischer und elektrostatischer Gitterpotentiale. Ann. Phys. 1921, 369, 253–287. [Google Scholar] [CrossRef] [Scilit]
  54. Wei, Y.; Wang, K.; Zuo, W. Neighborhood Component Feature Selection for High-Dimensional Data. J. Comput. 2012, 7, 161–168. [Google Scholar]
  55. Roweis, S.; Hinton, G.; Salakhutdinov, R. Neighbourhood component analysis. Adv. Neural Inf. Processing Syst. (NIPS) 2005, 17, 513–520. [Google Scholar]
  56. Qiao, Z.W.; Cheetham, A.K.; Jiang, J.W. Identifying the best metal-organic frameworks and unravelling different mechanisms for the separation of pentane isomers. Mol. Syst. Des. Eng. 2019, 4, 609–615. [Google Scholar] [CrossRef] [Scilit]
  57. Deng, X.M.; Yang, W.Y.; Li, S.H.; Liang, H.; Shi, Z.N.; Qiao, Z.W. Large-Scale Screening and Machine Learning to Predict the Computation-Ready, Experimental Metal-Organic Frameworks for CO2 Capture from Air. Appl. Sci. 2020, 10, 569. [Google Scholar] [CrossRef] [Scilit]
  58. Moghadam, P.Z.; Fairen-Jimenez, D.; Snurr, R.Q. Efficient identification of hydrophobic MOFs: Application in the capture of toxic industrial chemicals. J. Mater. Chem. A 2016, 4, 529–536. [Google Scholar] [CrossRef] [Scilit]
  59. Liang, H.; Yang, W.Y.; Peng, F.; Liu, Z.L.; Liu, J.; Qiao, Z.W. Combining large-scale screening and machine learning to predict the metal-organic frameworks for organosulfurs removal from high-sour natural gas. APL Mater. 2019, 7, 091101. [Google Scholar] [CrossRef] [Scilit]
  60. Tominaka, S.; Coudert, F.-X.; Dao, T.D.; Nagao, T.; Cheetham, A.K. Insulator-to-Proton-Conductor Transition in a Dense Metal–Organic Framework. J. Am. Chem. Soc. 2015, 137, 6428–6431. [Google Scholar] [CrossRef] [Scilit]
Nanomaterials 12 00159 g001
Figure 1. The relationship of selectivity S0[H2O/(N2+O2)] versus (a) LCD, (b) VSA, (c) ρ, and (d) PLD. The color code represents void fraction ϕ.
Figure 1. The relationship of selectivity S0[H2O/(N2+O2)] versus (a) LCD, (b) VSA, (c) ρ, and (d) PLD. The color code represents void fraction ϕ.
Nanomaterials 12 00159 g001
Nanomaterials 12 00159 g002
Figure 2. The relationship of selectivity S0[H2O/(N2+O2)] versus (a) Qst, (b) KH2O. The color code represents void fraction ϕ.
Figure 2. The relationship of selectivity S0[H2O/(N2+O2)] versus (a) Qst, (b) KH2O. The color code represents void fraction ϕ.
Nanomaterials 12 00159 g002
Nanomaterials 12 00159 g003aNanomaterials 12 00159 g003b
Figure 3. Model (a) NCA, (b) GBRT, and (c) RF trained by 6013 CoRE-MOFs. The color represents a base-e logarithm of the number of MOFs.
Figure 3. Model (a) NCA, (b) GBRT, and (c) RF trained by 6013 CoRE-MOFs. The color represents a base-e logarithm of the number of MOFs.
Nanomaterials 12 00159 g003aNanomaterials 12 00159 g003b
Nanomaterials 12 00159 g004
Figure 4. Relative importance of the six descriptors on the selectivity of MOFs by three ML prediction.
Figure 4. Relative importance of the six descriptors on the selectivity of MOFs by three ML prediction.
Nanomaterials 12 00159 g004
Nanomaterials 12 00159 g005
Figure 5. Model (a) NCA, (b) GBRT, and (c) RF prediction for 10,000 hMOFs. The color represents a base-e logarithm of the number of MOFs.
Figure 5. Model (a) NCA, (b) GBRT, and (c) RF prediction for 10,000 hMOFs. The color represents a base-e logarithm of the number of MOFs.
Nanomaterials 12 00159 g005
Table 1. Top 10 CoRE-MOFs with optimal performance of water harvesting.
Table 1. Top 10 CoRE-MOFs with optimal performance of water harvesting.
No.CSD Code aLCD (nm)ϕVSA
(m2·cm−3)		PLD (nm)ρ (kg·m−3)Qst (kJ·mol−1)KH2O
(mol·kg−1·Pa−1)		S0[H2O/(N2+O2)]
1QUTHAP0.5690.44654.970.4411257.79479.91 ± 8.312.78 × 101244.14 × 10128
2CAJWIV0.6200.49856.370.3801078.91307.79 ± 10.194.30 × 10776.85 × 1082
3PIBLUJ0.5950.39473.390.3521304.13261.19 ± 5.985.81 × 10412.35 × 1046
4LIRVAK0.3550.2217.880.3011535.50318.82 ± 7.427.16 × 10443.11 × 1045
5HUZSUR010.9880.621422.660.867842.16255.45 ± 8.233.18 × 10392.48 × 1043
6HEWFUL0.5580.16293.030.4941665.78271.03 ± 3.111.63 × 10361.31 × 1042
7YUJWAD0.3880.2616.620.2641429.41265.55 ± 9.256.35 × 10369.73 × 1041
8YUJWAD010.3980.2842.730.2701409.42261.01 ± 9.771.73 × 10361.30 × 1041
9- b0.3840.2610.460.2711414.41254.38 ± 9.031.85 × 10344.26 × 1039
10ECUFEP0.5320.22491.720.4472912.23247.36 ± 7.132.53 × 10321.17 × 1039
a CSD code is the number of MOFs in the Cambridge Structural Database. b This MOF came from Tominaka et al.’s work [60].
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Li, L.; Shi, Z.; Liang, H.; Liu, J.; Qiao, Z. Machine Learning-Assisted Computational Screening of Metal-Organic Frameworks for Atmospheric Water Harvesting. Nanomaterials 2022, 12, 159. https://doi.org/10.3390/nano12010159

AMA Style

Li L, Shi Z, Liang H, Liu J, Qiao Z. Machine Learning-Assisted Computational Screening of Metal-Organic Frameworks for Atmospheric Water Harvesting. Nanomaterials. 2022; 12(1):159. https://doi.org/10.3390/nano12010159

Chicago/Turabian Style

Li, Lifeng, Zenan Shi, Hong Liang, Jie Liu, and Zhiwei Qiao. 2022. "Machine Learning-Assisted Computational Screening of Metal-Organic Frameworks for Atmospheric Water Harvesting" Nanomaterials 12, no. 1: 159. https://doi.org/10.3390/nano12010159

APA Style

Li, L., Shi, Z., Liang, H., Liu, J., & Qiao, Z. (2022). Machine Learning-Assisted Computational Screening of Metal-Organic Frameworks for Atmospheric Water Harvesting. Nanomaterials, 12(1), 159. https://doi.org/10.3390/nano12010159

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop