Approaching Disordered Quantum Dot Systems by Complex Networks with Spatial and Physical-Based Constraints
Abstract
1. Introduction
2. Related Work
3. Theoretical Framework
3.1. The Density Operator
3.2. Electron Dynamics of the Open Quantum System S
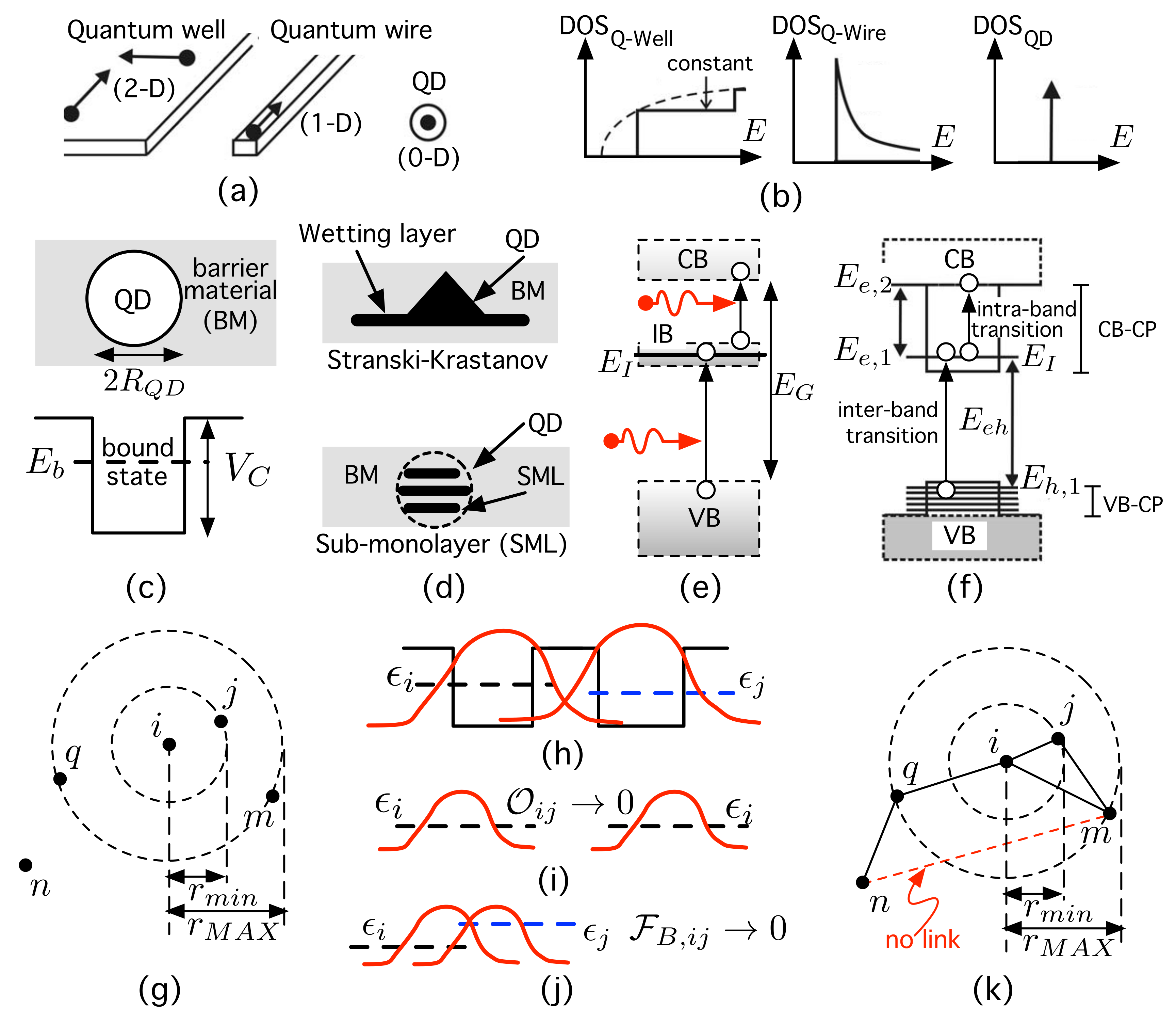
4. Approaching the QD System by a Network with Spatial and Physical-Based Constraints
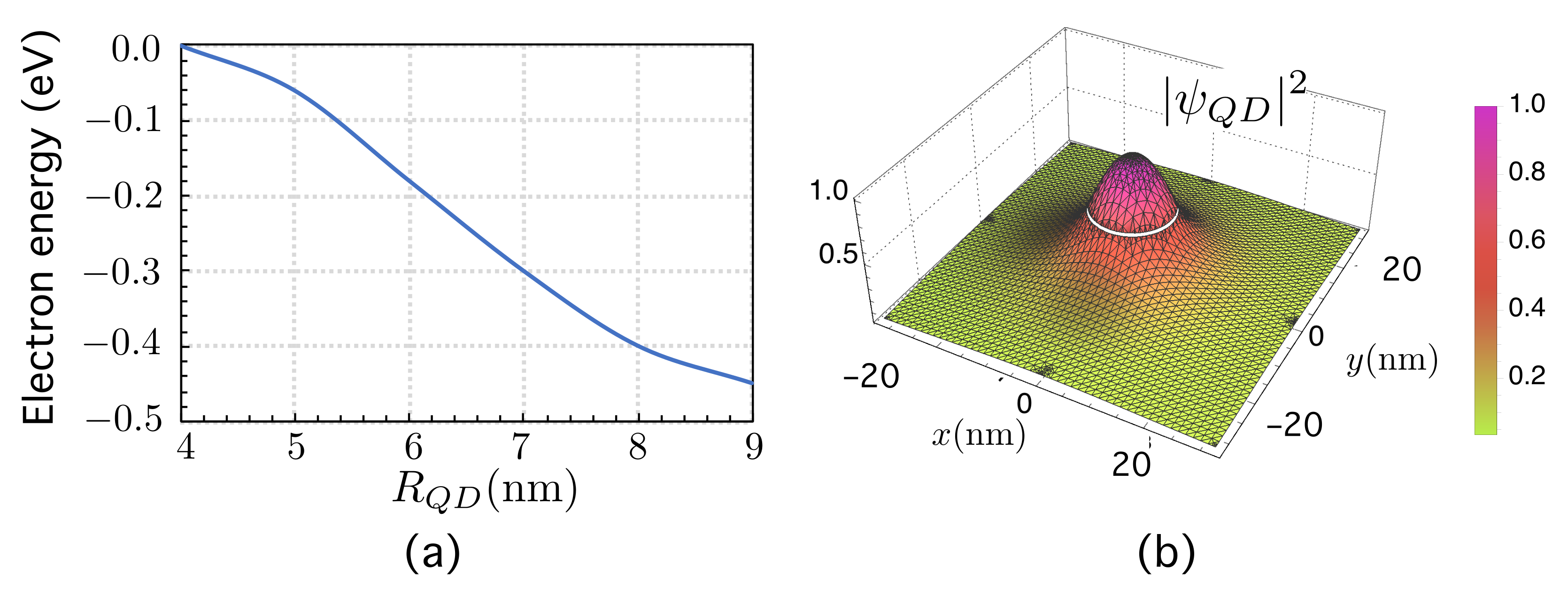
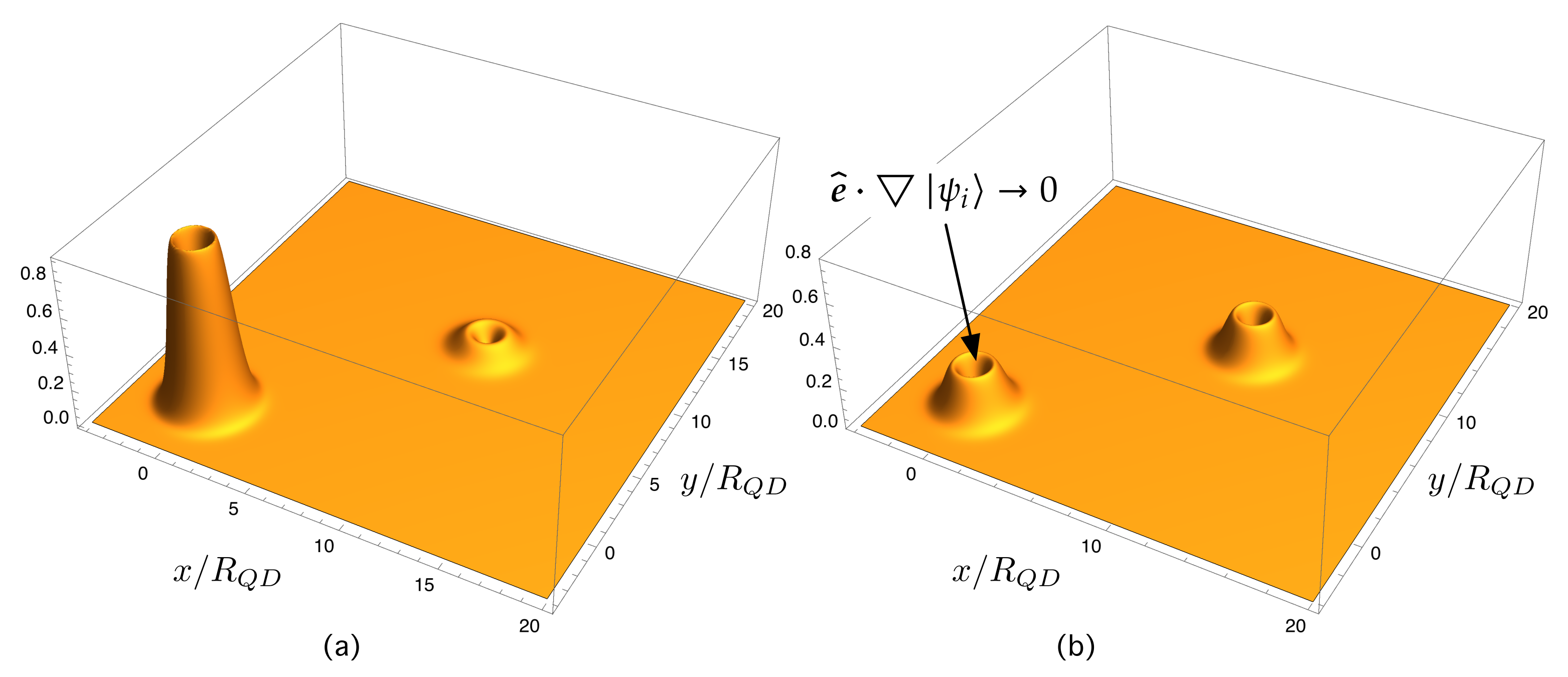
4.1. A Single QD
4.2. The Quantum System S
4.3. Generating the Network Associated to S System
5. Simulation Work
5.1. Methodology
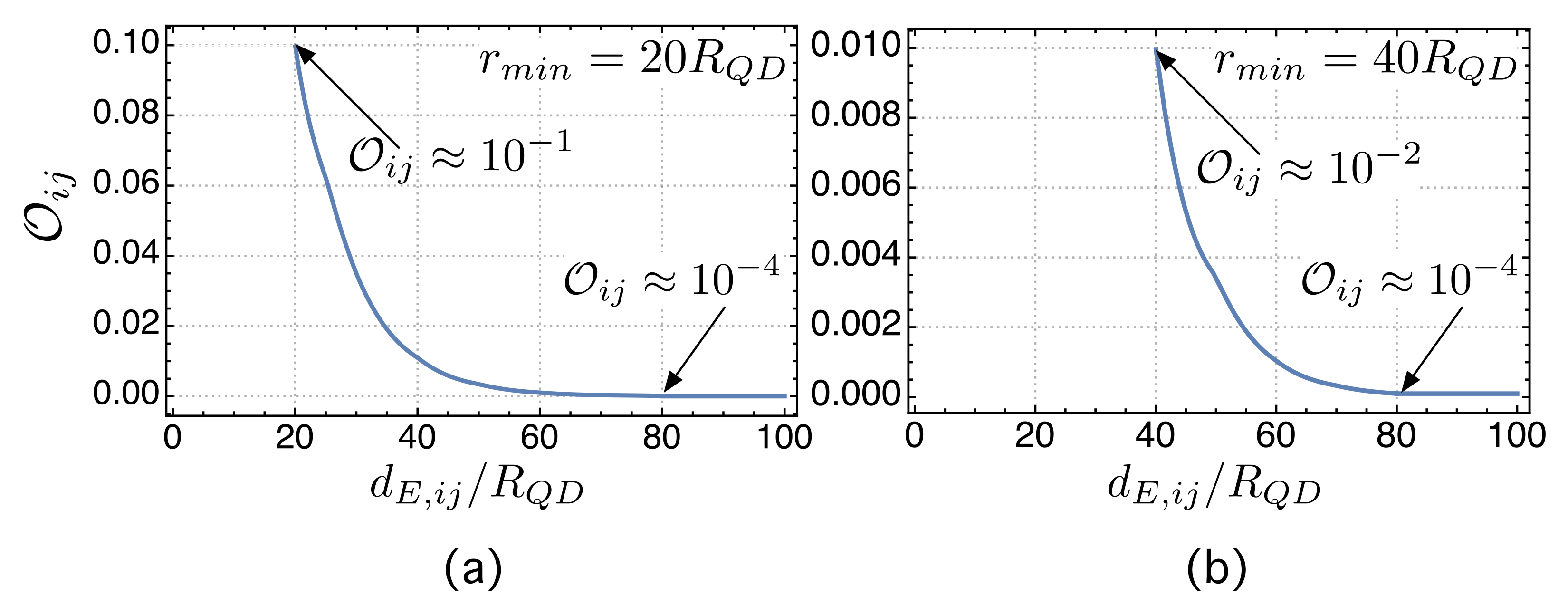
5.2. Testing the Weak Overlap Hypothesis
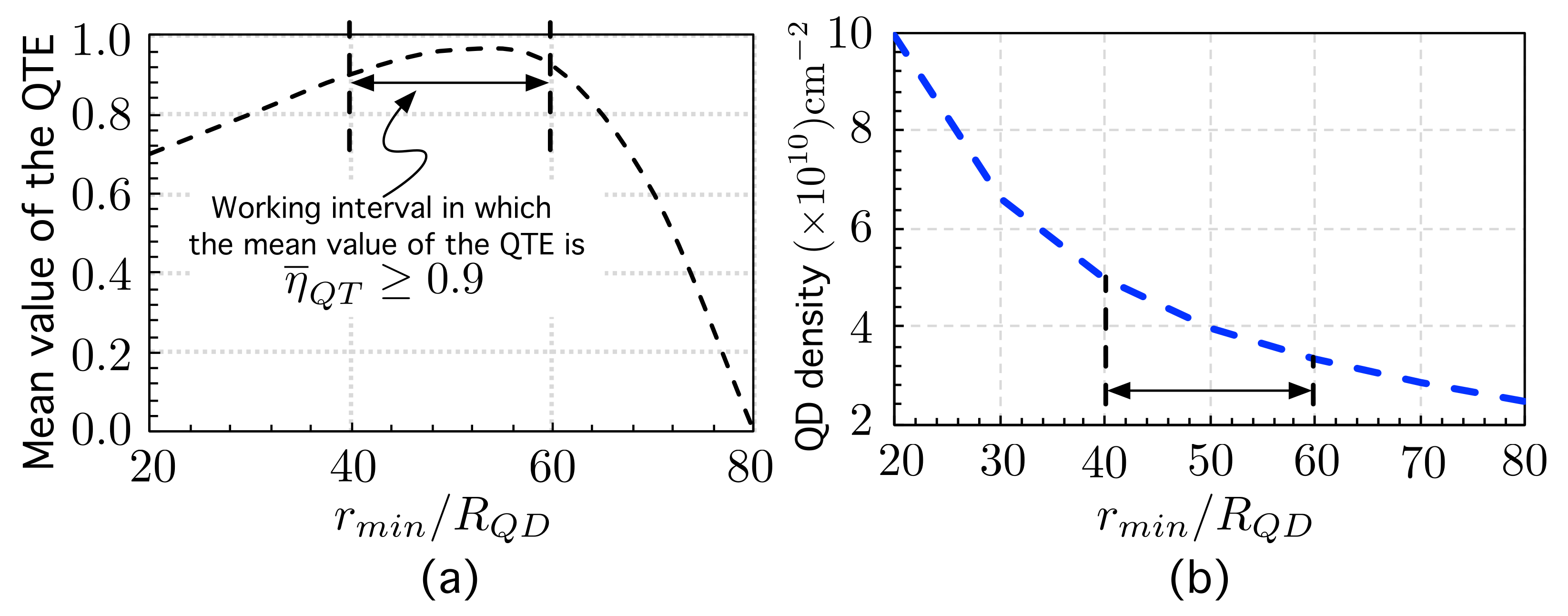
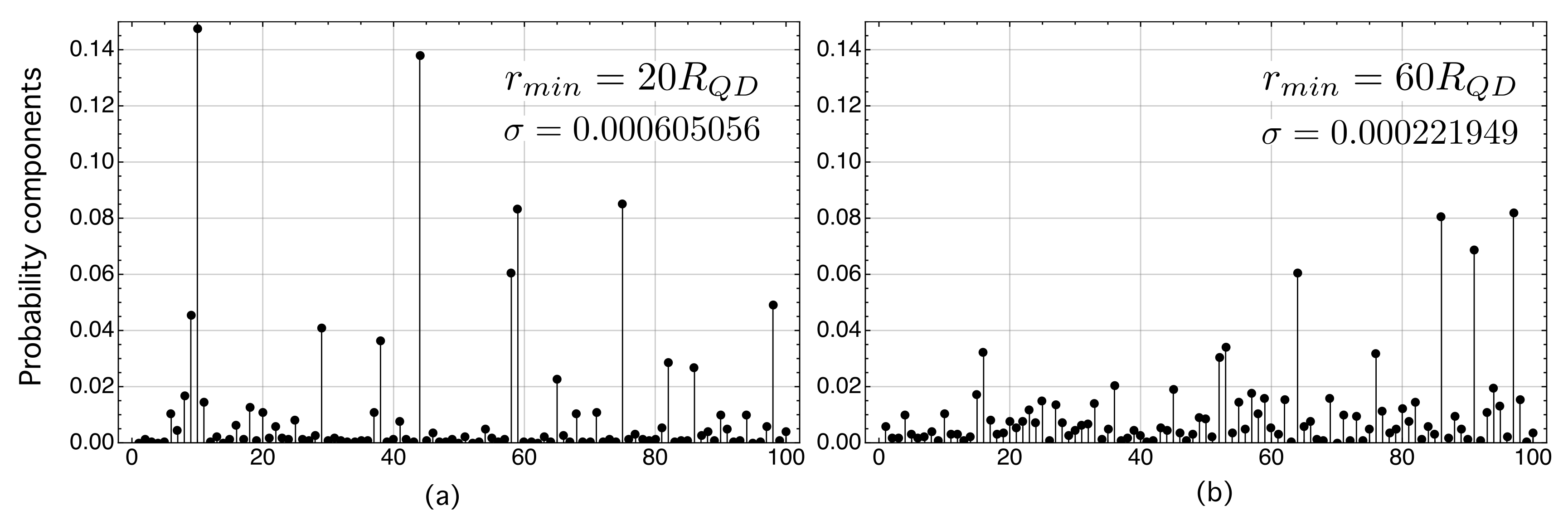
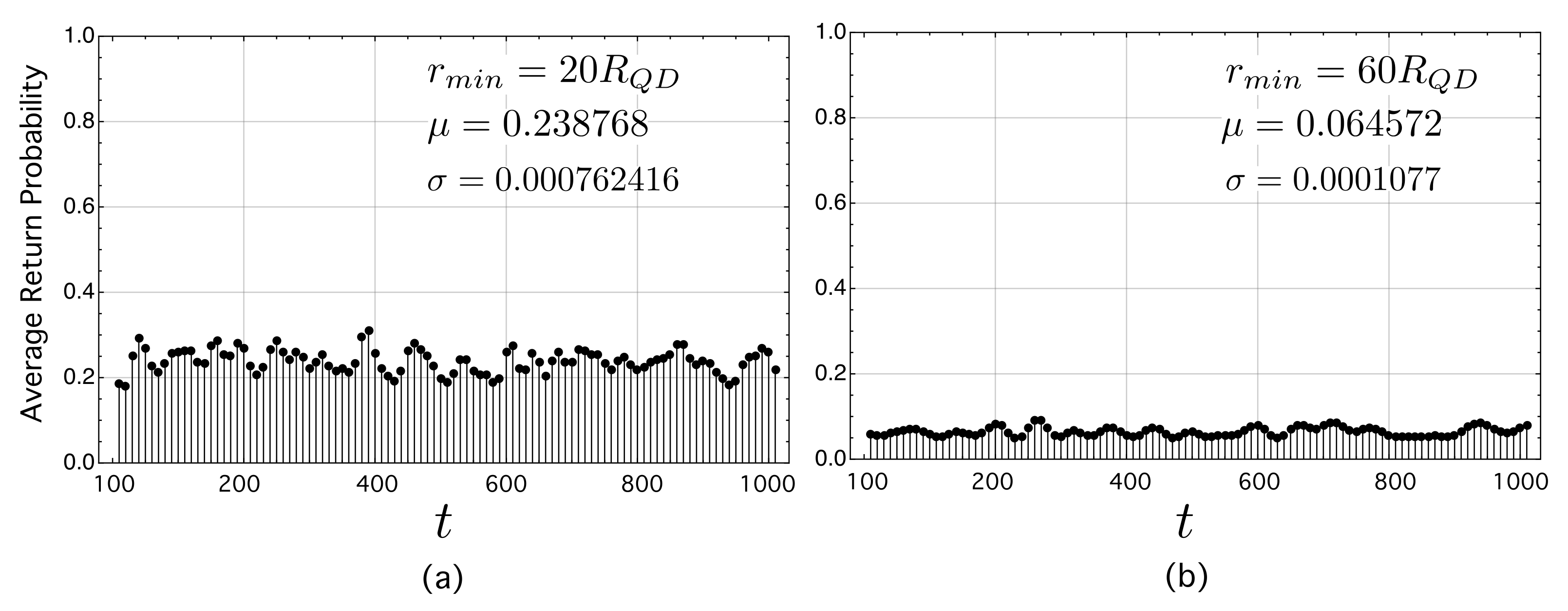
5.3. Influence of the Minimum Inter-Dot Distance on Quantum Transport
6. A Prospective Application
7. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations and Nomenclature
Abbreviations
| 0D | Zero-dimensional |
| 1D | One-dimensional |
| 2D | Two-dimensional |
| ARP | Average Return Probability |
| CB | Conduction Band |
| CN | Complex Networks |
| CP | Confinement Potential |
| CTQW | Continuous-Time Quantum Walks |
| DM | Dot Material |
| GS | Ground State |
| IB | Intermediate Band |
| IBSC | Intermediate-Band Solar Cell |
| LCAO | Linear Combination of Atomic Integrals |
| LME | Lindblad Master Equation |
| QD | Quantum Dot |
| QD-IBSC | Quantum Dot Intermediate-Band Solar Cell |
| QM | Quantum Mechanics |
| QT | Quantum Transport |
| QW | Quantum Walk |
| RGG | Random Geometric Graph |
| RN | Random Network |
| SAQDs | Self-Assembled Quantum Dots |
| SML-QDs | Sub-Monolayer Quantum Dots |
| SN | Spatial Network |
| SK | Stranski–Krastanow |
| SW | Small World |
| TB | Tight-binding |
| VB | Valence band |
| VW | Volmer–Weber |
| WL | Wetting layer |
Nomenclature
| Identity operator in Quantum Mechanics. | |
| Adjacency matrix of a graph . | |
| Element of the adjacency matrix . | |
| Average return probability. | |
| Node degree matrix: . It is the diagonal matrix formed from the nodes degrees. | |
| Euclidean distance between any pair of nodes i and j in a network. | |
| Distance between two nodes i and j. It is the length of the shortest path (geodesic path) between them, that is, the minimum number of links when going from one node to the other. | |
| Euclidean distance limit beyond which there is no link formation. | |
| Energy level of a confined electron in a quantum dot. | |
| Energy level of a confined hole in a quantum dot. | |
| Discrete electron energy in a quantum dot (QD). | |
| Quantum transport efficiency. | |
| Graph , where is the set of nodes (), is the set of links, and is weighted adjacency matrix that emerges from our method to link formation. | |
| Boltzmann factor. | |
| Hamiltonian operator corresponding to the total energy of a quantum system. | |
| Hamiltonian in matrix form. | |
| ℏ | Reduced Planck constant. |
| Hilbert space. | |
| Equilibrium Hilbert subspace. | |
| Ket vector in the Hilbert space . | |
| Bra vector in the dual space corresponding to the ket | |
| ℓ | Average path length of a network. It is the mean value of distances between any pair of nodes in the network. |
| Set of links (edges) of a network (graph). | |
| Laplacian matrix of a graph . | |
| Normalizad Laplacian matrix, . | |
| Electron mass. | |
| M | Size of a graph . It is the number of links in the set . |
| N | Order of a graph . It is the number of nodes in set , that is the cardinality of set : . |
| Set of nodes (or vertices) of a graph. | |
| Laplace operator. | |
| Probability density function giving the probability that a randomly selected node has k links. | |
| Ket or vector state in Dirac notation corresponding to the wave function . | |
| Radius of the quantum dot. | |
| Electron wavefunction in a quantum dot. | |
| Boltzmann time. | |
| Potential energy operator. | |
| Depth of confinement potential. | |
| Confining, spherical (depending only on the radial co-ordinate r), finite, and square potential energy. | |
| Time evolution operator generated by the normalizad Laplacian matrix . | |
| Weight of the link between node i and j. | |
| weighted adjacency matrix. |
References
- Harrison, P.; Valavanis, A. Quantum Wells, Wires and Dots: Theoretical and Computational Physics of Semiconductor Nanostructures; John Wiley & Sons: Chichester, UK, 2016. [Google Scholar]
- Cotta, M.A. Quantum Dots and Their Applications: What Lies Ahead? ACS Appl. Nano Mater. 2020, 3, 4920–4924. [Google Scholar] [CrossRef]
- Sengupta, S.; Chakrabarti, S. Structural, Optical and Spectral Behaviour of InAs-Based Quantum Dot Heterostructures: Applications for High-Performance Infrared Photodetectors; Springer: Singapore, 2017. [Google Scholar]
- Nowozin, T. Self-Organized Quantum Dots for Memories: Electronic Properties and Carrier Dynamics; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Bimberg, D.; Grundmann, M.; Ledentsov, N.N. Quantum Dot Heterostructures; John Wiley & Sons: Chichester, UK, 1999. [Google Scholar]
- Wang, Z.M. Self-Assembled Quantum Dots; Springer Science & Business Media: Berlin, Germany, 2007; Volume 1. [Google Scholar]
- Han, I.S.; Kim, J.S.; Shin, J.C.; Kim, J.O.; Noh, S.K.; Lee, S.J.; Krishna, S. Photoluminescence study of InAs/InGaAs sub-monolayer quantum dot infrared photodetectors with various numbers of multiple stack layers. J. Lumin. 2019, 207, 512–519. [Google Scholar] [CrossRef]
- Germann, T.; Strittmatter, A.; Pohl, J.; Pohl, U.; Bimberg, D.; Rautiainen, J.; Guina, M.; Okhotnikov, O. High-power semiconductor disk laser based on In As/Ga As submonolayer quantum dots. Appl. Phys. Lett. 2008, 92, 101123. [Google Scholar] [CrossRef]
- Xu, Z.; Birkedal, D.; Hvam, J.M.; Zhao, Z.; Liu, Y.; Yang, K.; Kanjilal, A.; Sadowski, J. Structure and optical anisotropy of vertically correlated submonolayer InAs/GaAs quantum dots. Appl. Phys. Lett. 2003, 82, 3859–3861. [Google Scholar] [CrossRef]
- Qi, H.; Wang, S.; Jiang, X.; Fang, Y.; Wang, A.; Shen, H.; Du, Z. Research progress and challenges of blue light-emitting diodes based on II–VI semiconductor quantum dots. J. Mater. Chem. C 2020, 8, 10160–10173. [Google Scholar] [CrossRef]
- Chen, J.; Du, W.; Shi, J.; Li, M.; Wang, Y.; Zhang, Q.; Liu, X. Perovskite quantum dot lasers. InfoMat 2020, 2, 170–183. [Google Scholar] [CrossRef]
- Geiregat, P.; Van Thourhout, D.; Hens, Z. A bright future for colloidal quantum dot lasers. NPG Asia Mater. 2019, 11, 1–8. [Google Scholar] [CrossRef]
- Norman, J.C.; Jung, D.; Zhang, Z.; Wan, Y.; Liu, S.; Shang, C.; Herrick, R.W.; Chow, W.W.; Gossard, A.C.; Bowers, J.E. A review of high-performance quantum dot lasers on silicon. IEEE J. Quantum Electron. 2019, 55, 1–11. [Google Scholar] [CrossRef]
- Bimberg, D.; Kirstaedter, N.; Ledentsov, N.; Alferov, Z.I.; Kop’Ev, P.; Ustinov, V. InGaAs-GaAs quantum-dot lasers. IEEE J. Sel. Top. Quantum Electron. 1997, 3, 196–205. [Google Scholar] [CrossRef]
- Vichi, S.; Bietti, S.; Khalili, A.; Costanzo, M.; Cappelluti, F.; Esposito, L.; Somaschini, C.; Fedorov, A.; Tsukamoto, S.; Rauter, P. Droplet epitaxy quantum dot based infrared photodetectors. Nanotechnology 2020, 31, 245203. [Google Scholar] [CrossRef]
- Ren, A.; Yuan, L.; Xu, H.; Wu, J.; Wang, Z. Recent progress of III–V quantum dot infrared photodetectors on silicon. J. Mater. Chem. C 2019, 7, 14441–14453. [Google Scholar] [CrossRef]
- Sogabe, T.; Shen, Q.; Yamaguchi, K. Recent progress on quantum dot solar cells: A review. J. Photonics Energy 2016, 6, 040901. [Google Scholar] [CrossRef]
- Lv, Z.; Wang, Y.; Chen, J.; Wang, J.; Zhou, Y.; Han, S.T. Semiconductor quantum dots for memories and neuromorphic computing systems. Chem. Rev. 2020, 120, 3941–4006. [Google Scholar] [CrossRef]
- Grundmann, M.; Stier, O.; Bimberg, D. InAs/GaAs pyramidal quantum dots: Strain distribution, optical phonons, and electronic structure. Phys. Rev. B 1995, 52, 11969. [Google Scholar] [CrossRef]
- Luque, A.; Martí, A. Increasing the efficiency of ideal solar cells by photon induced transitions at intermediate levels. Phys. Rev. Lett. 1997, 78, 5014. [Google Scholar] [CrossRef]
- Luque, A.; Linares, P.; Antolín, E.; Ramiro, I.; Farmer, C.; Hernández, E.; Tobías, I.; Stanley, C.; Martí, A. Understanding the operation of quantum dot intermediate band solar cells. J. Appl. Phys. 2012, 111, 044502. [Google Scholar] [CrossRef]
- López, E.; Datas, A.; Ramiro, I.; Linares, P.; Antolín, E.; Artacho, I.; Martí, A.; Luque, A.; Shoji, Y.; Sogabe, T.; et al. Demonstration of the operation principles of intermediate band solar cells at room temperature. Sol. Energy Mater. Sol. Cells 2016, 149, 15–18. [Google Scholar] [CrossRef]
- Luque, A.; Martí, A.; López, N.; Antolín, E.; Cánovas, E.; Stanley, C.; Farmer, C.; Caballero, L.; Cuadra, L.; Balenzategui, J. Experimental analysis of the quasi-Fermi level split in quantum dot intermediate-band solar cells. Appl. Phys. Lett. 2005, 87, 083505. [Google Scholar] [CrossRef]
- Martí, A.; Antolín, E.; Stanley, C.; Farmer, C.; López, N.; Díaz, P.; Cánovas, E.; Linares, P.; Luque, A. Production of photocurrent due to intermediate-to-conduction-band transitions: A demonstration of a key operating principle of the intermediate-band solar cell. Phys. Rev. Lett. 2006, 97, 247701. [Google Scholar] [CrossRef] [PubMed]
- Datas, A.; López, E.; Ramiro, I.; Antolín, E.; Martí, A.; Luque, A.; Tamaki, R.; Shoji, Y.; Sogabe, T.; Okada, Y. Intermediate band solar cell with extreme broadband spectrum quantum efficiency. Phys. Rev. Lett. 2015, 114, 157701. [Google Scholar] [CrossRef]
- Spielman, D. Spectral graph theory. In Combinatorial Scientific Computing; Number 18; Chapman and Hall/CRC: London, UK, 2012. [Google Scholar]
- Barabási, A.L. Network Science; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Cohen-Tannoudji, C.; Diu, B.; Laloe, F.; Dui, B. Quantum Mechanics; Wiley-Interscience: Weinheim, Germany, 2006. [Google Scholar]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.U. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Strogatz, S.H. Exploring complex networks. Nature 2001, 410, 268–276. [Google Scholar] [CrossRef]
- Cuadra, L.; Salcedo-Sanz, S.; Del Ser, J.; Jiménez-Fernández, S.; Geem, Z.W. A critical review of robustness in power grids using complex networks concepts. Energies 2015, 8, 9211–9265. [Google Scholar] [CrossRef]
- Cuadra, L.; Pino, M.D.; Nieto-Borge, J.C.; Salcedo-Sanz, S. Optimizing the structure of distribution smart grids with renewable generation against abnormal conditions: A complex networks approach with evolutionary algorithms. Energies 2017, 10, 1097. [Google Scholar] [CrossRef]
- Doyle, J.C.; Alderson, D.L.; Li, L.; Low, S.; Roughan, M.; Shalunov, S.; Tanaka, R.; Willinger, W. The “robust yet fragile” nature of the Internet. Proc. Natl. Acad. Sci. USA 2005, 102, 14497–14502. [Google Scholar] [CrossRef] [PubMed]
- Barthélemy, M. Spatial networks. Phys. Rep. 2011, 499, 1–101. [Google Scholar] [CrossRef]
- Montoya, J.M.; Solé, R.V. Small world patterns in food webs. J. Theor. Biol. 2002, 214, 405–412. [Google Scholar] [CrossRef] [PubMed]
- Chimal-Eguía, J.C.; Castillo-Montiel, E.; Paez-Hernández, R.T. Properties of the vascular networks in malignant tumors. Entropy 2020, 22, 166. [Google Scholar] [CrossRef] [PubMed]
- Guimera, R.; Amaral, L.A.N. Functional cartography of complex metabolic networks. Nature 2005, 433, 895–900. [Google Scholar] [CrossRef] [PubMed]
- Chung, F.R.; Graham, F.C. Spectral Graph Theory; Number 92; American Mathematical Society: Providence, RI, USA, 1997. [Google Scholar]
- Spielman, D.A. Algorithms, graph theory, and linear equations in Laplacian matrices. In Proceedings of the International Congress of Mathematicians 2010 (ICM 2010) (In 4 Volumes) Vol. I: Plenary Lectures and Ceremonies Vols. II–IV: Invited Lectures, 2010; World Scientific, Hyderabad, India, 19–27 August 2010; pp. 2698–2722. [Google Scholar]
- Iannelli, F.; Koher, A.; Brockmann, D.; Hövel, P.; Sokolov, I.M. Effective distances for epidemics spreading on complex networks. Phys. Rev. E 2017, 95, 012313. [Google Scholar] [CrossRef]
- Liu, C.; Wu, X.; Niu, R.; Wu, X.; Fan, R. A new SAIR model on complex networks for analysing the 2019 novel coronavirus (COVID-19). Nonlinear Dyn. 2020, 101, 1777–1787. [Google Scholar] [CrossRef] [PubMed]
- Pond, T.; Magsarjav, S.; South, T.; Mitchell, L.; Bagrow, J.P. Complex contagion features without social reinforcement in a model of social information flow. Entropy 2020, 22, 265. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Liu, C.; Yang, Z.; Liu, X.; Zhang, Y.; Wei, Z. Modeling the propagation of mobile malware on complex networks. Commun. Nonlinear Sci. Numer. Simul. 2016, 37, 249–264. [Google Scholar] [CrossRef]
- Ding, L.; Liu, S.Y.; Yang, Q.; Xu, X.K. Uncovering the Dependence of Cascading Failures on Network Topology by Constructing Null Models. Entropy 2019, 21, 1119. [Google Scholar] [CrossRef]
- Dobson, I.; Carreras, B.A.; Lynch, V.E.; Newman, D.E. Complex systems analysis of series of blackouts: Cascading failure, critical points, and self-organization. Chaos Interdiscip. J. Nonlinear Sci. 2007, 17, 026103. [Google Scholar] [CrossRef] [PubMed]
- Cuadra, L.; Nieto-Borge, J.C. Modeling Quantum Dot Systems as Random Geometric Graphs with Probability Amplitude-Based Weighted Links. Nanomaterials 2021, 11, 375. [Google Scholar] [CrossRef]
- Barthelemy, M. Morphogenesis of Spatial Networks; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Susskind, L.; Friedman, A. Quantum Mechanics: The Theoretical Minimum; Penguin Books: London, UK, 2015. [Google Scholar]
- Ritter, S.; Nölleke, C.; Hahn, C.; Reiserer, A.; Neuzner, A.; Uphoff, M.; Mücke, M.; Figueroa, E.; Bochmann, J.; Rempe, G. An elementary quantum network of single atoms in optical cavities. Nature 2012, 484, 195. [Google Scholar] [CrossRef]
- Mülken, O.; Dolgushev, M.; Galiceanu, M. Complex quantum networks: From universal breakdown to optimal transport. Phys. Rev. E 2016, 93, 022304. [Google Scholar] [CrossRef]
- Faccin, M.; Migdał, P.; Johnson, T.H.; Bergholm, V.; Biamonte, J.D. Community detection in quantum complex networks. Phys. Rev. X 2014, 4, 041012. [Google Scholar] [CrossRef]
- Mohseni, M.; Rebentrost, P.; Lloyd, S.; Aspuru-Guzik, A. Environment-assisted quantum walks in photosynthetic energy transfer. J. Chem. Phys. 2008, 129, 11B603. [Google Scholar] [CrossRef]
- Mülken, O.; Blumen, A. Efficiency of quantum and classical transport on graphs. Phys. Rev. E 2006, 73, 066117. [Google Scholar] [CrossRef]
- Mülken, O.; Blumen, A. Continuous-time quantum walks: Models for coherent transport on complex networks. Phys. Rep. 2011, 502, 37–87. [Google Scholar] [CrossRef]
- Venegas-Andraca, S.E. Quantum walks: A comprehensive review. Quantum Inf. Process. 2012, 11, 1015–1106. [Google Scholar] [CrossRef]
- Darázs, Z.; Kiss, T. Pólya number of the continuous-time quantum walks. Phys. Rev. A 2010, 81, 062319. [Google Scholar] [CrossRef]
- Mülken, O.; Volta, A.; Blumen, A. Asymmetries in symmetric quantum walks on two-dimensional networks. Phys. Rev. A 2005, 72, 042334. [Google Scholar] [CrossRef]
- Agliari, E.; Blumen, A.; Mülken, O. Dynamics of continuous-time quantum walks in restricted geometries. J. Phys. A Math. Theor. 2008, 41, 445301. [Google Scholar] [CrossRef]
- Mülken, O.; Bierbaum, V.; Blumen, A. Coherent exciton transport in dendrimers and continuous-time quantum walks. J. Chem. Phys. 2006, 124, 124905. [Google Scholar] [CrossRef] [PubMed]
- Agliari, E.; Blumen, A.; Muelken, O. Quantum-walk approach to searching on fractal structures. Phys. Rev. A 2010, 82, 012305. [Google Scholar] [CrossRef]
- Blumen, A.; Bierbaum, V.; Mülken, O. Coherent dynamics on hierarchical systems. Phys. A Stat. Mech. Appl. 2006, 371, 10–15. [Google Scholar] [CrossRef][Green Version]
- Mülken, O.; Blumen, A. Slow transport by continuous time quantum walks. Phys. Rev. E 2005, 71, 016101. [Google Scholar] [CrossRef]
- Xu, X.P.; Li, W.; Liu, F. Coherent transport on Apollonian networks and continuous-time quantum walks. Phys. Rev. E 2008, 78, 052103. [Google Scholar] [CrossRef]
- Xu, X.; Liu, F. Coherent exciton transport on scale-free networks. New J. Phys. 2008, 10, 123012. [Google Scholar] [CrossRef]
- Mülken, O.; Pernice, V.; Blumen, A. Quantum transport on small-world networks: A continuous-time quantum walk approach. Phys. Rev. E 2007, 76, 051125. [Google Scholar] [CrossRef] [PubMed]
- Salimi, S. Continuous-time quantum walks on star graphs. Ann. Phys. 2009, 324, 1185–1193. [Google Scholar] [CrossRef]
- Anishchenko, A.; Blumen, A.; Mülken, O. Enhancing the spreading of quantum walks on star graphs by additional bonds. Quantum Inf. Process. 2012, 11, 1273–1286. [Google Scholar] [CrossRef]
- Kulvelis, N.; Dolgushev, M.; Mülken, O. Universality at breakdown of quantum transport on complex networks. Phys. Rev. Lett. 2015, 115, 120602. [Google Scholar] [CrossRef] [PubMed]
- Gong, L.; Tong, P. von Neumann entropy and localization-delocalization transition of electron states in quantum small-world networks. Phys. Rev. E 2006, 74, 056103. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of “small-world” networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Caldarelli, G.; Vespignani, A. (Eds.) Large Scale Structure and Dynamics of Complex Networks: From Information Technology to Finance and Natural Science; World Scientific: Wood Dale, IL, USA, 2007; Volume 2. [Google Scholar]
- Newman, M.E.; Watts, D.J. Renormalization group analysis of the small-world network model. Phys. Lett. A 1999, 263, 341–346. [Google Scholar] [CrossRef]
- Cui, L.; Kumara, S.; Albert, R. Complex networks: An engineering view. Circuits Syst. Mag. IEEE 2010, 10, 10–25. [Google Scholar] [CrossRef]
- Bashan, A.; Berezin, Y.; Buldyrev, S.V.; Havlin, S. The extreme vulnerability of interdependent spatially embedded networks. Nat. Phys. 2013, 9, 667–672. [Google Scholar] [CrossRef]
- Zhao, J.; Li, D.; Sanhedrai, H.; Cohen, R.; Havlin, S. Spatio-temporal propagation of cascading overload failures in spatially embedded networks. Nat. Commun. 2016, 7, 10094. [Google Scholar] [CrossRef]
- Penrose, M. Random Geometric Graphs; Oxford University Press: Oxford, UK, 2003; Volume 5. [Google Scholar]
- Kenniche, H.; Ravelomananana, V. Random geometric graphs as model of wireless sensor networks. In Proceedings of the 2010 The 2nd International Conference on Computer and Automation Engineering (ICCAE), Singapore, 26–28 February 2010; IEEE: Piscataway, NJ, USA, 2010; Volume 4, pp. 103–107. [Google Scholar]
- Nemeth, G.; Vattay, G. Giant clusters in random ad hoc networks. Phys. Rev. E 2003, 67, 036110. [Google Scholar] [CrossRef] [PubMed]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Goldstein, S.; Lebowitz, J.L.; Mastrodonato, C.; Tumulka, R.; Zanghi, N. Approach to thermal equilibrium of macroscopic quantum systems. Phys. Rev. E 2010, 81, 011109. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, S.; Lebowitz, J.L.; Mastrodonato, C.; Tumulka, R.; Zanghì, N. Normal typicality and von Neumann’s quantum ergodic theorem. Proc. R. Soc. A Math. Phys. Eng. Sci. 2010, 466, 3203–3224. [Google Scholar] [CrossRef]
- Goldstein, S.; Hara, T.; Tasaki, H. Extremely quick thermalization in a macroscopic quantum system for a typical nonequilibrium subspace. New J. Phys. 2015, 17, 045002. [Google Scholar] [CrossRef]
- Manzano, D. A short introduction to the Lindblad master equation. AIP Adv. 2020, 10, 025106. [Google Scholar] [CrossRef]
- Wang, Y.S.; Nijjar, P.; Zhou, X.; Bondar, D.I.; Prezhdo, O.V. Combining Lindblad Master Equation and Surface Hopping to Evolve Distributions of Quantum Particles. J. Phys. Chem. B 2020, 124, 4326–4337. [Google Scholar] [CrossRef]
- Datta, S. Electronic Transport in Mesoscopic Systems; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Mandl, F. Quantum Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 1992. [Google Scholar]
- Galindo, A.; Pascual, P. Quantum Mechanics I; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Ballentine, L.E. Quantum Mechanics: A Modern Development; World Scientific Publishing Company: Wood Dale, IL, USA, 2014. [Google Scholar]
- Estrada, E. The electron density function of the Hückel (tight-binding) model. Proc. R. Soc. A Math. Phys. Eng. Sci. 2018, 474, 20170721. [Google Scholar] [CrossRef]
- Newman, M. Networks; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Ding, X.; Jiang, T. Spectral distributions of adjacency and Laplacian matrices of random graphs. Ann. Appl. Probab. 2010, 20, 2086–2117. [Google Scholar] [CrossRef]
- Farhi, E.; Gutmann, S. Quantum computation and decision trees. Phys. Rev. A 1998, 58, 915. [Google Scholar] [CrossRef]
- Faccin, M.; Johnson, T.; Biamonte, J.; Kais, S.; Migdał, P. Degree distribution in quantum walks on complex networks. Phys. Rev. X 2013, 3, 041007. [Google Scholar] [CrossRef]
- Mülken, O.; Blumen, A. From Continuous-Time Random Walks to Continuous-Time Quantum Walks: Disordered Networks. In Nonlinear Phenomena in Complex Systems: From Nano to Macro Scale; Springer: Berlin, Germany, 2014; pp. 189–197. [Google Scholar]
- Darázs, Z.; Anishchenko, A.; Kiss, T.; Blumen, A.; Mülken, O. Transport properties of continuous-time quantum walks on Sierpinski fractals. Phys. Rev. E 2014, 90, 032113. [Google Scholar] [CrossRef]
- Anishchenko, A.; Blumen, A.; Muelken, O. Geometrical aspects of quantum walks on random two-dimensional structures. Phys. Rev. E 2013, 88, 062126. [Google Scholar] [CrossRef]
- Ray, R.K. Solving Quantum Random Walker Using Steepest Entropy Ascent Ansatz: A Pathway Towards Typicality. arXiv 2019, arXiv:1907.04548. [Google Scholar]
- Gualtieri, V.; Benedetti, C.; Paris, M.G. Quantum-classical dynamical distance and quantumness of quantum walks. Phys. Rev. A 2020, 102, 012201. [Google Scholar] [CrossRef]
- Mülken, O.; Blumen, A. Spacetime structures of continuous-time quantum walks. Phys. Rev. E 2005, 71, 036128. [Google Scholar] [CrossRef] [PubMed]
- Stevanovic, D. Applications of graph spectra in quantum physics. In Selected Topics in Applications of Graph Spectra; Institute of the Serbian Academy of Sciences and Arts: Belgrade, Serbia, 2011; pp. 85–111. [Google Scholar]
- Datta, S. Quantum Phenomena; Modular Series on Solid State Devices; Addison-Wesley: Seattle, WA, USA, 1989. [Google Scholar]
- Li, M.F. Modern Semiconductor Quantum Physics; World Scientific: Singapore, 1995. [Google Scholar]
- Pankove, J.I. Optical Processes in Semiconductors; Courier Corporation: New York, NY, USA, 1975. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cuadra, L.; Nieto-Borge, J.C. Approaching Disordered Quantum Dot Systems by Complex Networks with Spatial and Physical-Based Constraints. Nanomaterials 2021, 11, 2056. https://doi.org/10.3390/nano11082056
Cuadra L, Nieto-Borge JC. Approaching Disordered Quantum Dot Systems by Complex Networks with Spatial and Physical-Based Constraints. Nanomaterials. 2021; 11(8):2056. https://doi.org/10.3390/nano11082056
Chicago/Turabian StyleCuadra, Lucas, and José Carlos Nieto-Borge. 2021. "Approaching Disordered Quantum Dot Systems by Complex Networks with Spatial and Physical-Based Constraints" Nanomaterials 11, no. 8: 2056. https://doi.org/10.3390/nano11082056
APA StyleCuadra, L., & Nieto-Borge, J. C. (2021). Approaching Disordered Quantum Dot Systems by Complex Networks with Spatial and Physical-Based Constraints. Nanomaterials, 11(8), 2056. https://doi.org/10.3390/nano11082056






