Dielectric Imaging of Fixed HeLa Cells by In-Liquid Scanning Dielectric Force Volume Microscopy
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Preparation
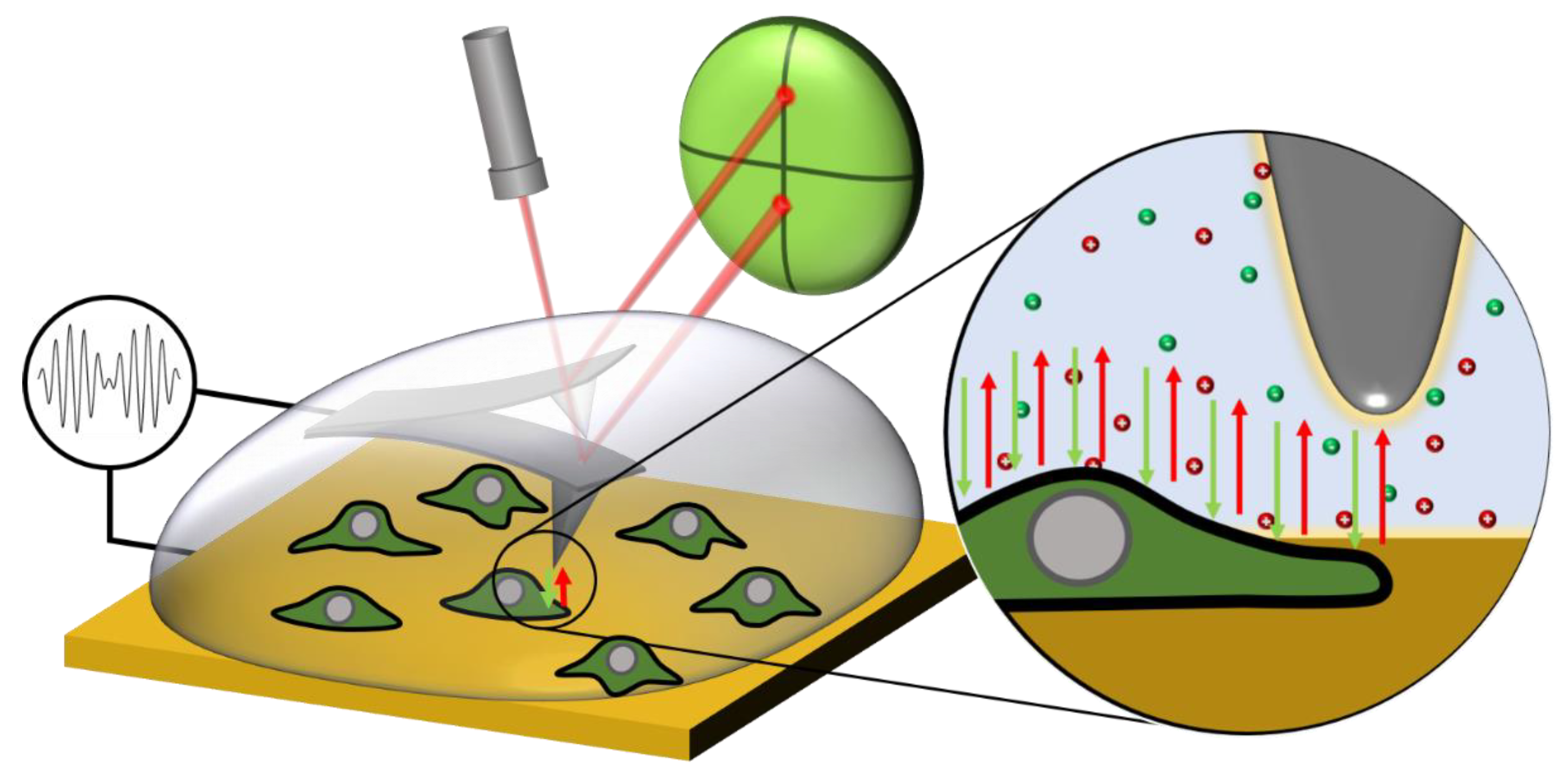
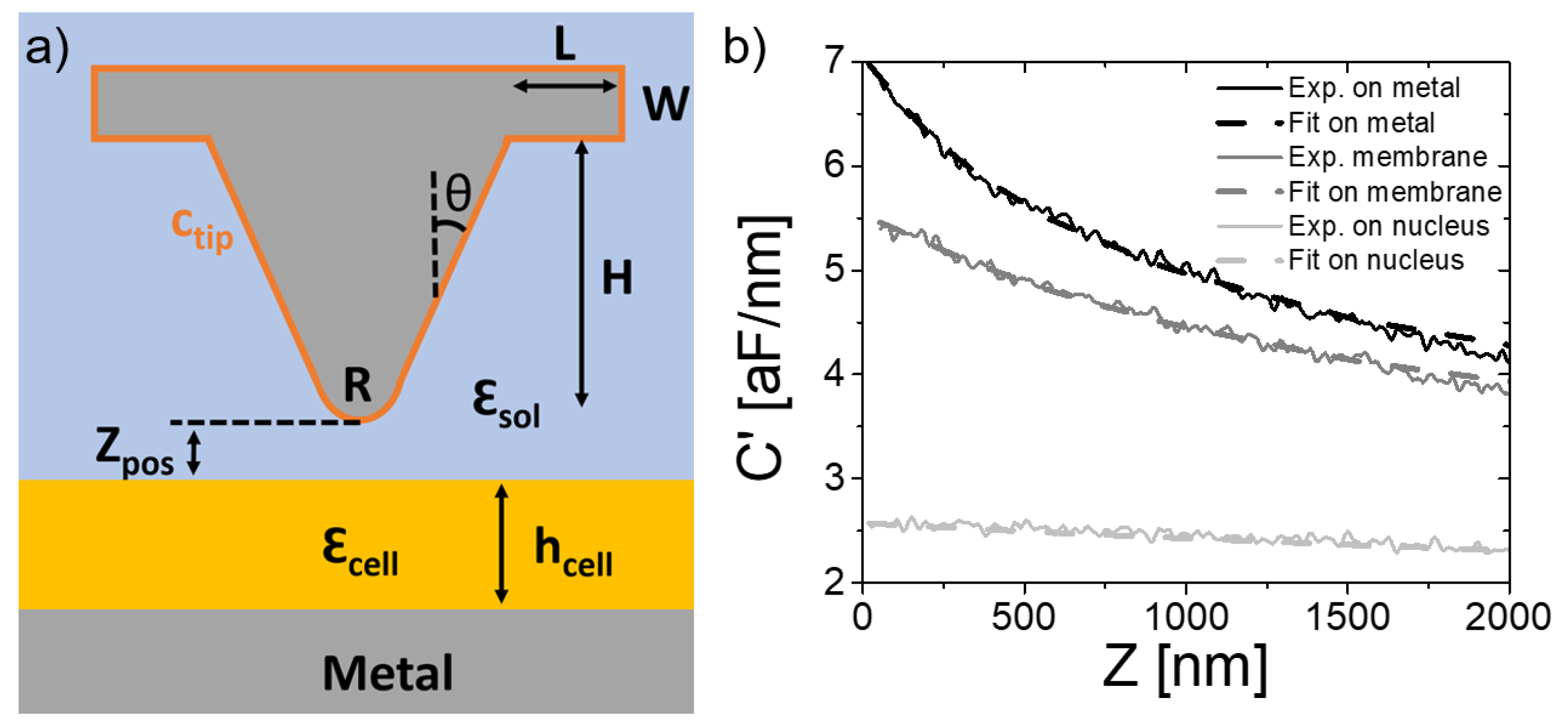
2.2. In-Liquid SDFVM
2.3. Dielectric Constant Mapping
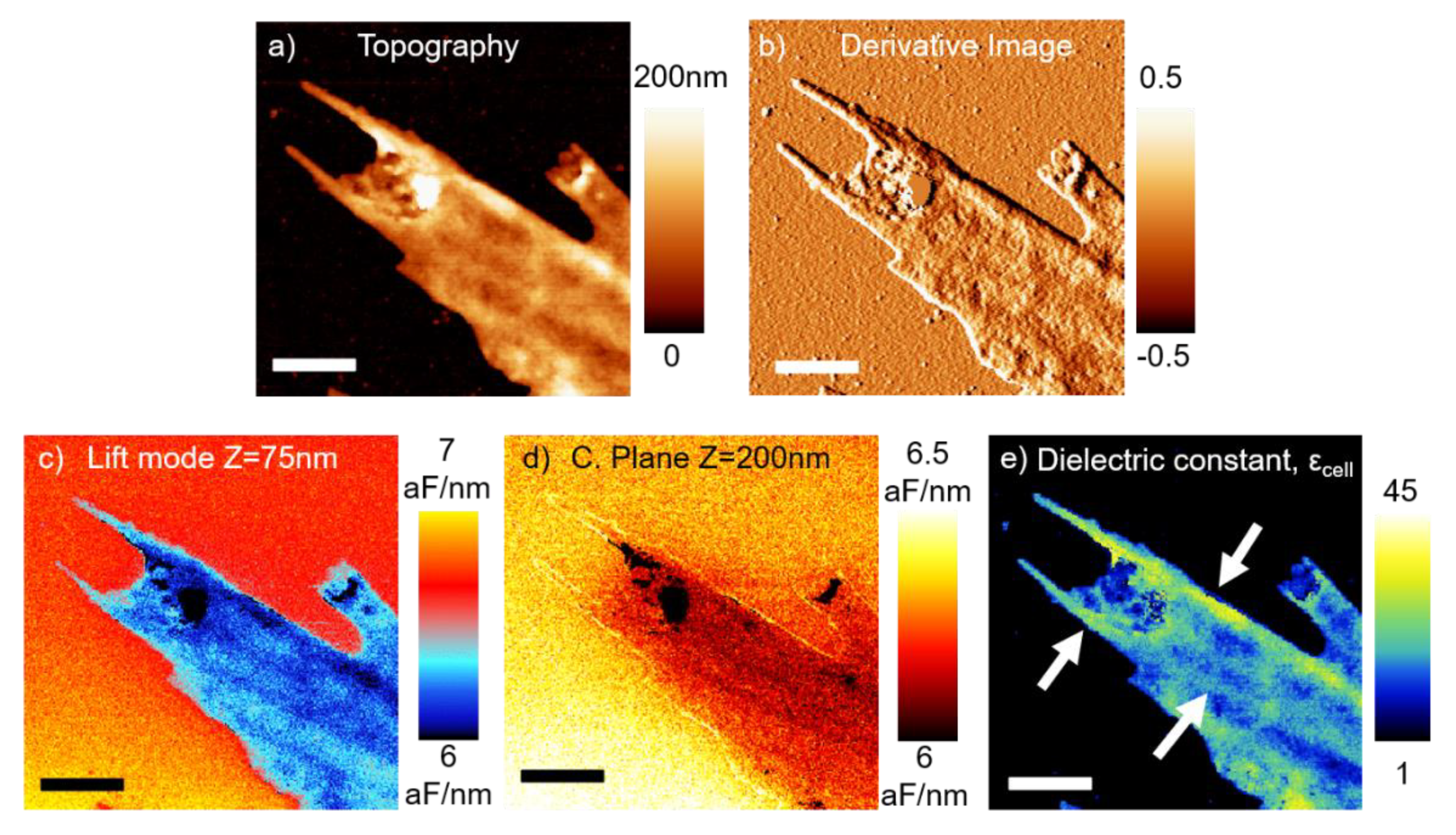
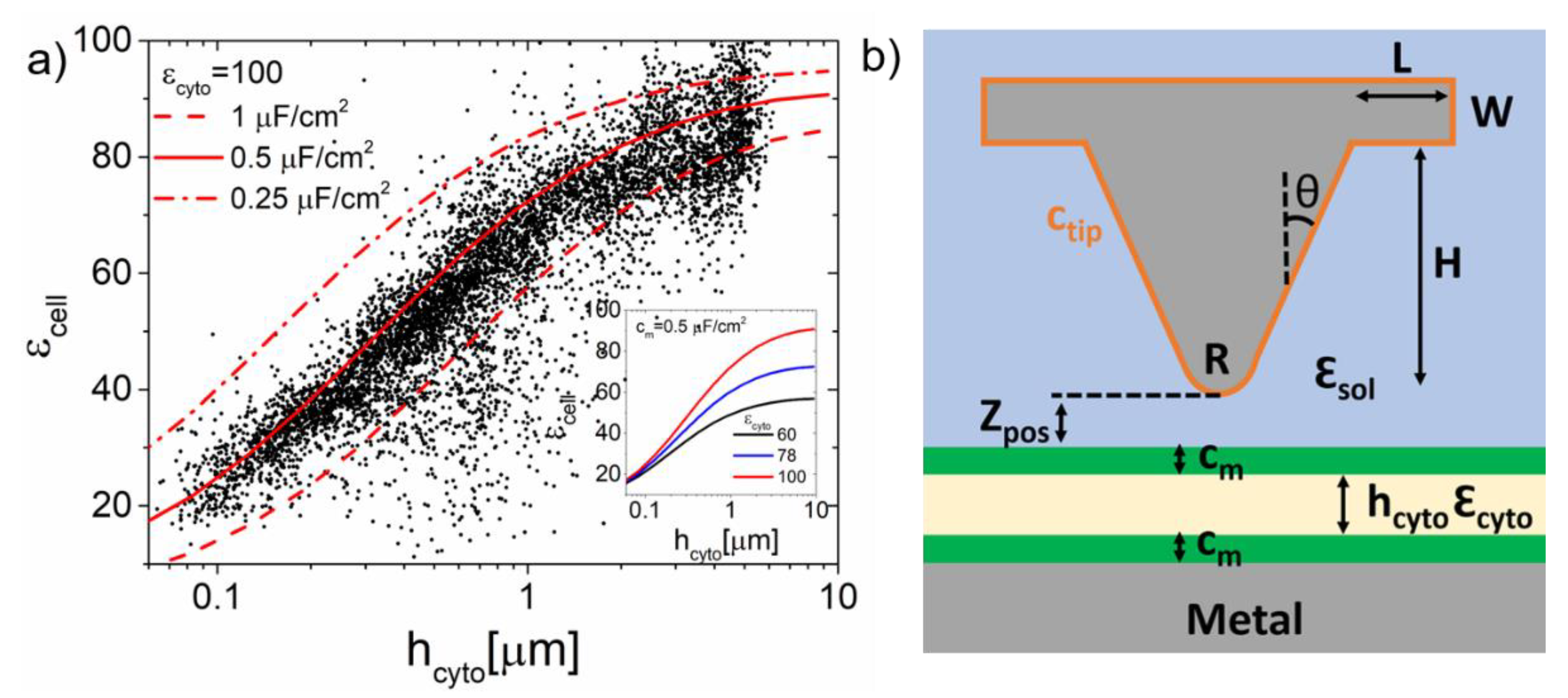
3. Results
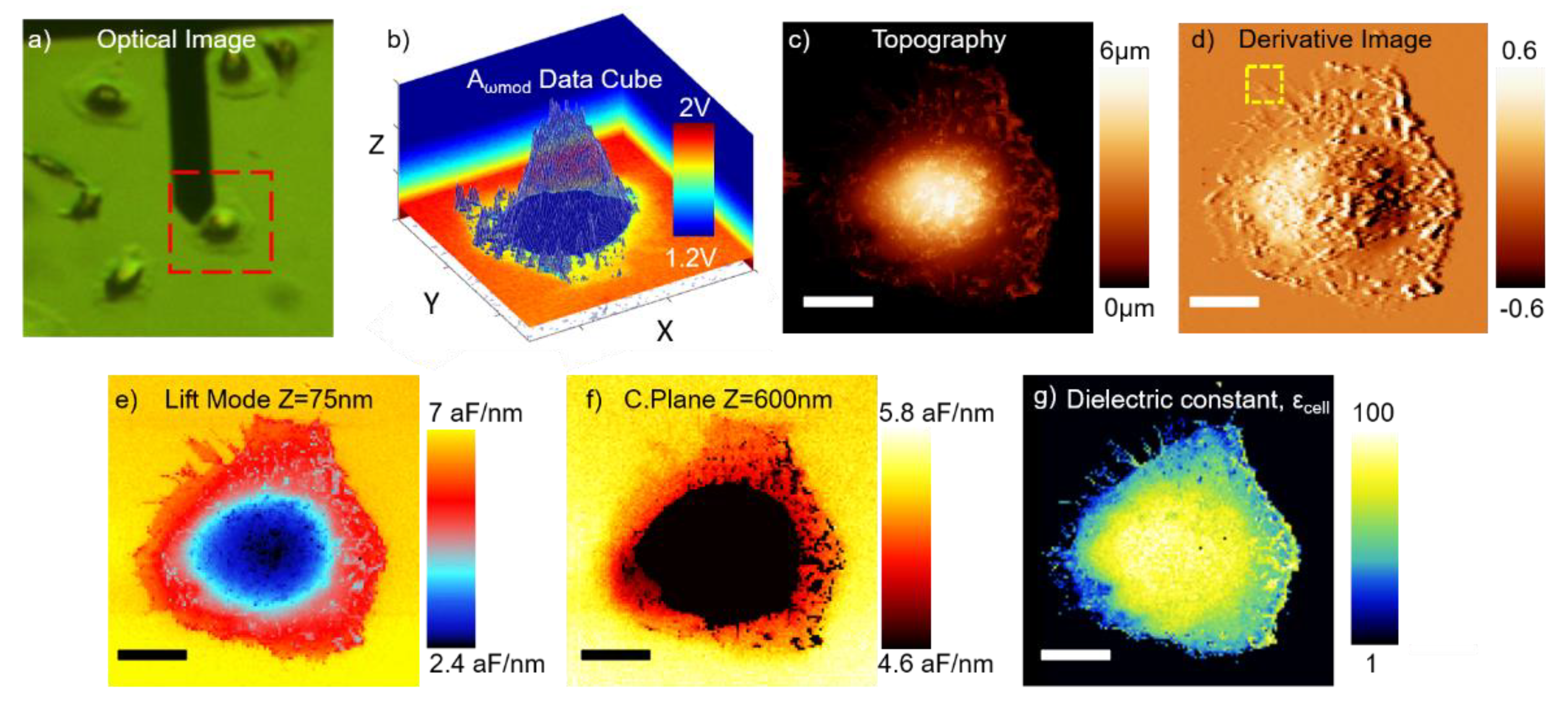
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gascoyne, P.R.C.; Wang, X.; Huang, Y.; Becker, F.F. Dielectrophoretic separation of cancer cells from blood. IEEE Trans. Ind. Appl. 1997, 33, 670–678. [Google Scholar] [CrossRef]
- Patel, P.; Markx, G.H. Dielectric measurement of cell death. Enzym. Microb. Technol. 2008, 43, 463–470. [Google Scholar] [CrossRef]
- Wang, X.; Becker, F.F.; Gascoyne, P.R.C. Membrane dielectric changes indicate induced apoptosis in HL-60 cells more sensitively than surface phosphatidylserine expression or DNA fragmentation. Biochim. Biophys. Acta 2002, 1564, 412–420. [Google Scholar] [CrossRef]
- Gentet, L.J.; Stuart, G.J.; Clements, J.D. Direct measurement of specific membrane capacitance in neurons. Biophys. J. 2000, 79, 314–320. [Google Scholar] [CrossRef]
- Devi, U.V.; Puri, P.; Sharma, N.N. Electrokinetics of cells in dielectrophoretic separation: A biological perspective. BioNanoSci. 2014, 4, 276–287. [Google Scholar] [CrossRef]
- Trainito, C.I.; Bayart, E.; Bisceglia, E.; Subra, F.; Français, O.; Le Pioufle, B. Le electrorotation as a versatile tool to estimate dielectric properties of multi-scale biological samples: From single cell to spheroid analysis. In Proceedings of the 1st World Congress on Electroporation and Pulsed Electric Fields in Biology, Medicine and Food and Environmental Technologies, IFMBE, Portorož, Slovenia, 6–10 September 2015; Springer: Singapore, 2016; Volume 53, pp. 75–78. ISBN 9789812878168. [Google Scholar]
- Cheung, K.; Gawad, S.; Renaud, P. Impedance spectroscopy flow cytometry: On-chip label-free cell differentiation. Cytom. Part A 2005, 65, 124–132. [Google Scholar] [CrossRef]
- Signore, G.; Abbandonato, G.; Storti, B.; Sto, M. Imaging the static dielectric constant in vitro and in living cells by bioconjugable GFP chromophore analog. Chem. Commun. 2013, 49, 2–4. [Google Scholar] [CrossRef]
- Knöpfel, T.; Song, C. Optical voltage imaging in neurons: Moving from technology development to practical tool. Nat. Rev. Neurosci. 2019, 20, 719–727. [Google Scholar] [CrossRef]
- Grienberger, C.; Konnerth, A. Imaging calcium in neurons. Neuron 2012, 73, 862–885. [Google Scholar] [CrossRef]
- Miccoli, B.; Lopez, C.M.; Goikoetxea, E.; Putzeys, J.; Sekeri, M.; Krylychkina, O.; Chang, S.W.; Firrincieli, A.; Andrei, A.; Reumers, V.; et al. High-density electrical recording and impedance imaging with a multi-modal CMOS multi-electrode array chip. Front. Neurosci. 2019, 13, 1–14. [Google Scholar] [CrossRef]
- Lee, G.H.; Pyun, J.C.; Cho, S. Electrical impedance characterization of cell growth on interdigitated microelectrode array. J. Nanosci. Nanotechnol. 2014, 14, 8342–8346. [Google Scholar] [CrossRef] [PubMed]
- Kyndiah, A.; Leonardi, F.; Tarantino, C.; Cramer, T.; Millan-Solsona, R.; Garreta, E.; Montserrat, N.; Mas-Torrent, M.; Gomila, G. Bioelectronic recordings of cardiomyocytes with accumulation mode electrolyte gated organic field effect transistors. Biosens. Bioelectron. 2020, 150, 111844. [Google Scholar] [CrossRef]
- Beaulieu, I.; Kuss, S.; Mauzeroll, J.; Geissler, M. Biological scanning electrochemical microscopy and its application to live cell studies. Anal. Chem. 2011, 83, 1485–1492. [Google Scholar] [CrossRef]
- Chen, F.; Panday, N.; Li, X.; Ma, T.; Guo, J.; Wang, X.; Kos, L.; Hu, K.; Gu, N.; He, J. Simultaneous mapping of nanoscale topography and surface potential of charged surfaces by scanning ion conductance microscopy. Nanoscale 2020, 12, 20737–20748. [Google Scholar] [CrossRef]
- Shkirskiy, V.; Kang, M.; McPherson, I.J.; Bentley, C.L.; Wahab, O.J.; Daviddi, E.; Colburn, A.W.; Unwin, P.R. Electrochemical impedance measurements in scanning ion conductance microscopy. Anal. Chem. 2020, 92, 12509–12517. [Google Scholar] [CrossRef]
- Asami, K. Simulation for the dielectric images of single biological cells obtained using a scanning dielectric microscope. J. Phys. D Appl. Phys. 2008, 41, 085501. [Google Scholar] [CrossRef]
- Asami, K. Dielectric imaging of biological cells. Colloid Polym. Sci. 1995, 273, 1095–1097. [Google Scholar] [CrossRef]
- Novak, P.; Li, C.; Shevchuk, A.I.; Stepanyan, R.; Caldwell, M.; Hughes, S.; Smart, T.G.; Gorelik, J.; Ostanin, V.P.; Lab, M.J.; et al. Nanoscale live-cell imaging using hopping probe ion conductance microscopy. Nat. Methods 2009, 6, 279–281. [Google Scholar] [CrossRef] [PubMed]
- Tselev, A.; Velmurugan, J.; Ievlev, A.V.; Kalinin, S.V.; Kolmakov, A. Seeing through walls at the nanoscale: Microwave microscopy of enclosed objects and processes in liquids. ACS Nano 2016, 10, 3562–3570. [Google Scholar] [CrossRef] [PubMed]
- Farina, M.; Jin, X.; Fabi, G.; Pavoni, E.; Donato, A.; Mencarelli, D.; Piacenza, F.; Al Hadi, R.; Zhao, Y.; Hwang, J.C.M.; et al. Inverted scanning microwave microscope for in vitro imaging and characterization of biological cells. Appl. Phys. Lett. 2019, 114, 093703. [Google Scholar] [CrossRef]
- Fumagalli, L.; Gomila, G. Probing dielectric constant at the nanoscale with scanning probe microscopy. In Capacitance Spectroscipy of Semiconductors; Pan Stanford Publishing: Singapore, 2018; ISBN 9789814774543. [Google Scholar]
- Valavade, A.V.; Date, K.S.; Press, M.R.; Kothari, D.C. Scanning dielectric constant microscopy for imaging single biological cells. Biomed. Phys. Eng. Express 2018, 4, 055023. [Google Scholar] [CrossRef]
- Valavade, A.V.; Kothari, D.C.; Löbbe, C. Dielectric constant microscopy for biological materials. Am. Inst. Phys. 2013, 1512, 1–3. [Google Scholar] [CrossRef]
- Birkenhauer, E.; Neethirajan, S. Characterization of electrical surface properties of mono- and co-cultures of Pseudomonas aeruginosa and methicillin-resistant Staphylococcus aureus using Kelvin probe force microscopy. RSC Adv. 2014, 4, 42432–42440. [Google Scholar] [CrossRef]
- Checa, M.; Millan-Solsona, R.; Mares, A.G.; Pujals, S.; Gomila, G. Fast label-free nanoscale composition mapping of eukaryotic cells via scanning dielectric force volume microscopy and machine learning. Small Methods 2021, 2100279. [Google Scholar] [CrossRef]
- Checa, M.; Millan-Solsona, R.; Blanco, N.; Torrents, E.; Fabregas, R.; Gomila, G. Mapping the dielectric constant of a single bacterial cell at the nanoscale with scanning dielectric force volume microscopy. Nanoscale 2019, 11, 20809–20819. [Google Scholar] [CrossRef] [PubMed]
- Collins, L.; Kilpatrick, J.I.; Kalinin, S.V.; Rodriguez, B.J. Towards nanoscale electrical measurements in liquid by advanced KPFM techniques: A review. Rep. Prog. Phys. 2018, 81, 086101. [Google Scholar] [CrossRef]
- Umeda, K.I.; Kobayashi, K.; Oyabu, N.; Hirata, Y.; Matsushige, K.; Yamada, H. Practical aspects of Kelvin-probe force microscopy at solid/liquid interfaces in various liquid media. J. Appl. Phys. 2014, 116, 134307. [Google Scholar] [CrossRef]
- Collins, L.; Jesse, S.; Kilpatrick, J.I.; Tselev, A.; Varenyk, O.; Okatan, M.B.; Weber, S.A.L.; Kumar, A.; Balke, N.; Kalinin, S.V.; et al. Probing charge screening dynamics and electrochemical processes at the solid-liquid interface with electrochemical force microscopy. Nat. Commun. 2014, 5, 1–8. [Google Scholar] [CrossRef]
- Collins, L.; Jesse, S.; Kilpatrick, J.I.; Tselev, A.; Okatan, M.B.; Kalinin, S.V.; Rodriguez, B.J. Kelvin probe force microscopy in liquid using electrochemical force microscopy. Beilstein J. Nanotechnol. 2015, 6, 201–214. [Google Scholar] [CrossRef]
- Collins, L.; Kilpatrick, J.I.; Vlassiouk, I.V.; Tselev, A.; Weber, S.A.L.; Jesse, S.; Kalinin, S.V.; Rodriguez, B.J. Dual harmonic Kelvin probe force microscopy at the graphene-liquid interface. Appl. Phys. Lett. 2014, 104, 133103. [Google Scholar] [CrossRef]
- Kobayashi, N.; Asakawa, H.; Fukuma, T. Dual frequency open-loop electric potential microscopy for local potential measurements in electrolyte solution with high ionic strength. Rev. Sci. Instrum. 2012, 83, 033709. [Google Scholar] [CrossRef]
- Gramse, G.; Edwards, M.A.; Fumagalli, L.; Gomila, G. Theory of amplitude modulated electrostatic force microscopy for dielectric measurements in liquids at MHz frequencies. Nanotechnology 2013, 24, 415709. [Google Scholar] [CrossRef] [PubMed]
- Gramse, G.; Edwards, M.A.; Fumagalli, L.; Gomila, G. Dynamic electrostatic force microscopy in liquid media. Appl. Phys. Lett. 2012, 101, 213108. [Google Scholar] [CrossRef]
- Millan-Solsona, R.; Checa, M.; Fumagalli, L.; Gomila, G. Mapping the capacitance of self-assembled monolayers at metal/electrolyte interfaces at the nanoscale by in-liquid scanning dielectric microscopy. Nanoscale 2020, 12, 20658–20668. [Google Scholar] [CrossRef] [PubMed]
- Kyndiah, A.; Checa, M.; Leonardi, F.; Millan-Solsona, R.; Di Muzio, M.; Tanwar, S.; Fumagalli, L.; Mas-Torrent, M.; Gomila, G. Nanoscale mapping of the conductivity and interfacial capacitance of an electrolyte-gated organic field-effect transistor under operation. Adv. Funct. Mater. 2021, 31, 1–8. [Google Scholar] [CrossRef]
- Di Muzio, M.; Millan-Solsona, R.; Borrell, J.H.; Fumagalli, L.; Gomila, G. Cholesterol effect on the specific capacitance of submicrometric DOPC bilayer patches measured by in-liquid scanning dielectric microscopy. Langmuir 2020, 36, 12963–12972. [Google Scholar] [CrossRef] [PubMed]
- Gramse, G.; Dols-Perez, A.; Edwards, M.A.; Fumagalli, L.; Gomila, G. Nanoscale measurement of the dielectric constant of supported lipid bilayers in aqueous solutions with electrostatic force microscopy. Biophys. J. 2013, 104, 1257–1262. [Google Scholar] [CrossRef]
- Di Muzio, M.; Millan-Solsona, R.; Dols-Perez, A.; Borrell, J.H.; Fumagalli, L.; Gomila, G. Dielectric properties and lamellarity of single liposomes measured by in-liquid scanning dielectric microscopy. J. Nanobiotechnol. (accepted for publication).
- Wright, C.J.; Francis, L.W.; Gonzalez, D.; Ryder, T.; Baer, K.; Rees, M.; White, J.O.; Conlan, R.S. Optimized sample preparation for high-resolution AFM characterization of fixed human cells. J. Microsc. 2010, 240, 111–121. [Google Scholar] [CrossRef]
- Checa, M.; Millan-Solsona, R.; Gomila, G. Frequency-dependent force between ac voltage biased plates in electrolyte solutions. Phys. Rev. E 2019, 100, 022604. [Google Scholar] [CrossRef]
- Benítez, R.; Moreno-Flores, S.; Bolós, V.J.; Toca-Herrera, J.L. A new automatic contact point detection algorithm for AFM force curves. Microsc. Res. Tech. 2013, 76, 870–876. [Google Scholar] [CrossRef] [PubMed]
- Gavara, N. Combined strategies for optimal detection of the contact point in AFM force-indentation curves obtained on thin samples and adherent cells. Sci. Rep. 2016, 6, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Riedel, C.; Arinero, R.; Tordjeman, P.; Leveque, G.; Schwartz, G.A.; Alegria, A.; Colmenero, J. Nanodielectric mapping of a model polystyrene-poly(vinyl acetate) blend by electrostatic force microscopy. Phys. Rev. E 2010, 81, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Van Der Hofstadt, M.; Fabregas, R.; Biagi, M.C.; Fumagalli, L.; Gomila, G. Nanoscale dielectric microscopy of non-planar samples by lift-mode electrostatic force microscopy. Nanotechnology 2016, 27, 405706. [Google Scholar] [CrossRef] [PubMed]
- Gomila, G.; Gramse, G.; Fumagalli, L. Finite-size effects and analytical modeling of electrostatic force microscopy applied to dielectric films. Nanotechnology 2014, 25, 255702. [Google Scholar] [CrossRef]
- Balakrishnan, H.; Millan-Solsona, R.; Checa, M.; Fabregas, R.; Fumagalli, L.; Gomila, G. Depth mapping of metallic nanowire polymer nanocomposites by scanning dielectric microscopy. Nanoscale 2021. [Google Scholar] [CrossRef]
- Fumagalli, L.; Esfandiar, A.; Fabregas, R.; Hu, S.; Ares, P.; Janardanan, A.; Yang, Q.; Radha, B.; Taniguchi, T.; Watanabe, K.; et al. Anomalously low dielectric constant of confined water. Science 2018, 360, 1339–1342. [Google Scholar] [CrossRef]
- Fumagalli, L.; Esteban-Ferrer, D.; Cuervo, A.; Carrascosa, J.L.; Gomila, G. Label-free identification of single dielectric nanoparticles and viruses with ultraweak polarization forces. Nat. Mater. 2012, 11, 808–816. [Google Scholar] [CrossRef]
- Guerrero, C.R.; Garcia, P.D.; Garcia, R. Subsurface imaging of cell organelles by force microscopy. ACS Nano 2019, 13, 9629–9637. [Google Scholar] [CrossRef]
- Kim, S.O.; Kim, J.; Okajima, T.; Cho, N.J. Mechanical properties of paraformaldehyde-treated individual cells investigated by atomic force microscopy and scanning ion conductance microscopy. Nano Converg. 2017, 4, 1–8. [Google Scholar] [CrossRef]
- Garcia, R. Nanomechanical mapping of soft materials with the atomic force microscope: Methods, theory and applications. Chem. Soc. Rev. 2020, 49, 5850–5884. [Google Scholar] [CrossRef] [PubMed]
- Gramse, G.; Kölker, A.; Škereň, T.; Stock, T.J.Z.; Aeppli, G.; Kienberger, F.; Fuhrer, A.; Curson, N.J. Nanoscale imaging of mobile carriers and trapped charges in delta doped silicon p–n junctions. Nat. Electron. 2020, 3, 531–538. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Checa, M.; Millan-Solsona, R.; Glinkowska Mares, A.; Pujals, S.; Gomila, G. Dielectric Imaging of Fixed HeLa Cells by In-Liquid Scanning Dielectric Force Volume Microscopy. Nanomaterials 2021, 11, 1402. https://doi.org/10.3390/nano11061402
Checa M, Millan-Solsona R, Glinkowska Mares A, Pujals S, Gomila G. Dielectric Imaging of Fixed HeLa Cells by In-Liquid Scanning Dielectric Force Volume Microscopy. Nanomaterials. 2021; 11(6):1402. https://doi.org/10.3390/nano11061402
Chicago/Turabian StyleCheca, Martí, Ruben Millan-Solsona, Adrianna Glinkowska Mares, Silvia Pujals, and Gabriel Gomila. 2021. "Dielectric Imaging of Fixed HeLa Cells by In-Liquid Scanning Dielectric Force Volume Microscopy" Nanomaterials 11, no. 6: 1402. https://doi.org/10.3390/nano11061402
APA StyleCheca, M., Millan-Solsona, R., Glinkowska Mares, A., Pujals, S., & Gomila, G. (2021). Dielectric Imaging of Fixed HeLa Cells by In-Liquid Scanning Dielectric Force Volume Microscopy. Nanomaterials, 11(6), 1402. https://doi.org/10.3390/nano11061402






