A Novel Long Short-Term Memory Based Optimal Strategy for Bio-Inspired Material Design
Abstract
1. Introduction
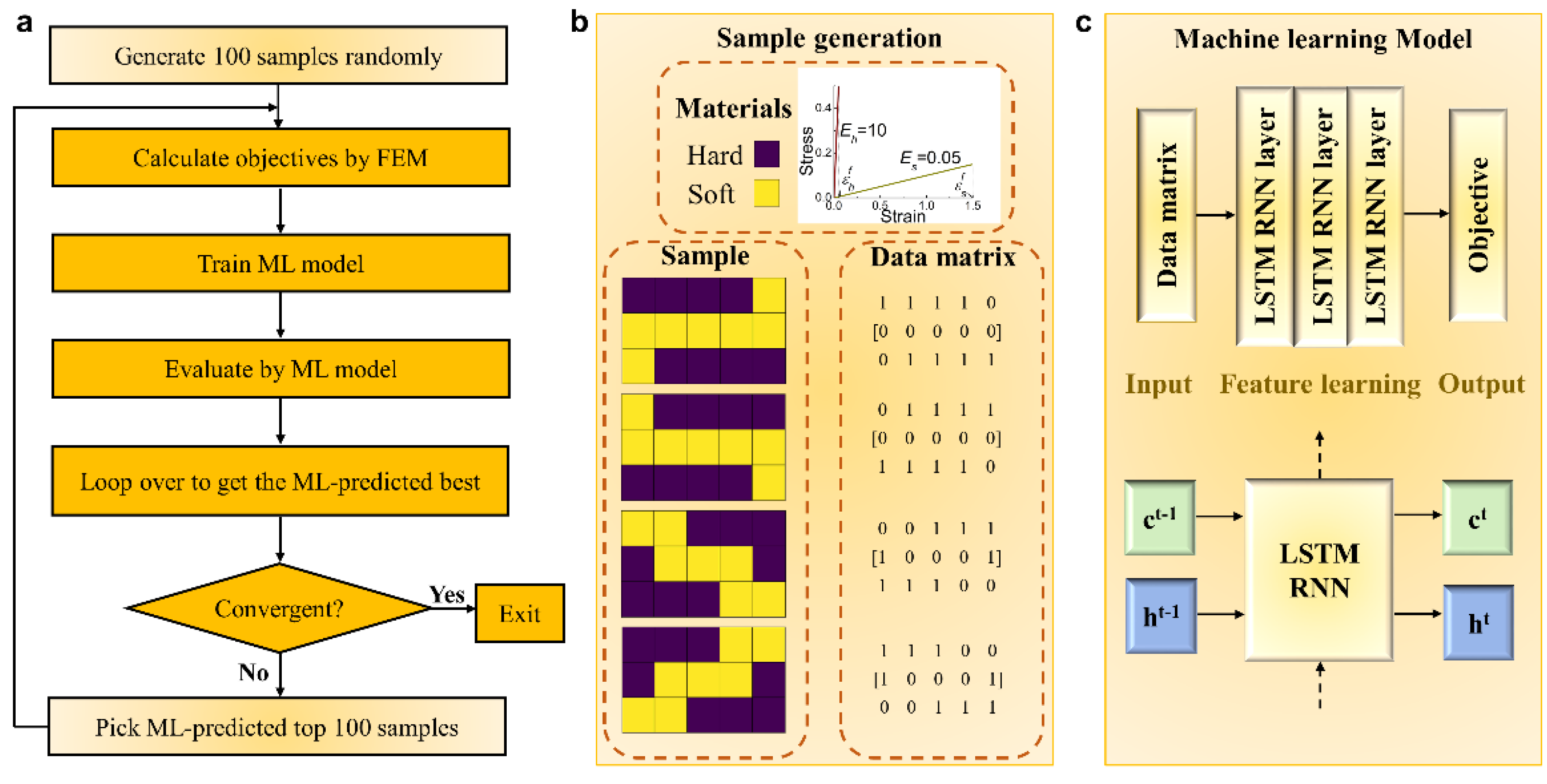
2. Methods
2.1. Sample Generation
2.2. Recurrent Neural Network
3. Results
4. Discussion
4.1. Comparisons with CNN-Based Optimal Strategy
4.2. Failure Mechanism of the Optimal Staggered Structure
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ritchie, R.O. The Conflicts between Strength and Toughness. Nat. Mater. 2011, 11, 817. [Google Scholar] [CrossRef]
- Porter, M.M.; Joanna, M. It’s Tough to Be Strong: Advances. Am. Ceram. Soc. Bull. 2014, 93, 18–24. [Google Scholar]
- Gao, H. Application of Fracture Mechanics Concepts to Hierarchical Biomechanics of Bone and Bone-like Materials. Int. J. Fract. 2006, 138, 101–137. [Google Scholar] [CrossRef]
- Gao, H.-L.; Chen, S.-M.; Mao, L.-B.; Song, Z.-Q.; Yao, H.-B.; Cölfen, H.; Luo, X.-S.; Zhang, F.; Pan, Z.; Meng, Y.-F.; et al. Mass production of bulk artificial nacre with excellent mechanical properties. Nat. Commun. 2017, 8, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Wat, A.; Lee, J.I.; Ryu, C.W.; Gludovatz, B.; Kim, J.; Tomsia, A.P.; Ishikawa, T.; Schmitz, J.; Meyer, A.; Alfreider, M.; et al. Bioinspired nacre-like alumina with a bulk-metallic glass-forming alloy as a compliant phase. Nat. Commun. 2019, 10, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Li, X.; Chu, M.; Sun, H.; Jin, J.; Yu, K.; Wang, Q.; Zhou, Q.; Chen, Y. Electrically assisted 3D printing of nacre-inspired structures with self-sensing capability. Sci. Adv. 2019, 5, eaau9490. [Google Scholar] [CrossRef]
- Yin, Z.; Hannard, F.; Barthelat, F. Impact-resistant nacre-like transparent materials. Science 2019, 364, 1260–1263. [Google Scholar] [CrossRef] [PubMed]
- Ji, B.; Gao, H. Mechanical properties of nanostructure of biological materials. J. Mech. Phys. Solids 2004, 52, 1963–1990. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Y.-W.; Gao, H. On optimal hierarchy of load-bearing biological materials. Proc. R. Soc. B Boil. Sci. 2010, 278, 519–525. [Google Scholar] [CrossRef] [PubMed]
- Begley, R.M.; Philips, N.R.; Compton, B.G.; Wilbrink, D.V.; Ritchie, R.O.; Utz, M. Micromechanical Models to Guide the Development of Synthetic ‘Brick and Mortar’composites. J. Mech. Phys. Solids 2012, 60, 1545–1560. [Google Scholar] [CrossRef]
- Shao, Y.; Zhao, H.-P.; Feng, X.-Q.; Gao, H. Discontinuous crack-bridging model for fracture toughness analysis of nacre. J. Mech. Phys. Solids 2012, 60, 1400–1419. [Google Scholar] [CrossRef]
- Abid, N.; Mirkhalaf, M.; Barthelat, F. Discrete-element modeling of nacre-like materials: Effects of random microstructures on strain localization and mechanical performance. J. Mech. Phys. Solids 2018, 112, 385–402. [Google Scholar] [CrossRef]
- Abid, N.; Pro, J.W.; Barthelat, F. Fracture mechanics of nacre-like materials using discrete-element models: Effects of microstructure, interfaces and randomness. J. Mech. Phys. Solids 2019, 124, 350–365. [Google Scholar] [CrossRef]
- Guo, X.; Gao, H. Bio-Inspired Material Design and Optimization. In IUTAM Symposium on Topological Design Optimization of Structures, Machines and Materials: Status and Perspectives; Bendsoe, M.P., Olhoff, N., Sigmund, O., Eds.; Springer: Dordrecht, The Netherlands, 2006; Volume 137, pp. 439–453. [Google Scholar]
- Samuel, A.L. Some Studies in Machine Learning Using the Game of Checkers. IBM J. Res. Dev. 1959, 44, 206–226. [Google Scholar] [CrossRef]
- Abueidda, D.W.; Seid, K.; Nahil, A.S. Topology Optimization of 2d Structures with Nonlinearities Using Deep Learning. Comput. Struct. 2020, 237, 106283. [Google Scholar] [CrossRef]
- Liu, X.; Christos, E.; Athanasiou, N.P.; Padture, B.; Sheldon, W.; Gao, H. A Machine Learning Approach to Fracture Mechanics Problems. Acta Mater. 2020, 190, 105–112. [Google Scholar] [CrossRef]
- Wang, T.; Shao, M.; Guo, R.; Tao, F.; Zhang, G.; Snoussi, H.; Tang, X. Surrogate Model via Artificial Intelligence Method for Accelerating Screening Materials and Performance Prediction. Adv. Funct. Mater. 2021, 31, 2006245. [Google Scholar] [CrossRef]
- Abueidda, D.W.; Koric, S.; Nahil, A.S.; Huseyin, S. Deep Learning for Plasticity and Thermo-Viscoplasticity. Int. J. Plast. 2021, 136, 102852. [Google Scholar] [CrossRef]
- Gu, G.X.; Chen, C.-T.; Buehler, M.J. De novo composite design based on machine learning algorithm. Extrem. Mech. Lett. 2018, 18, 19–28. [Google Scholar] [CrossRef]
- Gu, G.X.; Chen, C.-T.; Richmond, D.J.; Buehler, M.J. Bioinspired hierarchical composite design using machine learning: Simulation, additive manufacturing, and experiment. Mater. Horiz. 2018, 5, 939–945. [Google Scholar] [CrossRef]
- Abueidda, D.W.; Mohammad, A.; Rami, A.; Umberto, R.; Iwona, M.J.; Nahil, A.S. Prediction and Optimization of Mechanical Properties of Composites Using Convolutional Neural Networks. Compos. Struct. 2019, 227, 111264. [Google Scholar] [CrossRef]
- Hanakata, P.Z.; Cubuk, E.D.; Campbell, D.K.; Park, H.S. Accelerated Search and Design of Stretchable Graphene Kirigami Using Machine Learning. Phys. Rev. Lett. 2018, 121, 255304. [Google Scholar] [CrossRef] [PubMed]
- Mikolov, T.; Martin, K.; Lukáš, B.; Jan, Č.; Sanjeev, K. Recurrent neural network based language model. In Proceedings of the International Conference on Acoustics Speech and Signal Processing (ICASSP), Dallas, TX, USA, 15–19 March 2010; pp. 1045–1048. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Gulli, A.; Sujit, P. Deep Learning with Keras; Packt Publishing: Birmingham, UK, 2017. [Google Scholar]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, B.; Li, D.; Chen, Y. A Novel Long Short-Term Memory Based Optimal Strategy for Bio-Inspired Material Design. Nanomaterials 2021, 11, 1389. https://doi.org/10.3390/nano11061389
Ding B, Li D, Chen Y. A Novel Long Short-Term Memory Based Optimal Strategy for Bio-Inspired Material Design. Nanomaterials. 2021; 11(6):1389. https://doi.org/10.3390/nano11061389
Chicago/Turabian StyleDing, Bin, Dong Li, and Yuli Chen. 2021. "A Novel Long Short-Term Memory Based Optimal Strategy for Bio-Inspired Material Design" Nanomaterials 11, no. 6: 1389. https://doi.org/10.3390/nano11061389
APA StyleDing, B., Li, D., & Chen, Y. (2021). A Novel Long Short-Term Memory Based Optimal Strategy for Bio-Inspired Material Design. Nanomaterials, 11(6), 1389. https://doi.org/10.3390/nano11061389






