Directional Plasmonic Excitation by Helical Nanotips
Abstract
1. Introduction
2. Materials and Methods
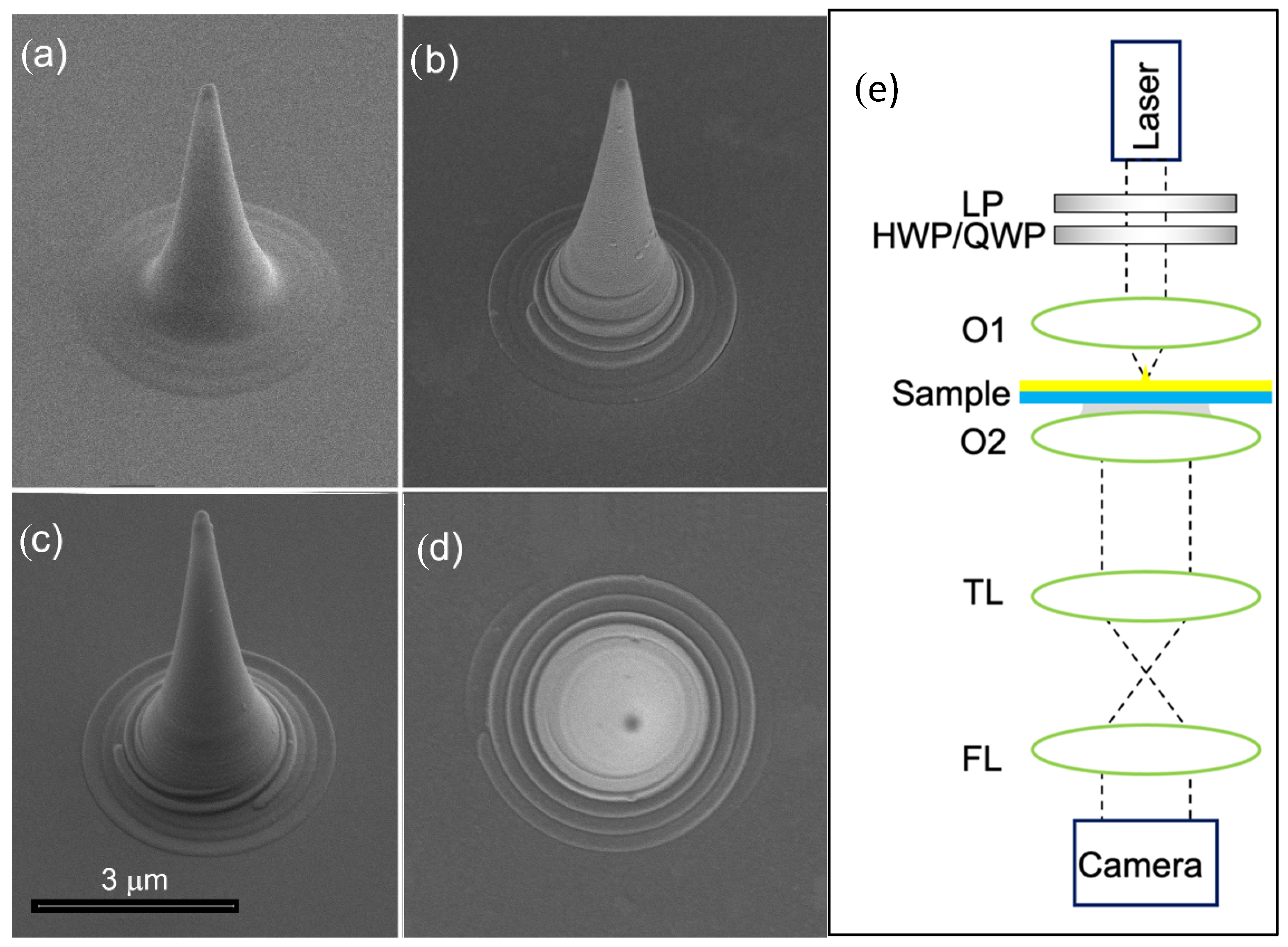
2.1. Nanotip Fabrication
2.2. Leakage Microscopy for k-Space Microscopy
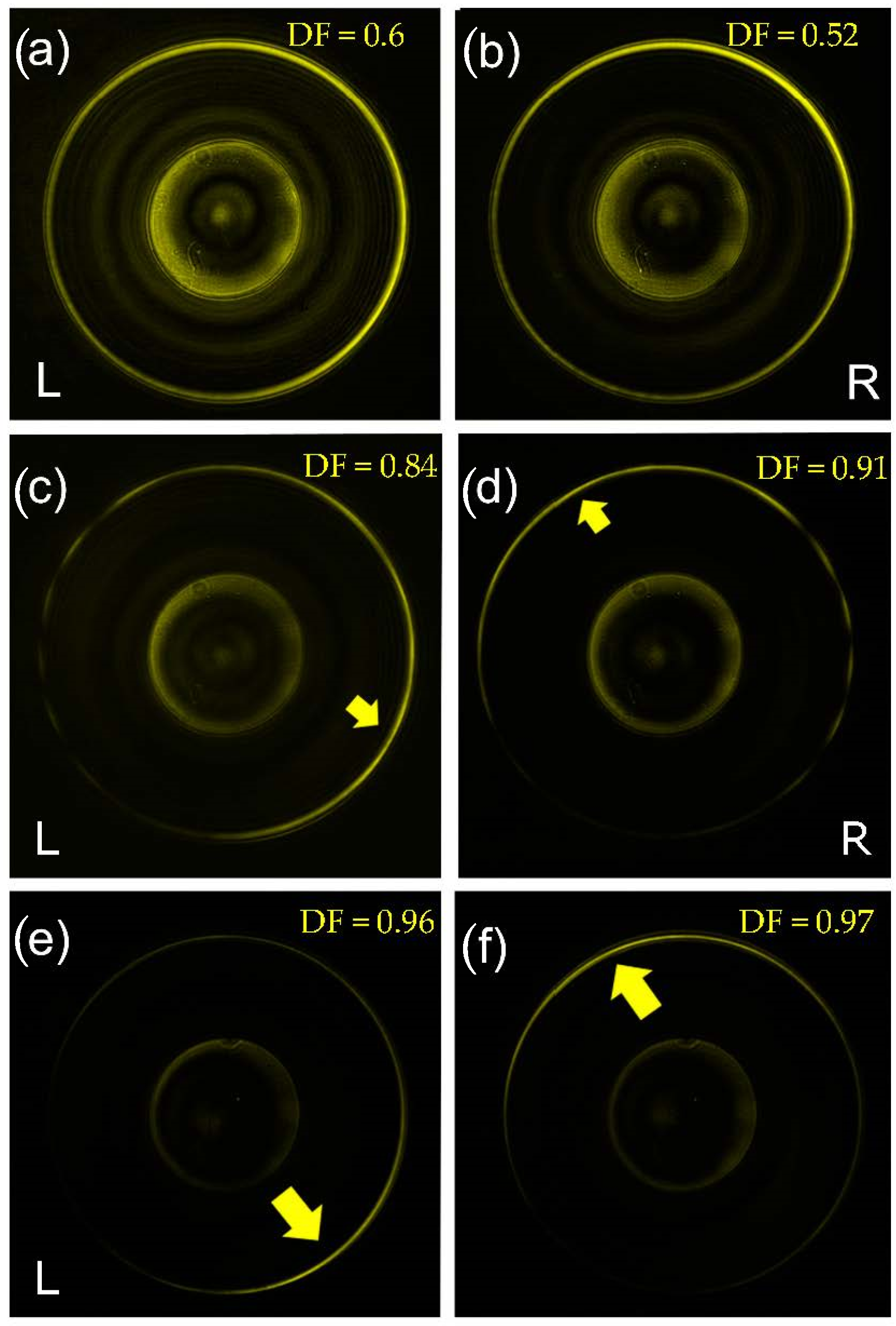
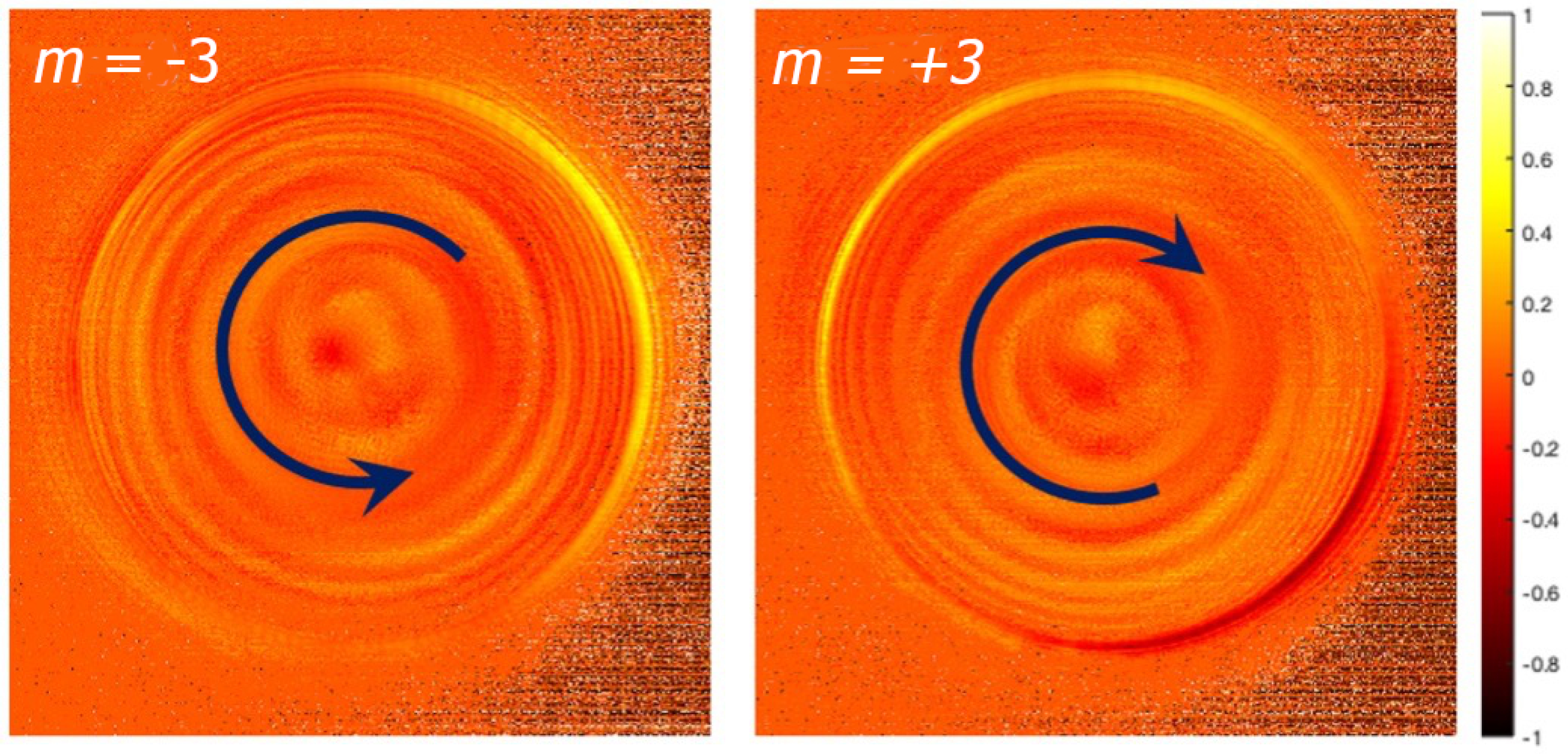
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shafiei, F.; Wu, C.; Wu, Y.; Khanikaev, A.B.; Putzke, P.; Singh, A.; Li, X.; Shvets, G. Plasmonic nano-protractor based on polarization spectro-tomography. Nat. Photonics 2013, 7, 367–372. [Google Scholar] [CrossRef]
- Nitzan, A.; Jortner, J. Line shape of a molecular resonance. Mol. Phys. 1972, 24, 109–131. [Google Scholar] [CrossRef]
- Nitzan, A. Photon absorption and scattering in Fano anti-resonances. Mol. Phys. 1974, 27, 65–80. [Google Scholar] [CrossRef]
- Miroshnichenko, A.E.; Flach, S.; Kivshar, Y.S. Fano resonances in nanoscale structures. Rev. Mod. Phys. 2010, 82, 2257–2298. [Google Scholar] [CrossRef]
- Joe, Y.S.; Satanin, A.M.; Kim, C.S. Classical analogy of Fano resonances. Phys. Scr. 2006, 74, 259–266. [Google Scholar] [CrossRef]
- Luk’Yanchuk, B.; Zheludev, N.I.; Maier, S.A.; Halas, N.J.; Nordlander, P.; Giessen, H.; Chong, C.T.; Limonov, M.F.; Rybin, M.V.; Poddubny, A.N.; et al. Fano resonances in photonics. Nat. Photonics 2010, 11, 543–554. [Google Scholar]
- McCutcheon, M.W.; Rieger, G.W.; Cheung, I.W.; Young, J.F.; Dalacu, D.; Frédérick, S.; Poole, P.J.; Aers, G.C.; Williams, R.L. Resonant scattering and second-harmonic spectroscopy of planar photonic crystal microcavities. Appl. Phys. Lett. 2005, 87, 221110. [Google Scholar] [CrossRef]
- Drezet, A.; Genet, C. Imaging Surface Plasmons: From Leaky Waves to Far-Field Radiation. Phys. Rev. Lett. 2013, 110, 1–5. [Google Scholar] [CrossRef]
- Berthel, M.; Jiang, Q.; Chartrand, C.; Bellessa, J.; Huant, S.; Genet, C.; Drezet, A. Coherence and aberration effects in surface plasmon polariton imaging. Phys. Rev. E 2015, 92, 033202. [Google Scholar] [CrossRef]
- Ott, C.; Kaldun, A.; Raith, P.; Meyer, K.; Laux, M.; Evers, J.; Keitel, C.H.; Greene, C.H.; Pfeifer, T. Lorentz Meets Fano in Spectral Line Shapes: A Universal Phase and Its Laser Control. Science 2013, 340, 716–720. [Google Scholar] [CrossRef]
- He, J.; Fan, C.; Ding, P.; Zhu, S.; Liang, E. Near-field engineering of Fano resonances in a plasmonic assembly for maximizing CARS enhancements. Sci. Rep. 2016, 6, 20777. [Google Scholar] [CrossRef]
- Rajesh, D.; Nechayev, S.; Cheskis, D.; Sternklar, S.; Gorodetski, Y. Probing spin-orbit interaction via Fano interference. Appl. Phys. Lett. 2018, 113, 261104. [Google Scholar] [CrossRef]
- Rybin, M.V.; Filonov, D.S.; Belov, P.A.; Kivshar, Y.S.; Limonov, M.F. Switching from Visibility to Invisibility via Fano Resonances: Theory and Experiment. Sci. Rep. 2015, 5, 8774. [Google Scholar] [CrossRef] [PubMed]
- Bliokh, K.Y.; Rodríguez-Fortuño, F.J.; Nori, F.; Zayats, A.V. Spin-orbit interactions of light. Nat. Photonics 2015, 9, 796–808. [Google Scholar] [CrossRef]
- Ni, J.; Hu, Y.; Liu, S.; Lao, Z.; Ji, S.; Pan, D.; Zhang, C.; Xu, B.; Li, J.; Wu, D.; et al. Controllable double-helical microstructures by photonic orbital angular momentum for chiroptical response. Opt. Lett. 2021, 46, 1401–1404. [Google Scholar] [CrossRef]
- Cheng, L.; Li, X.; Wang, Z.; Cao, P.; He, X.; Niu, T. AdjusTable 3D Plasmonic Archimedes Spiral Lens for Optical Manipulation. Appl. Sci. 2019, 9, 674. [Google Scholar] [CrossRef]
- Garoli, D.; Zilio, P.; De Angelis, F.; Gorodetski, Y. Helicity locking of chiral light emitted from a plasmonic nanotaper. Nanoscale 2017, 9, 6965–6969. [Google Scholar] [CrossRef] [PubMed]
- Garoli, D.; Zilio, P.; Gorodetski, Y.; Tantussi, F.; De Angelis, F. Beaming of Helical Light from Plasmonic Vortices via Adiabatically Tapered Nanotip. Nano Lett. 2016, 16, 6636–6643. [Google Scholar] [CrossRef]
- Liu, K.; Maccaferri, N.; Shen, Y.; Li, X.; Zaccaria, R.P.; Zhang, X.; Gorodetski, Y.; Garoli, D. Particle trapping and beaming using a 3D nanotip excited with a plasmonic vortex. Opt. Lett. 2020, 45, 823–826. [Google Scholar] [CrossRef]
- Maccaferri, N.; Gorodetski, Y.; Toma, A.; Zilio, P.; De Angelis, F.; Garoli, D. Magnetoplasmonic control of plasmonic vortices. Appl. Phys. Lett. 2017, 111, 201104. [Google Scholar] [CrossRef]
- Garoli, D.; Zilio, P.; Gorodetski, Y.; Tantussi, F.; De Angelis, F. Optical vortex beam generator at nanoscale level. Sci. Rep. 2016, 6, 29547. [Google Scholar] [CrossRef]
- Zilio, P.; Parisi, G.; Garoli, D.; Carli, M.; Romanato, F. Bilayer holey plasmonic vortex lenses for the far field transmission of pure orbital angular momentum light states. Opt. Lett. 2014, 39, 4899–4902. [Google Scholar] [CrossRef]
- Lin, J.; Mueller, J.P.B.; Wang, Q.; Yuan, G.; Antoniou, N.; Yuan, X.-C.; Capasso, F. Polarization-Controlled Tunable Directional Coupling of Surface Plasmon Polaritons. Science 2013, 340, 331–334. [Google Scholar] [CrossRef]
- Rodríguez-fortuño, F.J.; Martínez, A.; Wurtz, G.; Zayats, A.V. Electromagnetic Guided Modes. Science 2013, 328, 328–331. [Google Scholar]
- Shitrit, N.; Yulevich, I.; Maguid, E.; Ozeri, D.; Veksler, D.; Kleiner, V.; Hasman, E. Spin-Optical Metamaterial Route to Spin-Controlled Photonics. Science 2013, 340, 724–726. [Google Scholar] [CrossRef]
- Lefier, Y.; Salut, R.; Suarez, M.A.; Grosjean, T. Directing Nanoscale Optical Flows by Coupling Photon Spin to Plasmon Extrinsic Angular Momentum. Nano Lett. 2017, 18, 38–42. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Zhou, S.; Hu, C.; Zhang, W.; Xiao, X.; Zhang, J. Broadband spin-controlled surface plasmon polariton launching and radiation via L-shaped optical slot nanoantennas. Laser Photon. Rev. 2014, 8, 590–595. [Google Scholar] [CrossRef]
- Mueller, J.P.B.; Leosson, K.; Capasso, F. Polarization-Selective Coupling to Long-Range Surface Plasmon Polariton Waveguides. Nano Lett. 2014, 14, 5524–5527. [Google Scholar] [CrossRef]
- Drezet, A.; Hohenau, A.; Koller, D.; Stepanov, A.; Ditlbacher, H.; Steinberger, B.; Aussenegg, F.; Leitner, A.; Krenn, J. Leakage radiation microscopy of surface plasmon polaritons. Mater. Sci. Eng. B 2008, 149, 220–229. [Google Scholar] [CrossRef]
- Cuche, A.; Mollet, O.; Drezet, A.; Huant, S. “Deterministic” quantum plasmonics. Nano Lett. 2010, 10, 4566–4570. [Google Scholar] [CrossRef]
- Hohenau, A.; Krenn, J.R.; Drezet, A.; Mollet, O.; Huant, S.; Genet, C.; Stein, B.; Ebbesen, T.W. Surface plasmon leakage radiation microscopy at the diffraction limit. Opt. Express 2011, 19, 25749–25762. [Google Scholar] [CrossRef]
- Stein, B.; Laluet, J.-Y.; Devaux, E.; Genet, C.; Ebbesen, T.W. Fano Resonances and Leakage Radiation for High-Resolution Plasmonic Sensing. J. Phys. Chem. C 2012, 116, 6092–6096. [Google Scholar] [CrossRef]
- Gorodetski, Y.; Shitrit, N.; Bretner, I.; Kleiner, V.; Hasman, E. Observation of Optical Spin Symmetry Breaking in Nanoapertures. Nano Lett. 2009, 9, 3016–3019. [Google Scholar] [CrossRef]
- Epstein, E.D.; Singh, L.; Sternklar, S.; Gorodetski, Y. The role of plasmonic excitations in the optical activity of periodic structures with configurational chirality. Appl. Phys. Lett. 2020, 116, 131106. [Google Scholar] [CrossRef]
- Singh, L.; Epstein, E.D.; Cheskis, D.; Sternklar, S.; Gorodetski, Y. Experimental investigation of Kramers–Kronig relations in chiral metasurfaces with reduced rotational symmetry. J. Opt. 2020, 22, 12LT01. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, L.; Maccaferri, N.; Garoli, D.; Gorodetski, Y. Directional Plasmonic Excitation by Helical Nanotips. Nanomaterials 2021, 11, 1333. https://doi.org/10.3390/nano11051333
Singh L, Maccaferri N, Garoli D, Gorodetski Y. Directional Plasmonic Excitation by Helical Nanotips. Nanomaterials. 2021; 11(5):1333. https://doi.org/10.3390/nano11051333
Chicago/Turabian StyleSingh, Leeju, Nicolò Maccaferri, Denis Garoli, and Yuri Gorodetski. 2021. "Directional Plasmonic Excitation by Helical Nanotips" Nanomaterials 11, no. 5: 1333. https://doi.org/10.3390/nano11051333
APA StyleSingh, L., Maccaferri, N., Garoli, D., & Gorodetski, Y. (2021). Directional Plasmonic Excitation by Helical Nanotips. Nanomaterials, 11(5), 1333. https://doi.org/10.3390/nano11051333









