Dynamics of Stress-Driven Two-Phase Elastic Beams
Abstract
1. Introduction
2. Stress-Driven Mixture of Integral Elasticity
3. Scale-Dependent Free Vibrations
- Solving Equation (17) in terms of the vector of integration constants .
- Enforcing standard and constitutive boundary conditions to get a homogeneous algebraic linear system .
- Solving the characteristic nonlinear equationfor any fixed pair of parameters , to detect natural frequencies .
4. Case-Problems: Numerical Outcomes
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, J.; Zhang, X.; Wei, X.; Xue, Y.; Wan, H.; Wang, P. Recent advances in acoustic wave biosensors for the detection of disease-related biomarkers: A review. Anal. Chim. Acta 2021, 338321. [Google Scholar] [CrossRef]
- Soukarie, D.; Ecochard, V.; Salome, L. DNA-based nanobiosensors for monitoring of water quality. Int. J. Hyg. Environ. Health 2020, 226, 113485. [Google Scholar] [CrossRef]
- Ilyas, S.; Younis, M.I. Resonator-based M/NEMS logic devices: Review of recent advances. Sens. Actuators A 2020, 302, 111821. [Google Scholar] [CrossRef]
- Basutkar, R. Analytical modelling of a nanoscale series-connected bimorph piezoelectric energy harvester incorporating the flexoelectric effect. Int. J. Eng. Sci. 2019, 139, 42–61. [Google Scholar] [CrossRef]
- Udara, S.; Hadimani, H.C.; Krishnamurthy Revankar, P. Sensitivity and Selectivity Enhancement of MEMS/NEMS Cantilever by Coating of Polyvinylpyrrolidone. Mater. Today Proc. 2019, 18, 1610–1619. [Google Scholar] [CrossRef]
- De Bellis, M.L.; Bacigalupo, A.; Zavarise, G. Characterization of hybrid piezoelectric nanogenerators through asymptotic homogenization. Comput. Methods Appl. Mech. Eng. 2019, 355, 1148–1186. [Google Scholar] [CrossRef]
- Pourasghar, A.; Chen, Z. Effect of hyperbolic heat conduction on the linear and nonlinear vibration of CNT reinforced size-dependent functionally graded microbeams. Int. J. Eng. Sci. 2019, 137, 57–72. [Google Scholar] [CrossRef]
- Arora, R. Nanocomposite polyaniline for environmental and energy applications. Mater. Today Proc. 2020. [Google Scholar] [CrossRef]
- Rogula, D. Influence of spatial acoustic dispersion on dynamical properties of dislocations. Bull. Pol. Acad. Sci. 1965, 13, 337–385. [Google Scholar]
- Rogula, D. Nonlocal Theories of Material Systems; Ossolineum: Wrocław, Poland, 1965. [Google Scholar]
- Kröner, E. Elasticity theory of materials with long range cohesive forces. Int. J. Solids Struct. 1967, 3, 731–742. [Google Scholar] [CrossRef]
- Eringen, A.C. Linear theory of nonlocal elasticity and dispersion of plane waves. Int. J. Eng. Sci. 1972, 10, 425–435. [Google Scholar] [CrossRef]
- Eringen, A. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R.; Diaco, M.; Marotti de Sciarra, F. Constitutive boundary conditions and paradoxes in nonlocal elastic nanobeams. Int. J. Mech. Sci. 2017, 121, 151–156. [Google Scholar] [CrossRef]
- Eringen, A.C. Theory of nonlocal elasticity and some applications. Res. Mech. 1987, 21, 313–342. [Google Scholar]
- Zhu, X.; Wang, Y.; Dai, H.H. Buckling analysis of Euler–Bernoulli beams using Eringen’s two-phase nonlocal model. Int. J. Eng. Sci. 2017, 116, 130–140. [Google Scholar] [CrossRef]
- Wang, Y.B.; Zhu, X.W.; Dai, H.H. Exact solutions for the static bending of Euler-Bernoulli beams using Eringen’s two-phase local/nonlocal model. AIP Adv. 2016, 6, 085114. [Google Scholar] [CrossRef]
- Polizzotto, C. Nonlocal elasticity and related variational principles. Int. J. Solids Struct. 2001, 38, 7359–7380. [Google Scholar] [CrossRef]
- Pisano, A.A.; Fuschi, P. Closed form solution for a nonlocal elastic bar in tension. Int. J. Solids Struct. 2003, 40, 13–23. [Google Scholar] [CrossRef]
- Khodabakhshi, P.; Reddy, J. A unified integro-differential nonlocal model. Int. J. Eng. Sci. 2015, 95, 60–75. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R.; Diaco, M. On nonlocal integral models for elastic nano-beams. Int. J. Mech. Sci. 2017, 131–132, 490–499. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R. Nonlocal elasticity in nanobeams: The stress-driven integral model. Int. J. Eng. Sci. 2017, 115, 14–27. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R. Stress-driven versus strain-driven nonlocal integral model for elastic nano-beams. Compos. B Eng. 2017, 114, 184–188. [Google Scholar] [CrossRef]
- Zhang, P.; Qing, H.; Gao, C.F. Exact solutions for bending of Timoshenko curved nanobeams made of functionally graded materials based on stress-driven nonlocal integral model. Compos. Struct. 2020, 245, 112362. [Google Scholar] [CrossRef]
- Pinnola, F.P.; Vaccaro, M.S.; Barretta, R.; Marotti de Sciarra, F. Random vibrations of stress-driven nonlocal beams with external damping. Meccanica 2020. [Google Scholar] [CrossRef]
- Barretta, R.; Fabbrocino, F.; Luciano, R.; de Sciarra, F.M. Closed-form solutions in stress-driven two-phase integral elasticity for bending of functionally graded nano-beams. Phys. E Low-Dimens. Syst. Nanostruct. 2018, 97, 13–30. [Google Scholar] [CrossRef]
- Vaccaro, M.S.; Pinnola, F.P.; de Sciarra, F.M.; Canadija, M.; Barretta, R. Stress-driven two-phase integral elasticity for Timoshenko curved beams. Proc. Inst. Mech. Eng. Part J. Nanomater. Nanoeng. Nanosyst. 2021. [Google Scholar] [CrossRef]
- Apuzzo, A.; Barretta, R.; Luciano, R.; Marotti de Sciarra, F.; Penna, R. Free vibrations of Bernoulli-Euler nano-beams by the stress-driven nonlocal integral model. Compos. B Eng. 2017, 123, 105–111. [Google Scholar] [CrossRef]
- Lam, D.; Yang, F.; Chong, A.; Wang, J.; Tong, P. Experiments and theory in strain gradient elasticity. J. Mech. Phys. Solids 2003, 51, 1477–1508. [Google Scholar] [CrossRef]
- Abazari, A.M.; Safavi, S.M.; Rezazadeh, G.; Villanueva, L.G. Modelling the Size Effects on the Mechanical Properties of Micro/Nano Structures. Sensors 2015, 15, 28543–28562. [Google Scholar] [CrossRef] [PubMed]
- Savin, A.; Korznikova, E.; Dmitriev, S. Improving bending rigidity of graphene nanoribbons by twisting. Mech. Mater. 2019, 137, 103123. [Google Scholar] [CrossRef]
- Aifantis, E.C. On the role of gradients in the localization of deformation and fracture. Int. J. Eng. Sci. 1992, 30, 1279–1299. [Google Scholar] [CrossRef]
- Ru, C.; Aifantis, E. A simple approach to solve boundary-value problems in gradient elasticity. Acta Mech. 1993, 101, 59–68. [Google Scholar] [CrossRef]
- Altan, B.; Aifantis, E. On Some Aspects in the Special Theory of Gradient Elasticity. J. Mech. Behav. Mater. 1997, 8, 231–282. [Google Scholar] [CrossRef]
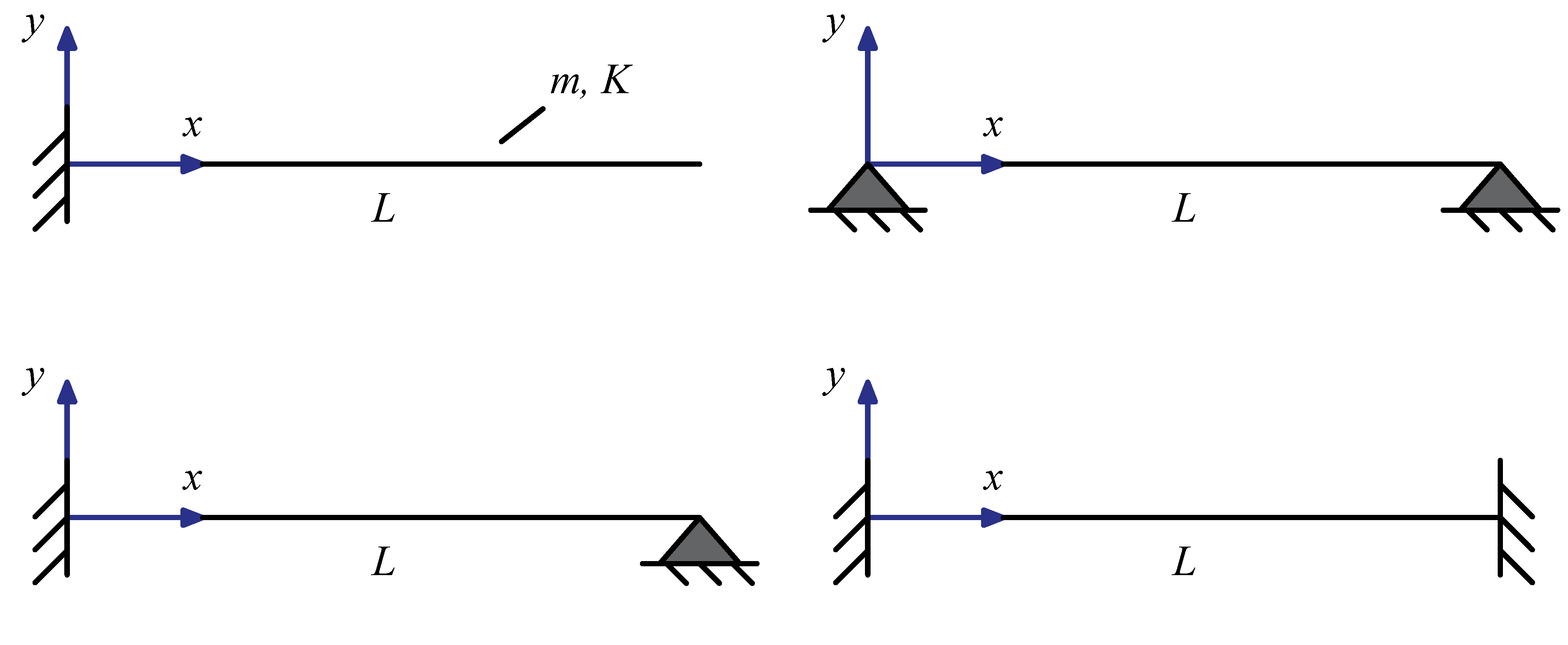



| GradEla | |||||||
|---|---|---|---|---|---|---|---|
| = 0 | = 0.2 | = 0.4 | = 0.6 | = 0.8 | = 1.0 | ||
| 0 | 3.5160 | 3.5160 | 3.5160 | 3.5160 | 3.5160 | 3.5160 | 3.5160 |
| 0.01 | 3.5515 | 3.5443 | 3.5372 | 3.5301 | 3.5230 | 3.5160 | 3.5168 |
| 0.02 | 3.5877 | 3.5731 | 3.5585 | 3.5442 | 3.5300 | 3.5160 | 3.5192 |
| 0.03 | 3.6246 | 3.6021 | 3.5800 | 3.5583 | 3.5370 | 3.5160 | 3.5230 |
| 0.04 | 3.6621 | 3.6315 | 3.6016 | 3.5724 | 3.5439 | 3.5160 | 3.5282 |
| 0.05 | 3.7002 | 3.6612 | 3.6232 | 3.5865 | 3.5507 | 3.5160 | 3.5348 |
| 0.06 | 3.7389 | 3.6911 | 3.6449 | 3.6004 | 3.5575 | 3.5160 | 3.5426 |
| 0.07 | 3.7781 | 3.7211 | 3.6666 | 3.6143 | 3.5642 | 3.5160 | 3.5515 |
| 0.08 | 3.8177 | 3.7514 | 3.6882 | 3.6281 | 3.5708 | 3.5160 | 3.5615 |
| 0.09 | 3.8577 | 3.7817 | 3.7098 | 3.6418 | 3.5773 | 3.5160 | 3.5725 |
| 0.10 | 3.8981 | 3.8120 | 3.7313 | 3.6553 | 3.5837 | 3.5160 | 3.5843 |
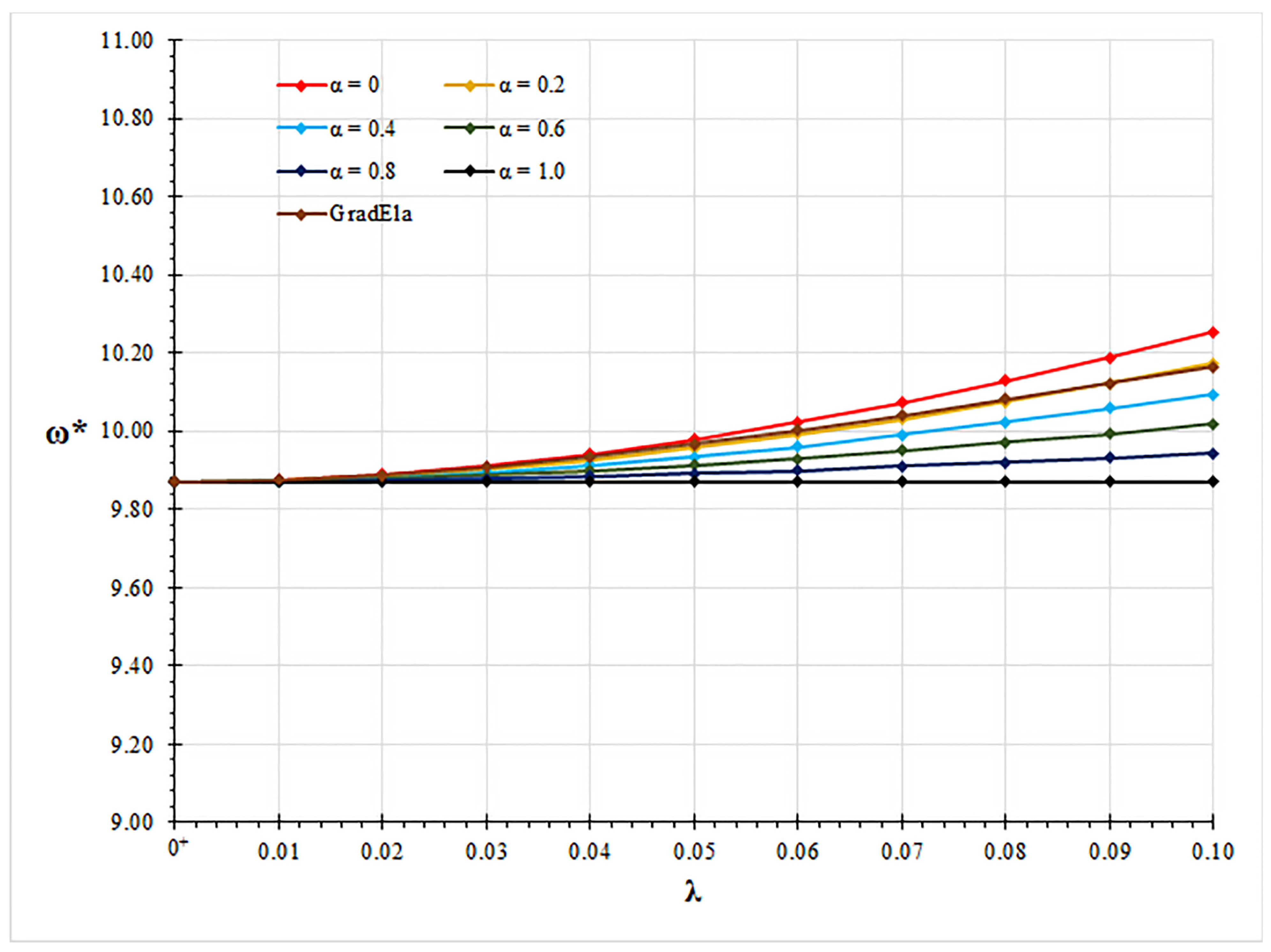
| GradEla | |||||||
|---|---|---|---|---|---|---|---|
| = 0 | = 0.2 | = 0.4 | = 0.6 | = 0.8 | = 1.0 | ||
| 0 | 9.8696 | 9.8696 | 9.8696 | 9.8696 | 9.8696 | 9.8696 | 9.8696 |
| 0.01 | 9.8744 | 9.8734 | 9.8725 | 9.8715 | 9.8706 | 9.8696 | 9.8743 |
| 0.02 | 9.8883 | 9.8845 | 9.8808 | 9.8771 | 9.8733 | 9.8696 | 9.8875 |
| 0.03 | 9.9107 | 9.9025 | 9.8942 | 9.8860 | 9.8778 | 9.8696 | 9.9081 |
| 0.04 | 9.9410 | 9.9266 | 9.9123 | 9.8980 | 9.8838 | 9.8696 | 9.9349 |
| 0.05 | 9.9786 | 9.9565 | 9.9346 | 9.9128 | 9.8911 | 9.8696 | 9.9666 |
| 0.06 | 10.0228 | 9.9916 | 9.9607 | 9.9300 | 9.8997 | 9.8696 | 10.0023 |
| 0.07 | 10.0729 | 10.0313 | 9.9901 | 9.9495 | 9.9093 | 9.8696 | 10.0407 |
| 0.08 | 10.1285 | 10.0751 | 10.0225 | 9.9708 | 9.9198 | 9.8696 | 10.0811 |
| 0.09 | 10.1888 | 10.1225 | 10.0575 | 9.9937 | 9.9311 | 9.8696 | 10.1224 |
| 0.10 | 10.2534 | 10.1731 | 10.0946 | 10.0179 | 9.9429 | 9.8696 | 10.1639 |
| GradEla | |||||||
|---|---|---|---|---|---|---|---|
| = 0 | = 0.2 | = 0.4 | = 0.6 | = 0.8 | = 1.0 | ||
| 0 | 15.4184 | 15.4183 | 15.4183 | 15.4183 | 15.4182 | 15.4182 | 15.4182 |
| 0.01 | 15.5854 | 15.5512 | 15.5174 | 15.4840 | 15.4509 | 15.4182 | 15.4385 |
| 0.02 | 15.7781 | 15.7030 | 15.6294 | 15.5575 | 15.4871 | 15.4182 | 15.4969 |
| 0.03 | 15.9958 | 15.8724 | 15.7532 | 15.6379 | 15.5263 | 15.4182 | 15.5897 |
| 0.04 | 16.2373 | 16.0583 | 15.8875 | 15.7242 | 15.5679 | 15.4182 | 15.7137 |
| 0.05 | 16.5016 | 16.2593 | 16.0310 | 15.8154 | 15.6115 | 15.4182 | 15.8657 |
| 0.06 | 16.7874 | 16.4737 | 16.1823 | 15.9105 | 15.6564 | 15.4182 | 16.0427 |
| 0.07 | 17.0931 | 16.7000 | 16.3399 | 16.0085 | 15.7023 | 15.4182 | 16.2419 |
| 0.08 | 17.4173 | 16.9364 | 16.5024 | 16.1084 | 15.7485 | 15.4182 | 16.4606 |
| 0.09 | 17.7585 | 17.1814 | 16.6686 | 16.2092 | 15.7947 | 15.4182 | 16.6965 |
| 0.10 | 18.1152 | 17.4332 | 16.8370 | 16.3103 | 15.8406 | 15.4182 | 16.9473 |
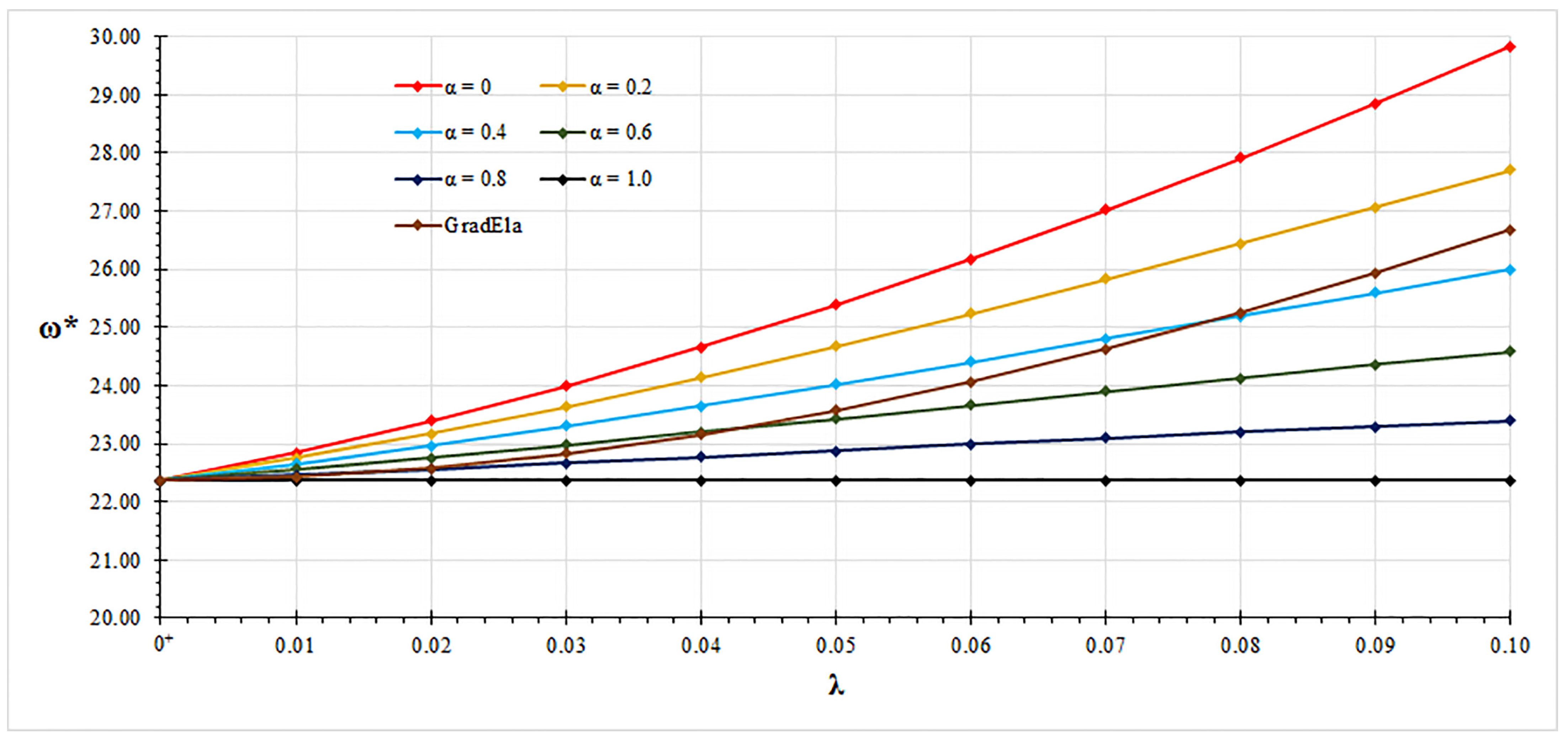
| GradEla | |||||||
|---|---|---|---|---|---|---|---|
| = 0 | = 0.2 | = 0.4 | = 0.6 | = 0.8 | = 1.0 | ||
| 0 | 22.3737 | 22.3736 | 22.3736 | 22.3735 | 22.3734 | 22.3733 | 22.3734 |
| 0.01 | 22.8518 | 22.7531 | 22.6559 | 22.5602 | 22.4660 | 22.3733 | 22.4268 |
| 0.02 | 23.3932 | 23.1758 | 22.9655 | 22.7618 | 22.5645 | 22.3733 | 22.5812 |
| 0.03 | 23.9976 | 23.6394 | 23.2993 | 22.9757 | 22.6674 | 22.3733 | 22.8284 |
| 0.04 | 24.6643 | 24.1412 | 23.6540 | 23.1991 | 22.7732 | 22.3733 | 23.1619 |
| 0.05 | 25.3918 | 24.6772 | 24.0259 | 23.4293 | 22.8804 | 22.3733 | 23.5762 |
| 0.06 | 26.1774 | 25.2430 | 24.4106 | 23.6632 | 22.9877 | 22.3733 | 24.0660 |
| 0.07 | 27.0180 | 25.8337 | 24.8038 | 23.8981 | 23.0937 | 22.3733 | 24.6266 |
| 0.08 | 27.9098 | 26.4440 | 25.2014 | 24.1312 | 23.1973 | 22.3733 | 25.2532 |
| 0.09 | 28.8488 | 27.0689 | 25.5994 | 24.3603 | 23.2976 | 22.3733 | 25.9412 |
| 0.10 | 29.8307 | 27.7033 | 25.9944 | 24.5837 | 23.3940 | 22.3733 | 26.6861 |
| CF | PP | CP | CC | |
|---|---|---|---|---|
| 0 | 3.5160 | 9.8696 | 15.4183 | 22.3735 |
| 0.01 | 3.5336 | 9.8720 | 15.5007 | 22.6079 |
| 0.02 | 3.5514 | 9.8789 | 15.5933 | 22.8628 |
| 0.03 | 3.5691 | 9.8901 | 15.6950 | 23.1355 |
| 0.04 | 3.5869 | 9.9051 | 15.8049 | 23.4228 |
| 0.05 | 3.6047 | 9.9237 | 15.9217 | 23.7212 |
| 0.06 | 3.6225 | 9.9453 | 16.0440 | 24.0272 |
| 0.07 | 3.6402 | 9.9697 | 16.1708 | 24.3370 |
| 0.08 | 3.6578 | 9.9965 | 16.3008 | 24.6473 |
| 0.09 | 3.6753 | 10.0254 | 16.4328 | 24.9549 |
| 0.10 | 3.6927 | 10.0560 | 16.5659 | 25.2573 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vaccaro, M.S.; Pinnola, F.P.; Marotti de Sciarra, F.; Barretta, R. Dynamics of Stress-Driven Two-Phase Elastic Beams. Nanomaterials 2021, 11, 1138. https://doi.org/10.3390/nano11051138
Vaccaro MS, Pinnola FP, Marotti de Sciarra F, Barretta R. Dynamics of Stress-Driven Two-Phase Elastic Beams. Nanomaterials. 2021; 11(5):1138. https://doi.org/10.3390/nano11051138
Chicago/Turabian StyleVaccaro, Marzia Sara, Francesco Paolo Pinnola, Francesco Marotti de Sciarra, and Raffaele Barretta. 2021. "Dynamics of Stress-Driven Two-Phase Elastic Beams" Nanomaterials 11, no. 5: 1138. https://doi.org/10.3390/nano11051138
APA StyleVaccaro, M. S., Pinnola, F. P., Marotti de Sciarra, F., & Barretta, R. (2021). Dynamics of Stress-Driven Two-Phase Elastic Beams. Nanomaterials, 11(5), 1138. https://doi.org/10.3390/nano11051138









