Omnipresence of Weak Antilocalization (WAL) in Bi2Se3 Thin Films: A Review on Its Origin
Abstract
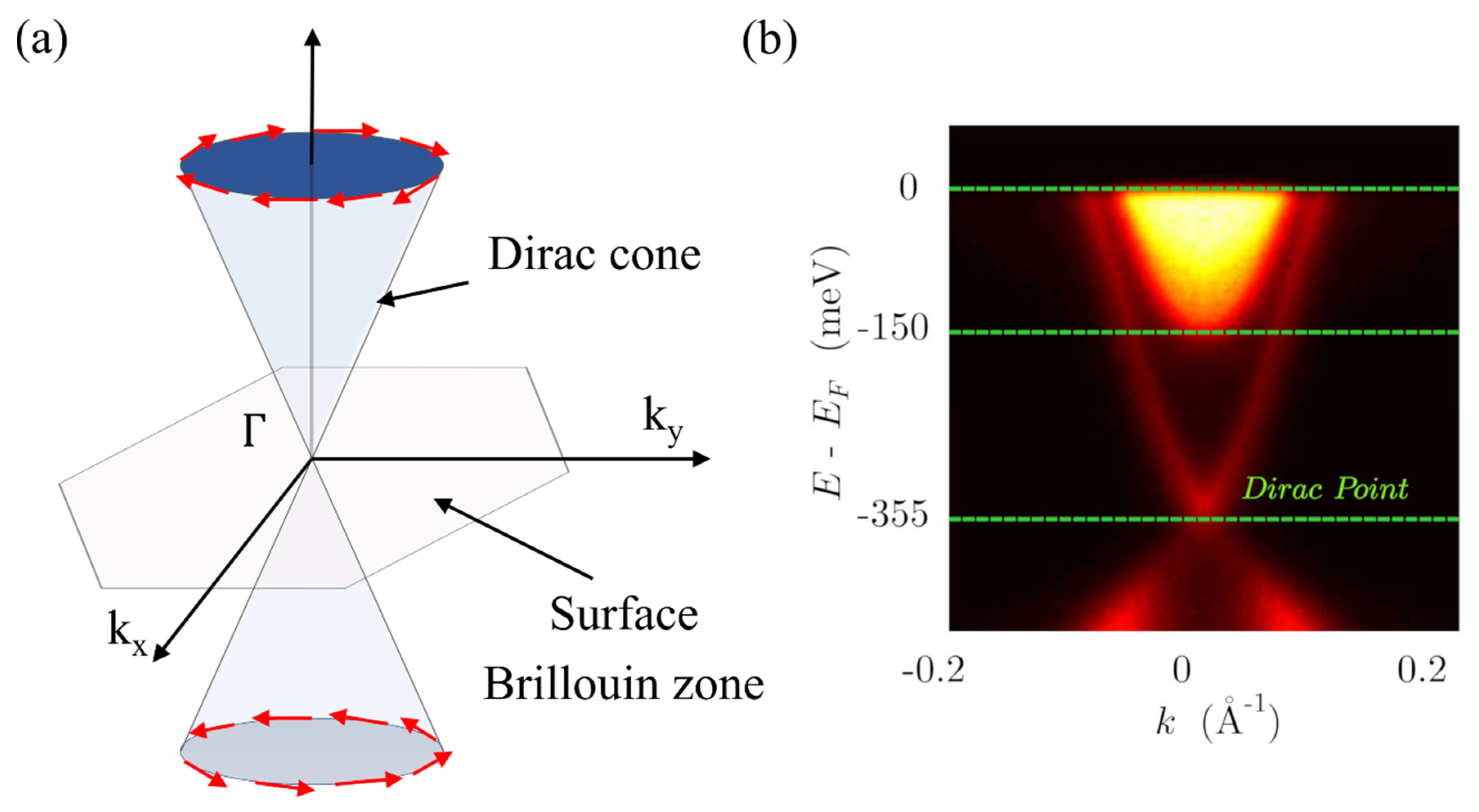
1. Introduction
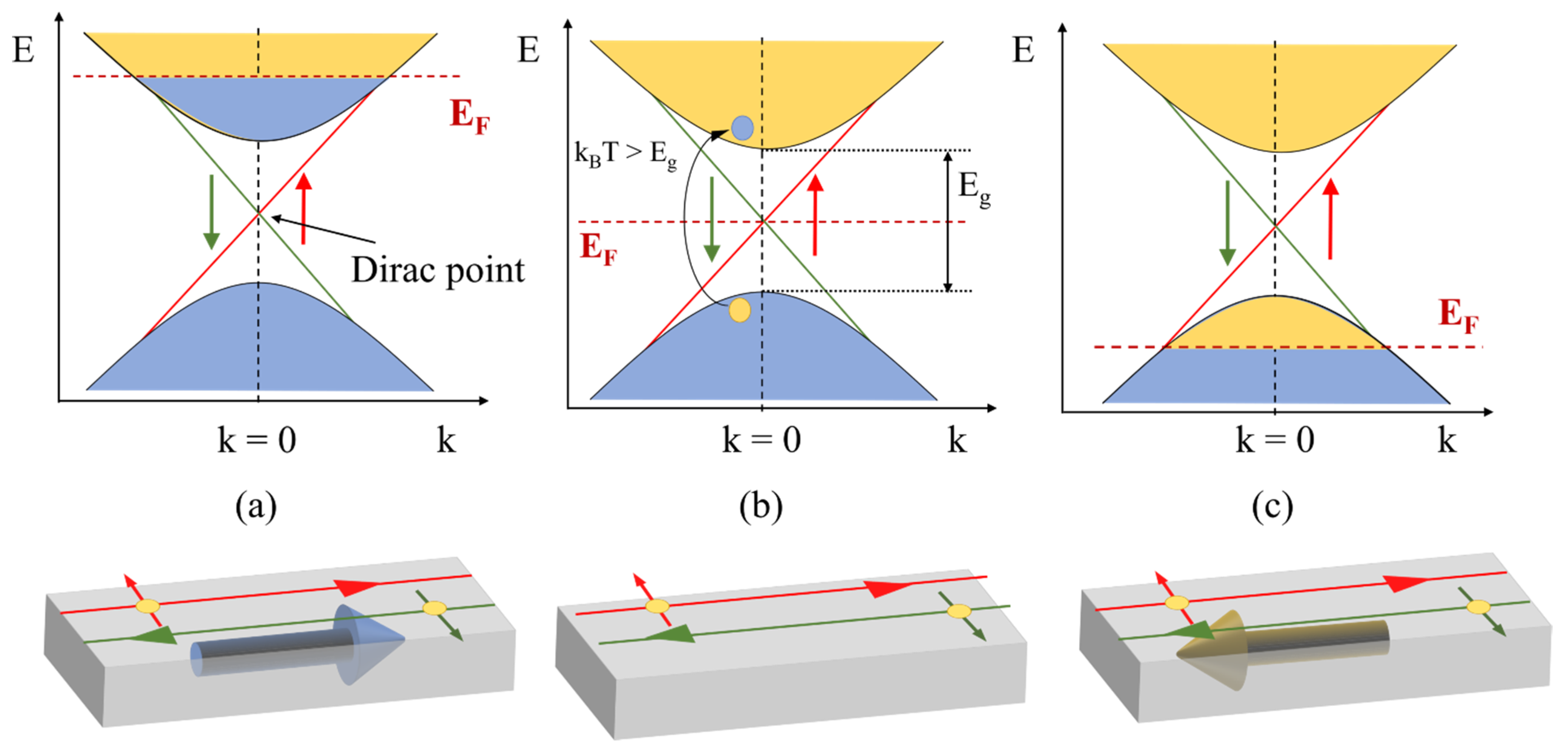
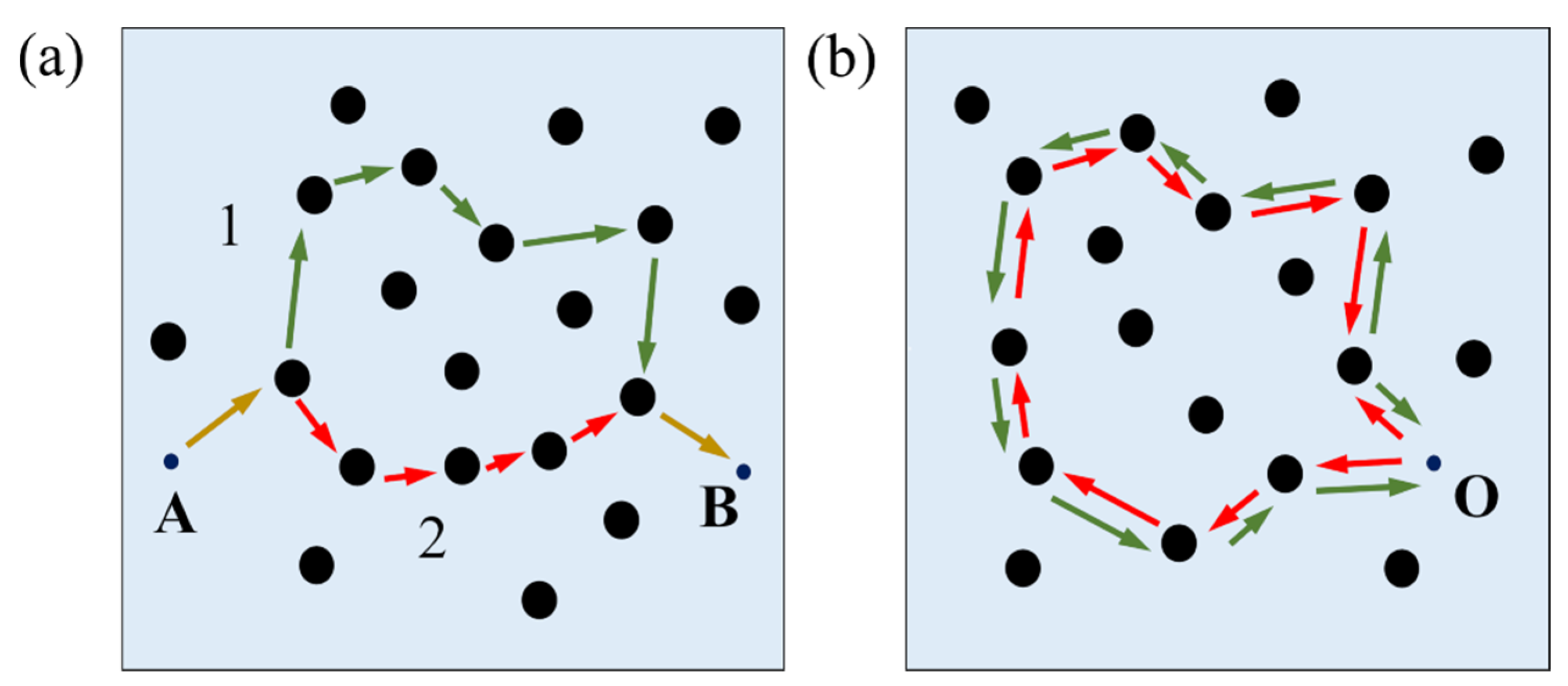
2. Weak-Antilocalization (WAL) Effect
2.1. Electronic Motion in the Quantum Diffusive Regime
2.2. WAL in Relevant Materials
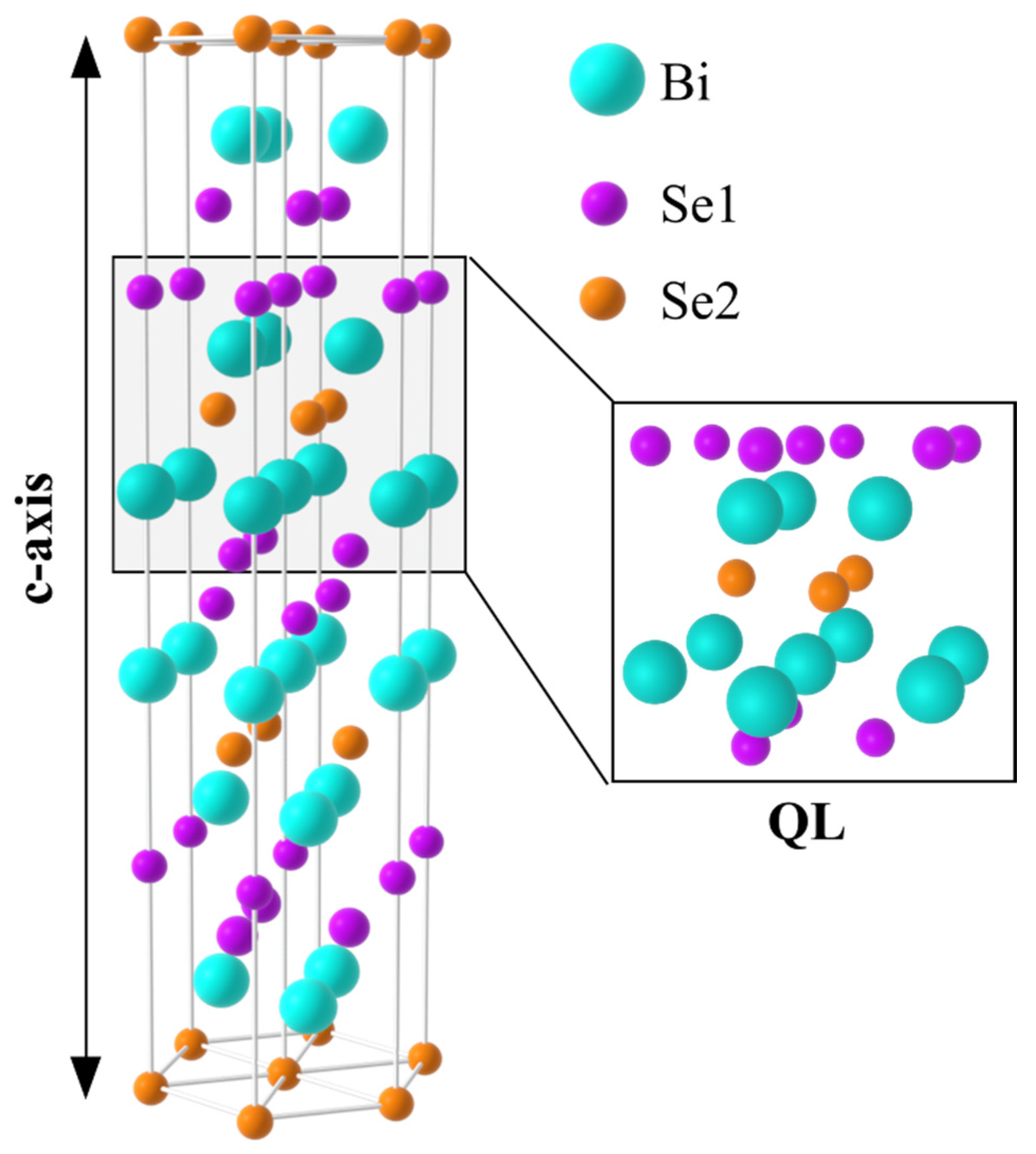
3. WAL in Bi2Se3 Thin Films
3.1. Growth Methods
3.2. Magnetotransport Properties and WAL Effect in Bi2Se3 Thin Films
4. Remarks and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Von Klitzing, K. The quantized Hall effect. Rev. Mod. Phys. 1986, 58, 519–531. [Google Scholar] [CrossRef]
- Moore, J. Topological insulators: The next generation. Nat. Phys. 2009, 5, 378–380. [Google Scholar] [CrossRef]
- Kane, C.L.; Mele, E.J. Quantum Spin hall effect in graphene. Phys. Rev. Lett. 2005, 95, 226801. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045–3067. [Google Scholar] [CrossRef]
- Fu, L.; Kane, C.L. Superconducting proximity effect and Majorana fermions at the surface of a topological insulator. Phys. Rev. Lett. 2008, 100, 096407. [Google Scholar] [CrossRef] [PubMed]
- Pesin, D.; MacDonald, A.H. Spintronics and pseudospintronics in graphene and topological insulators. Nat. Mater. 2012, 11, 409–416. [Google Scholar] [CrossRef] [PubMed]
- Analytis, J.G.; Chu, J.H.; Chen, Y.; Corredor, F.; McDonald, R.D.; Shen, Z.X.; Fisher, I.R. Bulk Fermi surface coexistence with Dirac surface state in Bi2Se3: A comparison of photoemission and Shubnikov-de Haas measurements. Phys. Rev. B Condens. Matter Mater. Phys. 2010, 81, 205407. [Google Scholar] [CrossRef]
- König, M.; Molenkamp, L.W.; Qi, X.; Zhang, S. Quantum Spin Hall Insulator State in HgTe Quantum Wells. Science 2007, 766, 766–771. [Google Scholar] [CrossRef] [PubMed]
- Hsieh, D.; Qian, D.; Wray, L.; Xia, Y.; Hor, Y.S.; Cava, R.J.; Hasan, M.Z. A topological Dirac insulator in a quantum spin Hall phase. Nature 2008, 452, 970–974. [Google Scholar] [CrossRef] [PubMed]
- Xia, Y.; Qian, D.; Hsieh, D.; Wray, L.; Pal, A.; Lin, H.; Bansil, A.; Grauer, D.; Hor, Y.S.; Cava, R.J.; et al. Observation of a large-gap topological-insulator class with a single Dirac cone on the surface. Nat. Phys. 2009, 5, 398–402. [Google Scholar] [CrossRef]
- Hsieh, D.; Xia, Y.; Qian, D.; Wray, L.; Meier, F.; Dil, J.H.; Osterwalder, J.; Patthey, L.; Fedorov, A.V.; Lin, H.; et al. Observation of time-reversal-protected single-dirac-cone topological-insulator states in Bi2Se3 and Sb2Te3. Phys. Rev. Lett. 2009, 103, 146401. [Google Scholar] [CrossRef]
- Chen, J.; Qin, H.J.; Yang, F.; Liu, J.; Guan, T.; Qu, F.M.; Zhang, G.H.; Shi, J.R.; Xie, X.C.; Yang, C.L.; et al. Gate-voltage control of chemical potential and weak antilocalization in Bi2Se3. Phys. Rev. Lett. 2010, 105, 176602. [Google Scholar] [CrossRef]
- Taskin, A.A.; Sasaki, S.; Segawa, K.; Ando, Y. Manifestation of Topological Protection in Transport Properties of Epitaxial Bi2Se3 Thin Films. Phys. Rev. Lett. 2012, 109, 066803. [Google Scholar] [CrossRef] [PubMed]
- Steinberg, H.; Laloë, J.B.; Fatemi, V.; Moodera, J.S.; Jarillo-Herrero, P. Electrically tunable surface-to-bulk coherent coupling in topological insulator thin films. Phys. Rev. B Condens. Matter Mater. Phys. 2011, 84, 233101. [Google Scholar] [CrossRef]
- Xue, L.; Zhou, P.; Zhang, C.X.; He, C.Y.; Hao, G.L.; Sun, L.Z.; Zhong, J.X. First-principles study of native point defects in Bi2Se3. AIP Adv. 2013, 3, 052105. [Google Scholar] [CrossRef]
- Scanlon, D.O.; King, P.D.C.; Singh, R.P.; De La Torre, A.; Walker, S.M.K.; Balakrishnan, G.; Baumberger, F.; Catlow, C.R.A. Controlling bulk conductivity in topological insulators: Key role of anti-site defects. Adv. Mater. 2012, 24, 2154–2158. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Qin, H.; Chen, J.; He, X.; Lu, L.; Li, Y.; Wu, K. Growth of topological insulator Bi2Se3 thin films on SrTiO3 with a large tunability in chemical potential. Adv. Funct. Mater. 2011, 21, 2351–2355. [Google Scholar] [CrossRef]
- Hor, Y.S.; Richardella, A.; Roushan, P.; Xia, Y.; Checkelsky, J.G.; Yazdani, A.; Hasan, M.Z.; Ong, N.P.; Cava, R.J. P -type Bi2Se3 for topological insulator and low-temperature thermoelectric applications. Phys. Rev. B Condens. Matter Mater. Phys. 2009, 79, 2–6. [Google Scholar] [CrossRef]
- Fu, L. Topological crystalline insulators. Phys. Rev. Lett. 2011, 106, 106802. [Google Scholar] [CrossRef] [PubMed]
- Hsieh, T.H.; Lin, H.; Liu, J.; Duan, W.; Bansil, A.; Fu, L. Topological crystalline insulators in the SnTe material class. Nat. Commun. 2012, 3, 1–7. [Google Scholar] [CrossRef]
- Tanaka, Y.; Ren, Z.; Sato, T.; Nakayama, K.; Souma, S.; Takahashi, T.; Segawa, K.; Ando, Y. Experimental realization of a topological crystalline insulator in SnTe. Nat. Phys. 2012, 8, 800–803. [Google Scholar] [CrossRef]
- Xu, S.Y.; Liu, C.; Alidoust, N.; Neupane, M.; Qian, D.; Belopolski, I.; Denlinger, J.D.; Wang, Y.J.; Lin, H.; Wray, L.A.; et al. Observation of a topological crystalline insulator phase and topological phase transition in Pb1-xSnxTe. Nat. Commun. 2012, 3, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Dziawa, P.; Kowalski, B.J.; Dybko, K.; Buczko, R.; Szczerbakow, A.; Szot, M.; Łusakowska, E.; Balasubramanian, T.; Wojek, B.M.; Berntsen, M.H.; et al. Topological crystalline insulator states in Pb1-xSnxSe. Nat. Mater. 2012, 11, 1023–1027. [Google Scholar] [CrossRef]
- Dzero, M.; Sun, K.; Galitski, V.; Coleman, P. Topological Kondo insulators. Phys. Rev. Lett. 2010, 104, 106408. [Google Scholar] [CrossRef] [PubMed]
- Xu, N.; Biswas, P.K.; Dil, J.H.; Dhaka, R.S.; Landolt, G.; Muff, S.; Matt, C.E.; Shi, X.; Plumb, N.C.; Radović, M.; et al. Direct observation of the spin texture in SmB6 as evidence of the topological Kondo insulator. Nat. Commun. 2014, 5, 1–5. [Google Scholar] [CrossRef]
- Liu, Z.K.; Zhou, B.; Zhang, Y.; Wang, Z.J.; Weng, H.M.; Prabhakaran, D.; Mo, S.K.; Shen, Z.X.; Fang, Z.; Dai, X.; et al. Discovery of a three-dimensional topological dirac semimetal, Na3Bi. Science 2014, 343, 864–867. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.Y.; Belopolski, I.; Alidoust, N.; Neupane, M.; Bian, G.; Zhang, C.; Sankar, R.; Chang, G.; Yuan, Z.; Lee, C.C.; et al. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 2015, 349, 613–617. [Google Scholar] [CrossRef] [PubMed]
- Das, A.; Ronen, Y.; Most, Y.; Oreg, Y.; Heiblum, M.; Shtrikman, H. Zero-bias peaks and splitting in an Al-InAs nanowire topological superconductor as a signature of Majorana fermions. Nat. Phys. 2012, 8, 887–895. [Google Scholar] [CrossRef]
- Sasaki, S.; Kriener, M.; Segawa, K.; Yada, K.; Tanaka, Y.; Sato, M.; Ando, Y.; Cu, T. Topological Superconductivity in CuxBi2Se3. Phys. Rev. Lett. 2011, 107, 217001. [Google Scholar] [CrossRef]
- Taskin, A.A.; Sasaki, S.; Segawa, K.; Ando, Y. Achieving surface quantum oscillations in topological insulator thin films of Bi2Se3. Adv. Mater. 2012, 24, 5581–5585. [Google Scholar] [CrossRef]
- Kim, Y.S.; Brahlek, M.; Bansal, N.; Edrey, E.; Kapilevich, G.A.; Iida, K.; Tanimura, M.; Horibe, Y.; Cheong, S.W.; Oh, S. Thickness-dependent bulk properties and weak antilocalization effect in topological insulator Bi2Se3. Phys. Rev. B Condens. Matter Mater. Phys. 2011, 84, 073109. [Google Scholar] [CrossRef]
- Chen, J.; He, X.Y.; Wu, K.H.; Ji, Z.Q.; Lu, L.; Shi, J.R.; Smet, J.H.; Li, Y.Q. Tunable surface conductivity in Bi2Se3 revealed in diffusive electron transport. Phys. Rev. B Condens. Matter Mater. Phys. 2011, 83, 1–5. [Google Scholar] [CrossRef]
- Bigi, C.; Orgiani, P.; Nardi, A.; Troglia, A.; Fujii, J.; Panaccione, G.; Vobornik, I.; Rossi, G. Robustness of topological states in Bi2Se3 thin film grown by Pulsed Laser Deposition on (001)-oriented SrTiO3 perovskite. Appl. Surf. Sci. 2019, 473, 190–193. [Google Scholar] [CrossRef]
- Lee, Y.F.; Punugupati, S.; Wu, F.; Jin, Z.; Narayan, J.; Schwartz, J. Evidence for topological surface states in epitaxial Bi2Se3 thin film grown by pulsed laser deposition through magneto-transport measurements. Curr. Opin. Solid State Mater. Sci. 2014, 18, 279–285. [Google Scholar] [CrossRef]
- Berry, M. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. London. A. Math. Phys. Sci. 1984, 392, 45–47. [Google Scholar] [CrossRef]
- Bergmann, G. Weak localization in thin films: A time-of-flight experiment with conduction electrons. Phys. Rep. 1986, 107, 1–58. [Google Scholar] [CrossRef]
- Sangiao, S.; Marcano, N.; Fan, J.; Morellón, L.; Ibarra, M.R.; De Teresa, J.M. Quantitative analysis of the weak anti-localization effect in ultrathin Bi films. Epl 2011, 95, 37002. [Google Scholar] [CrossRef]
- Hasan, M. Berry’s phase and quantization in topological insulators. Physics 2010, 3, 62. [Google Scholar] [CrossRef]
- Hikami, S.; Larkin, A.I.; Nagaoka, Y. Spin-Orbit Interaction and Magnetoresistance in the Two Dimensional Random System. Prog. Theor. Phys. 1980, 63, 707–710. [Google Scholar] [CrossRef]
- Brahlek, M.; Koirala, N.; Salehi, M.; Bansal, N.; Oh, S. Emergence of decoupled surface transport channels in bulk insulating Bi2Se3 thin films. Phys. Rev. Lett. 2014, 113, 026801. [Google Scholar] [CrossRef] [PubMed]
- Altshuler, B.L.; Aronov, A.G.; Khmelnitsky, D.E. Effects of electron-electron collisions with small energy transfers on quantum localization. J. Phys. C Solid State Phys. 1982, 15, 7367–7386. [Google Scholar] [CrossRef]
- Jing, Y.; Huang, S.; Zhang, K.; Wu, J.; Guo, Y.; Peng, H.; Liu, Z.; Xu, H.Q. Weak antilocalization and electron–electron interaction in coupled multiple-channel transport in a Bi2Se3 thin film. Nanoscale 2016, 18, 1879–1885. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; He, K.; Chang, C.Z.; Song, C.L.; Wang, L.L.; Chen, X.; Jia, J.F.; Fang, Z.; Dai, X.; Shan, W.Y.; et al. Crossover of the three-dimensional topological insulator Bi2Se3 to the two-dimensional limit. Nat. Phys. 2010, 6, 584–588. [Google Scholar] [CrossRef]
- Liu, Y.H.; Chong, C.W.; Jheng, J.L.; Huang, S.Y.; Huang, J.C.A.; Li, Z.; Qiu, H.; Huang, S.M.; Marchenkov, V.V. Gate-tunable coherent transport in Se-capped Bi2Se3 grown on amorphous SiO2/Si. Appl. Phys. Lett. 2015, 107, 012106. [Google Scholar] [CrossRef]
- Assaf, B.A.; Katmis, F.; Wei, P.; Satpati, B.; Zhang, Z.; Bennett, S.P.; Harris, V.G.; Moodera, J.S.; Heiman, D. Quantum coherent transport in SnTe topological crystalline insulator thin films. Appl. Phys. Lett. 2014, 105, 102108. [Google Scholar] [CrossRef]
- Lu, H.Z.; Shen, S.Q. Weak antilocalization and localization in disordered and interacting Weyl semimetals. Phys. Rev. B Condens. Matter Mater. Phys. 2015, 92, 1–13. [Google Scholar] [CrossRef]
- Lu, H.Z.; Shen, S.Q. Quantum transport in topological semimetals under magnetic fields. Front. Phys. 2017, 12, 1–18. [Google Scholar] [CrossRef]
- Zhao, B.; Cheng, P.; Pan, H.; Zhang, S.; Wang, B.; Wang, G.; Xiu, F.; Song, F. Weak antilocalization in Cd3As2 thin films. Sci. Rep. 2016, 6, 1–7. [Google Scholar] [CrossRef]
- Xiong, J.; Kushwaha, S.K.; Liang, T.; Krizan, J.W.; Hirschberger, M.; Wang, W.; Cava, R.J.; Ong, N.P. Evidence for the chiral anomaly in the Dirac semimetal Na3Bi. Science 2015, 350, 413–416. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Zhao, L.; Long, Y.; Wang, P.; Chen, D.; Yang, Z.; Liang, H.; Xue, M.; Weng, H.; Fang, Z.; et al. Observation of the chiral-anomaly-induced negative magnetoresistance: In 3D Weyl semimetal TaAs. Phys. Rev. X 2015, 5, 031023. [Google Scholar] [CrossRef]
- Liu, M.; Chang, C.Z.; Zhang, Z.; Zhang, Y.; Ruan, W.; He, K.; Wang, L.L.; Chen, X.; Jia, J.F.; Zhang, S.C.; et al. Electron interaction-driven insulating ground state in Bi2Se3 topological insulators in the two-dimensional limit. Phys. Rev. B Condens. Matter Mater. Phys. 2011, 83, 165440. [Google Scholar] [CrossRef]
- Li, H.D.; Wang, Z.Y.; Kan, X.; Guo, X.; He, H.T.; Wang, Z.; Wang, J.N.; Wong, T.L.; Wang, N.; Xie, M.H. The van der Waals epitaxy of Bi2Se3 on the vicinal Si(111) surface: An approach for preparing high-quality thin films of a topological insulator. New J. Phys. 2010, 12, 103038. [Google Scholar] [CrossRef]
- Le, P.H.; Wu, K.H.; Luo, C.W.; Leu, J. Growth and characterization of topological insulator Bi2Se3 thin films on SrTiO3 using pulsed laser deposition. Thin Solid Films 2013, 534, 659–665. [Google Scholar] [CrossRef]
- Yang, L.; Wang, Z.; Li, M.; Gao, X.P.A.; Zhang, Z. The dimensional crossover of quantum transport properties in few-layered Bi2Se3 thin films. Nanoscale Adv. 2019, 1, 2303–2310. [Google Scholar] [CrossRef]
- Brom, J.E.; Ke, Y.; Du, R.; Won, D.; Weng, X.; Andre, K.; Gagnon, J.C.; Mohney, S.E.; Li, Q.; Chen, K.; et al. Structural and electrical properties of epitaxial Bi2Se3 thin films grown by hybrid physical-chemical vapor deposition. Appl. Phys. Lett. 2012, 100, 162110. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, Y.S.; Lee, C.C.; Wu, J.K.; Lee, H.Y.; Te Liang, C.; Chang, Y.H. A study on the epitaxial Bi2Se3 thin film grown by vapor phase epitaxy. AIP Adv. 2016, 6, 065218. [Google Scholar] [CrossRef]
- Wang, W.J.; Gao, K.H.; Li, Z.Q. Thickness-dependent transport channels in topological insulator Bi2Se3 thin films grown by magnetron sputtering. Sci. Rep. 2016, 6, 1–9. [Google Scholar] [CrossRef]
- Richardella, A.; Zhang, D.M.; Lee, J.S.; Koser, A.; Rench, D.W.; Yeats, A.L.; Buckley, B.B.; Awschalom, D.D.; Samarth, N. Coherent heteroepitaxy of Bi2Se3 on GaAs (111)B. Appl. Phys. Lett. 2010, 97, 262104. [Google Scholar] [CrossRef]
- Bansal, N.; Kim, Y.S.; Edrey, E.; Brahlek, M.; Horibe, Y.; Iida, K.; Tanimura, M.; Li, G.H.; Feng, T.; Lee, H.D.; et al. Epitaxial growth of topological insulator Bi2Se3 film on Si(111) with atomically sharp interface. Thin Solid Films 2011, 520, 224–229. [Google Scholar] [CrossRef]
- Kim, N.; Lee, P.; Kim, Y.; Kim, J.S.; Kim, Y.; Noh, D.Y.; Yu, S.U.; Chung, J.; Kim, K.S. Persistent topological surface state at the interface of Bi2Se3 film grown on patterned graphene. ACS Nano 2014, 8, 1154–1160. [Google Scholar] [CrossRef]
- Kou, X.F.; He, L.; Xiu, F.X.; Lang, M.R.; Liao, Z.M.; Wang, Y.; Fedorov, A.V.; Yu, X.X.; Tang, J.S.; Huang, G.; et al. Epitaxial growth of high mobility Bi2Se3 thin films on CdS. Appl. Phys. Lett. 2011, 98, 2011–2014. [Google Scholar] [CrossRef]
- He, L.; Xiu, F.; Yu, X.; Teague, M.; Fan, Y.; Kou, X. Surface-Dominated Conduction in a 6 nm thick Bi2Se3 Thin Film. Nano Lett. 2012, 12, 1486–1490. [Google Scholar] [CrossRef] [PubMed]
- Guo, X.; Xu, Z.J.; Liu, H.C.; Zhao, B.; Dai, X.Q.; He, H.T.; Wang, J.N.; Liu, H.J.; Ho, W.K.; Xie, M.H. Single domain Bi2Se3 films grown on InP(111)A by molecular-beam epitaxy. Appl. Phys. Lett. 2013, 102, 151604. [Google Scholar] [CrossRef]
- Bansal, N.; Kim, Y.S.; Brahlek, M.; Edrey, E.; Oh, S. Thickness-independent transport channels in topological insulator Bi2Se3 thin films. Phys. Rev. Lett. 2012, 109, 116804. [Google Scholar] [CrossRef]
- Brahlek, M.; Koirala, N.; Bansal, N.; Oh, S. Transport properties of topological insulators: Band bending, bulk metal-to-insulator transition, and weak anti-localization. Solid State Commun. 2015, 215, 54–62. [Google Scholar] [CrossRef]
- Orgiani, P.; Bigi, C.; Kumar Das, P.; Fujii, J.; Ciancio, R.; Gobaut, B.; Galdi, A.; Sacco, C.; Maritato, L.; Torelli, P.; et al. Structural and electronic properties of Bi2Se3 topological insulator thin films grown by pulsed laser deposition. Appl. Phys. Lett. 2017, 110, 171601. [Google Scholar] [CrossRef]
- Zhang, M.; Wei, Z.; Jin, R.; Ji, Y.; Yan, Y.; Pu, X.; Yang, X.; Zhao, Y. Electrical transport properties and morphology of topological insulator Bi2Se3 thin films with different thickness prepared by magnetron sputtering. Thin Solid Films 2016, 603, 289–293. [Google Scholar] [CrossRef]
- Oveshnikov, L.N.; Prudkoglyad, V.A.; Nekhaeva, E.I.; Kuntsevich, A.Y.; Selivanov, Y.G.; Chizhevskii, E.G.; Aronzon, B.A. Magnetotransport in thin epitaxial Bi2Se3 films. JETP Lett. 2016, 104, 629–634. [Google Scholar] [CrossRef]
- Dey, R.; Roy, A.; Pramanik, T.; Guchhait, S.; Sonde, S.; Rai, A.; Register, L.F.; Banerjee, S.K. Localization and interaction effects of epitaxial Bi2Se3 bulk states in two-dimensional limit. J. Appl. Phys. 2016, 120, 164301. [Google Scholar] [CrossRef]
- You, A.; Be, M.A.Y.; In, I. Magnetotransport in Bi2Se3 thin films epitaxially grown on Ge (111). AIP Adv. 2018, 8, 115125. [Google Scholar] [CrossRef]
- Han, W.; Otani, Y.C.; Maekawa, S. Quantum materials for spin and charge conversion. npj Quantum Mater. 2018, 3, 1–16. [Google Scholar] [CrossRef]
- Wang, H.; Kally, J.; Lee, J.S.; Liu, T.; Chang, H.; Hickey, D.R.; Mkhoyan, K.A.; Wu, M.; Richardella, A.; Samarth, N. Surface-State-Dominated Spin-Charge Current Conversion in Topological-Insulator-Ferromagnetic-Insulator Heterostructures. Phys. Rev. Lett. 2016, 117, 076601. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Liu, C.; Xu, J.; Yang, F.; Miao, L.; Yao, M.; Gao, C.L.; Shen, C.; Ma, X.; Chen, X.; et al. The coexistence of superconductivity and topological order in the Bi2Se3 thin films. Science 2012, 336, 52–55. [Google Scholar] [CrossRef]
- Peng, H.; Lai, K.; Kong, D.; Meister, S.; Chen, Y.; Qi, X.L.; Zhang, S.C.; Shen, Z.X.; Cui, Y. Aharonov-Bohm interference in topological insulator nanoribbons. Nat. Mater. 2010, 9, 225–229. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; Qu, F.; Shen, J.; Ding, Y.; Chen, J.; Ji, Z.; Liu, G.; Fan, J.; Yang, C.; Fu, L.; et al. Proximity-effect-induced superconducting phase in the topological insulator Bi2Se3. Phys. Rev. B Condens. Matter Mater. Phys. 2012, 86, 134504. [Google Scholar] [CrossRef]
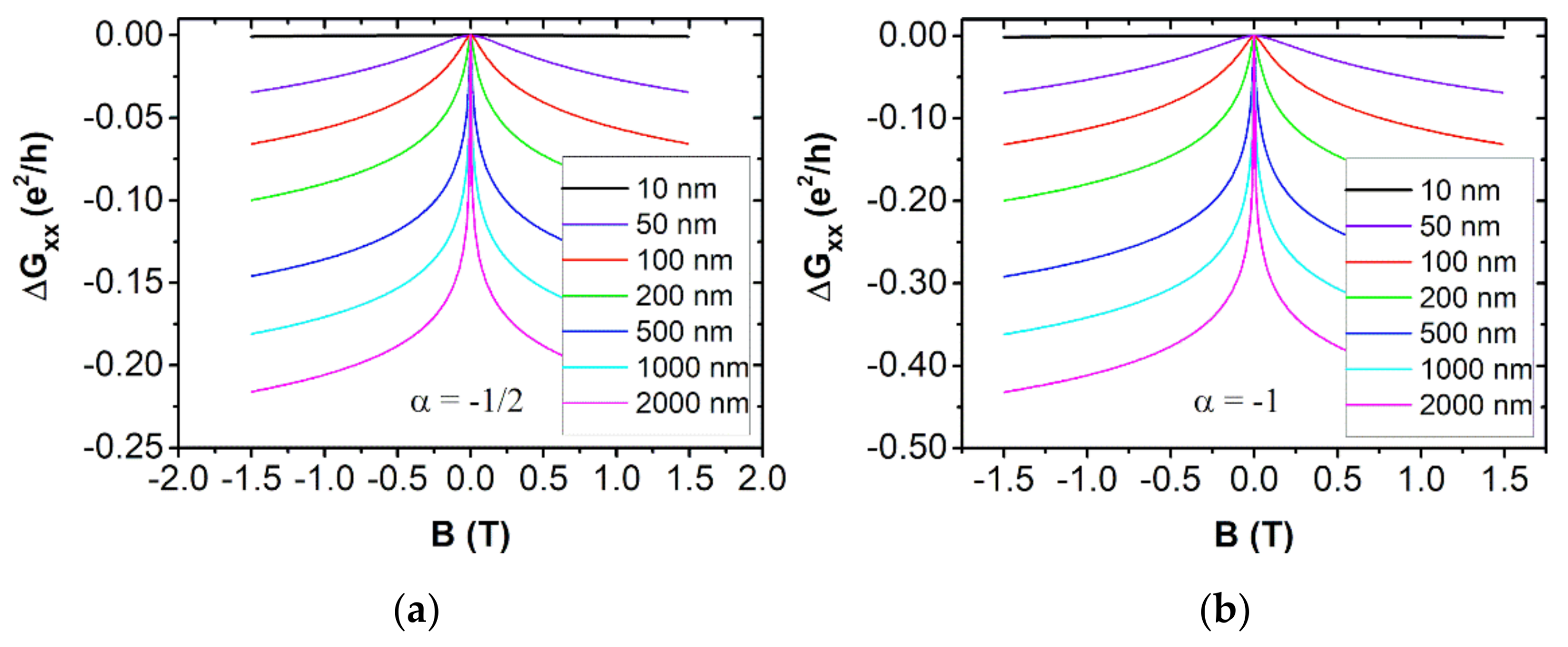
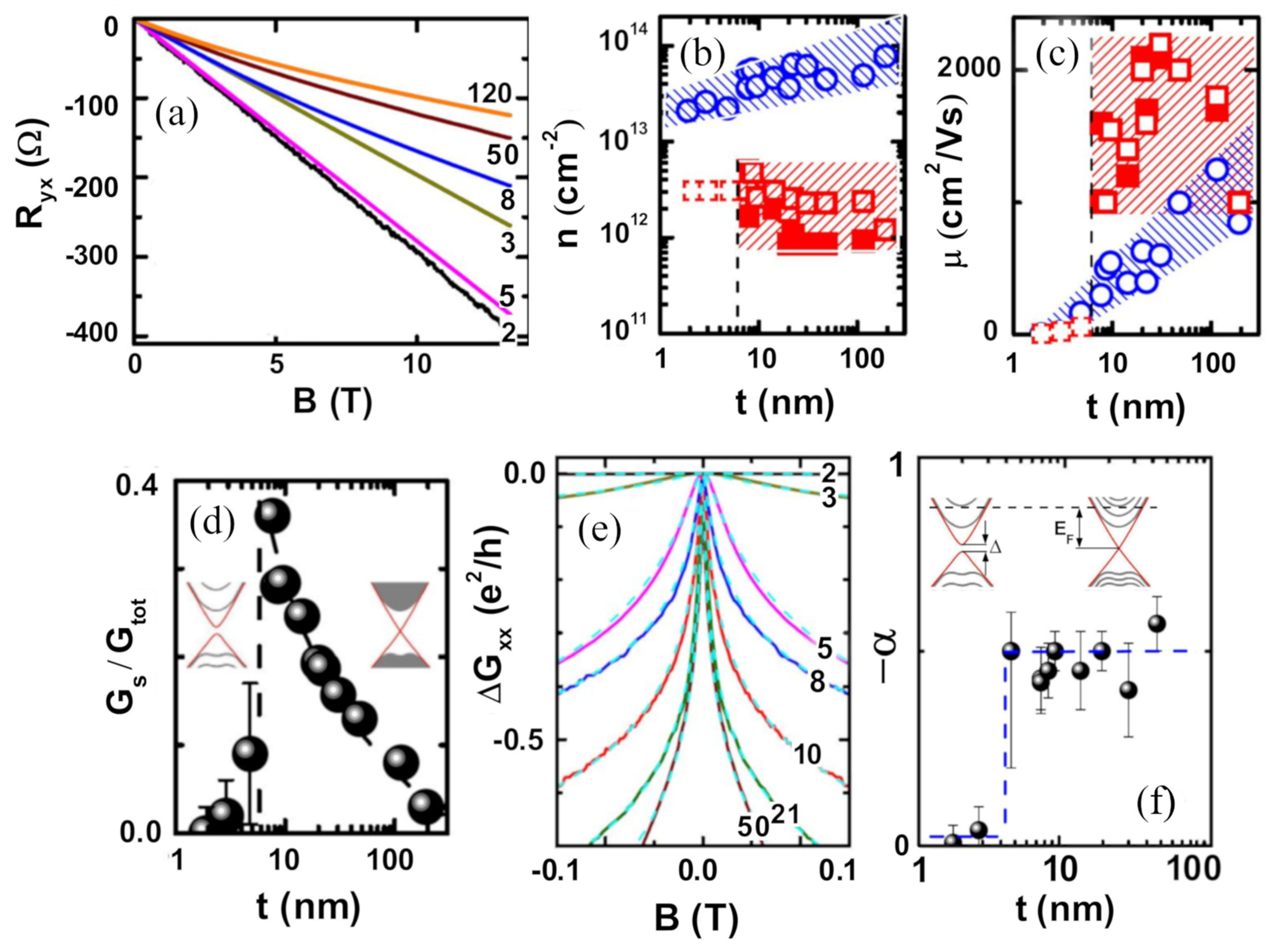



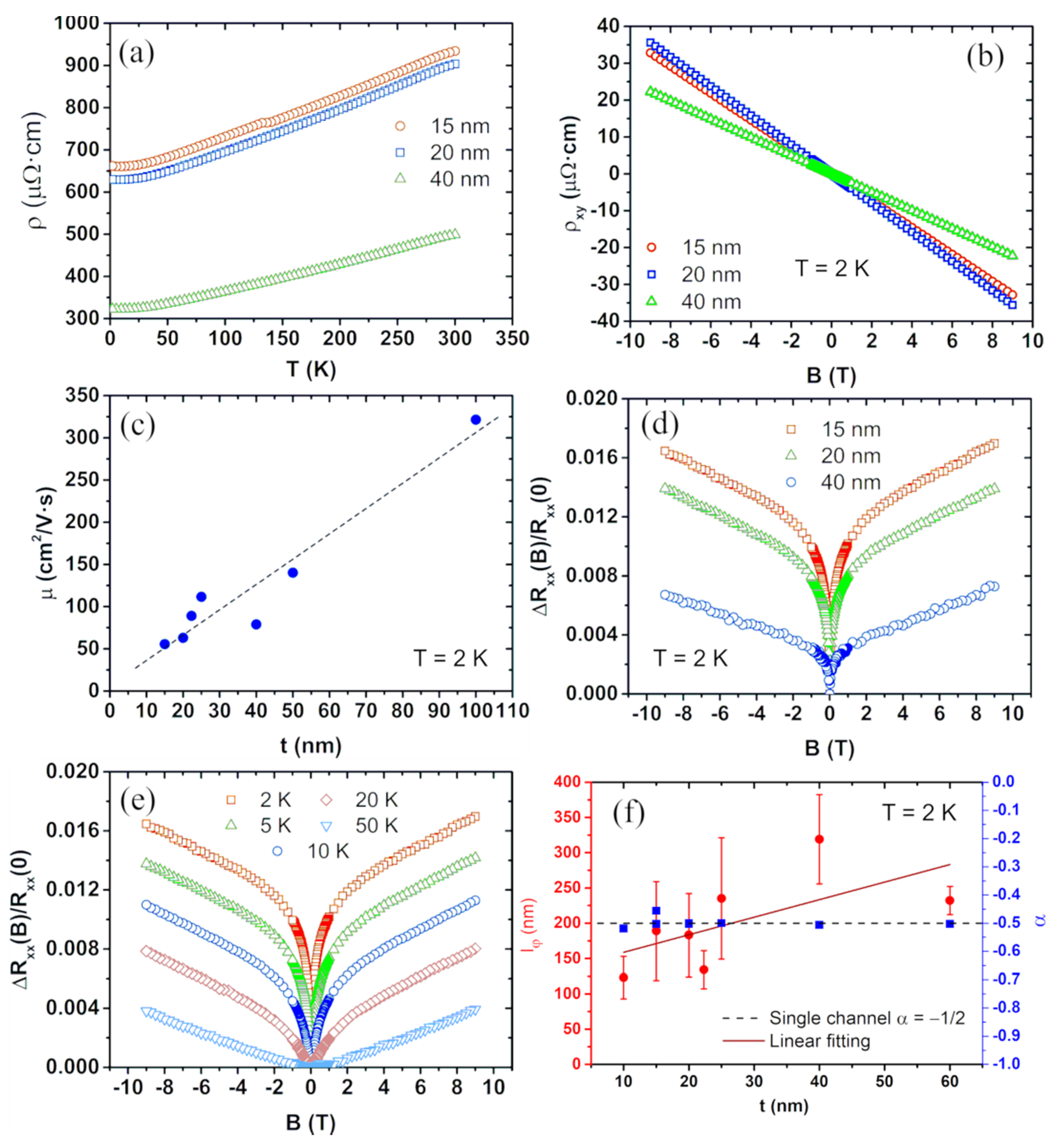
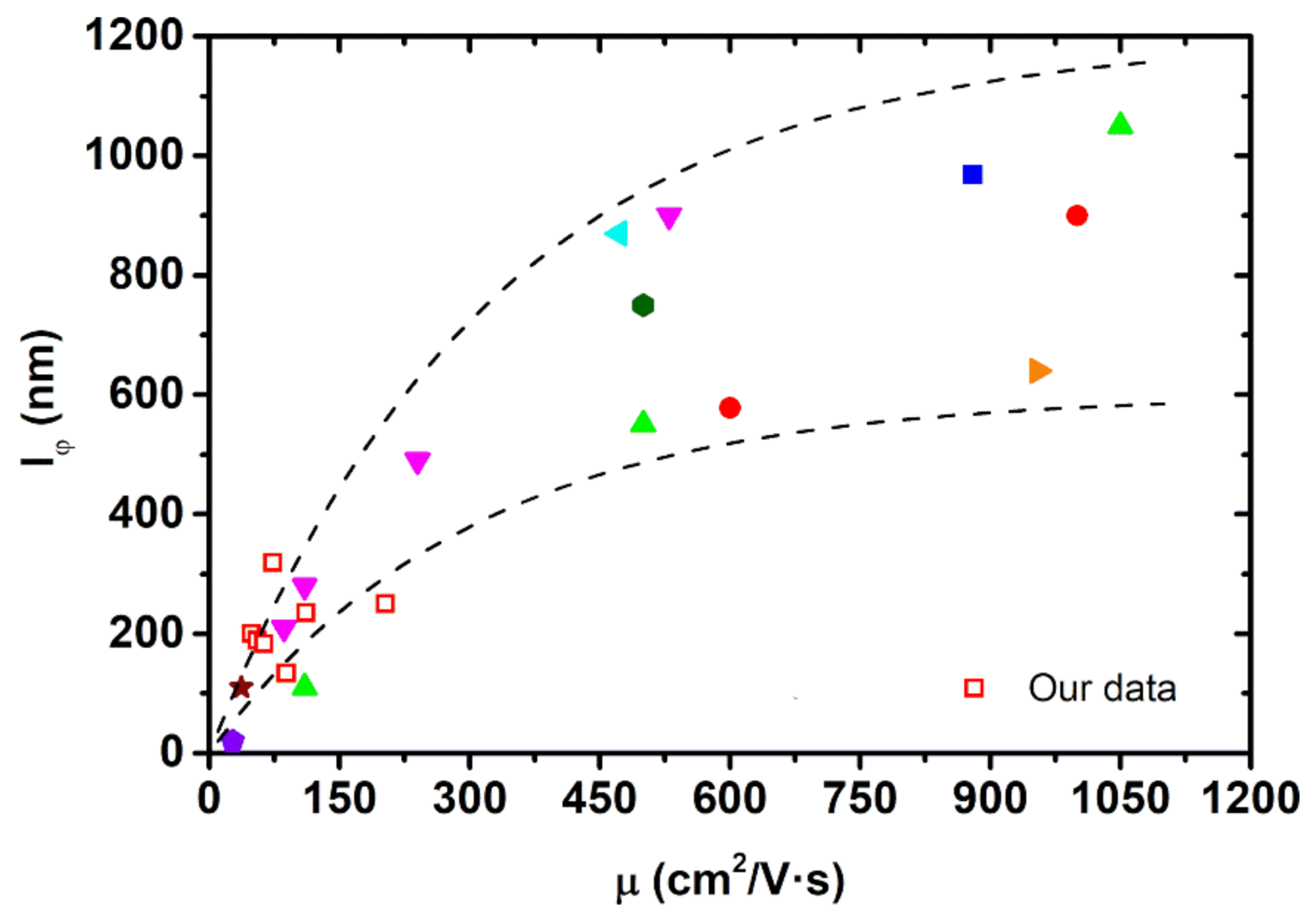
| Reference | t (nm) | n2D | n | μ | T | ||
|---|---|---|---|---|---|---|---|
| [13] | 2–50 | - | 4 | 100–1200 | 1.6 | 100–1000 | −0.5 |
| [14] | 20 | - | - | - | 0.3–10 | 80–300 | −1~−0.5 |
| [30] | ≈38 | 1 | 390–880 | 1.8 | 306–968 | −0.52 | |
| [31] | 1–100 | - | 0.1–6 | 70–1150 | 1.5 | 150–1000 | −0.6~0.5 |
| [32] | 5–20 | 0.8–8.6 | - | 20–1000 | 1.2 | 143–∞ | −0.5 |
| [42] | 10 | - | 6 | 472 | 0.4–10 | 150–870 | −0.6 |
| [44] | 7 | 1.5 | - | - | 2.5 | 55–90 | −0.6~−0.2 |
| [51] | 1–6 | 3.5 | - | 31–350 | 1.5 | 75–200 | −0.6~−0.3 |
| [54] | 6–22 | - | 3.5–6.5 | 80–530 | 2 | 200–900 | −0.55~−0.35 |
| [56] | 30 | - | 1.1 | 954 | 2 | 640 | −0.56 |
| [57] | 9–54 | ~100 | - | - | 2–9 | 10–159 | −1.08~0.16 |
| [64] | 10–245 | 3 | - | 500 | 1.5 | 750 | −0.6 |
| [67] | 30–300 | 0.81–3.25 | - | - | 10 | 318–879 | −0.72~−0.34 |
| [68] | 9.8–23 | 0.3 | - | - | 0.3–8 | 300–800 | −0.4 |
| [69] | 5 | - | 3 | 27 | 2–20 | 8–20 | −0.5 |
| [70] | 12 | - | 4.6 | 37 | 1.6–6 | 65–110 | −0.7~−0.6 |
| Our data | 15–60 | 7–50 | 7–50 | 50–150 | 2 | 120–325 | ~−0.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gracia-Abad, R.; Sangiao, S.; Bigi, C.; Kumar Chaluvadi, S.; Orgiani, P.; De Teresa, J.M. Omnipresence of Weak Antilocalization (WAL) in Bi2Se3 Thin Films: A Review on Its Origin. Nanomaterials 2021, 11, 1077. https://doi.org/10.3390/nano11051077
Gracia-Abad R, Sangiao S, Bigi C, Kumar Chaluvadi S, Orgiani P, De Teresa JM. Omnipresence of Weak Antilocalization (WAL) in Bi2Se3 Thin Films: A Review on Its Origin. Nanomaterials. 2021; 11(5):1077. https://doi.org/10.3390/nano11051077
Chicago/Turabian StyleGracia-Abad, Rubén, Soraya Sangiao, Chiara Bigi, Sandeep Kumar Chaluvadi, Pasquale Orgiani, and José María De Teresa. 2021. "Omnipresence of Weak Antilocalization (WAL) in Bi2Se3 Thin Films: A Review on Its Origin" Nanomaterials 11, no. 5: 1077. https://doi.org/10.3390/nano11051077
APA StyleGracia-Abad, R., Sangiao, S., Bigi, C., Kumar Chaluvadi, S., Orgiani, P., & De Teresa, J. M. (2021). Omnipresence of Weak Antilocalization (WAL) in Bi2Se3 Thin Films: A Review on Its Origin. Nanomaterials, 11(5), 1077. https://doi.org/10.3390/nano11051077










