Homogeneous and Multiphase Analysis of Nanofluids Containing Nonspherical MWCNT and GNP Nanoparticles Considering the Influence of Interfacial Layering
Abstract
1. Introduction
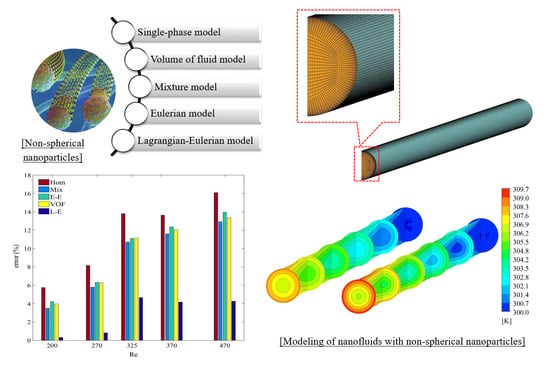
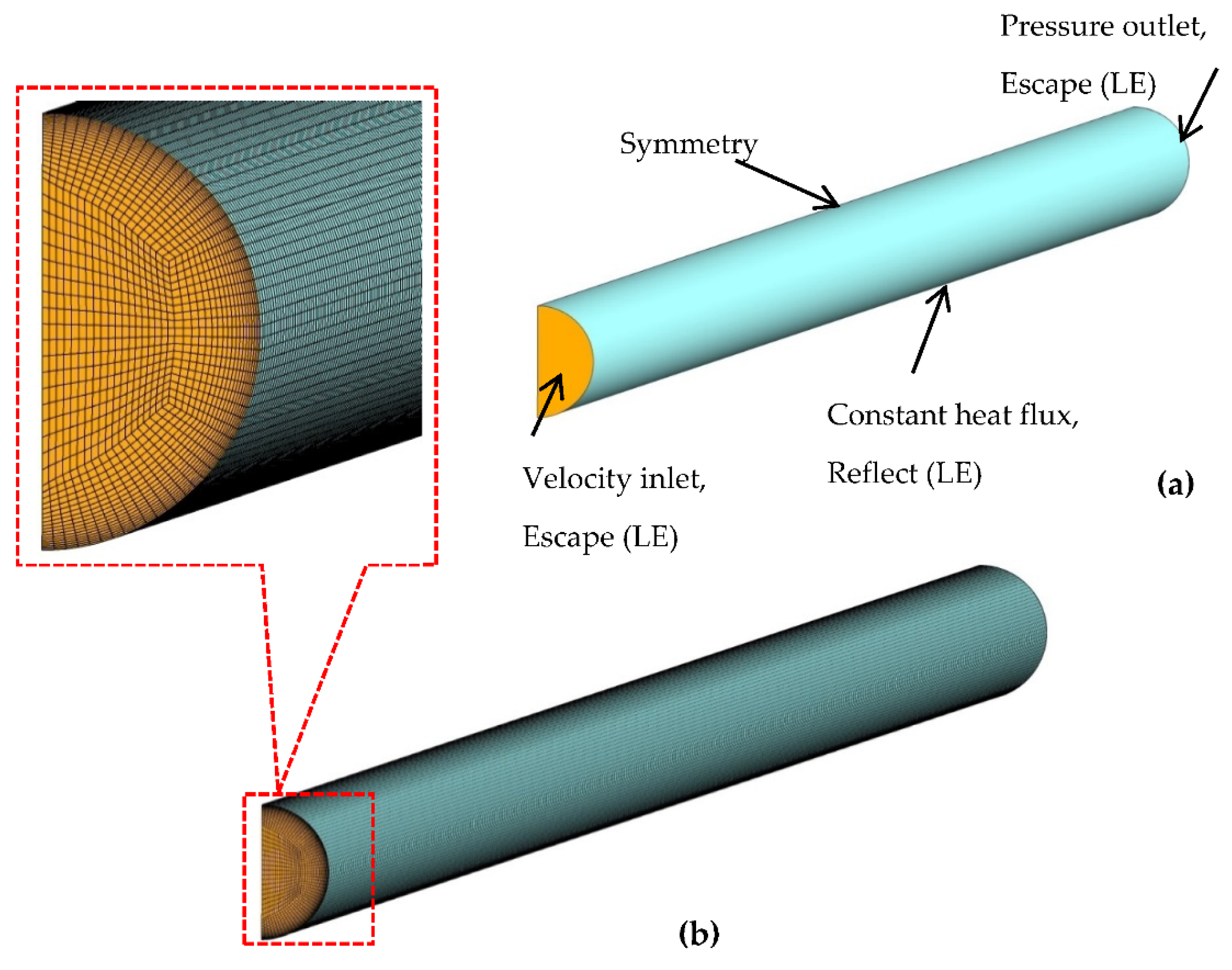
2. Problem Description
3. Mathematical Formulation
3.1. Single-Phase Model
3.2. Eulerian–Eulerian Model
3.2.1. Mixture Model
3.2.2. Volume of Fluid Model
3.2.3. Eulerian Model
3.3. Lagrangian–Eulerian Model
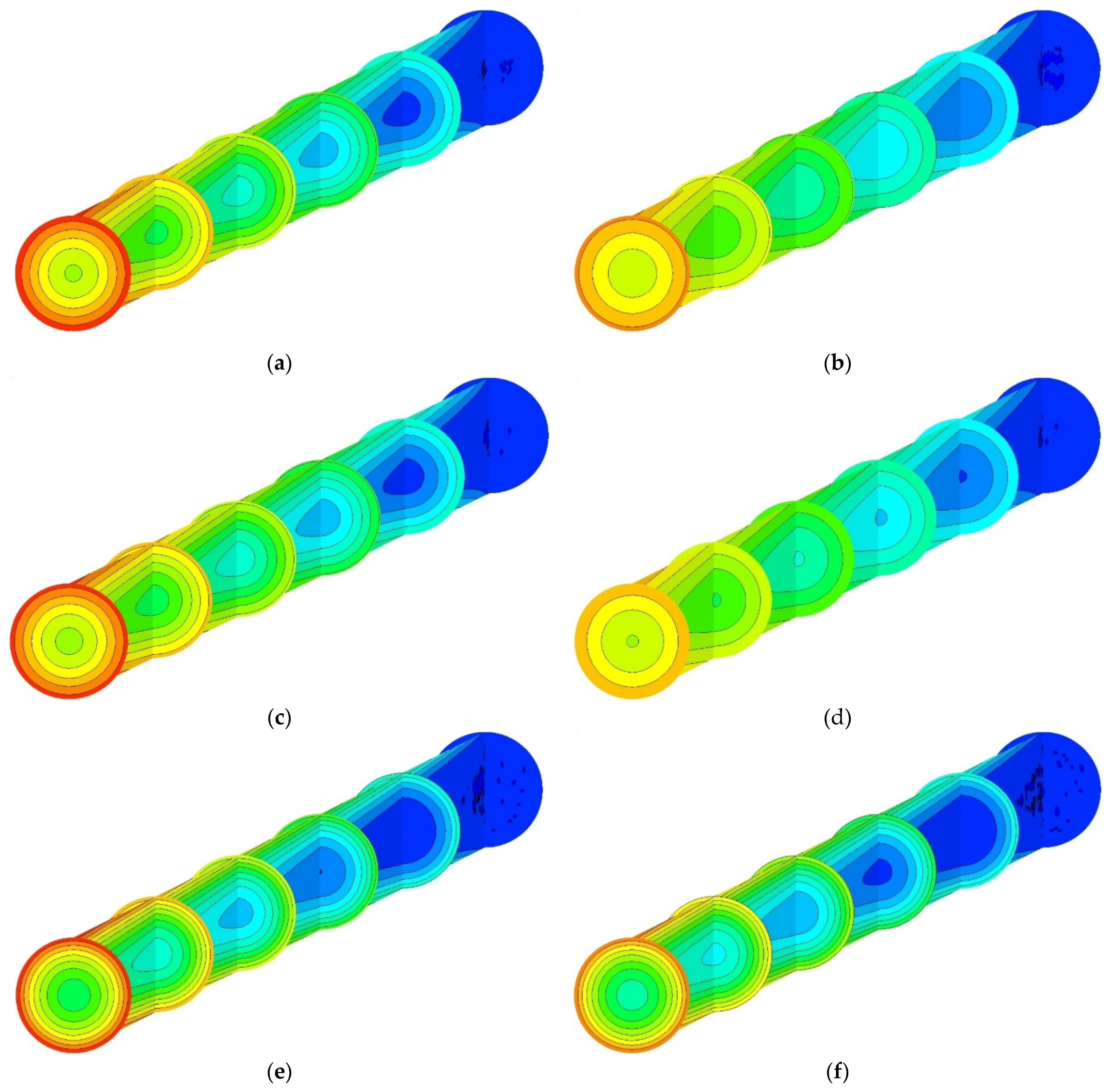
4. Numerical Details and Grid Independency
5. Results and Discussion
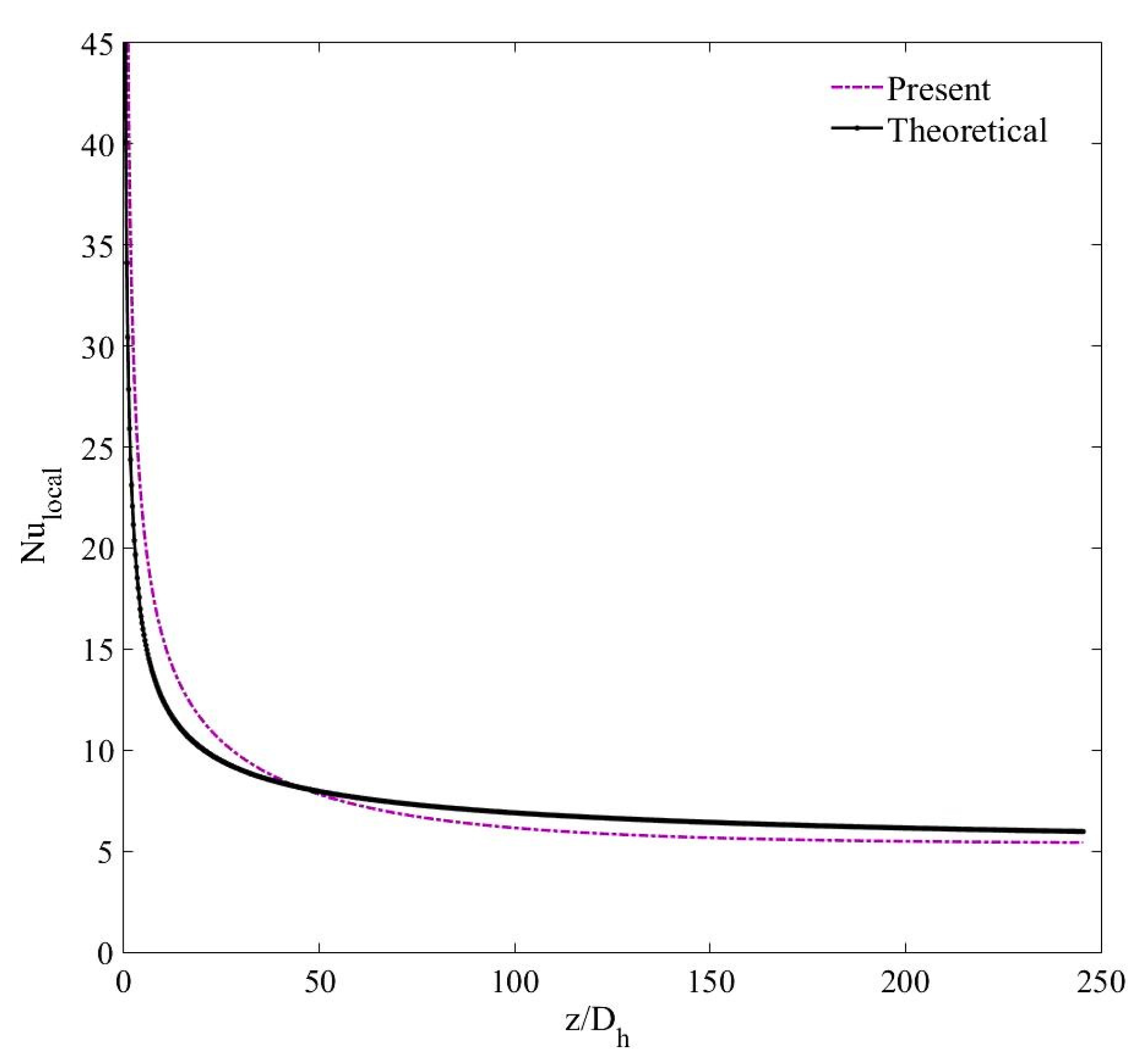
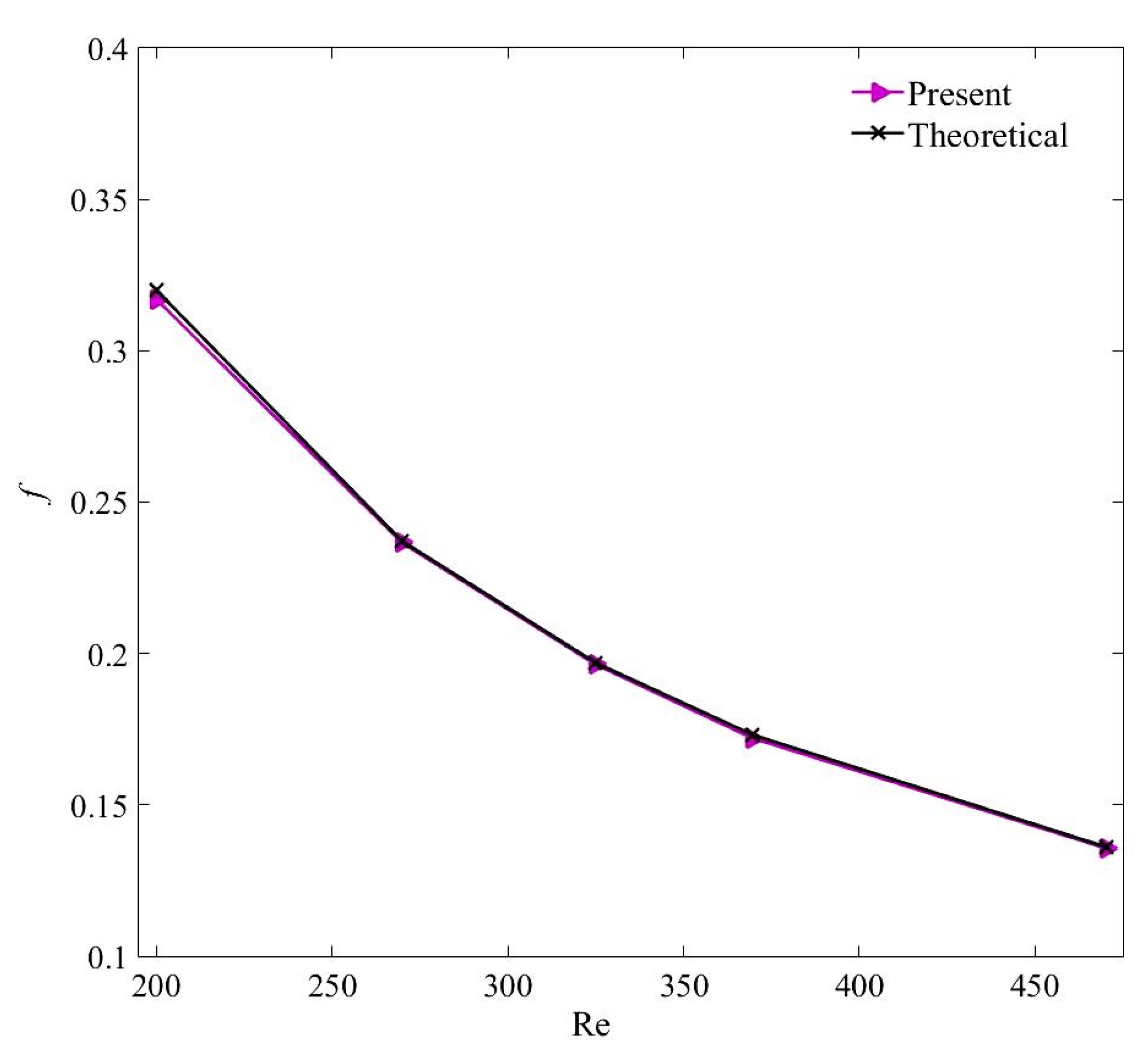
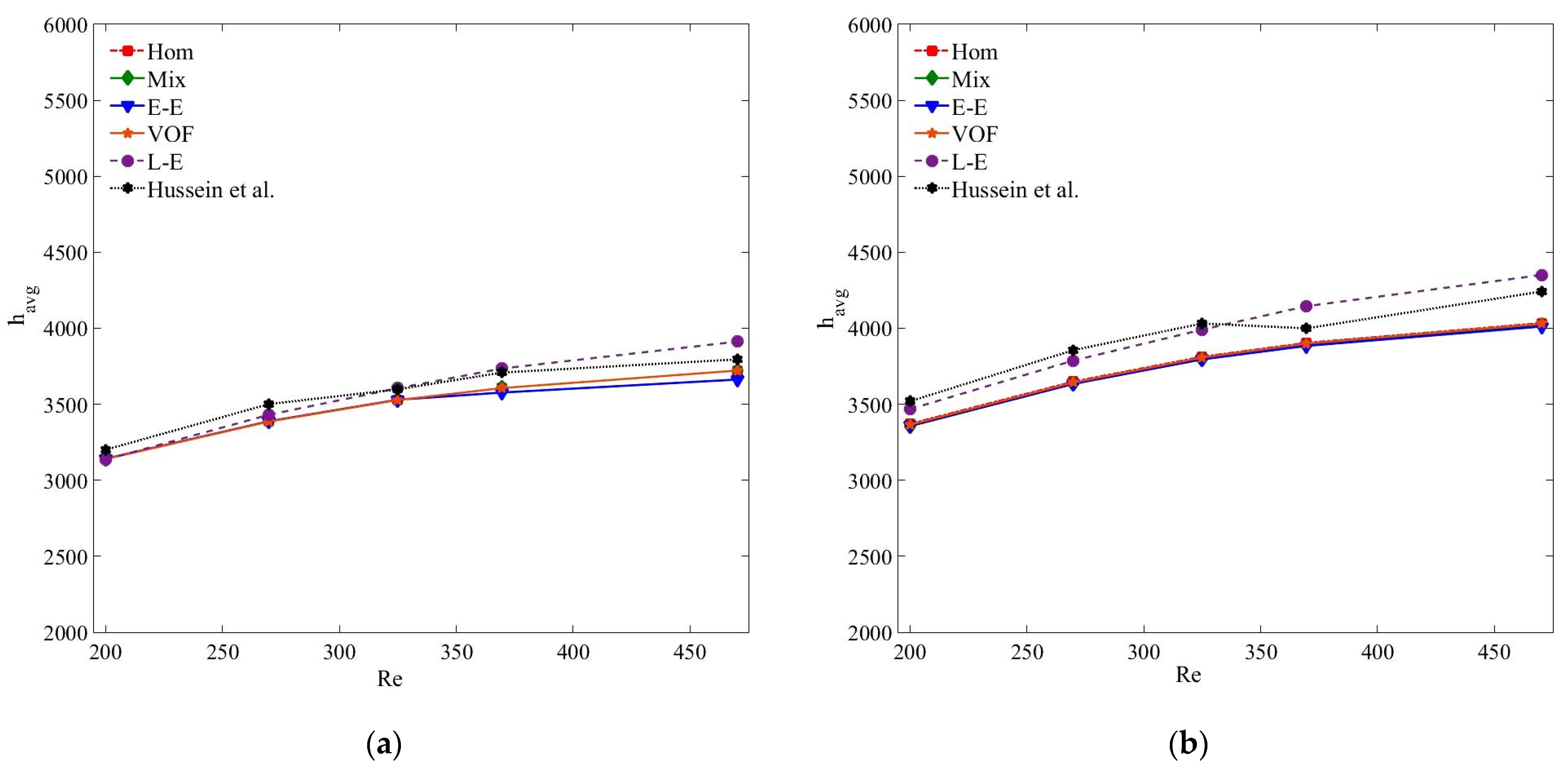
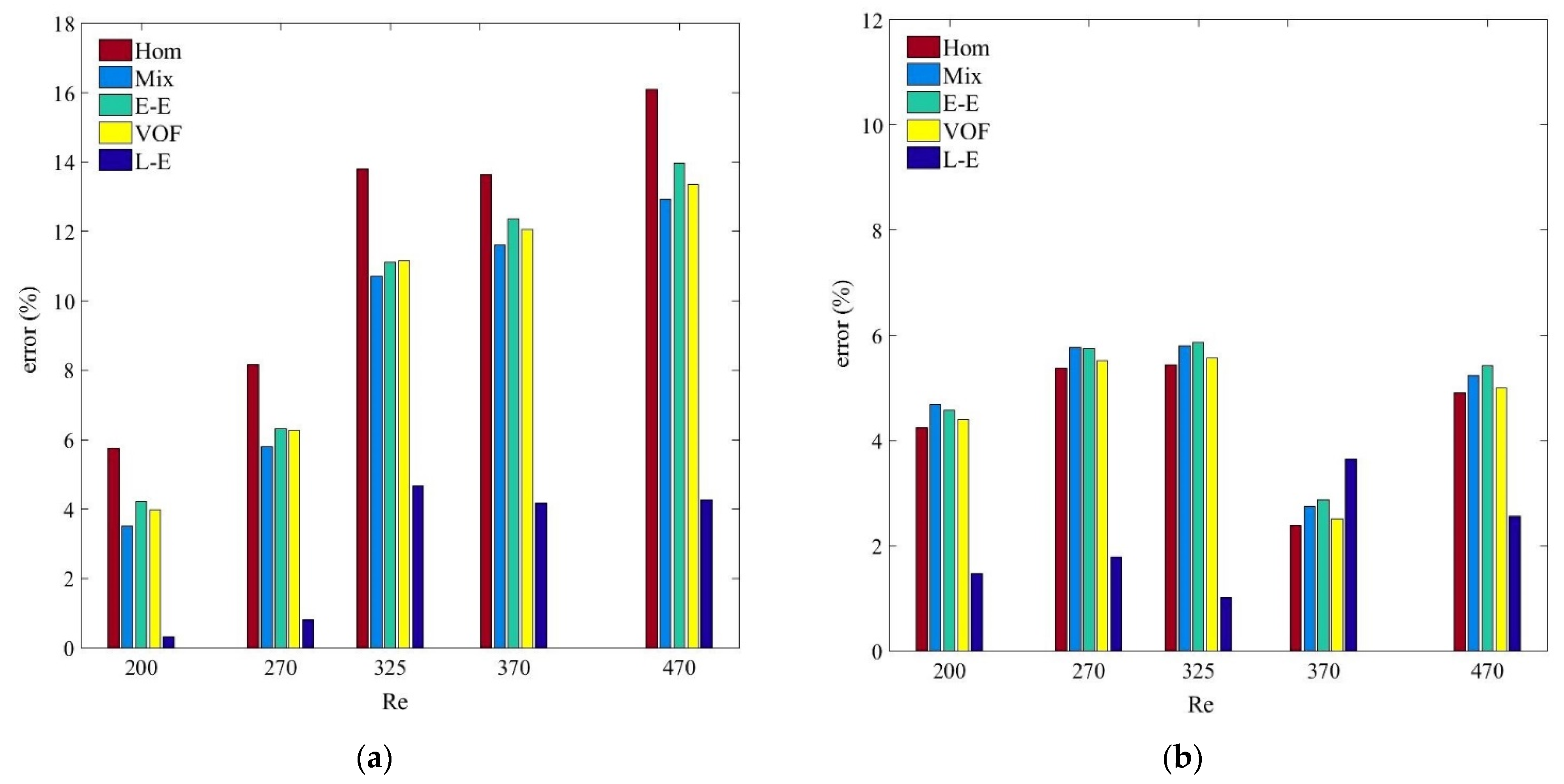
5.1. Validation of the Homogenous Model
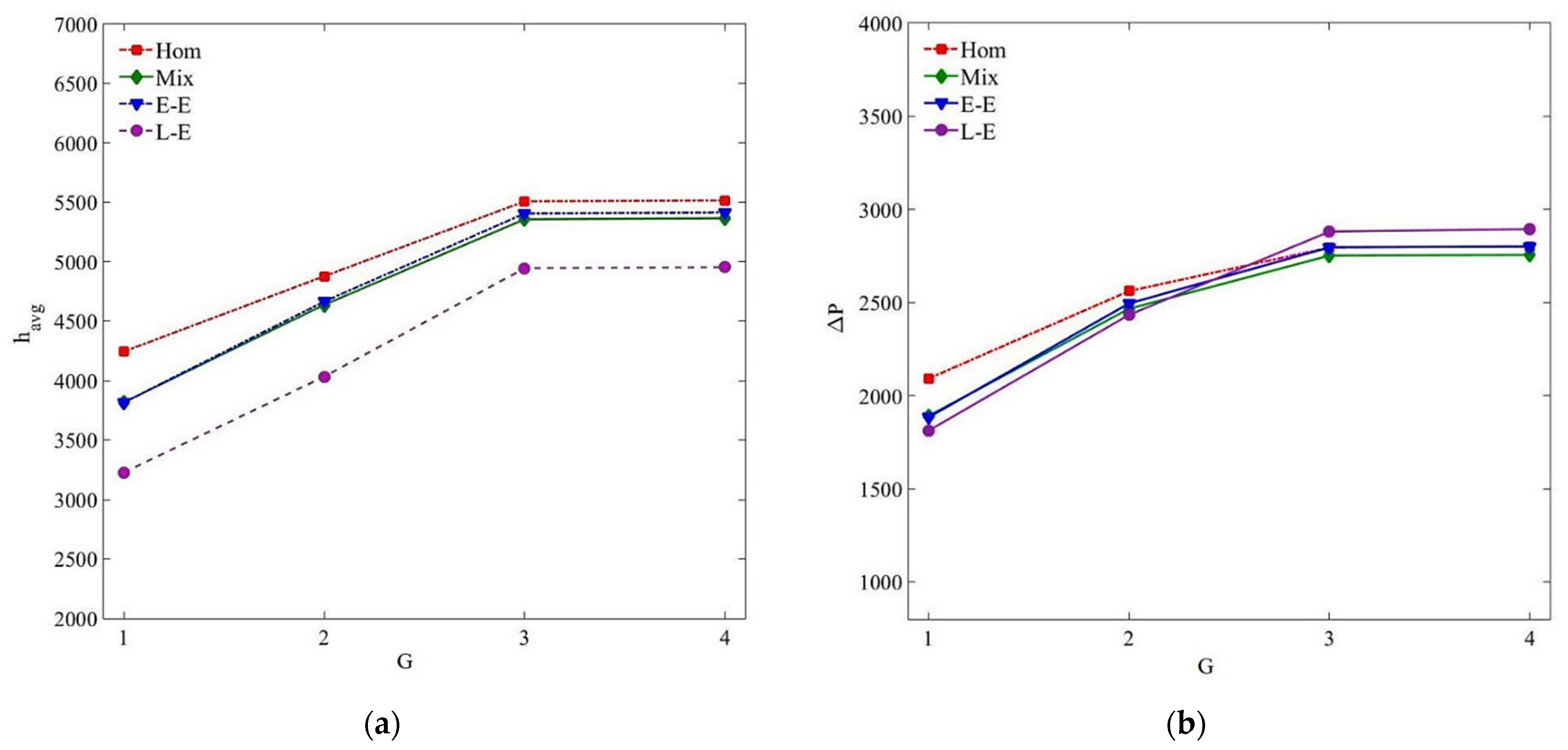
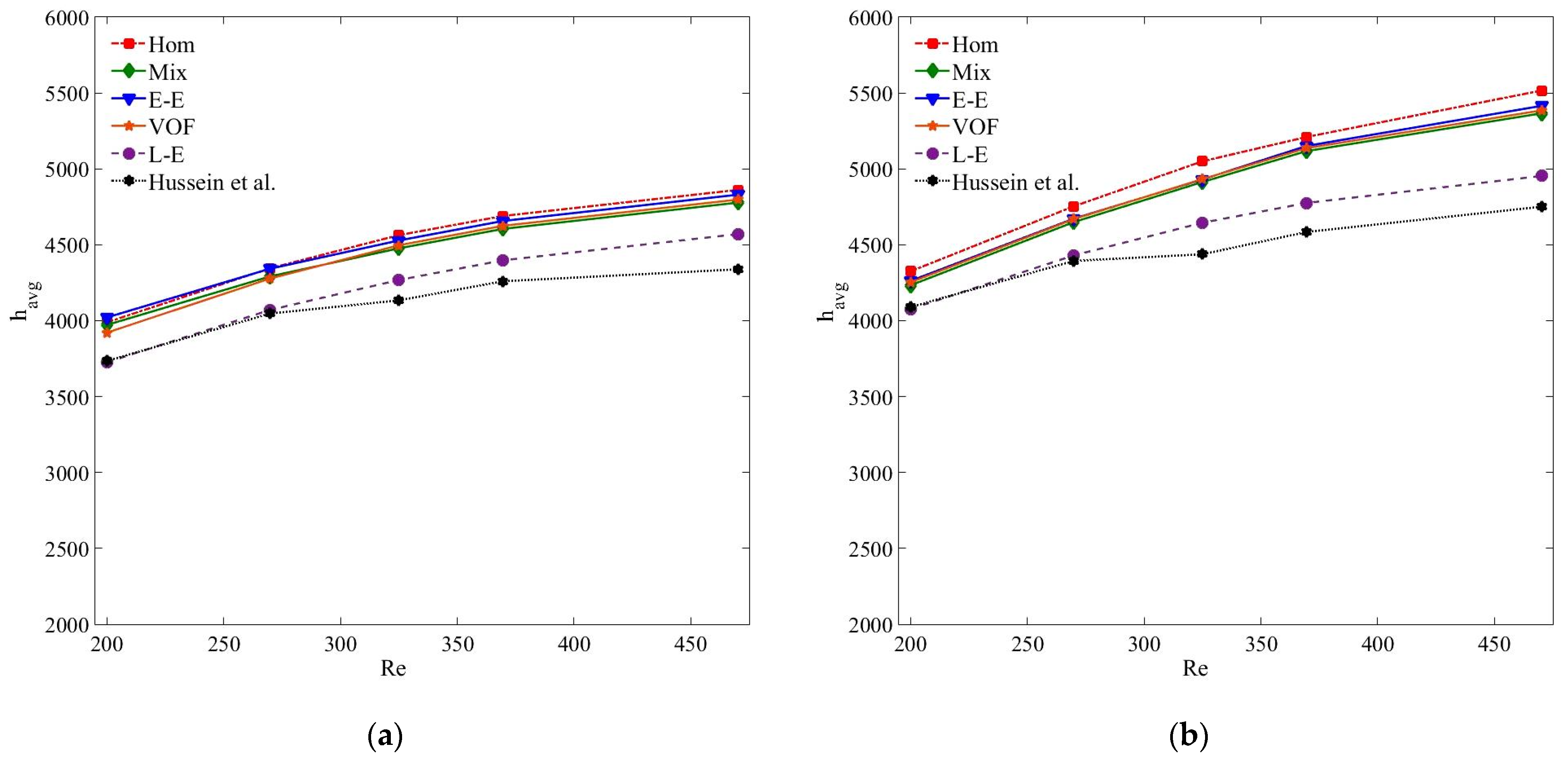
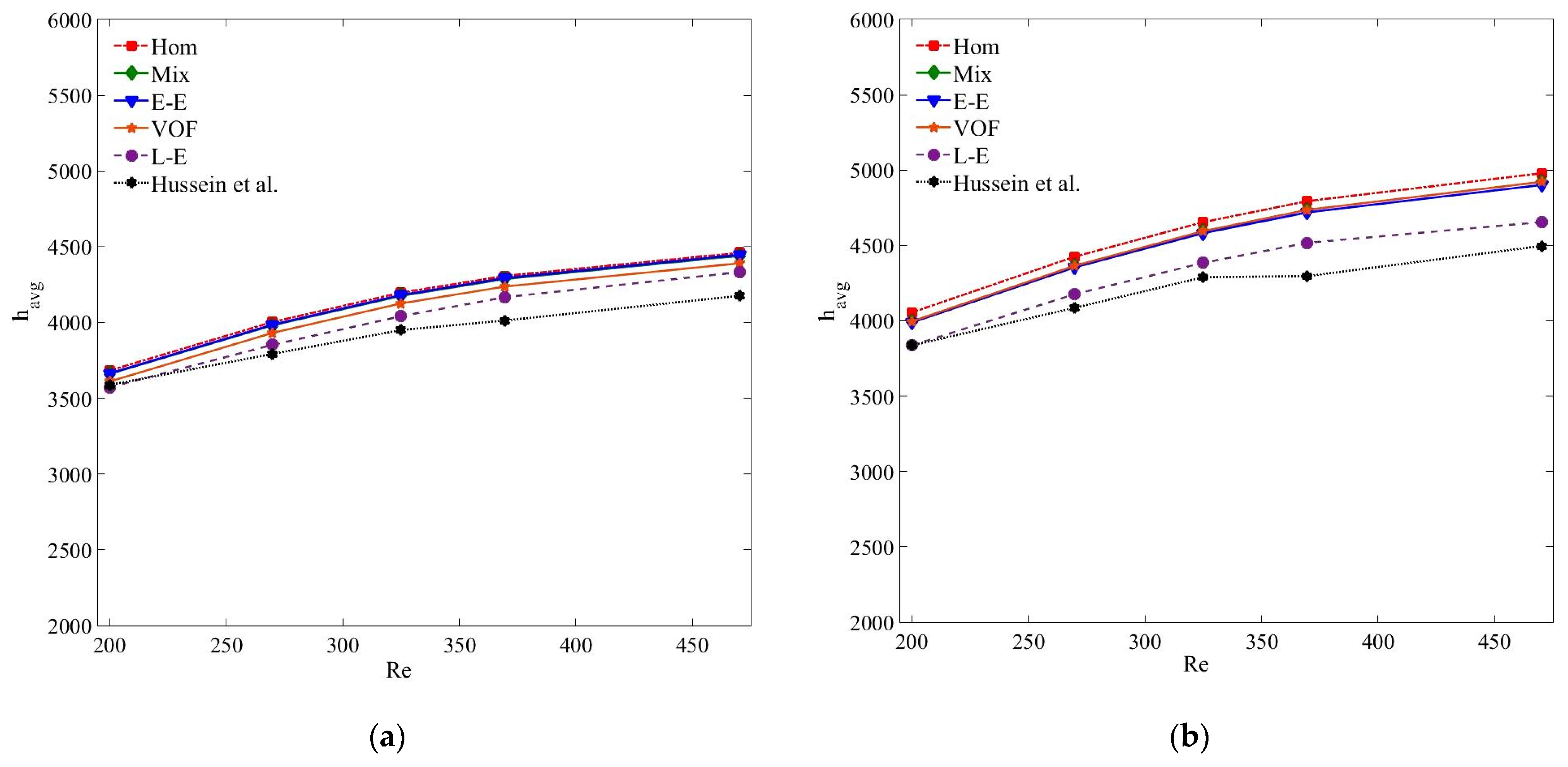
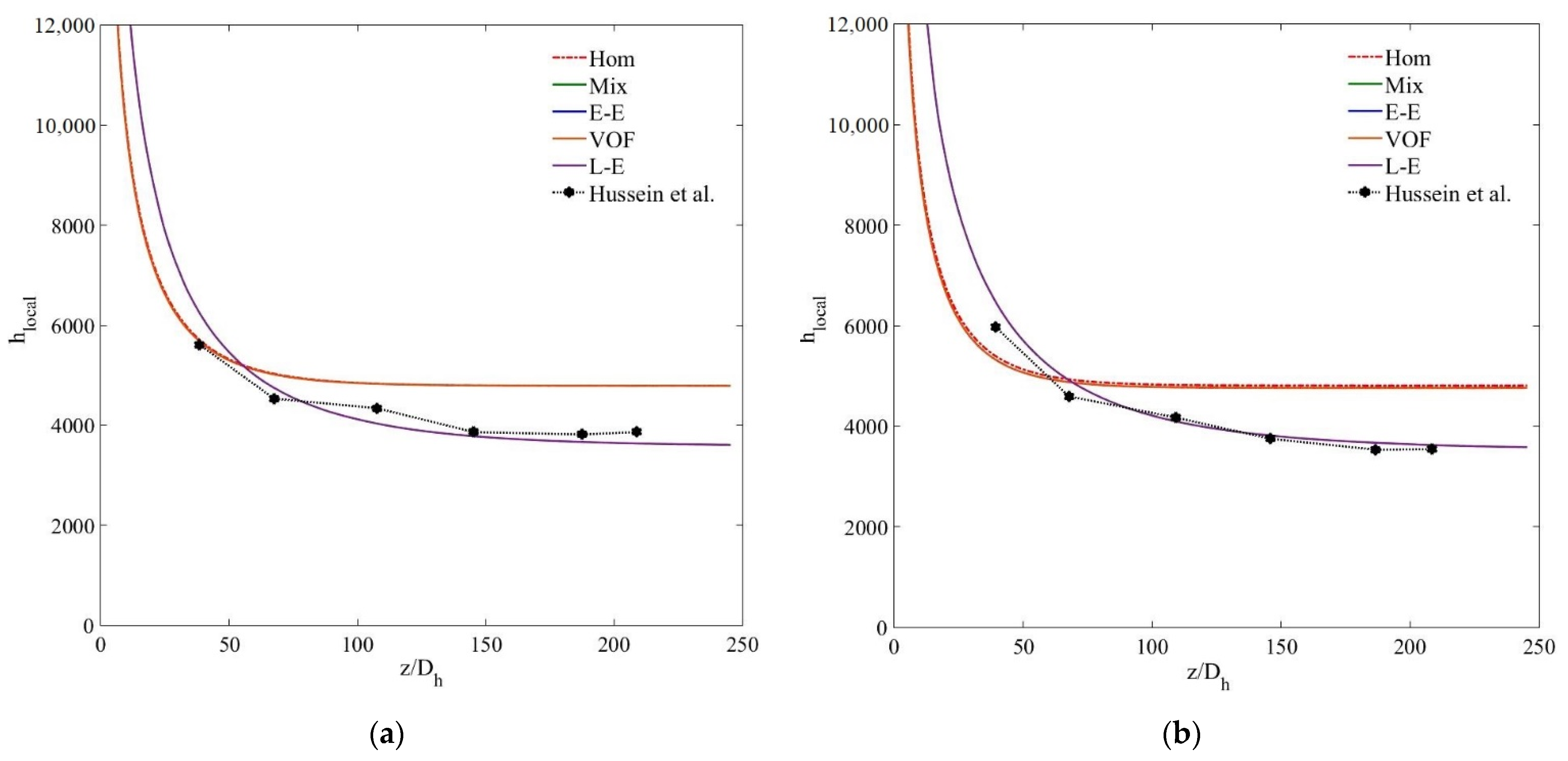
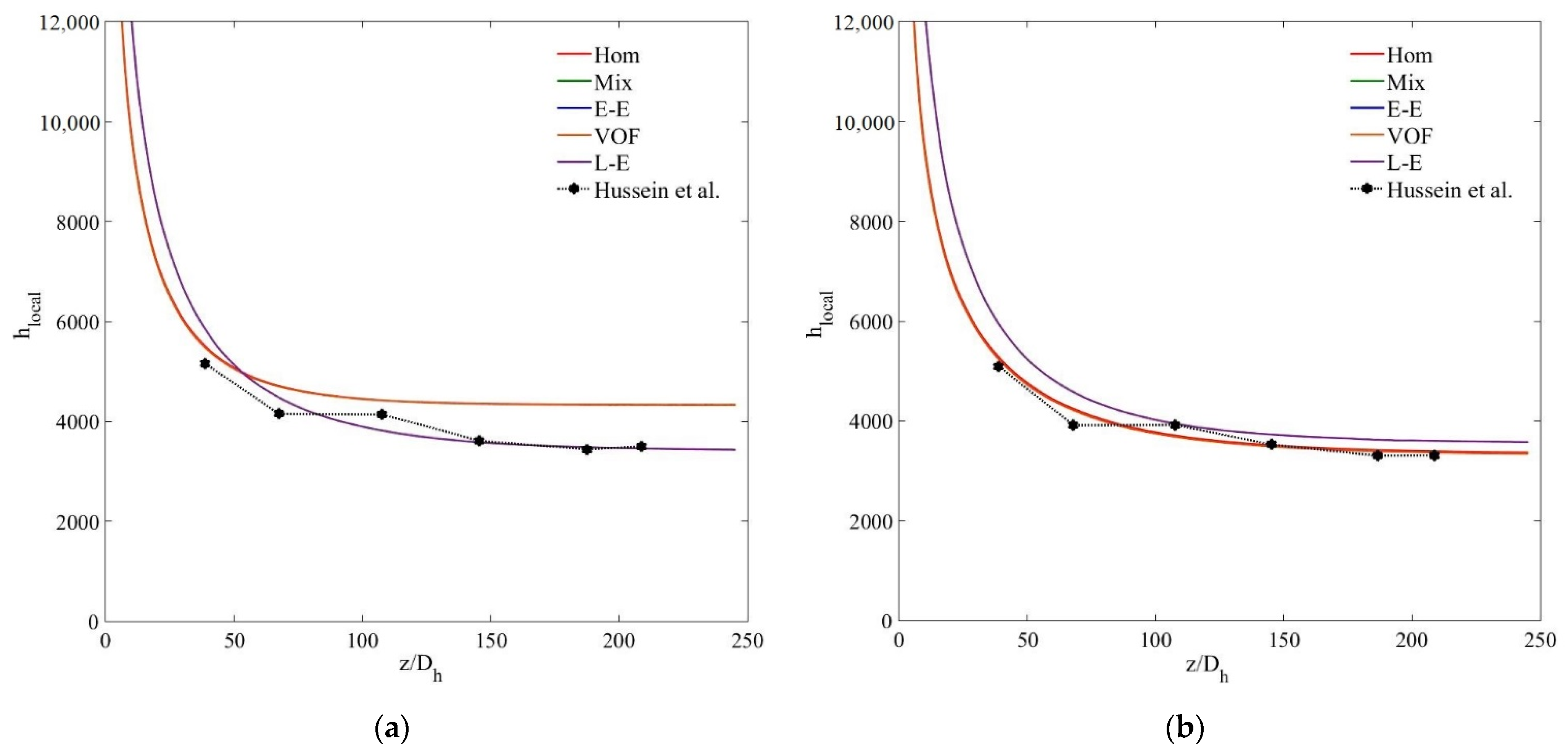
5.2. Heat Transfer Characteristics
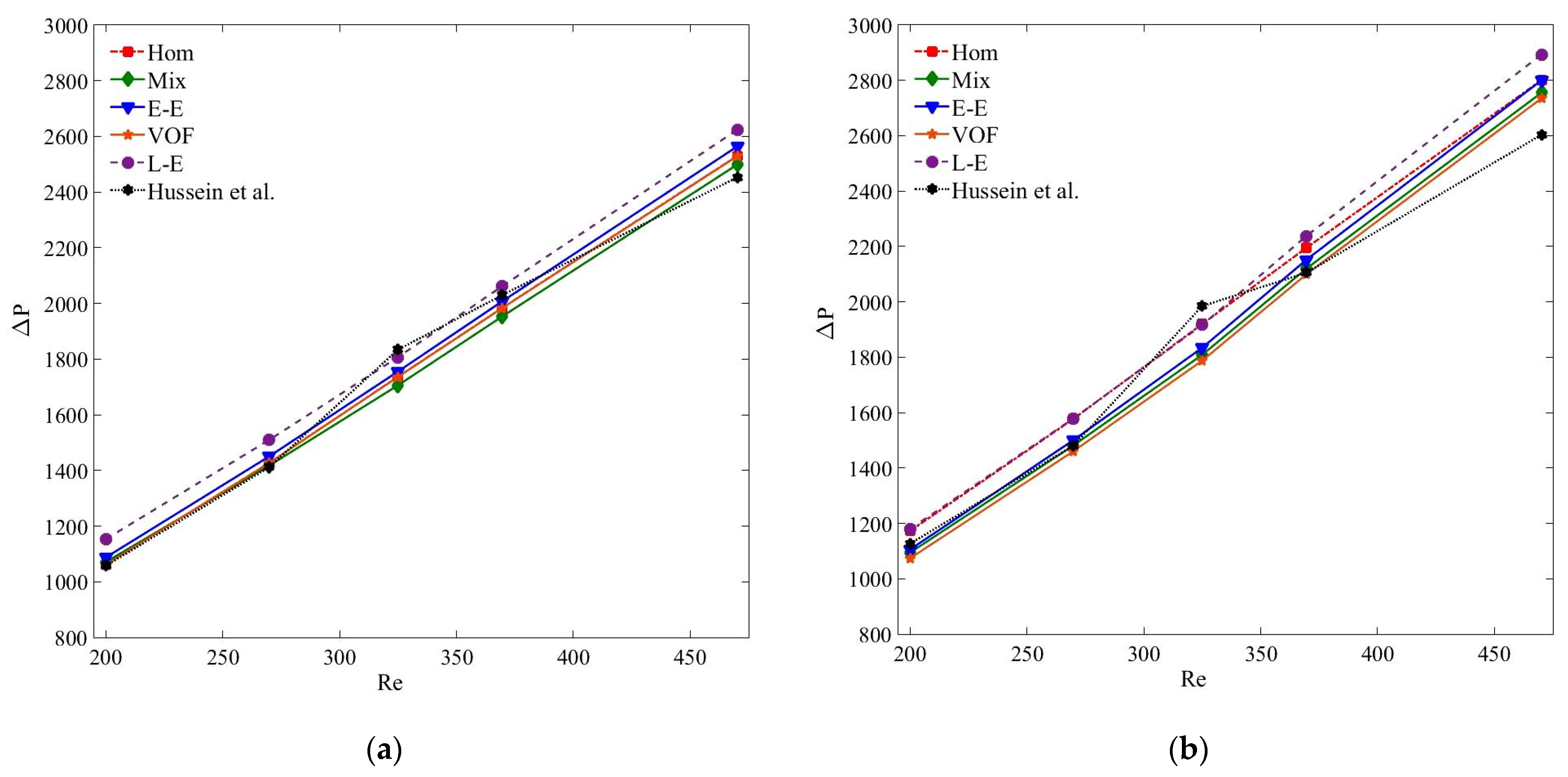
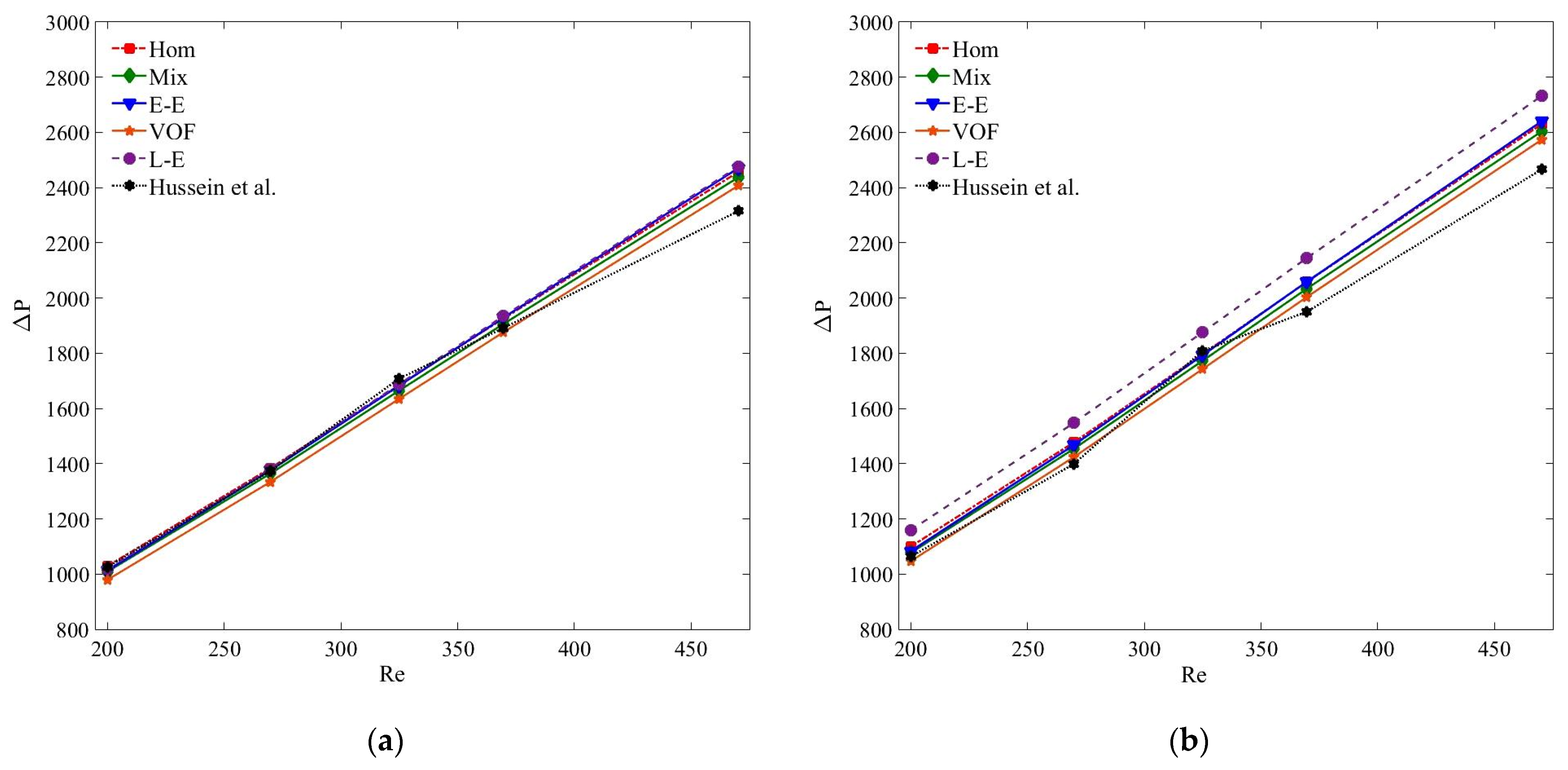
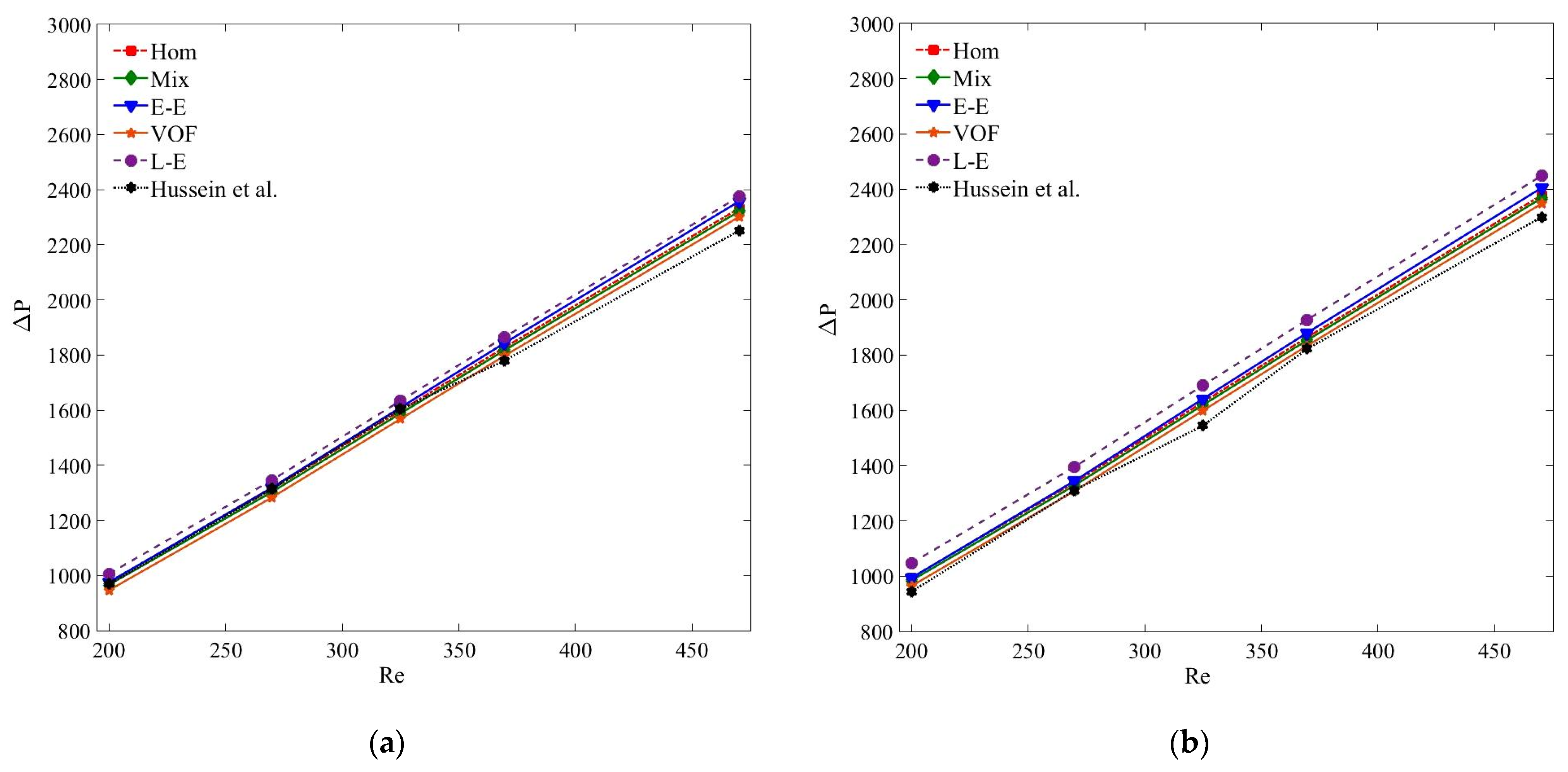
5.3. Pressure Drop Characteristics
6. Conclusions
- Single and all the multiphase numerical models estimate reasonably accurate convective heat transfer coefficient results for diluted nanofluids and at low Reynolds number when the interphase interactions are negligible.
- The single-phase and Eulerian–Eulerian models overestimate the thermal fields of the nanofluid with a more perceptible difference at high nanoparticle concentration and Reynolds number.
- The multiphase Eulerian–Eulerian approaches reveal marginal differences between average and local convective heat transfer coefficients results. The maximum deviation of the single-phase, VOF, mixture and Eulerian models are 10.73%, 9.5%, 9% and 9.4%, respectively, for the average heat transfer coefficient results of the MWCNT/GNP–H2O (0.25 wt%) nanofluid at Reynolds number of 470.
- Of all the tested models, the Lagrangian–Eulerian approximation of nanofluid provides the most accurate convective heat transfer coefficient with a maximum deviation of 5.34% for 0.25 wt% of MWCNT–water nanofluid at Reynolds number of 470. However, the model requires high memory and computational time to compute the trajectories of individual nanoparticles.
- Despite the thermal discrepancies, all numerical models determine quite accurate pressure drop results at all the studied nanoparticle concentrations and Reynolds numbers.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| AL2O3 | Aluminium oxide (-) | Prandtl number (-) | |
| Cunningham correlation (-) | Heat flux () | ||
| Drag coefficient (-) | Re | Reynolds number (-) | |
| Inertial coefficient (-) | Momentum source term (W/m3) | ||
| Specific heat () | Energy source term (N/m3) | ||
| Copper (-) | Temperature () | ||
| Diameter (m) | TiO2 | Titanium dioxide (-) | |
| Deformation tensor (s−1) | Time (s) | ||
| Channel hydraulic diameter (m) | Number of cells (-) | ||
| E-E | Eulerian model (-) | V | Velocity () |
| Drag force (ms−2) | VOF | Volume of fluid model | |
| Lift force (ms−2) | + | Wall distance of initial node (-) | |
| Collision force (ms−2) | Greek Symbols | ||
| Force due to gravity (ms−2) | μ | Viscosity () | |
| Brownian force (ms−2) | Nanoparticle aspect ratio (-) | ||
| Thermophoresis force (ms−2) | Stress-strain tensor (-) | ||
| Virtual mass force (ms−2) | ρ | Density () | |
| Pressure force (ms−2) | ψ | Particle weight fraction (-) | |
| Gravitation acceleration () | φ | Particle effective volume fraction (-) | |
| GNP | Graphene nanoplatelets | Relative viscosity of nanofluid (-) | |
| H | Height (m) | ϖ | Particle sphericity |
| h | Convective heat transfer coefficient (W m−2K−1) | Kinematic viscosity () | |
| Hom | Single-phase model (-) | Subscripts | |
| M | Mass () | avg | Average |
| Mix | Mixture model (-) | f | Liquid phase |
| Knudsen number (-) | h | Hydraulic diameter | |
| k | Thermal conductivity () | in | Inlet |
| Boltzmann constant () | local | Local | |
| Channel length () | m | Mixture | |
| L-E | Lagrangian–Eulerian model (-) | n | Nanoparticles |
| N | Avogadro’s number (-) | nf | Nanofluid |
| Nusselt number (-) | r | Relative | |
| M | Molar mass () | Nanoparticle phase | |
| MWCNT | Multiwalled carbon nanotubes (-) | Reference temperature | |
| P | Pressure () | t | Total |
| PEC | Performance evaluation criteria (-) | out | Outlet |
| n | Particle shape factor | w | Wall |
References
- Ghalandari, M.; Maleki, A.; Haghighi, A.; Shadloo, M.S.; Nazari, M.A.; Tlili, I. Applications of nanofluids containing carbon nanotubes in solar energy systems: A review. J. Mol. Liq. 2020, 313, 113476. [Google Scholar] [CrossRef]
- Ambreen, T.; Saleem, A.; Park, C.W. Analysis of hydro-thermal and entropy generation characteristics of nanofluid in an aluminium foam heat sink by employing Darcy-Forchheimer-Brinkman model coupled with multiphase Eulerian model. Appl. Therm. Eng. 2020, 173, 115231. [Google Scholar] [CrossRef]
- Alrashed, A.A.; Akbari, O.A.; Heydari, A.; Toghraie, D.; Zarringhalam, M.; Shabani, G.A.S.; Seifi, A.R.; Goodarzil, M. The numerical modeling of water/FMWCNT nanofluid flow and heat transfer in a backward-facing contracting channel. Phys. B Condens. Matter 2018, 537, 176–183. [Google Scholar] [CrossRef]
- Abdulrazzaq, T.; Togun, H.; Goodarzi, M.; Kazi, S.N.; Ariffin, M.K.A.; Adam, N.M.; Hooman, K. Turbulent heat transfer and nanofluid flow in an annular cylinder with sudden reduction. J. Therm. Anal. Calorim. 2020, 141, 373–385. [Google Scholar] [CrossRef]
- Aghaei, A.; Sheikhzadeh, G.A.; Goodarzi, M.; Hasani, H.; Damirchi, H.; Afrand, M. Effect of horizontal and vertical elliptic baffles inside an enclosure on the mixed convection of a MWCNTs-water nanofluid and its entropy generation. Eur. Phys. J. Plus 2018, 133, 486. [Google Scholar] [CrossRef]
- Gkountas, A.A.; Benos, L.T.; Sofiadis, G.N.; Sarris, I.E. A printed-circuit heat exchanger consideration by exploiting an Al2O3-water nanofluid: Effect of the nanoparticles interfacial layer on heat transfer. Therm. Sci. Eng. Prog. 2021, 22, 100818. [Google Scholar] [CrossRef]
- Vo, D.D.; Hedayat, M.; Ambreen, T.; Shehzad, S.A.; Sheikholeslami, M.; Shafee, A.; Nguyen, T.K. Effec-tiveness of various shapes of Al2O3 nanoparticles on the MHD convective heat transportation in porous medium: CVFEM modelling. J. Therm. Anal. Calorim. 2020, 139, 1345–1353. [Google Scholar] [CrossRef]
- Ambreen, T.; Kim, M.H. Influence of particle size on the effective thermal conductivity of nanofluids: A critical review. Appl. Energy 2020, 264, 114684. [Google Scholar] [CrossRef]
- Shehzad, S.A.; Sheikholeslami, M.; Ambreen, T.; Shafee, A. Convective MHD flow of hybrid-nanofluid within an elliptic porous enclosure. Phys. Lett. A 2020, 384, 126727. [Google Scholar] [CrossRef]
- Ambreen, T.; Kim, M.-H. Effects of variable particle sizes on hydrothermal characteristics of nanofluids in a microchannel. Int. J. Heat Mass Transf. 2018, 120, 490–498. [Google Scholar] [CrossRef]
- Bakthavatchalam, B.; Habib, K.; Saidur, R.; Baran, B.; Irshad, K. Comprehensive study on nanofluid and ionanofluid for heat transfer enhancement: A review on current and future perspective Distilled water. J. Mol. Liq. 2020, 305, 112787. [Google Scholar] [CrossRef]
- Ambreen, T.; Kim, M.-H. Heat transfer and pressure drop correlations of nanofluids: A state of art review. Renew. Sustain. Energy Rev. 2018, 91, 564–583. [Google Scholar] [CrossRef]
- Keblinski, P.; Phillpot, R.; Choi, S.; Eastman, A. Mechanisms of heat flow in suspensions of nano-sized particles (nanofluids). Int. J. Heat Mass Transf. 2002, 45, 855–863. [Google Scholar] [CrossRef]
- Wen, D.; Ding, Y. Experimental investigation into convective heat transfer of nanofluids at the entrance region under laminar flow conditions. Int. J. Heat Mass Transf. 2004, 47, 5181–5188. [Google Scholar] [CrossRef]
- Mahmoodi, M.; Kandelousi, S. Effects of thermophoresis and Brownian motion on nanofluid heat transfer and entropy generation. J. Mol. Liq. 2015, 211, 15–24. [Google Scholar] [CrossRef]
- Benos, L.T.; Sarris, I.E. The interfacial nanolayer role on magnetohydrodynamic natural convection of an Al2O3-water nanofluid. Heat Transf. Eng. 2021, 42, 89–105. [Google Scholar] [CrossRef]
- Shehzad, S.A.; Sheikholeslami, M.; Ambreen, T.; Shafee, A.; Babazadeh, H.; Ahmad, M. Heat transfer management of hybrid nanofluid including radiation and magnetic source terms within a porous domain. Appl. Nanosci. 2020, 10, 5351–5359. [Google Scholar] [CrossRef]
- Mahanthesh, B.; Shehzad, S.A.; Ambreen, T.; Khan, S.U. Significance of Joule heating and viscous heating on heat transport of MoS2–Ag hybrid nanofluid past an isothermal wedge. J. Therm. Anal. Calorim. 2020, 1–9. [Google Scholar] [CrossRef]
- Shehzad, S.A.; Sheikholeslami, M.; Ambreen, T.; Shafee, A.; Babazadeh, H. Examination of CVFEM for nanofluid free convection MHD flow through permeable medium. Appl. Nanosci. 2020, 10, 3269–3277. [Google Scholar] [CrossRef]
- Reddy, M.G.G.; Kumar, K.G.; Shehzad, S.A.; Javed, T.; Ambreen, T. Thermal transportation analy-sis of nanoliquid squeezed flow past a sensor surface with MCWCNT and SWCNT. Heat Transf. Asian Res. 2019, 48, 2262–2275. [Google Scholar] [CrossRef]
- Babazadeh, H.; Ambreen, T.; Shehzad, S.A.; Shafee, A. Ferrofluid non-Darcy heat transfer involving second law analysis: An application of CVFEM. J. Therm. Anal. Calorim. 2020, 1–18. [Google Scholar] [CrossRef]
- Kumar, K.G.; Lokesh, H.J.; Shehzad, S.A.; Ambreen, T. On analysis of Blasius and Rayleigh–Stokes hybrid nanofluid flow under aligned magnetic field. J. Therm. Anal. Calorim. 2019, 139, 2119–2127. [Google Scholar] [CrossRef]
- Ganesh Kumar, K.; Shehzad, S.A.; Ambreen, T.; Anwar, M.I. Heat transfer augmentation in water-based TiO2 nanoparti-cles through a converging/diverging channel by considering Darcy-Forchheimer porosity. Rev. Mex. Fís. 2019, 65, 373–381. [Google Scholar] [CrossRef]
- Moraveji, M.K.; Esmaeili, E. Comparison between single-phase and two-phases CFD modeling of laminar forced convection flow of nanofluids in a circular tube under constant heat flux. Int. Commun. Heat Mass Transf. 2012, 39, 1297–1302. [Google Scholar] [CrossRef]
- Akbari, M.; Galanis, N.; Behzadmehr, A. Comparative assessment of single and two-phase models for numerical studies of nanofluid turbulent forced convection. Int. J. Heat Fluid Flow 2012, 37, 136–146. [Google Scholar] [CrossRef]
- Albojamal, A.; Vafai, K. Analysis of single phase, discrete and mixture models, in predicting nanofluid transport. Int. J. Heat Mass Transf. 2017, 114, 225–237. [Google Scholar] [CrossRef]
- Hejazian, M.; Moraveji, M.K. A Comparative Analysis of Single and Two-Phase Models of Turbulent Convective Heat Transfer in a Tube for TiO2 Nanofluid with CFD. Numer. Heat Transf. Part A Appl. 2013, 63, 795–806. [Google Scholar] [CrossRef]
- Behroyan, I.; Ganesan, P.; He, S.; Sivasankaran, S. Turbulent forced convection of Cu–water nanofluid: CFD model comparison. Int. Commun. Heat Mass Transf. 2015, 67, 163–172. [Google Scholar] [CrossRef]
- Shafahi, M.; Bianco, V.; Vafai, K.; Manca, O. Thermal performance of flat-shaped heat pipes using nanofluids. Int. J. Heat Mass Transf. 2010, 53, 1438–1445. [Google Scholar] [CrossRef]
- Moghadassi, A.; Ghomi, E.; Parvizian, F. A numerical study of water based Al2O3 and Al2O3–Cu hybrid nanofluid effect on forced convective heat transfer. Int. J. Therm. Sci. 2015, 92, 50–57. [Google Scholar] [CrossRef]
- Akbari, M.; Galanis, N.; Behzadmehr, A. Comparative analysis of single and two-phase models for CFD studies of nanofluid heat transfer. Int. J. Therm. Sci. 2011, 50, 1343–1354. [Google Scholar] [CrossRef]
- Bahiraei, M.; Hosseinalipour, S.M. Thermal Dispersion Model Compared with Euler-Lagrange Approach in Simu-lation of Convective Heat Transfer for Nanoparticle Suspensions. J. Dispers. Sci. Technol. 2013, 34, 1778–1789. [Google Scholar] [CrossRef]
- Bahiraei, M. A numerical study of heat transfer characteristics of CuO-water nanofluid by Euler-Lagrange approach. J. Therm. Anal. Calorim. 2016, 123, 1591–1599. [Google Scholar] [CrossRef]
- Fard, M.H.; Esfahany, M.N.; Talaie, M. Numerical study of convective heat transfer of nanofluids in a circular tube two-phase model versus single-phase model. Int. Commun. Heat Mass Transf. 2010, 37, 91–97. [Google Scholar] [CrossRef]
- Behroyan, I.; Vanaki, S.M.; Ganesan, P.; Saidur, R. A comprehensive comparison of various CFD models for convective heat transfer of Al2O3 nanofluid inside a heated tube. Int. Commun. Heat Mass Transf. 2016, 70, 27–37. [Google Scholar] [CrossRef]
- Mojarrad, M.S.; Keshavarz, A.; Shokouhi, A. Nanofluids thermal behavior analysis using a new dispersion model along with single-phase. Heat Mass Transf. 2013, 49, 1333–1343. [Google Scholar] [CrossRef]
- Ebrahimnia-Bajestan, E.; Moghadam, M.C.; Niazmand, H.; Daungthongsuk, W.; Wongwises, S. Experimental and numerical investigation of nanofluids heat transfer characteristics for application in solar heat exchangers. Int. J. Heat Mass Transf. 2016, 92, 1041–1052. [Google Scholar] [CrossRef]
- Kumar, N.; Puranik, B.P. Numerical study of convective heat transfer with nanofluids in turbulent flow using a Lagrangian-Eulerian approach. Appl. Therm. Eng. 2017, 111, 1674–1681. [Google Scholar] [CrossRef]
- Hejazian, M.; Moraveji, M.K.; Beheshti, A. Comparative study of Euler and mixture models for turbulent flow of Al2O3 nanofluid inside a horizontal tube. Int. Commun. Heat Mass Transf. 2014, 52, 152–158. [Google Scholar] [CrossRef]
- Göktepe, S.; Atalik, K.; Ertürk, H. Comparison of single and two-phase models for nanofluid convection at the en-trance of a uniformly heated tube. Int. J. Therm. Sci. 2014, 80, 83–92. [Google Scholar] [CrossRef]
- Lotfi, R.; Saboohi, Y.; Rashidi, A. Numerical study of forced convective heat transfer of Nanofluids: Comparison of different approaches. Int. Commun. Heat Mass Transf. 2010, 37, 74–78. [Google Scholar] [CrossRef]
- Ambreen, T.; Kim, M.-H. Comparative assessment of numerical models for nanofluids’ laminar forced convection in micro and mini channels. Int. J. Heat Mass Transf. 2017, 115, 513–523. [Google Scholar] [CrossRef]
- Mahian, O.; Kolsi, L.; Amani, M.; Estellé, P.; Ahmadi, G.; Kleinstreuer, C.; Marshall, J.S.; Siavashi, M.; Taylor, R.A.; Niazmand, H.; et al. Recent advances in modeling and simulation of nanofluid flows—Part I: Fundamentals and theory. Phys. Rep. 2019, 790, 1–48. [Google Scholar] [CrossRef]
- Mahian, O.; Kolsi, L.; Amani, M.; Estellé, P.; Ahmadi, G.; Kleinstreuer, C.; Marshall, J.S.; Taylor, R.A.; Abu-Nada, E.; Rashidi, S.; et al. Recent advances in modeling and simulation of nanofluid flows—Part II: Applications. Phys. Rep. 2019, 791, 1–59. [Google Scholar] [CrossRef]
- Hussien, A.A.; Abdullah, M.Z.; Yusop, N.M.; Al-Nimr, M.A.; Atieh, M.A.; Mehrali, M. Experiment on forced convective heat transfer enhancement using MWCNTs/GNPs hybrid nanofluid and mini-tube. Int. J. Heat Mass Transf. 2017, 115, 1121–1131. [Google Scholar] [CrossRef]
- Xuan, Y.; Roetzel, W. Conceptions for heat transfer correlation of nanofluids. Int. J. Heat Mass Transf. 2000, 43, 3701–3707. [Google Scholar] [CrossRef]
- Batchelor, G.K. The effect of Brownian motion on the bulk stress in a suspension of spherical particles. J. Fluid Mech. 1977, 83, 97–117. [Google Scholar] [CrossRef]
- Hamilton, R.L.; Crosser, O.K. Thermal Conductivity of Heterogeneous Two-Component Systems. Ind. Eng. Chem. Fundam. 1962, 1, 187–191. [Google Scholar] [CrossRef]
- Kang, H.U.; Kim, S.H.; Oh, J.M. Estimation of Thermal Conductivity of Nanofluid Using Experimental Effective Particle Volume. Exp. Heat Transf. 2006, 19, 181–191. [Google Scholar] [CrossRef]
- Manninen, M.; Taivassalo, V. On the Mixture Model for Multiphase Flow. 1996. Available online: https://cris.vtt.fi/en/publications/on-the-mixture-model-for-multiphase-flow (accessed on 21 January 2021).
- Schiller, V.L. A Drag Coefficient Correlation. Z. Ver. Deutsch. Ing. 1933, 77, 318–320. [Google Scholar]
- Drew, D.A.; Lahey, R.T. Application of general constitutive principles to the derivation of multidimensional two-phase flow equations. Int. J. Multiph. Flow 1979, 5, 243–264. [Google Scholar] [CrossRef]
- Bouillard, J.X.; Lyczkowski, R.W.; Gidaspow, D. Porosity distributions in a fluidized bed with an immersed obstacle. AIChE J. 1989, 35, 908–922. [Google Scholar] [CrossRef]
- Ranz, W. Evaporation from drops 1. Chem. Eng. Prog. 1952, 48, 141–146. [Google Scholar]
- Saffman, P.G. The lift on a small sphere in a slow shear flow. J. Fluid Mech. 1965, 22, 385. [Google Scholar] [CrossRef]
- Tian, L.; Ahmadi, G.; Tu, J. Mobility of nanofiber, nanorod, and straight-chain nanoparticles in gases. Aerosol. Sci. Technol. 2017, 51, 587–601. [Google Scholar] [CrossRef][Green Version]
- Akhavan-Behabadi, M.; Shahidi, M.; Aligoodarz, M.; Fakoor-Pakdaman, M. An experimental investigation on rheological properties and heat transfer performance of MWCNT-water nanofluid flow inside vertical tubes. Appl. Therm. Eng. 2016, 106, 916–924. [Google Scholar] [CrossRef]
- Ansys. ANSYS FLUENT User’s Guide. 2013. Available online: https://www.ansys.com/products/ansys-fluent (accessed on 21 January 2021).
- Ramesh, K.; Shah, A.L. London, Laminar Flow Forced Convection in Ducts: A Source Book for Compact Heat Exchanger Analytical Data; Academic Press: Cambridge, MA, USA, 1978. [Google Scholar]
- Brown, G.O. The History of the Darcy-Weisbach Equation for Pipe Flow Resistance; American Society of Civil Engineers: Reston, VA, USA, 2002; pp. 34–43. [Google Scholar]
- Moraveji, M.K.; Ardehali, R.M. CFD modeling (comparing single and two-phase approaches) on thermal performance of Al2O3/water nanofluid in mini-channel heat sink. Int. Commun. Heat Mass Transf. 2013, 44, 157–164. [Google Scholar] [CrossRef]
- Vallejo, J.P.; Calviño, U.; Freire, I.; Fernández-seara, J.; Lugo, L. Convective heat transfer in pipe flow for glycolated water-based carbon nanofluids. A thorough analysis. J. Mol. Liq. 2020, 301, 112370. [Google Scholar] [CrossRef]
- Ali, H.M. In tube convection heat transfer enhancement: SiO2 aqua based nanofluids. J. Mol. Liq. 2020, 308, 113031. [Google Scholar] [CrossRef]
- Ambreen, T.; Saleem, A.; Park, C.W. Numerical analysis of the heat transfer and fluid flow characteristics of a nanofluid-cooled micropin-fin heat sink using the Eulerian-Lagrangian approach. Powder Technol. 2019, 345, 509–520. [Google Scholar] [CrossRef]
- Ambreen, T.; Saleem, A.; Park, C.W. Pin-fin shape-dependent heat transfer and fluid flow characteristics of water- and nanofluid-cooled micropin-fin heat sinks: Square, circular and triangular fin cross-sections. Appl. Therm. Eng. 2019, 158, 113781. [Google Scholar] [CrossRef]
| Material | Ref. | |||
|---|---|---|---|---|
| MWCNT | 2100 | 630 | 1500 | [57] |
| GNP | 2200 | 790 | 3000 | [45] |
| Grid | ||
|---|---|---|
| G1 | 0.058 | 826,541 |
| G2 | 0.044 | 1,102,676 |
| G3 | 0.031 | 1,442,556 |
| G4 | 0.023 | 2,302,986 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ambreen, T.; Saleem, A.; Park, C.W. Homogeneous and Multiphase Analysis of Nanofluids Containing Nonspherical MWCNT and GNP Nanoparticles Considering the Influence of Interfacial Layering. Nanomaterials 2021, 11, 277. https://doi.org/10.3390/nano11020277
Ambreen T, Saleem A, Park CW. Homogeneous and Multiphase Analysis of Nanofluids Containing Nonspherical MWCNT and GNP Nanoparticles Considering the Influence of Interfacial Layering. Nanomaterials. 2021; 11(2):277. https://doi.org/10.3390/nano11020277
Chicago/Turabian StyleAmbreen, Tehmina, Arslan Saleem, and Cheol Woo Park. 2021. "Homogeneous and Multiphase Analysis of Nanofluids Containing Nonspherical MWCNT and GNP Nanoparticles Considering the Influence of Interfacial Layering" Nanomaterials 11, no. 2: 277. https://doi.org/10.3390/nano11020277
APA StyleAmbreen, T., Saleem, A., & Park, C. W. (2021). Homogeneous and Multiphase Analysis of Nanofluids Containing Nonspherical MWCNT and GNP Nanoparticles Considering the Influence of Interfacial Layering. Nanomaterials, 11(2), 277. https://doi.org/10.3390/nano11020277