1. Introduction
The cancer burden is increasing exponentially. It was estimated to have risen to 18.1 million new cases and 9.6 million deaths worldwide in 2018 [
1]. The World Health Organization (WHO) estimated that 1/5 men and 1/6 women worldwide develop cancer and 1/8 men and 1/11 women die from the disease [
2]. The most common treatments of cancer are surgery, radiotherapy and chemotherapy. However, the lack of efficiency of these treatments in many cases, in addition to their side effects that have not yet been totally neutralized, indicates that the search for new cancer treatments and therapies is vital. One of the most interesting approaches is hyperthermia, which is a non-invasive technique to selectively kill target cancer cells by raising the microenvironment tumor temperature to 43 °C to 45 °C, resulting in cell apoptosis due to the irreversible cell damage caused by their low heat resistance, where on the other hand, normal cell damage is minimum due to their high resistance to heat [
3,
4].
There are various hyperthermia techniques, with only one of them currently being clinically used. It consists of using antennas at microwave frequencies combined with radiotherapy [
5] and chemotherapy [
6]. Hyperthemia showed various therapeutic benefits, such as some direct cytotoxicity due to heating, mild anti-tumor response [
7], and tumor sensitization [
5]. However, this work focuses on the nanomedical cancer treatment hyperthermia, or magnetic hyperthermia (MHT), where the temperature increase is mediated by magnetic nanoparticles (MNPs) [
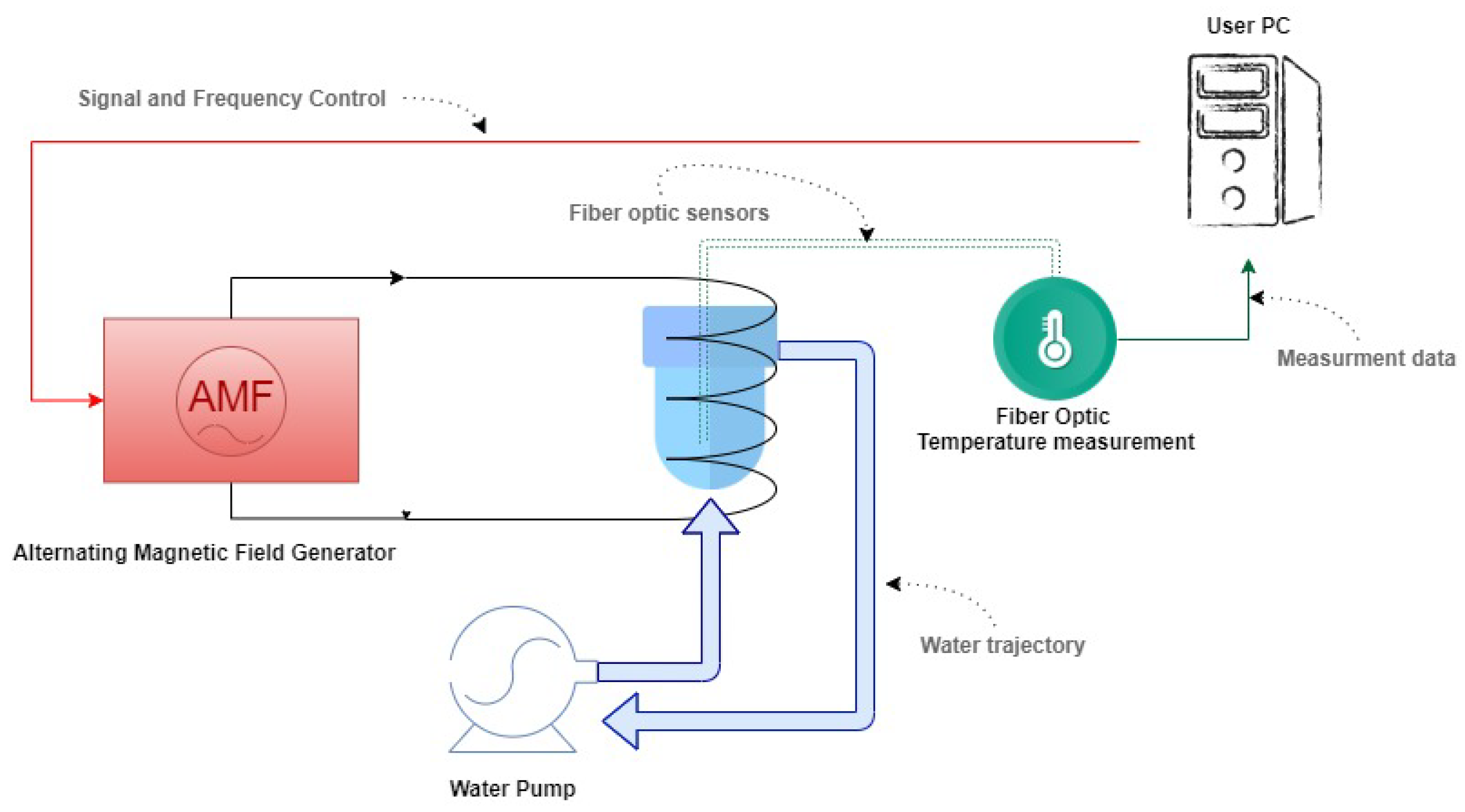
8]. It consists of placing superparamagnetic NPs under the influence of an alternating magnetic field (AMF), resulting in heat generation due to Néel and Brownian relaxation losses [
3]. The AMF, however, is generated through a coil connected to an AMF generator. It is essential to point out that AMFs applied at frequencies and intensities above 1 MHz and 1 T could be harmful to tissues and biological fluids [
9], which is not the case of the experiments in this study.
Nanoparticles (NPs) with different properties, such as gold, silver, or iron oxide, are commonly used by the scientific community to develop new applications, such as therapies or medical diagnostics [
10]. MNPs are well known and have many applications in the biomedical field: drug delivery [
11], tissue engineering [
12], magnetic resonance imaging (MRI) contrast agent [
8,
11] or heat mediators in optical hyperthermia [
10]. Iron oxide is the most commonly used material due to its high compatibility and biodistribution in the body [
13]. Furthermore, MNPs have been approved by the food and drug administration (FDA) for some applications, such as MRI contrast agents and heat mediators for drug release or cancer treatment using AMF [
13], as we previously mentioned. Furthermore, the iron oxide NPs are the most promising heating agent candidates [
14], which is why they were used in the MHT clinical trials of Magforce AG to test their NanoTherm
® therapy system [
15]. There are many different sizes and shapes of these NPs. The particle size affects its heat production because, theoretically, the size at which the magnetite particles change from Néel to Brown is around 12 nm [
16]. Thus, if the MNP is smaller than 12 nm, Néel Relaxation dominates its heating process; hence, it is dominated by frequency. On the other hand, if the MNP is larger than 12 nm; it is dominated by Brownian relaxation; hence, the heating generation depends on the AMF strength [
16]. The shape of the MNP also affects its performance, and there are many different iron oxide NPs, such as nanoflowers, spherical and hollow [
16,
17]. The worldwide scientific network is in a constant influx of information and basic research to obtain improvements and to consolidate developments cooperating in the advancement of MHT to obtain outcomes in clinical translation [
14].
In Sánchez et al. [
18], the cubic-shaped NPs were discussed, followed by their optimization for MHT application and their potential industrial implementation. They showed good heating performance, making them a promising type of particles for MHT. Duta et al. [
19] showed the development of malic acid and
-hydroxy acid grafted magnetic nanocarriers of spherical size, good magnetic responsiveness and excellent heating efficiency. As shown in Gustafson et al. [
20], it is vital for drug delivery agents to possess good biocompatibility and avoid the rapid clearance from the body by the reticuloendothelial system (RES), in addition to inertness and high loading affinity of drug molecules. The iron oxide superparamagnetic nanoparticles (SPIONs) showed a high specific absorption rate (
), a 72% loading efficiency and a slow and sustained release in a
-dependent manner over a period of time, making them suitable for MHT and controlled drug delivery. In Mille et al. [
21], the NP chain formation during MHT through the calorimetric method was studied using time-resolved high-frequency hysterisis loops. The study proved that the formation of the chains is dependent on time and magnetic field amplitude, whereas it is not dependent on the frequency in the range they experimented (between 9 and 78 kHz). The work also concluded that if the measurement time is shorter than the chain formation, the thermal power is underestimated. A fact that is vital for biological applications since the magnetic fields are applied for a longer duration than the heating power measurements. Similarly, in Iglesias et al. [
22], MHT through calorimetric methods was conducted in order to enhance the power losses calculation and clarify some irregularity parameters.
In this study, we will be using spherical iron oxide NPs, with a diameter of approximately nm at two different concentrations ( and 75 mgFe/mL). It is expected to have a difference in heating, where the heating efficiency decreases by half when going from the latter to the former concentration. Therefore, we will observe differences in heating efficiencies depending on the concentration and other variables explained in the Materials and Methods section.
1.1. Hyperthermia Limitations
Nevertheless, MHT faced various limitations, such as a significant efficiency decrease between in vivo and in vitro experiments and aggregation. In vivo MHT was described in Manuchehrabadi et al. [
12], demonstrating that the homogeneity of the temperature increase inside the organ was strongly dependent on the distribution of NPs. Furthermore, MHT experiments demonstrate that MNPs have a decreased energy absorption per unit mass, or
, once internalized in cells, ranging from
to
depending on particle size, shape and composition [
23,
24]. The aggregation effect, on the other hand, was demonstrated in Mejías et al. [
11], where the inefficiency of NPs to respond to AMF was observed due to NP massive aggregation, which led to the unpredictable NP orientation in tumor cell lysosomes. On the other hand, other research links this effect to Brownian mobility restriction [
24,
25].
As a result, greater efficacy in producing heat might alleviate most of the issues mentioned above, either by enhancing NP behavior, which is the most widely pursued area of research, or by enhancing energy delivery from the exciting magnetic field, which is the primary goal of this work.
To the best of the author’s knowledge, there are no experimental studies that use non-conventional AMF waveforms or systems capable of providing these waveforms. Thus, all MHT experiments in the articles are conducted using the conventional sinusoidal waveform.
1.2. Hypothesis
Rosensweig’s model calculates the NPs’ heat dissipation following its excitation by an AMF [
26]. The power dissipation formula is expressed by:
where
(H· m
) is the vacuum permeability,
is the equilibrium susceptibility,
f (s
) is the frequency,
(A· m
) is the amplitude of the magnetic field and
(s) is the relaxation time. However, the model was made for sinusoidal AMF waveforms, and no further models were developed using other waveforms.
Looking at Equation (
1), Rosensweig connected the magnetic field and frequency to the temperature rise after a certain amount of time (
) in NPs [
26], meaning that the heat dissipation of the NPs is dependent on
B and
f. It also depends on
; however, since we are using the same NPs throughout the experiments of this study, the
will not vary.
In initial studies conducted in our laboratory [
27], we observed that the heat production does not follow the Rosensweig rule for low magnetic intensities when using non-sinusoidal waveform and non-coupled slopes and peak intensities [
26]. Then, in [
28,
29], which was a continuation of the initial work, the results showed that, contrary to the Rosensweig rule, the frequency is not enough to define the heat production when all the other experimental conditions are kept equal. Furthermore, modifying the heat generation using only square waveforms of shifting duty cycles is conceivable, pointing to transients around the zeros as the primary source of heat dissipation once again. This means that the slope of the AMF signal, signal frequency and even particle size (tiny particles <10 nm) conditions the proportionality between
and
B.
Therefore, this paper will conduct experiments with a newly developed and enhanced AMF generator, which can reach higher frequencies, generate conventional and various unconventional AMF waveforms and produce higher intensity alternating currents (AC).
1.3. Objectives
The objective of the paper is to:
3. Results
The experiments were conducted in a way that allowed us to see the effect of the AMF strength, frequency and NP concentration on the heating efficiency while placed under conventional and conventional AMF waveforms. Then, the thermal power increment between the conventional and non-conventional signals is deduced by applying the acquired final temperatures in Equation (
6). Finally, to validate the relationship between the power dissipation and the waveform slope, Equation (
6) is adjusted to Equation (
7) and then used to calculate the normalized power dissipation (
).
3.1. Magnetic Field Effect
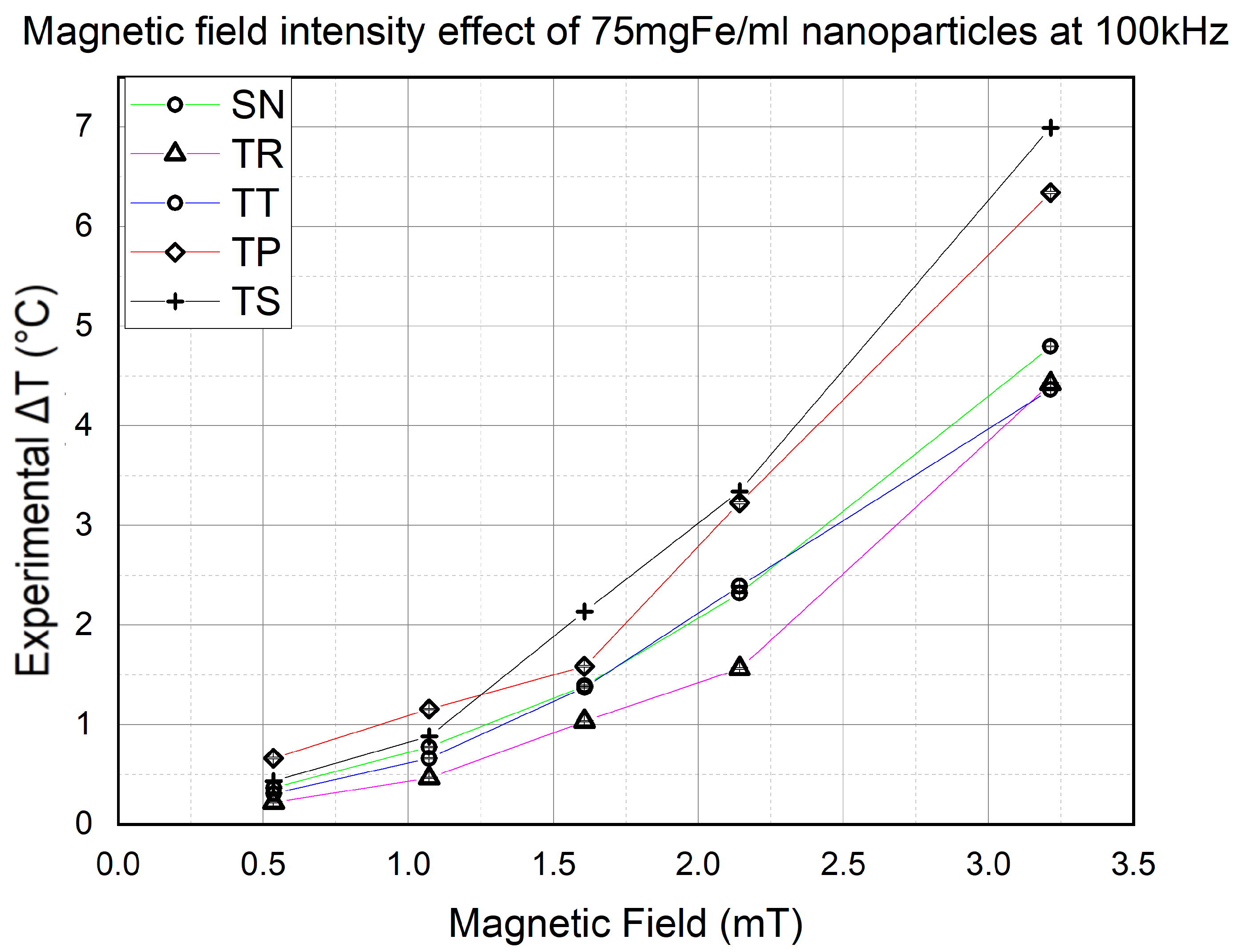
The first thing that needed to be confirmed was the proportional effect of the magnetic field on the final temperature. However, the impact of the waveform is not yet determined, so this section will help us determine the effect of the signal slope on the NP heat efficiency. Hence, using 75 mgFe/mL NPs at 100 kHz frequency, the AMF strength was variated from 0.5 mT to 3.3 mT. The results are shown in
Figure 8.
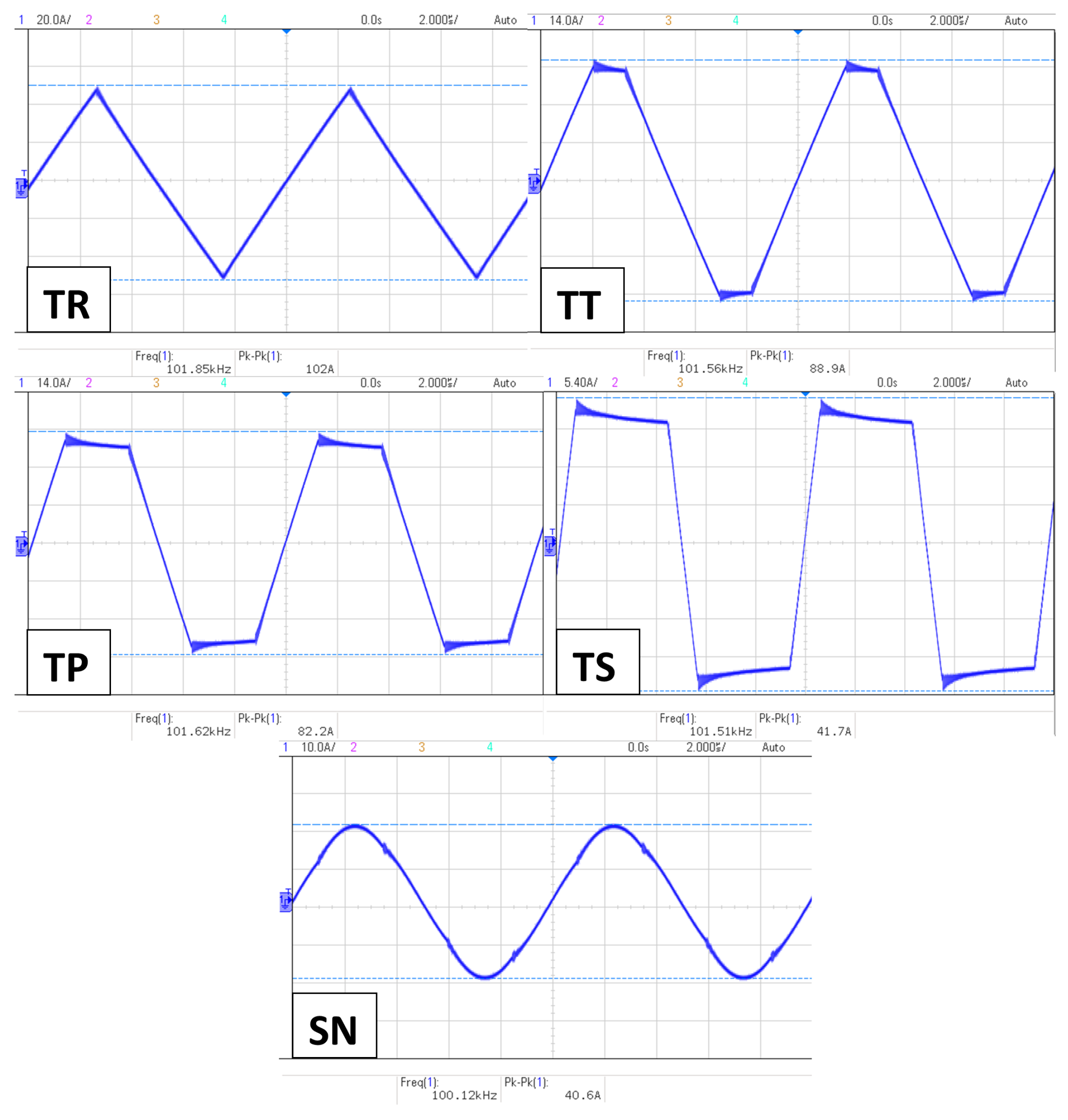
We noticed a dominance made by the signals with the higher slopes in heat efficiency over the rest of the waveforms. Furthermore, the higher the field intensity, the more significant the difference is. On the other hand, a conventional SN signal is always in third place behind the TS and TP waveforms, respectively, except at mT, where the TT signal marked a slightly higher value than the SN. However, TR signals have trails in heat efficiency throughout all the experiment’s magnetic field intensities.
The results of the experiments of this section proved to us the proportionality of the NP heating efficiency with the AMF strength. Furthermore, they showed us that TS and TP signals have higher heating capability than the SN signal. However, TP unexpectedly exceeded TS at and mT, scoring a slightly higher value of . This phenomenon is currently being investigated to determine if it occurs for specific reasons or because of the weak magnetic field intensity.
3.2. Frequency Effect
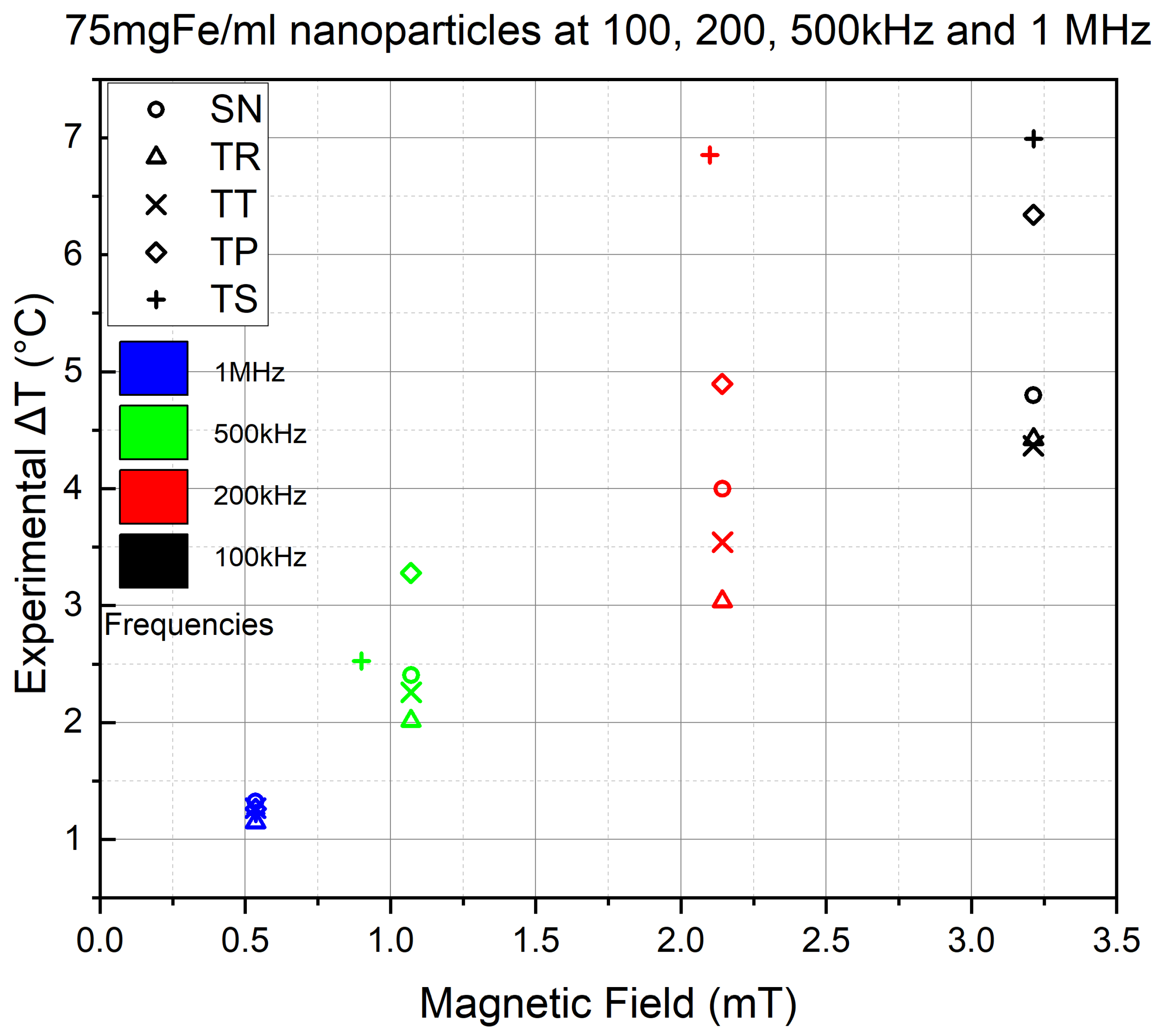
The experiments were conducted at four different frequencies and five AMF intensities to visualize the frequency effect on the NP’s heat efficiency. The objective is to see if we will see an increase in NP’s thermal performance by fixing the nanoparticle volume and concentration and varying the frequency.
Figure 9 shows the results of the inert experiments conducted at 100, 200, 500 kHz and 1 MHz frequency, using AMF intensities of
(in blue),
(in green),
(in magenta),
(in orange) and
(in red). Then, a connecting line was drawn between the
corresponding to the same AMF intensities at different frequencies, which allows the visualization of any variation in the NPs’ thermal power.
However, the coil suffered from overheating at higher frequencies, which is why
Figure 9 shows many inconsistencies in the experimental results. Furthermore, the orange color in the colormap has two AMF intensities, where the
mT was used only for the TS 500 kHz frequency experiment instead of the
mT because TS was unable to reach the latter AMF intensity due to severe thermal losses.
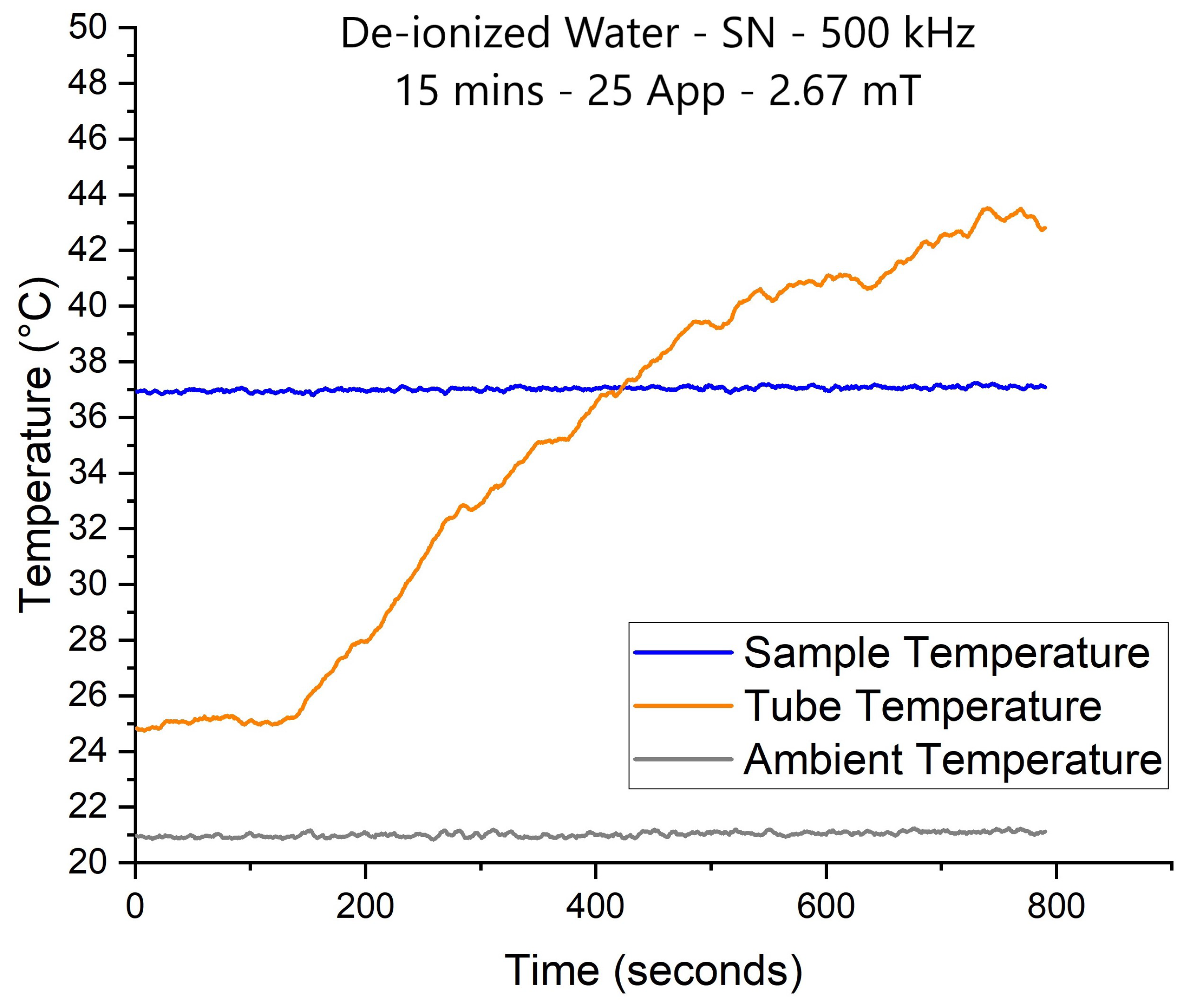
Nevertheless, the results still showed a linear increase in all AMF intensities for all signals. For example, this is seen in curves A and B, which represent the 2.14 mT AMF intensity (in green) of the SN and TR waveforms, respectively, at 100, 200 and 500 kHz. On the other hand, mT (blue) shows a sharper increase, but unfortunately, the experiments were only conducted at 100 and 200 kHz frequencies. In contrast, a less intense growth is witnessed at and mT intensities, whereas at mT, a moderate increase is seen throughout all four applied frequencies.
The coil overheating resulted in the discontinuity of many experiments, resulting in the absence of waveforms through the applied frequencies. Which is why we decided to represent the highest AMF intensity that was successfully experimented on all waveforms at each of the four frequencies.
Figure 10 represents the results of the 1 MHz experiments at
mT (equivalent to 5
output AC), the 500 kHz experiments at
mT except for the TS signal, which, due to heavy coil heating, was limited to
mT (equivalent to 10
and 8.4
output AC, respectively), the 200 kHz experiments at
mT (equivalent to 20
output AC) and the 100 kHz experiments at
mT AMF field intensity (equivalent to 30
output AC).
The 100 kHz (in black) results are similar to the maximum values in
Figure 8, yet the
T value of
at 200 kHz (in Red) /
mT is almost equal to the value of TS at 100 kHz/
mT. At 500 kHz (in green), although the
was placed at
mT lower than the rest of the waveforms, it still managed to reach a higher heat efficiency than the conventional AMF signal. However, at 1 MHz (in blue), the values are almost equal, but the conventional signal’s scored the highest final heating temperature.
The results of the experiments of this section proved to us that the proportionality of the NP heating efficiency with the AMF frequency. Similar to the previous section, they showed us that TS and TP signals have higher heating capability than the SN signal at higher frequencies (200 kHz and 500 kHz). However, at frequencies as high as 1 MHz, the TS and TP lose their dominance to the SN, which is also unexpected. In addition, the increase in the frequency effect at 0.5 mT is significantly decreased compared to 3.21 mT. It is unfortunate that the coil heating prohibited us from conducting experiments at a B higher than mT since we already witnessed irregularities at a magnetic field strength this low in the previous section on the one hand, and we were not able to see the thermal capability of high AMF intensities at high frequencies on the other.
3.3. Concentration Effect
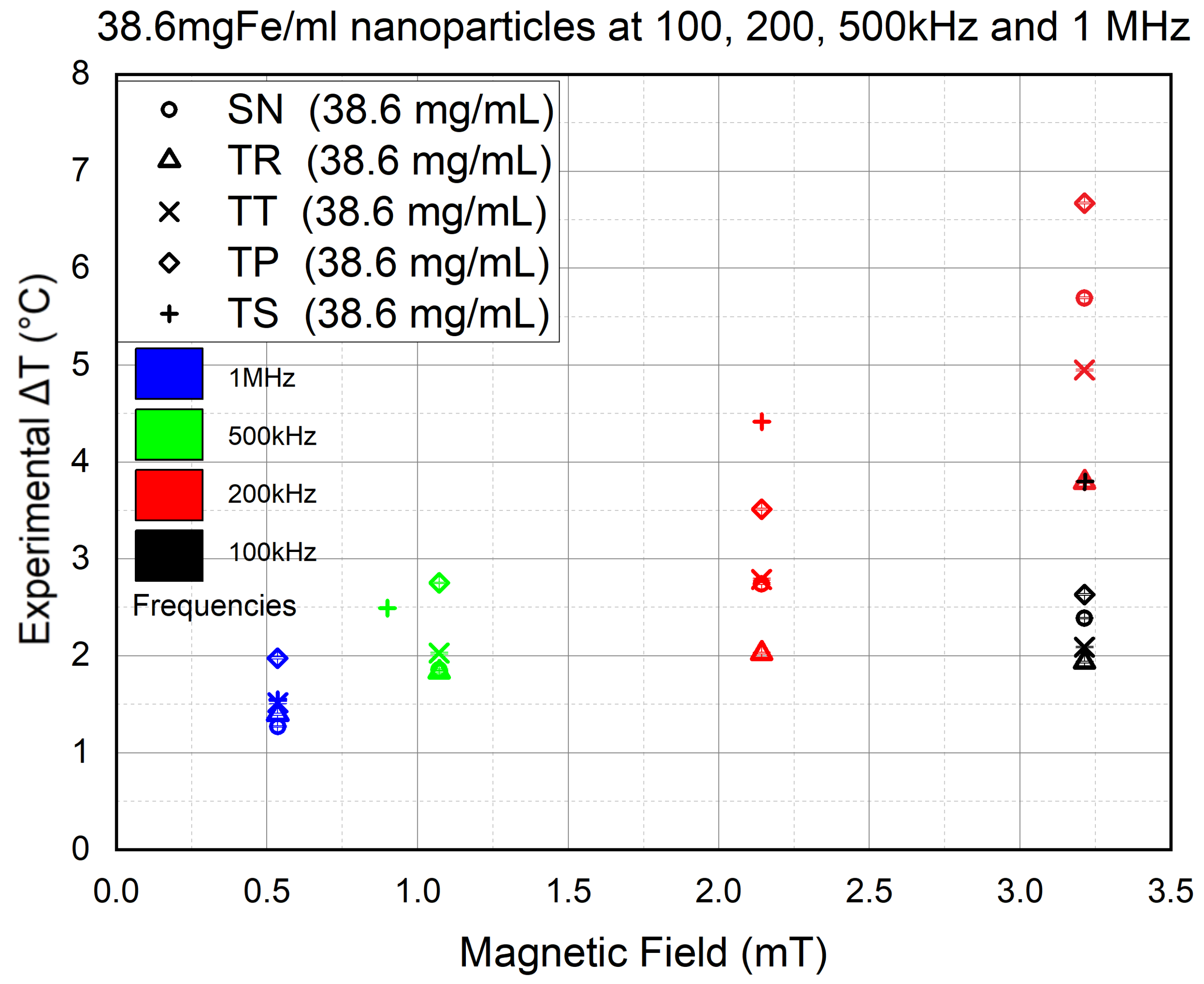
The effect of the concentration has been studied in tow suspensions at 75 mgFe/mL and another obtained by diluting the latter on at mgFe/mL. Therefore, in this section, we will determine the concentration effect on NP heating. Understanding the impact the concentration has on the results is vital, especially for the in vitro phase, where the toxicity factor will be taken into consideration.
Hence, we repeated the experiments of the previous section using the same frequencies, except for the 200 kHz experiments (in red) where the experiments were conducted at both
and
mT (equivalent to 20 and 30
output
) except for TS, which was applied at only
mT, due to the sever coil overheating that was suffered at
mT and kept interrupting the experiments. The results are shown in
Figure 11.
The results showed a decrease by half in the heat efficiency at 100 kHz (in black) compared to the 75 mgFe/mL experiments. At 200 kHz (in red), it required increasing B to mT to reach the same values the 75 mgFe/mL concentration had achieved at 100 kHz in the previous section. Hence, by decreasing the NP concentration by half, the heat efficiency also decreased by half. Since the decrease is linear, this means that there is no aggregation occurring in the experiments using 75 mgFe/mL concentration. Nevertheless, even if aggregation occurred, it would be identical in all the experiments since the same methodology was used throughout the study; hence, it would be hard to determine whether the AMF shape effects the NP aggregation.
On the other hand, TS followed by TP both showed a higher heat production than SN, as expected. On the other hand, at 500 kHz (in green), the final values are slightly lower than those achieved using 75 mgFe/mL NPs. However, still, the TS shows higher efficiency than SN, although the former was placed mT lower than the latter. However, at 1 MHz (in blue), we can see TP and TS regaining their superiority in heat efficiency compared to SN. The latter is even surpassed by TR and TT waveforms. Nevertheless, TP showing higher efficiency than TS is also unexpected, an irregularity seen in all the experiments conducted at B equal to mT.
The results of the experiments of this section confirmed the positive effect of the frequency on NP heating. It also showed that decreasing the NP concentration negatively affects lower frequencies (100 kHz and 200 kHz), although this effect is reduced significantly at 500 kHz. The results at 1 MHz, although irregular, still showed less clustering of values compared to the 75 mgFe/mL experiments. This could mean that lower concentrations are more responsive to unconventional waveforms at high frequencies, where a high concentration is more responsive to the conventional signal. Yet again, we cannot jump to conclusions until further investigation is conducted on the NPs’ behavior at very low magnetic field intensities.
3.4. Thermal Power Ratio
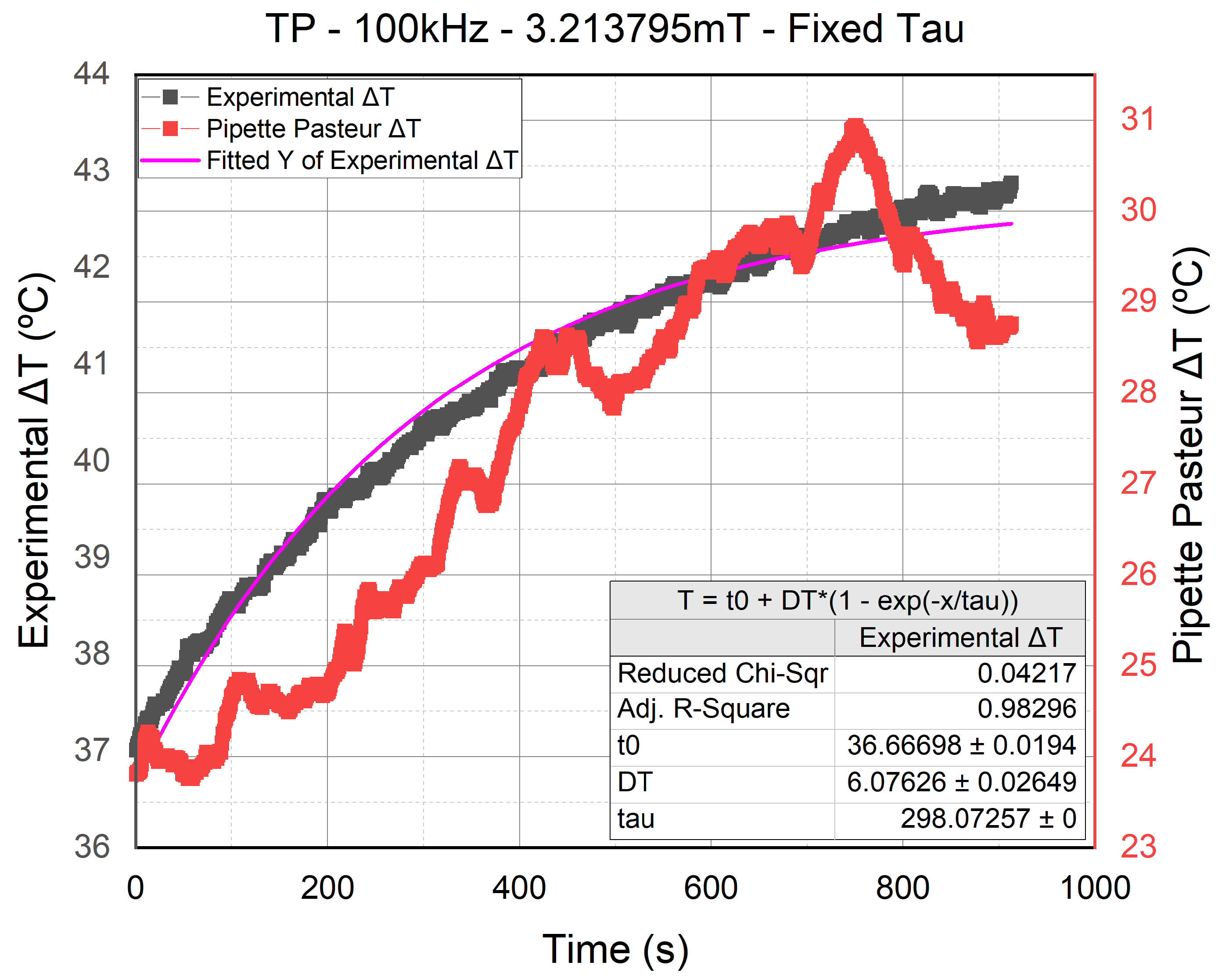
The power dissipation of the NPs is calculated using Equation (
1). However, when comparing the
deduced from the calorimeter calibration in Rosales et al. [
27] to the
we deduced using the error
approach, we found a significant difference. By comparing the fitting conducted using our
in
Figure 7 (in clear blue) to the one conducted using the
from the calibration in
Figure 12 (in violet), it can be seen that the
acquired from the calibration was not reliable. Hence, until we have enhanced the calorimeter calibration and acquire a
almost equal to the
we deduced in the previous sections, the Power dissipation calculation will not be reliable. Therefore, we decided to use a different approach to analyze the heating capabilities of each signal.
Using Equation (
6), we were able to establish a ratio determining the unconventional waveform’s efficiency compared to the conventional sinusoidal, where a negative and a positive
refer to a lesser and higher efficiency, respectively. Furthermore, the
value was calculated based on the
-
method described in Wildeboer et al. [
31], using the
deduced from the
-
described previously. However, the thermal capacitance
was taken from the calibration results in Rosales et al. [
27], although the value is probably inaccurate since the
acquired from the same calibration was also unreliable. However, similar to the
, we merely aim to analyze and compare the
values of each signal. The results are represented in
Table 2.
In both concentrations found in
Table 2, the TS and TP were more efficient than the SN waveform in the entire experimental conditions except at 1 MHz while using 75 mgFe/mL NPs. Even then, SN had a thermal power more efficient by only
% compared to TS and
% in the case of TP. TS dominated SN in the rest of the experiments, achieving maximum efficiency at 200 kHz/
mT, with
equal to
% at both 75 mgFe/mL and
mgFe/mL. These results prove that AMF waveforms with higher slopes have a higher impact on the NP’s heating efficiency and the overall MNP hyperthermia technique.
3.5. Power Dissipation Dependency on the Waveform’s Slope
In order to determine the dependency of NPs’ power dissipation on the signal slope, we have to go back to the Rosensweig equation in Equation (
1). We set our focus upon the magnetic field intensity
and the frequency
f while neglecting the other variable. The thermal power depends on the product of
f and
to the power two, which means if normalized by dividing to the product of
f·
to the power two, the thermal power should be essentially almost constant since the NP denominator
varies slightly with the frequency. Next, we go back to the
formula in Equation (
2), and we also focus on the same variables. Looking at these two equations, we notice that by dividing the thermal power from Equation (
1) by the product of
·
from Equation (
2) to the power of two, we can determine the relationship between the former and the waveform slope.
Since we do not possess an actual thermal power value, we will use the
from
Table 2. However, zero and negative values cannot be included in the calculations, so instead of subtracting
in Equation (
6), we carried it out as follows:
The objective in Equation (
7) is to set
at 100 instead of 0. Next, we divide the previous result by the slope as follows:
All the values of
used in this study and represented in
Figure 8,
Figure 10,
Figure 11 and
Table 2 were applied in Equation (
7) to then deduce their corresponding
from Equation (
8).
The values were so small that they were plotted using a
scale plot, as shown in
Figure 13.
In
Figure 13, the experiment results using 75 mgFe/mL are represented in black, whereas the ones conducted using
mgFe/mL are represented in red, and every waveform used in the experiments is represented by its own sign.
Although
should be almost constant or very slightly dependent on frequency, following the Rosensweig equation, it actually strongly depends on the
(
·
f),
and
f, as can be seen in
Figure 13. Of course, this does not contradict that
positively depends on the
and that, specifically, the
that keeps the frequency and magnetic field peak equal also determines the
value as a function of the waveform, as shown in
Figure 13. The explanation for this phenomenon still deserves further investigation and may be related to recent studies [
34,
35].
4. Discussion
The experimental results in this study showed the heat generation superiority of TS and TP compared to the SN, TT and TR signals. Moreover, in some instances, TS reached a
higher efficiency in thermal power generation than the SN, with TP closely behind. In Allia et al. [
34] and Barrera et al. [
35], theoretical studies were conducted to analyze the effect of the hysteresis loop on NPs’ heating efficiency. The simulation results showed the superiority of a square signal over the conventional sinusoidal signal. However, since generating a pure square AC signal at these frequencies is intrinsically very difficult and not possible with the equipment we have now, a more realistic simulation should be conducted in the future to compare the results with the experimental ones. Furthermore, an intensive theoretical study and simulations will focus on the consequences of replacing a single SN term with the Fourier sum of the unconventional signals, in addition to the analysis of the waveforms’ Fourier spectrum and determining the latter’s relationship with the frequency and relaxation time dependence on the dissipated power from Equation (
1).
The results showed the effect of the frequency on small NPs, as mentioned in Roca et al. [
16], where a temperature increase was witnessed even at small magnetic field strengths. Furthermore, the experiments showed that a
mgFe/mL NP concentration is more responsive to unconventional than conventional AMF waveforms at 1 MHz frequencies, where all waveforms exceeded SN in heat dissipation by
at best by TP and by
% at worst by TR. On the other hand, at lower frequencies, the concentration of the MNPs were proportional to their heating efficiency. This fact led to the assumption that no aggregation occurred during the experiments since the lowering of the NP concentration by half led to the loss of almost half of the heat efficiency, which showed the adequacy of the experimental protocols used in these experiments. In contrast, abnormal phenomena appeared at magnetic field strengths below
mT, where NP showed unexpected
results. This might be due to the chains’ formation effect discussed in Mille et al. [
21]. This should be investigated further to determine if the cause is the exposure time,
B, to what extent the MNPs’ concentration has an effect on the formation of the chains, and if the waveform shape has any impact on it. Furthermore, it is vital to determine whether the AMF shape affects the NP aggregation and to identify each waveform’s affect magnitude for different NP concentrations, frequencies and AMF strength conditions.
These results confirm the conclusion in Rosales et al. [
27] that using a low SPION concentration and exposing them to AMF waveforms with more significant slopes, such as TS and TP, at high frequencies has a higher efficiency than those with higher frequencies conventional signals. This will result in MNP hyperthermia therapies with lower NP toxicity risk and lower magnetic field intensity requirements. However, since the concentration effect is now determined, the shape effect should be targeted in future experiments. In Avugadda et al. [
36] and Abenojar et al. [
37], the cubic-shaped particles showed a higher
than the spherical-shaped, in addition to the promising results shown in Sánchez et al. [
18], so perhaps the cubic-shaped would perform even better with non-conventional signals.
Furthermore, following the calculation of
, the results showed the dependency of the thermal power generated by the NP on the waveform’s slope, as it was previously hypothesized in Garcia et al. [
28], Zeinoun et al. [
30] and Urbano et al. [
29]. However, further investigation is required in order to determine the factor that TR and TT are aligned exponentially, while TS, TP and SN are aligned horizontally.
To summarize, the experiments showed higher heat production efficiency of TS and TP AMF waveforms at best by
% and
%, respectively, over the conventional SN waveform. Furthermore, the results showed that the higher the frequency, the lower concentration is required to create the most efficient conditions for the MNPs. Finally, the
calculation results proved the dependency of the power dissipation on the waveform’s slope and not only
B and
f, as mentioned in Rosensweig et al. [
26].
5. Conclusions
We have successfully shown the higher efficiency of AMF waveforms of significant slopes over the conventional SN in MNP hyperthermia. The experiments showed higher heat production efficiency of TS and TP AMF waveforms at best by % and %, respectively, over the conventional SN waveform. However, it might not be the highest efficiency available, which is why further investigation will be conducted to search for a waveform that might even surpass the % superiority over SN.
Furthermore, we have demonstrated the effectiveness of the slope, frequency and NP concentration on the therapy. We concluded that the ideal conditions for low concentrations of SPIONs are the use of signals with more significant slopes (TS and TP) at radiofrequencies, which will result in increasing the efficiency of the therapy while lowering the toxicity levels.
Future Work
The hyperthermia system requires a coil suited for radiofrequency operations in addition to an adequate cooling system for it. This will allow us to exploit the full capability of the AMF generator and conduct high-frequency experiments at higher intensities without overheating issues.
Furthermore, a glass-based in vitro sample holder is currently being designed to conduct in vitro studies since the current calorimeter is only for MR tubes. Our objective is to design a sample holder that can fit a dish (35 mm Ø, 10 cm) inside and have the ability to isolate the sample and block the external temperature interferences.