Geometrical Nonlinearity for a Timoshenko Beam with Flexoelectricity
Abstract
:1. Introduction
2. A Linear Theory of Direct Flexoelectricity
- Essential b.c.:
- Natural b.c.:wherethe traction vector and the electric charge are defined as follows:with , is the Dirac delta function, and is the Cartesian component of the unit tangent vector on Γ.
3. Timoshenko Beam with Flexoelectric Effect and Nonlinear Strains
- (i)
- Total shear force or the beam deflection vanishes at the end of the beam:
- (ii)
- Total bending moment or rotation of the cross-section vanishes at the end of the beam:
- (iii)
- Higher-order shear force or the deflection slope vanishes at the end of the beam:
- (iv)
- Higher-order bending moment or gradient of rotation vanishes at the end of the beam:
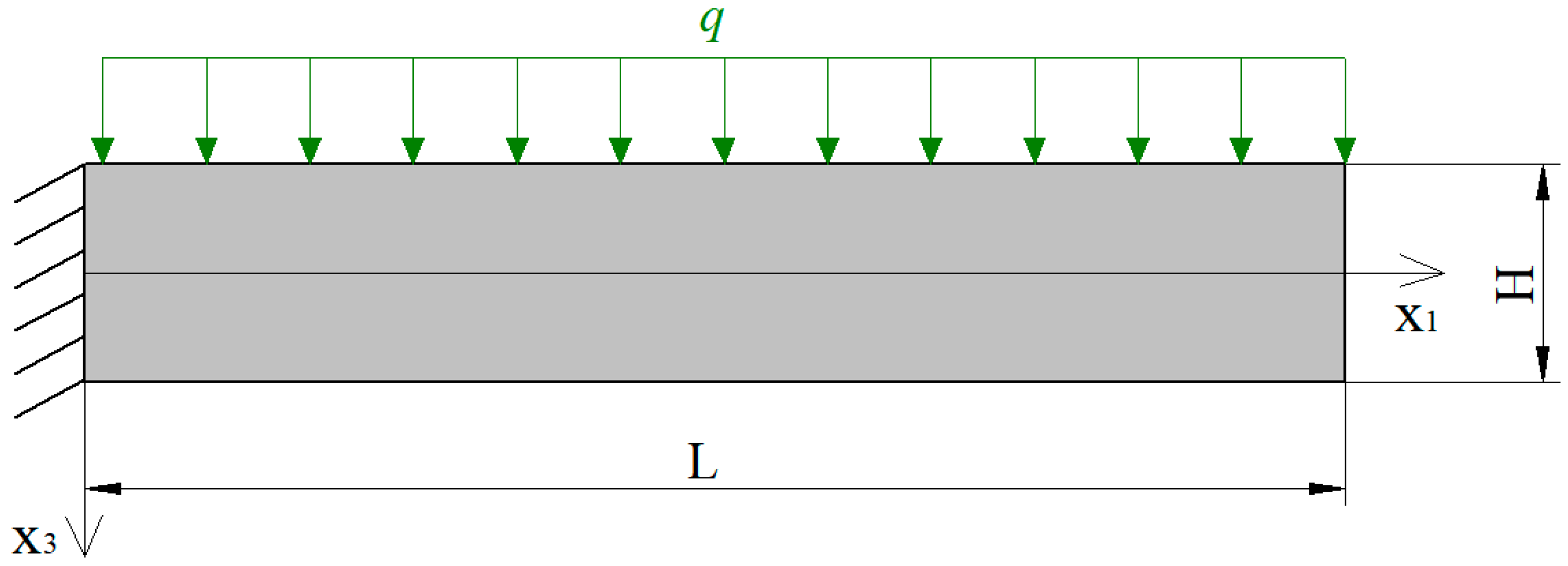
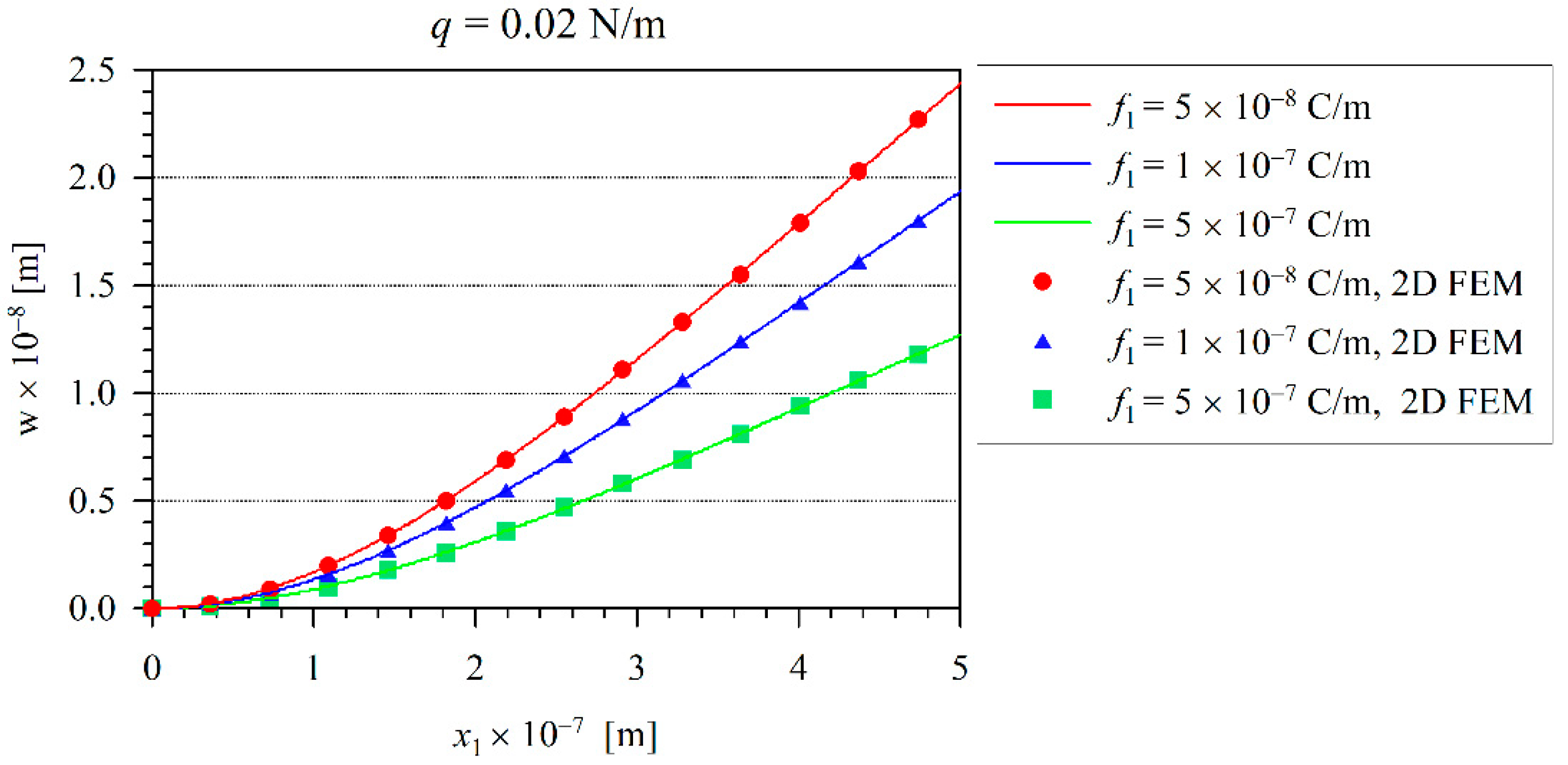
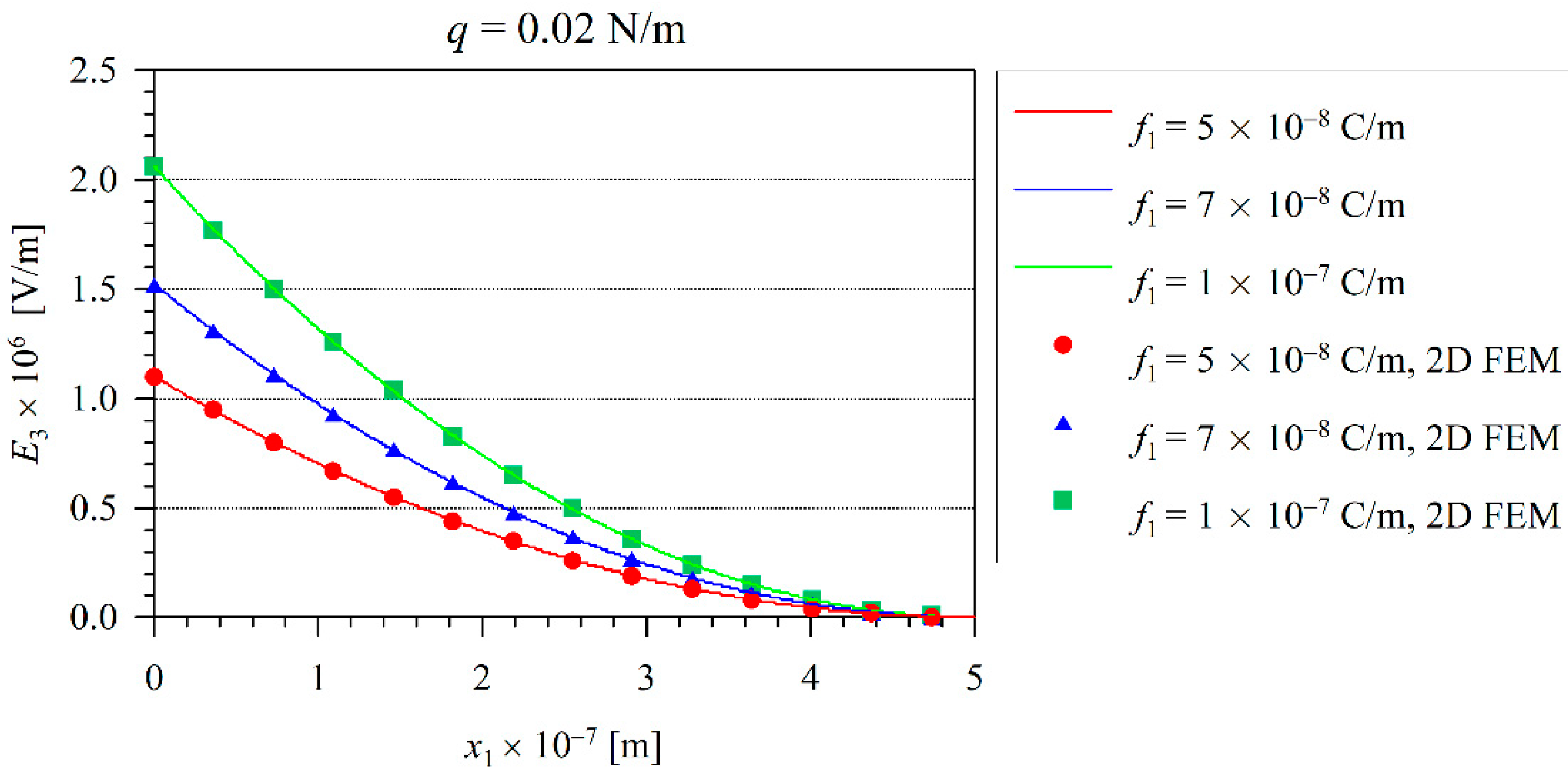
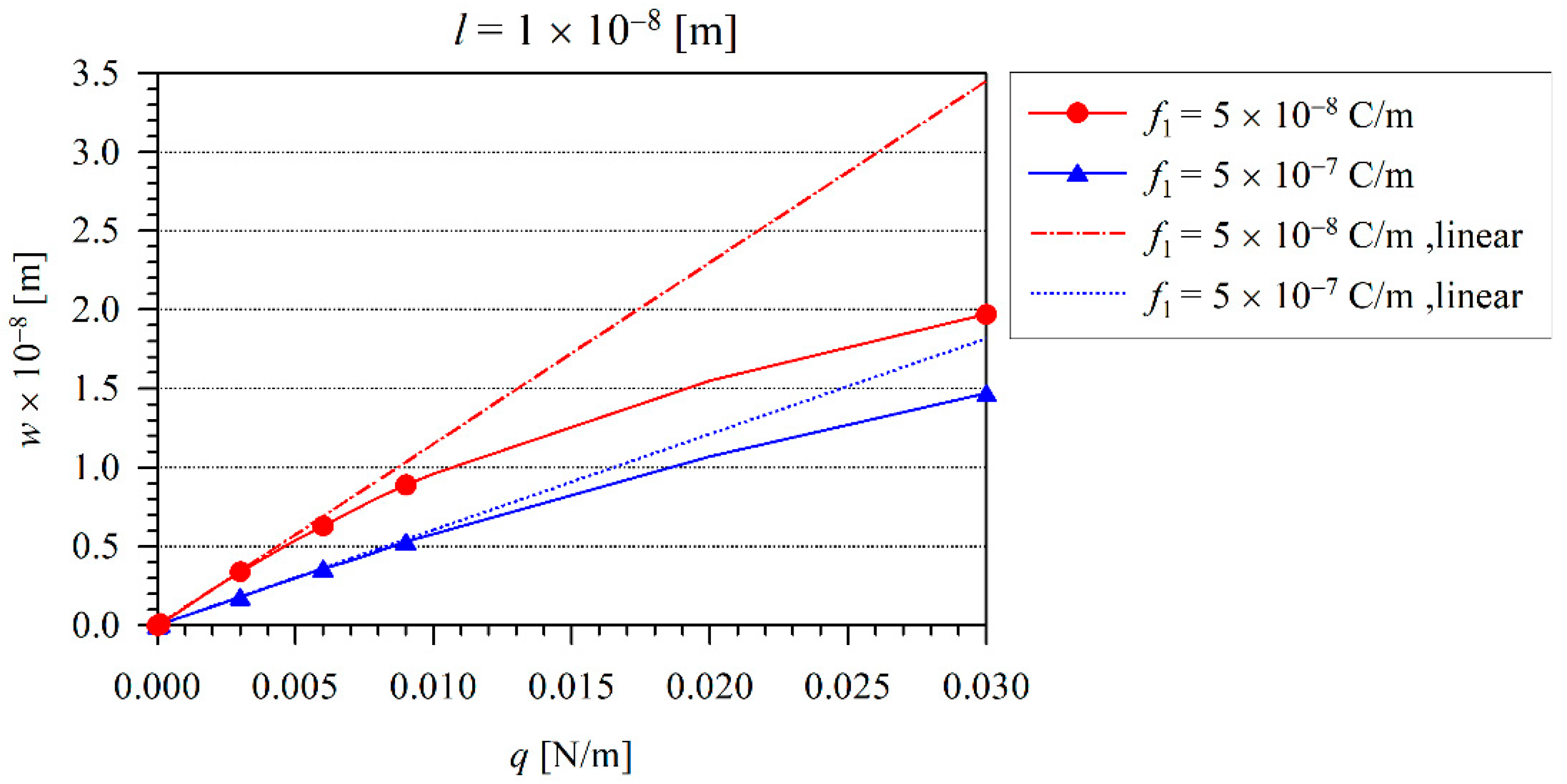
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yaghoubi, S.T.; Mousavi, S.M.; Paavola, J. Buckling of centrosymmetric anisotropic beam structures within strain gradient elasticity. Int. J. Solids Struct. 2017, 109, 84–92. [Google Scholar] [CrossRef]
- Reddy, J. An Introduction to Nonlinear Finite Element Analysis; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Wang, K.F.; Zeng, S.; Wang, B.L. Large amplitude free vibration of electrically actuated nanobeams with surface energy and thermal effects. Int. J. Mech. Sci. 2017, 131–132, 227–233. [Google Scholar] [CrossRef]
- Faroughi, S.; Rojas, E.F.; Abdelkefi, A.; Park, Y.H. Reduced-order modeling and usefulness of non-uniform beams for flexoelectric energy harvesting applications. Acta Mech. 2019, 230, 2339–2361. [Google Scholar] [CrossRef]
- Majdoub, M.S.; Sharma, P.; Cagin, T. Enhanced size dependent piezoelectricity and elasticity in nanostructures due to the flexoelectric effect. Phys. Rev. B 2008, 77, 125424. [Google Scholar] [CrossRef] [Green Version]
- Tagantsev, A.K. Piezoelectricity and flexoelectricity in crystalline dielectrics. Phys. Rev. B 1986, 34, 5883–5889. [Google Scholar] [CrossRef] [PubMed]
- Tagantsev, A.K.; Meunier, V.; Sharma, P. Novel electromechanical phenomena at the nanoscale: Phenomenological theory and atomistic modelling. MRS Bull. 2009, 34, 643–647. [Google Scholar] [CrossRef]
- Maranganti, R.; Sharma, N.D.; Sharma, P. Electromechanical coupling in non-piezoelectric materials due to nanoscale nonlocal size effects: Green’s function solutions and embedded inclusions. Phys. Rev. B 2006, 74, 014110. [Google Scholar] [CrossRef] [Green Version]
- Tagantsev, A. Theory of flexoelectric effect in crystals. JETP Lett. 1985, 88, 2108–2122. [Google Scholar]
- Yudin, P.; Tagantsev, A. Fundamentals of Flexoelectricity in Solids. Nanotechnology 2013, 24, 432001. [Google Scholar] [CrossRef]
- Jiang, X.; Huang, W.; Zhang, S. Flexoelectric nano-generator: Materials, structures and devices. Nano Energy 2013, 2, 1079–1092. [Google Scholar] [CrossRef]
- Hu, S.; Shen, S. Variational principles and governing equations in nano-dielectrics with the flexoelectric effect. Sci. China Phys. Mech. Astron. 2010, 53, 1497–1504. [Google Scholar] [CrossRef]
- Wang, K.F.; Wang, B.L. An analytical model for nanoscale unimorph piezoelectric energy harvesters with flexoelectric effect. Compos. Struct. 2016, 153, 253–261. [Google Scholar] [CrossRef]
- Mindlin, R.; Tiersten, H. Effects of couple-stresses in linear elasticity. Arch. Ration. Mech. Anal. 1962, 11, 415–448. [Google Scholar] [CrossRef]
- Mindlin, R.D. Second gradient of strain and surface tension in linear elasticity. Int. J. Solids Struct. 1965, 1, 417–438. [Google Scholar] [CrossRef]
- Ma, H.; Gao, X.L.; Reddy, J. A microstructure-dependent Timoshenko beam model based on a modified couple stress theory. J. Mech. Phys. Solids 2008, 56, 3379–3391. [Google Scholar] [CrossRef]
- Deng, Q.; Kammoun, M.; Erturk, A.; Sharma, P. Nanoscale flexoelectric energy harvesting. Int. J. Solids Struct. 2014, 51, 3218–3225. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.F.; Wang, B.L. Non-linear flexoelectricity in energy harvesting. Int. J. Eng. Sci. 2017, 116, 88–103. [Google Scholar] [CrossRef]
- Ansari, R.; Pourashraf, T.; Gholami, R. An exact solution for the nonlinear forced vibration of functionally graded nanobeams in thermal environment based on surface elasticity theory. Thin Wall. Struct. 2015, 93, 169–176. [Google Scholar] [CrossRef]
- Thai, T.Q.; Rabczuk, T.; Zhuang, X. A large deformation isogeometric approach for flexoelectricity and soft materials. Comp. Methods App. Mech. Eng. 2018, 341, 718–739. [Google Scholar] [CrossRef]
- Barati, M.R. On non-linear vibrations of flexoelectric nanobeams. Int. J. Eng. Sci. 2017, 121, 143–153. [Google Scholar] [CrossRef]
- Malikan, M.; Eremeyev, V.A. On nonlinear bending study of a piezo-flexomagnetic nanobeam based on an analytical-numerical solution. Nanomaterials 2020, 10, 1762. [Google Scholar] [CrossRef] [PubMed]
- Malikan, M.; Eremeyev, V.A. On the geometrically nonlinear vibration of a piezo-flexomagnetic nanotube. Math. Methods App. Sci. 2021. [Google Scholar] [CrossRef]
- Malikan, M.; Eremeyev, V.A. On the dynamics of a visco-piezo-flexoelectric nanobeam. Symmetry 2020, 12, 643. [Google Scholar] [CrossRef] [Green Version]
- Sahmani, S.; Aghdam, M.M. Nonlocal strain gradient beam model for nonlinear vibration of prebuckled and postbuckled multilayer functionally graded GPLRC nanobeams. Comp. Struct. 2017, 179, 77–88. [Google Scholar] [CrossRef]
- Malikan, M. Electro-mechanical shear buckling of piezoelectric nanoplate using modified couple stress theory based on simplified first order shear deformation theory. Appl. Math. Model. 2017, 48, 196–207. [Google Scholar] [CrossRef]
- Hu, S.L.; Shen, S.P. Electric field gradient theory with surface effect for nano-dielectrics. CMC: Computers. Mater. Contin. 2009, 13, 63–87. [Google Scholar]
- Parton, V.Z.; Kudryavtsev, B.A. Electromagnetoelasticity: Piezoelectrics and Electrically Conductive Solids; Taylor & Francis: Abingdon, UK, 1988. [Google Scholar]
- Shen, S.P.; Hu, S.L. A theory of flexoelectricity with surface effect for elastic dielectrics. J. Mech. Phys. Solids 2010, 58, 665–677. [Google Scholar] [CrossRef]
- Gitman, I.; Askes, H.; Kuhl, E.; Aifantis, E. Stress concentrations in fractured compact bone simulated with a special class of anisotropic gradient elasticity. Int. J. Solids Struct. 2010, 47, 1099–1107. [Google Scholar] [CrossRef]
- Deng, F.; Deng, Q.; Yu, W.; Shen, S. Mixed finite elements for flexoelectric solids. J. App. Mech. 2017, 84, 0810041. [Google Scholar] [CrossRef]
- Lekhnitskii, S.G. Theory of Elasticity of an Anisotrophic Elastic Body; Holden-Day: San Francisco, CA, USA, 1963. [Google Scholar]
- Sladek, J.; Sladek, V.; Wunsche, M.; Zhang, C. Effects of electric field and strain gradients on cracks in piezoelectric solids. Eur. J. Mech.—A/Solids 2018, 71, 187–198. [Google Scholar] [CrossRef]
- Chen, W.; Liang, X.; Shen, S. Forced vibration of piezoelectric and flexoelectric Euler-Bernoulli beams by dynamic Green’s functions. Acta Mech. 2021, 232, 449–460. [Google Scholar] [CrossRef]
- McMeeking, R.M. The energy release rate for a Griffith crack in a piezoelectric material. Eng. Fract. Mech. 2004, 71, 1149–1163. [Google Scholar] [CrossRef]
- Tian, X.; Sladek, J.; Sladek, V.; Deng, Q.; Li, Q. A collocation mixed finite element method for the analysis of flexoelectric solids. Int. J. Solids Struct. 2021, 217/218, 27–39. [Google Scholar] [CrossRef]
- Wen, P.H.; Aliabadi, M.H.; Young, A. Post buckling analysis of Reissner plates by the boundary element method. J. Strain Anal. Eng. 2006, 41, 239–252. [Google Scholar] [CrossRef]
- Wen, P.H.; Hon, Y.C. Geometrically nonlinear analysis of Reissener–Mindlin plate by meshless computation. Comput. Model. Eng. Sci. 2007, 21, 177–191. [Google Scholar]
- Sladek, V.; Sladek, J.; Krahulec, S.; Pan, E. The MLPG analyses of large deflections of magnetoelectroelastic plates. Eng. Anal. Bound. Elem. 2013, 37, 673–682. [Google Scholar] [CrossRef]
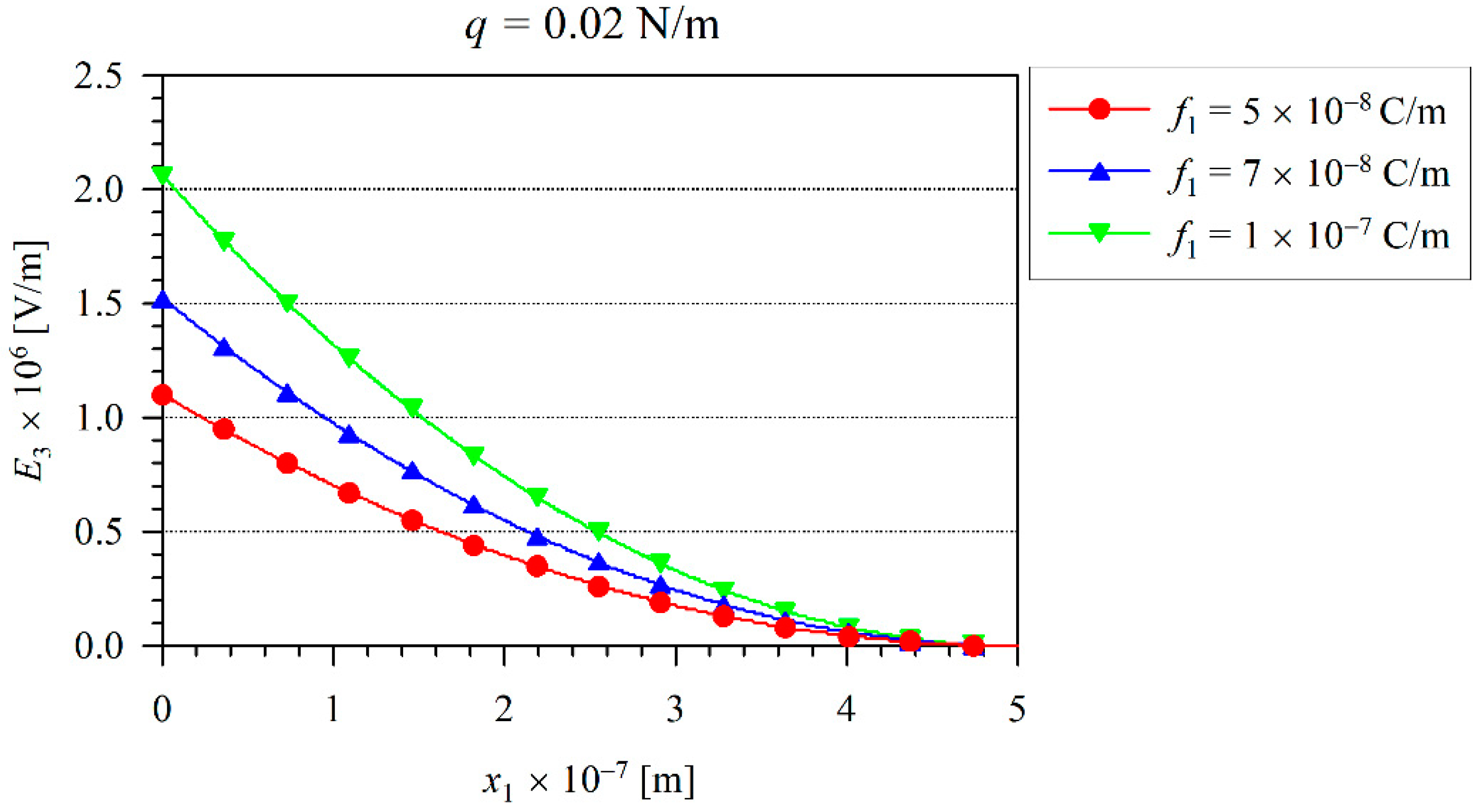
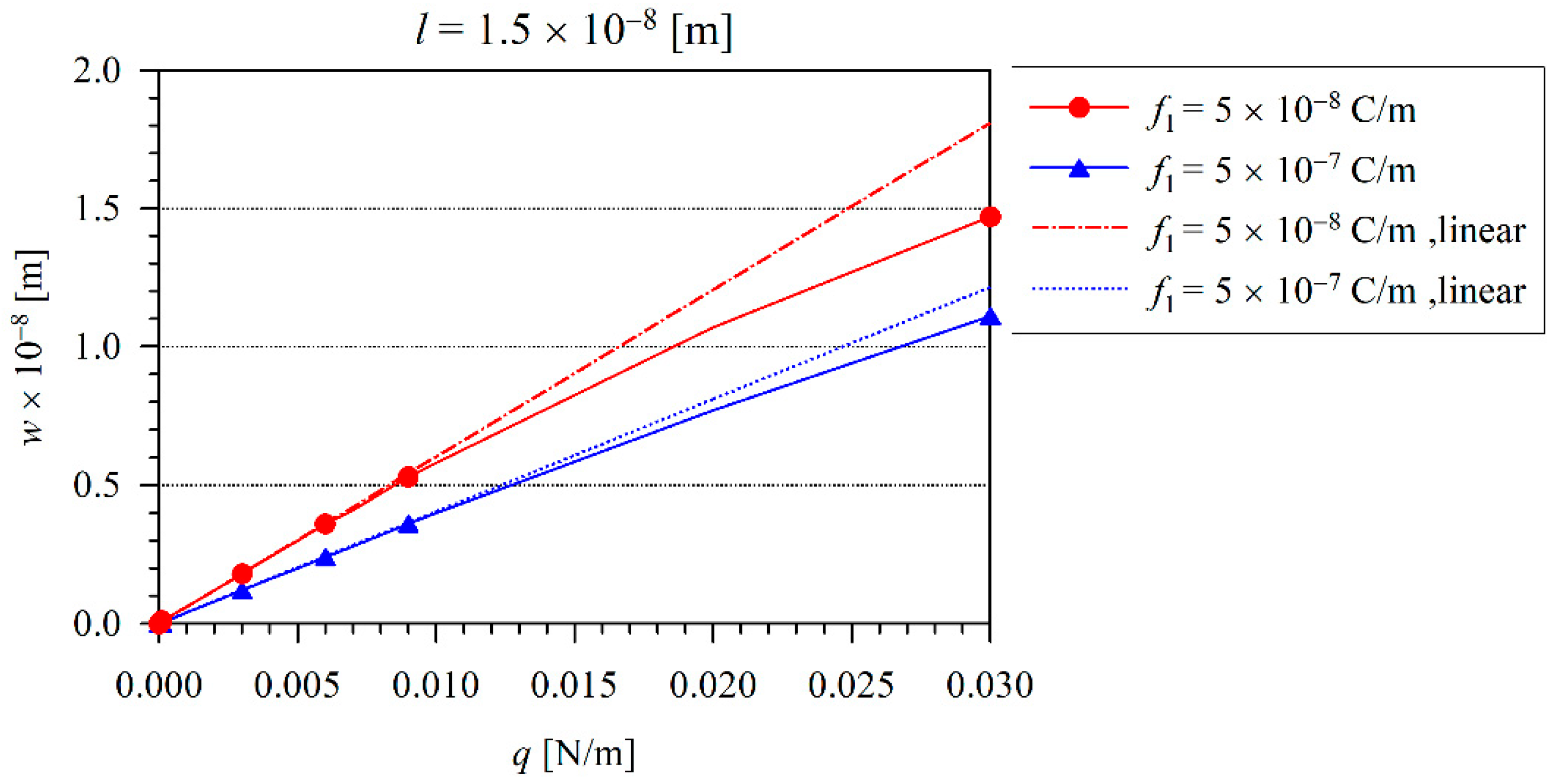

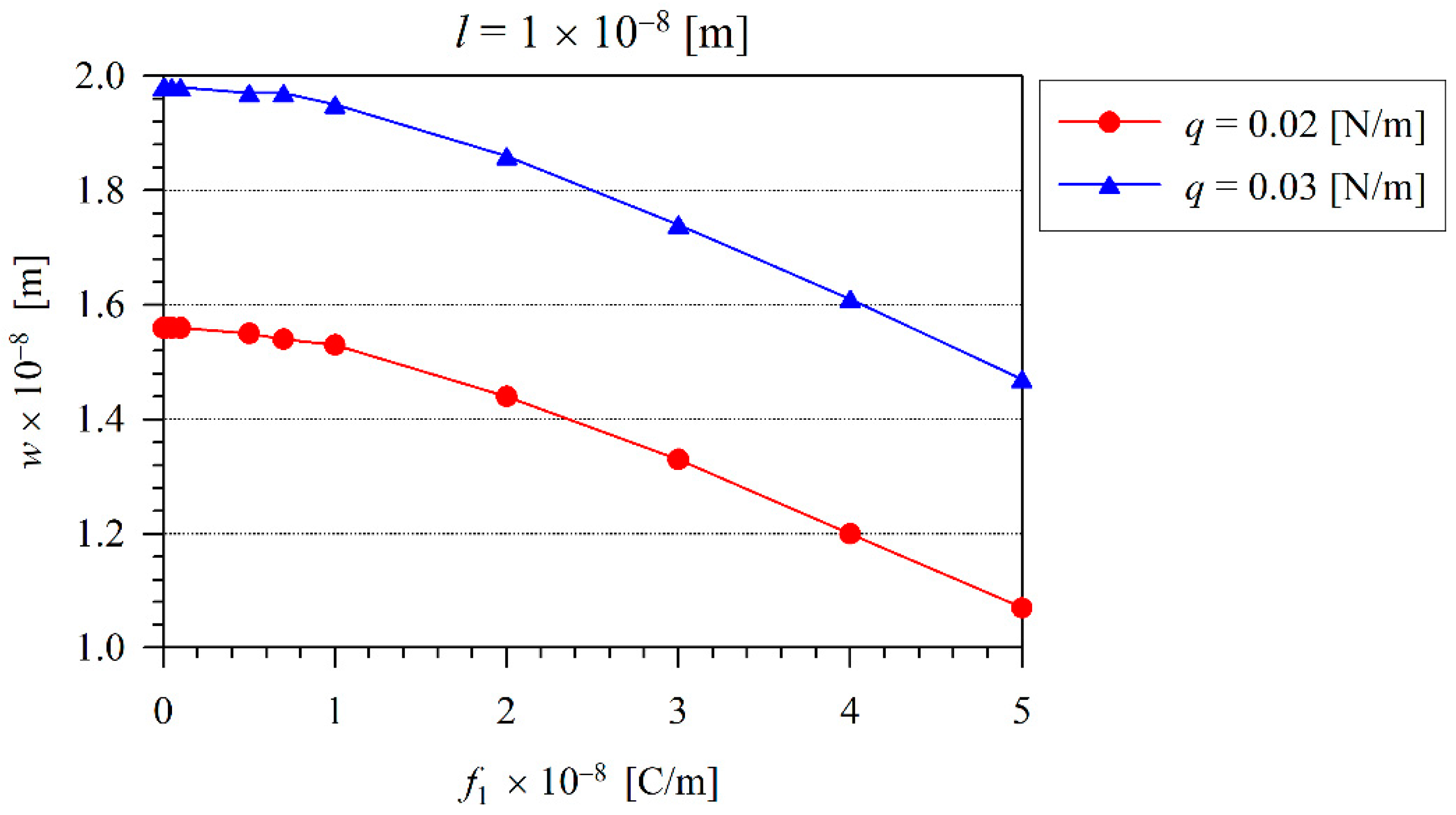
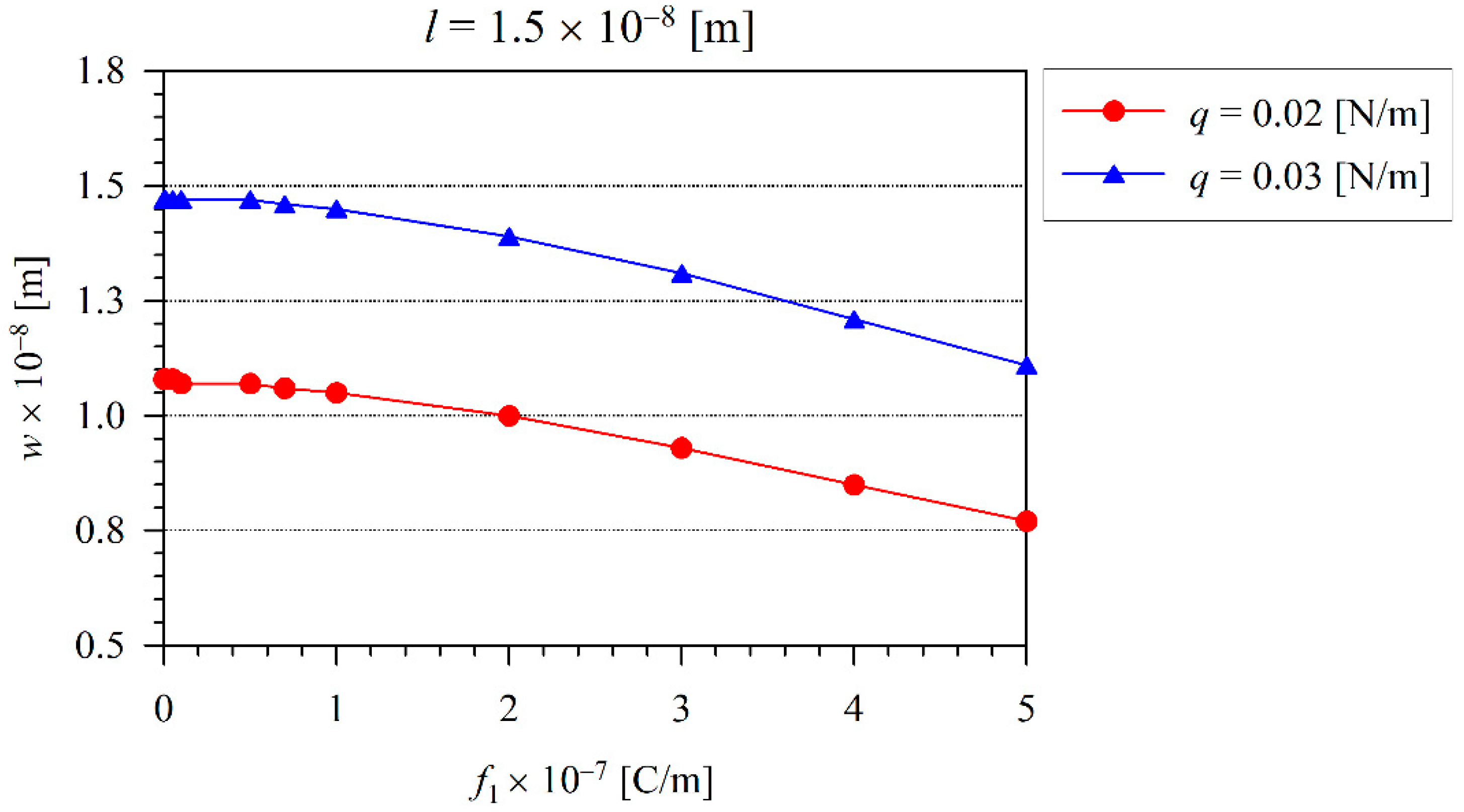
| Number of Elements | w (x1 = 2.5 × 10−7) |
|---|---|
| 10 elements | 6.353723 × 10−9 |
| 20 elements | 6.750830 × 10−9 |
| 50 elements | 6.750842 × 10−9 |
| 100 elements | 6.750842 × 10−9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Repka, M.; Sladek, J.; Sladek, V. Geometrical Nonlinearity for a Timoshenko Beam with Flexoelectricity. Nanomaterials 2021, 11, 3123. https://doi.org/10.3390/nano11113123
Repka M, Sladek J, Sladek V. Geometrical Nonlinearity for a Timoshenko Beam with Flexoelectricity. Nanomaterials. 2021; 11(11):3123. https://doi.org/10.3390/nano11113123
Chicago/Turabian StyleRepka, Miroslav, Jan Sladek, and Vladimir Sladek. 2021. "Geometrical Nonlinearity for a Timoshenko Beam with Flexoelectricity" Nanomaterials 11, no. 11: 3123. https://doi.org/10.3390/nano11113123
APA StyleRepka, M., Sladek, J., & Sladek, V. (2021). Geometrical Nonlinearity for a Timoshenko Beam with Flexoelectricity. Nanomaterials, 11(11), 3123. https://doi.org/10.3390/nano11113123






