Dielectric Confinement and Exciton Fine Structure in Lead Halide Perovskite Nanoplatelets
Abstract
:1. Introduction
2. Electronic and Dielectric Confinement Effects on the Exciton Energy
2.1. Theoretical Methods
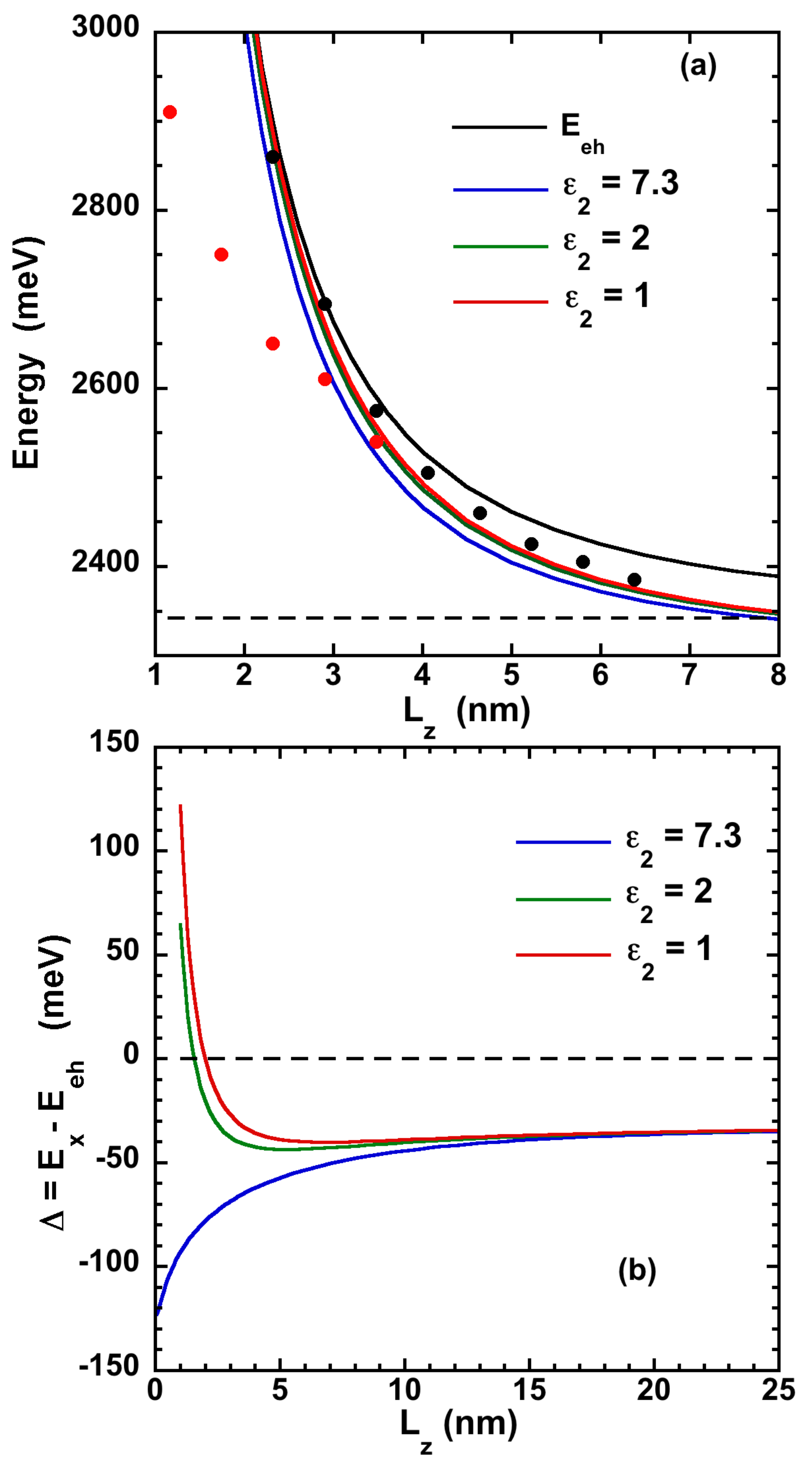
2.2. Results and Discussion on Exciton Energy
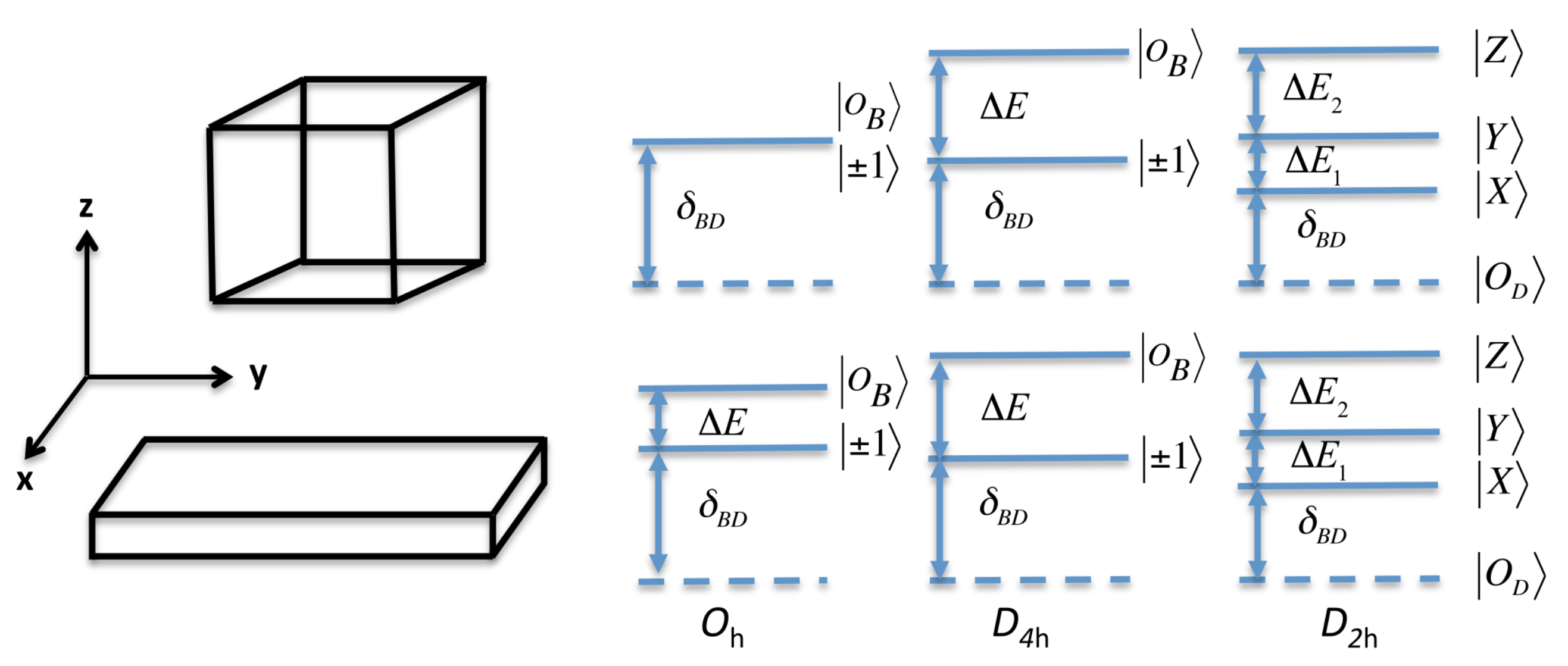
3. Electronic and Dielectric Confinement Effects on the Exciton Fine Structure
3.1. Theoretical Methods
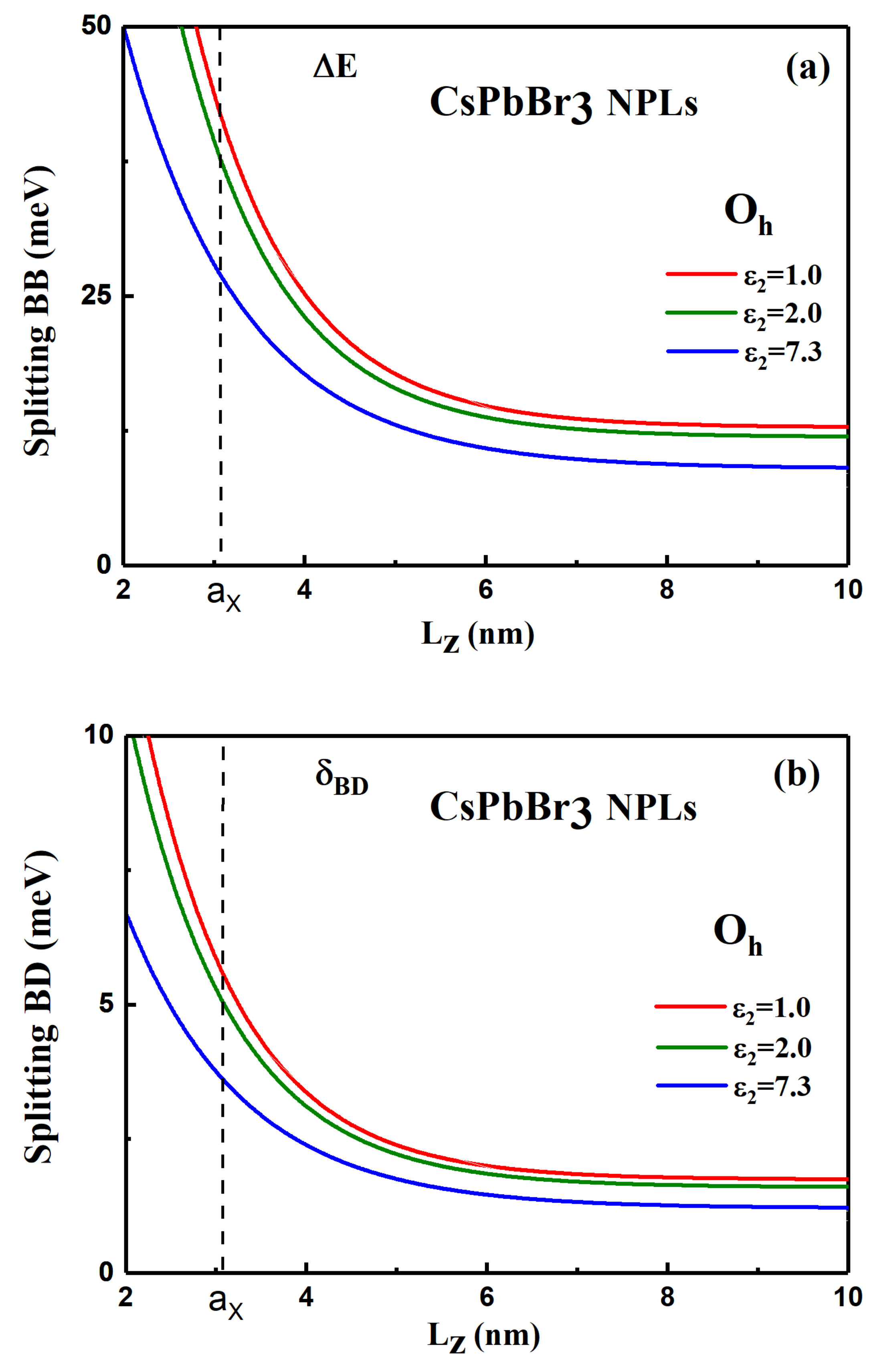
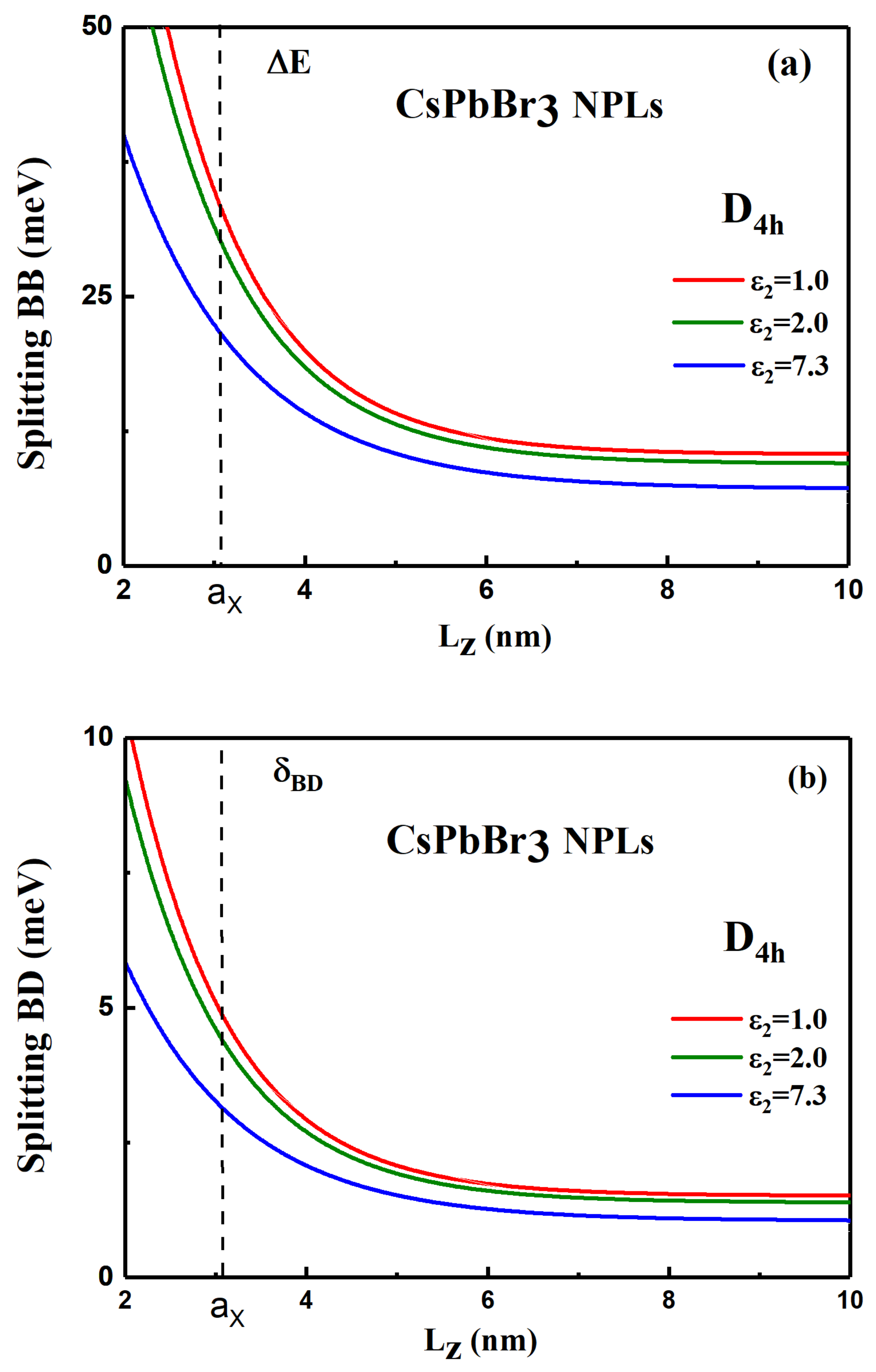
3.2. Results and Discussion on Exciton FSS
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Joo, J.; Na, H.B.; Yu, T.; Yu, J.H.; Kim, Y.W.; Wu, F.; Zhang, J.Z.; Hyeon, T. Generalized and Facile Synthesis of Semiconducting Metal Sulfide Nanocrystals. J. Am. Chem. Soc. 2003, 125, 11100–11105. [Google Scholar] [CrossRef] [PubMed]
- Ithurria, S.; Dubertret, B. Quasi 2D Colloidal CdSe Platelets with Thickness Controlled at the Atomic Level. J. Am. Chem. Soc. 2008, 130, 16504–16505. [Google Scholar] [CrossRef]
- Achtstein, A.W.; Antanovich, A.; Prudnikau, A.; Scott, R.; Woggon, U.; Artemyev, M.V. Linear Absorption in CdSe Nanoplates: Thickness and Lateral Size Dependency of the Intrinsic Absorption. J. Phys. Chem. C 2015, 119, 20156–20161. [Google Scholar] [CrossRef]
- Naeem, A.; Masia, F.; Christodoulou, S.; Moreels, I.; Borri, P.; Langbein, W. Giant Exciton Oscillator Strength and Radiatively Limited Dephasing in Two-Dimensional Platelets. Phys. Rev. B Condens. Matter Mater. Phys. 2015, 91, 121302. [Google Scholar] [CrossRef]
- Ithurria, S.; Tessier, M.D.; Mahler, B.; Lobo, R.P.S.M.; Dubertret, B.; Efros, A.L. Colloidal Nanoplatelet with Two-Dimensional Electronic Structure. Nat. Mater. 2011, 10, 936–941. [Google Scholar]
- Scott, R.; Achtstein, A.W.; Prudnikau, A.; Antanovich, A.; Christodoulou, S.; Moreels, I.; Artemyev, M.; Woggon, U. Two Photon Absorption in II-VI Semiconductors: The Influence of Dimensionnality and Size. Nano Lett. 2015, 15, 4985. [Google Scholar] [CrossRef] [PubMed]
- Protesescu, L.; Yakunin, S.; Bodnarchuk, M.I.; Krieg, F.; Caputo, R.; Hendon, C.H.; Yang, R.X.; Walsh, A.; Kovalenko, M.V. Nanocrystals of Cesium Lead Halide Perovskites (CsPbX3, X = Cl, Br, and I): Novel Optoelectronic Materials Showing Bright Emission with Wide Color Gamut. Nano Lett. 2015, 15, 3692–3696. [Google Scholar] [CrossRef] [Green Version]
- Bekenstein, Y.; Koscher, B.A.; Eaton, S.W.; Yang, P.; Alivisatos, A.P. Highly Luminescent Colloidal Nanoplates of Perovskite Cesium Lead Halide and Their Oriented Assemblies. J. Am. Chem. Soc. 2015, 137, 16008–16011. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Akkerman, Q.A.; Motti, S.G.; Srimath Kandada, A.R.; Mosconi, E.; D’Innocenzo, V.; Bertoni, G.; Marras, S.; Kamino, B.A.; Miranda, L.; De Angelis, F.; et al. Solution Synthesis Approach to Colloidal Cesium Lead Halide Perovskite Nanoplatelets with Monolayer-Level Thickness Control. J. Am. Chem. Soc. 2016, 138, 1010–1016. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Almeida, G.; Goldoni, L.; Akkerman, Q.; Dang, Z.; Khan, A.H.; Marras, S.; Moreels, I.; Manna, L. Role of Acid-Base Equilibria in the Size, Shape, and Phase Control of Cesium Lead Bromide Nanocrystals. ACS Nano 2018, 12, 1704–1711. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Swarnkar, A.; Ravi, V.K.; Nag, A. Beyond Colloidal Cesium Lead Halide Perovskite Nanocrystals: Analogous Metal Halides and Doping. ACS Energy Lett. 2017, 2, 1089–1098. [Google Scholar] [CrossRef]
- Wang, J.; Su, R.; Xing, J.; Bao, D.; Diederichs, C.; Liu, S.; Liew, T.C.H.; Chen, Z.; Xiong, Q. Room Temperature Coherently Coupled Exciton–Polaritons in Two-Dimensional Organic–Inorganic Perovskite. ACS Nano 2018, 12, 8382–8389. [Google Scholar] [CrossRef] [PubMed]
- Kumagai, M.; Takagahara, T. Excitonic and Non-Linear-Optical Properties of Dielectric Quantum-Well Structures. Phys. Rev. B Condens. Matter Mater. Phys. 1989, 40, 12359–12381. [Google Scholar] [CrossRef] [PubMed]
- Takagahara, T. Effects of Dielectric Confinement and Electron-Hole Exchange Interaction on Excitonic States in Semiconductor Quantum Dots. Phys. Rev. B Condens. Matter Mater. Phys. 1993, 47, 4569–4584. [Google Scholar] [CrossRef] [PubMed]
- Achtstein, A.W.; Schliwa, A.; Prudnikau, A.; Hardzei, M.; Artemyev, M.V.; Antanovich, A.; Thomsen, C.; Woggon, U. Electronic Structure and Exciton-Phonon Interaction in Two-Dimensional Colloidal CdSe Nanosheets. Nano Lett. 2012, 12, 3151–3157. [Google Scholar] [CrossRef] [PubMed]
- Rajadell, F.; Climente, J.I.; Planelles, J. Exciton in Core-Only, Core-Shell and Core-Crown CdSe Nanoplatelets: Interplay Between in-Plane Electron-Hole Correlation, Spatial Confinement and Dielectric Confinement. Phys. Rev. B Condens. Matter Mater. Phys. 2017, 96, 035307. [Google Scholar] [CrossRef] [Green Version]
- Benchamekh, R.; Gippius, N.A.; Even, J.; Nestoklon, M.O.; Jancu, J.-M.; Ithurria, S.; Dubertret, B.; Efros, A.L.; Voisin, P. Tight-Binding Calculations of Image-Charge Effects in Colloidal Nanoscale Platelet CdSe. Phys. Rev. B Condens. Matter Mater. Phys. 2014, 89, 035307. [Google Scholar] [CrossRef] [Green Version]
- Sapori, D.; Kepenekian, M.; Pedesseau, L.; Katan, C.; Even, J. Quantum Confinement and Dielectric Profiles of Colloidal Nanoplatelets of Halide Inorganic and Hybrid Organic–Inorganic Perovskites. Nanoscale 2016, 8, 6369–6378. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sometani, T.; Kenroku, H. Method for Solving Electrostatic Problems Having a Simple Dielectric Boundary. Am. J. Phys. 1977, 45, 918–921. [Google Scholar] [CrossRef]
- Keldysh, L.V. Coulomb Interaction in Thin Semiconductor and Semimetal Films. J. Exp. Theor. Phys. Lett. 1979, 29, 658. [Google Scholar]
- Keldysh, L.V. Excitons and Polaritons in Semiconductor/Insulator Quantum Wells and Superlattices. Superlattices Microstruct. 1988, 4, 637–642. [Google Scholar] [CrossRef]
- Keldysh, L.V. Excitons in Semiconductor-Dielectric Nanostructures. Phys. Stat. Sol. 1997, 164, 3–12. [Google Scholar] [CrossRef]
- Cudazzo, P.; Tokatly, I.V.; Rubio, A. Dielectric Screening in Two-Dimensional Insulators: Implications for Excitonic and Impurity States in Graphane. Phys. Rev. B Condens. Matter Mater. Phys. 2011, 84, 085406. [Google Scholar] [CrossRef] [Green Version]
- Shinozuka, Y.; Matsuura, M. Wannier Exciton in Quantum Wells. Phys. Rev. B Condens. Matter Mater. Phys. 1983, 28, 4878–4881. [Google Scholar] [CrossRef]
- Bayer, M.; Walck, S.N.; Reinecke, T.L.; Forchel, A. Exciton Binding Energies and Diamagnetic Shifts in Semiconductor Quantum Wires and Quantum Dots. Phys. Rev. B Condens. Matter Mater. Phys. 1998, 57, 6584–6591. [Google Scholar] [CrossRef]
- Yang, Z.; Surrente, A.; Galkowski, K.; Miyata, A.; Portugall, O.; Sutton, R.J.; Haghighirad, A.A.; Snaith, H.J.; Maude, D.K.; Plochocka, P.; et al. Impact of the Halide Cage on the Electronic Properties of Fully Inorganic Cesium Lead Halide Perovskite. ACS Energy Lett. 2017, 2, 1621–1627. [Google Scholar] [CrossRef] [Green Version]
- Baranowski, M.; Plochocka, P.; Sui, R.; Legrand, L.; Barisien, T.; Bernardot, F.; Xiong, Q.; Testelin, C.; Chamarro, M. Exciton Binding Energy and Effective Mass of CsPbCl3: A Magneto-Optical Study. Photon. Res. 2020, 8, A50–A55. [Google Scholar] [CrossRef]
- Steinmetz, V.; Ramade, J.; Legrand, L.; Barisien, T.; Bernardot, F.; Lhuillier, E.; Bernard, M.; Vabre, M.; Saïdi, I.; Ghribi, A.; et al. Anisotropic Shape of CsPbBr3 Colloidal Nano-Crystals: From 1D to 2D Confinement Effects. Nanoscale 2020, 12, 18978–18986. [Google Scholar] [CrossRef] [PubMed]
- Bohn, J.B.; Tong, Y.; Gramlich, M.; Lai, M.L.; Doblinger, M.; Wanf, K.; Hoye, R.L.Z.; Müller-Buschbaum, P.; Stranks, S.D.; Urban, A.S.; et al. Boosting Tunable Blue Luminescence of Halide Perovskite Nanoplatelets through Postsynthetic Surface Trap Repair. Nano Lett. 2018, 18, 5231–5238. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sichert, J.A.; Tong, Y.; Mutz, N.; Vollmer, M.; Fisher, S.; Milowska, K.Z.; Cortadella, R.G.; Nickel, B.; Cardenas-Daw, C.; Stolarczyk, J.K.; et al. Quantum Size Effect in Organometal Halide Perovskite Nanoplatelets. Nano Lett. 2015, 15, 6521–6527. [Google Scholar] [CrossRef] [PubMed]
- Haug, H.; Koch, S.W. Quantum Theory of the Optical and Electronic Properties of Semiconductors; World Scientific: Singapore, 2004; pp. 174–177. [Google Scholar]
- Chen, Y.; Gil, B.; Lefebvre, P.; Mathieu, M. Exchange Effects on Excitons in Quantum Wells. Phys. Rev. B Condens. Matter Mater. Phys. 1988, 37, 6429–6432. [Google Scholar] [CrossRef]
- Chamarro, M.; Gourdon, C.; Lavallard, P.; Lublinskaya, O.; Ekimov, A.I. Enhancement of Electron-Hole Exchange Interaction in CdSe Nanocrystals: A Quantum Confinement Effect. Phys. Rev. B Condens. Matter Mater. Phys. 1996, 53, 1336–1342. [Google Scholar] [CrossRef] [PubMed]
- Micic, O.I.; Cheong, H.M.; Fu, H.; Zunger, A.; Sprague, J.R.; Mascarenhas, A.; Nozik, A.J. Size-Dependent Spectroscopy of InP Quantum Dots. J. Phys. Chem. B 1997, 101, 4904–4912. [Google Scholar] [CrossRef]
- Tamarat, P.; Hou, L.; Trebbia, J.-B.; Swarnkar, A.; Biadala, L.; Louyer, Y.; Bodnarchuk, M.I.; Kovalenko, M.V.; Even, J.; Lounis, B. The Dark Exciton Ground State Promote Photon-Pair Emission in Individual Perovskite Nanocrystals. Nat. Commun. 2020, 11, 6001. [Google Scholar] [CrossRef] [PubMed]
- Fu, M.; Tamarat, P.; Huang, H.; Even, J.; Rogach, A.L.; Lounis, B. Neutral and Charged Exciton Fine Structure in Single Lead Halide Perovskite Nanocrystals Revealed by Magneto-Optical Spectroscopy. Nano Lett. 2017, 17, 2895–2901. [Google Scholar] [CrossRef]
- Pikus, G.E.; Bir, G.L. Exchange Interaction in Excitons in Semiconductors. Zh. Eksp. Teor. Fiz. 1971, 60, 195–208, Sov. Phys. JETP1971, 33, 108–114. [Google Scholar]
- Bir, G.L.; Pikus, G.E. Symmetry and Strain Induced Effects in Semiconductors; Wiley: New York, NY, USA, 1975. [Google Scholar]
- Denisov, M.M.; Makarov, V.P. Longitudinal and Transverse Excitons in Semiconductors. Phys. Stat. Sol. 1973, 56, 9–59. [Google Scholar] [CrossRef]
- Gupalov, S.V.; Ivchenko, E.L.; Kavokin, A.V. Fine Structure of Localized Excitons Levels in Quantum Wells. J. Exp. Theor. Phys. 1998, 86, 388–394. [Google Scholar] [CrossRef]
- Efros, A.L.; Rosen, M.; Kuno, M.; Nirmal, M.; Norris, D.J.; Bawendi, M. Band-Edge Exciton in Quantum Dots of Semiconductors with a Degenerate Valence Band: Dark and Bright Exciton States. Phys. Rev. B Condens. Matter Mater. Phys. 1996, 54, 4843–4856. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Romestain, R.; Fishman, G. Excitonic Wave Function, Correlation Energy, Exchange Energy, and Oscillator Strength in a Cubic Quantum Dot. Phys. Rev. B Condens. Matter Mater. Phys. 1994, 49, 1774–1781. [Google Scholar] [CrossRef] [PubMed]
- Franceschetti, A.; Zunger, A. Direct Pseudopotential Calculation of Exciton Coulomb and Exchange Energies in Semiconductor Quantum Dots. Phys. Rev. Lett. 1997, 78, 915–918. [Google Scholar] [CrossRef] [Green Version]
- Tong, H.; Wu, M.W. Theory of Excitons in Cubic III-V Semiconductor GaAs, InAs and GaN Quantum Dots: Fine Structure and Spin Relaxation. Phys. Rev. B Condens. Matter Mater. Phys. 2011, 83, 235323. [Google Scholar] [CrossRef] [Green Version]
- Nestoklon, M.O.; Goupalov, S.V.; Dzhioev, R.I.; Ken, O.S.; Korenev, V.L.; Kusrayev, Y.G.; Sapega, V.F.; de Weerd, C.; Gomez, L.; Gregorkiewicz, T.; et al. Optical Orientation and Alignment of Excitons in Ensembles of Inorganic Perovskite Nanocrystals. Phys. Rev. B Condens. Matter Mater. Phys. 2018, 97, 235304. [Google Scholar] [CrossRef] [Green Version]
- Ben Aich, R.; Saïdi, I.; Ben Radhia, S.; Boujdaria, K.; Barisien, T.; Legrand, L.; Bernardot, F.; Chamarro, M.; Testelin, C. Bright-Exciton Splittings in Inorganic Cesium Lead Halide Perovskite Nanocrystals. Phys. Rev. Appl. 2019, 11, 034042. [Google Scholar] [CrossRef]
- Sercel, P.C.; Lyons, J.L.; Wickramaratne, D.; Vaxenburg, R.; Bernstein, N.; Efros, A.L. Exciton Fine Structure in Perovskite Nanocrystals. Nano Lett. 2019, 19, 4068–4077. [Google Scholar] [CrossRef] [PubMed]
- Ben Aich, R.; Ben Radhia, S.; Boujdaria, K.; Chamarro, M.; Testelin, C. Multiband k.p Model for Tetragonal Crystals: Application to Hybrid Halide Perovskite Nanocrystals. J. Phys. Chem. Lett. 2020, 11, 808–817. [Google Scholar] [CrossRef]
- Sercel, P.C.; Lyons, J.L.; Bernstein, N.; Efros, A.L. Quasicubic Model for Metal Halide Perovskite Nanocrystals. J. Chem. Phys. 2019, 151, 234106. [Google Scholar] [CrossRef] [Green Version]
- Rössler, U.; Trebin, H.-R. Exchange and Polaron Corrections for Excitons in the Degenerate-Band Case. Phys. Rev. B Condens. Matter Mater. Phys. 1981, 23, 1961–1970. [Google Scholar] [CrossRef]
- Ramade, J.; Andriambariarijaona, L.M.; Steinmetz, V.; Goubet, N.; Legrand, L.; Barisien, T.; Bernardot, F.; Testelin, C.; Lhuillier, E.; Bramati, A.; et al. Fine Structure of Excitons and Electron–Hole Exchange Energy in Polymorphic CsPbBr3 Single Nanocrystals. Nanoscale 2018, 10, 6393–6401. [Google Scholar] [CrossRef]
- Gupalov, S.V.; Ivchenko, E.L. The Fine Structure of Excitonic Levels in CdSe Nanocrystals. Phys. Solid State 2000, 42, 2030–2038. [Google Scholar] [CrossRef]
- Rossi, D.; Liu, X.; Lee, Y.; Khurana, M.; Puthenpurayil, J.; Kim, K.; Akimov, A.V.; Cheon, J.; Son, D.H. Intense Dark Exciton Emission from Strongly Quantum-Confined CsPbBr3 Nanocrystals. Nano Lett. 2020, 20, 7321–7326. [Google Scholar] [CrossRef]
- Shamsi, J.; Dang, Z.; Bianchini, P.; Canale, C.; Di Stasio, F.; Brescia, R.; Prato, M.; Manna, L. Colloidal Synthesis of Quantum Confined Single Crystal CsPbBr3 Nanosheets with Lateral Size Control up to the Micrometer Range. J. Am. Chem. Soc. 2016, 138, 7240–7243. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brescia, R.; Toso, S.; Ramasse, Q.; Manna, L.; Shamsi, J.; Downing, C.; Calzolari, A.; Bertoni, G. Bandgap Determination from Individual Orthorhombic thin Cesium Lead Bromide Nanosheets by Electron Energy-Loss Spectroscopy. Nanoscale Horiz. 2020, 5, 1610–1617. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, D.; Kisielowski, C.; Dou, L.; Lornieko, N.; Bekenstein, Y.; Wong, A.B.; Alivisatos, A.P.; Yang, P. Atomic Resolution Imaging of Halide Perovskites. Nano Lett. 2016, 16, 7530–7535. [Google Scholar] [CrossRef] [Green Version]
- Bertolotti, F.; Nedelcu, G.; Vivani, A.; Cervellino, A.; Masciocchi, N.; Guagliardi, A.; Kovalenko, M.V. Crystal Structure, Morphology, and Surface Termination of Cyan-Emissive, Six-Monolayers-Thick CsPbBr3 Nanoplatelets from X-ray Total Scattering. ACS Nano 2019, 13, 14294–14307. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shornokova, E.V.; Biadala, L.; Yakovlev, D.R.; Sapega, D.R.; Sapega, V.F.; Kusrayev, Y.G.; Mitioglu, A.A.; Ballotin, M.V.; Christianen, P.M.C.; Belykh, V.V.; et al. Addressing the exciton fine structure in colloidal nanocrystals: The case of CdSe nanoplatelets. Nanoscale 2018, 10, 646–656. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sercel, P.C.; Efros, A.I. Band-Edge Exciton in CdSe and Other II–VI and III–V Compound Semiconductor Nanocrystals—Revisited. Nanoscale 2018, 18, 4061–4068. [Google Scholar] [CrossRef]
- Rodina, A.V.; Efros, A.L. Effect of Dielectric Confinement on Optical Properties of Colloidal Nanostructures. J. Exp. Theor. Phys. 2016, 122, 554–566. [Google Scholar] [CrossRef]
- Huo, C.; Fong, C.F.; Amara, M.R.; Huang, Y.; Chen, B.; Zhang, H.; Guo, L.; Li, H.; Huang, W.; Diederichs, C.; et al. Optical Spectroscopy of Single Colloidal CsPbBr3 Perovskite Nanoplatelets. Nano Lett. 2020, 20, 3673–3680. [Google Scholar] [CrossRef] [PubMed]
- Do, T.T.H.; Del Aguila, A.G.; Zhang, D.; Xing, J.; Liu, S.; Prosnikov, M.A.; Gao, W.; Chang, K.; Christianen, P.C.M.; Xiong, Q. Bright Exciton Fine-Structure in Two-Dimensional Lead Halide Perovskites. Nano Lett. 2020, 20, 5141–5148. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghribi, A.; Ben Aich, R.; Boujdaria, K.; Barisien, T.; Legrand, L.; Chamarro, M.; Testelin, C. Dielectric Confinement and Exciton Fine Structure in Lead Halide Perovskite Nanoplatelets. Nanomaterials 2021, 11, 3054. https://doi.org/10.3390/nano11113054
Ghribi A, Ben Aich R, Boujdaria K, Barisien T, Legrand L, Chamarro M, Testelin C. Dielectric Confinement and Exciton Fine Structure in Lead Halide Perovskite Nanoplatelets. Nanomaterials. 2021; 11(11):3054. https://doi.org/10.3390/nano11113054
Chicago/Turabian StyleGhribi, Amal, Rim Ben Aich, Kaïs Boujdaria, Thierry Barisien, Laurent Legrand, Maria Chamarro, and Christophe Testelin. 2021. "Dielectric Confinement and Exciton Fine Structure in Lead Halide Perovskite Nanoplatelets" Nanomaterials 11, no. 11: 3054. https://doi.org/10.3390/nano11113054
APA StyleGhribi, A., Ben Aich, R., Boujdaria, K., Barisien, T., Legrand, L., Chamarro, M., & Testelin, C. (2021). Dielectric Confinement and Exciton Fine Structure in Lead Halide Perovskite Nanoplatelets. Nanomaterials, 11(11), 3054. https://doi.org/10.3390/nano11113054







