Assessing the Viscoelasticity of Photopolymer Nanowires Using a Three-Parameter Solid Model for Bending Recovery Motion
Abstract
:1. Introduction
2. Theoretical Considerations
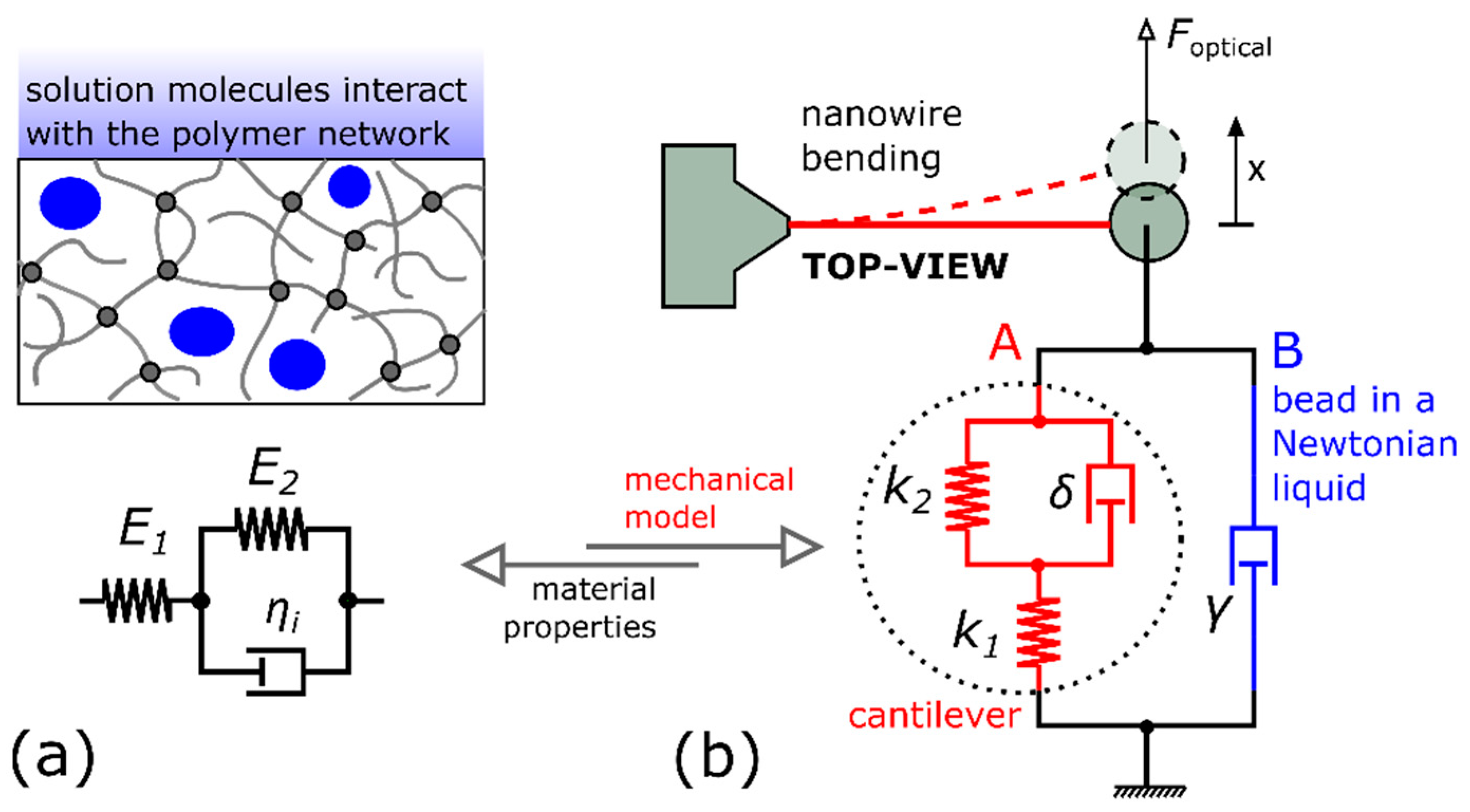
2.1. The Three-Parameter Solid Model
2.2. The Mechanical Model of the Microstructure
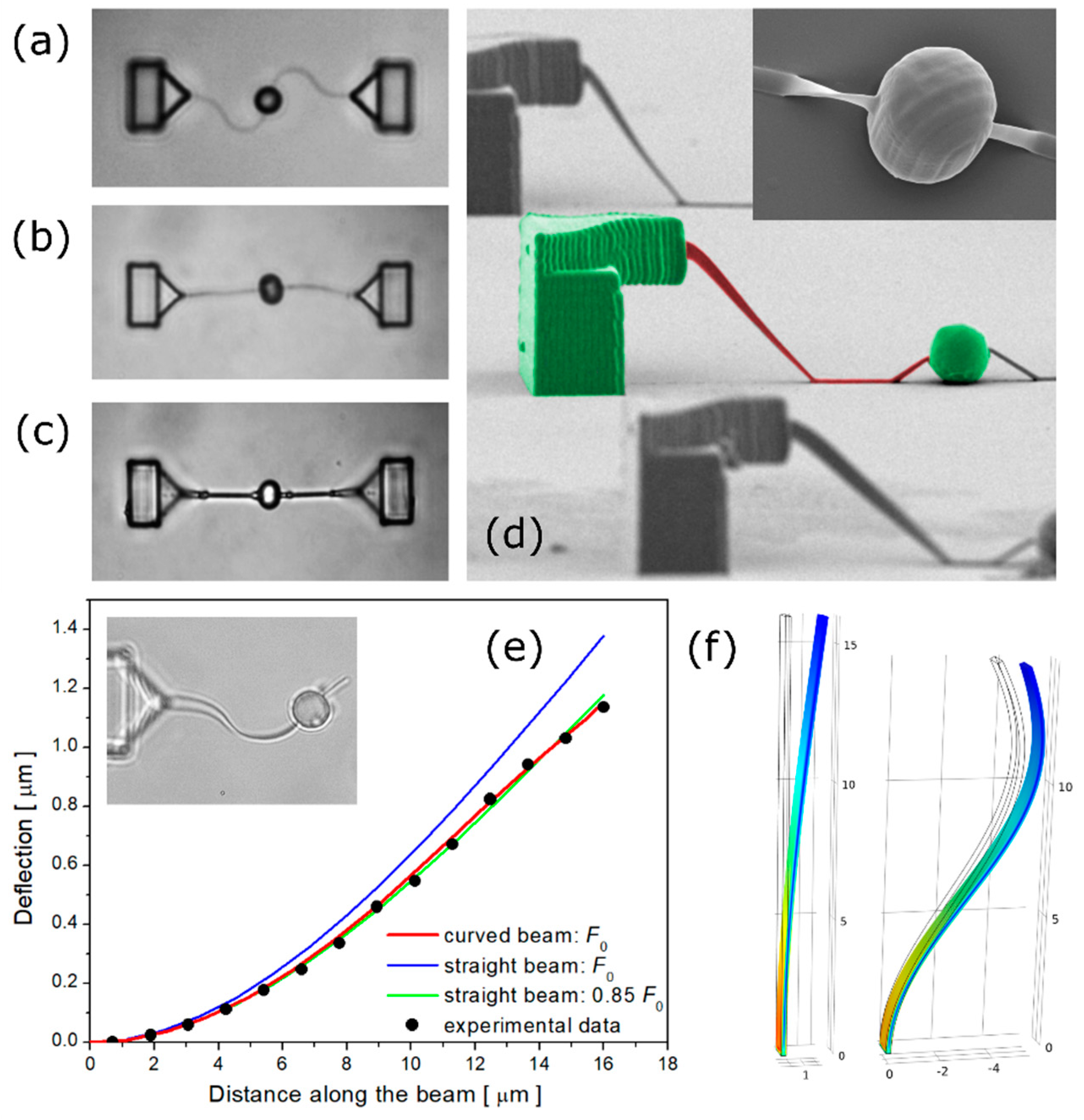
2.3. The Bending Recovery Motion
2.4. The Inverse Problem
3. Materials and Methods
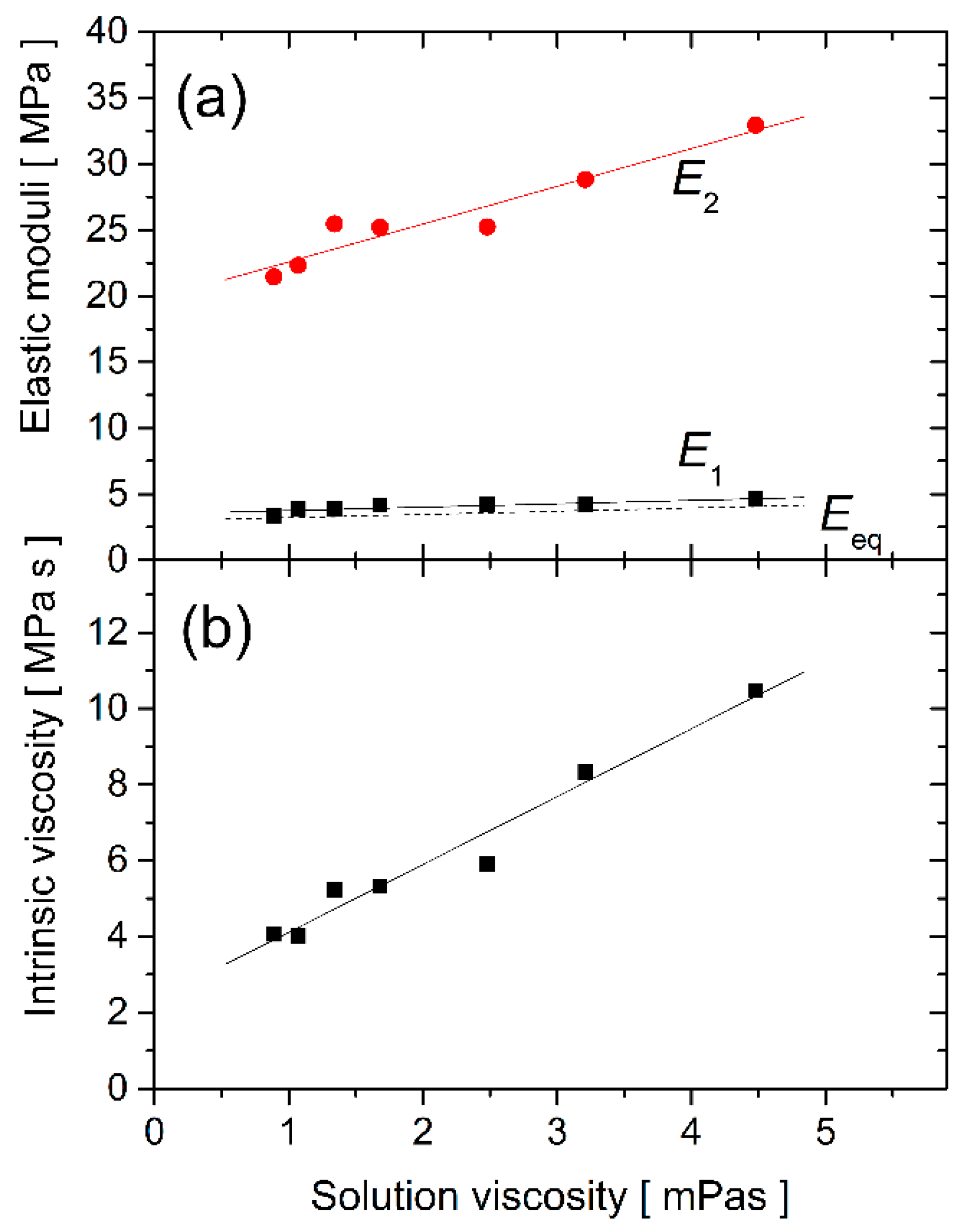
4. Results and Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Otuka, A.; Tomazio, N.; Paula, K.; Mendonça, C. Two-Photon Polymerization: Functionalized Microstructures, Micro-Resonators, and Bio-Scaffolds. Polymers 2021, 13, 1994. [Google Scholar] [CrossRef] [PubMed]
- LaFratta, C.N.; Fourkas, J.T.; Baldacchini, T.; Farrer, R.A. Multiphoton Fabrication. Angew. Chem. Int. Ed. 2007, 46, 6238–6258. [Google Scholar] [CrossRef] [PubMed]
- Malinauskas, M.; Farsari, M.; Piskarskas, A.; Juodkazis, S. Ultrafast laser nanostructuring of photopolymers: A decade of advances. Phys. Rep. 2013, 533, 1–31. [Google Scholar] [CrossRef]
- Gräfe, D.; Walden, S.L.; Blinco, J.; Wegener, M.; Blasco, E.; Barner-Kowollik, C. It’s in the Fine Print: Erasable Three-Dimensional Laser-Printed Micro- and Nanostructures. Angew. Chem. Int. Ed. 2019, 59, 6330–6340. [Google Scholar] [CrossRef]
- Jonušauskas, L.; Baravykas, T.; Andrijec, D.; Gadišauskas, T.; Purlys, V. Stitchless support-free 3D printing of free-form micromechanical structures with feature size on-demand. Sci. Rep. 2019, 9, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Haske, W.; Chen, V.W.; Hales, J.; Dong, W.; Barlow, S.; Marder, S.R.; Perry, J.W. 65 nm feature sizes using visible wavelength 3-D multiphoton lithography. Opt. Express 2007, 15, 3426–3436. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Gattass, R.R.; Gershgoren, E.; Hwang, H.; Fourkas, J.T. Achieving λ/20 Resolution by One-Color Initiation and Deactivation of Polymerization. Science 2009, 324, 910–913. [Google Scholar] [CrossRef] [PubMed]
- LaFratta, C.N.; Baldacchini, T. Two-Photon Polymerization Metrology: Characterization Methods of Mechanisms and Microstructures. Micromachines 2017, 8, 101. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.-B.; Takada, K.; Kawata, S. Elastic force analysis of functional polymer submicron oscillators. Appl. Phys. Lett. 2001, 79, 3173–3175. [Google Scholar] [CrossRef]
- Nakanishi, S.; Shoji, S.; Kawata, S.; Sun, H.-B. Giant elasticity of photopolymer nanowires. Appl. Phys. Lett. 2007, 91, 063112. [Google Scholar] [CrossRef]
- Ushiba, S.; Masui, K.; Taguchi, N.; Hamano, T.; Kawata, S.; Shoji, S. Size dependent nanomechanics of coil spring shaped polymer nanowires. Sci. Rep. 2015, 5, 17152. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, S.-J.; Li, Y.; Wang, Y.-K.; Liu, L.-P.; Wang, H.-D.; Xiao, Y.-F.; Yang, H.; Gong, Q. Controlling Young’s modulus of polymerized structures fabricated by direct laser writing. Appl. Phys. A 2014, 118, 437–441. [Google Scholar] [CrossRef]
- Shin, C.-S.; Li, T.-J.; Lin, C.-L. Alleviating Distortion and Improving the Young’s Modulus in Two-Photon Polymerization Fabrications. Micromachines 2018, 9, 615. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bayindir, Z.; Sun, Y.; Naughton, M.J.; LaFratta, C.N.; Baldacchini, T.; Fourkas, J.; Stewart, J.R.; Saleh, B.E.A.; Teich, M.C. Polymer microcantilevers fabricated via multiphoton absorption polymerization. Appl. Phys. Lett. 2005, 86, 064105. [Google Scholar] [CrossRef] [Green Version]
- Bauer, J.; Izard, A.G.; Zhang, Y.; Baldacchini, T.; Valdevit, L. Programmable Mechanical Properties of Two-Photon Polymerized Materials: From Nanowires to Bulk. Adv. Mater. Technol. 2019, 4. [Google Scholar] [CrossRef]
- Ladner, I.S.; Cullinan, M.A.; Saha, S.K. Tensile properties of polymer nanowires fabricated via two-photon lithography. RSC Adv. 2019, 9, 28808–28813. [Google Scholar] [CrossRef] [Green Version]
- Cicha, K.; Koch, T.; Torgersen, J.; Li, Z.; Liska, R.; Stampfl, J. Young’s modulus measurement of two-photon polymerized micro-cantilevers by using nanoindentation equipment. J. Appl. Phys. 2012, 112, 094906. [Google Scholar] [CrossRef]
- Greiner, A.M.; Richter, B.; Bastmeyer, M. Micro-Engineered 3D Scaffolds for Cell Culture Studies. Macromol. Biosci. 2012, 12, 1301–1314. [Google Scholar] [CrossRef]
- Klein, F.; Striebel, T.; Fischer, J.; Jiang, Z.; Franz, C.M.; von Freymann, G.; Wegener, M.; Bastmeyer, M. Elastic Fully Three-dimensional Microstructure Scaffolds for Cell Force Measurements. Adv. Mater. 2010, 22, 868–871. [Google Scholar] [CrossRef]
- Liu, Y.-J.; Yang, J.-Y.; Nie, Y.-M.; Lu, C.-H.; Huang, E.D.; Shin, C.-S.; Baldeck, P.; Lin, C.-L. A simple and direct reading flow meter fabricated by two-photon polymerization for microfluidic channel. Microfluid. Nanofluid. 2014, 18, 427–431. [Google Scholar] [CrossRef]
- Song, Y.; Panas, R.M.; Chizari, S.; Shaw, L.A.; Jackson, J.A.; Hopkins, J.B.; Pascall, A.J. Additively manufacturable micro-mechanical logic gates. Nat. Commun. 2019, 10, 882. [Google Scholar] [CrossRef] [PubMed]
- Kaynak, M.; Dirix, P.; Sakar, M.S. Addressable Acoustic Actuation of 3D Printed Soft Robotic Microsystems. Adv. Sci. 2020, 7. [Google Scholar] [CrossRef] [PubMed]
- Kaynak, M.; Ozcelik, A.; Nourhani, A.; Lammert, P.E.; Crespi, V.H.; Huang, T.J. Acoustic actuation of bioinspired microswimmers. Lab Chip 2016, 17, 395–400. [Google Scholar] [CrossRef] [Green Version]
- Keshavarz, B.; Zarket, B.; Amin, S.; Rughani, R.; Muthukrishnan, S.; Holten-Andersen, N.; McKinley, G.H. Characterizing viscoelastic properties of synthetic and natural fibers and their coatings with a torsional pendulum. Soft Matter 2021, 17, 4578–4593. [Google Scholar] [CrossRef]
- Lakes, R.S. Viscoelastic measurement techniques. Rev. Sci. Instrum. 2004, 75, 797. [Google Scholar] [CrossRef] [Green Version]
- Cayll, D.R.; Ladner, I.S.; Cho, J.H.; Saha, S.K.; Cullinan, M.A. A MEMS dynamic mechanical analyzer for in situ viscoelastic characterization of 3D printed nanostructures. J. Micromech. Microeng. 2020, 30, 075008. [Google Scholar] [CrossRef]
- Kubacková, J.; Iványi, G.T.; Kažiková, V.; Strejčková, A.; Hovan, A.; Žoldák, G.; Vizsnyiczai, G.; Kelemen, L.; Tomori, Z.; Bánó, G. Bending dynamics of viscoelastic photopolymer nanowires. Appl. Phys. Lett. 2020, 117, 013701. [Google Scholar] [CrossRef]
- Bánó, G.; Kubacková, J.; Hovan, A.; Strejčková, A.; Iványi, G.; Vizsnyiczai, G.; Kelemen, L.; Žoldák, G.; Tomori, Z.; Horvath, D. Power Spectral Density Analysis of Nanowire-Anchored Fluctuating Microbead Reveals a Double Lorentzian Distribution. Mathematics 2021, 9, 1748. [Google Scholar] [CrossRef]
- Schizas, C.; Karalekas, D. Mechanical characteristics of an Ormocomp® biocompatible hybrid photopolymer. J. Mech. Behav. Biomed. Mater. 2011, 4, 99–106. [Google Scholar] [CrossRef]
- Flügge, W. Viscoelasticity; Springer: Berlin/Heidelberg, Germany, 1975. [Google Scholar]
- Sarkar, S.; Baker, P.J.; Chan, E.P.; Lin-Gibson, S.; Chiang, M.Y.M. Quantifying the sensitivity of the network structure and properties from simultaneous measurements during photopolymerization. Soft Matter 2017, 13, 3975–3983. [Google Scholar] [CrossRef]
- Takada, K.; Wu, N.; Chen, Q.-D.; Shoji, S.; Xia, H.; Kawata, S.; Sun, H.-B. Size-dependent behaviors of femtosecond laser-prototyped polymer micronanowires. Opt. Lett. 2009, 34, 566–568. [Google Scholar] [CrossRef] [Green Version]
- Berg-Sorensen, K.; Flyvbjerg, H. Power spectrum analysis for optical tweezers. Rev. Sci. Instrum. 2004, 75, 594–612. [Google Scholar] [CrossRef] [Green Version]
- Singh, A.; Scotti, G.; Sikanen, T.; Jokinen, V.; Franssila, S. Laser Direct Writing of Thick Hybrid Polymers for Microfluidic Chips. Micromachines 2014, 5, 472–485. [Google Scholar] [CrossRef]
- Jamal, M.; Zarafshar, A.M.; Gracias, D.H. Differentially photo-crosslinked polymers enable self-assembling microfluidics. Nat. Commun. 2011, 2, 1–6. [Google Scholar] [CrossRef]
- Gieseler, J.; Gomez-Solano, J.R.; Magazzù, A.; Castillo, I.P.; García, L.P.; Gironella-Torrent, M.; Viader-Godoy, X.; Ritort, F.; Pesce, G.; Arzola, A.V.; et al. Optical tweezers—From calibration to applications: A tutorial. Adv. Opt. Photonics 2021, 13, 74–241. [Google Scholar] [CrossRef]
- Baldacchini, T.; Zimmerley, M.; Kuo, C.-H.; Potma, E.O.; Zadoyan, R. Characterization of Microstructures Fabricated by Two-Photon Polymerization Using Coherent Anti-Stokes Raman Scattering Microscopy. J. Phys. Chem. B 2009, 113, 12663–12668. [Google Scholar] [CrossRef] [Green Version]
- Jiang, L.J.; Zhou, Y.S.; Xiong, W.; Gao, Y.; Huang, X.; Jiang, L.; Baldacchini, T.; Silvain, J.-F.; Lu, Y.F. Two-photon polymerization: Investigation of chemical and mechanical properties of resins using Raman microspectroscopy. Opt. Lett. 2014, 39, 3034–3037. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cacopardo, L.; Guazzelli, N.; Nossa, R.; Mattei, G.; Ahluwalia, A. Engineering hydrogel viscoelasticity. J. Mech. Behav. Biomed. Mater. 2019, 89, 162–167. [Google Scholar] [CrossRef]

| k1 pN/nm | k2 pN/nm | keq pN/nm | δ 10−6 kg s−1 | γ 10−6 kg s−1 | E1 MPa | E2 MPa | Eeq MPa | ηi MPa s | |
|---|---|---|---|---|---|---|---|---|---|
| water | 0.0017 | 0.011 | 0.0015 | 2.1 | 0.042 | 3.4 | 21 | 2.9 | 4.1 |
| 400 mg/mL glucose | 0.0024 | 0.017 | 0.0021 | 5.4 | 0.21 | 4.6 | 33 | 4.1 | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kubacková, J.; Slabý, C.; Horvath, D.; Hovan, A.; Iványi, G.T.; Vizsnyiczai, G.; Kelemen, L.; Žoldák, G.; Tomori, Z.; Bánó, G. Assessing the Viscoelasticity of Photopolymer Nanowires Using a Three-Parameter Solid Model for Bending Recovery Motion. Nanomaterials 2021, 11, 2961. https://doi.org/10.3390/nano11112961
Kubacková J, Slabý C, Horvath D, Hovan A, Iványi GT, Vizsnyiczai G, Kelemen L, Žoldák G, Tomori Z, Bánó G. Assessing the Viscoelasticity of Photopolymer Nanowires Using a Three-Parameter Solid Model for Bending Recovery Motion. Nanomaterials. 2021; 11(11):2961. https://doi.org/10.3390/nano11112961
Chicago/Turabian StyleKubacková, Jana, Cyril Slabý, Denis Horvath, Andrej Hovan, Gergely T. Iványi, Gaszton Vizsnyiczai, Lóránd Kelemen, Gabriel Žoldák, Zoltán Tomori, and Gregor Bánó. 2021. "Assessing the Viscoelasticity of Photopolymer Nanowires Using a Three-Parameter Solid Model for Bending Recovery Motion" Nanomaterials 11, no. 11: 2961. https://doi.org/10.3390/nano11112961
APA StyleKubacková, J., Slabý, C., Horvath, D., Hovan, A., Iványi, G. T., Vizsnyiczai, G., Kelemen, L., Žoldák, G., Tomori, Z., & Bánó, G. (2021). Assessing the Viscoelasticity of Photopolymer Nanowires Using a Three-Parameter Solid Model for Bending Recovery Motion. Nanomaterials, 11(11), 2961. https://doi.org/10.3390/nano11112961







