Electrodynamics of Topologically Ordered Quantum Phases in Dirac Materials
Abstract
:1. Introduction
2. Theoretical and Computational Details
2.1. First-Principles Calculations
2.2. Emergence of Topological Order in Electronic Phases
2.3. Relationships with Other Models of Transport via Emergent Topological Quantum Phases
2.4. Time-Propagation TDDFT of the Topological Electronic Phase
3. Results and Discussion
3.1. Electronic Properties
3.1.1. Renormalized Electronic Ground State
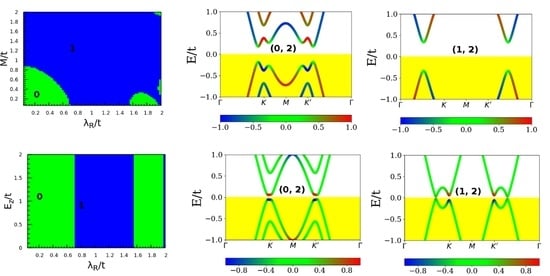
3.1.2. Characterizing the Topological Order and Quantum Phase Transitions
3.1.3. Tuning the Topological Order Using Material-Dependent Potentials
3.2. Optoelectronic Properties
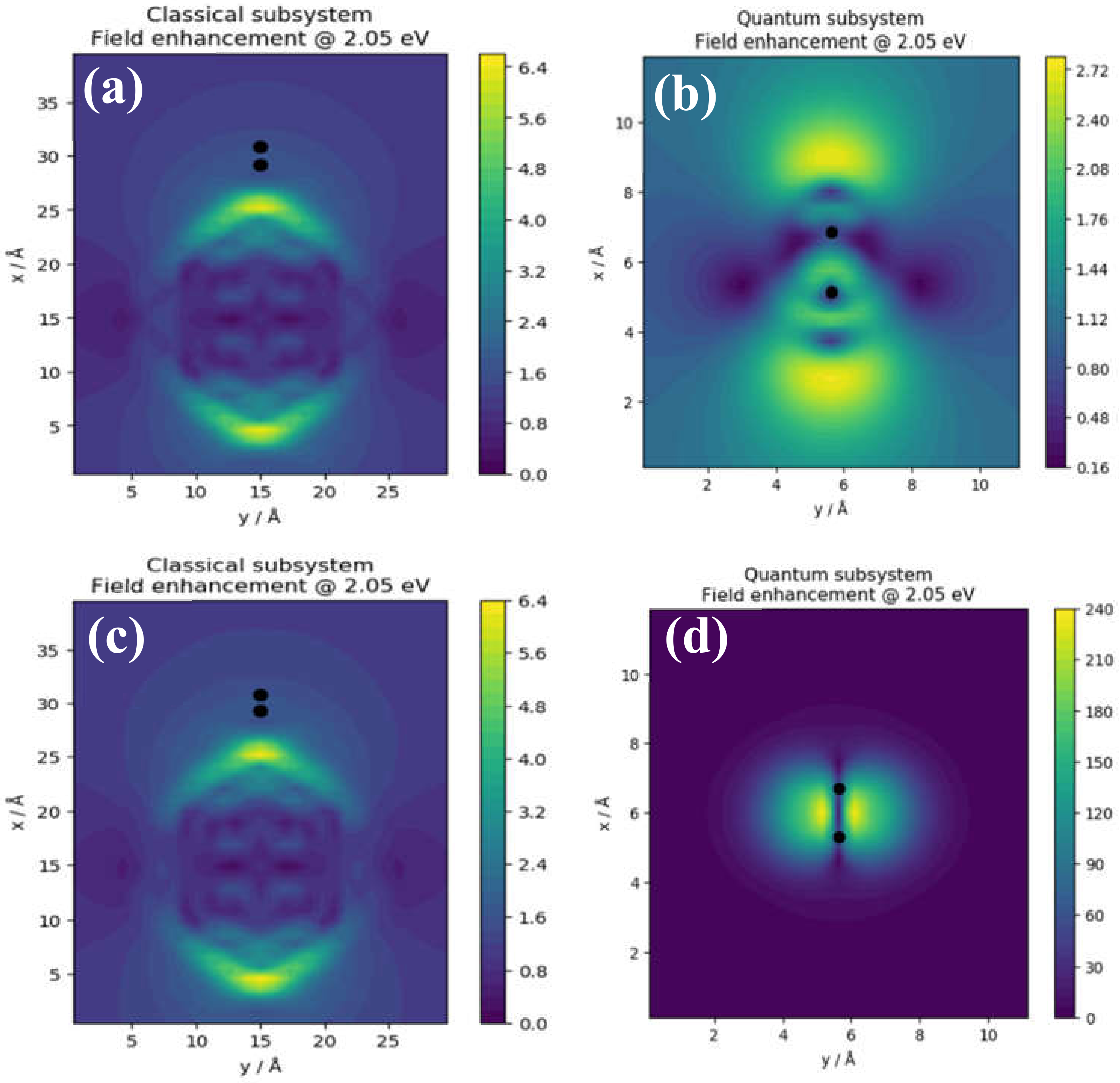
3.2.1. Near-Field Electrodynamics of Topological Electronic Phases
3.2.2. Optical Photoabsorption
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Leshen, J.; Kavai, M.; Giannakis, I.; Kaneko, Y.; Tokura, Y.; Mukherjee, S.; Lee, W.-C.; Aynajian, P. Emergent charge order near the doping-induced Mott-insulating quantum phase transition in Sr3Ru2O7. Commun. Phys. 2019, 2, 36. [Google Scholar] [CrossRef]
- Wehling, T.O.; Black-Schaffer, A.M.; Balatsky, A.V. Dirac materials. Adv. Phys. 2014, 76, 1. [Google Scholar] [CrossRef] [Green Version]
- Pan, H.; Li, X.; Jiang, H.; Yao, Y.G.; Yang, S.Y.A. Phase-change memory function of correlated electrons in organic conductors. Phys. Rev. B 2015, 91, 045404. [Google Scholar] [CrossRef] [Green Version]
- Pan, H.; Li, Z.S.; Liu, C.C.; Zhu, G.B.; Qiao, Z.H.; Yao, Y.G. Valley-polarized quantum anomalous hall effect in silicene. Phys. Rev. Lett. 2014, 112, 106802. [Google Scholar] [CrossRef] [Green Version]
- Ganeshan, S.; Sun, K.; Das Sarma, S. Topological zero-energy modes in gapless commensurate Aubry-André-Harper models. Phys. Rev. Lett. 2013, 110, 180403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hadad, Y.; Khanikaev, A.B.; Alu, A. Self-induced topological transitions and edge states supported by nonlinear staggered potentials. Phys. Rev. B 2016, 93, 155112. [Google Scholar] [CrossRef] [Green Version]
- Downing, C.A.; Weick, G. Topological plasmons in dimerized chains of nanoparticles: Robustness against long-range quasistatic interactions and retardation effects. Eur. Phys. J. B 2018, 91, 253. [Google Scholar] [CrossRef]
- Shapiro, J. The bulk-edge correspondence in three simple cases. Rev. Math. Phys. 2020, 32, 2030003. [Google Scholar] [CrossRef] [Green Version]
- Salahuddin, S.; Ni, K.; Datta, S. Progress and future prospects of negative capacitance electronics: A materials perspective. Nat. Electron. 2018, 1, 442. [Google Scholar] [CrossRef]
- Ukpong, A.M. Axial field induced spin response in Fe/hBN-based tunnel junctions. Phys. Rev. B 2019, 100, 035424. [Google Scholar] [CrossRef]
- Ukpong, A.M. Tunable magnetotransport in Fe/hBN/graphene/hBN/Pt(Fe) epitaxial multilayers. J. Phys. D: Appl. Phys. 2018, 51, 095302. [Google Scholar] [CrossRef]
- Ukpong, A.M. Ab initio studies of coherent spin transport in Fe-hBN/graphene van der Waals multilayers. J. Phys. Condens. Matter 2017, 29, 285302. [Google Scholar] [CrossRef] [PubMed]
- Ukpong, A.M. First principles study of van der Waals heterobilayers. Comput. Condens. Matter 2015, 2, 1. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.-Y.; Shen, M.; An, X.-T.; Sun, Q.-F.; Xie, X.-C.; Chang, K.; Li, S.-S. Coexistence and decoupling of bulk and edge states in disordered two-dimensional topological insulators. Phys. Rev. B 2014, 90, 054205. [Google Scholar] [CrossRef] [Green Version]
- Seibel, C.; Bentmann, H.; Braun, J.; Minár, J.; Maaß, H.; Sakamoto, K.; Arita, M.; Shimada, K.; Ebert, H.; Reinert, F. Connection of a Topological Surface State with the Bulk Continuum in Sb2Te3(0001). Phys. Rev. Lett. 2015, 114, 066802. [Google Scholar] [CrossRef]
- Kitagawa, T.; Oka, T.; Brataas, A.; Fu, L.; Demler, E. Transport properties of nonequilibrium systems under the application of light: Photoinduced quantum Hall insulators without Landau levels. Phys. Rev. B 2011, 84, 235108. [Google Scholar] [CrossRef] [Green Version]
- Lindner, N.H.; Refael, G.; Galitski, V. Floquet topological insulator in semiconductor quantum wells. Nat. Phys. 2011, 7, 490. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.H.; Steinberg, H.; Jarillo-Herrero, P.; Gedik, N. Observation of Floquet-Bloch states on the surface of a topological insulator. Science 2013, 342, 453. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mikami, T.; Kitamura, S.; Yasuda, K.; Tsuji, N.; Oka, T.; Aoki, H. Brillouin-Wigner theory for high-frequency expansion in periodically driven systems: Application to Floquet topological insulators. Phys. Rev. B 2016, 93, 144307. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Wang, Y.; Classen, M.; Moritz, B.; Devereaux, T.P. Observing photo-induced chiral edge states of graphene nanoribbons in pump-probe spectroscopies. NPJ Quantum Mater. 2020, 5, 84. [Google Scholar] [CrossRef]
- Jangjan, M.; Hosseini, M.V. Floquet engineering of topological metal states and hybridization of edge states with bulk states in dimerized two-leg ladders. Sci. Rep. 2020, 10, 14256. [Google Scholar]
- Oka, T.; Aoki, H. Photovoltaic Hall effect in graphene. Phys. Rev. B 2009, 79, 081406. [Google Scholar] [CrossRef] [Green Version]
- Cavalleri, A. Photo-induced superconductivity. Contemp. Phys. 2018, 59, 31–46. [Google Scholar] [CrossRef]
- Fausti, D.; Tobey, R.I.; Dean, N.; Kaiser, S.; Dienst, A.; Hoffmann, M.C.; Pyon, S.; Takayama, T.; Takagi, H.; Cavalleri, A. Light-Induced Superconductivity in a Stripe-Ordered Cuprate. Science 2011, 331, 189. [Google Scholar] [CrossRef] [Green Version]
- Mitrano, M.; Cantaluppi, A.; Nicoletti, D.; Kaiser, S.; Perucchi, A.; Lupi, S.; Di Pietro, P.; Pontiroli, D.; Riccò, M.; Clark, S.R.; et al. Possible light-induced superconductivity in K3C60 at high temperature. Nature 2016, 530, 461. [Google Scholar] [CrossRef] [PubMed]
- McIver, J.W.; Schulte, B.; Stein, F.-U.; Matsuyama, T.; Jotzu, G.; Meier, G.; Cavalleri, A. Light-induced anomalous Hall effect in graphene. Nat. Phys. 2020, 16, 38. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.-L.; Xu, S.-Y.; Belopolski, I.; Yuan, Z.; Lin, Z.; Tong, B.; Bian, G.; Alidoust, N.; Lee, C.-C.; Huang, S.-M.; et al. Signatures of the Adler–Bell–Jackiw chiral anomaly in a Weyl fermion semimetal. Nat. Commun. 2016, 7, 10735. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorno Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef] [Green Version]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [Green Version]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Methfessel, M.; Paxton, A. High-precision sampling for Brillouin-zone integration in metals. Phys. Rev. B 1989, 40, 3616. [Google Scholar] [CrossRef] [Green Version]
- Blount, E.I. Bloch Electrons in a Magnetic Field. Phys. Rev. 1962, 126, 1636. [Google Scholar] [CrossRef]
- Wannier, G.H. Dynamics of Band Electrons in Electric and Magnetic Fields. Rev. Mod. Phys. 1962, 34, 645. [Google Scholar] [CrossRef]
- Luttinger, J.M. The Effect of a Magnetic Field on Electrons in a Periodic Potential. Phys. Rev. 1951, 84, 814. [Google Scholar] [CrossRef]
- Kohn, W. Theory of Bloch Electrons in a Magnetic Field: The Effective Hamiltonian. Phys. Rev. 1959, 115, 1460. [Google Scholar] [CrossRef]
- Fischbeck, H.J. Theory of Bloch Electrons in a Magnetic Field. Phys. Status Solidi B 1970, 38, 11–62. [Google Scholar] [CrossRef]
- Chae, S.J.; Güneş, F.; Kim, K.K.; Kim, E.S.; Han, G.H.; Kim, S.M.; Shin, H.-J.; Yoon, S.-M.; Choi, J.-Y.; Park, M.H.; et al. Synthesis of large-area graphene layers on poly-nickel substrate by chemical vapor deposition: Wrinkle formation. Adv. Mater. 2009, 21, 2328. [Google Scholar] [CrossRef]
- Tse, W.K.; Qiao, Z.; Yao, Y.; MacDonald, A.H.; Niu, Q. Quantum anomalous Hall effect in single-layer and bilayer graphene. Phys. Rev. B 2011, 83, 155447. [Google Scholar] [CrossRef] [Green Version]
- Min, H.; Hill, J.E.; Sinitsyn, N.A.; Sahu, B.R.; Kleinman, L.; MacDonald, A.H. Intrinsic and Rashba spin-orbit interactions in graphene sheets. Phys. Rev. B 2006, 74, 165310. [Google Scholar] [CrossRef] [Green Version]
- Sheng, D.N.; Weng, Z.Y.; Sheng, L.; Haldane, F.D. Quantum spin-Hall effect and topologically invariant Chern numbers. Phys. Rev. Lett. 2006, 97, 036808. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qiao, Z.; Yang, S.A.; Feng, W.; Tse, W.-K.; Ding, J.; Yao, Y.; Wang, J.; Niu, Q. Quantum anomalous Hall effect in graphene from Rashba and exchange effects. Phys. Rev. B 2010, 82, 161414R. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Xu, Z.; Sheng, L.; Wang, B.; Xing, D.Y.; Sheng, D.N. Time-reversal-symmetry-broken quantum spin Hall effect. Phys. Rev. Lett. 2011, 107, 066602. [Google Scholar] [CrossRef] [Green Version]
- Villanueva, J.L. Topological Electronic Phases in Graphene. PhD Thesis, University of Santiago de Compostela, Galicia, Spain, 2016. [Google Scholar]
- Thouless, D.J. Quantization of particle transport. Phys. Rev. B 1983, 27, 6083. [Google Scholar] [CrossRef]
- Beugeling, W.; Goldman, N.; Morais Smith, C. Topological phases in a two-dimensional lattice: Magnetic field versus spin-orbit coupling. Phys. Rev. B 2012, 86, 075118. [Google Scholar] [CrossRef] [Green Version]
- Balents, L. Weyl electrons kiss. Physics 2011, 4, 36. [Google Scholar] [CrossRef] [Green Version]
- Xiao, D.; Chang, M.C.; Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 2010, 82, 1959. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.-C.; Jiang, H.; Yao, Y. Low-energy effective Hamiltonian involving spin-orbit coupling in silicene and two-dimensional germanium and tin. Phys. Rev. B 2011, 84, 195430. [Google Scholar] [CrossRef] [Green Version]
- Qi, X.L.; Zhang, S.C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057. [Google Scholar] [CrossRef] [Green Version]
- Schluter, M.; Hybertsen, M.S. The electronic structure of La2CuO4: Renormalization from density functional theory to strong coupling models. Physica 1989, 162–164, 583–586. [Google Scholar] [CrossRef]
- Hybertsen, M.S.; Stechel, E.B.; Schluter, M.; Jennison, D.R. Renormalization from density-functional theory to strong-coupling models for electronic states in Cu-O materials. Phys. Rev. B 1990, 41, 11068. [Google Scholar] [CrossRef] [PubMed]
- Jefferson, J.H.; Eskes, H.; Feiner, L.F. Derivation of a single-band model for CuO2 planes by a cell-perturbation method. Phys. Rev. B 1992, 45, 7959. [Google Scholar] [CrossRef]
- Kane, C.J.; Mele, E.J. Z2 topological order and the quantum spin Hall effect. Phys. Rev. Lett. 2005, 95, 146802. [Google Scholar] [CrossRef] [Green Version]
- Kane, C.J.; Mele, E.J. Quantum spin Hall effect in graphene. Phys. Rev. Lett. 2005, 95, 226801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cayssol, J. Introduction to Dirac materials and topological insulators. Comptes Rendus Phys. 2013, 14, 760–778. [Google Scholar] [CrossRef] [Green Version]
- Saxena, R.; Rao, S.; Kundu, A. Bulk-edge correspondence and new topological phases in periodically driven spin-orbit coupled materials in the low frequency limit. J. Phys. Commun. 2020, 4, 075019. [Google Scholar] [CrossRef]
- Srivastav, S.K.; Sahu, M.R.; Watanabe, K.; Taniguchi, T.; Banerjee, S.; Das, A. Universal quantized thermal conductance in graphene. Sci. Adv. 2019, 5, eaaw5798. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schneider, J. Understanding the Finite-Difference Time-Domain Method. 2020. Available online: https://eecs.wsu.edu/~schneidj/ufdtd/ufdtd.pdf (accessed on 19 June 2021).
- Sato, S.A.; McIver, J.W.; Nuske, M.; Tang, P.; Jotzu, G.; Schulte, B.; Hüubener, H.; De Giovannini, U.; Mathey, L.; Sentef, M.A.; et al. Microscopic theory for the light-induced anomalous Hall effect in graphene. Phys. Rev. B 2019, 99, 214302. [Google Scholar] [CrossRef] [Green Version]
- Kuisma, M.; Sakko, A.; Rossi, T.P.; Larsen, A.H.; Enkovaara, J.; Lehtovaara, L.; Rantala, T.T. Localized surface plasmon resonance in silver nanoparticles: Atomistic first-principles time-dependent density-functional theory calculations. Phys. Rev. B 2015, 91, 115431. [Google Scholar] [CrossRef] [Green Version]
- Mortensen, J.J.; Hansen, L.B.; Jacobsen, K.W. Real-space grid implementation of the projector augmented wave method. Phys. Rev. B 2005, 71, 035109. [Google Scholar] [CrossRef] [Green Version]
- Buckeridge, J.; Jevdokimovs, D.; Catlow, C.R.A.; Sokol, A.A. Bulk electronic, elastic, structural, and dielectric properties of the Weyl semimetal TaAs. Phys. Rev. B 2016, 93, 125205. [Google Scholar] [CrossRef] [Green Version]
- Yan, B.; Felser, C. Topological Materials: Weyl Semimetals. Annu. Rev. Condens. Matter Phys. 2017, 8, 337. [Google Scholar] [CrossRef] [Green Version]
- Weng, H.; Fang, V.; Fang, Z.; Bernevig, B.A.; Dai, X. Weyl semimetal phase in noncentrosymmetric transition-metal monophosphides. Phys. Rev. X 2015, 5, 011029. [Google Scholar] [CrossRef]
- Huang, S.-M.; Xu, S.-Y.; Belopolski, I.; Lee, C.-C.; Chang, G.; Wang, B.; Alidoust, N.; Bian, G.; Neupane, M.; Zhang, C.; et al. A Weyl Fermion semimetal with surface Fermi arcs in the transition metal monopnictide TaAs class. Nat. Commun. 2015, 6, 7373. [Google Scholar] [CrossRef]
- Bukov, M.; D’Alessio, L.; Polkovnikov, A. Universal high-frequency behavior of periodically driven systems: From dynamical stabilization to Floquet engineering. Adv. Phys. 2015, 64, 139. [Google Scholar] [CrossRef] [Green Version]
- Avsar, A.; Tan, J.Y.; Taychatanapat, T.; Balakrishnan, J.; Koon, G.K.W.; Yeo, Y.; Lahiri, J.; Carvalho, A.; Rodin, A.S.; O’Farrell, E.C.T.; et al. Spin-dependent thermoelectric effects in graphene-based superconductor junctions. Nat. Commun. 2014, 5, 4875. [Google Scholar] [CrossRef]
- Konschuh, S.; Gmitra, M.; Fabian, F. Tight-binding theory of the spin-orbit coupling in graphene. Phys. Rev. B 2010, 82, 245412. [Google Scholar] [CrossRef] [Green Version]
- Murakami, S.; Iso, S.; Avishai, Y.; Onoda, M.; Nagaosa, N. Tuning phase transition between quantum spin Hall and ordinary insulating phases. Phys. Rev. B 2007, 76, 205304. [Google Scholar] [CrossRef] [Green Version]
- Moore, J.E.; Balents, L. Topological invariants of time-reversal-invariant band structures. Phys. Rev. B 2007, 75, 121306. [Google Scholar] [CrossRef] [Green Version]
- Haldane, F.D. Model for a Quantum Hall Effect without Landau Levels: Condensed matter realization of the "parity anomaly". Phys. Rev. Lett. 1988, 61, 2015. [Google Scholar] [CrossRef]
- Teleman, N. The index theorem for topological manifolds. Acta Math. 1984, 153, 117. [Google Scholar] [CrossRef]
- Zhang, L.; Tong, P. Staggered potential and magnetic field tunable electronic switch in a kagome nanoribbon junction. Phys. Condens. Matter 2019, 31, 305302. [Google Scholar] [CrossRef]
- Topsakal, M.; Akturk, E.; Ciraci, S. First-principles study of two- and one-dimensional honeycomb structures of boron nitride. Phys. Rev. B 2009, 79, 115442. [Google Scholar] [CrossRef]
- Giovannetti, G.; Khomyakov, P.A.; Brocks, G.; Kelly, P.J.; van den Brink, J. Substrate-induced band gap in graphene on hexagonal boron nitride: Ab initio density functional calculations. Phys. Rev. B 2007, 76, 073103. [Google Scholar] [CrossRef] [Green Version]
- Ukpong, A.M. Emergence of nontrivial spin textures in frustrated van der Waals ferromagnets. Nanomaterials 2021, 11, 1770. [Google Scholar] [CrossRef] [PubMed]
- Coomar, A.; Arntsen, C.; Lopata, K.A.; Pistinner, S.; Neuhauser, D. Monitoring the growth dynamics of colloidal gold-silver core-shell nanoparticles using in situ second harmonic generation and extinction spectroscopy. J. Chem. Phys. 2011, 135, 084121. [Google Scholar] [CrossRef]
- Marchesin, F.; Koval, P.; Barbry, M.; Aizpurua, J.; Sánchez-Portal, D. Plasmonic response of metallic nanojunctions driven by single atom motion: Quantum transport revealed in optics. ACS Photonics 2016, 3, 269. [Google Scholar] [CrossRef] [Green Version]
- Fukuoka, N.; Tanabe, K. Lightning-Rod Effect of Plasmonic Field Enhancement on Hydrogen-Absorbing Transition Metals. Nanomaterials 2019, 9, 1235. [Google Scholar] [CrossRef] [Green Version]
- Urbieta, M.; Barbry, M.; Zhang, Y.; Zabala, N.; Aizpurua, J. Atomic-Scale Lightning Rod Effect In Plasmonic Picocavities: A Classical View To A Quantum Effect. ACS Nano 2018, 12, 585. [Google Scholar] [CrossRef] [PubMed]
- Ngwenya, T.B.; Ukpong, A.M.; Chetty, N. Defect states of complexes involving a vacancy on the boron site in boronitrene. Phys. Rev. B 2011, 84, 245425. [Google Scholar] [CrossRef] [Green Version]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussien, M.A.M.; Ukpong, A.M. Electrodynamics of Topologically Ordered Quantum Phases in Dirac Materials. Nanomaterials 2021, 11, 2914. https://doi.org/10.3390/nano11112914
Hussien MAM, Ukpong AM. Electrodynamics of Topologically Ordered Quantum Phases in Dirac Materials. Nanomaterials. 2021; 11(11):2914. https://doi.org/10.3390/nano11112914
Chicago/Turabian StyleHussien, Musa A. M., and Aniekan Magnus Ukpong. 2021. "Electrodynamics of Topologically Ordered Quantum Phases in Dirac Materials" Nanomaterials 11, no. 11: 2914. https://doi.org/10.3390/nano11112914
APA StyleHussien, M. A. M., & Ukpong, A. M. (2021). Electrodynamics of Topologically Ordered Quantum Phases in Dirac Materials. Nanomaterials, 11(11), 2914. https://doi.org/10.3390/nano11112914