Self-Limitations of Heat Release in Coupled Core-Shell Spinel Ferrite Nanoparticles: Frequency, Time, and Temperature Dependencies
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
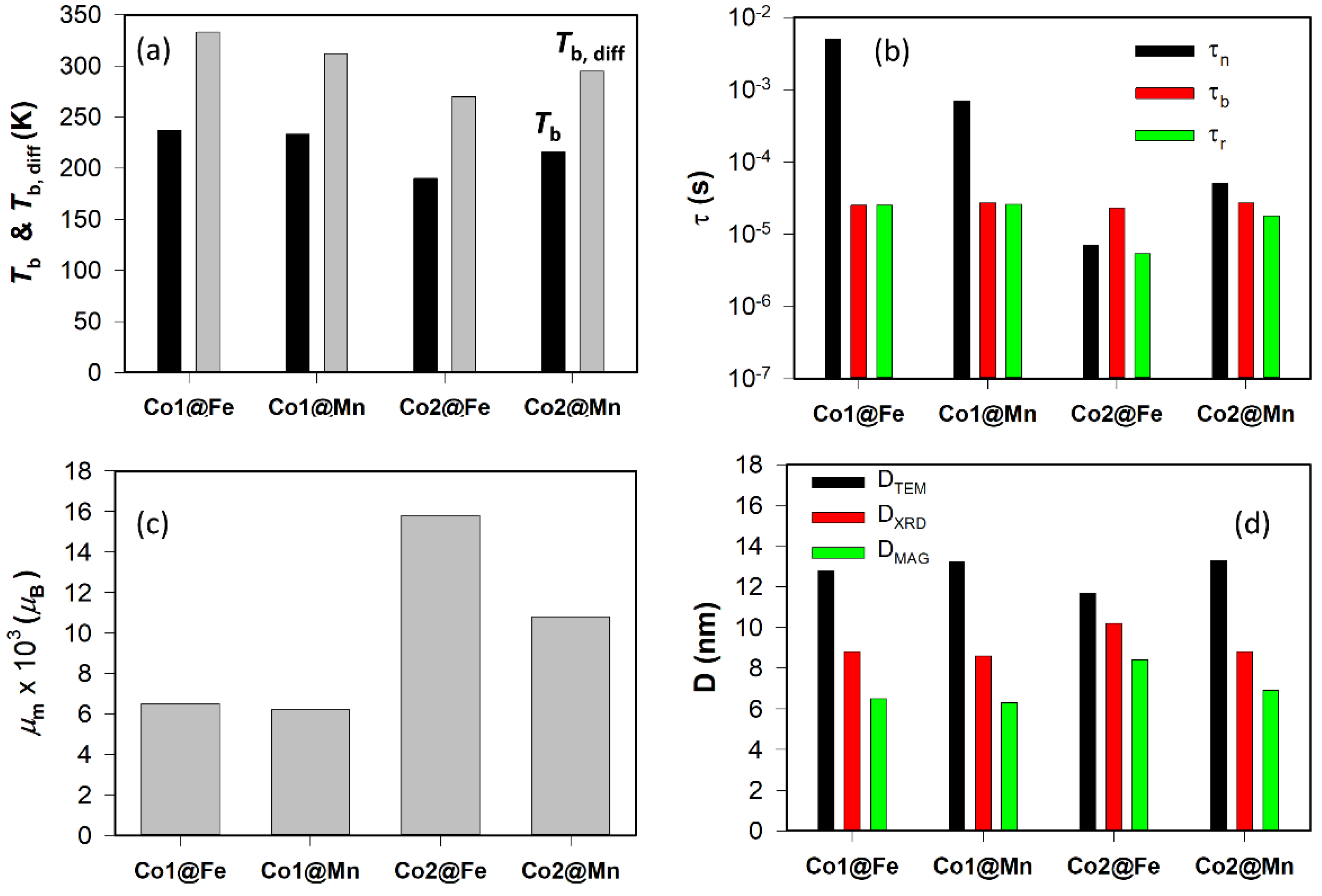
3.1. Basic Characterization
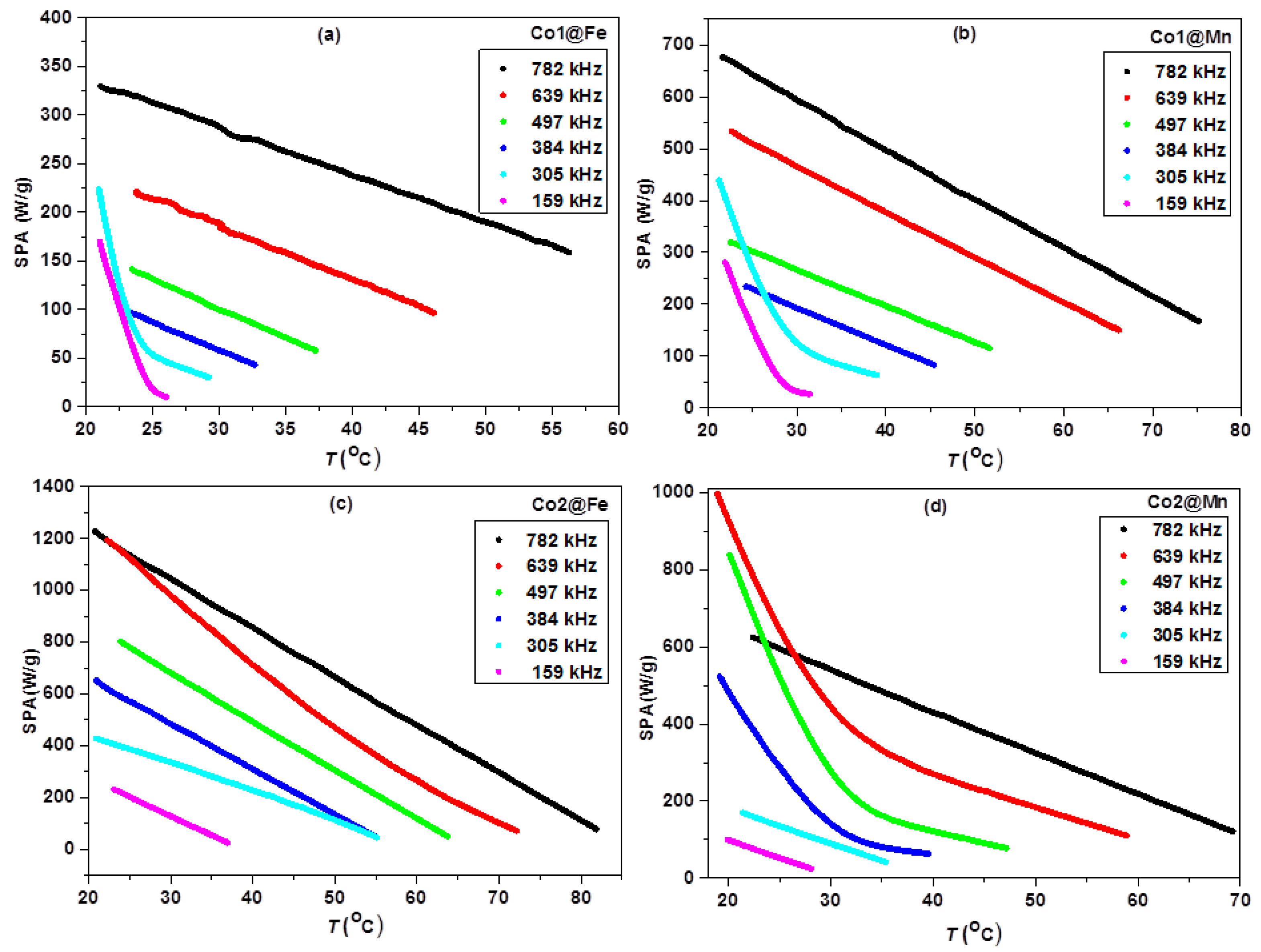
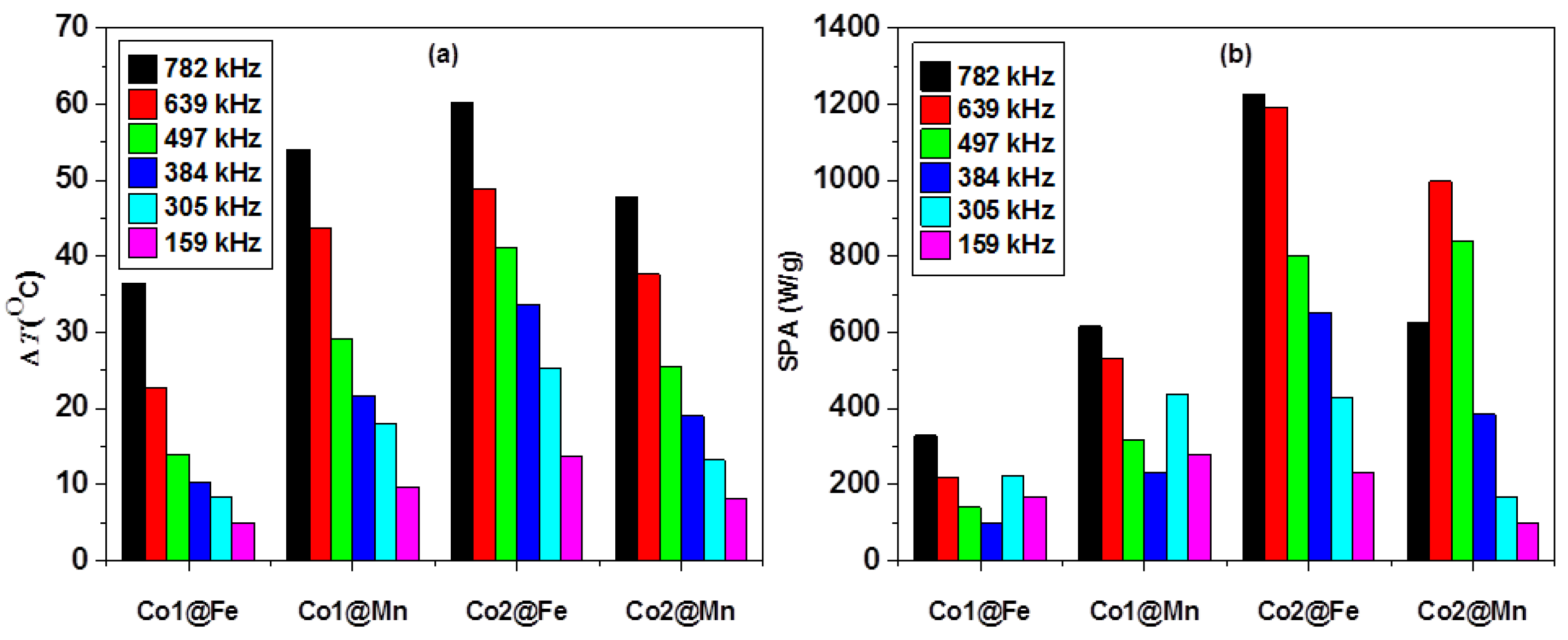
3.2. Heating Properties
3.3. Heating Abilities in the Context of MNPs’ Parameters
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Khandhar, A.P.; Ferguson, R.M.; Krishnan, K.M. Monodispersed magnetite nanoparticles optimized for magnetic fluid hyperthermia: Implications in biological systems. J. Appl. Phys. 2011, 109, 10–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kita, E.; Hashimoto, S.; Kayano, T.; Minagawa, M.; Yanagihara, H.; Kishimoto, M.; Yamada, K.; Oda, T.; Ohkohchi, N.; Takagi, T.; et al. Heating characteristics of ferromagnetic iron oxide nanoparticles for magnetic hyperthermia. J. Appl. Phys. 2010, 107, 09B321. [Google Scholar] [CrossRef]
- Chomoucka, J.; Drbohlavova, J.; Huska, D.; Adam, V.; Kizek, R.; Hubalek, J. Magnetic nanoparticles and targeted drug delivering. Pharmacol. Res. 2010, 62, 144–149. [Google Scholar] [CrossRef] [PubMed]
- Reiss, G.; Hütten, A. Applications beyond data storage. Nat. Mater. 2005, 4, 725–726. [Google Scholar] [CrossRef] [PubMed]
- Akbarzadeh, A.; Samiei, M.; Davaran, S. Magnetic nanoparticles: Preparation, physical properties, and applications in biomedicine. Nanoscale Res. Lett. 2012, 7, 144. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tartaj, P.; del Puerto Morales, M.; Veintemillas-Verdaguer, S.; Gonzalez-Carreño, T.; Serna, C.J. The preparation of magnetic nanoparticles for applications in biomedicine. J. Phys. D Appl. Phys. 2003, 36, R182. [Google Scholar] [CrossRef]
- Chatterjee, D.K.; Diagaradjane, P.; Krishnan, S. Nanoparticle-mediated hyperthermia in cancer therapy. Ther. Deliv. 2011, 2, 1001–1014. [Google Scholar] [CrossRef] [Green Version]
- Dewey, W.C.; Hopwood, L.E.; Sapareto, S.A.; Gerweck, L.E. Cellular Responses to Combinations of Hyperthermia and Radiation. Radiology 1977, 123, 463–474. [Google Scholar] [CrossRef] [PubMed]
- Meffre, A.; Mehdaoui, B.; Connord, V.; Carrey, J.; Fazzini, P.F.; Lachaize, S.; Respaud, M.; Chaudret, B. Complex Nano-objects Displaying Both Magnetic and Catalytic Properties: A Proof of Concept for Magnetically Induced Heterogeneous Catalysis. Nano Lett. 2015, 15, 3241–3248. [Google Scholar] [CrossRef]
- Ceylan, S.; Coutable, L.; Wegner, J.; Kirschning, A. Inductive heating with magnetic materials inside flow reactors. Chem. Eur. J. 2011, 17, 1884–1893. [Google Scholar] [CrossRef]
- Bordet, A.; Lacroix, L.-M.; Fazzini, P.-F.; Carrey, J.; Soulantica, K.; Chaudret, B. Magnetically Induced Continuous CO 2 Hydrogenation Using Composite Iron Carbide Nanoparticles of Exceptionally High Heating Power. Angew. Chem. 2016, 128, 16126–16130. [Google Scholar] [CrossRef]
- Asensio, J.M.; Miguel, A.B.; Fazzini, P.F.; van Leeuwen, P.W.N.M.; Chaudret, B. Hydrodeoxygenation Using Magnetic Induction: High-Temperature Heterogeneous Catalysis in Solution. Angew. Chem., Int. Ed. 2019, 58, 11306–11310. [Google Scholar] [CrossRef] [PubMed]
- Rosensweig, R.E. Heating magnetic fluid with alternating magnetic field. J. Magn. Magn. Mater. 2002, 252, 370–374. [Google Scholar] [CrossRef]
- Ruta, S.; Chantrell, R.; Hovorka, O. Unified model of hyperthermia via hysteresis heating in systems of interacting magnetic nanoparticles. Sci. Rep. 2015, 5, 9090. [Google Scholar] [CrossRef] [Green Version]
- Mohapatra, J.; Xing, M.; Liu, J.P. Inductive Thermal Effect of Ferrite Magnetic Nanoparticles. Materials 2019, 12, 3208. [Google Scholar] [CrossRef] [Green Version]
- Deatsch, A.E.; Evans, B.A. Heating efficiency in magnetic nanoparticle hyperthermia. J. Magn. Magn. Mater. 2014, 354, 163–172. [Google Scholar] [CrossRef]
- Etemadi, H.; Plieger, P.G. Magnetic Fluid Hyperthermia Based on Magnetic Nanoparticles: Physical Characteristics, Historical Perspective, Clinical Trials, Technological Challenges, and Recent Advances. Adv. Ther. 2020, 3, 2000061. [Google Scholar] [CrossRef]
- Tong, S.; Zhu, H.; Bao, G. Magnetic iron oxide nanoparticles for disease detection and therapy. Mater. Today 2019, 31, 86–99. [Google Scholar] [CrossRef] [PubMed]
- Carrey, J.; Mehdaoui, B.; Respaud, M. Simple models for dynamic hysteresis loop calculations of magnetic single-domain nanoparticles: Application to magnetic hyperthermia optimization. J. Appl. Phys. 2011, 109, 083921. [Google Scholar] [CrossRef]
- Hergt, R.; Dutz, S.; Zeisberger, M. Validity limits of the Néel relaxation model of magnetic nanoparticles for hyperthermia. Nanotechnology 2009, 21, 015706. [Google Scholar] [CrossRef] [PubMed]
- Mamiya, H.; Jeyadevan, B. Hyperthermic effects of dissipative structures of magnetic nanoparticles in large alternating magnetic fields. Sci. Rep. 2011, 1, 157. [Google Scholar] [CrossRef] [Green Version]
- Usov, N.A.; Nesmeyanov, M.S.; Tarasov, V.P. Magnetic Vortices as Efficient Nano Heaters in Magnetic Nanoparticle Hyperthermia. Sci. Rep. 2018, 8, 1224. [Google Scholar] [CrossRef] [PubMed]
- Usov, N.A.; Rytov, R.A.; Bautin, V.A. Properties of assembly of superparamagnetic nanoparticles in viscous liquid. Sci. Rep. 2021, 11, 6999. [Google Scholar] [CrossRef]
- Torres, T.E.; Lima, E.; Calatayud, M.P.; Sanz, B.; Ibarra, A.; Fernández-Pacheco, R.; Mayoral, A.; Marquina, C.; Ibarra, M.R.; Goya, F.G. The relevance of Brownian relaxation as power absorption mechanism in Magnetic Hyperthermia. Sci. Rep. 2019, 9, 3992. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Coey, J.M.D.; Khalafalla, D. Superparamagnetic γ-Fe2O3. Phys. Status Solidi 1972, 11, 229–241. [Google Scholar] [CrossRef]
- Kittel, C. Theory of the Structure of Ferromagnetic Domains in Films and Small Particles. Phys. Rev. 1946, 70, 965–971. [Google Scholar] [CrossRef]
- Kolhatkar, A.G.; Jamison, A.C.; Litvinov, D.; Willson, R.C.; Lee, T.R. Tuning the magnetic properties of nanoparticles. Int. J. Mol. Sci. 2013, 14, 15977–16009. [Google Scholar] [CrossRef] [Green Version]
- Abenojar, E.C.; Wickramasinghe, S.; Bas-Concepcion, J.; Samia, A.C.S. Structural effects on the magnetic hyperthermia properties of iron oxide nanoparticles. Prog. Nat. Sci. Mater. Int. 2016, 26, 440–448. [Google Scholar] [CrossRef] [Green Version]
- Choi, H.; An, M.; Eom, W.; Lim, S.W.; Shim, I.-B.; Kim, C.S.; Kim, S.J. Crystallographic and Magnetic Properties of the Hyperthermia Material CoFe2O4@AlFe2O4. J. Korean Phys. Soc. 2017, 70, 173–176. [Google Scholar] [CrossRef]
- Tong, S.; Quinto, C.A.; Zhang, L.; Mohindra, P.; Bao, G. Size-Dependent Heating of Magnetic Iron Oxide Nanoparticles. ACS Nano 2017, 11, 6808–6816. [Google Scholar] [CrossRef]
- Song, Q.; Zhang, Z.J. Controlled synthesis and magnetic properties of bimagnetic spinel ferrite CoFe2O4 and MnFe2O4 nanocrystals with core-shell architecture. J. Am. Chem. Soc. 2012, 134, 10182–10190. [Google Scholar] [CrossRef]
- Masala, O.; Hoffman, D.; Sundaram, N.; Page, K.; Proffen, T.; Lawes, G.; Seshadri, R. Preparation of magnetic spinel ferrite core/shell nanoparticles: Soft ferrites on hard ferrites and vice versa. Solid State Sci. 2006, 8, 1015–1022. [Google Scholar] [CrossRef]
- Lee, J.-H.; Jang, J.; Choi, J.; Moon, S.H.; Noh, S.; Kim, J.; Kim, J.-G.; Kim, I.-S.; Park, K.I.; Cheon, J. Exchange-coupled magnetic nanoparticles for efficient heat induction. Nat. Nanotechnol. 2011, 6, 418–422. [Google Scholar] [CrossRef]
- Angelakeris, M.; Li, Z.A.; Hilgendorff, M.; Simeonidis, K.; Sakellari, D.; Filippousi, M.; Tian, H.; Van Tendeloo, G.; Spasova, M.; Acet, M.; et al. Enhanced biomedical heat-triggered carriers via nanomagnetism tuning in ferrite-based nanoparticles. J. Magn. Magn. Mater. 2015, 381, 179–187. [Google Scholar] [CrossRef] [Green Version]
- Kafrouni, L.; Savadogo, O. Recent progress on magnetic nanoparticles for magnetic hyperthermia. Prog. Biomater. 2016, 5, 147–160. [Google Scholar] [CrossRef] [Green Version]
- Serantes, D.; Simeonidis, K.; Angelakeris, M.; Chubykalo-Fesenko, O.; Marciello, M.; Morales, M.d.P.; Baldomir, D.; Martinez-Boubeta, C. Multiplying Magnetic Hyperthermia Response by Nanoparticle Assembling. J. Phys. Chem. C 2014, 118, 5927–5934. [Google Scholar] [CrossRef]
- Ranoo, S.; Lahiri, B.B.; Muthukumaran, T.; Philip, J. Enhancement in hyperthermia efficiency under in situ orientation of superparamagnetic iron oxide nanoparticles in dispersions. Appl. Phys. Lett. 2019, 115, 43102. [Google Scholar] [CrossRef]
- de la Presa, P.; Luengo, Y.; Multigner, M.; Costo, R.; Morales, M.P.; Rivero, G.; Hernando, A. Study of Heating Efficiency as a Function of Concentration, Size, and Applied Field in γ-Fe2O3 Nanoparticles. J. Phys. Chem. C 2012, 116, 25602–25610. [Google Scholar] [CrossRef]
- Cobianchi, M.; Lascialfari, A.; Kusigerki, V.; Mrakovic, A.; Knezevic, N.; Peddis, D.; Illes, E. Effects of organic coating on hyperthermic efficiencies. In Proceedings of the 2017 IEEE International Magnetics Conference (INTERMAG), Dublin, Ireland, 24–28 April 2017; p. 1. [Google Scholar]
- Liu, X.; Chen, H.J.; Alfadhl, Y.; Chen, X.; Parini, C.; Wen, D. Conductivity and frequency dependent specific absorption rate. J. Appl. Phys. 2013, 113, 074092. [Google Scholar] [CrossRef]
- Conde-Leboran, I.; Baldomir, D.; Martinez-Boubeta, C.; Chubykalo-Fesenko, O.; del Puerto Morales, M.; Salas, G.; Cabrera, D.; Camarero, J.; Teran, F.J.; Serantes, D. A Single Picture Explains Diversity of Hyperthermia Response of Magnetic Nanoparticles. J. Phys. Chem. C 2015, 119, 15698–15706. [Google Scholar] [CrossRef]
- Mehdaoui, B.; Meffre, A.; Carrey, J.; Lachaize, S.; Lacroix, L.-M.; Gougeon, M.; Chaudret, B.; Respaud, M. Optimal Size of Nanoparticles for Magnetic Hyperthermia: A Combined Theoretical and Experimental Study. Adv. Funct. Mater. 2011, 21, 4573–4581. [Google Scholar] [CrossRef] [Green Version]
- Shaterabadi, Z.; Nabiyouni, G.; Soleymani, M. Physics responsible for heating efficiency and self-controlled temperature rise of magnetic nanoparticles in magnetic hyperthermia therapy. Prog. Biophys. Mol. Biol. 2018, 133, 9–19. [Google Scholar] [CrossRef] [PubMed]
- Sanna Angotzi, M.; Mameli, V.; Cara, C.; Musinu, A.; Sangregorio, C.; Niznansky, D.; Xin, H.L.; Vejpravova, J.; Cannas, C. Coupled hard-soft spinel ferrite-based core-shell nanoarchitectures: Magnetic properties and heating abilities. Nanoscale Adv. 2020, 2, 3191–3201. [Google Scholar] [CrossRef]
- Sanna Angotzi, M.; Mameli, V.; Zákutná, D.; Kubániová, D.; Cara, C.; Cannas, C. Evolution of the Magnetic and Structural Properties with the Chemical Composition in Oleate-Capped MnxCo1–xFe2O4 Nanoparticles. J. Phys. Chem. C 2021, 125, 20626–20638. [Google Scholar] [CrossRef]
- Sanna Angotzi, M.; Musinu, A.; Mameli, V.; Ardu, A.; Cara, C.; Niznansky, D.; Xin, H.L.; Cannas, C. Spinel Ferrite Core-Shell Nanostructures by a Versatile Solvothermal Seed-Mediated Growth Approach and Study of Their Nanointerfaces. ACS Nano 2017, 11, 7889–7900. [Google Scholar] [CrossRef] [PubMed]
- Pacakova, B.; Kubickova, S.; Salas, G.; Mantlikova, A.R.; Marciello, M.; Morales, M.P.; Niznansky, D.; Vejpravova, J. The internal structure of magnetic nanoparticles determines the magnetic response. Nanoscale 2017, 9, 5129–5140. [Google Scholar] [CrossRef]
- Vatansever, E.; Acharyya, M. Nonequilibrium multiple transitions in the core-shell Ising nanoparticles driven by randomly varying magnetic fields. J. Magn. Magn. Mater. 2021, 527, 167721. [Google Scholar] [CrossRef]
- Kneller, E.F.; Hawig, R. The exchange-spring magnet: A new material principle for permanent magnets. IEEE Trans. Magn. 1991, 27, 3560–3588. [Google Scholar] [CrossRef]
- Ruta, S.; Rannala, E.; Serantes, D.; Hovorka, O.; Chantrell, R. Optimisation of properties for magnetic hyperthermia beyond LRT. In Proceedings of the 2nd Workshop on Magnetic Nanoparticles for Hypothermia, Challenges and Opportunities, Santiago de Compostela, Spain, 15 July 2019. [Google Scholar]
- Ota, S.; Takemura, Y. Characterization of Néel and Brownian Relaxations Isolated from Complex Dynamics Influenced by Dipole Interactions in Magnetic Nanoparticles. J. Phys. Chem. C 2019, 123, 28859–28866. [Google Scholar] [CrossRef] [Green Version]
- Shasha, C.; Krishnan, K.M. Nonequilibrium Dynamics of Magnetic Nanoparticles with Applications in Biomedicine. Adv. Mater. 2021, 33, 48–50. [Google Scholar] [CrossRef]
- Garaio, E.; Sandre, O.; Collantes, J.M.; Garcia, J.A.; Mornet, S.; Plazaola, F. Specific absorption rate dependence on temperature in magnetic field hyperthermia measured by dynamic hysteresis losses (ac magnetometry). Nanotechnology 2015, 26, 015704. [Google Scholar] [CrossRef] [PubMed] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khanal, S.; Sanna Angotzi, M.; Mameli, V.; Veverka, M.; Xin, H.L.; Cannas, C.; Vejpravová, J. Self-Limitations of Heat Release in Coupled Core-Shell Spinel Ferrite Nanoparticles: Frequency, Time, and Temperature Dependencies. Nanomaterials 2021, 11, 2848. https://doi.org/10.3390/nano11112848
Khanal S, Sanna Angotzi M, Mameli V, Veverka M, Xin HL, Cannas C, Vejpravová J. Self-Limitations of Heat Release in Coupled Core-Shell Spinel Ferrite Nanoparticles: Frequency, Time, and Temperature Dependencies. Nanomaterials. 2021; 11(11):2848. https://doi.org/10.3390/nano11112848
Chicago/Turabian StyleKhanal, Shankar, Marco Sanna Angotzi, Valentina Mameli, Miroslav Veverka, Huolin L. Xin, Carla Cannas, and Jana Vejpravová. 2021. "Self-Limitations of Heat Release in Coupled Core-Shell Spinel Ferrite Nanoparticles: Frequency, Time, and Temperature Dependencies" Nanomaterials 11, no. 11: 2848. https://doi.org/10.3390/nano11112848
APA StyleKhanal, S., Sanna Angotzi, M., Mameli, V., Veverka, M., Xin, H. L., Cannas, C., & Vejpravová, J. (2021). Self-Limitations of Heat Release in Coupled Core-Shell Spinel Ferrite Nanoparticles: Frequency, Time, and Temperature Dependencies. Nanomaterials, 11(11), 2848. https://doi.org/10.3390/nano11112848