Characterizing Polymer Hydration Shell Compressibilities with the Small-System Method
Abstract
1. Introduction
2. Methods
3. Results and Discussion
3.1. Isothermal Compressibility of SPC/E Water: Sampling Fluctuations in Cylindrical Observation Volumes
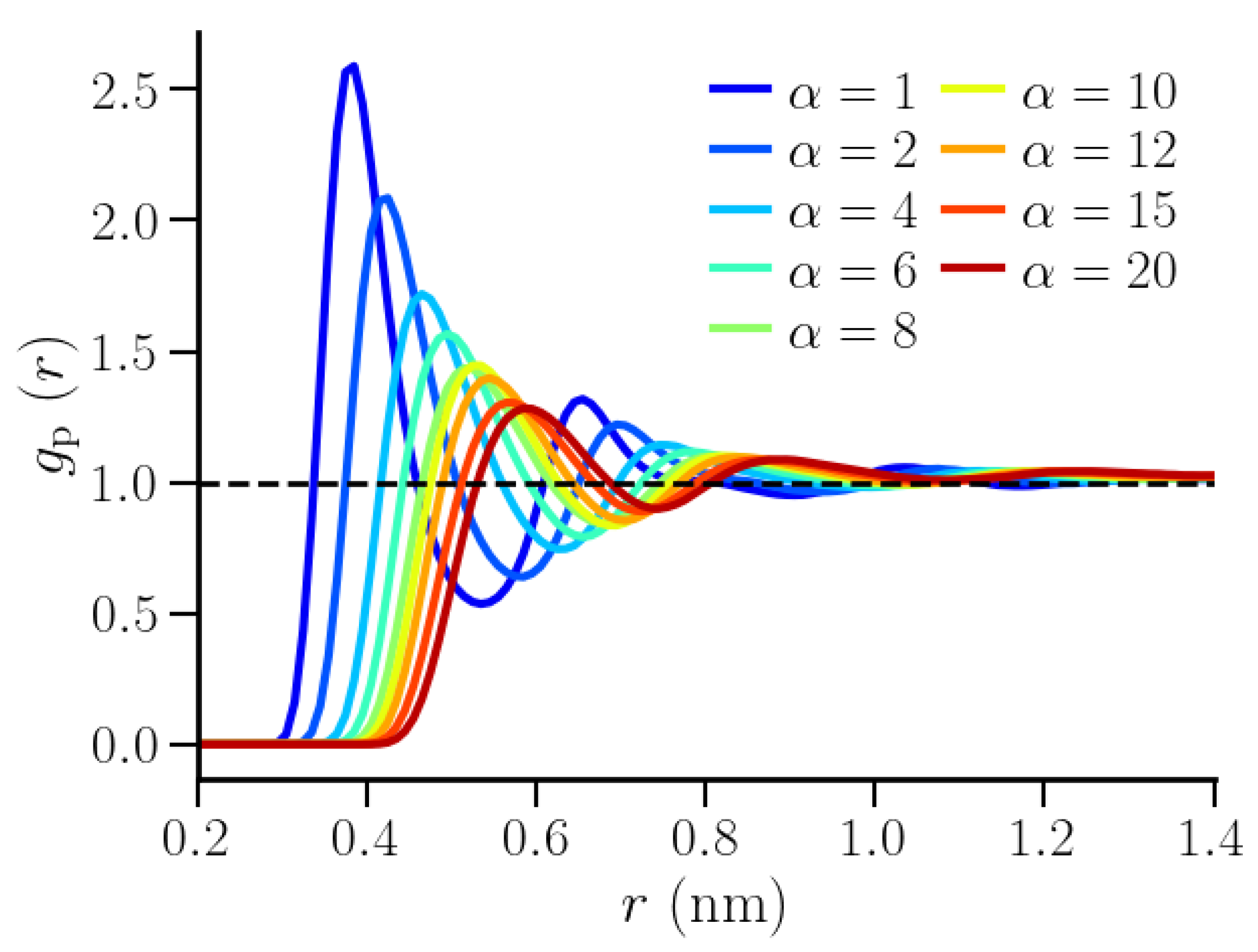
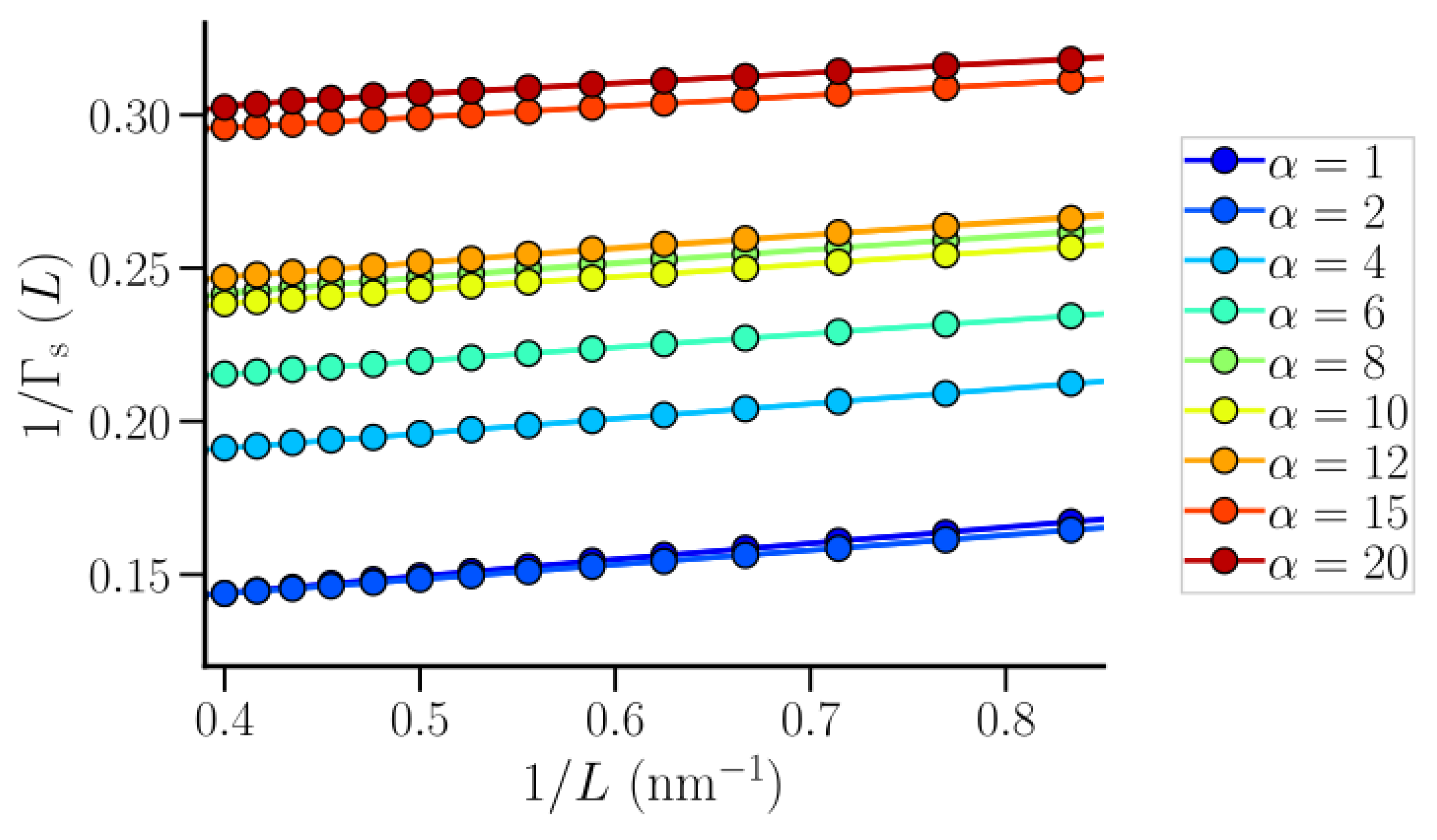
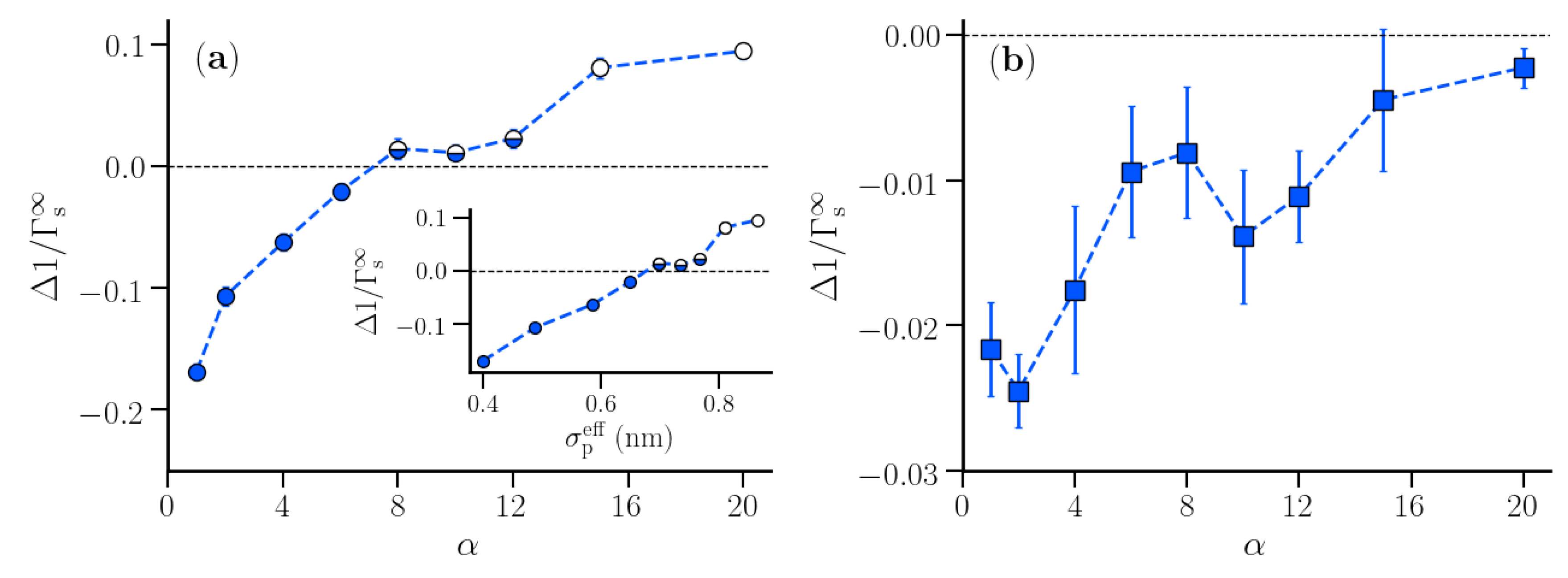
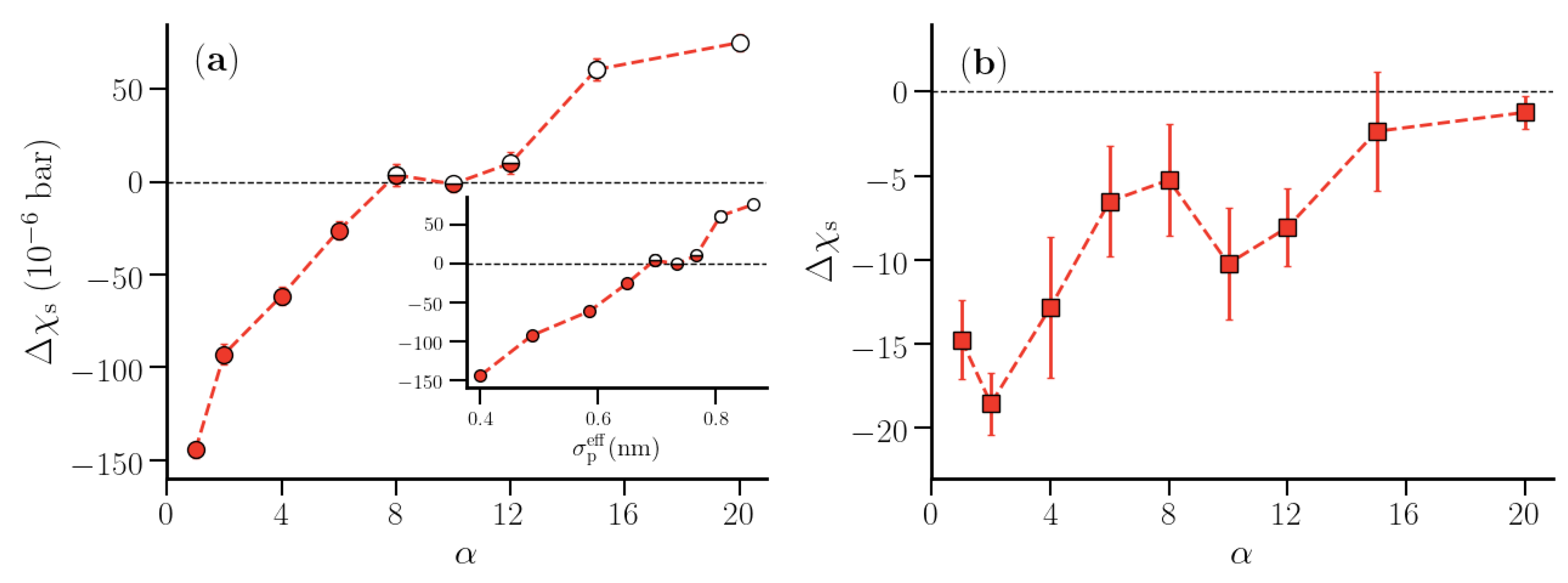
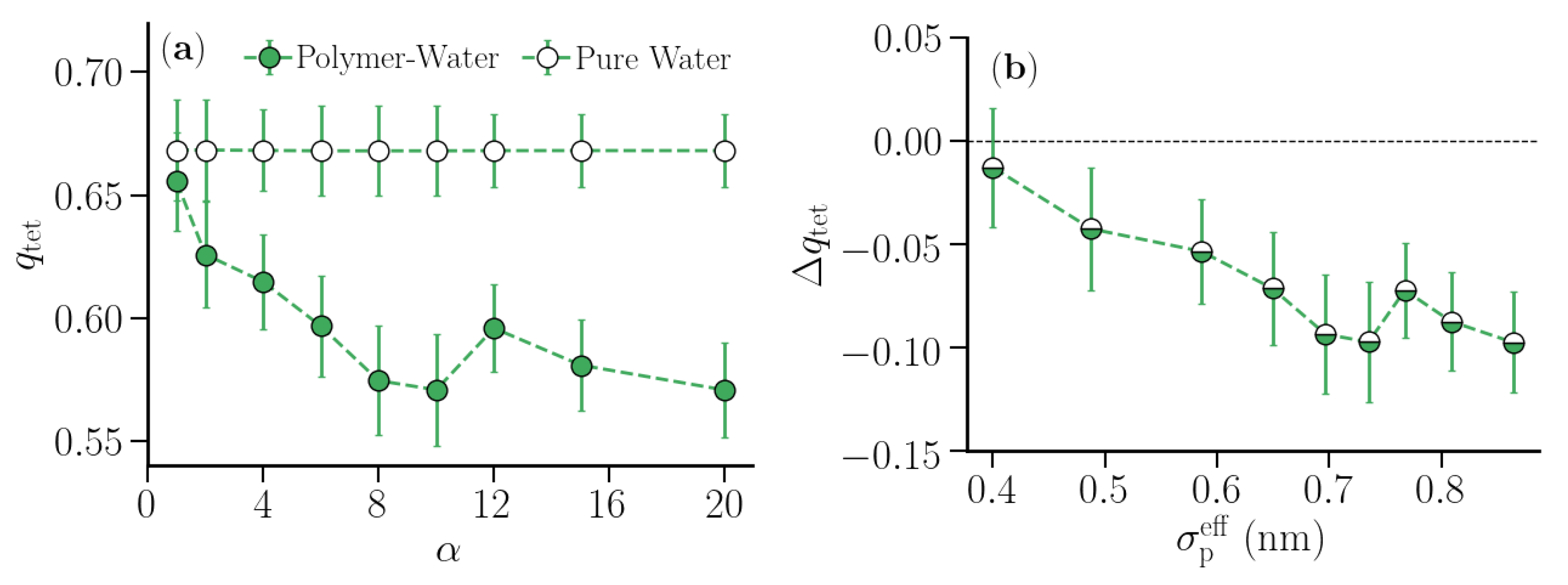
3.2. Thermodynamic Properties of Polymer Hydration Shells
4. Scope and Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| TL | Thermodynamic Limit |
| SSM | Small-System Method |
| KBI | Kirkwood-Buff Integral |
| RDF | Radial Distribution Function |
| pRDF | Proximal pair correlation function |
References
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications, 2nd ed.; Academic Press, Inc.: New York, NY, USA, 2001. [Google Scholar]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids, 2nd ed.; Clarendon Press: Oxford, UK, 2017. [Google Scholar] [CrossRef]
- Lebowitz, J.L.; Percus, J.K. Long-Range Correlations in a Closed System with Applications to Nonuniform Fluids. Phys. Rev. 1961, 122, 1675–1691. [Google Scholar] [CrossRef]
- Perera, A.; Zoranić, L.; Sokolić, F.; Mazighi, R. A Comparative Molecular Dynamics Study of Water-Methanol and Acetone-Methanol Mixtures. J. Mol. Liq. 2011, 159, 52–59. [Google Scholar] [CrossRef]
- Ganguly, P.; van der Vegt, N.F.A. Convergence of Sampling Kirkwood-Buff Integrals of Aqueous Solutions with Molecular Dynamics Simulations. J. Chem. Theory Comput. 2013, 9, 1347–1355. [Google Scholar] [CrossRef] [PubMed]
- Krüger, P.; Schnell, S.K.; Bedeaux, D.; Kjelstrup, S.; Vlugt, T.J.H.; Simon, J.M. Kirkwood-Buff Integrals for Finite Volumes. J. Phys. Chem. Lett. 2013, 4, 235–238. [Google Scholar] [CrossRef] [PubMed]
- Krüger, P.; Vlugt, T.J.H. Size and Shape Dependence of Finite-Volume Kirkwood-Buff Integrals. Phys. Rev. E 2018, 97, 051301. [Google Scholar] [CrossRef]
- Dawass, N.; Krüger, P.; Schnell, S.K.; Bedeaux, D.; Kjelstrup, S.; Simon, J.M.; Vlugt, T.J.H. Finite-Size Effects of Kirkwood-Buff Integrals from Molecular Simulations. Mol. Simul. 2018, 44, 599–612. [Google Scholar] [CrossRef]
- Milzetti, J.; Nayar, D.; van der Vegt, N.F.A. Convergence of Kirkwood–Buff Integrals of Ideal and Nonideal Aqueous Solutions Using Molecular Dynamics Simulations. J. Phys. Chem. B 2018, 122, 5515–5526. [Google Scholar] [CrossRef]
- Schnell, S.K.; Vlugt, T.J.H.; Simon, J.M.; Bedeaux, D.; Kjelstrup, S. Thermodynamics of a Small System in a μT Reservoir. Chem. Phys. Lett. 2011, 504, 199–201. [Google Scholar] [CrossRef]
- Schnell, S.K.; Liu, X.; Simon, J.M.; Bardow, A.; Bedeaux, D.; Vlugt, T.J.H.; Kjelstrup, S. Calculating Thermodynamic Properties from Fluctuations at Small Scales. J. Phys. Chem. B 2011, 115, 10911–10918. [Google Scholar] [CrossRef]
- Hill, T.L. Thermodynamics of Small Systems. J. Chem. Phys. 1962, 36, 3182–3197. [Google Scholar] [CrossRef]
- Hill, T.L. Thermodynamics of Small Systems; Dover Publications: Mineola, NY, USA, 1994. [Google Scholar]
- Schnell, S.K.; Skorpa, R.; Bedeaux, D.; Kjelstrup, S.; Vlugt, T.J.H.; Simon, J.M. Partial Molar Enthalpies and Reaction Enthalpies from Equilibrium Molecular Dynamics Simulation. J. Chem. Phys. 2014, 141, 144501. [Google Scholar] [CrossRef] [PubMed]
- Strøm, B.A.; Simon, J.M.; Schnell, S.K.; Kjelstrup, S.; He, J.; Bedeaux, D. Size and Shape Effects on the Thermodynamic Properties of Nanoscale Volumes of Water. Phys. Chem. Chem. Phys. 2017, 19, 9016–9027. [Google Scholar] [CrossRef] [PubMed]
- Schnell, S.K.; Englebienne, P.; Simon, J.M.; Kruger, P.; Balaji, S.P.; Kjelstrup, S.; Bedeaux, D.; Bardow, A.; Vlugt, T.J.H. How to Apply the Kirkwood-Buff Theory to Individual Species in Salt Solutions. Chem. Phys. Lett. 2013, 582, 154–157. [Google Scholar] [CrossRef]
- Erdös, M.; Galteland, O.; Bedeaux, D.; Kjelstrup, S.; Moultos, O.; Vlugt, T. Gibbs Ensemble Monte Carlo Simulation of Fluids in Confinement: Relation between the Differential and Integral Pressures. Nanomaterials 2020, 10, 293. [Google Scholar] [CrossRef] [PubMed]
- Rauter, M.; Galteland, O.; Erdös, M.; Moultos, O.; Vlugt, T.; Schnell, S.; Bedeaux, D.; Kjelstrup, S. Two-Phase Equilibrium Conditions in Nanopores. Nanomaterials 2020, 10, 608. [Google Scholar] [CrossRef]
- Jamali, S.H.; Bardow, A.; Vlugt, T.J.H.; Moultos, O.A. Generalized Form for Finite-Size Corrections in Mutual Diffusion Coefficients of Multicomponent Mixtures Obtained from Equilibrium Molecular Dynamics Simulation. J. Chem. Theory Comput. 2020, 16, 3799–3806. [Google Scholar] [CrossRef]
- Trinh, T.T.; Bedeaux, D.; Simon, J.M.; Kjelstrup, S. Thermodynamic Characterization of Two Layers of CO2 on a Graphite Surface. Chem. Phys. Lett. 2014, 612, 214–218. [Google Scholar] [CrossRef]
- Trinh, T.T.; van Erp, T.S.; Bedeaux, D.; Kjelstrup, S.; Grande, C.A. A Procedure to Find Thermodynamic Equilibrium Constants for CO2 and CH4 Adsorption on Activated Carbon. Phys. Chem. Chem. Phys. 2015, 17, 8223–8230. [Google Scholar] [CrossRef][Green Version]
- Lum, K.; Chandler, D.; Weeks, J.D. Hydrophobicity at Small and Large Length Scales. J. Phys. Chem. B 1999, 103, 4570–4577. [Google Scholar] [CrossRef]
- Chandler, D. Interfaces and the Driving Force of Hydrophobic Assembly. Nature 2005, 437, 640–647. [Google Scholar] [CrossRef]
- Sarupria, S.; Garde, S. Quantifying Water Density Fluctuations and Compressibility of Hydration Shells of Hydrophobic Solutes and Proteins. Phys. Rev. Lett. 2009, 103, 037803. [Google Scholar] [CrossRef] [PubMed]
- Mittal, J.; Hummer, G. Static and Dynamic Correlations in Water at Hydrophobic Interfaces. Proc. Natl. Acad. Sci. USA 2008, 105, 20130–20135. [Google Scholar] [CrossRef] [PubMed]
- Huang, D.M.; Geissler, P.L.; Chandler, D. Scaling of Hydrophobic Solvation Free Energies. J. Phys. Chem. B 2001, 105, 6704–6709. [Google Scholar] [CrossRef]
- Patel, A.J.; Varilly, P.; Chandler, D. Fluctuations of Water Near Extended Hydrophobic and Hydrophilic Surfaces. J. Phys. Chem. B 2010, 114, 1632–1637. [Google Scholar] [CrossRef]
- Rego, N.B.; Xi, E.; Patel, A.J. Protein Hydration Waters Are Susceptible to Unfavorable Perturbations. J. Am. Chem. Soc. 2019, 141, 2080–2086. [Google Scholar] [CrossRef]
- Rajamani, S.; Truskett, T.M.; Garde, S. Hydrophobic Hydration from Small to Large Lengthscales: Understanding and Manipulating the Crossover. Proc. Natl. Acad. Sci. USA 2005, 102, 9475–9480. [Google Scholar] [CrossRef]
- Zangi, R.; Zhou, R.; Berne, B.J. Urea’s Action on Hydrophobic interactions. J. Am. Chem. Soc. 2009, 131, 1535–1541. [Google Scholar] [CrossRef]
- Kanduč, M.; Chudoba, R.; Palczynski, K.; Kim, W.K.; Roa, R.; Dzubiella, J. Selective Solute Adsorption and Partitioning Around Single PNIPAM Chains. Phys. Chem. Chem. Phys. 2017, 19, 5906–5916. [Google Scholar] [CrossRef]
- Abascal, J.L.F.; Vega, C. A General Purpose Model for the Condensed Phases of Water: TIP4P/2005. J. Chem. Phys. 2005, 123, 234505. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High Performance Molecular Simulations Through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1-2, 19–25. [Google Scholar] [CrossRef]
- Hess, B. P-LINCS: A Parallel Linear Constraint Solver for Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 116–122. [Google Scholar] [CrossRef] [PubMed]
- Darden, T.; York, D.; Pedersen, L. Particle Mesh Ewald: An N·logN Method for Ewald Sums in Large Systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical Sampling Through Velocity Rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef]
- Nosé, S. A Molecular Dynamics Method for Simulations in the Canonical Ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular Dynamics with Coupling to an External Bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic Transitions in Single Crystals: A New Molecular Dynamics Method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Grigera, J.R.; Straatsma, T.P. The Missing Term in Effective Pair Potentials. J. Phys. Chem. 1987, 91, 6269–6271. [Google Scholar] [CrossRef]
- Chau, P.L.; Hardwick, A.J. A New Order Parameter for Tetrahedral Configurations. Mol. Phys. 1998, 93, 511–518. [Google Scholar] [CrossRef]
- Errington, J.R.; Debenedetti, P.G. Relationship Between Structural Order and the Anomalies of Liquid Water. Nature 2005, 409, 318–321. [Google Scholar] [CrossRef]
- Heidari, M.; Kremer, K.; Potestio, R.; Cortes-Huerto, R. Finite-Size Integral Equations in the Theory of Liquids and the Thermodynamic Limit in Computer Simulations. Mol. Phys. 2018, 116, 3301–3310. [Google Scholar] [CrossRef]
- Pi, H.L.; Aragones, J.L.; Vega, C.; Noya, E.G.; Abascal, J.L.; Gonzalez, M.A.; McBride, C. Anomalies in Water as Obtained from Computer Simulations of the TIP4P/2005 Model: Density Maxima, and Density, Isothermal Compressibility and Heat Capacity Minima. Mol. Phys. 2009, 107, 365–374. [Google Scholar] [CrossRef]
- Pathak, H.; Palmer, J.C.; Schlesinger, D.; Wikfeldt, K.T.; Sellberg, J.A.; Pettersson, L.G.M.; Nilsson, A. The Structural Validity of Various Thermodynamical Models of Supercooled Water. J. Chem. Phys. 2016, 145, 134507. [Google Scholar] [CrossRef] [PubMed]
- Pettersson, L.G.; Nilsson, A. The Structure of Water; From Ambient to Deeply Supercooled. J. Non-Cryst. Solids 2015, 407, 399–417. [Google Scholar] [CrossRef]
- Román, F.L.; White, J.A.; Velasco, S. Fluctuations in an Equilibrium Hard-Disk Fluid: Explicit Size Effects. J. Chem. Phys. 1997, 107, 4635–4641. [Google Scholar] [CrossRef]
- Jamadagni, S.N.; Godawat, R.; Garde, S. Hydrophobicity of Proteins and Interfaces: Insights from Density Fluctuations. Annu. Rev. Chem. Biomol. Eng. 2011, 2, 147–171. [Google Scholar] [CrossRef] [PubMed]
- Duboué-Dijon, E.; Laage, D. Characterization of the Local Structure in Liquid Water by Various Order Parameters. J. Phys. Chem. B 2015, 119, 8406–8418. [Google Scholar] [CrossRef]
- Stillinger, F.H. Structure in Aqueous Solutions of Nonpolar Solutes from the Standpoint of Scaled-Particle Theory. J. Solut. Chem. 1973, 2, 141–158. [Google Scholar] [CrossRef]
- Nayar, D.; van der Vegt, N.F.A. Cosolvent Effects on Polymer Hydration Drive Hydrophobic Collapse. J. Phys. Chem. B 2018, 122, 3587–3595. [Google Scholar] [CrossRef]
- Dalgicdir, C.; Rodríguez-Ropero, F.; van der Vegt, N.F.A. Computational Calorimetry of PNIPAM Cononsolvency in Water/Methanol Mixtures. J. Phys. Chem. B 2017, 121, 7741–7748. [Google Scholar] [CrossRef]
- Rodríguez-Ropero, F.; van der Vegt, N.F.A. On the Urea Induced Hydrophobic Collapse of a Water Soluble Polymer. Phys. Chem. Chem. Phys. 2015, 17, 8491–8498. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tripathy, M.; Bharadwaj, S.; B., S.J.; van der Vegt, N.F.A. Characterizing Polymer Hydration Shell Compressibilities with the Small-System Method. Nanomaterials 2020, 10, 1460. https://doi.org/10.3390/nano10081460
Tripathy M, Bharadwaj S, B. SJ, van der Vegt NFA. Characterizing Polymer Hydration Shell Compressibilities with the Small-System Method. Nanomaterials. 2020; 10(8):1460. https://doi.org/10.3390/nano10081460
Chicago/Turabian StyleTripathy, Madhusmita, Swaminath Bharadwaj, Shadrack Jabes B., and Nico F. A. van der Vegt. 2020. "Characterizing Polymer Hydration Shell Compressibilities with the Small-System Method" Nanomaterials 10, no. 8: 1460. https://doi.org/10.3390/nano10081460
APA StyleTripathy, M., Bharadwaj, S., B., S. J., & van der Vegt, N. F. A. (2020). Characterizing Polymer Hydration Shell Compressibilities with the Small-System Method. Nanomaterials, 10(8), 1460. https://doi.org/10.3390/nano10081460