Comparing Methods for Calculating Nano Crystal Size of Natural Hydroxyapatite Using X-Ray Diffraction
Abstract
1. Introduction
2. Materials and Experiments
2.1. Preparation of Hydroxyapatite Powders
2.2. XRD Analysis of Samples
3. Results and Discussions
3.1. Scherrer Method
3.1.1. Straight Line Model in Scherrer Method
3.1.2. Model of Straight Line Passing the Origin in Scherrer Method
3.1.3. Average Model in Scherrer Equation
3.2. Modified Scherrer Equation (Monshi–Scherrer Method)
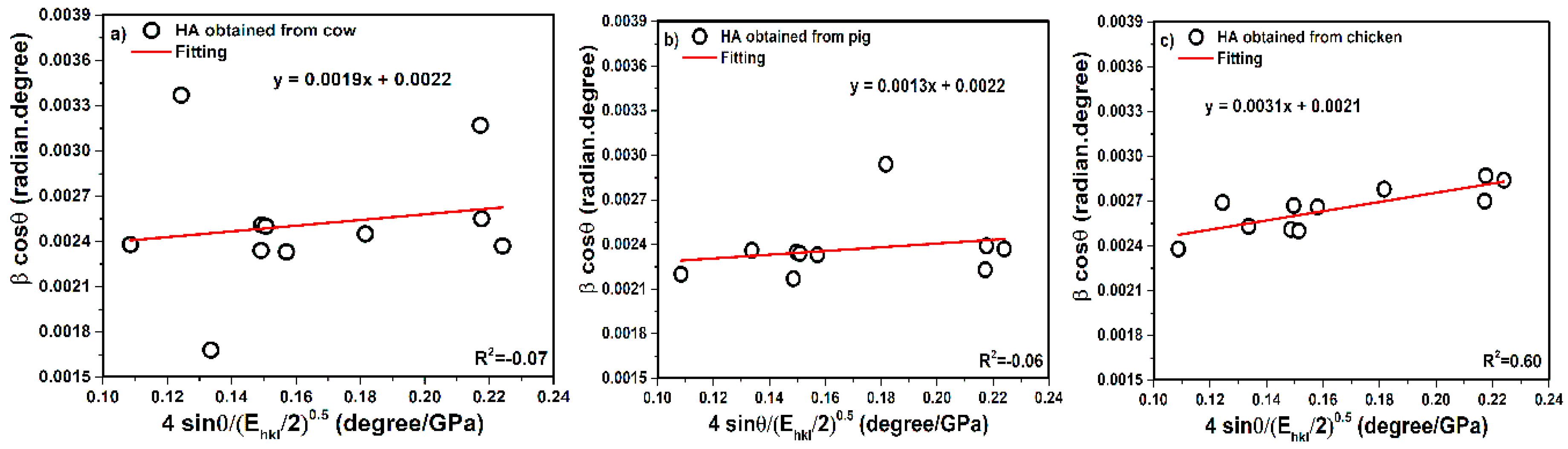
3.3. Williamson–Hall Method of Analysis
3.3.1. Uniform Deformation Model (UDM)
3.3.2. Uniform Stress Deformation Model (USDM)
3.3.3. Uniform Deformation Energy Density Model (UDEDM)
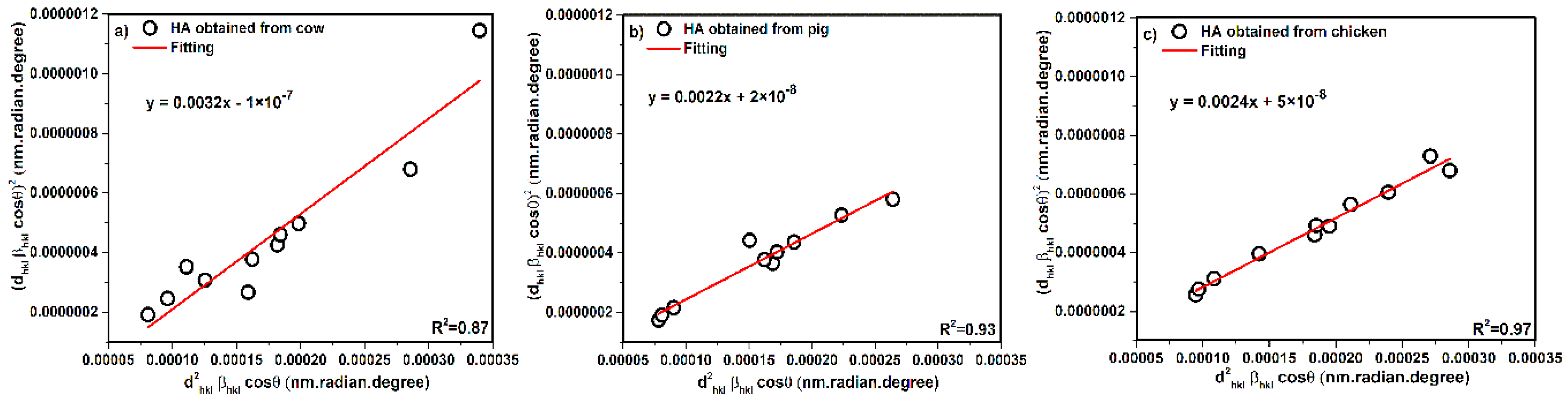
3.4. Halder–Wagner Method (H-W)
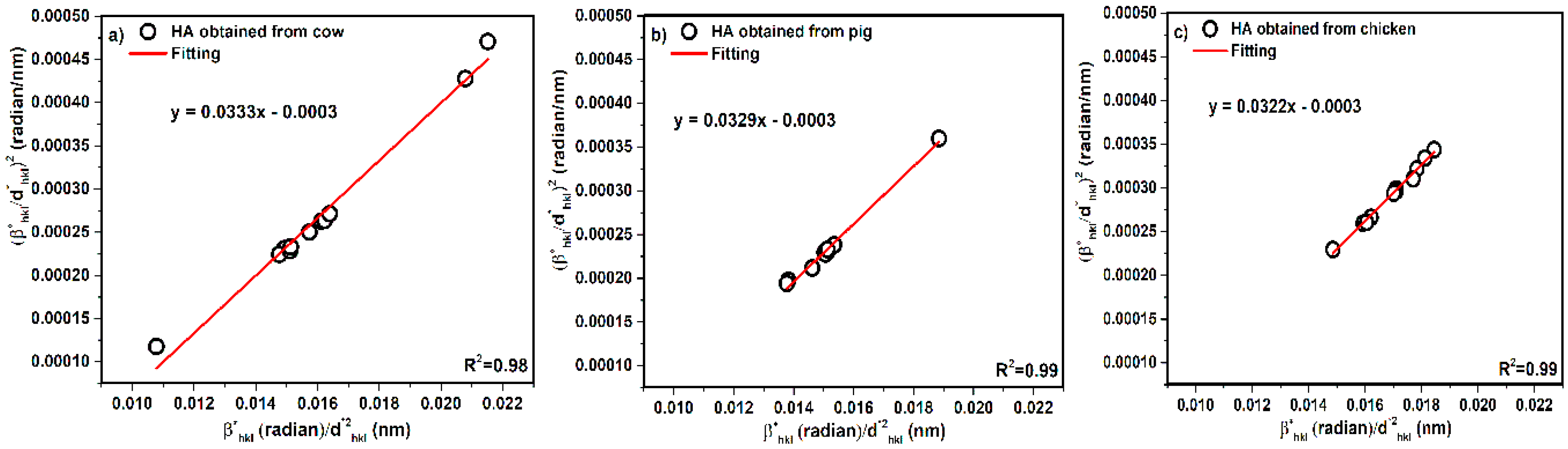
3.5. Size Strain Plot Method (SSP)
3.6. Specific Surface Area by Gas Adsorption (BET Method)
3.7. Study of TEM Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Guggenheim, S.; Bain, D.C.; Bergaya, F.; Brigatti, M.F.; Drits, V.A.; Eberl, D.D.; Formoso, M.L.L.; Galán, E.; Merriman, R.J.; Peacor, D.R.; et al. Report of the Association Internationale pour l’Etude des Argiles (AIPEA) Nomenclature Committee for 2001: Order, disorder and crystallinity in phyllosilicates and the use of the Crystallinity Index. Clay Miner. 2002, 37, 389–393. [Google Scholar] [CrossRef]
- Santos, P.d.S.; Coelho, A.C.V.; Samohdntos, H.d.S.; Kiyohara, P.K. Hydrothermal synthesis of well-crystallised boehmite crystals of various shapes. Mater. Res. 2009, 12, 437–445. [Google Scholar] [CrossRef]
- Scherrer, P. Bestimmung der Grösse und der Inneren Struktur von Kolloidteilchen Mittels Röntgenstra-hlen. J. Nachrichten von der Gesellschaft der Wissenschaften, Göttingen. Math. Phys. Kl. 1918, 2, 98–100. [Google Scholar]
- Londoño-Restrepo, S.M.; Jeronimo-Cruz, R.; Malo, B.M.; Muñoz, E.R.; García, M.R. Efect of the Nano Crystal Size on the X-ray Difraction Patterns of Biogenic Hydroxyapatite from Human, Bovine, and Porcine Bones. Sci. Rep. 2019, 9, 5915. [Google Scholar] [CrossRef]
- Mohd Pu’ad, N.A.S.; Koshy, P.; Abdullah, H.Z.; Idris, M.I.; Lee, T.C. Syntheses of hydroxyapatite from natural sources. Heliyon 2019, 5, e01588. [Google Scholar] [CrossRef]
- Lee, S.J.; Lee, Y.C.; Yoon, Y.S. Characteristics of calcium phosphate powders synthesized from cuttlefish bone and phosphoric acid. J. Ceram. Process. Res. 2007, 8, 427–430. [Google Scholar]
- Manalu1, J.L.; Soegijono, B.; Indrani, D.J. Characterization of Hydroxyapatite Derived from Bovine Bone. Asian J. Appl. Sci. 2015, 3, 758–765. [Google Scholar]
- Herliansyah, M.K.; Nasution, D.A.; Hamdi, M.; Ide-Ektessabi, A.; Wildan, M.W.; Tontowi, A.E. Preparation and Characterization of Natural Hydroxyapatite: A Comparative Study of Bovine Bone Hydroxyapatite and Hydroxyapatite from Calcite. Mater. Sci. Forum 2007, 561–565, 1441–1444. [Google Scholar] [CrossRef]
- Bahrololoom, M.E.; Javidia, M.; Javadpoura, S.; Ma, J. Characterisation of natural hydroxyapatite extracted from bovine cortical bone ash. J. Ceram. Process. Res. 2009, 10, 129–138. [Google Scholar]
- Shahabi, S.; Najafi, F.; Majdabadi, A.; Hooshmand, T.; Haghbin, M.; Karimi, B.; Fatemi, S.M. Effect of Gamma Irradiation on Structural and Biological Properties of a PLGA-PEG-Hydroxyapatite Composite. Sci. World J. 2014, 420616, 9. [Google Scholar] [CrossRef] [PubMed]
- Markovic, M.; Fowler, B.O.; Tung, M.S. Preparation and Comprehensive Characterization of a Calcium Hydroxyapatite Reference Material. J. Res. Natl. Inst. Stand. Technol. 2004, 109, 553–568. [Google Scholar] [CrossRef] [PubMed]
- Madhavi, S.; Ferraris, C.; White, T.J. Synthesis and crystallization of macroporous hydroxyapatite. J. Solid State Chem. 2005, 178, 2838–2845. [Google Scholar] [CrossRef]
- Esmaeilkhanian, A.; Sharifianjazi, F.; Abouchenari, A.; Rouhani, A.; Parvin, N.; Irani, M. Synthesis and Characterization of Natural Nano-hydroxyapatite Derived from Turkey Femur-Bone Waste. Appl. Biochem. Biotechnol. 2019, 189, 919–932. [Google Scholar] [CrossRef] [PubMed]
- Das, R.; Nath, S.S.; Bhattacharjee, R. Preparation of linoleic acid capped gold nanoparticles and their spectra. Phys. E Low Dimens. Syst. Nanostruct. 2010, 43, 224–227. [Google Scholar] [CrossRef]
- Dey, P.C.; Das, R. Effect of silver doping on the elastic properties of CdS nanoparticles. J. Indian J. Phys. 2018, 92, 1099–1108. [Google Scholar] [CrossRef]
- De, M.; Gupta, S.P.S. Lattice imperfection studies in polycrystalline materials by x-ray diffraction line-profile analysis. Pramana 1984, 23, 721–744. [Google Scholar] [CrossRef]
- Prabhu, Y.T.; Rao, K.V.; Kumar, V.S.S.; Kumari, B.S. X-Ray Analysis by Williamson-Hall and Size-Strain Plot Methods of ZnO Nanoparticles with Fuel Variation. World J. Nano Sci. Eng. 2014, 4, 21–28. [Google Scholar] [CrossRef]
- Monshi, A.; Messer, P.F. Ratio of slopes method for quantitative X-ray diffraction analysis. J. Mater. Sci. 1991, 26, 3623–3627. [Google Scholar] [CrossRef]
- Monshi, A.; Foroughi, M.R.; Monshi, M.R. Modified Scherrer Equation to Estimate More Accurately Nano-Crystallite Size Using XRD. World J. Nano Sci. Eng. 2012, 2, 154–160. [Google Scholar] [CrossRef]
- Nath, D.; Singh, F.; Das, R. X-ray diffraction analysis by Williamson-Hall, Halder-Wagner and size-strain plot methods of CdSe nanoparticles—A comparative study. Mater. Chem. Phys. 2019, 239, 122021. [Google Scholar] [CrossRef]
- Jacob, R.; Isac, J. X-ray diffraction line profile analysis of Ba0.6Sr0.4FexTi(1−x) O3-δ, (x = 0.4). Int. J. Chem. Stud. 2015, 2, 12–21. [Google Scholar]
- Warren, B.E.; Averbach, B.L. The separation of cold-work distortion and particle size broadening in X-ray patterns. J. Appl. Phys. 1952, 23, 497. [Google Scholar] [CrossRef]
- Adachi, S. Handbook on Physical Properties of Semiconductors; Springer: New York, NY, USA, 2004; ISBN 1402077475. [Google Scholar]
- Bodke, M.; Gawai, U.; Patil, A.; Dole, B. Estimation of accurate size, lattice strain using Williamson-Hall models, SSP and TEM of Al doped ZnO nanocrystals. Matériaux Tech. 2018, 106, 602. [Google Scholar] [CrossRef]
- Zhang, J.M.; Zhang, Y.; Xu, K.W.; Ji, V. General compliance transformation relation and applications for anisotropic hexagonal metals. Solid State Commun. 2006, 139, 87–91. [Google Scholar] [CrossRef]
- Katz, J.L.; Ukraincik, K. On the anisotropic elastic properties of hydroxyapatite. J. Biomech. 1971, 4, 221–227. [Google Scholar] [CrossRef]
- Mote, V.D.; Purushotham, Y.; Dole, B.N. Williamson-Hall analysis in estimation of lattice strain in nanometer-sized ZnO particles. J. Theor. Appl. Phys. 2012, 6, 2251–7235. [Google Scholar] [CrossRef]
- Motevalizadeh, L.; Heidary, Z.; Abrishami, M.E. Facile template-free hydrothermal synthesis and microstrain measurement of ZnO nano rods. J. Bull. Mater. Sci. 2014, 37, 397–405. [Google Scholar] [CrossRef]
- Halder, N.C.; Wagner, C.N.J. Separation of particle size and lattice strain in integral breadth measurements. Acta Cryst. 1966, 20, 312–331. [Google Scholar] [CrossRef]
- Balzar, D.; Ledbetter, H. Voigt-function modeling in fourier analysis of size- and strain-broadened X-ray diffraction peaks. J. Appl. Crystal. 1993, 26, 97–103. [Google Scholar] [CrossRef]
- Mazhidi, M.; Khani, P.H. Structural characterization of ZnO and ZnO: Mn nanoparticles prepared by reverse micelle method. Int. J. Nano Dim. 2008, 4, 233. [Google Scholar] [CrossRef]
- Joscheki, S.; Nies, B.; Krotz, R.; Goferich, A. Chemical and physicochemical characterization of porous hydroxyapatite ceramics made of natural bone. Biomaterials 2000, 21, 1645–1658. [Google Scholar] [CrossRef]
- Misra, D.N.; Bowen, R.L.; Mattamal, G.L. Surface area of dental enamel, bone, and hydroxyapatite: Chemisorption from solution. J. Calcif. Tissue Res. 1978, 26, 139–142. [Google Scholar] [CrossRef]
- Doostmohammadi, A.; Monshi, A.; Salehi, R.; Fathi, M.H.; Karbasi, S.; Pieles, U.; Daniels, A.U. Preparation, chemistry and physical properties of bone-derived hydroxyapatite particles having a negative zeta potential. Mater. Chem. Phys. 2012, 132, 446–452. [Google Scholar] [CrossRef]
- Ruksudjarit, A.; Pengpat, K.; Rujijanagul, G.; Tunkasiri, T. Synthesis and characterization of nanocrystalline hydroxyapatite from natural bovine bone. Curr. Appl. Phys. 2008, 8, 270–272. [Google Scholar] [CrossRef]
- Mayo, M.J. Processing of nanocrystalline ceramics from ultrafine particles. Int. Mater. Rev. 1996, 41, 85–115. [Google Scholar] [CrossRef]
- Janus, A.M.; Faryna, M.; Haberko, K.; Rakowska, A.; Panz, T. Chemical and microstructural characterization of natural hydroxyapatite derived from pig bones. Microchim. Acta 2008, 161, 349–353. [Google Scholar] [CrossRef]
- Paul, S.; Pal, A.; Choudhury, A.R.; Bodhak, S.; Balla, V.K.; Sinha, A.; Das, M. Effect of trace elements on the sintering effect of fish scale derived hydroxyapatite and its bioactivity. Ceram. Int. 2017, 43, 15678–15684. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Yahya, M.Y.; Shirazi, H.A.; Hassan, S.A. Mechanical and tribological properties of hydroxyapatite nanoparticles extracted from natural bovine bone and the bone cement developed by nano-sized bovine hydroxyapatite filler. Ceram. Int. 2015, 41, 10818–10827. [Google Scholar] [CrossRef]
- Foroughi, M.R.; Karbasi, S.; Kahrizsangi, R.E. Physical and mechanical properties of a poly-3-hydroxybutyratecoated nanocrystalline hydroxyapatite scaffold for bone tissue engineering. J. Porous Mater. 2012, 19, 667–675. [Google Scholar] [CrossRef]
- Ofudje, E.A.; Rajendran, A.; Adeogun, A.I.; Idowu, M.A.; Kareem, S.O.; Pattanayak, D. Synthesis of organic derived hydroxyapatite scaffold from pig bone waste for tissue engineering applications. Adv. Powder Technol. 2018, 29, 1–8. [Google Scholar] [CrossRef]
- Mondal, B.; Mondal, S.; Mondal, A.; Mandal, N. Fish scale derived hydroxyapatite scaffold for bone tissue engineering. Mater. Charact. 2016, 121, 112–124. [Google Scholar] [CrossRef]
- Pal, A.; Maity, S.; Chabri, S.; Bera, S.; Chowdhury, A.R.; Das, M.; Sinha, A. Mechanochemical synthesis of nanocrystalline hydroxyapatite from Mercenaria clam shells and phosphoric acid. Biomed. Phys. Eng. Express 2017, 3, 015010. [Google Scholar] [CrossRef]

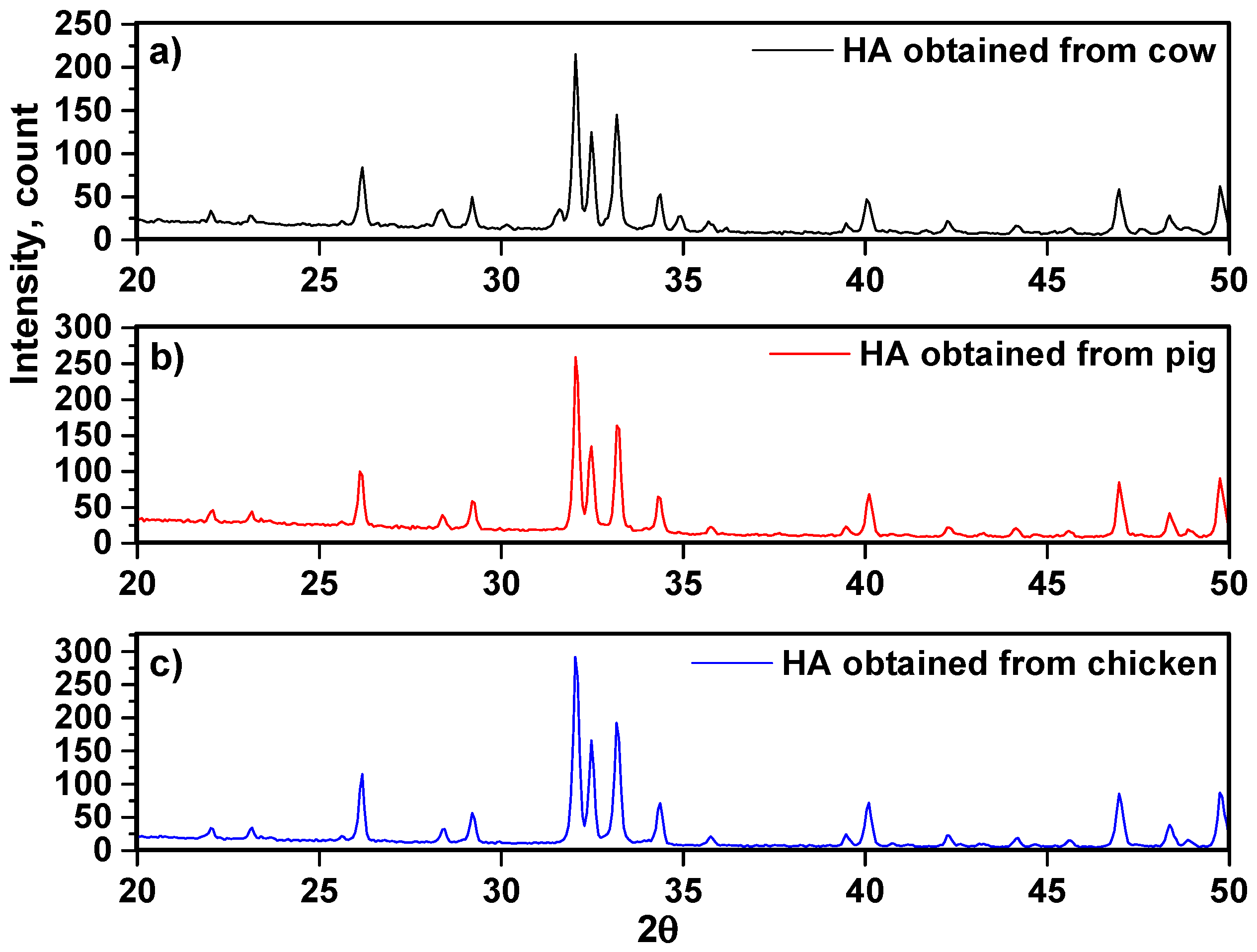

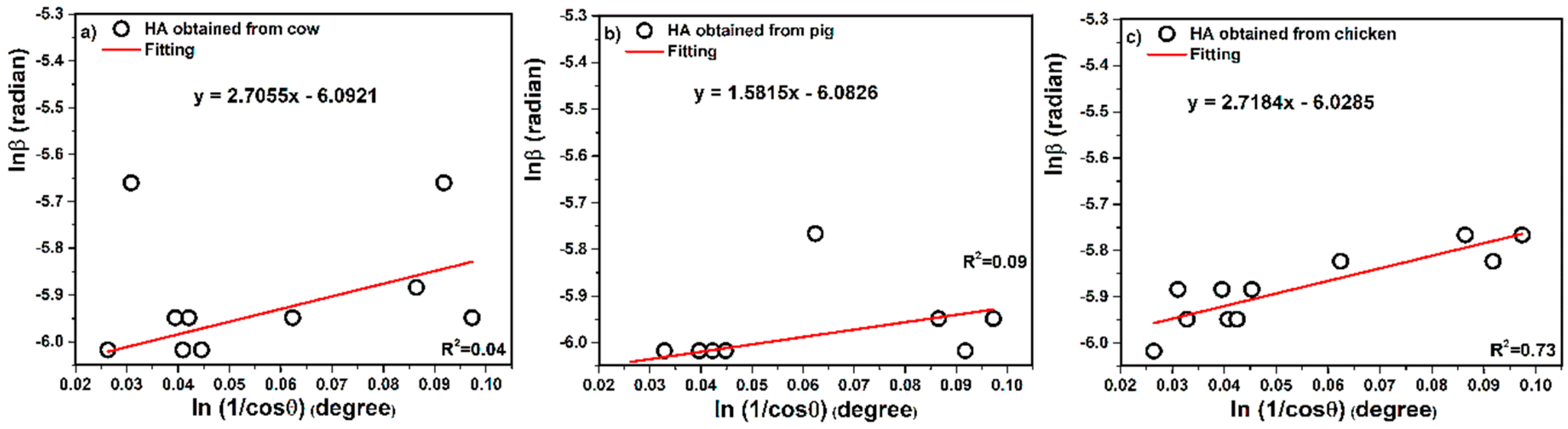
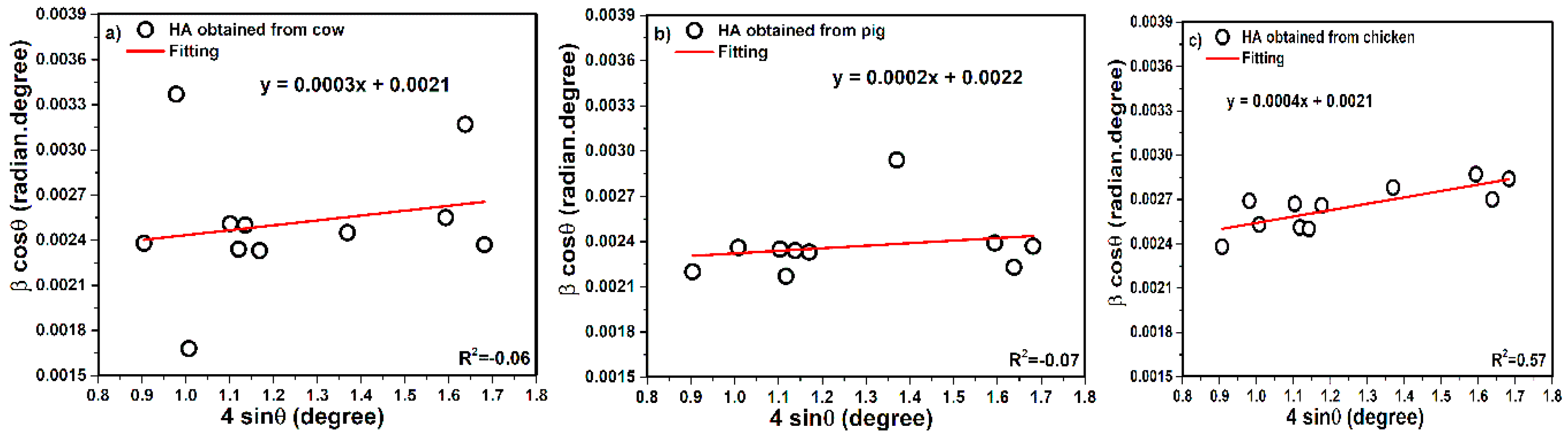
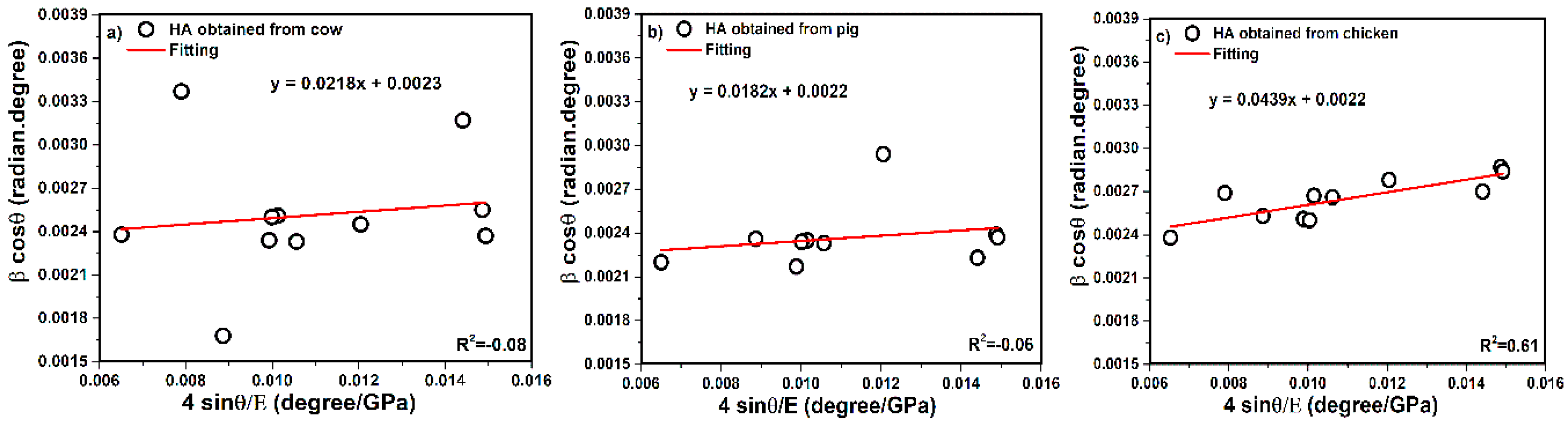

| Cow | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2θ (Degree) | β = FWHM (Degree) | θ (Degree) | cosθ (Degree) | 1/cosθ (Degree) | Ln(1/cosθ) (Degree) | β = FWHM (Radian) | Ln β (Radian) | 4 sinθ (Degree) | β(Radian).cosθ (Degree) | hkl | |
| 26.15 | 0.14 | 13.07 | 0.9740 | 1.02669 | 0.02634 | 0.00244 | −6.0174 | 0.9045 | 0.00238 | 002 | 3.46500 |
| 28.32 | 0.2 | 14.16 | 0.9696 | 1.03135 | 0.03087 | 0.00348 | −5.66072 | 0.9785 | 0.00337 | 102 | 3.17485 |
| 29.18 | 0.1 | 14.59 | 0.9677 | 1.03338 | 0.03283 | 0.00174 | −6.35387 | 1.007 | 0.00168 | 210 | 3.07687 |
| 31.96 | 0.15 | 15.98 | 0.9613 | 1.04026 | 0.03947 | 0.00261 | −5.94841 | 1.1012 | 0.00251 | 211 | 2.81215 |
| 32.54 | 0.14 | 16.27 | 0.9599 | 1.04178 | 0.04093 | 0.00244 | −6.0174 | 1.1206 | 0.00234 | 112 | 2.78900 |
| 32.98 | 0.15 | 16.49 | 0.9588 | 1.04297 | 0.04207 | 0.00261 | −5.94841 | 1.1353 | 0.0025 | 300 | 2.71354 |
| 33.97 | 0.14 | 16.98 | 0.9564 | 1.04559 | 0.04458 | 0.00244 | −6.0174 | 1.1681 | 0.00233 | 202 | 2.63845 |
| 40.03 | 0.15 | 20.01 | 0.9396 | 1.06428 | 0.0623 | 0.00261 | −5.94841 | 1.3687 | 0.00245 | 310 | 2.26285 |
| 46.94 | 0.16 | 23.47 | 0.9172 | 1.09027 | 0.08643 | 0.00278 | −5.88387 | 1.5930 | 0.00255 | 222 | 1.94339 |
| 48.35 | 0.2 | 24.17 | 0.9123 | 1.09613 | 0.09179 | 0.00348 | −5.66072 | 1.6377 | 0.00317 | 320 | 1.87176 |
| 49.73 | 0.15 | 24.86 | 0.9073 | 1.10217 | 0.09728 | 0.00261 | −5.94841 | 1.6816 | 0.00237 | 213 | 1.84732 |
| Pig | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2θ (Degree) | β = FWHM (Degree) | θ (Degree) | cosθ (Degree) | 1/cosθ (Degree) | Ln(1/cosθ) (Degree) | β = FWHM (Radian) | Ln β (Radian) | 4 sinθ (Degree) | β(Radian).cosθ (Degree) | hkl | |
| 26.12 | 0.13 | 13.06 | 0.9741 | 1.02659 | 0.02624 | 0.00226 | −6.09151 | 0.9038 | 0.0022 | 002 | 3.46500 |
| 29.20 | 0.14 | 14.60 | 0.9677 | 1.03338 | 0.03283 | 0.00244 | −6.0174 | 1.0082 | 0.00236 | 210 | 3.07687 |
| 32.04 | 0.14 | 16.02 | 0.9611 | 1.04047 | 0.03968 | 0.00244 | −6.0174 | 1.1038 | 0.00235 | 211 | 2.81215 |
| 32.44 | 0.13 | 16.22 | 0.9601 | 1.04156 | 0.04072 | 0.00226 | −6.09151 | 1.1173 | 0.00217 | 112 | 2.78900 |
| 33.07 | 0.14 | 16.53 | 0.9586 | 1.04319 | 0.04228 | 0.00244 | −6.0174 | 1.1380 | 0.00234 | 300 | 2.71354 |
| 34.02 | 0.14 | 17.01 | 0.9562 | 1.04581 | 0.04479 | 0.00244 | −6.0174 | 1.1701 | 0.00233 | 202 | 2.63845 |
| 40.07 | 0.18 | 20.03 | 0.9395 | 1.0644 | 0.06241 | 0.00313 | −5.76608 | 1.3700 | 0.00294 | 310 | 2.26285 |
| 46.96 | 0.15 | 23.48 | 0.9171 | 1.09039 | 0.08654 | 0.00261 | −5.94841 | 1.5937 | 0.00239 | 222 | 1.94339 |
| 48.34 | 0.14 | 24.17 | 0.9123 | 1.09613 | 0.09179 | 0.00244 | −6.0174 | 1.6377 | 0.00223 | 320 | 1.87176 |
| 49.73 | 0.15 | 24.86 | 0.9073 | 1.10217 | 0.09728 | 0.00261 | −5.94841 | 1.6816 | 0.00237 | 213 | 1.84732 |
| Chicken | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2θ (Degree) | β = FWHM (Degree) | θ (Degree) | cosθ (Degree) | 1/cosθ (Degree) | Ln(1/cosθ) (Degree) | β = FWHM (Radian) | Ln β (Radian) | 4 sinθ (Degree) | β(Radian).cosθ (Degree) | hkl | |
| 26.20 | 0.14 | 13.10 | 0.9739 | 1.0268 | 0.02645 | 0.00244 | −6.0174 | 0.9066 | 0.00238 | 002 | 3.46500 |
| 28.39 | 0.16 | 14.19 | 0.9694 | 1.03157 | 0.03108 | 0.00278 | −5.88387 | 0.9805 | 0.00269 | 102 | 3.17485 |
| 29.19 | 0.15 | 14.59 | 0.9677 | 1.03338 | 0.03283 | 0.00261 | −5.94841 | 1.0076 | 0.00253 | 210 | 3.07687 |
| 32.03 | 0.16 | 16.01 | 0.9612 | 1.04037 | 0.03957 | 0.00278 | −5.88387 | 1.1032 | 0.00267 | 211 | 2.81215 |
| 32.45 | 0.15 | 16.22 | 0.9601 | 1.04156 | 0.04072 | 0.00261 | −5.94841 | 1.1173 | 0.00251 | 112 | 2.78900 |
| 33.16 | 0.15 | 16.58 | 0.9584 | 1.04341 | 0.04249 | 0.00261 | −5.94841 | 1.1414 | 0.0025 | 300 | 2.71354 |
| 34.21 | 0.16 | 17.10 | 0.9557 | 1.04635 | 0.04531 | 0.00278 | −5.88387 | 1.1761 | 0.00266 | 202 | 2.63845 |
| 40.05 | 0.17 | 20.02 | 0.9395 | 1.0644 | 0.06241 | 0.00296 | −5.82324 | 1.3693 | 0.00278 | 310 | 2.26285 |
| 46.95 | 0.18 | 23.47 | 0.9172 | 1.09027 | 0.08643 | 0.00313 | −5.76608 | 1.5930 | 0.00287 | 222 | 1.94339 |
| 48.34 | 0.17 | 24.17 | 0.9123 | 1.09613 | 0.09179 | 0.00296 | −5.82324 | 1.6377 | 0.0027 | 320 | 1.87176 |
| 49.74 | 0.18 | 24.87 | 0.9072 | 1.10229 | 0.09739 | 0.00313 | −5.76608 | 1.6822 | 0.00284 | 213 | 1.84732 |
| Bone | Crystal System | a | c | c/a | Cell Volume (Å3) | Crystal Density (g/cm3) |
|---|---|---|---|---|---|---|
| Cow | Hexagonal | 9.4000 | 6.9300 | 0.7340 | 530.30 | 3.14 |
| Pig | Hexagonal | 9.4210 | 6.8930 | 0.7316 | 529.83 | 3.14 |
| Chicken | Hexagonal | 9.4210 | 6.8800 | 0.7302 | 528.83 | 3.18 |
| Cow | Pig | Chicken | |||
|---|---|---|---|---|---|
| x | y | x | y | x | y |
| 409.83 | 0.974 | 442.47 | 0.9741 | 409.83 | 0.9739 |
| 287.35 | 0.9696 | 409.83 | 0.9677 | 359.71 | 0.9694 |
| 574.71 | 0.9677 | 409.83 | 0.9611 | 383.14 | 0.9677 |
| 383.14 | 0.9613 | 442.47 | 0.9601 | 359.71 | 0.9612 |
| 409.83 | 0.9599 | 409.83 | 0.9586 | 383.14 | 0.9601 |
| 383.14 | 0.9588 | 409.83 | 0.9562 | 383.14 | 0.9584 |
| 409.83 | 0.9564 | 319.48 | 0.9395 | 359.71 | 0.9557 |
| 383.14 | 0.9396 | 383.14 | 0.9171 | 337.83 | 0.9395 |
| 359.71 | 0.9172 | 409.83 | 0.9123 | 319.48 | 0.9172 |
| 287.35 | 0.9123 | 383.14 | 0.9073 | 337.83 | 0.9123 |
| 383.14 | 0.9073 | - | - | 319.48 | 0.9072 |
| 57.60 | 62.32 | 57.60 |
| 40.68 | 58.09 | 50.96 |
| 81.60 | 58.34 | 54.19 |
| 54.62 | 63.18 | 51.35 |
| 58.59 | 58.59 | 54.62 |
| 54.84 | 58.84 | 54.84 |
| 58.84 | 46.63 | 51.54 |
| 55.96 | 57.36 | 49.31 |
| 53.76 | 61.48 | 47.77 |
| 43.25 | 57.85 | 50.77 |
| 57.85 | - | 48.27 |
| 56 | 58 | 52 |
| Elastic Compliances (GPa) | Stiffness Constants (GPa) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| C11 | C12 | C13 | C33 | C44 | S11 | S12 | S13 | S33 | S44 |
| 137 | 42.5 | 54.9 | 172 | 39.6 | 0.88 | −0.18 | −0.22 | 0.72 | 2.52 |
| Cow | Pig | Chicken | |||
|---|---|---|---|---|---|
| 2θ (Degree) | E (GPa) | 2θ (Degree) | E (GPa) | 2θ (Degree) | E (GPa) |
| 26.15 | 138.889 | 26.12 | 138.889 | 26.20 | 138.889 |
| 28.32 | 123.935 | 29.20 | 113.636 | 28.39 | 124.121 |
| 29.18 | 113.636 | 32.04 | 108.694 | 29.19 | 113.636 |
| 31.96 | 108.734 | 32.44 | 113.02 | 32.03 | 108.684 |
| 32.54 | 112.887 | 33.07 | 113.636 | 32.45 | 113.054 |
| 32.98 | 113.636 | 34.02 | 110.706 | 33.16 | 113.636 |
| 33.97 | 110.598 | 40.07 | 113.636 | 34.21 | 110.733 |
| 40.03 | 113.636 | 46.96 | 107.155 | 40.05 | 113.636 |
| 46.94 | 107.161 | 48.34 | 113.636 | 46.95 | 107.154 |
| 48.35 | 113.636 | 49.73 | 112.702 | 48.34 | 113.636 |
| 49.73 | 112.571 | - | - | 49.74 | 112.734 |
| Size of Crystallites | Scherrer (All Peaks/New Model/Average Model) | Monshi–Scherrer | Williamson–Hall (UDM/USDM/UDEDM) | H-W | SSP | BET | TEM |
|---|---|---|---|---|---|---|---|
| Lcow (nm) | 1371/60/56 | 60 | 65/60/62 | 4 | 43 | 56 | ~ 50 |
| Lpig (nm) | 457/60/58 | 60 | 62/62/62 | 4 | 62 | 52 | ~ 50 |
| Lchicken (nm) | 196/53/52 | 57 | 65/62/65 | 4 | 57 | 49 | ~ 50 |
| Williamson–Hall | SSP | |||||
|---|---|---|---|---|---|---|
| UDM | USDM | UDEDM | ||||
| Strain (ε) × 10−4 | Stress (MPa) | Strain (ε) × 10−4 | Strain (ε) × 10−3 | LED (KJ/m3) | Strain (ε) × 10−4 | |
| cow | 3 | 22 | 1.89 | 0.87 | 43.67 | - |
| pig | 2 | 18 | 1.59 | 0.73 | 29.70 | 2.83 |
| chicken | 4 | 44 | 3.81 | 0.70 | 28.28 | 4.48 |
| Number | Source | Method of Preparation | Temperature of Heat Treatment | Crystallite Phases | Size of Crystal (L) (nm) | Shape | Reference |
|---|---|---|---|---|---|---|---|
| 1 | Bovine bone | Thermal treatment | 800 °C | hydroxyapatite | <100 (58 and 62) | Needle | [35] |
| 2 | Bovine bone | Thermal treatment | 800 °C | hydroxyapatite | 70–180 | Irregular | [37] |
| 3 | Fish scale | Thermal treatment | 800 °C | hydroxyapatite | 30 | Irregular | [38] |
| 4 | Bovine bone | Thermal treatment | 900 °C | hydroxyapatite | 30 | - | [39] |
| 5 | Bovine bone | Thermal treatment | 900 °C | hydroxyapatite | 70–80 | Spherical | [40] |
| 6 | Pig bone | Thermal treatment | 1000 °C | hydroxyapatite | 38–52 | Rod like | [41] |
| 7 | Fish scale | Thermal treatment | 1000 °C | hydroxyapatite | 76 | Nearly spherical | [42] |
| 8 | Clam shell | Thermal treatment | 1000 °C | hydroxyapatite | 53–67 | Agglomerate | [43] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rabiei, M.; Palevicius, A.; Monshi, A.; Nasiri, S.; Vilkauskas, A.; Janusas, G. Comparing Methods for Calculating Nano Crystal Size of Natural Hydroxyapatite Using X-Ray Diffraction. Nanomaterials 2020, 10, 1627. https://doi.org/10.3390/nano10091627
Rabiei M, Palevicius A, Monshi A, Nasiri S, Vilkauskas A, Janusas G. Comparing Methods for Calculating Nano Crystal Size of Natural Hydroxyapatite Using X-Ray Diffraction. Nanomaterials. 2020; 10(9):1627. https://doi.org/10.3390/nano10091627
Chicago/Turabian StyleRabiei, Marzieh, Arvydas Palevicius, Ahmad Monshi, Sohrab Nasiri, Andrius Vilkauskas, and Giedrius Janusas. 2020. "Comparing Methods for Calculating Nano Crystal Size of Natural Hydroxyapatite Using X-Ray Diffraction" Nanomaterials 10, no. 9: 1627. https://doi.org/10.3390/nano10091627
APA StyleRabiei, M., Palevicius, A., Monshi, A., Nasiri, S., Vilkauskas, A., & Janusas, G. (2020). Comparing Methods for Calculating Nano Crystal Size of Natural Hydroxyapatite Using X-Ray Diffraction. Nanomaterials, 10(9), 1627. https://doi.org/10.3390/nano10091627






