Application of Magnetosomes in Magnetic Hyperthermia
Abstract
1. Introduction
2. Model and Methods
3. Results
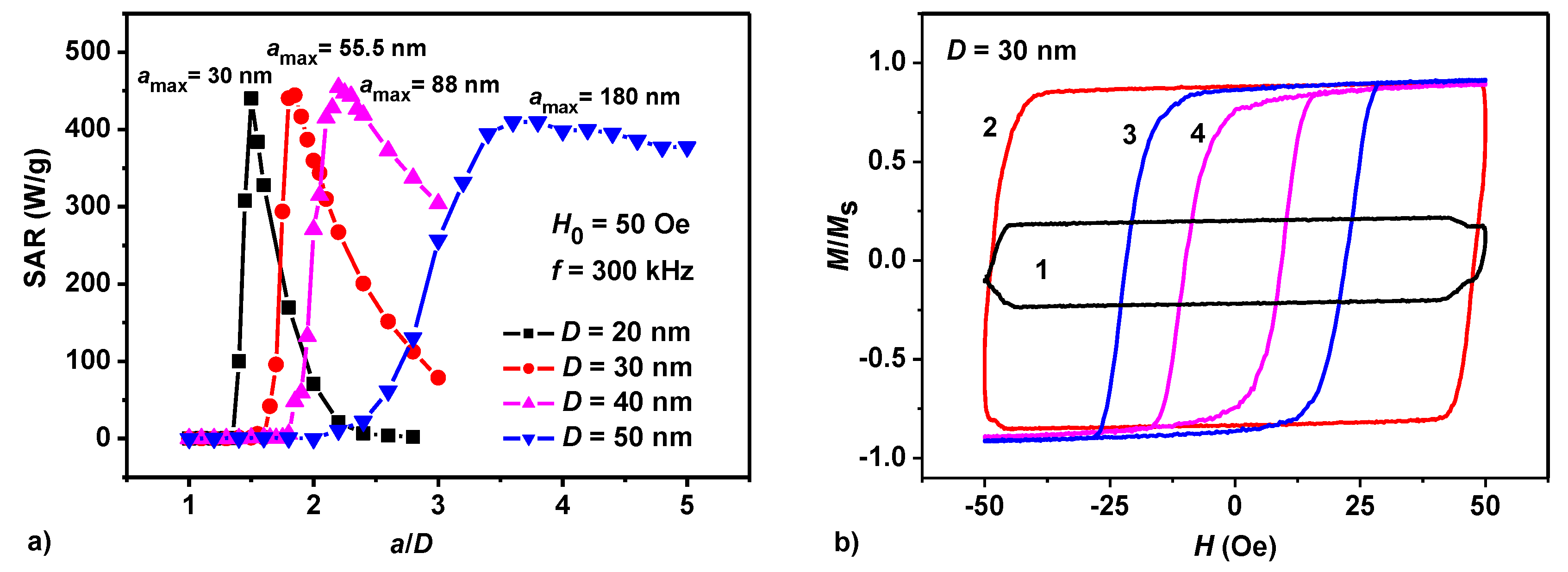
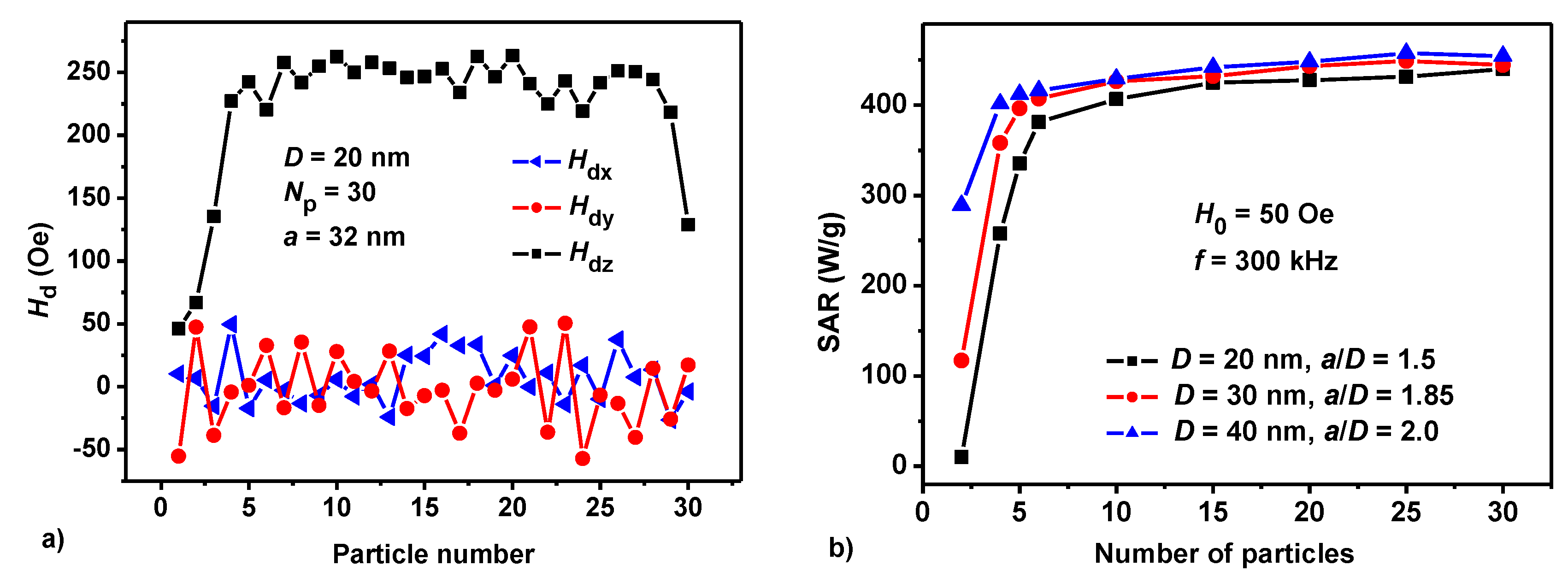
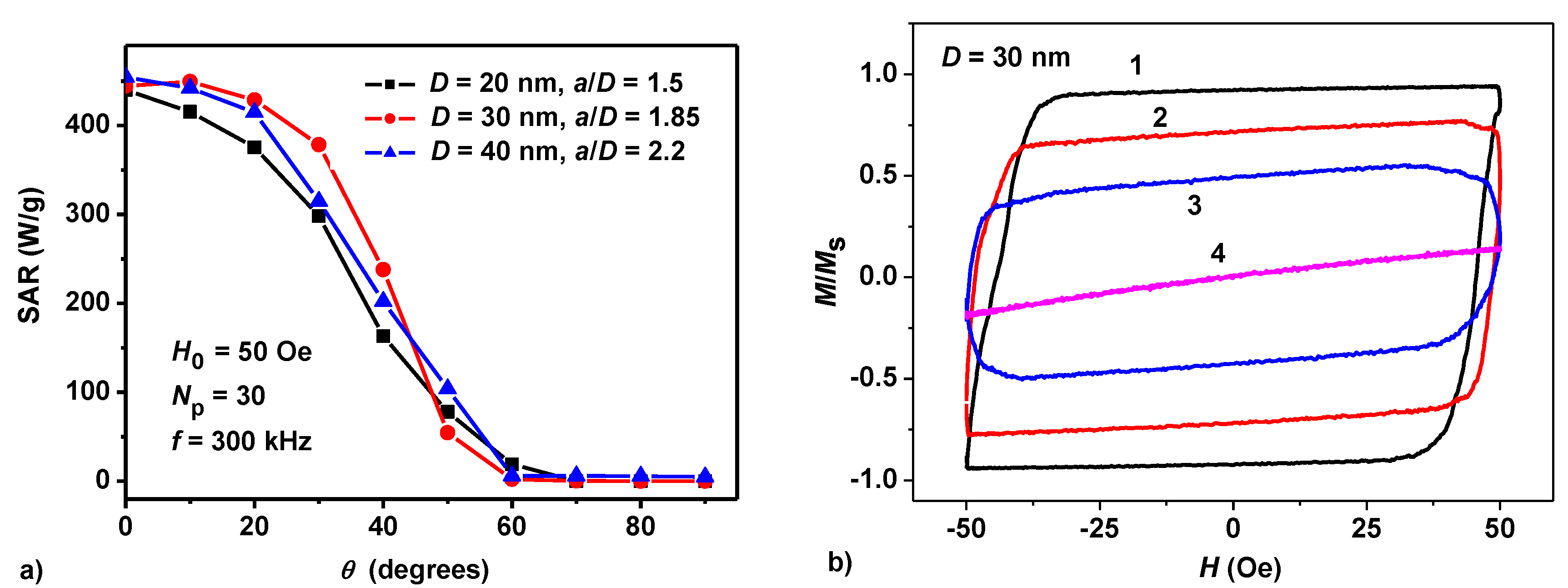
3.1. Dilute Chain Assembly
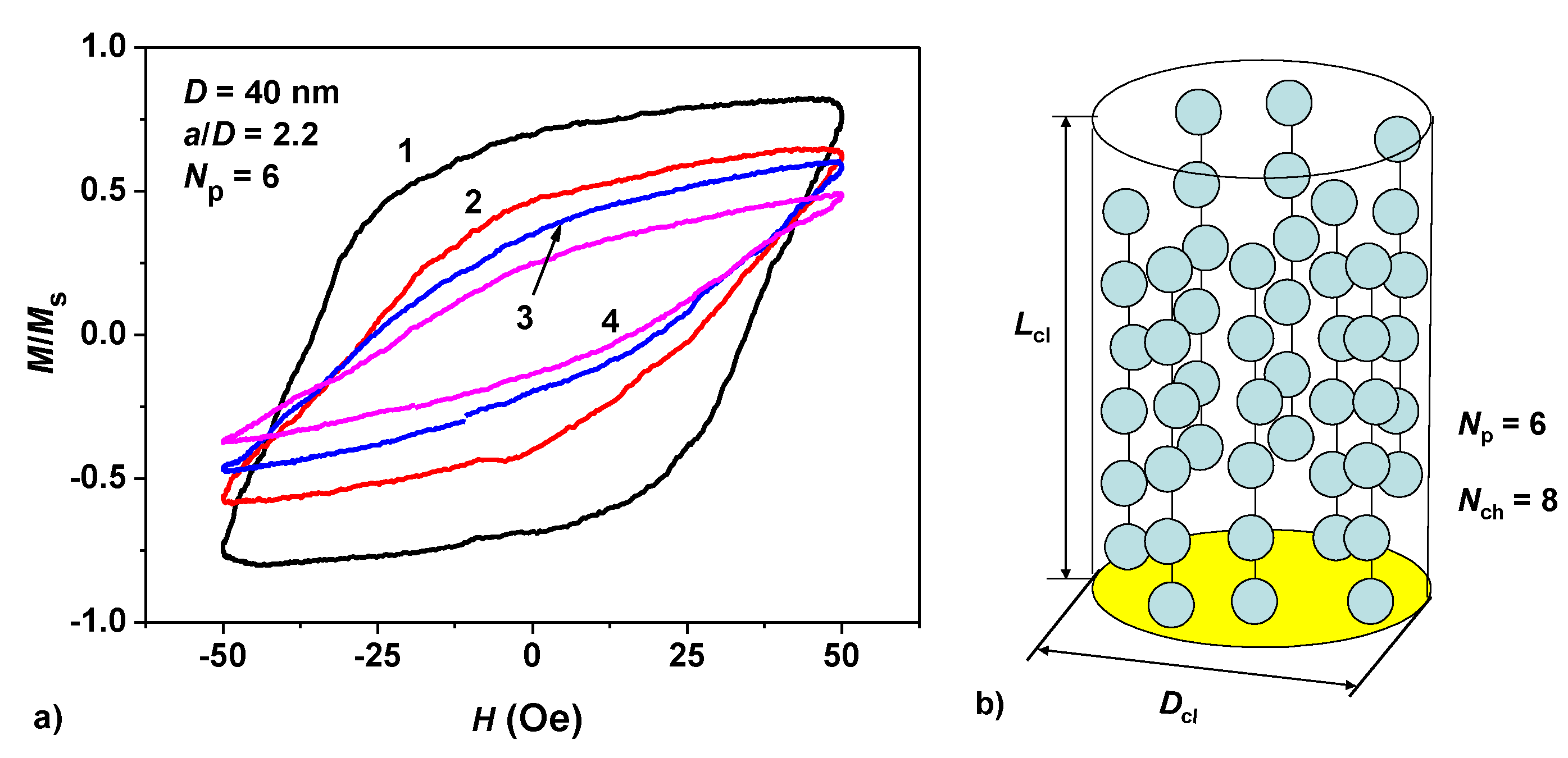
3.2. Interaction of Magnetosome Chains
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Périgo, E.A.; Hemery, G.; Sandre, O.; Ortega, D.; Garaio, E.; Plazaola, F.; Teran, F.J. Fundamentals and Advances in Magnetic Hyperthermia. Appl. Phys. Rev. 2015, 2, 041302. [Google Scholar] [CrossRef]
- Blanco-Andujar, C.; Teran, F.J.; Ortega, D. Current Outlook and Perspectives on Nanoparticle-Mediated Magnetic Hyperthermia. In Iron Oxide Nanoparticles for Biomedical Applications; Mahmoudi, M., Laurent, S., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 197–245. [Google Scholar] [CrossRef]
- Mahmoudi, K.; Bouras, A.; Bozec, D.; Ivkov, R.; Hadjipanayis, C. Magnetic hyperthermia therapy for the treatment of glioblastoma: A review of the therapy’s history, efficacy and application in humans. Int. J. Hyperth. 2018, 34, 1316–1328. [Google Scholar] [CrossRef] [PubMed]
- Ito, A.; Tanaka, K.; Kondo, K.; Shinkai, M.; Honda, H.; Matsumoto, K.; Saida, T.; Kobayashi, T. Tumor regression by combined immunotherapy and hyperthermia using magnetic nanoparticles in an experimental subcutaneous murine melanoma. Cancer Sci. 2003, 94, 308–313. [Google Scholar] [CrossRef] [PubMed]
- Alphandéry, E.; Faure, S.; Seksek, O.; Guyot, F.; Chebbi, I. Chains of magnetosomes extracted from AMB 1 magnetotactic bacteria for application in alternative magnetic field cancer therapy. ACS Nano 2011, 5, 6279–6296. [Google Scholar] [CrossRef]
- Kobayashi, T. Cancer hyperthermia using magnetic nanoparticles. Biotechnol. J. 2011, 6, 1342–1347. [Google Scholar] [CrossRef]
- Alphandéry, E.; Idbaih, A.; Adam, C.; Delattre, J.-Y.; Schmitt, C.; Guyot, F.; Chebbi, I. Development of non-pyrogenic magnetosome minerals coated with poly-l-lysine leading to full disappearance of intracranial U87-Luc glioblastoma in 100% of treated mice using magnetic hyperthermia. Biomaterials 2017, 141, 210–222. [Google Scholar] [CrossRef]
- Johannsen, M.; Gneveckow, U.; Eckelt, L.; Feussner, A.; Waldofner, N.; Scholz, R.; Deger, S.; Wust, P.; Loening, S.A.; Jordan, A. Clinical hyperthermia of prostate cancer using magnetic nanoparticles: Presentation of a new interstitial technique. Int. J. Hyperth. 2005, 21, 637–647. [Google Scholar] [CrossRef]
- van Landeghem, F.K.; Maier-Hauff, K.; Jordan, A.; Hoffmann, K.T.; Gneveckow, U.; Scholz, R.; Thiesen, B.; Brück, W.; von Deimling, A. Post-mortem studies in glioblastoma patients treated with thermotherapy using magnetic nanoparticles. Biomaterials 2009, 30, 52–57. [Google Scholar] [CrossRef]
- Matsumine, A.; Takegami, K.; Asanuma, K.; Matsubara, T.; Nakamura, T.; Uchida, A.; Sudo, A. A novel hyperthermia treatment for bone metastases using magnetic materials. Int. J. Clin. Oncol. 2011, 16, 101–108. [Google Scholar] [CrossRef]
- Pankhurst, Q.A.; Thanh, N.T.K.; Jones, S.K.; Dobson, J. Progress in applications of magnetic nanoparticles in biomedicine. J. Phys. D Appl. Phys. 2009, 42, 224001. [Google Scholar] [CrossRef]
- Dutz, S.; Hergt, R. Magnetic nanoparticle heating and heat transfer on a microscale: Basic principles, realities and physical limitations of hyperthermia for tumour therapy. Int. J. Hyperth. 2013, 29, 790–800. [Google Scholar] [CrossRef] [PubMed]
- El-Sayed, I.H.; Huang, X.; El-Sayed, M.A. Selective laser photo-thermal therapy of epithelial carcinoma using anti-EGFR antibody conjugated gold nanoparticles. Cancer Lett. 2006, 239, 129–135. [Google Scholar] [CrossRef] [PubMed]
- Espinosa, A.; Kolosnjaj-Tabi, J.; Abou-Hassan, A.; Sangnier, A.P.; Curcio, A.; Silva, A.K.A.; Di Corato, R.; Neveu, S.; Pellegrino, T.; Liz-Marzán, L.M.; et al. Magnetic (hyper)thermia or photo-thermia? Progressive comparison of iron oxide and gold nanoparticles heating in water, in cells, and in vivo. Adv. Funct. Mater. 2018, 28, 1803660. [Google Scholar] [CrossRef]
- Brezovich, I.A. Low frequency hyperthermia: Capacitive and ferromagnetic thermoseed methods. Med. Phys. Monogr. 1988, 16, 82–111. [Google Scholar]
- Hergt, R.; Dutz, S.; Müller, R.; Zeisberger, M. Magnetic Particle Hyperthermia: Nanoparticle Magnetism and Materials Development for Cancer Therapy. J. Phys. Condens. Matter 2006, 18, S2919–S2934. [Google Scholar] [CrossRef]
- Reddy, L.H.; Arias, J.L.; Nicolas, J.; Couvreur, P. Magnetic Nanoparticles: Design and Characterization, Toxicity and Biocompatibility, Pharmaceutical and Biomedical Applications. Chem. Rev. 2012, 112, 5818–5878. [Google Scholar] [CrossRef]
- Silva, A.K.A.; Espinosa, A.; Kolosnjaj-Tabi, J.; Wilhelm, C.; Gazeau, F. Medical applications of iron oxide nanoparticles. In Iron Oxides: From Nature to Applications; Faivre, D., Ed.; Wiley-VCH: Weinheim, Germany, 2016; pp. 425–471. [Google Scholar] [CrossRef]
- Kolosnjaj-Tabi, J.; Lartigue, L.; Javed, Y.; Luciani, N.; Pellegrino, T.; Wilhelm, C.; Alloyeau, D.; Gazeau, F. Biotransformations of magnetic nanoparticles in the body. Nano Today 2016, 11, 280–284. [Google Scholar] [CrossRef]
- Sun, S.; Zeng, H. Size-controlled synthesis of magnetite nanoparticles. J. Am. Chem. Soc. 2002, 124, 8204–8205. [Google Scholar] [CrossRef]
- Daou, T.J.; Pourroy, G.; Bégin-Colin, S.; Grenèche, J.M.; Ulhaq-Bouillet, C.; Legaré, P.; Bernhardt, P.; Leuvrey, C.; Rogez, G. Hydrothermal Synthesis of Monodisperse Magnetite Nanoparticles. Chem. Mater. 2006, 18, 4399–4404. [Google Scholar] [CrossRef]
- Hui, C.; Shen, C.; Yang, T.; Bao, L.; Tian, J.; Ding, H.; Li, C.; Gao, H.-J. Large-Scale Fe3O4 Nanoparticles Soluble in Water Synthesized by a Facile Method. J. Phys. Chem. C 2008, 112, 11336–11339. [Google Scholar] [CrossRef]
- Bautin, V.A.; Seferyan, A.G.; Nesmeyanov, M.S.; Usov, N.A. Properties of polycrystalline nanoparticles with uniaxial and cubic types of magnetic anisotropy of individual grains. J. Magn. Magn. Mater. 2018, 460, 278–284. [Google Scholar] [CrossRef]
- Kallumadil, M.; Tada, M.; Nakagawa, T.; Abe, M.; Southern, P.; Pankhurst, Q.A. Suitability of commercial colloids for magnetic hyperthermia. J. Magn. Magn. Mater. 2009, 321, 1509–1513. [Google Scholar] [CrossRef]
- Muela, A.; Munoz, D.; Martin-Rodriguez, R.; Orue, I.; Garaio, E.; Abad Diaz de Cerio, A.; Alonso, J.; Garcia, J.A.; Fdez-Gubieda, M.L. Optimal Parameters for Hyperthermia Treatment Using Biomineralized Magnetite Nanoparticles: A Theoretical and Experimental Approach. J. Phys. Chem. C 2016, 120, 24437–24448. [Google Scholar] [CrossRef]
- Etheridge, M.L.; Hurley, K.R.; Zhang, J.; Jeon, S.; Ring, H.L.; Hogan, C.; Haynes, C.L.; Garwood, M.; Bischof, J.C. Accounting for biological aggregation in heating and imaging of magnetic nanoparticles. Technology 2014, 2, 214–228. [Google Scholar] [CrossRef] [PubMed]
- Sanz, B.; Calatayud, M.P.; Biasi, E.D.; Lima, E., Jr.; Mansilla, M.V.; Zysler, R.D.; Ibarra, M.R.; Goya, G.F. In silico before in vivo: How to predict the heating efficiency of magnetic nanoparticles within the intracellular space. Sci. Rep. 2016, 6, 38733. [Google Scholar] [CrossRef] [PubMed]
- Usov, N.A. Low frequency hysteresis loops of superparamagnetic nanoparticles with uniaxial anisotropy. J. Appl. Phys. 2010, 107, 123909. [Google Scholar] [CrossRef]
- Carrey, J.; Mehdaoui, B.; Respaud, M. Simple models for dynamic hysteresis loop calculations of magnetic single-domain nanoparticles: Application to magnetic hyperthermia optimization. J. Appl. Phys. 2011, 109, 83921. [Google Scholar] [CrossRef]
- Jonasson, C.; Schaller, V.; Zeng, L.; Olsson, E.; Frandsen, C.; Castro, A.; Nilsson, L.; Bogart, L.K.; Southern, P.; Pankhurst, Q.A.; et al. Modelling the effect of different core sizes and magnetic interactions inside magnetic nanoparticles on hyperthermia performance. J. Magn. Magn. Mater. 2019, 477, 198–202. [Google Scholar] [CrossRef]
- Mehdaoui, B.; Meffre, A.; Carrey, J.; Lachaize, S.; Lacroix, L.-M.; Gougeon, M.; Chaudret, B.; Respaud, M. Optimal Size of Nanoparticles for Magnetic Hyperthermia: A Combined Theoretical and Experimental Study. Adv. Funct. Mater. 2011, 21, 4573–4581. [Google Scholar] [CrossRef]
- Guardia, P.; Di Corato, R.; Lartigue, L.; Wilhelm, C.; Espinosa, A.; Garcia-Hernandez, M.; Gazeau, F.; Manna, L.; Pellegrino, T. Water-soluble iron oxide nanocubes with high values of specific absorption rate for cancer cell hyperthermia treatment. ACS Nano 2012, 6, 3080–3091. [Google Scholar] [CrossRef]
- Di Corato, R.; Espinosa, A.; Lartigue, L.; Tharaud, M.; Chat, S.; Pellegrino, T.; Ménager, C.; Gazeau, F.; Wilhelm, C. Magnetic hyperthermia efficiency in the cellular environment for different nanoparticle designs. Biomaterials 2014, 35, 6400–6411. [Google Scholar] [CrossRef]
- Unni, M.; Uhl, A.M.; Savliwala, S.; Savitzky, B.H.; Dhavalikar, R.; Garraud, N.; Arnold, D.P.; Kourkoutis, L.F.; Andrew, J.S.; Rinaldi, C. Thermal decomposition synthesis of iron oxide nanoparticles with diminished magnetic dead layer by controlled addition of oxygen. ACS Nano 2017, 11, 2284–2303. [Google Scholar] [CrossRef] [PubMed]
- Nemati, Z.; Alonso, J.; Rodrigo, I.; Das, R.; Garaio, E.; Garcia, J.A.; Orue, I.; Phan, M.-H.; Srikanth, H. Improving the heating efficiency of iron oxide nanoparticles by tuning their shape and size. J. Phys. Chem. C 2018, 122, 2367–2381. [Google Scholar] [CrossRef]
- Navarro, E.; Luengo, Y.; Veintemillas, S.; Morales, M.P.; Palomares, F.J.; Urdiroz, U.; Cebollada, F.; González, J.M. Slow magnetic relaxation in well crystallized, monodispersed, octahedral and spherical magnetite nanoparticles. AIP Adv. 2019, 9, 125143. [Google Scholar] [CrossRef]
- Hergt, R.; Hiergeist, R.; Zeisberger, M.; Schuïer, D.; Heyen, U.; Hilger, I.; Kaiser, W.A. Magnetic properties of bacterial magnetosomes as potential diagnostic and therapeutic tools. J. Magn. Magn. Mater. 2005, 293, 80–86. [Google Scholar] [CrossRef]
- Alphandéry, E.; Chebbi, I.; Guyot, F.; Durand-Dubief, M. Use of bacterial magnetosomes in the magnetic hyperthermia treatment of tumours: A review. Int. J. Hyperth. 2013, 29, 801–809. [Google Scholar] [CrossRef] [PubMed]
- Timko, M.; Molcan, M.; Hashim, A.; Skumiel, A.; Müller, M.; Gojzewski, H.; Jozefczak, A.; Kovac, J.; Rajnak, M.; Makowski, M.; et al. Hyperthermic effect in suspension of magnetosomes prepared by various methods. IEEE Trans. Magn. 2013, 49, 250–254. [Google Scholar] [CrossRef]
- Alphandéry, E. Application of magnetosomes synthesized by magnetotactic bacteria in medicine. Front. Bioeng. Biotechnol. 2014, 2, 5. [Google Scholar] [CrossRef]
- Mandawala, C.; Chebbi, I.; Durand-Dubief, M.; Le Fèvre, R.; Hamdous, Y.; Guyot, F.; Alphandery, E. Biocompatible and stable magnetosome minerals coated with poly-l-lysine, citric acid, and carboxy-methyl-dextran for application in the magnetic hyperthermia treatment of tumors. J. Mater. Chem. B 2017, 5, 7644–7660. [Google Scholar] [CrossRef]
- Le Fèvre, R.; Durand-Dubief, M.; Chebbi, I.; Mandawala, C.; Lagroix, F.; Valet, J.-P.; Idbaih, A.; Adam, C.; Delattre, J.-Y.; Schmitt, C.; et al. Enhanced antitumor efficacy of biocompatible magnetosomes for the magnetic hyperthermia treatment of glioblastoma. Theranostics 2017, 7, 4618–4631. [Google Scholar] [CrossRef]
- Marcano, L.; Muñoz, D.; Martin-Rodriguez, R.; Orue, I.; Alonso, J.; Garcia-Prieto, A.; Serrano, A.; Valencia, S.; Abrudan, R.; FernándezBarquin, L.; et al. Magnetic Study of Co-Doped Magnetosome Chains. J. Phys. Chem. C 2018, 122, 7541–7550. [Google Scholar] [CrossRef]
- Orue, I.; Marcano, L.; Bender, P.; García-Prieto, A.; Valencia, S.; Mawass, M.A.; Gil-Cartón, D.; Alba Venero, D.; Honecker, D.; Garcıa-Arribas, A.; et al. Configuration of the magnetosome chain: A natural magnetic nanoarchitecture. Nanoscale 2018, 10, 7407–7419. [Google Scholar] [CrossRef] [PubMed]
- Gandia, D.; Gandarias, L.; Rodrigo, I.; Robles-Garcia, J.; Das, R.; Garaio, E.; Garcia, J.A.; Phan, M.-H.; Srikanth, H.; Orue, I.; et al. Unlocking the Potential of Magnetotactic Bacteria as Magnetic Hyperthermia Agents. Small 2019, 15, 1902626. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Boubeta, C.; Simeonidis, K.; Makridis, A.; Angelakeris, M.; Iglesias, O.; Guardia, P.; Cabot, A.; Yedra, L.; Estrade, S.; Peiro, F.; et al. Learning from nature to improve the heat generation of iron–oxide nanoparticles for magnetic hyperthermia applications. Sci. Rep. 2013, 3, 1652. [Google Scholar] [CrossRef] [PubMed]
- Serantes, D.; Simeonidis, K.; Angelakeris, M.; Chubykalo-Fesenko, O.; Marciello, M.; Morales, M.P.; Baldomir, D.; Martinez-Boubeta, C. Multiplying Magnetic Hyperthermia Response by Nanoparticle Assembling. J. Phys. Chem. C 2014, 118, 5927–5934. [Google Scholar] [CrossRef]
- Simeonidis, K.; Morales, M.P.; Marciello, M.; Angelakeris, M.; de la Presa, P.; Lazaro-Carrillo, A.; Tabero, A.; Villanueva, A.; Chubykalo-Fesenko, O.; Serantes, D. In-situ particles reorientation during magnetic hyperthermia application: Shape matters twice. Sci. Rep. 2016, 6, 38382. [Google Scholar] [CrossRef]
- Brown, W.F., Jr. Thermal fluctuations of a single-domain particle. Phys. Rev. 1963, 130, 1677–1686. [Google Scholar] [CrossRef]
- Garcia-Palacios, J.L.; Lazaro, F.J. Langevin-dynamics study of the dynamical properties of small magnetic particles. Phys. Rev. B 1998, 58, 14937–14958. [Google Scholar] [CrossRef]
- Scholz, W.; Schrefl, T.; Fidler, J. Micromagnetic simulation of thermally activated switching in fine particles. J. Magn. Magn. Mater. 2001, 233, 296–304. [Google Scholar] [CrossRef]
- Coffey, W.T.; Kalmykov, Y.P.; Waldron, J.T. The Langevin Equation: With Applications to Stochastic Problems in Physics, Chemistry and Electrical Engineering, 2nd ed.; World Scientific: Singapore, 2004; p. 704. ISBN 978-981-238-462-1. [Google Scholar]
- Usov, N.A.; Peschany, S.E. Theoretical hysteresis loops of single-domain particles with cubic anisotropy. J. Magn. Magn. Mater. 1997, 174, 247–260. [Google Scholar] [CrossRef]
- Usov, N.A.; Serebryakova, O.N.; Tarasov, V.P. Interaction effects in assembly of magnetic nanoparticles. Nanoscale Res. Lett. 2017, 12, 489. [Google Scholar] [CrossRef] [PubMed]
- Usov, N.A.; Nesmeyanov, M.S.; Gubanova, E.M.; Epshtein, N.B. Heating ability of magnetic nanoparticles with cubic and combined anisotropy. Beilstein J. Nanotechnol. 2019, 10, 305–314. [Google Scholar] [CrossRef] [PubMed]
- Gudoshnikov, S.A.; Grebenshchikov, Y.B.; Ljubimov, B.Y.; Palvanov, P.S.; Usov, N.A.; Ipatov, M.; Zhukov, A.; Gonzalez, J. Ground state magnetization distribution and characteristic width of head to head domain wall in Fe-rich amorphous microwire. Phys. Stat. Sol. 2009, 206, 613–617. [Google Scholar] [CrossRef]
- Aharoni, A. Nucleation of magnetization reversal in ESD magnets. IEEE Trans. Magn. 1969, 5, 207–210. [Google Scholar] [CrossRef]
- Branquinho, L.C.; Carriao, M.S.; Costa, A.S.; Zufelato, N.; Sousa, M.H.; Miotto, R.; Ivkov, R.; Bakuzis, A.F. Effect of magnetic dipolar interactions on nanoparticle heating efficiency: Implications for cancer hyperthermia. Sci. Rep. 2013, 3, 2887. [Google Scholar] [CrossRef]
- Conde-Leboran, I.; Baldomir, D.; Martinez-Boubeta, C.; Chubykalo-Fesenko, O.; Morales, M.P.; Salas, G.; Cabrera, D.; Camarero, J.; Teran, F.J.; Serantes, D. A single picture explains diversity of hyperthermia response of magnetic nanoparticles. J. Phys. Chem. C 2015, 119, 15698–15706. [Google Scholar] [CrossRef]
- Gudoshnikov, S.A.; Liubimov, B.Y.; Popova, A.V.; Usov, N.A. The influence of a demagnetizing field on hysteresis losses in a dense assembly of superparamagnetic nanoparticles. J. Magn. Magn. Mater. 2012, 324, 3690–3695. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Usov, N.A.; Gubanova, E.M. Application of Magnetosomes in Magnetic Hyperthermia. Nanomaterials 2020, 10, 1320. https://doi.org/10.3390/nano10071320
Usov NA, Gubanova EM. Application of Magnetosomes in Magnetic Hyperthermia. Nanomaterials. 2020; 10(7):1320. https://doi.org/10.3390/nano10071320
Chicago/Turabian StyleUsov, Nikolai A., and Elizaveta M. Gubanova. 2020. "Application of Magnetosomes in Magnetic Hyperthermia" Nanomaterials 10, no. 7: 1320. https://doi.org/10.3390/nano10071320
APA StyleUsov, N. A., & Gubanova, E. M. (2020). Application of Magnetosomes in Magnetic Hyperthermia. Nanomaterials, 10(7), 1320. https://doi.org/10.3390/nano10071320





